Open Access Article
Open Access ArticleThe disclosure of mesoscale behaviour of a 3d-SMM monolayer on Au(111) through a multilevel approach†
Guglielmo
Fernandez Garcia
 ab,
Alessandro
Lunghi
ab,
Alessandro
Lunghi
 ac,
Federico
Totti
ac,
Federico
Totti
 *a and
Roberta
Sessoli
*a and
Roberta
Sessoli
 a
a
aUniversità degli Studi di Firenze. Dipartimento di Chimica “Ugo Schiff”, Via della Lastruccia 3-13, 50019, Sesto Fiorentino, FI, Italy. E-mail: federico.totti@unifi.it
bInstitut des Sciences Chimiques de Rennes, UMR 6226 CNRS, Université de Rennes 1, 263 Avenue du Général Leclerc, 35042 Cedex Rennes, France
cSchool of Physics, CRANN and AMBER, Trinity College Dublin 2, Ireland
First published on 12th February 2018
Abstract
Here we present a computational study of a full- and a half-monolayer of a Fe4 single molecule magnet ([Fe4(L)2(dpm)6], where H3L = 2-hydroxymethyl-2-phenylpropane-1,3-diol and Hdpm = dipivaloylmethane, Fe4Ph) on an unreconstructed surface of Au(111). This has been possible through the application of an integrated approach, which allows the explicit inclusion of the packing effects in the classical dynamics to be used in a second step in periodic and non-periodic high level DFT calculations. In this way we can obtain access to mesoscale geometrical data and verify how they can influence the magnetic properties of interest of the single Fe4 molecule. The proposed approach allows to overcome the ab initio state-of-the-art approaches used to study Single Molecule Magnets (SMMs), which are based on the study of one single adsorbed molecule and cannot represent effects on the scale of a monolayer. Indeed, we show here that it is possible to go beyond the computational limitations inherent to the use, for such complex systems, of accurate calculation techniques (e.g. ab initio molecular dynamics) without losing the level of accuracy necessary to gain new detailed insights, hardly reachable at the experimental level. Indeed, long-range and edge effects on the Fe4 structures and their easy axis of magnetization orientations have been evidenced as their different contributions to the overall macroscopic behavior.
1. Introduction
Nanotechnology is the branch of technology related to the engineering of devices with dimensions of less than a few tens of nanometers. However, smallness in itself does not represent the only goal. Indeed, the realization of nanodevices by innovative structures with new or ad hoc intrinsic properties can enable breakthroughs in fundamental science and technological applications.1–3 One of the possible ways to achieve smallness and novel properties at the same time is represented by the deposition of molecular systems with peculiar properties (catalytic,4 magnetic5 and conduction6) on different surfaces. Recently, a class of molecules with peculiar magnetic properties have been deposited on a surface.7 The reason for the interest lies in the fact that this class of molecules show a slow relaxation of their molecular magnetization at low temperature: hence the name Single Molecule Magnets (SMMs).8 The possibility to retain their appealing magnetic properties in addition to the ability to tune them through an external stimulus once adsorbed on a surface can open the way to ultra-high density storage devices9,10 and to molecule-based quantum-computing.11 However, the conservation or the enhancement at the surface of the properties observed for the non-adsorbed SMM system is still an open issue. Indeed, the SMM–surface interaction can easily lead to the suppression of the target properties if wet approaches are used12,13 or even to the SMM fragmentation in the case of deposition occurring through sublimation.14–16Such issues can be very relevant for the kind of SMM of interest in this work (polynuclear complexes). Indeed, even small surface induced structural variations and/or packing effects might dramatically influence the magnetic properties of interest, that, in the case of the SMM class of systems, are the exchange coupling constants J and the magnetic anisotropy parameter D. Therefore, maintaining or improving the balance of the J values, which define the total spin ground state S, and the D values, which define the spin thermal relaxation barrier (U ∝ |D|S2), becomes crucial upon surface absorption.
For these reasons, with the increasing complexity of the system (e.g. shape or electronic structure for the adsorbed molecule and band structure for the surface) the study of the targeted properties becomes a challenging task, both at the experimental level and from a theoretical and computational point of view. The development of experiments and theoretical models, able to gain insights into such complex hybrid systems, is, therefore, a cutting-edge topic in this field.17
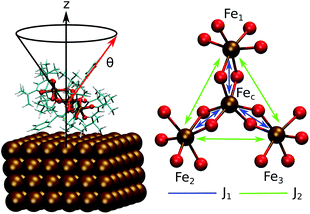
This work focuses on the computational study of the evolution of the deposition process on a metallic surface of single molecule magnets not just modeling it through a single SMM unit adsorbed on the surface but using a whole monolayer of SMM molecules, therefore, including also the packing effects on the properties of interest. The SMM studied in this work is the cluster [Fe4(L)2(dpm)6]18 where Hdpm is dipivaloylmethane and H3L is the tripodal ligand 2-hydroxymethyl-2-phenylpropane-1,3-diol. This SMM, Fe4Ph hereafter, is a member of the propeller-shape Fe4 family and has been evaporated on an unrecostructured Au(111) surface. As shown by Accorsi et al. in the crystal phase these molecules have an S = 5 ground state due to the coupling of the central high spin Fe3+ ion (Fec), via double oxygen-bridges, with three peripheral high spin Fe3+ ions (Fei or Fe1, Fe2, and Fe3, see Fig. 1).
Some fundamental and yet missing pieces of the understanding of the Fe4Ph@Au(111) system are the microscopic organization of molecules on the substrate. Although STM images with molecular resolution of 2D arrays have been recorded,19,20 the orientation of individual molecules (in the packing), how they interact with each other and how this interaction affects their magnetic properties are still unknown. These three aspects critically influence the properties of the final macroscopic devices, so their understanding and control is of topical interest.
From a computational perspective, both static7 (e.g. geometry optimization) and dynamical methods21 (e.g. ab initio molecular dynamics – AIMD) have been employed to study this class of adsorbed systems. The former approaches offer the chance to obtain important information within limited computational efforts. To obtain a higher level of information, a more accurate exploration of the Potential Energy Surface (PES), to identify its multiple energy minima, is mandatory. In this framework, molecular dynamics methods become extremely valuable, as recently reported. The study of the SMM self-assembling also requires severe extensions of both length- and time-scales of simulation, up to several nm and ns, respectively. To overcome inherent computational limitations of first-principles methods, we exploited a previously presented and validated multi-scale molecular dynamics methodology,22 where periodic Density Functional Theory (pDFT) is coupled to a force field (FF) based Molecular Mechanics (MM). The computational protocol is reviewed in the Methods section and in the ESI.† In such a framework, we addressed packing and long-range interaction effects on Fe4Ph@Au by mimicking two in silico experimental setups: for the former, a simulation cell was chosen containing a number of molecules equal to the experimental surface density (full monolayer, FM) for a total of 72 molecules, while for the latter a simulation cell with half of the molecules (half monolayer, HM) was used. For each system we analyzed both large-scale aggregation dynamics and its effect upon the internal structure of a single molecule by MM/(p)DFT. Finally, to comprehensively characterize the Fe4Ph@Au system we also calculated the magnetic properties for each significant conformation highlighted by pDFT/DFT. Through our approach, it was possible to overcome the computational limitations of more accurate calculation techniques (e.g. AIMD), without losing the desired information. Even more important, it was possible to gain new insights at a higher level of detail, hardly reachable at the experimental level. Indeed, the different contributions of the long-range and edge effects on the Fe4 structure and their orientations to the overall macroscopic behavior have been evidenced. To our knowledge, this is the first time that insights at the mesoscopic level have been obtained for a structurally complex SMM, such as Fe4Ph.
2. Methods and computational details
The flow-chart of the adopted computational protocol is sketched in Fig. 2 and it represents the extension of the one previously developed and validated on the single Fe4Ph molecule adsorbed on Au(111).22 The main computational details are shown below.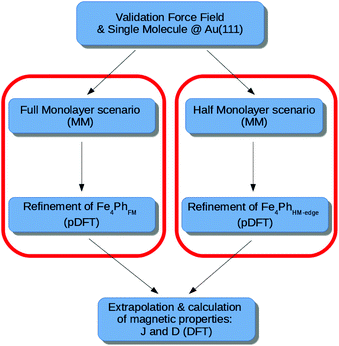 | ||
| Fig. 2 Flowchart of the approach proposed in the paper, for both the Full Monolayer (FM) and Half Monolayer (HM) scenario. | ||
2.1. Force field calculations
The Hessian obtained at the pDFT level (vide infra) for the Fe4 system was used to derive a full set of parameters for the description of the metal core via a classical potential (Force Field – FF). The reference FF is GAFF23,24 where the bonding between the metal and the ligands is described by a simple harmonic function, while the non-bonded interactions are described by a 6–12 Lennard-Jones potential and a Coulomb term. A new modified GAFF was validated through a full benchmark testing procedure on model systems. Among them, since the inter-cluster interactions are fundamental for an accurate description of the packing dynamics, we chose to reproduce the crystal packing of Fe4Me which is isostructural to Fe4Ph. The accurate results achieved indicate that standard GAFF non-bonded terms are suited for reproducing inter-Fe4 interactions. This was not true for Au–Haromatic and Au–Caromatic which had to be mimicked by an ad hoc Morse term, instead. More details are reported elsewhere.22Both the simulation cells for FM and HM scenarios are hexagonal and their dimensions are 138 × 134 × 80 Å. The Au(111) surface is represented by six layers with the bottom one held fixed to mimic the bulk. The number of the Fe4Ph present in the cell is 72 (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 total atoms including the surface) and 36 (24
120 total atoms including the surface) and 36 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 336 total atoms) for FM and HM, respectively. All MD/MM calculations are performed with the LAMMPS package25 with Ewald summation (10−6 accuracy in forces), time step of 1 fs, and cutoff of pairwise interactions of 20 Å with tail corrections. The equation of motion was integrated with a standard velocity-Verlet integrator. Before all simulation runs, we performed geometry optimization with the Hessian-free truncated Newton algorithm and a thermalization run of 1 ns, with temperature rescaling, up to 300 K. All the MD runs lasted 10 ns in the microcanonical ensemble (NVE, constant number of particles, N, volume, V, and energy, E).
336 total atoms) for FM and HM, respectively. All MD/MM calculations are performed with the LAMMPS package25 with Ewald summation (10−6 accuracy in forces), time step of 1 fs, and cutoff of pairwise interactions of 20 Å with tail corrections. The equation of motion was integrated with a standard velocity-Verlet integrator. Before all simulation runs, we performed geometry optimization with the Hessian-free truncated Newton algorithm and a thermalization run of 1 ns, with temperature rescaling, up to 300 K. All the MD runs lasted 10 ns in the microcanonical ensemble (NVE, constant number of particles, N, volume, V, and energy, E).
2.2. Ab initio cell set up from MD dynamics cells
To access the electronic information (pDFT) of the MM/MD structures containing thousands of atoms and, at the same time, saving the packing effects, we had to reduce the cell where only one Fe4Ph is present. To do so, we cooled the MM structure down to 200 K with a 0.5 ns run and through a tailored cut we extracted the pDFT cell from the MM/MD one. For the FM system, this resulted in a hexagonal 17 × 17 × 60 Å cell (388 atoms of which 144 Au), while for the HM system a 20 × 23 × 60 Å cubic cell has been used. Such new cells were also refined by a thermal annealing procedure at the pDFT level lowering the temperature to 0 K. It is important to emphasize that this structure is not representative of the full ensemble explored by the simulation, but just a single sampling. However, previous studies21,22 already explored the reliability of this procedure and its limits, so, based on these grounds, we employed it as an assay to gain partial but reliable insights into the packing effects on the single molecule properties.2.3. Ab initio calculations
CP2K26 and ORCA27 packages were employed for the DFT description. For all the calculations involving the metal surface the CP2K code was used with the meta-GGA TPSS functional,28 rVV10 corrections for dispersion forces29 and periodic boundary conditions (PBC). The CP2K code uses a GPW approach (hybrid Gaussian – Plane Wave) in which the electronic density obtained by the Kohn–Sham orbitals in a GTO basis set is mapped to an auxiliary plane wave basis set. The molecular optimized DZVP-MOLOPT-SR-GTH basis set was used along with a cutoff of 450 Ry for the plane wave expansion. To account for the metallic character of the surface, a smearing of the occupation numbers of the molecular orbitals with a Fermi–Dirac distribution with a temperature of 1500 K was considered. All the simulation cells present four layers of gold with the bottom layer kept fixed to mimic the bulk and only one Fe4Ph molecule in it. Their dimensions and symmetry are chosen depending on the MM/MD results obtained for the FM and HM scenarios as discussed in details in the following sections.2.4. Calculation of magnetic properties
The isotropic exchange coupling in the Fe4 family can be described by the spin Hamiltonian: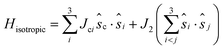 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 are negligible at difference in the geometrical deformations induced by the adsorption process. The isotropic exchange coupling constants were computed within the broken symmetry31,32 framework with the PBE0 + rVV10 functional.33 The calculations of anisotropic tensors for the ground state S = 5, DS=5, were performed within the Giant Spin Approximation (GSA):
21 are negligible at difference in the geometrical deformations induced by the adsorption process. The isotropic exchange coupling constants were computed within the broken symmetry31,32 framework with the PBE0 + rVV10 functional.33 The calculations of anisotropic tensors for the ground state S = 5, DS=5, were performed within the Giant Spin Approximation (GSA):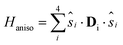 | (2) |
| HGSAaniso = S{·}DS=5{·}S | (3) |
3. Results and discussion
3.1. Full monolayer (FM) scenario – MM structural characterization
The scenario, in which the packing and long-range effects are maximized, is the one where the highest density of Fe4Ph is obtained. Relying on the fact that the substrate–molecule interaction has been previously elucidated by us,22 to understand the effects of the close packing arrangement on Fe4Ph's structure, conformations and, consequently, on its magnetic properties, we have chosen to mimic the scenario in which the highest coverage density value of Fe4Ph was derived by experimental STM images20 (see Fig. 3d). Fig. 3c shows a snapshot after the geometry optimization and at the end of the 10 ns (see the ESI† for the initial snapshot): the Fe4Ph monolayer exhibits extensive and stable bidimensional hexagonal-like domains. In detail, once optimized, the system readily evolves in the first ns towards an almost regular compact pattern which is retained over the complete trajectory. Indeed, being that the Fe4Ph molecules are quasi-spherical and not charged, the inter-molecular interactions are mainly driven by van der Waals interactions. In this case, the hexagonal packing is the most favorable one since it maximizes the number of contacts and, consequently, the density of Fe4Ph on gold. The calculated average distance between the Fec (mass center) of different molecules along all the trajectory and averaged on all the possible couples shows to be in very good agreement with the average one measured between the spherical objects present in the STM images and associated with the Fe4Ph molecules.20 Moreover, in order to verify how much regular the Fe4Ph packing symmetry is, we have calculated the g(r) (radial distribution function) between the Fec of different molecules. The g(r) plot, as shown in Fig. 3b, presents regular patterns with several maxima and minima spaced by almost zero values. The latter indicates the absence of important diffusion processes in the trajectory and a high level of order in the monolayer. Similar to the solid state case, we can map each peak in Fig. 3b through 2D Miller indices (Fig. 3a). In such a framework, the first sharp peak would correspond to the [10] plane and, consequently, to an estimate of the Fe4Ph monolayer lattice constant. The other peaks, whose slightly broader shapes reveal a thermal contribution, present a regular recurrence, which maps a hexagonal lattice. As already observed in the single Fe4Ph molecule, no particular contact has been found between the Au(111) and Fe4Ph monolayer lattices, ruling out any surface imprinting effects on the symmetry of the Fe4Ph monolayer.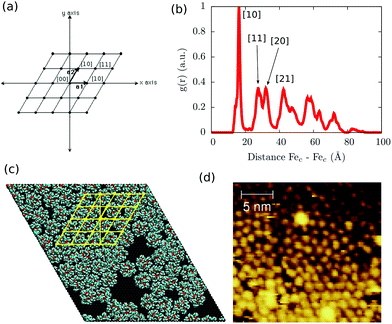 | ||
| Fig. 3 (a) Bidimensional hexagonal Miller notation; (b) radial distribution function (g(r)) of the intermolecular distance along with the interpretation of the first peaks in terms of Miller indices; (c) final snapshot of the MM dynamic run for the FM scenario along with a hexagonal lattice (yellow lines); (d) experimental STM images reported by Malavolti et al.20 | ||
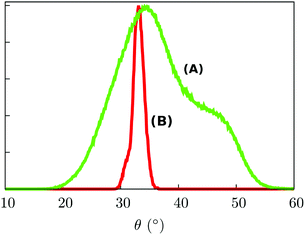
Such a result is of extreme importance since the presence of a sort of “crystallographic” symmetry represents a prerequisite for 2D engineering and the exploitation of system properties of relevance for technological applications.36 The other fundamental aspect resides in the eventual correlation between the supramolecular order and the magnetic properties.37 With the aim of exploring this aspect, we have studied the evolution of the angle θ, defined as the direction of the easy-axis of magnetization with the normal to the surface (see Fig. 1), for each of the adsorbed Fe4Ph molecules. As already shown in previous studies,9 the direction of the magnetization vector in the Fe4 family is approximately perpendicular to the plane formed by the four iron atoms. Two distributions of θ were calculated (see Fig. 4). Distribution (A) is the average of the θ distributions calculated for each single Fe4Ph in the whole trajectory. Instead (B) is the θ distribution averaged at each time-step for all the 72 Fe4Ph molecules. The two quantities give different insights into the time evolution of the monolayer: (A) is an estimation of the possible range of θ values spanned during the dynamics by each single Fe4Ph (i.e. single molecule properties), but averaged on the ensemble of molecules; (B) is the distribution of the mean value (i.e. average ensemble properties), where the weight of the single molecule fluctuations at a given time-step is reduced by the procedure. For such a reason, (B) distribution can be directly compared with the experimental values obtained by those experimental techniques sensitive to the average orientation of the molecule on the surface as, for example, an X-ray magnetic circular dichroism (XMCD) experiment. In such a framework, (B) is in good agreement with previous calculations and experimental findings.20 It is important to note that (B) distribution computed for the FM scenario is slightly different from the one computed for the single Fe4Ph molecule (θ = 30°), hinting an active packing effect. In contrast, (A) distribution seems to be a superposition of two broad bands centered at two different θ values: 34° and 44°. This means that each single molecule can span a wider range of θ values than suggested by the (B) distribution and that a larger number of Fe4Ph molecules span around θ = 34° than θ = 44°. However, on the basis of the results obtained for the single molecule in a previous work22 the actual θ range values can be considered the most likely to be spanned by Fe4Ph and, therefore, other significant distributions can be excluded.
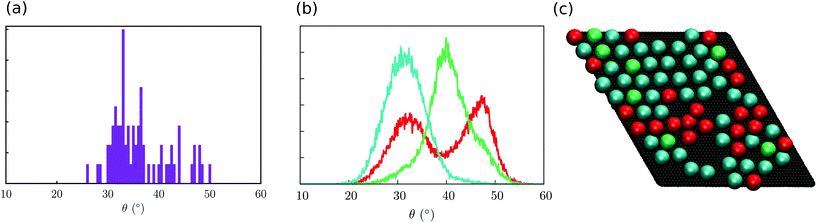
With the aim to identify the two different sub-ensembles of Fe4Ph molecules, we explored the distribution of each single molecule without making the average on the whole trajectory that leads to (A). In Fig. 5a the distribution of the maximum θ value found for each single molecule distribution is shown. It is possible to observe two main distributions centred at 34° and 44°, respectively. The latter is pretty wide while the former is narrower and accounts for a much larger number of θ values. However, such an approach does not allow the demonstration of more complex behaviors, i.e. the presence of distributions with two or more maxima. For this reason, we divided the distributions of θ in three families and we mapped each one on the last snapshot of the trajectory (in Fig. 5b the distributions of three representative molecules are reported while in Fig. 5c the last snapshot is presented): one distribution is peaked at 44° (color green); one distribution peaked at 34° (color blue); one wide distribution spanning the two other Fe4Ph sub-ensembles (color red). Such an analysis revealed that distribution (A) is not a superposition of only two distributions, but a third sub-ensemble of molecules is present. The mapping shows a detailed degree of disorder that was not evident from the mean values calculated for (A) and (B) distributions. From such an analysis, it has been possible to evidence that when a hexagonal monolayer-like packing is present (Fig. 5b), a single color is dominant (cyan colored spheres); however, in the presence of lower molecule density a more disordered pattern (different colors) is observed. Interestingly, this mapping procedure hints the presence of subtle border effects, i.e. where the density of the packing is lower. In detail, 30% of the population shows this distribution. We also note the presence of broad distribution for 9% of the total population, referring to molecules experiencing a bulk-like environment that occasionally visit the conformation with θ at 44°. On the basis of this analysis, we can affirm that the averaged values of θ are close but different from the ones found for the isolated molecule and that they are also affected by the density of the Fe4Ph molecules.
3.2. FM scenario – pDFT structural refining and magnetic characterization
To obtain information on the electronic structure it is necessary to refine the MM results at a pDFT level as already presented.22 Since we are interested, first of all, to gain insights into the fine structural effects induced by the monolayer packing, we chose to perform thermal annealing on a single Fe4Ph molecule experiencing a hexagonal packing, i.e. corresponding to the Fe4Ph molecules colored with cyan (highest density). To do so, we tailored the pDFT cell on the basis of the hexagonal packing observed in the MM simulation cell as explained in Methods and computational details. The interaction with the neighboring Fe4Ph molecules is assured by periodic boundary conditions. The final geometry obtained by the thermal annealing refinement (called Fe4PhFM) shows close resemblance for both the metal core and ligands with the one obtained from the same computational protocol when only a single molecule adsorbed on Au(111) was considered (see the ESI† for all the important internal degrees of freedom). For example Table 1 shows the values of the improper dihedral angle ϕ of the phenyl ring of the ligand towards the surface. As already seen for a single molecule on Au(111), the ϕ angle is an important structural parameter to understand the interaction with the surface. It is clear that it does not vary substantially in the two cases, confirming the similarity of the observed structures. However, magnetic properties are strictly correlated the with structural parameters35,38 of the metal core such as the distance Fec–Fep, the angle FeÔFe and the γ-pitch angle. The metal core shows a more pronounced deviation from the pseudo-C3 symmetry towards a C2 one, but FeÔFe and γ-pitch angles (as reported in Table 1) show values that are in the high probability region in the distribution curve computed for the single Fe4Ph molecule.22 The packing effects can be somehow correlated to the average of the improper dihedral angles Chfac,centralOhfacOhfacFe, δ, related to the hfac− ligands (see the ESI†): indeed, it is possible to observe a trend as δ(Exp.) > δ(single Fe4Ph) > δ(Fe4PhHM-edge) > δ(Fe4PhFM), suggesting a non-innocent effect of the monolayer formation.| <FeÔFe> (°) | <γ-Pitch> (°) | <Fec-Fep> (Å) | ϕ (°) | |
|---|---|---|---|---|
| Fe4PhFM | 103.7 | 68.6 | 3.12 | 15.2 |
| Fe4PhHM-edge | 102.4 | 70.5 | 3.14 | 90 |
| Single Fe4Ph@Au | 102.6 | 62.2 | 3.10 | 15.7 |
| Exp. | 102.2 | 68.9 | 3.07 | — |
A larger isotropic coupling constant J1 is observed (21.36 cm−1vs. 16.05 cm−1 found for the single molecule on the surface) resulting in an increase of 20 cm−1 of the separation between the ground S = 5 state and the first excited S = 4 state. Regarding D and E/D, only small differences with respect to the bulk have been found, as for the single Fe4Ph@Au(111) (Table 2). Moreover, as suggested by distribution (B) in Fig. 4, the narrower distribution of θ values indicates that the anisotropy axis orientations are expected to be restricted to the cone defined by the θ angle, in agreement with what was experimentally observed.7 We can conclude that the inclusion of the packing effects is likely not to introduce sensitive modifications on the core structure and, therefore, on the magnetic structure.
| (cm−1) | Fe4PhFM | Fe4PhHM-edge | Exp. |
|---|---|---|---|
| J c1 | 21.05 | 22.57 | — |
| J c2 | 23.91 | 18.26 | — |
| J c3 | 19.13 | 23.87 | — |
| J 1 | 21.36 | 21.57 | 16.37 |
| J 2 | 0.25 | 0.03 | 0.29 |
| D c | −1.22 | −0.96 | — |
| E/Dc | 0.23 | 0.21 | — |
| D 1 | 0.35 | 0.54 | 0.71 |
| E/D1 | 0.28 | 0.15 | 0.11 |
| D 2 | 0.58 | 0.45 | 0.60 |
| E/D2 | 0.12 | 0.20 | 0.17 |
| D 3 | 0.66 | 0.59 | 0.60 |
| E/D3 | 0.14 | 0.14 | 0.17 |
| D S=5 | −0.42 | −0.41 | −0.42 |
| E/DS=5 | 0.13 | 0.07 | 0.02 |
Having access to the g tensor of the individual Fe ions, we have also calculated the dipolar contribution to the isotropic exchange interactions, i.e. the non-vanishing trace of the dipolar interaction, taking a pair of neighboring Fe4Ph as the upper limit (see the ESI†). The computed Jdip's are of order of 10−7 cm−1 as expected for the long intermolecular Fe–Fe distances. The leading anisotropic part of the dipolar interaction depends on the magnetic polarization of the monolayer and its evolution during the magnetization process is known to affect resonant tunneling of the magnetization.39 The investigation of this aspect will be the subject of a future publication.
3.3. Half monolayer (HM) scenario – MM structural characterization
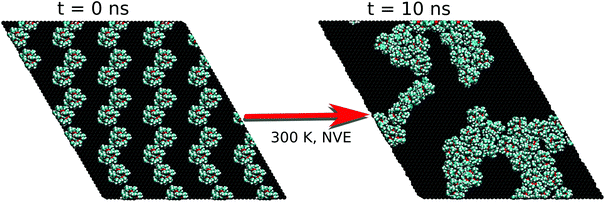
To verify whether the FM results were somehow biased by the chosen experimental high density of Fe4Ph on gold, we repeated the procedure starting from a halved number of Fe4Ph molecules on the same surface. In other words, we aimed at understanding if the system reaches an ordered state spontaneously, starting from a geometry far away from the full monolayer scenario. We have chosen the HM model because it represents a good compromise between the possibility of having a sparse guess and at the same time a significant chance to observe effective Fe4Ph interactions in a relatively short time for an MD simulation. For other concentrations as 1/3 and 2/3, for instance, only one of the two above conditions would be privileged with respect to the other. As evident in the snapshot reported in Fig. 6, the Fe4Ph molecules readily start to arrange themselves in the hexagonal packing as soon as they start interacting with each other. In the following, the formation of clusters with a hexagonal pattern becomes even more evident and it can be straightforwardly supposed that they can act as seeding structures for a more compact and extended surface covering. To ensure that the convergence on that ordered stucture is not biased by the starting geometry and its symmetry, trial calculations (1 ns after thermalization) were performed on a cubic cell, with a starting position in which the Fe4Ph molecules were positioned on a square 2D lattice. Also in this case we observed the same hexagonal pattern after the first ns (see the ESI†).On the basis of these results, the analysis of the hexagonal cell is consistent with the one reported for the FM case. In such a scenario, most of the molecules present a very similar structure to those examined in the FM scenario while a few (11%) of them have explored a different minimum of the conformational space. Indeed, the latter present a θ angle equal to 90°. They are found in low density regions of the surface that correspond to borders of the self-assembled aggregates, suggesting the presence of domain edge effects (from now on Fe4PhHM-edge). The possibilities of having a low percentage of Fe4Ph owing to a θ larger than 35° was somehow predicted by Mannini et al.:7 indeed, the XMCD data therein presented were fitted by considering also the presence of a low percentage of Fe4Ph molecules with θ larger than 35°. However, it is important to point out that any other direct or indirect indication of the presence of such a conformer is not present in the literature. Notably this new Fe4PhHM-edge conformer was not accessible in the single molecule MD, since its presence is a direct consequence of the formation of the bidimensional lattice in a low density scenario. Moreover, the interaction between this conformer and its neighbor is driven by the intermolecular π–π interaction between the phenyl rings, that are found lying parallel to each other and with the surface. However, since this has been observed only for a low percentage of molecules, to have a more quantitative analysis on these aspects it would be necessary to perform a molecular dynamics study on a simulation box built starting from this conformer.
3.4. HM scenario – pDFT structural refining and magnetic characterization
On the basis of the similarities observed between the structures of Fe4Ph molecules in FM and HM scenarios, we focused our pDFT analysis over the Fe4PhHM-edge conformer, with a θ equal to 90°. We performed thermal annealing on one of these structures, following the same idea explained for Fe4PhFM but, in contrast, it was not necessary to respect the geometry of the packing, since the conformer is present in low density areas (see Fig. 7). Therefore a cubic cell has been used, as explained in the Methods and computational details. The laying of the molecule with the trigonal axis parallel to the surface does not affect heavily the structural parameters (FeÔFe, γ-pitch) and the same symmetry of the metal core observed for the full monolayer (Fe4PhFM) is retained. In fact, the direct contact with the surface of the hfac− ligands is reflected in an average δ dihedral angle which is comparable to the one observed for Fe4PhFM (see Fig. 7 and ESI†). On the other hand, the metal core is shown to be quite rigid (Table 1), with only minor distortions with respect to the Fe4PhFM, since the major distortions are accounted for by the aforementioned more flexible hfac− ligands. Indeed, from a magnetic point of view, the isotropic couplings remain unchanged with respect to Fe4PhFM and only slight differences are found for the magnetic anisotropy. Since the interaction between the phenyl ring of the tripodal ligand and the surface is weaker in this case, the ϕ angle results in 90°.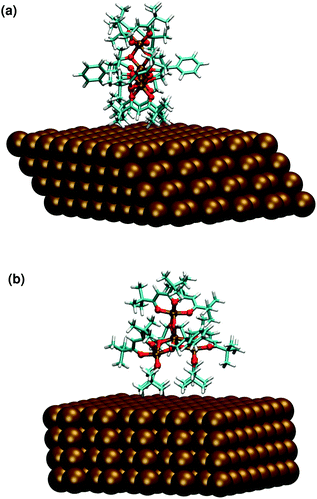 | ||
| Fig. 7 Optimized geometry of the Fe4PhHM-edge conformer computed at the pDFT level: side (a) and frontal (b) view. | ||
The presence of this conformer might be a “lead” to future 2D crystal engineering, in which each Fe4Ph has the terminal phenyl rings in contact with the neighbors’ benzene ring, forming some sort of supramolecular chains on the surface. The possibility to form a regular and stable pattern of such conformers would represent an interesting achievement. Indeed, the disorder of the easy axis of magnetization would be significantly reduced and the orientation would be parallel to the surface. Such a situation is not common to our knowledge in the case of adsorbed SMMs. Moreover, in the case that Fe4PhHM-edge could be switched to Fe4PhFM with external stimuli acting on rotovibrational degree of freedom (laser light, for instance) this would make feasible the control of the easy axis orientation of the Fe4Ph molecules in the absence of external magnetic or electric fields.
4. Conclusions
In this work a multi-scale molecular dynamics computational scheme has been used to study a monolayer of single molecule magnets adsorbed on a metallic surface. This novel approach made it possible to significantly extend simulation length- and time-scales unlocking the possibility to include in the model fundamental features such as the inter-molecular interactions. The model led to the corroboration of previous experimental evidence, like the formation of a 2D hexagonal lattice of molecules on the substrate and the overall stability of the packing. It was also able to prove, for the first time, the formation of a multitude of stable and transient conformers in the self-assembly of Fe4Ph@Au(111). These effects cannot directly be extracted from experimental analysis and their presence has so far been only predicted. Finally, a complete characterization of the spin-Hamiltonian of adsorbed Fe4Ph has revealed the effect of packing and the variability of conformers. Most importantly, these results has been analyzed from a “device” perspective, highlighting the impact of local disorder on single molecule measurements that can have an influence on the performance of the hybrid interface of molecular spintronic devices. On the other hand, the possibility to have access to several possible conformations revealed the prospect to design, for instance, new packing arrangements with different magnetic properties tunable by external stimuli. The understanding and control of the large-scale self-assembly of these systems is indeed a key factor for their technological applications and constitutes a current and future challenge in the manufacturing of molecular devices.The level of detailed information obtained with the presented model (as the distribution of the θ angle) is something hardly achievable at the experimental level and, moreover, the MM model overcomes the intrinsic computational difficulty DFT of mimicking, on a large scale, complex systems containing transition metals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the support from the European Research Council (Advanced Grant No. 267746 – MolNanoMaS), the European Union's Horizon2020 Research and Innovation Programme under grant agreement No. 737709 (FEMTOTERABYTE, http://www.physics.gu.se/femtoterabyte) and the MOLSPIN COST action CA15128.References
- A. R. Rocha, V. M. García-Suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335–339 CrossRef CAS PubMed.
- W. Wernsdorfer, Nat. Mater., 2007, 6, 174–176 CrossRef CAS PubMed.
- F. E. Kalff, M. P. Rebergen, E. Fahrenfort, J. Girovsky, R. Toskovic, J. L. Lado, J. Fernández-Rossier and A. F. Otte, Nat. Nanotechnol., 2016, 11, 926–929 CrossRef CAS PubMed.
- R. Coppage, J. M. Slocik, H. Ramezani-Dakhel, N. M. Bedford, H. Heinz, R. R. Naik and M. R. Knecht, J. Am. Chem. Soc., 2013, 135, 11048–11054 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458–4464 CrossRef CAS PubMed.
- M. Cinchetti, V. A. Dediu and L. E. Hueso, Nat. Mater., 2017, 16, 507–515 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M.-A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- F. Allouche, G. Lapadula, G. Siddiqi, W. W. Lukens, O. Maury, B. Le Guennic, F. Pointillart, J. Dreiser, V. Mougel, O. Cador and C. Copéret, ACS Cent. Sci., 2017, 3(3), 244–249 CrossRef CAS PubMed.
- M. Urdampilleta, N. V. Nguyen, J. P. Cleuziou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Int. J. Mol. Sci., 2011, 12, 6656–6667 CrossRef CAS PubMed.
- L. Rigamonti, M. Piccioli, L. Malavolti, L. Poggini, M. Mannini, F. Totti, B. Cortigiani, A. Magnani, R. Sessoli and A. Cornia, Inorg. Chem., 2013, 52, 5897–5905 CrossRef CAS PubMed.
- J. Dreiser, A. M. Ako, C. Wäckerlin, J. Heidler, C. E. Anson, A. K. Powell, C. Piamonteze, F. Nolting, S. Rusponi and H. Brune, J. Phys. Chem. C, 2015, 119, 3550–3555 Search PubMed.
- V. Lanzilotto, L. Malavolti, S. Ninova, I. Cimatti, L. Poggini, B. Cortigiani, M. Mannini, F. Totti, A. Cornia and R. Sessoli, Chem. Mater., 2016, 28, 7693–7702 CrossRef CAS.
- P. Erler, P. Schmitt, N. Barth, A. Irmler, S. Bouvron, T. Huhn, U. Groth, F. Pauly, L. Gragnaniello and M. Fonin, Nano Lett., 2015, 15, 4546–4552 CrossRef CAS PubMed.
- S. Rauschenbach, F. L. Stadler, E. Lunedei, N. Malinowski, S. Koltsov, G. Costantini and K. Kern, Small, 2006, 2, 540–547 CrossRef CAS PubMed.
- A. Caneschi, D. Gatteschi and F. Totti, Coord. Chem. Rev., 2015, 289–290, 357–378 CrossRef CAS.
- S. Accorsi, A.-L. Barra, A. Caneschi, G. Chastanet, A. Cornia, A. C. Fabretti, D. Gatteschi, C. Mortalo, E. Olivieri, F. Parenti, P. Rosa, R. Sessoli, L. Sorace, W. Wernsdorfer and L. Zobbi, J. Am. Chem. Soc., 2006, 128, 4742–4755 CrossRef CAS PubMed.
- J. A. Burgess, L. Malavolti, V. Lanzilotto, M. Mannini, S. Yan, S. Ninova, F. Totti, S. Rolf-Pissarczyk, A. Cornia, R. Sessoli and S. Loth, Nat. Commun., 2015, 6, 8216 CrossRef PubMed.
- L. Malavolti, V. Lanzilotto, S. Ninova, L. Poggini, I. Cimatti, B. Cortigiani, L. Margheriti, D. Chiappe, E. Otero, P. Sainctavit, F. Totti, A. Cornia, M. Mannini and R. Sessoli, Nano Lett., 2015, 15, 535–541 CrossRef CAS PubMed.
- A. Lunghi, M. Iannuzzi, R. Sessoli and F. Totti, J. Mater. Chem. C, 2015, 3, 7294–7304 RSC.
- G. Fernandez Garcia, A. Lunghi, F. Totti and R. Sessoli, J. Phys. Chem. C, 2016, 120, 14774–14781 CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- J. Tao, J. Perdew, V. Staroverov and G. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- R. Sabatini, T. Gorni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 4–7 CrossRef.
- S. Ninova, V. Lanzilotto, L. Malavolti, L. Rigamonti, B. Cortigiani, M. Mannini, F. Totti and R. Sessoli, J. Mater. Chem. C, 2014, 2, 9599–9608 RSC.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS.
- A. Bencini and F. Totti, J. Chem. Theory Comput., 2009, 5, 144–154 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Lunghi and F. Totti, J. Mater. Chem. C, 2014, 2, 8333–8343 RSC.
- B. Moulton, J. Lu, R. Hajndl, S. Hariharan and M. J. Zaworotko, Angew. Chem., Int. Ed., 2002, 41, 2821–2824 CrossRef CAS PubMed.
- L. Su, W.-C. Song, J. P. Zhao and F.-C. Liu, Chem. Commun., 2016, 52, 8722–8725 RSC.
- T. Gupta, T. Rajeshkumar and G. Rajaraman, Phys. Chem. Chem. Phys., 2014, 16, 14568 RSC.
- L. Vergnani, A. L. Barra, P. Neugebauer, M. J. Rodriguez-Douton, R. Sessoli, L. Sorace, W. Wernsdorfer and A. Cornia, Chem. – Eur. J., 2012, 18, 3390–3398 CrossRef CAS PubMed.
- L. Rigamonti, A. Cornia, A. Nava, M. Perfetti, M.-E. Boulon, A.-L. Barra, X. Zhong, K. Park and R. Sessoli, Phys. Chem. Chem. Phys., 2014, 16, 17220 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C7NR06320B |
| This journal is © The Royal Society of Chemistry 2018 |