Pathway-engineering for highly-aligned block copolymer arrays

Abstract

While the ultimate driving force in self-assembly is energy minimization and the corresponding evolution towards equilibrium, kinetic effects can also play a very strong role. These kinetic effects, such as trapping in metastable states, slow coarsening kinetics, and pathway-dependent assembly, are often viewed as complications to be overcome. Here, we instead exploit these effects to engineer a desired final nano-structure in a block copolymer thin film, by selecting a particular ordering pathway through the self-assembly energy landscape. In particular, we combine photothermal shearing with high-temperature annealing to yield hexagonal arrays of block copolymer cylinders that are aligned in a single prescribed direction over macroscopic sample dimensions. Photothermal shearing is first used to generate a highly-aligned horizontal cylinder state, with subsequent thermal processing used to reorient the morphology to the vertical cylinder state in a templated manner. Finally, we demonstrate the successful transfer of engineered morphologies into inorganic replicas.

---

Introduction

Self-assembly is a powerful paradigm for controlling order at the nanoscale, wherein molecules are designed and synthesized to encode a desired structural motif. During assembly, molecules segregate, pack, and align in order to minimize energy, thereby spontaneously giving rise to a well-defined nanoscale morphology. The spontaneous ordering ensures that the encoded morphology appears simultaneously throughout the entire material, allowing rapid wide-area patterning at the nanoscale. However, the stochastic nature of this assembly process makes it difficult to control, with defects, a distribution of orientations, and even competing phases frequently appearing. While the fundamental structural motif is defined by equilibrium considerations, the actual nano-structures observed experimentally are typically determined by kinetic effects, including trapping in transient states, slow grain coarsening kinetics, and a strong dependence on the processing history. While kinetic trapping and pathway-dependent assembly are typically viewed as a complicating nuisance—limiting one's ability to generate defect-free phases—one can instead take advantage of the complex energy landscape underlying self-assembly to enforce a particular global nanostructure by selecting an appropriate pathway through the landscape.

Block copolymers (BCPs) are a well-studied and versatile class of self-assembling materials, where chemically distinct polymer blocks are covalently bonded. The strong driving force towards phase-separation of the blocks is frustrated by the covalent link; at equilibrium the energy compromise involves local segregation of a size and shape dictated by the chain architecture, and thus the emergence of a periodic morphology, such as hexagonally packed cylinders, or alternating lamellae.^1,2 Ordering of BCPs is strongly influenced by kinetic effects, especially owing to the large molecular dimensions, which lead to large energy barriers for defect annihilation,^3,4 and correspondingly slow coarsening kinetics.^5–8 Enormous effort has gone into accelerating ordering in block copolymers,⁸ including through the use of microwave⁹ or high-temperature^10–12 thermal annealing, vapor^13,14 or direct immersion^15,16 solvent annealing, and sweeping a thermal zone through the material.^17–21 Self-assembling materials are responsive and thus their ordering can be directed,^22,23 with boundary conditions or external fields breaking symmetry and selecting a desired morphology or orientation. It is interesting to note that the majority of demonstrated methods rely on controlling the conditions under which ordering occurs, but otherwise treat assembly as a single-step process. Conceptually, such approaches are using applied environments to modify the self-assembly energy landscape so that the desired structure is both the energy-minimum, and is readily accessible to the ordering process (i.e. the system evolves naturally ‘downhill’ into this minimum, without encountering undue barriers). Of course, kinetic effects appear also. For instance, in solvent vapor annealing, the final order can depend strongly on the swelling and quench rates.^24–26 The formation of Frank-Kasper phases depends sensitively on the cooling protocol.^27,28 Zone annealing^18,29,30 and shearing^31–34 involve manifestly non-uniform process history. Applying the appropriate processing conditions to achieve a particular kind of order can be viewed as selecting a particular pathway through the self-assembly energy landscape. We have recently demonstrated a striking example of pathway-dependent assembly in block copolymers,³⁵ wherein applying a rapid shear pulse—so short that phase separation does not have an opportunity to progress appreciably—can induce ‘latent alignment’ in an otherwise disordered block copolymer film. Subsequent isotropic thermal annealing then easily gives rise to a highly-aligned morphology (in-plane cylinders with long-axis uniaxially aligned along the original shear direction), as the system naturally evolves into the global energy minimum. This multi-step processing is to be contrasted with conventional (one-step) oven annealing, where a poly-grain morphology develops owing to the succession of energy barriers for defect annihilation. Moreover, the processing is manifestly pathway-dependent, since the same processing steps in the opposite order (thermal annealing followed by a very brief shear pulse) cannot induce a highly-aligned phase.

Here, we exploit the complex structure of the multi-dimensional energy landscape that underlies block copolymer self-assembly, in order to control the final nano-structure that forms. We combine enforcement of environment conditions (interfacial energies and film thickness), along with appropriate selection of the pathway through the energy landscape (via processing protocol). This pathway-engineering allows us to access morphologies that would normally be inaccessible to single-step processing. In particular, we demonstrate that a cylinder-forming BCP thin film, coated on a chemically neutral substrate, can be shear-processed to yield a highly-aligned in-plane (horizontal) cylinder morphology. Subsequent isotropic thermal processing of this state allows the cylinders to reorient to be out-of-plane (vertical), consistent with the neutral substrate condition. However, the pre-aligned horizontal morphology templates this reorientation transition,³⁰ causing the final vertical cylinder morphology to exhibit uniform biaxial alignment over the entire macroscopic sample dimensions. Out-of-plane orientation is ultimately induced by interfacial energy, while the in-plane alignment direction is selected via the shear-processing step. Overall, this multi-step ordering can be viewed as an efficient pathway through the energy landscape, which both bypasses problematic energy barriers, while also selecting the subspace of the landscape with the desired alignment. The final morphology is an aligned array of hexagonally-packed nano-dots; aligned hexagonal BCP arrays have also been demonstrated via topographic^36,37 and chemical³⁸ epitaxy. Conversion of these phases into inorganic nanoparticle arrays is potentially useful for nano-electronics^39,40 or high-density bit-patterned data storage.^37,41,42 We demonstrate conversion of the aligned hexagonal morphology into a macroscopic array of germanium nano-dots, without any sample area sacrificed towards guide patterns. Overall, the presented results point towards a powerful paradigm for controlling ordering in certain self-assembling materials. Pathway-engineering involves understanding the self-assembly energy landscape, and thereafter selecting a sequence of processing steps that navigate this complex space towards the desired final structure. This strategy can in principle be applied to any self-assembling material that exhibits a well-defined responsiveness to processing conditions.

Results and discussion

We have recently demonstrated how photothermal annealing¹⁷ can be combined with ‘soft-shear’⁴³ effects in order to rapidly shear-align block copolymer (BCP) morphologies.^34,44 In this method (SS-LZA), a thermal zone passing through the material induces phase separation and morphological ordering. A simultaneous shear field is induced through differential thermal expansion. The combination of heating and shear induces an aligned morphology (with the alignment direction selected based on the morphology/orientation that minimizes energy dissipation). Here, we demonstrate how this method can be combined with conventional thermal annealing in order to select a particular ordering pathway, and thus enforce a target final structure, in block copolymer materials. An as-cast thin film of cylinder-forming polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) is initially unordered (Fig. 1a, upper left). Thermal annealing of this BCP material on a chemically ‘neutral’ substrate (roughly equal interaction energy with both BCP blocks) gives rise to a vertical cylinder orientation (cylinder axes perpendicular to substrate plane), but without any preferred in-plane orientation of the hexagonal lattice. The morphology is highly defective, exhibiting small grains and a uniform distribution of grain orientations (poly-grain, Fig. 1a upper row). Although thermal annealing can be used to improve order—via defect diffusion and annihilation—this grain coarsening is extremely slow, and achieving a uniaxial in-plane orientation over macroscopic areas is effectively impossible. However, a correctly selected processing sequence (Fig. 1a, second row) can yield exactly such a morphology. Photothermal shearing (soft-shear laser zone annealing, SS-LZA) can be used to orient the BCP cylinder phase along the shear direction, yielding a highly aligned state (ESI Fig. S1†) over the macroscopic samples dimensions (as confirmed using X-ray scattering, Fig. 1b). This shearing force is sufficiently strong to override the interface-directed ordering; i.e. shearing generates a horizontal cylinder orientation (cylinder axes parallel to substrate). For the selected film thickness, a monolayer of horizontal cylinder develops. Subsequent thermal annealing induces a reorientation of the cylinder axes from horizontal to vertical, owing to substrate neutrality and the general propensity for a BCP to order vertically at the free surface.⁴⁵ Importantly, the vertical cylinder morphology is templated from the preexisting horizontal state. Thus, the final state achieved is a highly-ordered vertical cylinder morphology, where the cylinder rows (close-packed planes) are aligned—throughout the entire sample—along the direction selected during the shear-processing step. This excellent biaxial alignment control can be verified locally via scanning electron microscopy (SEM, ESI Fig. S2 and S3†), and over the macroscopic sample dimensions using small-angle X-ray scattering (SAXS, Fig. 1c). This multi-step processing allows orientation to be controlled in both the out-of-plane and in-plane directions. The thermal annealing and substrate conditions induce a vertical cylinder orientation, while the shear processing step selects a particular in-plane alignment direction. Thus, one can program a diverse range of orientations by appropriately selecting processing steps (shear direction, thermal reorientation).

Fig. 1 (a) Pathway-engineering allows a desired final structure to be enforced by selecting an appropriate sequence of processing steps. A spun-cast film of cylinder-forming block copolymer begins in a disordered state (left). This state will organize into hexagonally-packed cylinders upon thermal annealing. Neutral substrate conditions induce a vertical orientation of the cylinders, but grains form without any control of in-plane orientation, resulting in isotropic (poly-grain) order. If the as-cast film is shear-aligned (using Soft-Shear Laser Zone Annealing, SS-LZA), it forms an aligned horizontal cylinder morphology (monolayer of cylinders). Upon thermal post-processing, this morphology will convert into a well-aligned vertical cylinder morphology. Although the thermal processing is isotropic (no directionality), the cylinder rows inherit the order of the shear-aligned morphology, forming a state that is well-aligned both in-plane and out-of-plane over the entire sample. X-ray scattering (SAXS) of the (b) shear-aligned horizontal cylinder state, and the (c) aligned vertical cylinder state demonstrate that the prescribed order is preserved over the macroscopic sample dimensions.

A key feature of the ordering process is that in-plane orientational order is inherited when the film converts from a horizontal to a vertical cylinder orientation. Fig. 2 shows transmission-mode X-ray scattering (SAXS) measurements of this final vertical-cylinder state. The sharp six-fold peaks, including higher-orders (Fig. 2a), demonstrates clearly that the morphology is well-aligned in a conserved direction over the entire beam footprint (0.1 mm × 0.1 mm). Additional SAXS measurements at different positions in the sample further confirmed that the hexagonal packing was aligned with respect to the initial shear direction over the entire macroscopic sample dimensions. The material thus has a single well-preserved orientation across arbitrary distances (the orientational correlation length is effectively unbounded); nevertheless, the ordering clearly exhibits some amount of positional disorder (cf. ESI Fig. S2†), which can be seen in the SAXS image as the finite peak width in the q-direction (Fig. 2c; from the q-width, we estimate⁴⁶ a correlation length of ξ ≈ 440 nm). The orientational spread of the morphology about the nominal shear direction can be quantified both from SEM image analysis (ESI Fig. S2c†) and by integrating the SAXS data along the angular direction, ϕ (Fig. 2b). The extremely sharp peaks in the angular direction confirm the excellent alignment and templated ordering of the final vertical-cylinder state (FWHM ≈ 6°). An interesting feature of the angular linecut is that the peaks at ϕ = 0° and ϕ = 180° are notably sharper than the other peaks (ϕ = ±60° and ϕ = ±120°). The former peaks arise from the cylinder rows that directly inherited positional order from the previous horizontal-cylinder axes, whereas the other peaks arise from the row-spacings which formed during reorientation and were only indirectly templated. Thus the orientational order is strongest in the direction dictated by the previous morphology. With respect to the BCP morphology, the slight differences in peak width imply that there are small random distortions to the hexagonal unit cells. In particular, the scattering peaks at ϕ = 0°/180° probe the orientation of the cylinder–cylinder nearest-neighbor vectors that are aligned with the shear direction, while the other scattering peaks (ϕ = ±60°/±120°) probe the nearest-neighbor vectors along other directions. The difference in the angular spread of these different directions suggests that the small random distortions to the unit cells are different along different directions, leading to a biased population of (slightly) distorted unit cells.

Fig. 2 Transmission-mode small-angle X-ray scattering (SAXS) analysis of a highly-aligned vertical-cylinder morphology. In the presented data, the BCP thin film was shear-aligned (2× sweeps of SS-LZA at 80 μm s⁻¹), and subsequently annealed using rapid thermal processing (RTP, 1 min at 340 °C). The sample was then converted to AlO_x to improve the scattering contrast for the transmission experiments. (a) The two-dimensional SAXS pattern exhibits a hexagonal arrangement of peaks, confirming that the cylinder morphology is aligned over the entire beam profile (0.10 mm × 0.10 mm). Measurements at different positions on the sample confirm that this alignment is preserved over the entire macroscopic dimensions of the processed material. The appearance of higher-order peaks confirms the excellent ordering. (b) An angular linecut through the first-order peak demonstrates the excellent alignment of the hexagonal phase. (c) From the width of the first-order peak of the circularly-averaged data, we estimate a typical correlation length (ξ) for the ordering (after accounting for instrumental broadening⁴⁶). (d) The angular spread of the peaks at 0° and 180° are notably smaller than the (e) other peaks (±60° and ± 120°). The former are FWHM ≈ 6°; the latter are FWHM ≈ 9°. This suggests that the orientational order is strongest in the shear-alignment direction.

This interesting disparity in the alignment along different directions strongly demonstrates that the observed reorientation transition from horizontal to vertical cylinders is a templated process, with horizontal-cylinder rows breaking up to form vertical-cylinder dots positioned along those rows. The ordering in adjacent rows is not independent, with hexagonal registry developing spontaneously to satisfy local BCP chain packing constraints. Given this templated reordering, one can moreover ascribe the small orientational spread of the hexagonal order in the vertical-cylinder state to undulations of the cylinder long axes in the preceding horizontal-cylinder state.

The observed reorientation process shares characteristics with assembly observed in other two-dimensional systems with in-plane anisotropy. For example, the subtle difference between the six first-order diffraction spots (Fig. 2) is also seen in template-directed assembly of colloidal spheres on patterned substrates, in which parallel grooves on the underlying substrate promote the formation of highly oriented hexagonal 2D arrays.^47–49 The key difference is that while in colloidal assembly the template is provided externally by the substrate, here the BCP self-templates, with the BCP vertical cylinders inheriting the positional order of the horizontal cylinders as they break up and reform. An analogy can also be drawn to cases of 2D or quasi-2D systems of chain-like molecules, such as hexatic phases of Langmuir monolayers⁵⁰ and smectic liquid crystals,^51,52 in which a nonzero molecular tilt away from the layer normal gives rise to in-plane anisotropy. In these systems, the degree of in-plane positional correlations is found to be the highest in the direction perpendicular to the molecular tilt direction.^50,51 The reorientation process observed in the BCP thin films can be considered as the “untilting” of cylindrical domains, and as such, the oriented BCP films exhibit the highest lateral positional correlations in the direction orthogonal to the domain tilt direction.

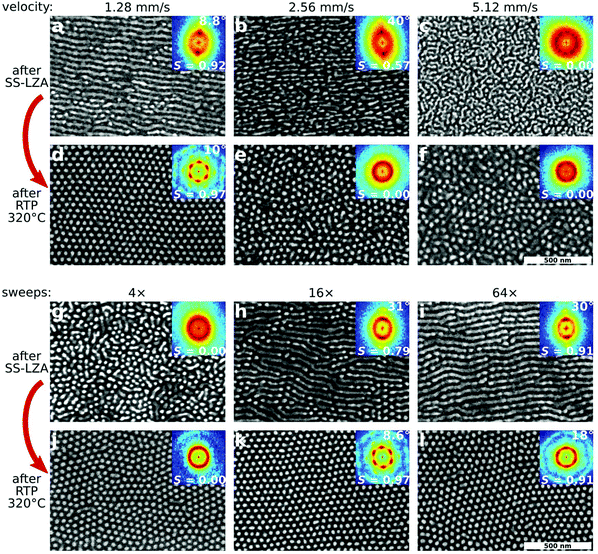
Because the ordering phenomenon described here is pathway-dependent, it is strongly sensitive to initial material parameters, and the processing conditions at each step. Thus, the final order can be optimized by identifying the ideal ordering pathway. The reorientation step requires thermal annealing in order to allow the morphology to reorient. We tested both conventional vacuum oven annealing, as well as rapid thermal processing (RTP) using an infrared (IR) heating source, which is able to achieve higher maximum temperatures and faster thermal ramp rates. We found that both methods succeed in converting horizontal cylinders to vertical cylinders in a templated manner, however final order is much better when using RTP, owing both to the achievable temperature and heating rate. Fig. 3a–f shows the influence of shear velocity on the initial (horizontal cylinder) and final (vertical cylinder) morphologies. Higher velocities induce stronger shear forces, but shorter processing/annealing times.³⁴ If the initial shear-alignment is too fast (Fig. 3b and c), the initial order is insufficient to template a well-aligned state after RTP.

Fig. 3 Influence of process history. SEM images are shown with FFT inset; for non-isotropic samples, the angular spread of the morphology is denoted in the upper-right. The orientational order parameter (S) is also noted. (a–f) The translation velocity used during the SS-LZA shear step (noted above images) influences the order (2× sweeps for presented data). If the initial shear-alignment is too fast (b, c), the initial order is insufficient to template an aligned state after RTP. (g–l) The number of shear sweeps used to pre-align the morphology is extremely important (presented data for shear velocity 0.32 mm s⁻¹). Insufficient shearing gives rise to poor order (g) and thus no templated re-assembly (j). Conversely, overly aggressive shearing (i) forms states that are difficult to reorder (l). Optimized shear processing (h) can be used as a template for efficient reordering into a well-aligned vertical cylinder state (k).

Fig. 3g–l demonstrates the influence of the number of SS-LZA sweeps (a larger number of repeated shear sweeps increases the overall processing/annealing time). Insufficient shearing (Fig. 3g) yields a poorly-ordered initial state, from which no templated reorientation can occur. As expected, increased shearing cycles improve the alignment of the morphology with the shear direction (as noted by the increasing value of S).^34,53 Interestingly, overly aggressive shearing (Fig. 3i, S = 0.91) forms states that are so highly-ordered that they are in fact difficult to reorder (Fig. 3l). The optimal shearing conditions (Fig. 3h) are those which yield an intermediate amount of ordering for the initial state, where the horizontal-cylinder state is well-developed and clearly aligned, but not perfectly ordered (S = 0.79). This suggests a key feature of the underlying energy landscape: reordering from a perfect, defect-free state is extremely difficult since the system is in a deep energy minimum. It is more efficient to reorder from a slightly defective morphology (higher-energy part of the energy landscape).

It is surprising to note that during the horizontal-to-vertical reorientation, the quality of in-plane alignment is not only preserved, but in fact improved. When comparing the alignment of the initial state (after SS-LZA) to the final state (after RTP) across a range of different processing conditions (ESI Fig. S4†), we find that a critical amount of initial alignment is required (FWHM < 40°) for templating to occur. When this criterion is met, however, the final hexagonal state is always more aligned (smaller orientational spread) than the initial state. Similar trends are observed for other measures of order, such as the orientational order parameter (S) or defect density (ρ_d); refer to ESI Tables S1 and S2† for details. This suggests that during the transformation through higher-energy intermediate states which accompany the horizontal-to-vertical reorientation, the system is able to eliminate defects and relax into a more aligned configuration. In terms of the energy landscape, the system must transit over an energy barrier along the ‘reorientation axis’, during which it can simultaneously transit across the barriers that exist along the ‘correlation length axis’ (ESI Fig. S9†).

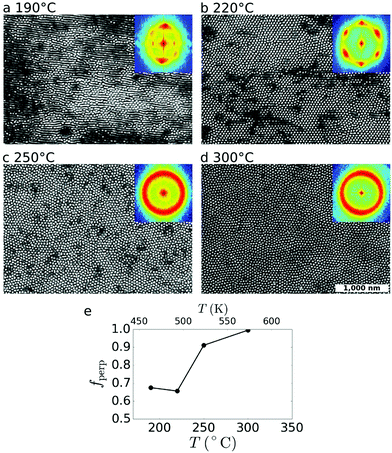
The temperature of the thermal reorientation step plays a key role in controlling the final order (Fig. 4). If the annealing temperature is too low, the cylinder phase does not effectively reorient from horizontal to vertical. As temperature is increased, the reorientation becomes more efficient (Fig. 4e), achieving complete reorientation (f_perp = 1) for T = 300 °C. Multiple effects likely contribute to this trend. Fundamentally, higher temperature increases system mobility and the energy available to overcome reordering barriers. Because the rate of block copolymer ordering is exponential in temperature,⁸ even prolonged annealing at a lower temperature may be insufficient to properly activate the reorientation. It is also worth noting that the different temperature-dependences of the PS and PMMA surface tensions implies that at certain temperatures, the vertical orientation will be more strongly preferred (especially where the surface energies of the two blocks are roughly equal).^54,55 Finally, rapid heating induces strong film thermal expansion in the vertical direction, which has been suggested to induce vertical orientation of BCP materials.^29,56,57

Fig. 4 Influence of post-processing temperature on out-of-plane alignment of morphology (a–c oven annealing; d RTP annealing). For the data presented here, SS-LZA was performed using T_b = 120 °C, and processing using 2× sweeps at 320 μm s⁻¹. The orientation of the morphology is characterized using image analysis (f_perp = 0 indicates horizontal orientation, f_perp = 1 indicates perfect vertical orientation). An optimized post-processing temperature is crucial to induce complete reorientation of the morphology.

It is also interesting to consider the role of the BCP repeat-spacing (L₀). For the material studied here (cylinder-forming BCP with molecular weight 99 kg mol⁻¹), the BCP forms a hexagonal phase with a repeat-spacing of L₀ = 43 nm between cylinder rows (i.e. an inter-cylinder distance of ), based on FFT analysis of SEM imagery. To a first approximation, the templated conversion of a monolayer of cylinders from horizontal to vertical cylinders would appear to be impossible, since the morphological repeat-spacings are incompatible (ESI Fig. S5†). In the horizontal state, the system exhibits the spacing of the cylinder-cylinder distance (d); whereas the templated vertical state must align subsequent cylinder rows (which are spaced by L₀) along these lines. However, it is known that L₀ is (weakly) temperature-dependent,^58–60 with chain relaxation at elevated temperature (towards a more ideal Gaussian coil configuration) leading a decreased L₀.⁴⁵ Thus, one can select different annealing temperatures for the two processing steps, such that d(T) for SS-LZA processing roughly matches L₀(T) for subsequent thermal annealing (note that exact match between these two quantities is not strictly required, since BCPs can accommodate some amount of lattice distortion through chain stretching^61,62). In this regard, photothermal SS-LZA processing is crucial as the initial shear-alignment step, since it allows access to high temperatures,¹⁷ and correspondingly smaller d. This can be confirmed by analyzing the SAXS data, where we measure a repeat-spacing in the initial horizontal aligned state (Fig. 1b) of 43.2 nm, and a spacing in the final vertical state (Fig. 1c) of 42.5 nm. The small (<2%) difference in spacings can evidently be accommodated by the inherent flexibility of the underlying polymer chains.

A crucial parameter in the ordering of block copolymer thin films is the overall film thickness, which can influence both morphology^63,64 and orientation.⁶⁵ Shear-alignment is also sensitive to film thickness, with thicker films responding more strongly (and monolayers being conversely difficult to shear-align) and near-commensurate thicknesses (with respect to cylinder row layering) more easily giving rise to well-ordered horizontal cylinder states.^34,66 That trend is also observed here for near-monolayer films (Fig. 5). Interestingly, the ideal thickness for a well-aligned horizontal cylinder state (36 nm, Fig. 5b) is not the ideal thickness for the eventual conversion to a well-ordered templated vertical cylinder state (30 nm, Fig. 5c). A 36 nm film yields a well-ordered horizontal state after SS-LZA (S = 0.96, ρ_d = 32 μm⁻²), with order improving slightly upon reorientation to a vertical state (S = 0.98, ρ_d = 15 μm⁻²). However, a slightly more defective 32 nm film (S = 0.92, ρ_d = 107 μm⁻²) yields greatly improved order upon reorientation (S = 0.99, ρ_d = 7 μm⁻²). Thus, overall processing conditions must be selected based on the desired final state, rather than attempting to optimize order for intermediate states (refer to ESI Table S1† for further examples). As noted previously, reorientation requires overcoming energy barriers; it is thus not desirable for the initial state to be perfectly ordered. Instead, we observe that a small amount of disorder in the initial configuration (i.e. a slightly higher-energy part of the landscape) allows the system to reorder most efficiently. More explicitly, it is likely that sites of imperfection in the initial horizontal state (morphological defects, breaks in the cylinder lines, isolated vertical cylinders, etc.) act as nucleation sites for the reorientation into the vertical state.

Fig. 5 Influence of film thickness on pathway-dependent ordering. For the data presented here, SS-LZA processing was performed at T_b = 120 °C, and using 2× sweeps at 80 μm s⁻¹. (a–d) SEM images (FFT inset) are shown for films of different thickness after SS-LZA processing (left column) and subsequent thermal post-processing at 320 °C (right column). Film thickness has a strong influence on the quality of alignment in both the initial horizontal state, and the final vertical state. Idealized conditions for well-aligned horizontal cylinders are not necessarily optimal for the final vertical cylinder state. (e, f) Below a critical thickness, the BCP film does not maintain continuity, and instead dewets into isolated islands of material.

The trends described herein can be understood as a form of pathway-dependent ordering occurring in a complex, multi-dimensional energy landscape. The ESI (Fig. S6–S9†) provides conceptual schematics of the overall shape of this energy space;^29,35Fig. 6 shows a schematic representation of a particular slice through this landscape. For the experiments described here, the primary axes relevant to ordering are: (1) the strong driving force towards phase separation of the two block components is quantified using the interfacial width (W), where the interfaces are broad in the disordered (as-cast) state, but sharpen as annealing proceeds; (2) the out-of-plane orientation is quantified by the fraction of perpendicular (vertical cylinder) domains (f_perp); and (3) the in-plane order is quantified by a correlation length (ξ), which can be interpreted either as the grain size or the degree-of-alignment. The as-cast film is highly disordered, as the material is kinetically trapped in a random configuration during the rapid solvent evaporation that accompanies spin-coating (W is large and ξ is small). Conventional thermal annealing involves rapid phase separation of the two block components (with W rapidly decreasing), owing to the chemical mismatch between the blocks. This strong driving force thus involves a strong gradient in the energy landscape; the system naturally first orders along this phase-separation direction. Unfortunately, this results in a population of nano-domains that are extremely poorly ordered; i.e. the formation of locally hexagonal packing motifs without any long-range order (small grain size ξ). If the substrate surface energy is neutral (roughly equal interaction with both blocks), the system will naturally adopt a vertical cylinder orientation (f_perp ≈ 1). As thermal annealing proceeds, topological defects in the morphology will randomly diffuse, and occasionally annihilate one another. This stochastic process involves a substantial energy barrier, and is thus extremely slow (ξ ∝ t^α, where t is time and α ≈ 0.25).⁸ This ‘natural’ ordering pathway thus traps the system in a portion of the energy landscape where further improvements in order are difficult (Fig. 6, vertical poly-grain). In this metastable state, a succession of energy barriers must be crossed for defects to be removed and order to be improved. Experimentally, most BCP systems will exhibit only micron-sized grains after even days of thermal annealing; materials are thus kinetically prevented from reaching the equilibrium state (global energy minimum), which would be a single, macroscopic grain with a common orientation throughout. Moreover, although the equilibrium state is for the system to form a single grain throughout the entire sample (which thus has little orientational spread), there is an energy degeneracy among all possible in-plane orientations. Thus, a particular alignment of this hexagonal phase cannot be selected from this ordering pathway.

Fig. 6 Schematic depiction of a selected slice through the multi-dimensional energy landscape which underlies block copolymer self-assembly. Here, the ordering with respect to out-of-plane orientation (f_perp) and in-plane order (ξ) is emphasized. When an as-cast (disordered) thin film is thermally annealed (red arrow), it forms a vertical cylinder orientation with only short-range order (vertical poly-grain). Coarsening of this morphology is extremely slow owing to the succession of energy barriers. Aggressive shear-alignment of an as-cast film (green arrows) generates a highly-aligned material before phase separation has completed (latent alignment), allowing this pathway to bypass the energy barriers for defect annihilation (dashed green arrow). Continued shearing yields a well-aligned horizontal cylinder state. Thermal annealing of this state then induces a reorientation to a vertical state (f_perp = 1). This reordering occurs in a templated manner, since the system naturally evolves from the initial horizontal aligned state towards the nearby vertical orientation energy minimum.

The engineered pathway described herein avoids the portions of the energy landscape where this kinetic trapping occurs, and instead navigates efficiently towards the desired portion of the landscape. The initial disordered film is first sheared using SS-LZA, which involves both high temperatures and aggressive shear rates. This causes the material to become aligned even before phase-separation has had an opportunity to appreciably proceed (Fig. 6, latent alignment).³⁵ In the multi-dimensional energy landscape (ESI Fig. S6†), rapid shearing bypasses numerous energy barriers, imposing a preferred orientation to the unordered material. As shearing proceeds, the material phase separates (W decreasing) owing to the concomitant heating, forming a morphology aligned with the shear direction. Shear is able to align a BCP morphology since it inherently selects an orientation that minimizes energy dissipation. In particular, the horizontal cylinder orientation is stable (remains morphologically unchanged) during a shear-distortion, whereas a vertical cylinder orientation (or horizontal cylinders aligned against the shear direction) would be continually stretched and distorted as shearing continues. SS-LZA shearing is sufficiently strong to overcome the interfacial energy influences, and thus drives the system to a non-equilibrium portion of the energy landscape (f_perp = 0). Once the system is resident in this portion of the energy landscape (Fig. 6, horizontal aligned), it can be easily reordered in a templated fashion into the desired structure (Fig. 6, vertical aligned). In particular, thermal annealing invokes a pathway where the system reorients form horizontal (f_perp = 0) to vertical (f_perp = 1), since the latter is lower-energy. Within the energy landscape, the system naturally orders towards the nearest vertical-cylinder configuration, which maintains the in-plane orientational order (large ξ). Thus, the reorientation is templated. This reorientation from a horizontal to vertical state involves an energy barrier (with thermal annealing providing the requisite excitation over this barrier). As noted before, and shown schematically in Fig. 6, this barrier-crossing involves two additional unique features: it provides an opportunity for the system to eliminate defects and relax into an even more highly-aligned state (with ξ increasing), and there is an advantage in preparing the horizontal state such that it is not perfectly ordered. The reorientation process is facilitated by this initial state being somewhat higher-energy (which decreases the effective energy barrier). Overall, the selected multi-step ordering pathway takes advantage of both kinetic and thermodynamic aspects. The system thermodynamically favors the vertical cylinder orientation, which is ultimately exploited to reorient the nanophase. On the other hand, the initial ordering steps are strongly non-equilibrium, with strongly time-varying thermal and shear fields used to order the material, and select a particular in-plane direction for morphological alignment. Most important, these processing steps are applied with the correct sequence, so as to navigate the energy landscape towards the desired final state.

By optimizing all available conditions (film thickness, SS-LZA and RTP processing), we can obtain highly-ordered hexagonal arrays of BCP cylinders (FWHM = 4.0°, S = 0.99, ρ_d = 7.1 μm⁻²). The highly-ordered morphology generated through pathway-engineering can be converted into an inorganic replica in order to generate functional nanostructures. In Fig. 7, we demonstrate the formation of an array of metallic germanium nano-dots fabricated using pathway-engineering (additional examples in ESI Fig. S10†). The organic BCP phase was converted into a metal oxide (AlO_x) replica using sequential infiltration synthesis (SIS), which involves exposure to a vapor-phase organometallic precursor, and water vapor.^67,68 The metal oxide forms preferentially within the PMMA cylinder cores, while subsequent plasma etching is used to remove the remaining organic PS matrix. This alumina replica of the BCP phase can be used as an etch mask, to then convert the nanostructure into a Ge replica by etching into the underlying Ge layer. The high-fidelity replica (Fig. 7e) demonstrates that the ordered phases obtained through pathway-engineering are viable candidates for fabricating functional nanostructures, with order being controlled over wide areas through the underlying self-assembly process.

Fig. 7 Transfer of engineered pattern to inorganic replicas. (a) The ordered BCP phase is selectively infiltrated with inorganic precursors from the vapor phase (trimethyl aluminum into the PMMA minority phase). (b) Cycles of precursor and H₂O exposure are used to generate a metal oxide phase (AlO_x). (c) Oxygen plasma is used to remove remaining organic material (PS matrix, and remaining PMMA). (d) The inorganic replica of the BCP phase can be further used as an etch mask to pattern substrate layers. (e) SEM tilt-view of an engineered BCP phase used to pattern a Ge layer deposited on a glass substrate (inset shows FFT of a wide-area top-view SEM). The good fidelity transfer demonstrates that pathway-engineering can be used to rapidly pattern arbitrary materials over large areas.

Conclusions

We have demonstrated how pathway-engineering of self-assembling block copolymer thin films can be exploited to form wide-area arrays of aligned nanodots. Cylinder-forming BCP material under conventional thermal annealing will form a hexagonal packing of cylinders at the nanoscale, but the long-range order is heavily limited by kinetic effects. In other words, the system becomes trapped in a part of the self-assembly energy landscape characterized by a succession of energy barriers for defect annihilation, such that even with prolonged annealing the system remains defective, with modest grain sizes. What is demonstrated here is a rationally-selected process history that navigates the energy landscape, bringing the system to the desired final configuration. Photothermal shearing is used to first form a well-ordered horizontal cylinder state, where the cylinder long axes are aligned along the shear direction. This bypasses the usual energy barriers to grain coarsening, giving rise to a system exhibiting long-range order (and with an essentially infinite orientational correlation length). When such a state is then thermally annealed, the morphology reorients to yield vertical cylinders (consistent with interfacial energy driving forces). This reorientation occurs in a templated manner, such that rows of vertical cylinders form exactly along the pre-existing long-axes of horizontal cylinders. This templated reorientation can again be rationalized in terms of the energy landscape, where the system evolves towards the ‘nearby’ energy minimum.

This multi-step ordering is manifestly pathway-dependent, since the order of the processing steps is crucial to yield the desired structure. Moreover, the final structure could not be obtained with a simpler single-step processing. For instance, while thin films of aligned horizontal cylinders can be obtained via shear, it is not possible using shear alone to yield aligned vertical cylinder (hexagonally-packed dots) morphologies. The presented processing strategy can likely be applied to other materials that respond to shear-forces, such as crystalline polymers or liquid crystals.^69,70 Other self-assembling materials may be responsive to different processing methods (thermal zones, electric or magnetic fields, solvent evaporation fronts), in which case those process variables could be used to navigate the energy landscape. Overall, pathway-engineering is a promising strategy for controlling the ultimate order in self-assembling systems, where sequences of processing steps are devised to efficiently navigate the multi-dimensional energy landscape.

Methods

Polymer film preparation

Polystyrene-block-poly(methyl methacrylate) block copolymer (PS-b-PMMA) material of molecular weight 99 kg mol⁻¹ (minority volume fraction f_PMMA = 0.3, polydispersity = 1.1) was obtained from Polymer Source Inc. This BCP material exhibits a cylinder row-row repeat-spacing of L₀ = 42.5 nm (i.e. an inter-cylinder distance of ), as measured for a well-ordered vertical-cylinder morphology. Substrates were coated in a neutralizing brush to promote a vertical domain orientation (under equilibrium conditions). The brush material is a PS-r-PMMA-OH random copolymer (provided by the Dow Chemical Company), of composition 61 mol% styrene, and total molecular weight M_n = 9.2 kg mol⁻¹, and polydispersity 1.35. The neutral brush was applied by spin coating at 750 rpm, followed by annealing at 220 °C for 5 min to promote adhesion, and finally rinsing in toluene to remove excess material. Thin films of block copolymer were spin cast from toluene solutions (1 wt%), with spin speed (1500 rpm to 5000 rpm) used to control film thickness.

Shear processing

Sample shearing was performed using our previously-described photothermal method: laser zone annealing (LZA)¹⁷ combined with soft-shear (SS).⁴³ Briefly, this SS-LZA method^34,35 uses a high-power (3 W) green (532 nm) laser (Melles Griot 85 GHS 309), which is focused to a sharp line at the sample position (20 μm FWHM along the sweep direction, ∼20 mm breadth in the orthogonal direction). This laser line is swept through the sample via sample translation. Substrates consisted of glass coated with a thin (100 nm) Ge layer, with an additional (10 nm) protective SiN_x layer. The laser-light is absorbed by the Ge layer, generating a local hot-zone that anneals the film. Films were LZA processed with a soft elastomeric cladding (0.5 mm thick polydimethylsiloxane, PDMS); differential thermal expansion of the PDMS layer (relative to the substrate) induces a transient shear field travelling along with the annealing hot-zone. The SS-LZA annealing protocol was varied by changing the sample sweep velocity, and/or the number of repeated sweeps through the hot-zone, and by altering the temperature of the sample-supporting base stage (T_b). The laser power was adjusted to 79% of its maximum intensity using a neutral density filter; under these conditions, the hot-zone induces a characteristic temperature rise (half-maximum of thermal spike) ∼190 °C above ambient. For the T_b = 120 °C conditions used here, the hot-zone thus has a characteristic temperature of T_HM ≈ 310 °C.

Thermal processing

Thermal processing using both oven annealing and a rapid thermal processor (RTP) were investigated. Oven annealing was performed under vacuum at temperatures ranging from 190 °C to 250 °C. RTP was performed using IR heating in an argon atmosphere using a silicon wafer as a carrier. RTP target temperatures ranging from 190 °C to 370 °C were used, with the samples kept at this temperature for 1 minute before cooling back to room temperature.

Imaging

Samples were imaged using scanning electron microscopy (SEM) in a Hitachi S-4800 instrument. Images were analyzed in order to quantify the morphological order, using published image analysis methods,^8,71 and custom-written code in the Python programming language, which exploits libraries for image manipulation (Python Image Library), numerical computations (numpy⁷²), and plotting (matplotlib⁷³). We establish one estimate of orientational spread by computing the Fast Fourier Transform (FFT) of the image, and extracting the intensity as a function of in-plane angle (ϕ) from the two-dimensional FFT around the location of the peak corresponding to the morphology (q ≈ 0.14 nm⁻¹). The orientational spread in the peak in I(ϕ) is estimated using the Full-Width at Half-Maximum (FWHM), while a two-dimensional (Hermans) orientational order parameter (S) is computed in the usual way.⁸ For this metric, S = 1 indicates perfect uniaxial alignment, while S = 0 indicates a completely isotropic state. For horizontal cylinder (‘fingerprint’) morphologies, we compute image gradients in order to establish the local orientation of the morphology.^18,21 From the histogram of orientations, we compute another estimate of orientational order. For vertical cylinder (‘hexagonal’) morphologies, we identify the positions of individual cylinders using thresholding, compute local morphological orientation using vectors between neighboring cylinders,³⁰ and obtain angular spread from the histogram of orientations. The out-of-plane orientation of the morphology was calculated by manual image thresholding and computing pixel areas, and reported as f_perp, where f_perp = 0 indicates a fully parallel orientation (horizontal cylinders) and f_perp = 1 indicates a perfectly perpendicular orientation (vertical cylinders).

Material conversion

To improve SEM imaging, BCP films were converted into metal oxide (AlO_x) replicas using Sequential Infiltration Synthesis (SIS); that is, by sequential exposure to a vapor-phase organometallic precursor, and water vapor.^67,68 We followed our previously-published protocol,^44,74 where samples were exposed to four cycles of trimethylaluminum (TMA), followed by water vapor, using a Cambridge Nanotech atomic layer deposition (ALD) tool (2 min exposures to ∼10 Torr of both TMA and H₂O at 85 °C). The infiltrated materials can be ashed to remove organic materials using oxygen plasma etching (20 W, 100 mTorr, for 3 min at room temperature). We further demonstrate the transfer of the BCP nanopattern to the Ge substrate by using the AlO_x replica as a mask for etching, using SF₆/O₂ reactive ion etching (40% O₂, 80 mTorr pressure, 20 W power, 30 s of etching).

X-ray scattering

Transmission-mode small-angle X-ray scattering (SAXS) experiments were performed at the Coherent Hard X-ray (CHX, 11-ID) and Complex Materials Scattering (CMS, 11-BM) beamlines at the National Synchrotron Light Source II, on AlO_x replicas of the BCP phases. For the results presented (CMS beamline), X-ray beam energy was set to 13.5 keV (wavelength 0.0918 nm) using a double multilayer monochromator, and beam size (0.1 mm × 0.1 mm) and divergence (0.10 mrad) were adjusted using slits. Beam flux was measured to be approximately 3 × 10¹⁰ photons per s. SAXS images were collected using a pixel-array detector (Dectris Pilatus 300k). Detector distance (5.033 m) was calibrated using a silver behenate standard sample; resolution at the detector position (instrumental broadening <0.0007 Å⁻¹) was estimated by measuring a high-quality lithographic line grating. Grain size estimates from scattering peak widths were performed using a Scherrer analysis, taking into account instrumental resolution.⁴⁶ In the analysis, ϕ = 0° is defined to be the +q_z direction in the two-dimensional SAXS image, where the SS-LZA sweep is along the horizontal (q_x direction). Since scattering peaks appear along the corresponding realspace repeat-spacing, the peaks along ±q_z (ϕ = 0° and ϕ = 180°) correspond to the shear-aligned order.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research used resources of the Center for Functional Nanomaterials, and the National Synchrotron Light Source II, which are U.S. DOE Office of Science Facilities, at Brookhaven National Laboratory under Contract No. DE-SC0012704. C. O. and Y. C. acknowledge NSF support by DMR-1410568. P. W. M. acknowledges support of the Foundation for Polish Science, through the First Team program, co-financed by the EU under the European Regional Development Fund.

References

1. M. J. Fasolka and A. M. Mayes, Annu. Rev. Mater. Res., 2001, 31, 323–355.
2. I. W. Hamley, Prog. Polym. Sci., 2009, 34, 1161–1210.
3. H. Takahashi, N. Laachi, K. T. Delaney, S.-M. Hur, C. J. Weinheimer, D. Shykind and G. H. Fredrickson, Macromol., 2012, 45, 6253–6265.
4. B. Kim, N. Laachi, K. T. Delaney, M. Carilli, E. J. Kramer and G. H. Fredrickson, J. Appl. Polym. Sci., 2014, 131, 40790.
5. H. J. Dai, N. P. Balsara, B. A. Garetz and M. C. Newstein, Phys. Rev. Lett., 1996, 77, 3677–3680.
6. C. Harrison, D. H. Adamson, Z. Cheng, J. M. Sebastian, S. Sethuraman, D. A. Huse, R. A. Register and P. M. Chaikin, Science, 2000, 290, 1558–1560.
7. C. T. Black and K. W. Guarini, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 1970–1975.
8. P. W. Majewski and K. G. Yager, J. Phys.: Condens. Matter, 2016, 28, 403002.
9. X. Zhang, K. D. Harris, N. L. Y. Wu, J. N. Murphy and J. M. Buriak, ACS Nano, 2010, 4, 7021–7029.
10. M. Perego, F. Ferrarese Lupi, M. Ceresoli, T. J. Giammaria, G. Seguini, E. Enrico, L. Boarino, D. Antonioli, V. Gianotti, K. Sparnacci and M. Laus, J. Mater. Chem. C, 2014, 2, 6655–6664.
11. M. Ceresoli, F. G. Volpe, G. Seguini, D. Antonioli, V. Gianotti, K. Sparnacci, M. Laus and M. Perego, J. Mater. Chem. C, 2015, 3, 8618–8624.
12. T. J. Giammaria, F. Ferrarese Lupi, G. Seguini, M. Perego, F. Vita, O. Francescangeli, B. Wenning, C. K. Ober, K. Sparnacci, D. Antonioli, V. Gianotti and M. Laus, ACS Appl. Mater. Interfaces, 2016, 8, 9897–9908.
13. D. Posselt, J. Zhang, D.-M. Smilgies, A. V. Berezkin, I. I. Potemkin and C. M. Papadakis, Prog. Polym. Sci., 2017, 66, 80–115.
14. C. Jin, B. C. Olsen, E. J. Luber and J. M. Buriak, Chem. Mater., 2017, 29, 176–188.
15. W. I. Park, J. M. Kim, J. W. Jeong and Y. S. Jung, ACS Nano, 2014, 8, 10009–10018.
16. A. Modi, S. M. Bhaway, B. D. Vogt, J. F. Douglas, A. Al-Enizi, A. Elzatahry, A. Sharma and A. Karim, ACS Appl. Mater. Interfaces, 2015, 7, 21639–21645.
17. P. W. Majewski and K. G. Yager, ACS Nano, 2015, 9, 3896–3906.
18. K. G. Yager, N. J. Fredin, X. Zhang, B. C. Berry, A. Karim and R. L. Jones, Soft Matter, 2010, 6, 92–99.
19. D. E. Angelescu, J. H. Waller, D. H. Adamson, R. A. Register and P. M. Chaikin, Adv. Mater., 2007, 19, 2687–2690.
20. K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Polymer, 2008, 49, 5146–5157.
21. B. C. Berry, A. W. Bosse, J. F. Douglas, R. L. Jones and A. Karim, Nano Lett., 2007, 7, 2789–2794.
22. J. Y. Cheng, C. A. Ross, H. I. Smith and E. L. Thomas, Adv. Mater., 2006, 18, 2505–2521.
23. H. Hu, M. Gopinadhan and C. O. Osuji, Soft Matter, 2014, 10, 3867–3889.
24. S. H. Kim, M. J. Misner, T. Xu, M. Kimura and T. P. Russell, Adv. Mater., 2004, 16, 226–231.
25. S. P. Paradiso, K. T. Delaney, C. J. García-Cervera, H. D. Ceniceros and G. H. Fredrickson, ACS Macro Lett., 2014, 3, 16–20.
26. W. Bai, K. G. Yager and C. A. Ross, Macromol., 2015, 48, 8574–8584.
27. S. Lee, M. J. Bluemle and F. S. Bates, Science, 2010, 330, 349–353.
28. K. Kim, M. W. Schulze, A. Arora, R. M. Lewis, M. A. Hillmyer, K. D. Dorfman and F. S. Bates, Science, 2017, 356, 520–523.
29. S. Samant, J. Strzalka, K. G. Yager, K. Kisslinger, D. Grolman, M. Basutkar, N. Salunke, G. Singh, B. Berry and A. Karim, Macromol., 2016, 49, 8633–8642.
30. P. W. Majewski and K. G. Yager, Soft Matter, 2016, 12, 281–294.
31. K. A. Koppi, M. Tirrell and F. S. Bates, Phys. Rev. Lett., 1993, 70, 1449.
32. D. E. Angelescu, J. H. Waller, D. H. Adamson, P. Deshpande, S. Y. Chou, R. A. Register and P. M. Chaikin, Adv. Mater., 2004, 16, 1736–1740.
33. Y.-R. Hong, D. H. Adamson, P. M. Chaikin and R. A. Register, Soft Matter, 2009, 5, 1687–1691.
34. P. W. Majewski and K. G. Yager, Macromol., 2015, 48, 4591–4598.
35. P. W. Majewski and K. G. Yager, Nano Lett., 2015, 15, 5221–5228.
36. I. Bita, J. K. W. Yang, Y. S. Jung, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943.
37. S. Park, D. H. Lee, J. Xu, B. Kim, S. W. Hong, U. Jeong, T. Xu and T. P. Russell, Science, 2009, 323, 1030–1033.
38. R. Ruiz, H. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. de Pablo and P. F. Nealey, Science, 2008, 321, 936–939.
39. C. T. Black, R. Ruiz, G. Breyta, J. Y. Cheng, M. E. Colburn, K. W. Guarini, H.-C. Kim and Y. Zhang, IBM J. Res. Dev., 2007, 51, 605.
40. M. A. Morris, Microelectron. Eng., 2015, 132, 207–217.
41. B. D. Terris and T. Thomson, J. Phys. D: Appl. Phys., 2005, 38, R199–R222.
42. G. Rhys Alun, W. Aled, O. Chloe, R. Jonathan, V. Aravind and T. Thomas, J. Phys. D: Appl. Phys., 2013, 46, 503001.
43. G. Singh, K. G. Yager, B. Berry, H.-C. Kim and A. Karim, ACS Nano, 2012, 6, 10335–10342.
44. P. W. Majewski, A. Rahman, C. T. Black and K. G. Yager, Nat. Commun., 2015, 6, 7448.
45. C. Forrey, K. G. Yager and S. P. Broadaway, ACS Nano, 2011, 5, 2895–2907.
46. D.-M. Smilgies, J. Appl. Crystallogr., 2009, 42, 1030–1034.
47. K.-h. Lin, J. C. Crocker, V. Prasad, A. Schofield, D. A. Weitz, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2000, 85, 1770–1773.
48. Y.-H. Ye, S. Badilescu, V.-V. Truong, P. Rochon and A. Natansohn, Appl. Phys. Lett., 2001, 79, 872–874.
49. M. Allard, E. H. Sargent, P. C. Lewis and E. Kumacheva, Adv. Mater., 2004, 16, 1360–1364.
50. V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819.
51. E. B. Sirota, P. S. Pershan, L. B. Sorensen and J. Collett, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 2890–2901.
52. J. D. Brock, A. Aharony, R. J. Birgeneau, K. W. Evans-Lutterodt, J. D. Litster, P. M. Horn, G. B. Stephenson and A. R. Tajbakhsh, Phys. Rev. Lett., 1986, 57, 98–101.
53. R. L. Davis, B. T. Michal, P. M. Chaikin and R. A. Register, Macromol., 2015, 48, 5339–5347.
54. P. Mansky, T. P. Russell, C. J. Hawker, J. Mays, D. C. Cook and S. K. Satija, Phys. Rev. Lett., 1997, 79, 237.
55. E. Han, K. O. Stuen, M. Leolukman, C.-C. Liu, P. F. Nealey and P. Gopalan, Macromol., 2009, 42, 4896–4901.
56. G. Singh, K. G. Yager, D.-M. Smilgies, M. M. Kulkarni, D. G. Bucknall and A. Karim, Macromol., 2012, 45, 7107–7117.
57. G. Singh, S. Batra, R. Zhang, H. Yuan, K. G. Yager, M. Cakmak, B. Berry and A. Karim, ACS Nano, 2013, 7, 5291–5299.
58. T. Hashimoto, M. Shibayama and H. Kawai, Macromol., 1983, 16, 1093–1101.
59. T. Ohta and K. Kawasaki, Macromol., 1986, 19, 2621–2632.
60. P. Mansky, O. K. C. Tsui, T. P. Russell and Y. Gallot, Macromol., 1999, 32, 4832–4837.
61. H. Yokoyama, T. E. Mates and E. J. Kramer, Macromol., 2000, 33, 1888–1898.
62. M. Roerdink, M. A. Hempenius, U. Gunst, H. F. Arlinghaus and G. J. Vancso, Small, 2007, 3, 1415–1423.
63. M. J. Fasolka, P. Banerjee, A. M. Mayes, G. Pickett and A. C. Balazs, Macromol., 2000, 33, 5702–5712.
64. G. E. Stein, E. J. Kramer, X. Li and J. Wang, Macromol., 2007, 40, 2453–2460.
65. S.-W. Kim, E. Kim, H. Lee, B. C. Berry, H.-C. Kim and D. Y. Ryu, Polymer, 2015, 74, 63–69.
66. R. L. Davis, P. M. Chaikin and R. A. Register, Macromol., 2014, 47, 5277–5285.
67. Q. Peng, Y.-C. Tseng, S. B. Darling and J. W. Elam, Adv. Mater., 2010, 22, 5129–5133.
68. M. Ramanathan, Y.-C. Tseng, K. Ariga and S. B. Darling, J. Mater. Chem. C, 2013, 1, 2080–2091.
69. C. R. Safinya, E. B. Sirota and R. J. Plano, Phys. Rev. Lett., 1991, 66, 1986–1989.
70. A. Jákli, I. Jánossy, L. Bata and A. Buka, Cryst. Res. Technol., 1988, 23, 949–954.
71. J. N. Murphy, K. D. Harris and J. M. Buriak, PLoS One, 2015, 10, e0133088.
72. T. E. Oliphant, Comput. Sci. Eng., 2007, 9, 10–20.
73. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
74. A. Rahman, P. W. Majewski, G. Doerk, C. T. Black and K. G. Yager, Nat. Commun., 2016, 7, 13988.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr06069f

---