Orbital control over the metal vs. ligand reduction in a series of neutral and cationic bis(cyclopentadienyl) Ti(IV) complexes†
Annemarie
Kuhn
 and
Jeanet
Conradie
and
Jeanet
Conradie
 *
*
Department of Chemistry, University of the Free State, PO Box 339, Bloemfontein, 9300, South Africa. E-mail: conradj@ufs.ac.za; Fax: +27-51-4017295; Tel: +27-51-4012194
First published on 27th November 2017
Abstract
Quantum chemistry calculations showed that the first reduction, as experimentally observed by cyclic voltammetry for a series of neutral and cationic functionalised bis(cyclopentadienyl) titanium(IV) derivatives, is metal based, involving the chemically and electrochemically reversible TiIV/TiIII redox couple. The second reduction peak observed is chemically and electrochemically irreversible. For the neutral [Cp2TiIV(ligand)n] (n = 1 or 2) complexes (Cp = cyclopentadienyl), the second irreversible reduction peak is metal-based, while for the cationic [Cp2TiIV(ligand)]+ complexes, the second irreversible reduction peak involves ligand reduction, leading to a TiIII species coupled to a ligand radical. The electronic properties of the substituents directly influence electron density at the reduction centre when π-interactions between the electro-active centre and the substituent groups exist in the lowest unoccupied molecular orbital (LUMO) of the complexes. In this case, a number of relationships between the electronic properties of the substituents and the reduction potentials have been affirmed, yielding linear relationship between experimentally measured reduction potentials and DFT calculated energies (energy of the LUMO, electron affinity, Mulliken electronegativity and global electrophilicity index). However, the substituent effect is ill defined when the LUMO is highly localised without π-interaction between the electro-active centre and the substituents.
1. Introduction
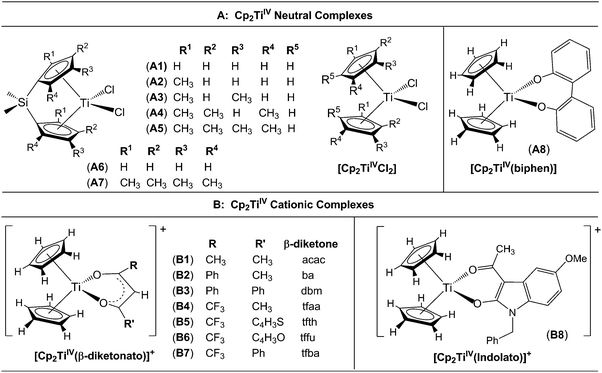
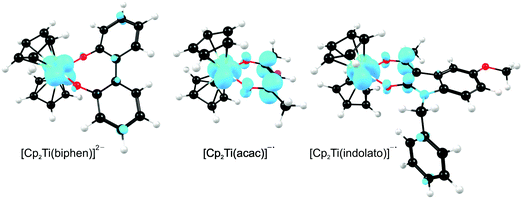
A large number of ‘bent-sandwich’ titanocene(IV) derivatives have been developed due to their role in industrial processes, including catalysis1–6 and as reagents for organic synthesis.7–9 For the development of homogeneous catalysts it is necessary to fine-tune the electronic properties of the active metal, using functionalised ligands, such that there is electronic interaction between the substituents and the metal centre via the ligand. The redox chemistry (electron transfer, oxidative addition, reductive elimination) of transition metal complexes is one of their defining features. Normally these redox processes take place on the metal, however, certain ligands can actively participate in electron transfer. Although the electrochemical behaviour of [Cp2TiCl2] (Cp = cyclopentadienyl) and substituted derivatives has been rigorously studied,10–17 attempts to directly relate the reduction potentials of substituted complexes to the electronic effects of substituents are often unsuccessful. Therefore understanding the influence of a substituent on the redox-potentials, for example, knowing when and how the electronic properties of the substituents are expected to have an influence on the reduction potentials, will help in the design of new compounds with controlled activity.In this contribution we present a comparative electrochemical study of two families, neutral and cationic, functionalised bis(cyclopentadienyl) titanium(IV) derivatives, using cyclic voltammetric data and DFT (Density Functional Theory) calculations determining the nature of the reductions, i.e., metal-centred vs. ligand-based reduction and predict the substituent effect on reduction potentials. Substitution of the Cp2TiIVCl2 derivatives in this study, involves the cyclopentadienyl ligands as well as replacing the labile dichloro ligands with redox active bidentate ligands. Neutral complexes are [(C5H5−nMen)2TiCl2] (n = 0–5) and ansa-compounds [Me2Si(C5H4−nMen)2TiCl2] (n = 0 or 4) (A1–A7), and [(C5H5)2Ti(biphen)] (A8). Cationic complexes are [(C5H5)2Ti(RCOCHCOR′)]+ with combinations of R, R′ = CF3, C4H3S, C4H3O, Ph(C6H5) and CH3 (B1–B7), and [(C5H5)2Ti(indolato)]+ (B8) see Fig. 1.
2. Experimental
2.1 Theoretical approach
Density functional theory (DFT) calculations were performed using the PW91/TZP (triple ζ polarized) functional18 and basis sets as implemented in the Amsterdam Density Functional (ADF2014).19 Geometry relaxed (adiabatic) energies of the molecule (N electron system), the corresponding N − 1 (reduced) and N + 1 (oxidized) electron systems were calculated to determine the electron affinity (EA) and ionization potential (IP) values of complexes.2.2 Electrochemistry
Electrochemical data of neutral and cationic bis(cyclopentadienyl) TiIV complexes form the basis of a density functional theory study presented in this contribution. The cyclic voltammetry measurements of the complexes used in this study, obtained from literature, were obtained under varying experimental conditions; series A1–A7 (THF),11 series B2–B7 (CH3CN)13 and B8 (C3H7CN).14 Cyclic voltammetry measurements done in this study for A1 (DCM), A8 and B1 (CH3CN), were performed on 0.002 mole dm−3 solutions of the complexes in dry solvent with (nBu4N)(PF6) as supporting electrolyte and using a glassy carbon working electrode, Pt auxiliary electrode, Ag/Ag+ reference electrode. All cited potentials were referenced against the Fc/Fc+ couple as suggested by IUPAC,20 with ferrocene used as internal standard.2.3 Synthesis of compounds
Titanocene dichloride, A1, (Fluka) was purified by recrystallization from hot toluene and complex B1 was prepared as described in ref. 13. In the preparation of [Cp2Ti(biphen)], A8, titanocene dichloride, [Cp2TiCl2] (0.249 g/1.0 mmole) was dissolved in H2O/THF, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (9 ml) and stirred under nitrogen for ½ h. The solution was cooled down on an ice-bath before silver perchlorate, AgClO4, (0.406 g/1.96 mmole) dissolved in water (2 ml) was added. The cooled mixture was stirred for a further ½ h. AgClO4 is light sensitive and the reaction must be light protected. A white precipitate, AgCl, was filtered off and washed with H2O/THF (2 ml). 2,2′-biphenol (0.372 g, 2 mmole) dissolved in cold THF (2 ml, ca. 4 °C) was added dropwise to the clear orange filtrate while stirring with an immediate colour change (orange to dark red). After ½ h of stirring the solution was removed and left for 4 days to precipitate at room temperature. The precipitate was washed with water, filtered and dissolved in diethyl ether. The solvent was removed with reduced pressure. The solid was washed with MeOH to remove unreacted 2,2′-biphenol yielding pure [Cp2Ti(biphen)].
1 mixture (9 ml) and stirred under nitrogen for ½ h. The solution was cooled down on an ice-bath before silver perchlorate, AgClO4, (0.406 g/1.96 mmole) dissolved in water (2 ml) was added. The cooled mixture was stirred for a further ½ h. AgClO4 is light sensitive and the reaction must be light protected. A white precipitate, AgCl, was filtered off and washed with H2O/THF (2 ml). 2,2′-biphenol (0.372 g, 2 mmole) dissolved in cold THF (2 ml, ca. 4 °C) was added dropwise to the clear orange filtrate while stirring with an immediate colour change (orange to dark red). After ½ h of stirring the solution was removed and left for 4 days to precipitate at room temperature. The precipitate was washed with water, filtered and dissolved in diethyl ether. The solvent was removed with reduced pressure. The solid was washed with MeOH to remove unreacted 2,2′-biphenol yielding pure [Cp2Ti(biphen)].
Yield 25% (0.0820 g). Colour: red. 1H NMR (600 MHz, δ/ppm, acetone-d6): 6.34 (s, 10H, 2× CpH), 6.71 (d, 2H; biphenH), 6.86 (t, 2H, biphenH), 7.18 (t, 2H, biphenH), 7.23 (t, 2H, biphenH). 1H NMR (300 MHz, δ/ppm, CDCl3): 6.26 (s, 10H, 2× CpH), 6.67 (d, 2H; biphenH), 6.93 (t, 2H, biphenH), 7.26 (m, 4H, biphenH). Elemental anal. calc. for TiC22H18O2: C, 72.9; H, 5.0. Found: C, 73.1; H, 4.93%.
3. Results and discussion
3.1 Cyclic voltammetry
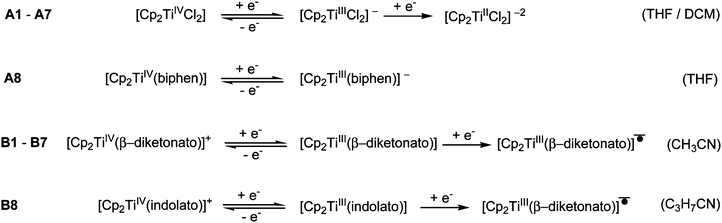
In the electrochemical reduction of neutral substituted Cp2TiIV dichloro complexes, A1–A7 (THF11 or DCM), the first two electron transfer reactions are; a reversible redox couple followed by an irreversible reduction peak with a large potential separation of ca. 1.2 V between the electron transfer reactions. See Fig. 2(a) for a representative CV of the series, A1. The first electron transfer was found to be completely reversible at scan rates of 0.05 V s−1, followed by an irreversible reduction in THF.11 The nature of the reduced species [Cp2TiCl2]− and [Cp2TiCl2]2− was not described,11 though it was suggested that the second reduction could lead to halogen cleavage. In this study, on ground of the DFT study presented below, the first electron transfer, which is completely reversible at scan rates of 0.1 V s−1 (Fig. 2(a)), is ascribed to TiIV/TiIII reduction and the following irreversible reduction is assigned to a second metal TiIII/TiII reduction.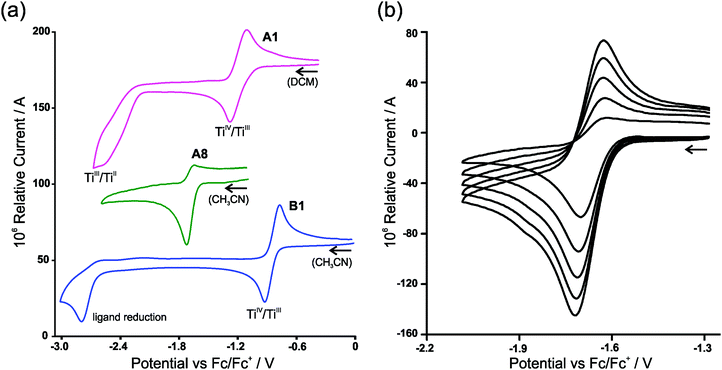 | ||
| Fig. 2 (a) Cyclic voltammograms (vs. Fc/Fc+) of A1, A8 and B1 in 0.1 mol dm−3 (nBu4N)(PF6) at a scan rate of 0.100 V s−1. A1 is conducted in DCM due to solvent coordination in CH3CN, giving rise to two oxidation peaks as a result of the solvent coordinated complex.10 (b) Cyclic voltammograms (vs. Fc/Fc+) of [Cp2Ti(biphen)]A8 in 0.1 mol dm−3 (nBu4N)(PF6)/(CH3CN), at scan rates 0.100–0.500 V s−1 showing the dependence of reversibility on scan rate. | ||
For [Cp2Ti(biphen)] (A8), a one-electron irreversible TiIV/TiIII reduction was observed in CH3CN at a scan rate of 0.1 V s−1 but as the scan rate increased the corresponding oxidation wave appeared at −1.63 V, with the current ratio, ipa/ipc dependent on scan rate (see Table 1 and Fig. 2(b)). However, in THF the reduction of [Cp2Ti(biphen)] is completely reversible and the corresponding anion, stable enough to be detected by e.s.r. techniques.12 The reported reduction potential, Epc (vs. Fc/Fc+) = −1.68 V is in good agreement with the value reported in this study, −1.67 V (Table 2). The more negative reduction potential of [Cp2Ti(biphen)] compared to [Cp2TiCl2], i.e., −1.7 vs. −1.3 V respectively, is expected because the Cl ligand is more electron withdrawing than oxygen (bonded to Ti in the O,O-bidentate biphen ligand) and hence the dichloro derivative A1 is easier to reduce than A8.
| ν (V s−1) | E pc (V) | ΔEp (V) | E 0′ (V) | i pc (106 A) | i pa/ipc |
|---|---|---|---|---|---|
| 0.10 | −1.701 | — | — | — | — |
| 0.20 | −1.709 | 0.079 | −1.670 | 36 | 0.40 |
| 0.30 | −1.711 | 0.081 | −1.671 | 56 | 0.51 |
| 0.40 | −1.714 | 0.084 | −1.672 | 76 | 0.61 |
| 0.50 | −1.718 | 0.091 | −1.673 | 93 | 0.69 |
| 1.00 | −1.727 | 0.110 | −1.673 | 160 | 0.86 |
| Complex | Reduction 1 | Reduction 2 | Free ligand | ||
|---|---|---|---|---|---|
| E 0′/V | E pc/V | E pc/V | |||
| A: neutral complexes | TiIV/TiIII | TiIII/TiII | Solvent | Ref. | |
| a SCE relative NHE = 0.244 V and Fc/Fc+ relative NHE = 0.400 V,22 therefore Epcvs. Fc/Fc+ relative SCE = −0.156 V (0.400–0.244 V). | |||||
| A1 [Cp2TiCl2] | −1.19 | −2.58 | — | DCM | This study |
| A1 | −1.16 | — | — | DCM | 10 |
| A1 | −0.90 | — | — | CH3CN | 10 |
| A1 | −1.28 | — | — | THF | 10 |
| A1 | −1.31 | −2.53 | — | THF | 11 |
| A2 | −1.40 | −2.58 | — | THF | 11 |
| A3 | −1.48 | −2.64 | — | THF | 11 |
| A4 | −1.59 | −2.70 | — | THF | 11 |
| A5 | −1.62 | −2.73 | — | THF | 11 |
| A6 | −1.28 | −2.52 | — | THF | 11 |
| A7 | −1.62 | −2.60 | — | THF | 11 |
| A8 [Cp2Ti(biphen)] | −1.67 | — | −1.93 | CH3CN | This study |
| −1.68 | — | — | THF | 12 | |
| Complex | Reduction 1 | Reduction 2 | Free ligand | ||
|---|---|---|---|---|---|
| Eo′/V | E pc/V | E pc/V | |||
| B: cationic complexes | TiIV/TiIII | ligand | Solvent | Ref. | |
| B1 [Cp2Ti(acac)]+ | −0.85 | −2.80 | −2.56 | CH3CN | This study |
| B1 | −0.86 | −2.85 | — | C3H7CN | 14 |
| B2 | −0.84 | −2.31 | −2.14 | CH3CN | 13 and 21 |
| B2 | −0.85 | −2.33 | — | C3H7CN | 14 |
| B3 | −0.82 | −2.11 | −1.93 | CH3CN | 13 and 21 |
| B4 | −0.63 | −2.16 | −1.85 | CH3CN | 13 and 21 |
| B5 | −0.62 | −1.89 | −1.54 | CH3CN | 13 and 21 |
| B6 | −0.62 | −1.92 | −1.54 | CH3CN | 13 and 21 |
| B7 | −0.62 | −1.92 | −1.56 | CH3CN | 13 and 21 |
| B8 [Cp2Ti(indolato)]+ | −0.85 | −2.93 | −2.63 | C3H7CN | 14 |
A second reduction peak for A8 was not observed in this study, see Fig. 2(a) where the CV scan was reversed at −2.6 V. The second metal TiIII/TiII reduction would only be expected around −3.0 V if the separation between the first and second reduction, was similar to the separation observed in A1. A ligand reduction could be possible for A8, since the free 2,2′-biphenol ligand is redox active, with an irreversible reduction, Epc (vs. Fc/Fc+) = −1.93 V at 0.1 V s−1 (see ESI†) similar to the irreversible reduction of free β-diketones21 and functionalized indole ligand.14
The electrochemical reduction of cationic [Cp2TiIV(β-diketonato)]+ complexes B1–B7 in CH3CN, yielded two separate electron transfers; a reversible redox couple followed by an irreversible reduction peak with a large potential separation between the electron transfer reactions, see Fig. 2(a) for a representative CV of the series, B1. The first reversible electron transfer, is assigned to TiIV/TiIII reduction, while the second irreversible reduction is ascribed to a ligand-based β-diketonato reduction.13 The electrochemical reduction of [Cp2Ti(indolato)]+ (B8), reported by Bond,14 is very similar to that of [Cp2Ti(acac)]+ (B1), with a reversible TiIV/TiIII reduction (E0′ = −0.85 V and −0.85 V respectively) followed by the second ligand-based irreversible reduction (Epc = −2.93 V and −2.80 V respectively). In both cases, the ligands themselves are redox active, Epc = −2.56 and −2.63 V14 respectively for the free ligands of B1 and B8. In all the examples of this study, the chelation of the bidentate ligand to the metal centre, forming a delocalised π-system, results in the coordinated ligand possessing higher electron density (in the electroactive centre) relative to the uncoordinated ligand and hence is more difficult to reduce at a more negative potential. It is significantly easier to reduce the cationic complexes B1–B8 compared to the neutral complexes A1–A8 because there is a residual positive charge on the complex making it easier to accept an electron.
In summary the observed electrochemical behaviour in the potential range 0 to −2.70 V vs. Fc/Fc+, of the neutral and cationic bis(cyclopentadienyl) Ti(IV) derivatives can be simplified (not indicating solvent substitution) and described by the following reactions equations depending on the solvent used.
3.2 Theoretical approach
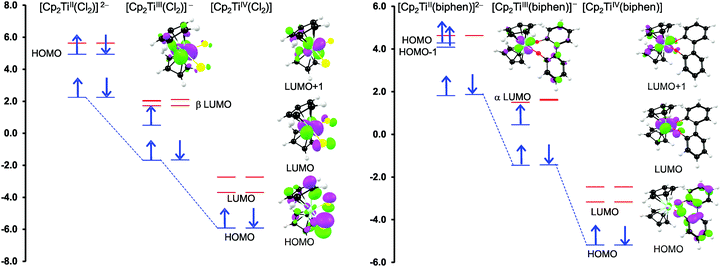
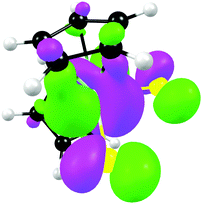
From a quantum chemistry view, the nature of the reduction centre of a complex can be identified by evaluating the character of the lowest unoccupied molecular orbital (LUMO) of the optimized complex, since reduction involves the addition of an electron into this orbital. Similarly the nature of the second reduction centre can be determined from the LUMO of the reduced complex if the first reduction is chemically reversible. DFT calculations were performed on representative samples of the neutral [Cp2TiCl2] (A1) and [Cp2Ti(biphen)] (A8) and cationic [Cp2Ti(acac)]+ (B1) and [Cp2Ti(indolato)]+ (B8) derivatives. In all four cases, the DFT calculations showed that the first reductions are metal based (TiIV/TiIII) as the LUMO is mainly of dz2 character localized on titanium, see Fig. 4 and 5. The distribution of the electron gained in the first reduction, as visualized by the Mulliken spin density plot of the reduced complex, is shown in Fig. 3.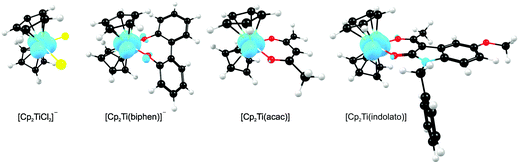 | ||
| Fig. 3 The Mulliken spin density plots of the first reduced species showing the distribution of the single unpaired electron located mainly on titanium. | ||
The nature of the second reduction centre, determined in the same manner as above but using the optimized reduced species, is more complicated and reveals that the character of the second reduction is not identical in the four examples. For A1, the lowest energy second reduced complex [Cp2TiCl2]2− is diamagnetic (q = −2, S = 0) with the second electron added to the β LUMO which is mainly of dz2 character located on titanium (Fig. 4), consistent with, TiIII/TiII second reduction. For A8, the lowest energy second reduced species [Cp2Ti(biphen)]2− is paramagnetic (q = −2, S = 1), 0.15 eV lower in energy than the diamagnetic option. The second electron is added to the α LUMO, mainly of dx2−y2 character and consistent with the second reduction also being the metal, TiIII/TiII reduction (Fig. 4). The spin plot of the DFT calculated double reduced complex [Cp2Ti(biphen)]2− in Fig. 6 shows the distribution of the two added unpaired electron, with a 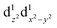 configuration.
configuration.
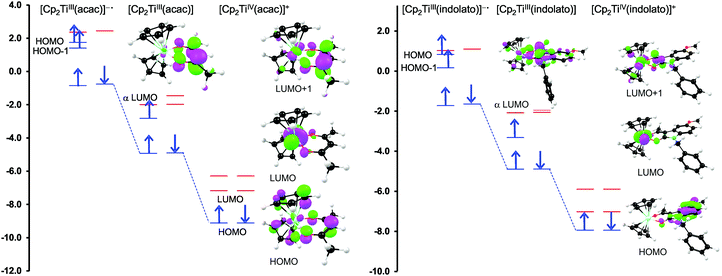
For both the cationic complexes [Cp2Ti(acac)]+ (B1) and [Cp2Ti(indolato)]+ (B8), the lowest energy doubly reduced species are paramagnetic (q = −1, S = 1), with the second electron added to the α LUMO. However in this case, the α LUMO is located on the ligand, i.e., the β-diketonato ligand for [Cp2TiIII(acac)] and the indolato ligand for [Cp2TiIII(indolato)] (Fig. 5), consistent with the second reduction being ligand based. The spin density plots of [Cp2Ti(acac)]− and [Cp2TiIII(indolato)]− (Fig. 6) show the distribution of the two added unpaired electrons, located on titanium as well as on the ligand. These results support the experimental cyclic voltammetry observations in which the cationic complexes B1 and B8 have a reversible metal reduction followed by an irreversible ligand reduction forming an unstable ligand radical. One can also conclude that although the second reduction of [Cp2Ti(biphen)] (A8) is not observed experimentally by cyclic voltammetry due to the solvent window, one would predict a TiIII/II reduction instead of the possible ligand reduction as is the case for B1 and B8. According these DFT results, [Cp2Ti(biphen)] should behave is a similar manner to [Cp2TiCl2], with two consecutive metal reductions, even though it has a redox active ligand.
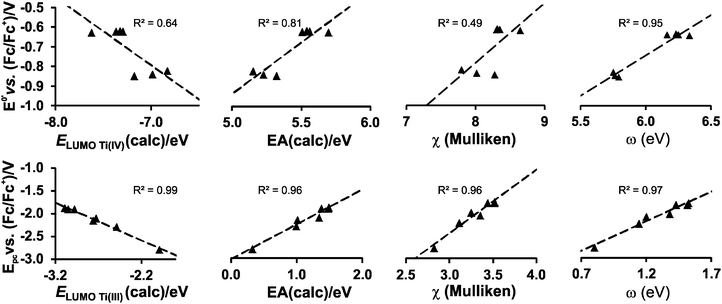
While the character of the LUMOs discussed above gave information on the reduction centres, the energy of the LUMOs is related to the reduction potentials; the lower the energy of the LUMO, the easier an electron can be accepted and the easier the reduction (less negative experimental Epc). It has been shown that linear relationships exist between experimentally measured reduction potentials Epc of a series of related compounds and calculated energies; i.e., LUMO energy (ELUMO), electron affinity (EA), Mulliken electronegativity (χ), global electrophilicity index (ω) and to a variety of empirical quantities, used to describe the electron-withdrawing power of R substituents on the ligand, i.e., Gordy scale group electronegativities, Hammett substituent constants and Lever electronic parameters.23–28
The following DFT calculated energies, reflecting the electronic properties of substituent groups on the electron density of the titanium, were used:
(DFT calculated energy values are recorded in Table S1 of the ESI†).
Strong correlations between LUMO energies, ELUMO, and reduction potentials, Epc, have been reported for a related series of compounds, substituted with electron-withdrawing or electron-donating groups. For example, the electro-reduction of functionalised β-diketones21 and nitrobenzenes33 forming radical anions, yielded reduction potentials which gave excellent correlations in the linear relationship between experimental Epcvs. calculated ELUMO (R2 = 0.99). In these investigations involving ligand reductions, the LUMOs presented effective π-conjugation between the electroactive centre and the substituent groups and hence the electronic properties of the substituents significantly influence the redox properties of the compounds. In the case of metal-centred reductions, the LUMOs can range from being highly metal localised with strong d character to having metal–ligand π-interactions. The investigation of octahedral [Ti(R1COCHCOR2)2biphen], containing electron withdrawing or electron donating substituents (R1,R2), showed that the LUMOs had efficient β-diketonato-metal π-conjugation,34 hence the observed reduction potentials were excellently correlated to LUMO energies (R2 = 0.98).
In the present investigation the substituent groups are located at different sites; series A the substituents (R1, R2…R5) are located on the Cp rings while in series B they are located on the β-diketonato ligand (RCOCHCOR′)−, see Fig. 1. The LUMO of A1 shows a small but significant π-interaction between titanium and the Cp rings, with 74% metal, and 9.0% Cp rings contributions (Fig. 7). The reduction potentials, E0′, of A1–A7 correlate linearly with DFT calculated energies, ELUMO, EA, χ and ω, (R2 = 0.80–0,98), see Fig. 8, showing a moderately strong influence of the substituents on the electron density at titanium.
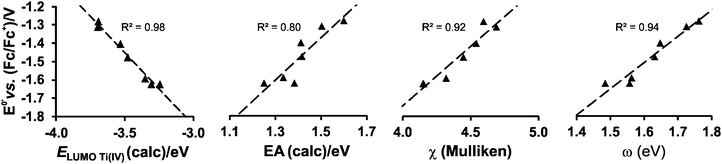 | ||
| Fig. 8 The relationship between the formal reduction potential, E0′, of titanium and the indicated DFT calculated energies for complexes A1–A7. | ||
However, the LUMO of complex B1 is metal centred and highly localised with 82% titanium d character. No π-interaction between the metal centre and the acetylacetonato ligand are indicated, thus the electronic properties of the substituents (R,R′) of the β-diketonato ligand in B1–B7 are not expected to have a clearly defined influence on the reduction potential of the TiIV/TiIII couple. This trend is observed in the poor correlation of the linear relationships between the formal reduction potential (E0′) of the TiIV/TiIII couple and the DFT calculated energies, ELUMO, EA, χ and ω (see Fig. 9 (top)). The reduction potentials appear in two groups depending on the number of CF3 groups present on the β-diketonato ligand. The strong electron-withdrawing CF3 groups clearly affect the electron density at the metal center with a notable shift of 0.2 V in the reduction potentials. Since electron density at the redox centre is regulated by both inductive (through the σ-system) and resonance effects (through the π-system), if direct π resonance (as a result of p-orbital overlap) is absent, CF3 substituent groups can withdraw electron density from the TiIV centre through strong electron-withdrawing induction. In a study of alkyloxy- and aryloxy-functionalized titanocenes, where the characteristic TiIV/III reduction was correlated to Hammett substituent constants, a relatively strong influence of the substituents on the electron density at titanium was observed.35 However the LUMOs were not calculated, and thus the substituent effect could not be related to the nature of the LUMO.
In contrast, when considering the second reduction, the LUMO of the reduced B1 species [Cp2TiIII(acac)] is distributed over the acetylacetonato ligand with π-character enhancing the communication between the electro-active ligand centre and the substituent groups (R,R′). In this case the extensive communication between the β-diketonato ligand reduction centre and the substituents, suggest that the electronic properties of the substituent groups of the β-diketonato ligand should have a clearly determinable influence on the second reduction. This is indeed observed when relating the experimental second reduction potentials Epc (that is ascribed to the reduction of the β-diketonato ligand) to the DFT calculated energies, ELUMO, EA, χ and ω (see Fig. 9 (bottom)). There is significantly larger substituent effect on the second redox-potentials, than on the first reduction potentials. The energy values are more consistently distributed over the energy range with a linear fit of higher accuracy (R2 = 0.96–0.99) compared to the relationships of the first reduction potentials, E0′versus ELUMO, EA, χ and ω in Fig. 7 (top), (R2 = 0.49–0.95).
4. Conclusions
In summary we demonstrated that the nature of the reduction, i.e., metal-centred vs. ligand-based, of functionalised bis(cyclopentadienyl) titanium(IV) derivatives can be predicted using Quantum Chemistry Techniques. DFT calculations in agreement with reported CV data showed that the first experimentally observed reduction is metal based involving the reversible TiIV/III couple, and the second experimentally observed reduction is either metal or ligand-based depending on the electronic structure of the LUMO of the species involved. For the neutral titanium(IV) complexes, the second reduction is metal based, TiIII/TiII, while for the cationic titanium(IV) complexes, it is a ligand reduction. The free bidentate O,O′-ligands, coordinated in both the neutral and cationic complexes, are also redox active but the reduction of the coordinated O,O′-ligands are only observed in the cationic complexes, in agreement with DFT calculations.We have also shown the conditions needed in the LUMO for the electronic properties of the substituents on the ligands to influence the reduction potentials. The electron-withdrawing or electron-donating properties of the substituents directly influence electron density at the redox centre when π-interactions between the electro-active centre and the substituent groups exist in the LUMO. In this case, a number of relationships between the electronic properties of the substituents and the redox behaviour have been affirmed, showing excellent correlation in the linear relationship between experimentally measured reduction potentials vs. DFT calculated energies, ELUMO, EA, χ and ω. This was demonstrated for the first reduction in Cp functionalized [Cp2TiIVCl2] derivatives, series A and the second reduction of β-diketonato functionalized [Cp2TiIV(β-diketonato)]+ derivatives, series B. However, the substituent effect was erratic and nonlinear (poor correlation of linear relationships) for the first reduction of series B, confirmed by the LUMO being highly localised with no π-interaction between the metal centre and the substituents on the β-diketonato ligand. Hence using DFT we have been able to determine when it is possible to fine-tune the electronic properties of the electro-active metal, using functionalised ligands for the design of metallocene catalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received support from the South African National Research Foundation and the Central Research Fund of the University of the Free State, Bloemfontein, South Africa. A grant of computer time from the Norwegian supercomputing program NOTUR (Grant No. NN4654K) is gratefully acknowledged.References
- D. S. Henriques, K. Zimmer, S. Klare, A. Meyer, E. Rojo-Wiechel, M. Bauer, R. Sure, S. Grimme, O. Schiemann, R. A. Flowers and A. Gansäuer, Highly Active Titanocene Catalysts for Epoxide Hydrosilylation: Synthesis, Theory, Kinetics, EPR Spectroscopy, Angew. Chem., Int. Ed. Engl., 2016, 55, 7671–7675 CrossRef CAS PubMed
.
- S. Ghosh and H. Hagihara, Polystyrene with half-titanocene/MAO catalysts: Influence of 2,6-diisopropylphenol, Appl. Catal., A, 2009, 360, 126–129 CrossRef CAS
.
- B. Wang, Ansa-Metallocene Polymerization Catalysts: Effects of the Bridges on the Catalytic Activities, Coord. Chem. Rev., 2006, 250, 242–258 CrossRef CAS
.
- Y. Qian, J. Huang, M. D. Bala, B. Lian, H. Zhang and H. Zhang, Synthesis, Structures, and Catalytic Reactions of Ring-Substituted Titanium(IV) Complexes, Chem. Rev., 2003, 103, 2633 CrossRef CAS PubMed
.
- L. Resconi, L. Cavallo, A. Fait and F. Piemontesi, Selectivity in Propene Polymerization with Metallocene Catalysts, Chem. Rev., 2000, 100, 1253–1345 CrossRef CAS PubMed
.
- P. C. Mohring and N. J. Coville, Homogeneous group 4 metallocene ziegler-natta catalysts: The influence of cyclopentadienyl-ring substituents, J. Organomet. Chem., 1994, 479, 1–29 CrossRef
.
- O. Vassylyev, A. Panarello and J. G. Khinast, Enantioselective hydrogenations with chiral titanocenes, Molecules, 2005, 10, 587–619 CrossRef CAS PubMed
.
- P. Jutzi and T. Redeker, Efficient recycling of a versatile titanocene precatalyst - significance of side-chain functionalization, Organometallics, 1997, 16, 1343–1344 CrossRef CAS
.
- F. N. Tebbe, G. W. Parshall and G. S. Reddy, Olefin homologation with titanium methylene compounds, J. Am. Chem. Soc., 1978, 100, 3611–3613 CrossRef CAS
.
- M. A. Vorotyntsev, M. Casalta, E. Pousson, L. Roullier, G. Boni and C. Moise, Redox properties of titanocene-pyrrole derivative and its electropolymerization, Electrochim. Acta, 2001, 46, 4017–4033 CrossRef CAS
.
- J. Langmaier, Z. Samec, V. Varga, M. Horáček and K. Mach, Substituent effects in cyclic voltammetry of titanocene dichlorides, J. Organomet. Chem., 1999, 579, 348–355 CrossRef CAS
.
- A. Chaloyard, A. Dormond and J. Tirouflet, and N. El Murr, Electrosynthesis of alkyl and aryloxy titanium(III) complexes; electrochemical and spectroscopic characterization, J. Chem. Soc., Chem. Commun., 1980, 214–216 RSC
.
- A. Kuhn and J. Conradie, J. Electrochemical and Density Functional Theory Study of bis(cyclopentadienyl) mono(β-diketonato) titanium(IV) cationic complexes, Electrochim. Acta, 2010, 56, 57–264 CrossRef
.
- A. M. Bond, R. Colton, U. Englert, H. Hügel and F. Marken, Characterization of titanocene(III) complexes of β-diketonates by electrochemical, spectroscopic and crystallographic methods: stabilization of oxidized and reduced β-diketonate radicals by acetyl and titanocene derivatization, respectively, Inorg. Chim. Acta, 1995, 235, 117–126 CrossRef CAS
.
- E. Erasmus, J. Conradie, A. Muller and J. C. Swarts, Synthesis, crystal structure and electrochemistry of tetrahedral mono-β-diketonato titanocenyl complexes, Inorg. Chim. Acta, 2007, 360, 2277–2283 CrossRef CAS
.
- E. Samuel and J. Vedelt, Electrochemical and Chemical Reduction of Titanocene Dihalides-An EPR Study, Organometallics, 1989, 8, 237–241 CrossRef CAS
.
- R. J. Enemærke, J. Larsen, T. Skrydstrup and K. Daasbjerg, Mechanistic Investigation of the Electrochemical Reduction of Cp2TiX2, Organometallics, 2004, 23, 1866–1874 CrossRef
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS
.
- The ADF program system was obtained from Scientific Computing and Modeling, Amsterdam (http://www.scm.com/). For a description of the methods used in ADF, see: G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. J. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
- G. Gritzner and J. Kuta, Recommendations on reporting electrode potentials in non-aqueous solvents, Pure Appl. Chem., 1984, 56, 461–466 CrossRef
.
- A. Kuhn, K. G. von Eschwege and J. Conradie, Electrochemical and density theory modelled reduction of enolized 1,3-diketones, Electrochim. Acta, 2011, 56, 6211 CrossRef CAS
.
- H.-M. Koepp, H. Wendt and H. Strehlow, Comparison of the Potential Series in Different Solvents, Z. Elektrochem., 1960, 64, 483–491 CAS
.
- J. Conradie, Density functional theory calculations of Rh-β-diketonato complexes, Dalton Trans., 2015, 44, 1503–1515 RSC
.
- M. M. Conradie and J. Conradie, Electrochemical behaviour of Tris(β-diketonato)iron(III) complexes: A DFT and experimental study, Electrochim. Acta, 2015, 152, 512–519 CrossRef CAS
.
- R. Freitag and J. Conradie, Electrochemical and Computational Chemistry Study of Mn(β-diketonato)3 complexes, Electrochim. Acta, 2015, 158, 418–426 CrossRef CAS
.
- R. Liu and J. Conradie, Tris(β diketonato)chromium(III) complexes: Effect of the -β-diketonate ligand on the redox properties, Electrochim. Acta, 2015, 185, 288–296 CrossRef CAS
.
- H. Ferreira, K. G. von Eschwege and J. Conradie, Electronic properties of Fe charge transfer complexes – A combined experimental and theoretical approach, Electrochim. Acta, 2016, 216, 339–346 CrossRef CAS
.
- H. Ferreira, M. M. Conradie, K. G. von Eschwege and J. Conradie, Electrochemical and DFT study of the reduction of substituted phenanthrolines, Polyhedron, 2017, 122, 147–154 CrossRef CAS
.
- R. S. Mulliken and A. New Electroaffinity, Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities, J. Chem. Phys., 1934, 2, 782 CrossRef CAS
.
- M. V. Putz, N. Russo and E. Sicilia, About the Mulliken electronegativity in DFT, Theor. Chem. Acc., 2005, 114, 38 CrossRef CAS
.
- F. De Proft, W. Langenaeker and P. Geerlings, Ab initio determination of substituent constants in a density functional theory formalism: calculation of intrinsic group electronegativity, hardness, and softness, J. Phys. Chem., 1993, 97, 1826 CrossRef CAS
.
- R. G. Parr, L. V. Szentpaly and S. Liu, Electrophilicity Index, J. Am. Chem. Soc., 1999, 121, 1922 CrossRef CAS
.
- A. Kuhn, K. G. von Eschwege and J. Conradie, Reduction potentials of para-substituted nitrobenzenes—an infrared, nuclear magnetic resonance, and density functional theory study, J. Phys. Org. Chem., 2011, 25, 58–68 CrossRef
.
- A. Kuhn and J. Conradie, Synthesis, Electrochemical and DFT study of octahedral bis(β-diketonato)-titanium(IV) complexes, Inorg. Chim. Acta, 2016, 247, 247–256 CrossRef
.
- S. Kocher, B. Walfort, G. Rheinwald, T. Ruffer and H. Lang, Alkyloxy- and aryloxy-titanocenes: Synthesis, solid-state structure and cyclic voltammetric studies, J. Organomet. Chem., 2008, 693, 3213–3222 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional electrochemical data, DFT calculated energies and optimized coordinates of the DFT calculations. See DOI: 10.1039/c7nj03746e |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2018 |