Size dependent surface reconstruction in detonation nanodiamonds†
Shery L. Y.
Chang
 *a,
Christian
Dwyer
b,
Eiji
Ōsawa
c and
Amanda S.
Barnard
*a,
Christian
Dwyer
b,
Eiji
Ōsawa
c and
Amanda S.
Barnard
 d
d
aJohn M. Cowley Center for High Resolution Electron Microscopy, Arizona State University, Tempe, USA. E-mail: shery.chang@asu.edu
bDepartment of Physics, Arizona State University, Tempe, USA
cNanoCarbon Research Institute, Ueda, Japan
dData61, CSIRO, Docklands, Australia
First published on 15th December 2017
Abstract
Nanometer-sized diamond particles are used in bio-medical applications, where the nature of the nanodiamond surfaces is crucial to achieving correct functionalisation. Herein, using high-resolution transmission electron microscopy and electronic structure calculations, we study the surface reconstructions that occur in detonation-synthesized nanodiamonds. Our results show that particles smaller than 3 nm exhibit size- and shape-dependent surface reconstructions, and that the surfaces can exhibit a higher-than-expected fraction of sp2+x bonding. This indicates an aliphatic character for sub-3 nm nanodiamond particles. Such behaviour impacts the functionality of nanodiamonds, where both size and surface charge can drive performance. Our observations offer a potential strategy for better functionalization control via the size range of the particles.
Conceptual insightsDetonation nanodiamonds are rapidly expanding for use in a wide range of biotechnological applications spanning from imaging, sensing to medical treatment. The success of the field relies on the control of surface properties for specific applications. However, our current understanding of the surface is based on some incorrect pervasive assumptions. This highlights the urgent need for detailed understanding of surface atomic and electronic structures of nanodiamonds. We conclusively show that the surface reconstruction of nanodiamonds is size dependent. More importantly, the surface of a nanodiamond has more nonhexagonal rings when the particle size is smaller than 3 nm, giving an aliphatic surface character, rather than aromatic. This is contrary to the common assumption, where surface graphitization has traditionally implied the formation of graphene, which we find to be a minority component at these sizes. This finding has a significant impact on the existing design principle of the binding and release of biological molecules to nanodiamond particle surfaces. Our results also provide a rapid screening strategy to use size selection to realise a more effective treatment of nanodiamond platforms and separation processes to tune samples for specific applications. |
Nanodiamond particles have recently attracted a surge of interest due to successful demonstrations in bio-medical applications. These include drug delivery,1–3 bio-sensing,4,5 and diagnostic imaging.6,7 For drug delivery applications in particular, it is desirable to use small nanodiamond particles with a large surface area to allow better loading of the biological molecules. Such nanodiamond particles can be synthesized via a detonation process, termed detonation nanodiamond (DND), producing particles typically 3–5 nm in size.8 It is generally accepted that DND particles consist of diamond-like cores and fullerene-like surfaces.9 The surfaces can be tuned to exhibit negative or positive surface electrostatic potentials, which provides the advantages of both aliphatic and aromatic surface characteristics in one material. For example, positive surface charges can moderate the uptake of nanoparticles by various metabolic systems and facilitate the binding of nanoparticles to cell membranes. In contrast, negatively charged surfaces can enable pH-triggered drug delivery, whereby drugs which are positively-charged under physiological conditions attach to the nanoparticles until perturbed by the lower pH of cells at the delivery site.10 The efficiency of such interactions depends crucially on the electronic structure at the surface.
From a materials design perspective, optimizing surface functionalization requires a detailed understanding of the surface structure of DND.11,12 Gaining such an understanding requires a combination of experimental observation and theory-based modelling. Of the numerous noteworthy experimental measurements of the electronic structures of DND,9,13–16 a seminal work using a combination of X-ray absorption spectroscopy (XAS) and density functional theory calculations9 showed that the surfaces of DND reconstruct to a buckminsterfullerene-like structure composed of hexagons, pentagons, etc. The presence of non-hexagonal polygons implies the presence of sp2+x electronic structure components.17 Theoretical calculations have further suggested that the DND surface structure should depend on the size and shape of the particle core,18,19 potentially offering ways to tune functionalization. However, it is not possible to verify such behaviour using spectroscopy methods such as XPS or Raman, since the spatial resolution of these methods can only probe the average sample structure, and they cannot differentiate the effect of particle size.
In the present work, we study DND surfaces using a combination of high-resolution transmission electron microscopy (HRTEM) and electronic structure modelling based on density-functional tight-binding (DFTB) theory. TEM was performed using a spherical-(Cs) and chromatic-(Cc) aberration-corrected instrument, which has the significant advantage of being able to directly image the surface atomic structure of individual DND particles. Our combined experimental observations and calculations show that the surface structures have strong dependence on the particle size and shape: the smaller the particle size, the greater the probability of five- and seven-membered rings in the aromatic shell; however, particle shape, and specifically facet geometry, plays an influential role; for particles larger than ∼3 nm in diameter, the surface structure approaches that of bulk diamond, which is dominated by aliphatic carbon.
The DND studied here was prepared by a six-step procedure in which the major step is ball-milling of nanodiamond agglutinates with 30 mm zirconia beads (details in the ESI†). Dispersed particles in aqueous solution were drop cast directly onto a TEM grid coated with holey amorphous carbon and dried under vacuum at room temperature for approximately 20 minutes.
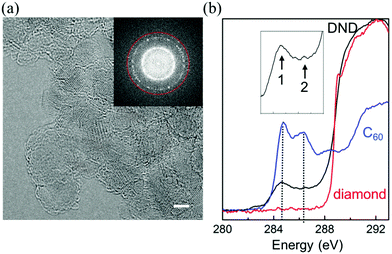
Fig. 1(a) shows an HRTEM image which is representative of the DND sample. Although HRTEM has been used to study nanodiamond particles in the past,20–22 here we use a lower beam energy (80 keV) to reduce radiation damage20,23 while maintaining the necessary spatial information transfer (0.1 nm) via the correction of spherical and chromatic aberration. Fig. 1(b) shows an electron energy-loss carbon-K spectrum from DND, collected from many hundreds of particles. A comparison with the spectra from bulk diamond and C60 reveals an sp2+x bonding component in DND, which is attributable to 5- and 7-membered-polygonal surface carbon, as discussed further below.
Fig. 2(a and b) show HRTEM images exemplar of larger and smaller DND particles (additional images are in Fig. S1, ESI†). Larger particles often exhibit easily-recognizable low-index facets, such as the 2.4 nm particle in Fig. 2(a) which exhibits an outmost {111} surface (indicated by the red arrow). The atomic columns at the surface are seen to have relaxed outwards compared to the {111} spacing in the core. The relaxation is nonuniform, producing a slightly convex surface. This behaviour is entirely different to that of the extended {111} surfaces in bulk diamond, which undergo a (2 × 1) reconstruction (Pandey chain structure).24 Smaller DND particles, such as the 1.6 nm particle in Fig. 2(b), often exhibit significantly more convex surfaces. These surfaces have the appearance of fullerene-like shells, as termed previously.18 We also observe that the core of the smaller particle in Fig. 2(b) is highly strained, as shown by the disordered appearance of the atomic columns. These results provide clear evidence of the manner in which highly convex fullerene-like shells can develop to accommodate strain in small DND particles.18
Another behaviour frequently observed in DND is the presence of high-density twins.20 As shown in Fig. 2(c), it appears that such twins can influence the surface structure, acting as pinning points, dividing the surface into smaller fragments.
To gain a deeper understanding of the size- and shape-dependent surface behaviour, we have performed extensive modelling of nanodiamonds using DFTB theory.25 Particle sizes ranging from 1.6 to 4 nm (matching our experiments) and 12 different shapes with varying ratios of {111}, {100} and {110} facets were calculated26 (see the ESI† and Fig. S2). Fig. 3 shows two selected shapes, namely, the doubly-truncated octahedron and the rhombicuboctahedron, which have different fractions of {111}, {100} and {110} facets. In order to facilitate the correct interpretation of the experimental HRTEM images and to compare with the theoretical models, high-resolution TEM image simulations were conducted using the theoretical atomic model as the structure input and the carefully calibrated experimental imaging conditions as the image simulation parameters.
It can be readily seen from Fig. 2 and 3 that DFTB predicts surface reconstructions in nanodiamonds in good accord with our experimental observations of DND. In Fig. 3, DFTB predicts that the reconstruction depends on both the size and the shape of the particle. For particles smaller than 2.8 nm, the surface structure relaxes and shows convex curvature. The {111} surfaces of larger particles also show concave areas which arise as the surfaces begin to adapt to the diamond sp3 structure beneath, generating a cross-link between the surface and the core.27
A Comparison of the two shape categories in Fig. 3(a and b) reveals that their surface reconstructions differ. While the doubly-truncated octahedra show a fullerene-like shell, the {111} surfaces of rhombicuboctahedra are terminated by {111}/{111} and {111}/{100} edges which appear to act as pinning points, giving rise to {111} surfaces with high local curvature. It is also worth noting that DFTB predicts strain in the particle cores. The strain is most pronounced in the smallest particles but it is also present in the sub-surface layer of larger particles. These theoretical findings agree well with our experimental observations, particularly the trend of convex surfaces for particles <2.8 nm, and the more pronounced strain in smaller particles.
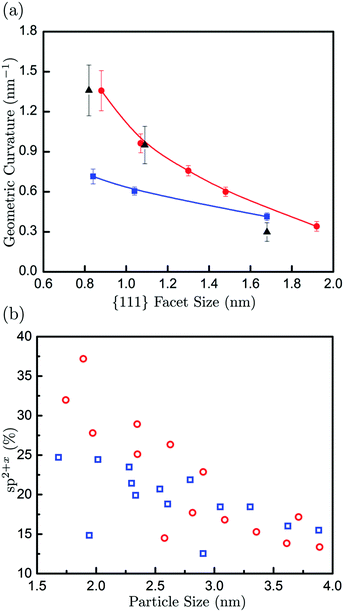
As a further comparison of our experimental and computational results, we have measured the surface curvature as a function of the surface facet size. The surface curvature gives an indication, although indirect, of the sp2+x contribution in nanodiamond particles, as higher curvature implies a higher concentration of non-hexagonal polygons and the associated sp2+x bonding. Fig. 4(a) shows curvatures measured from both the experimentally-observed and calculated particles, which show good agreement, particularly with the rhombicuboctahedra-shaped particles. A clear decrease in surface curvature with increasing facet size is observed. Low curvatures for facet sizes of about 2 nm (and larger) are indicative of surface structures cross-linked to the diamond core. It is interesting to point out that the calculated curvatures for rhombicuboctahedra are significantly higher than for doubly truncated octahedra at small facet sizes, whereas the influence of particle shape becomes negligible for larger facets. Fig. 4(b) shows the calculated fraction of sp2+x bonded carbons as a function of particle size. It is apparent that the sp2+x fraction increases with decreasing particle size for both selected shapes. Here, the calculated results exhibit a clear correlation between surface curvature and sp2+x fraction for particle sizes smaller than about 3 nm. Rhombicuboctahedra exhibit the highest curvatures and sp2+x fractions. This particular shape contains {110} facets, which have been shown to be important features of nanodiamond samples in the past.28 The DFTB calculations show that these facets are aliphatic. The aforementioned size dependence of the sp2+x fraction is also a function of the particle shape. For example, octahedral particles show relatively little sp2+x fraction size dependence, whereas particles containing a significant proportion of {110} surfaces show more pronounced behaviour (with the sp2+x fraction inversely proportional to particle size).
In summary, using low-voltage HRTEM imaging and electronic structure calculations we have elucidated the way in which nanodiamonds can exhibit reconstructed “fullerene-like” surfaces. The surface reconstruction is size dependent, with higher surface curvatures observed in very small particles and the curvature becoming negligible for particles larger than about 3 nm (or {111} facets larger than about 2 nm). The correlation between surface curvature and sp2+x fraction suggests that the detonation nanodiamond particles have a relatively high fraction of sp2+x-bonded carbon on the surface, and that this fraction can be substantially increased in very small particles. While our experimental and theoretical comparisons here do not include the effect of impurities such as nitrogen, which is commonly observed in DND, we estimate that such an effect to the surface curvature is negligible. Based on the size ranges of the particles and the experimentally measured nitrogen content in the sample (2–3%), we estimate that there is about 1% probability of nitrogen on the surface. Although the impact of nitrogen on the surface structure is currently not verified, considering our good agreement between the experiment and the nitrogen-free theoretical models, any deviation due to the 1% of N on the surface is largely insignificant. The size-dependent surface structure of nanodiamonds has important consequences for their functionality. For example, the surfaces with a high fraction of sp2+x-bonded carbon in smaller nanodiamond particles can give a near neutral surface electrostatic potential. This could potentially inhibit the opportunity to use strongly aromatic (negatively charged) or aliphatic (positively charged) facets exclusively for pH-triggered drug delivery, but could alternatively provide more efficient binding sites for other functional linker molecules such as polyethylene glycol29 or carboxyl.30 Moreover, knowledge of the size-dependent surface structure is an important starting point to tackle the challenging issues of surface structure and chemistry uniformity that are required for many nanodiamond applications, and may offer a route to control surface functionalisation, enabling better selectivity and higher rates of surface molecule attachment.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. L. Y. C. acknowledges Forschungszentrum Juelich for the use of PICO instrument and LeRoy Eyring Center for Solid State Science for the use of monochromated-aberration corrected Titan. Computational resources for this project have been supplied by the Australian National Computing Infrastructure national facility under Grant q27.References
- E. K. Chow, X. Zhang, M. Chen, R. Lam, E. Robinson, H. Huang, D. Schaffer, A. Goga, E. Ōsawa and D. Ho, Sci. Transl. Med., 2011, 3, 73ra21 CrossRef PubMed.
- A. Schroeder, D. Heller, M. Winslow, J. Dahlman, G. Pratt, R. Langer, T. Jacks and D. Anderson, Nat. Rev., 2012, 39, 12 Search PubMed.
- G. Hong, S. Diao, A. L. Antaris and H. Dai, Chem. Rev., 2015, 115, 10816 CrossRef CAS PubMed.
- W. Zhang, K. Patel, A. Schexnider, S. Banu and A. D. Radadia, ACS Nano, 2014, 8, 1419 CrossRef CAS PubMed.
- Z. Wang and Z. Dai, Nanoscale, 2015, 7, 6420 RSC.
- L. M. Manus, D. J. Mastarone, E. A. Waters, X. Zhang, E. A. Schultz-Sikma, K. W. MacRenaris, D. Ho and T. J. Meade, Nano Lett., 2010, 10, 484 CrossRef CAS PubMed.
- S. Mitragotri, D. G. Anderson, X. Chen, E. K. Chow, D. Ho, A. V. Kabanov, J. M. Karp, K. Kataoka, C. A. Mirkin, S. H. Petrosko, J. Shi, M. M. Stevens, S. Sun, S. Teoh, S. S. Venkatraman, Y. Younan Xia, S. Wang, Z. Gu and C. C. Xu, ACS Nano, 2015, 9, 6644 CrossRef CAS PubMed.
- E. Ōsaws, in Chemistry of Nanocarbons, ed. F. Wudl, S. Nagase and K. Akasaka, John Wiley & Sons, 2010, ch. 17 Search PubMed.
- J. Raty, G. Galli, C. Bostedt, T. W. van Buuren and L. J. Terminello, Phys. Rev. Lett., 2003, 90, 037401 CrossRef PubMed.
- X. Chen, L. Liu and C. Jiang, Acta Pharm. Sin. B, 2016, 6, 261 CrossRef PubMed.
- S. Sotoma, K. Akagi, S. Hosokawa, R. Igarashi, H. Tochio, Y. Haradae and M. Shirakawa, RSC Adv., 2015, 5, 13818 RSC.
- A. Krueger and D. Lang, Adv. Funct. Mater., 2012, 22, 890 CrossRef CAS.
- L. A. Garvie, Meteorit. Planet. Sci., 2006, 41, 667 CrossRef CAS.
- J. Birrell, J. E. Gerbi, O. Auciello, J. M. Gibson, D. M. Gruen and J. A. Carlisle, J. Appl. Phys., 2003, 93, 5606 CrossRef CAS.
- S. L. Y. Chang, A. S. Barnard, C. Dwyer, C. B. Boothroyd, R. K. Hocking, E. Osawa and R. J. Nicholls, Nanoscale, 2016, 8, 10548 RSC.
- M. Mermoux, J. Phys. Chem. C, 2014, 118, 23415 CAS.
- M. Dresselhaus, G. Dresselhaus and P. Eklund, Science of fullerenes and carbon nanotubes, Elsevier Inc., 2003 Search PubMed.
- A. S. Barnard, S. P. Russo and I. K. Snook, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 073406 CrossRef.
- A. S. Barnard, Mater. Horiz., 2014, 1, 289 RSC.
- S. Turner, O. Shenderova, F. D. Pieve, Y. Lu, E. Yücelen, J. Verbeeck, D. Lamoen and G. Van Tendeloo, Phys. Status Solidi A, 2013, 210, 1976 CrossRef CAS.
- K. Iakoubovskii, K. Mitsuishi and K. Furuya, Nanotechnology, 2008, 19, 155705 CrossRef CAS PubMed.
- P. Wesolowski, Y. Y. Lyutovich, F. Banhart, H. D. Carstanjen and H. Kronmuller, Appl. Phys. Lett., 1997, 71, 6 CrossRef.
- J. Hiraki, H. Mori, E. Taguchi, H. Yasuda, H. Kinoshita and N. Ohmae, Appl. Phys. Lett., 2005, 86, 223101 CrossRef.
- B. B. Pate, Surf. Sci., 1986, 165, 83 CrossRef CAS.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678 CrossRef CAS PubMed.
- A. S. Barnard, Nanodiamond Data Set. v1, CSIRO Data Collection, 2016 DOI:10.4225/08/571F076D050B1.
- A. S. Barnard and M. Sternberg, J. Mater. Chem., 2007, 17, 4811 RSC.
- L. Y. Chang, E. Ōsawa and A. S. Barnard, Nanoscale, 2011, 3, 958 RSC.
- A. S. Barnard, Nanoscale, 2017, 9, 70 RSC.
- L. Lai and A. S. Barnard, Nanoscale, 2014, 6, 14185 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Synthesis of dispersed elementary particles of detonation nanodiamond; (2) HRTEM imaging using monochromated-aberration corrected TEM; (3) HRTEM image simulations; (4) DFTB calculations of nanodiamond particles; and (5) geometric curvature measurement. See DOI: 10.1039/c7nh00125h |
| This journal is © The Royal Society of Chemistry 2018 |