Open Access Article
Open Access ArticleScreening of nutritional and genetic anemias using elastic light scattering†
Lieshu
Tong
a,
Josef
Kauer
bc,
Xi
Chen
de,
Kaiqin
Chu
a,
Hu
Dou
*d and
Zachary J.
Smith
 *a
*a
aDepartment of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei, Anhui, China. E-mail: zsmith@ustc.edu.cn
bBeuth Hochschule für Technik Berlin, Berlin, Germany
cNeuroCure Clinical Research Center, Charité - Universitätsmedizin Berlin, corporate member of Freie Universität Berlin, Humboldt-Universität zu Berlin, and Berlin Institute of Health, Berlin, Germany
dDepartment of Clinical laboratory, Ministry of Education Key Laboratory of Child Development and Disorders, Key Laboratory of Pediatrics in Chongqing, Chongqing International Science and Technology Cooperation Center for Child Development and Disorders, Children's Hospital of Chongqing Medical University, Chongqing, China. E-mail: 375009808@qq.com
eCenter for Clinical Molecular Medicine, Children's Hospital of Chongqing Medical University, China
First published on 28th September 2018
Abstract
Anemia affects more than ¼ of the world's population, mostly concentrated in low-resource areas, and carries serious health risks. Yet current screening methods are inadequate due to their inability to separate iron deficiency anemia (IDA) from genetic anemias such as thalassemia trait (TT), thus preventing targeted supplementation of oral iron. Here we present an accurate approach to diagnose anemia and anemia type using measures of pediatric red cell morphology determined through machine learning applied to optical light scattering measurements. A partial least squares model shows that our system can accurately extract mean cell volume, red cell size heterogeneity, and mean cell hemoglobin concentration with high accuracy. These clinical parameters (or the raw data itself) can be submitted to machine learning algorithms such as quadratic discriminants or support vector machines to classify a patient into healthy, IDA, or TT. A clinical trial conducted on 268 Chinese children, of which 49 had IDA and 24 had TT, shows >98% sensitivity and specificity for diagnosing anemia, with 81% sensitivity and 86% specificity for discriminating IDA and TT. The majority of the misdiagnoses are IDA patients with particularly severe anemia, possibly requiring hospital care. Therefore, in a screening paradigm where anyone testing positive for TT is sent to the hospital for gold-standard diagnosis and care, we maximize patient benefit while minimizing use of scarce resources.
Introduction
Anemia is a wide-spread and persistent public health concern. Estimates of the global prevalence of anemia place the burden at approximately 1/4 to 1/3 of the world's population, primarily concentrated in low-resource settings with poor access to healthcare.1,2 Despite anemia's vague clinical manifestation (fatigue, pale skin, tingling in limbs), anemia carries serious health risks, including slowed cognitive development in children,3,4 significantly increased mortality for mother and child during pregnancy,5,6 reduced productive work capacity,7 and increased susceptibility to infection,8 with anemia being an independent predictor of mortality in the elderly.9Anemia can have many underlying causes. In this work we are primarily concerned with nutritional and genetic causes. The most common form of anemia worldwide is iron deficiency anemia (IDA), which can be easily treated with iron supplementation. To address the heavy global burden of anemia, some researchers have explored widespread, population-level iron supplementation,10 including iron-fortified staple crops such as millet and rice.11 However, anemia persists as a public health issue due to the potential dangers of iron over-supplementation. The famous Pemba study, found that widespread iron supplementation in areas where genetic anemias are prevalent led to an overall adverse outcome for subjects who received supplementation but were already iron replete,12 with this result confirmed in additional clinical trials.13–15 While the cause of iron-associated toxicity is not fully elucidated, it is believed to be related to the fact that iron supplements bypass the body's typical mechanisms for iron extraction and storage from food, increasing serum iron levels and interfering with inflammatory and other processes in the body,16 including interfering with pregnancy,17 and increasing susceptibility to and severity of Plasmodium falciparum malaria.18 This is particularly critical for areas where Thalassemia trait (TT) is endemic. TT is a collection of genetic anemias where the body has a reduced capacity for synthesis of either the α, β, or δ chain of hemoglobin. TT carriers have a markedly reduced capacity to process iron, and therefore excess iron can easily lead to toxic iron overload.19,20
In many parts of the world genetic anemias can be highly prevalent. For example, in South-eastern China, estimates of TT prevalence are greater than 10% of the population.21,22 Thus, iron supplementation must be accompanied by population-level screening to determine anemia status in order to safely deliver potential benefits without risk to the otherwise healthy. Point of care technologies to screen for anemia have a long history, with methods such as Tallquist's paper-based colorimetric scale having nearly 100 years of use.23 Methods have traditionally focused on measuring hemoglobin concentration, with commercial point-of-care assays such as HemoCue24 already part of established clinical practice. Newer noninvasive tests of hemoglobin concentration based on diffuse light propagation through tissue are also under development and have seen limited deployment,25 while paper-based assays have also seen renewed interest.26 However, these methods all rely on hemoglobin measurements that cannot determine anemia type, rendering it of limited use for supplementation purposes in areas where genetic anemias are common.
Clinical tests for nutritional deficiency measure serum iron, serum ferritin, zinc protoporphyrin, and other chemical markers. Hennig et al. have developed a non-invasive method of screening for iron deficiency by determining serum ferritin concentration using autofluorescence of zinc protoporphyrin (ZPP) measured in the inner lip.27 However, ZPP levels can fluctuate with inflammation and other disorders, and thus as a screening method it lacks sensitivity. In developed countries with low levels of hemoglobinopathies and parasitic illnesses, ZPP has shown promise,28 but elsewhere it has limited diagnostic ability29,30 with some cautioning against its use as a screening indicator.31 Meanwhile, Srinivasan et al. recently reported a paper-based test of serum iron using a cell phone as a colorimetric reader, however with rather poor accuracy when used in whole human blood.32 Further, neither of these methods test for the presence of genetic disorders. Thus, multiparametric tests that screen for, and differentiate, both iron and genetic status are still needed.
The most robust method for testing genetic status is through gel electrophoresis or polymerase chain reaction (PCR). However, these tests require highly trained operators working in well-staffed clinical laboratories, rendering them impractical for population-level screening in areas where genetic anemias are common. When considering genetic anemias, besides reductions in hemoglobin concentrations and alterations in hemoglobin structure, these anemias also manifest through altered red cell morphology (with the crescent-shaped blood cells of sickle disease being the most famous example). For TT, researchers have long proposed using cell morphology, including mean cell volume (MCV), red cell distribution width (RDW), and mean cell hemoglobin concentration (MCHC) as a sensitive and specific method for anemia screening.33,34 We previously reported that quadratic discriminant analysis (QDA) applied to the three red cell parameters MCV, RDW, and MCHC outperformed established indices in discriminating healthy from anemic patients, and IDA from TT patients in Chinese children.35 However, these parameters are currently measured in the hospital by a complex flow cytometry system that requires regular maintenance and operation by a highly trained user. This makes their measurement by standard methods unsuitable for wide-spread population-level screening. Further, variations in genetic profiles worldwide also lead to varying performance of established diagnostic indices in different populations. MCV, RDW, and MCHC are related to the size, polydispersity, and average refractive index of red blood cells, respectively. Elastic light scattering is an established metrology method with nanometer-scale precision that can extract exactly these parameters from polydisperse suspensions such as latexes, nanoparticles, as well as biological cells.36–38 We previously demonstrated the proof-of-concept of a cost-effective red cell analyzer for measuring light scattering from whole blood, without sample flow or any moving parts, to quickly determine red cell morphology.35,37 However, as our prior work was primarily focused on establishing, through historical review, that cell morphology could accurately separate anemia types, the validation of our instrument was strictly limited to a 10-patient proof of concept study of healthy adult subjects.
In this study we expand on our prior work through three advances: (1) a full-scale clinical study on more than 200 pediatric subjects, including a substantial fraction suffering from IDA and TT. (2) A machine-learning based analysis scheme, not previously reported on elastic light scattering data, which improves both robustness and accuracy compared with our prior reported physics-based model. (3) Improved construction of our system to enable it to be transported out of a laboratory setting, enabling all of the measurements to be performed at a field site. The results show that the sensitivity and specificity using our simple instrument coupled with machine learning methods outperforms prior results using established morphometric indices and gold-standard laboratory equipment. Further, our method is easy to perform, requiring only 10 μL of blood that is simply obtained via finger stick or heel prick, and has a per-test cost of ∼US$1. This makes it amenable to operation by minimally trained users in field settings, as phlebotomy is not required. It gives results in minutes, allowing relatively high throughput for large population screening. The high sensitivity and specificity of the method, particularly for separating healthy and anemic subjects, indicates it holds great promise for use as a wide-spread screening method for nutritional and genetic anemias in Southeast Asia and elsewhere that TT and IDA are endemic.
Materials and methods
Collection of clinical data and reference laboratory testing
In order to test the feasibility of our device, blood was tested from 268 children at the Children's Hospital of Chongqing Medical University, including 195 healthy children, 49 children with IDA and 24 with TT from December 2017 to February 2018. Our study was approved by the Ethics Committee of the Children's Hospital of Chongqing Medical University, approval number (2016) . Our experiments were performed using discarded, anonymized samples that were collected as part of routine clinical practice at the Children's Hospital of Chongqing Medical University and not for the purposes of this study. Therefore, informed consent was not required.
. Our experiments were performed using discarded, anonymized samples that were collected as part of routine clinical practice at the Children's Hospital of Chongqing Medical University and not for the purposes of this study. Therefore, informed consent was not required.
WHO diagnostic criteria were used to distinguish different types of anemia. Patients 6 months to 6 years old with hemoglobin less than 110 g L−1 and those 6 to 14 years old with hemoglobin less than 120 g L−1 were considered anemic. For diagnosis of IDA, the serum iron of patients must be less than 11 μmol L−1. For deletion α-thalassemia patients, polymerase chain reaction reverse dot blot (PCR-RDB) technology was used to detect the −α3.7, −α4.2 and −SEA α-thalassemia deletion genes. For mutation α-thalassemia patients, PCR-RDB technology was used to detect the common Quong Sze (QS), Constant spring (CS) and Westmead (WS) mutation sites. For β-thalassemia patients, PCR-RDB technology was used to detect the following common mutation sites and start codons: CD41-42(−TCTT), IVS-2-654 C → T, CD17 A → T, -28 A → G, CD26 G → A, CD71-72(+A), CD43 G → T, -29 A → G. PRC-RDB was also used to identify the following nine rare mutation sites: ATG → AGG, CD14-15(+G), CD27-28(+C), -32 C → A, -30 T → C, IVS-1-1 G → T, IVS-1-5 G → C, CD31(−C), CAP +40−+43 (−AAAC).
After being collected, blood samples were stored in an ethylene diamine tetra-acetic acid (EDTA)-coated anticoagulation tube. Reference clinical values of red cell parameters were measured using Sysmex XE-2100 hematology analyzer, a specialized flow cytometer where blood is split into multiple measurement channels and analyzed using a combination of fluorescence, forward- and side-scattered light, and electrical impedance. Serum iron was measured using a Johnson & Johnson VITROS 5.1 FS biochemical analyzer. Genetic testing was performed using an ABI Verity PCR amplifier, UVP HB-100 hybridizer, and Bio-Rad electrophoresis and gel imaging systems with its supporting reagents. Thalassemia genetic testing utilized a PCR amplifier (Verity, ABI Corporation, USA), HB-1000 hybridizer (UVP Corporation, USA), and electrophoresis and gel imaging systems. In performing these analyses, we utilized Yaneng BIO α-thalassemia and β-thalassemia point mutation gene detection kits.
Elastic light scattering system
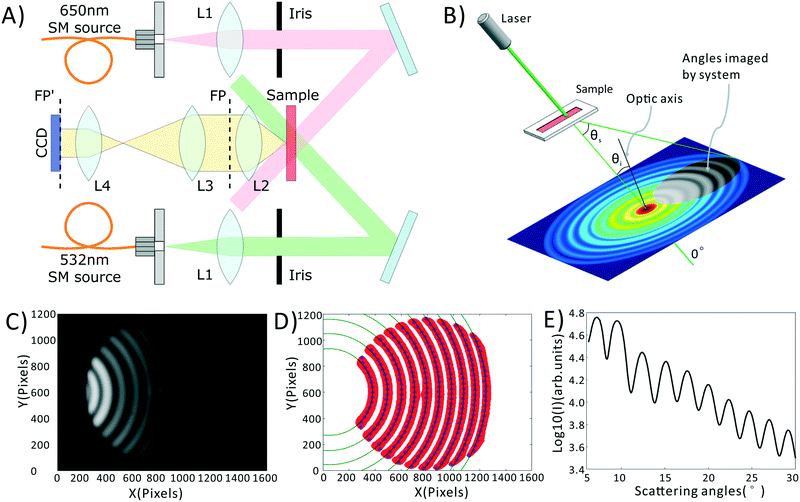
A schematic of our system is shown in Fig. 1A, a photograph of the as-built prototype is shown in ESI† Fig. S1, along with the details of cost and portability of the system. Light from inexpensive 532 nm and 650 nm laser diodes are coupled into single mode fibers to ensure high wavefront quality. Light emerging from these fibers is collimated and the central portion of the beam is selected by irises. The light is then directed at an angle onto a sample chamber containing diluted, sphered whole blood. Incident light is not collected by the detection system, while scattered light is directed onto a 14-bit CCD camera (Microvision, EM200, China). Light incident on a collection of spheres gives rise to a scattering pattern of circular fringes as seen in Fig. 1B and C, whose spacing, fringe contrast, and intensity can be related to the mean scatterer size, scatterer polydispersity, and average scatterer refractive index. The optical arrangement is designed to capture this angularly-dependent scattering pattern by imaging the Fourier plane of the collection lens (L2) onto the CCD with an appropriate magnification (0.24× in our system). In the Fourier plane, scattering angle θs is mapped to the radial coordinate of a polar coordinate system, as shown in Fig. 1B. The zero degree scattering is defined by the propagation direction of the incident beam, while our optical system collects the forward-directed portion of the 4π-steradian sphere of scattering angles. Compared to our prior-reported system,35 the utilized wavelengths have been changed, and the optical system has been redesigned to eliminate a dichroic mirror, reducing cost while minimizing wavefront aberrations that can interfere with the generation of a clean scattering pattern.Blood preparation
In order to obtain the most robust estimates of cell morphology, we dilute the blood, such that each photon passing through the sample undergoes at most one scattering event before reaching the detector. We also sphere the red blood cells using an isovolumetric sphering buffer such that their scattering is orientation independent.39,40 A photographic depiction of the blood preparation process is given in the ESI† Fig. S2. Briefly, 10 μL of whole blood is diluted 300 times in phosphate buffered saline (PBS) containing 0.26 μmol sodium dodecyl sulfate (SDS). SDS is an anionic surfactant which intercalates in the red cell membrane altering the surface tension of blood cells and forcing them into a uniform spherical shape. 10 μL of this diluted sample is then placed within a disposable, 100 μm thick sample chamber (Life Technologies, C10228) and measured. The measurement process consists of taking images at both the green and red wavelengths, with a total measurement time of about 2 minutes. These images are then averaged via a process described in the Data Processing section, below, to obtain the final data, shown in Fig. 1C.Data processing
All data processing and analysis was performed using MATLAB (R2017a, The MathWorks, Natick, MA). Statistical comparisons were performed using SPSS 13.0 (IBM, Armonk, NY). Prior to regression and classification analysis, raw data was converted from two-dimensional images into one-dimensional scattering patterns, as shown in Fig. 1C–E. Fig. 1C is the original scattering image obtained by the CCD camera. First, we subtract a constant offset representing the average dark noise level in the camera. Then we use an adaptive binarization algorithm to identify each fringe in the scattering pattern (shown as the red region in Fig. 1D). Following this we use a polynomial fitting algorithm to calculate the X position of maximum intensity for each Y position in each fringe (shown as the blue points in Fig. 1D). Finally, we use a least squares circle-fitting algorithm applied to the blue points to find the best-fitting circles for each fringe (shown in green in Fig. 1D) and use this to determine each fringe's center point. Using the average center position among all fringes, and angle calibration information obtained using a NIST-traceable polystyrene sphere sample (see the ESI† Fig. S3), we can determine the scattering angle for every point in the scattering pattern. This allows us to azimuthally average the scattering pattern due to its circular symmetry. We take the azimuthal median value, which neglects streaks in the scattering pattern caused by scratches in the plastic sample chamber. The final averaged scattering curve is shown in Fig. 1E.As described later in the text, PLS regression was used to extract clinical parameters from the scattering data, and was implemented using a linear kernel. PCA–SVM and QDA were used to classify the samples as healthy, IDA, or TT. PCA–SVM was performed using a radial basis function kernel and standardized variables. PLS regressions, QDA classifications, and PCA–SVM classifications were all validated using 10-fold cross validation, where 90% of the data is used to construct the regression or classification model, and the remaining 10% is tested. The calibration and testing procedure is repeated 10 times until all samples have been used as both calibration and test samples.
Results and discussion
Overview of clinical data
Table 1 presents the major descriptive statistics of the 268 patients analyzed in our pilot study. A complete table including age and gender breakdowns is provided in the ESI† Table S1. Significance testing between two groups was conducted with the Bonferroni test in the case of homogeneous variances, and with Dunnett T3 for inhomogeneous variances. The Chi-square test and Fisher exact test were used to compare the rates of multiple groups for continuous and categorical variables (age group and sex), respectively. All tests were performed at an α = 0.05 level of significance. There was no statistically significant difference in sex between groups (p > 0.05). There were significant differences in the age and age composition of each group (p < 0.01), as anemia is most common among infants and young children in China, and tends to decrease with age. The differences between MCV, MCHC and RDW for anemic patients of any kind versus healthy controls (HC group) were statistically significant. Furthermore, the MCV, was statistically different between IDA and TT groups, as expected based on prior results.| Variable | HC | IDA | TT |
|---|---|---|---|
| a Significantly different compared with HC group, p < 0.05. b Significantly different compared with IDA group, p < 0.05. | |||
| No. of samples | 195 | 49 | 24 |
| MCV (fL) | 85.50 ± 3.35 | 70.98 ± 7.79a | 63.15 ± 6.56ab |
| MCHC (g L−1) | 32.72 ± 0.73 | 31.61 ± 1.91a | 31.02 ± 0.93a |
| RDW (%) | 13.02 ± 0.78 | 16.44 ± 3.25a | 16.72 ± 2.04a |
Extracting red cell morphology from elastic scattering curves using partial least squares
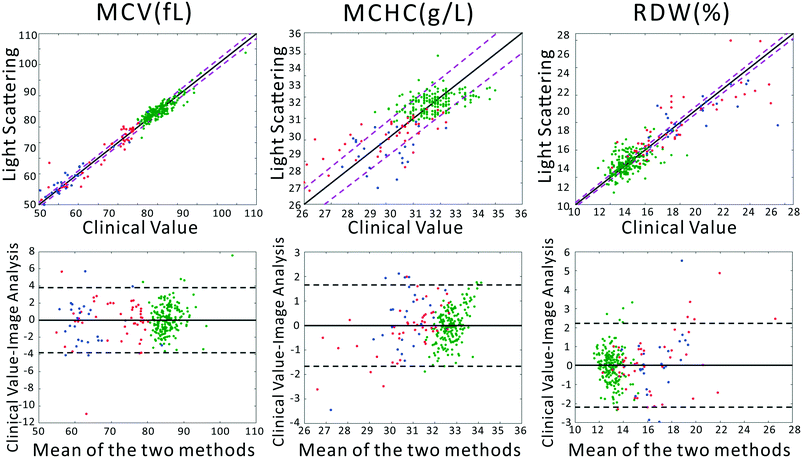
To confirm that our light scattering system can accurately report red cell size and refractive index, we extracted the MCV, MCHC, and RDW from the scattering patterns. Previously, we utilized a strict physical model to fit the scattering patterns. In that model, theoretical scattering from various size distributions are simulated, and the best fit to the experimental data is determined. However, in our testing we discovered that the physics-based model was highly intolerant of slight deviations of our pattern from theory, caused by variations in optical throughput at different angles, and slight sample-dependent backgrounds. Therefore, we utilized the chemometric method partial least squares (PLS) regression to correlate changes in the scattering patterns with clinical parameters. A full introduction to PLS can be found in the classic paper of Haaland and Thomas.41 It should be acknowledged that PLS regression generally assumes a linear model correlating observed signals and the underlying variables. This would be the case for, say, Raman spectra of a complex chemical mixture. In our measurements the scattering pattern can be thought of as a linear combination of scattering patterns from all individual scatterers. However, the required model rank for such a complete model is much too large. Despite this, in our dataset, maximum model accuracy was obtained using a model rank of 12, beyond which adding additional vectors to the PLS model did not increase accuracy. We note that due to the modest size of the dataset, particularly among diseased subjects, the errors must be interpreted as the errors of cross validation. However, as we show in the ESI,† the ultimate performance of the PLS-extracted values to discriminate anemia status does not strongly depend on the PLS model rank.A comparison between the clinical values and the PLS predictions based on the scattering patterns are shown in Fig. 2. The top row shows the correlation between our method and the clinical analyzer, while the bottom row presents the results of a Bland–Altman analysis. The results of our analysis on the three groups of blood samples demonstrates quite close agreement with clinical results, especially for MCV and MCHC, where the majority of the points fall within the 95% CI of the clinical analyzer. This agreement is in spite of the fact that clinical analyzers measure cells one at a time using complex flow cytometry, guaranteeing highly accurate results. By contrast, our method requires no flow or moving parts and measures population-level information in a single shot. Therefore we obtain highly accurate information despite using substantially simpler instrumentation.
These extracted parameters can then be used to separate healthy and anemic subjects, as well as IDA from TT subjects. Further, these values may find use in other clinical tasks such as in diagnosis or monitoring of other diseases known to alter cell morphology, such as macrocytic anemias due to liver dysfunction, B12 or folate deficiencies.42
Anemia screening using light scattering
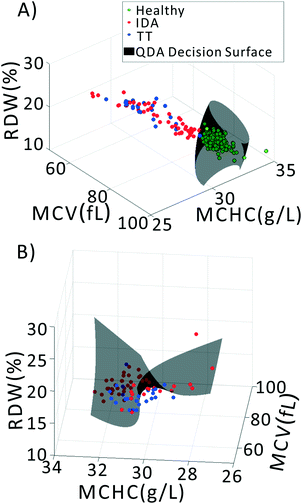
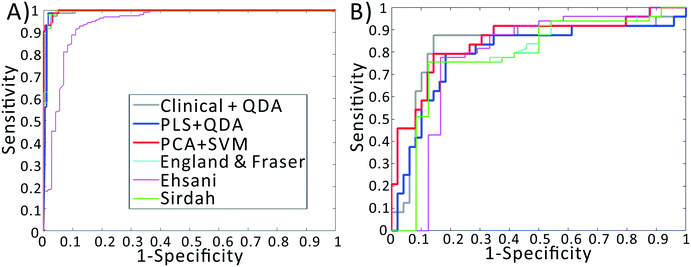
We previously demonstrated that using quadratic discriminants analysis (QDA), healthy, IDA, and TT samples could be separated using just three clinical parameters: MCV, MCHC, and RDW, as measured by a gold-standard analyzer. Using the results from our PLS analysis, we generated QDA decision surfaces to separate healthy and anemic patients, and to separate IDA and TT. The calculated decision boundaries are shown as black shaded surfaces in Fig. 3. We performed an identical QDA analysis using the MCV, MCHC, and RDW values determined by the gold standard analyzer (surfaces shown in the ESI† Fig. S4). Receiver operating characteristic (ROC) curves were generated to analyze the performance of each method for both separating healthy and anemic subjects and for discriminating between IDA and TT. These are shown in Fig. 4A and B, respectively. We can see that for discriminating healthy vs. anemia, both the gold-standard parameters (grey line) and the PLS-determined parameters (blue line) have excellent performance, reaching nearly 100% sensitivity and specificity, as seen in Table 2, which tabulated area under the curve (AUC), sensitivity, specificity, and Youden's index (YI)43 for each curve in Fig. 4A. However, when considering IDA vs. TT, the performance of the PLS-determined values drops somewhat. This is due to our light scattering system having slightly higher error in determining MCHC relative to the gold standard method. As shown in the ESI† Fig. S5, for IDA patients there is a linear relationship between MCV and hemoglobin. Thus, IDA patients with severe anemia (HGB lower than 90 g L−1) have MCV values similar to TT subjects. The major parameter separating severe IDA subjects and TT subjects is a small difference in MCHC. A potential solution to this dilemma would be to set up a second measurement channel that determines the absorption of the sample to provide a separate (and more accurate) measure of hemoglobin.44,45 A tabulation of performance metrics for each curve in Fig. 4B is shown in Table 3.| Index | AUC | Sens | Spec | YI |
|---|---|---|---|---|
| CLI + QDA | 99.46 | 97.44 | 97.26 | 0.94 |
| PLS + QDA | 99.28 | 98.46 | 98.63 | 0.97 |
| PCA + SVM | 99.75 | 99.49 | 93.15 | 0.93 |
| EF | 98.79 | 95.89 | 99.49 | 0.95 |
| E | 94.00 | 80.82 | 96.41 | 0.77 |
| Si | 98.94 | 95.89 | 99.49 | 0.95 |
| Index | AUC | Sens | Spec | YI |
|---|---|---|---|---|
| CLI + QDA | 83.50 | 87.50 | 85.71 | 0.73 |
| PLS + QDA | 79.59 | 79.17 | 81.63 | 0.61 |
| PCA + SVM | 84.86 | 81.17 | 85.71 | 0.67 |
| EF | 78.53 | 75.51 | 87.50 | 0.63 |
| E | 78.23 | 87.67 | 66.67 | 0.54 |
| Si | 78.32 | 75.51 | 87.50 | 0.63 |
As described above, PLS expects a linear model between the observed data and underlying latent variables. This assumption is violated to some degree in our dataset, potentially limiting the PLS performance. While the PLS-determined clinical values are useful for clinical interpretation, our goal is simply classification of a sample into healthy, IDA, or TT. Therefore, another option is to forgo the intermediate step of using PLS to extract the red cell parameters, and create a machine learning model that directly uses the raw scattering data to classify the patients into healthy, IDA, or TT. This has the advantage of not requiring any model of the data but relying purely on pattern matching. A principal component analysis decomposition of the dataset shows that even the first three principal component scores demonstrate strong visual separation of the data into healthy, IDA, and TT groups (see ESI† Fig. S6), indicating that a classification method based on a simple PCA decomposition of the raw data may have good performance.
To implement this, we created a principal components analysis–support vector machines (PCA–SVM) classification model starting from the raw data, and validated using 10-fold cross validation. For each round of validation, the PCA decomposition utilized only training data, preventing any information from the test set from being used in the calibration process. The first 10 principal component scores for each sample were used to create the SVM classification model. The remaining test samples were projected into the PCA space defined by the calibration set, and then classified using the established SVM model. As seen in the red line in Fig. 4B, the PCA–SVM model outperforms the PLS–QDA model, with an AUC similar to the QDA model using the gold-standard clinical data, albeit with somewhat reduced sensitivity. Similarly to the PLS validation, the optimum number of PC scores to pass to SVM was selected via cross validation. However, as detailed in the ESI,† the PCA–SVM performance does not strongly vary with model rank, indicating the robustness of the method.
Our results can also be compared with previously developed diagnostic functions that use red cell morphology to discriminate IDA and TT. While several diagnostic functions have been reported in the literature, our prior results have indicated the top-performing indices are:
(1) England and Fraser index (EF): MCV-RBC-(5 *Hb)-5.19;46
(2) Ehsani index (E): MCV-10*RBC;47 and
(3) Sirdah index (Si): MCV-RBC-3*Hb.48
Note that these functions require additional parameters, typically including the red cell count and the hemoglobin value, available only using complex instrumentation. When examining the ROC curves and Tables 2 and 3, we see that, despite using values determined by complex gold-standard clinical equipment, these indices all have lower performance than our method for discriminating IDA and TT, indicated by lower AUC and YI values.
Conclusions
In order to address the need for targeted prescription of iron supplementation in areas of the world where both IDA and Thalassemia trait are endemic, a large-population screening technique that can separate nutritional and genetic anemias is needed. In this paper we have addressed this challenge by presenting a screening method based on measurement of red cell morphology that can accurately screen for anemia and separate anemia into IDA and TT in Chinese children. Advantages of our system over traditional methods of determining red cell morphology is that ours requires: (i) only 10 μL of blood, easily extracted by a finger stick or heel prick; (ii) has no flow or other moving parts, meaning it should not require maintenance and would be optimal for use by an untrained user; (iii) is small enough to be portable and placed in small clinics, with potential for further size reductions in the future; and (iv) is more than one order of magnitude less expensive than current clinical instrumentation, increasing its utility for widespread deployment in low resource settings. By exploiting a Fourier imaging scheme, a large number of scattering angles can be captured simultaneously with azimuthal redundancy in the data, yielding high information content with high SNR. Using a partial least squares model, we are able to extract the mean cell volume, red cell distribution width, and mean cell hemoglobin concentration with high accuracy compared a clinical gold standard blood analyzer, although inaccuracy in MCHC determination does lead to confusion between TT subjects and those with severe IDA.Data from our system was used to separate healthy, IDA, and TT subjects in a large cohort of Chinese children, with excellent performance. In particular, the performance of our system using a support vector machines classification model was approximately equivalent to classification using raw data from the gold standard instrument, further confirming that our system can accurately probe red cell morphology, despite not requiring any flow or other moving parts. The majority of misclassifications of IDA vs. TT (∼75% of misclassifications) were IDA patients that were misclassified as TT. As the majority of the classification power in our data is found in the MCV, and as MCV for IDA subjects is correlated with hemoglobin concentration, the IDA patients misdiagnosed as TT may indicate moderate to severe anemia.
In a wide-scale population screening program for anemia, the goal is to provide the greatest benefit to the population while minimizing use of scarce resources. A proposed paradigm is to measure all subjects using the portable light scattering instrument. Based on the red cell morphology, subjects classified as healthy or those with IDA will be discharged or prescribed iron supplementation, respectively. Those registering as TT will be sent to the hospital for further gold-standard testing. Given that the IDA misclassifications are typically those IDA subjects with more serious anemia, and given that those with severe anemia may already be suffering deleterious effects of iron deficiency, evaluation in a hospital setting may be called for. Therefore, if all patients who register as TT on our instrument are sent for gold-standard testing, we can speculate that the “wasted” resources of IDA patients being sent to the hospital may be mitigated by the fact that their symptoms may warrant observation by a doctor. Additionally, the sensitivity and specificity of our system may be improved by adding an additional measurement channel to probe hemoglobin through simple absorbance measurements.
Further, in low-resource settings IDA often persists despite nutritional interventions due to helminth and other parasitic infections of which IDA is merely a symptom.49 Therefore, our system can act not only as a screening tool, but also as a method to conveniently monitor response of patients to therapy, identifying those patients for whom nutritional interventions are not sufficient.
Finally, as described in the introduction, point of care tests of iron status are currently under active research. These chemical tests may be combined synergistically with the morphological assay presented here, providing orthogonal and multiparametric information about anemia status at the point of care.
Author contributions
LT, JK, KC, and ZJS were responsible for methodology and software. LT was responsible for investigation and data curation using our prototype system, while XC was responsible for investigation and data curation using the clinical gold standard methods. LT and ZJS were responsible for formal analysis and visualization. KC, HD, and ZJS were responsible for conceptualization, resources, supervision, and project administration. HD and ZJS were responsible for Funding Acquisition. All authors contributed to writing and editing the paper.Conflicts of interest
The authors state that there are no conflicts to declare.Acknowledgements
Z. J. S. acknowledges funding from The Ministry of Science and Technology of the People's Republic of China National Key Research and Development Program (2016YFA0201303), and the 1000 Young Talents Global Recruitment Plan. H. D. and Z. J. S. acknowledge funding support from the Chongqing Municipal Science and Technology Commission (award cstc2017shmsA130083).References
- N. Milman, Ann. Hematol., 2011, 90, 369–377 CrossRef PubMed.
- G. A. Stevens, M. M. Finucane, L. M. De-Regil, C. J. Paciorek, S. R. Flaxman, F. Branca, J. P. Pena-Rosas, Z. A. Bhutta, M. Ezzati and N. I. M. S. Grp, Lancet Glob. Health, 2013, 1, E16–E25 CrossRef PubMed.
- S. Chang, L. Wang, Y. Wang, I. D. Brouwer, F. J. Kok, B. Lozoff and C. Chen, Pediatrics, 2011, 127, e927–933 CrossRef PubMed.
- R. C. Carter, J. L. Jacobson, M. J. Burden, R. Armony-Sivan, N. C. Dodge, M. L. Angelilli, B. Lozoff and S. W. Jacobson, Pediatrics, 2010, 126, e427–434 CrossRef PubMed.
- A. Levy, D. Fraser, M. Katz, M. Mazor and E. Sheiner, Eur. J. Obstet. Gynecol. Reprod. Biol., 2005, 122, 182–186 CrossRef PubMed.
- C. Breymann, Semin. Hematol., 2015, 52, 339–347 CrossRef PubMed.
- J. D. Haas and T. T. Brownlie, J. Nutr., 2001, 131, 676S–688S CrossRef CAS PubMed , discussion 688S-690S.
- J. R. Dunne, D. Malone, J. K. Tracy, C. Gannon and L. M. Napolitano, J. Surg. Res., 2002, 102, 237–244 CrossRef PubMed.
- O. Paltiel and A. M. Clarfield, Can. Med. Assoc. J., 2009, 181, 129–130 CrossRef PubMed.
- A. M. Prentice, Y. A. Mendoza, D. Pereira, C. Cerami, R. Wegmuller, A. Constable and J. Spieldenner, Nutr. Rev., 2017, 75, 49–60 CrossRef PubMed.
- J. L. Finkelstein, J. D. Haas and S. Mehta, Curr. Opin. Biotechnol., 2017, 44, 138–145 CrossRef CAS PubMed.
- S. Sazawal, R. E. Black, M. Ramsan, H. M. Chwaya, R. J. Stoltzfus, A. Dutta, U. Dhingra, I. Kabole, S. Deb, M. K. Othman and F. M. Kabole, Lancet, 2006, 367, 133–143 CrossRef CAS.
- S. Soofi, S. Cousens, S. P. Iqbal, T. Akhund, J. Khan, I. Ahmed, A. K. M. Zaidi and Z. A. Bhutta, Lancet, 2013, 382, 29–40 CrossRef CAS.
- S. Zlotkin, S. Newton, A. M. Aimone, I. Azindow, S. Amenga-Etego, K. Tchum, E. Mahama, K. E. Thorpe and S. Owusu-Agyei, JAMA, J. Am. Med. Assoc., 2013, 310, 938–947 CrossRef CAS PubMed.
- J. Veenemans, P. Milligan, A. M. Prentice, L. R. A. Schouten, N. Inja, A. C. van der Heijden, L. C. C. de Boer, E. J. S. Jansen, A. E. Koopmans, W. T. M. Enthoven, R. J. Kraaijenhagen, A. Y. Demir, D. R. A. Uges, E. V. Mbugi, H. F. J. Savelkoul and H. Verhoef, PLoS Med., 2011, 8, e1001125 CrossRef CAS PubMed.
- O. Fontaine, Food Nutr. Bull., 2007, 28, S621–S627 CrossRef.
- T. O. Scholl, Am. J. Clin. Nutr., 2005, 81, 1218s–1222s CrossRef CAS PubMed.
- M. A. Clark, M. M. Goheen, A. Fulford, A. M. Prentice, M. A. Elnagheeb, J. Patel, N. Fisher, S. M. Taylor, R. S. Kasthuri and C. Cerami, Nat. Commun., 2014, 5, 4446 CrossRef CAS PubMed.
- A. Piperno, R. Mariani, C. Arosio, A. Vergani, S. Bosio, S. Fargion, M. Sampietro, D. Girelli, M. Fraquelli, D. Conte, G. Fiorelli and C. Camaschella, Br. J. Haematol., 2000, 111, 908–914 CAS.
- K. Thakerngpol, S. Fucharoen, P. Boonyaphipat, K. Srisook, S. Sahaphong, V. Vathanophas and T. Stitnimankarn, BioMetals, 1996, 9, 177–183 CrossRef CAS PubMed.
- W. Chen, X. Zhang, X. Shang, R. Cai, L. Li, T. Zhou, M. Sun, F. Xiong and X. Xu, BMC Med. Genet., 2010, 11, 31 CrossRef PubMed.
- X. Y. Yao, J. Yu, S. P. Chen, J. W. Xiao, Q. C. Zheng, H. Y. Liu, L. Zhang, Y. Xian and L. Zou, Gene, 2013, 532, 120–124 CrossRef CAS PubMed.
- H. L. Alt, Am. J. Clin. Pathol., 1934, 4, 354–361 CrossRef CAS.
- F. Sanchis-Gomar, J. Cortell-Ballester, H. Pareja-Galeano, G. Banfi and G. Lippi, J. Lab. Autom., 2013, 18, 198–205 CrossRef PubMed.
- C. R. Crowley, N. W. Solomons and K. Schumann, Adv. Nutr., 2012, 3, 560–569 CrossRef CAS PubMed.
- X. Yang, N. Z. Piety, S. M. Vignes, M. S. Benton, J. Kanter and S. S. Shevkoplyas, Clin. Chem., 2013, 59, 1506–1513 CrossRef CAS PubMed.
- G. Hennig, C. Homann, I. Teksan, U. Hasbargen, S. Hasmuller, L. M. Holdt, N. Khaled, R. Sroka, T. Stauch, H. Stepp, M. Vogeser and G. M. Brittenham, Nat. Commun., 2016, 7, 10776 CrossRef CAS PubMed.
- Z. G. Mei, R. C. Flores-Ayala, L. M. Grummer-Strawn and G. M. Brittenham, Nutrients, 2017, 9, 557 CrossRef PubMed.
- M. N. Mwangi, K. S. Phiri, A. Abkari, M. Gbane, R. Bourdet-Sicard, V. A. Braesco, M. B. Zimmermann and A. M. Prentice, Nutrients, 2017, 9, 576 CrossRef PubMed.
- M. B. Zimmermann, L. Molinari, F. Staubli-Asobayire, S. Y. Hess, N. Chaouki, P. Adou and R. F. Hurrell, Am. J. Clin. Nutr., 2005, 81, 615–623 CrossRef CAS PubMed.
- M. N. Mwangi, S. Maskey, P. E. Andang o, N. K. Shinali, J. M. Roth, L. Trijsburg, A. M. Mwangi, H. Zuilhof, B. van Lagen, H. F. Savelkoul, A. Y. Demir and H. Verhoef, BMC Med., 2014, 12, 229 CrossRef PubMed.
- B. Srinivasan, D. O'Dell, J. L. Finkelstein, S. Lee, D. Erickson and S. Mehta, Biosens. Bioelectron., 2018, 99, 115–121 CrossRef CAS PubMed.
- E. Silvestroni and I. Bianco, Br. Med. J., 1983, 286, 1007–1009 CrossRef CAS PubMed.
- C. Shen, Y. M. Jiang, H. Shi, J. H. Liu, W. J. Zhou, Q. K. Dai and H. Yang, J. Pediatr. Hematol./Oncol., 2010, 32, e218–222 CrossRef PubMed.
- L. Tong, J. Kauer, S. Wachsmann-Hogiu, K. Chu, H. Dou and Z. J. Smith, Sci. Rep., 2017, 7, 10510 CrossRef PubMed.
- Z. J. Smith and A. J. Berger, Opt. Lett., 2008, 33, 714–716 CrossRef PubMed.
- Z. J. Smith, K. Chu and S. Wachsmann-Hogiu, PLoS One, 2012, 7, e46030 CrossRef CAS PubMed.
- I. Itzkan, L. Qiu, H. Fang, M. M. Zaman, E. Vitkin, L. C. Ghiran, S. Salahuddin, M. Modell, C. Andersson, L. M. Kimerer, P. B. Cipolloni, K. H. Lim, S. D. Freedman, I. Bigio, B. P. Sachs, E. B. Hanlon and L. T. Perelman, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17255–17260 CrossRef CAS PubMed.
- Y. R. Kim and L. Ornstein, Cytometry, 1983, 3, 419–427 CrossRef CAS PubMed.
- D. H. Tycko, M. H. Metz, E. A. Epstein and A. Grinbaum, Appl. Opt., 1985, 24, 1355–1365 CrossRef CAS PubMed.
- D. M. Haaland and E. V. Thomas, Anal. Chem., 1988, 60, 1193–1202 CrossRef CAS.
- P. R. Sarma, in Clinical Methods: The History, Physical, and Laboratory Examinations, ed. H. K. Walker, W. D. Hall and J. W. Hurst, Boston, 1990 Search PubMed.
- V. Bewick, L. Cheek and J. Ball, Crit. Care, 2004, 8, 508–512 CrossRef PubMed.
- T. J. Gao, Z. J. Smith, T. Y. Lin, D. C. Holt, S. M. Lane, D. L. Matthews, D. M. Dwyre, J. Hood and S. Wachsmann-Hogiu, Anal. Chem., 2015, 87, 11854–11862 CrossRef CAS PubMed.
- H. Y. Zhu, I. Sencan, J. Wong, S. Dimitrov, D. Tseng, K. Nagashima and A. Ozcan, Lab Chip, 2013, 13, 1282–1288 RSC.
- J. M. England and P. M. Fraser, Lancet, 1973, 1, 449–452 CrossRef CAS.
- M. Ehsani, A. Darvish, A. Aslani and F. Seighali, Turk. J. Hematol., 2005, 22, 268 Search PubMed.
- M. Sirdah, I. Tarazi, E. Al Najjar and R. Al Haddad, Int. J. Lab. Hematol., 2008, 30, 324–330 CrossRef CAS PubMed.
- J. L. Finkelstein, S. Mehta, C. P. Duggan, D. Spiegelman, S. Aboud, R. Kupka, G. I. Msamanga and W. W. Fawzi, Public Health Nutr., 2012, 15, 928–937 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc00377g |
| This journal is © The Royal Society of Chemistry 2018 |