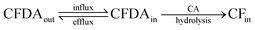Do protocells preferentially retain macromolecular solutes upon division/fragmentation? A study based on the extrusion of POPC giant vesicles
Alessio
Fanti†
a,
Leandro
Gammuto†
a,
Fabio
Mavelli
 b,
Pasquale
Stano‡
b,
Pasquale
Stano‡
 *c and
Roberto
Marangoni
*c and
Roberto
Marangoni
 *ad
*ad
aBiology Department, University of Pisa, Via Derna 1, I-56126 Pisa, Italy. E-mail: roberto.marangoni@unipi.it; Fax: +39 050 2211527; Tel: +39 050 2211525
bChemistry Department, University of Bari, Via E. Orabona 4, I-70125, Bari, Italy
cScience Department, Roma Tre University, Viale G. Marconi 446, I-00146, Rome, Italy
dCNR – Institute of Biophysics, Via G. Moruzzi 1, I-56124, Pisa, Italy
First published on 30th November 2017
Abstract
A key process of protocell behaviour is their recursive growth and division. In order to be sustainable, the latter must be characterized by an even and homogeneous partition of the solute molecules initially present in the parent protocell among the daughter ones. Here we have investigated, by means of an artificial division model (extrusion of giant lipid vesicles) and confocal microscopy, the fate of solutes when a large vesicle fragments into many smaller vesicles. Solutes of low- and high-molecular weight such as pyranine, calcein, albumin-FITC, dextran–FITC and carbonic anhydrase have been employed. Although the vesicle extrusion brings about a release of their inner content in the environment, the results shown in this initial report indicate that macromolecules can be partially retained when compared with low-molecular weight ones. Results are discussed from the viewpoint of the life cycle of primitive cells. In particular, the findings suggest that a similar mechanism operating during the critical step of vesicle growth–division could have contributed to primitive evolution.
Insight, innovation, integrationBy combining experimental and modelling techniques, this study provides the first evidence of macromolecular preferential retention (over small molecules) inside POPC vesicles during vesicle fragmentation (division) by mechanical extrusion. The true heterogeneous nature of vesicles originated by spontaneous self-assembly (“vesicle diversity”) is also highlighted. Its relevance is twofold. First, when lipid vesicles are intended as primitive cell models, this result suggests how and why macromolecules are entrapped, stored, and transmitted over protocell division, allowing the emergence of early cells. Second, this work contributes to the ongoing research on lipid vesicles used as synthetic cell-like structures in bottom-up synthetic biology, by a detailed characterization of giant vesicle extrusion (which can be a viable route to prepare solute-filled conventional vesicles otherwise difficult to obtain). |
1 Introduction
One of the major goals of synthetic biology is the creation of synthetic minimal cell models for addressing open questions in the biology domain and for developing new tools for biotechnology.1–3 Ongoing research on primitive cell models and artificial prototype cells (here both indicated as ‘protocells’) benefits from a synthetic biology approach. It adopts the constructive paradigm (understanding by building) and integrates quantitative analysis with mathematical tools. Lipid vesicles (liposomes) are often used to build cellular models of various complexities. These models range from ‘empty’ fatty acid vesicles, for instance those that are able to undergo spontaneous self-reproduction,4–6 up to much more complex systems, such as those hosting in the vesicle lumen the whole transcription–translation biomachinery.7–11When protocells are studied for deciphering some physical aspect of primitive cell formation and proliferation, the capture and the retention of molecular solutes are two fundamental features to consider. With respect to solute capture, it has been shown that when formation of vesicles occurs in a protein- or nucleic acid-solution, vesicles easily entrap these solutes in their lumen.12–14 Recent observations have revealed that under certain conditions, a small number of vesicles are filled with a very high number of solute molecules.15–18
With respect to the second issue (solute retention), the starting, and perhaps obvious, consideration is that in order to proliferate, protocells have to grow and divide. The self-reproduction of fatty acid vesicles has been reported,4–6 but with few exceptions5,19–22 not much interest has been devoted to understanding what happens to the encapsulated molecules during growth/division. Starting from a functional ‘mother’ protocell, similarly functional ‘daughter’ protocells can be obtained only if the molecules initially contained in the mother are evenly redistributed among the daughters. Protocell proliferation can be seriously hampered by solute loss or unpaired solute redistribution. In other words, while solute capture is a fundamental step for protocell emergence from separated components, protocell self-reproduction (growth/division) must be especially robust with respect to the retention and partition of the entrapped molecules.23
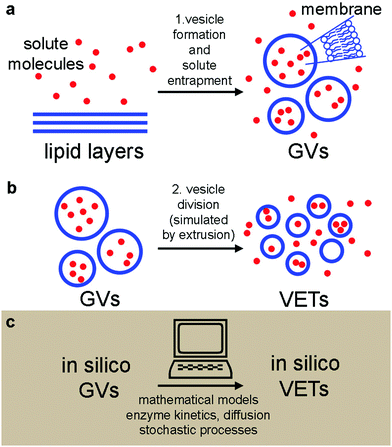
Here we present an experimental and computational study on vesicle formation and solute capture, followed by vesicle fragmentation and solute partition. The study has been carried out to mimic the formation of protocells from another protocell, following a process of growth–division. Our experimental model is based on (i) the spontaneous formation of solute-filled phospholipid giant vesicles (GVs) (Fig. 1a), and (ii) their fragmentation into several small daughter vesicles via a mechanical process24 that simulates protocell self-reproduction21 (Fig. 1b). In other words, we have simply applied the extrusion method as a way to create many small daughter vesicles from large ones (the mothers). Although it has been suggested that such an approach could model protocell division in porous rocks,21 it should be recalled that operating under conditions favouring spontaneous vesicle division, i.e., by addition or production of membrane-forming compounds,6,25–27 would be a better model for addressing the solute retention problem.
Based on the experimentally obtained GV populations, we constructed in silico vesicles undergoing the same transformations as real vesicles (Fig. 1c). In silico vesicle populations strictly obey physico-chemical rules and follow purely random stochastic paths. The in silico vesicles can be useful for hypothesis testing, just by contrasting their behaviour with the experimental outcomes. By combining wet-lab experiments and numerical modelling, here we provide novel evidence on the retention and partition of solutes, in particular with respect to their molecular weight (MW). Larger molecules are retained much better than small molecules. This might suggest that a basic physical mechanism (based on solute size) could have been a source of selective pressure in prebiotic times, favouring the transition from small to large molecules, as the latter ones are better retained during vesicle division. Such a mechanism could operate before the onset of sophisticated control mechanisms of solute partition during the key event of cell reproduction.
2 Results
We have applied a combination of bottom-up synthetic biology and systems biology, blending experimental approaches and theoretical modelling (Fig. 1). The experimental model is based on the preparation of giant lipid vesicles (GVs) by the natural swelling method (Fig. 1a), followed by a mechanical GV division to give conventional sub-micron vesicles by the extrusion technique (VETs) (Fig. 1b). The GVs contained solutes with different MWs (from 0.5 to 150 kDa) and different chemical structures. We have measured the size and content of the vesicles before and after extrusion and compared the results with the null hypotheses:• before extrusion: H0,I, the mean intra-GV solute concentration, 〈CGVs〉, is equal to the bulk concentration, Cbulk, of the solute in the solution, which has been used to prepare the GVs; i.e., 〈CGVs〉 = Cbulk;
• after extrusion: H0,II, the mean intra-VET and the mean intra-GV solute concentrations are equal; i.e. 〈CVETs〉 = 〈CGVs〉.
In addition to H0,I and H0,II, we have also checked additional less-restrictive hypotheses (h0,I and h0,II) based on the likelihood that a certain concentration value belongs or not – in a statistical sense – to a certain ‘parent’ distribution (see Section 5.4 for details). No statistical tests were carried out to compare the GV size distributions, because they derive from a fractionation procedure which likely introduces both a size bias and a variance contribution that cannot be easily estimated.
In parallel to experiments, all physical processes have been simulated by stochastic numerical modelling (Fig. 1c) in order to compare the observed and the simulated patterns. Stochastic analysis is essential in vesicle population analysis, as vesicles always display heterogeneity with respect to size and content.18,28–33 A population of solute-filled GVs has been artificially generated in silico and filled with solutes, based on parameters obtained by experiments. Next, the transformation of GVs into VETs is simulated by taking into account the initial and final size distributions, while the solutes have been partitioned by algorithms that model physical stochastic effects as purely random ones.
2.1 Experimental model
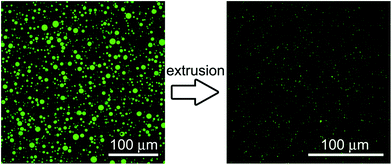
POPC GVs have been produced by the natural swelling method, which consists in the unperturbed swelling of a lipid film in the presence of solutes of interest. Although POPC cannot be considered a primitive lipid for the construction of protocells, it has been often used in studies when the focus is not on the chemical nature of the bilayer, rather on the solute compartmentation.19,20,34,35 Pyranine (0.52 kDa) and calcein (0.62 kDa) have been used as low molecular weight solutes, whereas bovine serum albumin-FITC (BSA–FITC, 69 kDa), dextran–FITC (150 kDa), and carbonic anhydrase (CA, 30 kDa) have been used as macromolecular ones. Pyranine, calcein, BSA–FITC, and dextran–FITC are fluorescent molecules, whose concentration can be easily measured. CA has been quantified by probing its esterase activity,36,37 with the fluorogenic substrate 6-carboxyfluorescein diacetate (CFDA) as discussed separately in Section 2.3.Solute-filled GVs have been easily prepared irrespective of the type and concentration of the solute (pyranine, calcein, albumine-FITC, dextran–FITC, carbonic anhydrase). After fractionation, GVs with an average radius ranging between 2.6 and 4.4 μm are obtained (Table 1), with a positively skewed size distribution (Fig. 3).
| Solutes | GVs | VETs |
|---|---|---|
| Pyranine | 4.4 ± 1.6 (496) | 0.41 ± 0.07 (4394) |
| Calcein | 3.7 ± 1.5 (814) | 0.42 ± 0.13 (7554) |
| BSA–FITC | 3.6 ± 1.1 (265) | 0.46 ± 0.13 (4440) |
| Dextran–FITC | 2.6 ± 0.9 (179) | 0.41 ± 0.07 (9634) |
| CA | 3.2 ± 1.8 (285) | 0.76 ± 0.34 (233) |
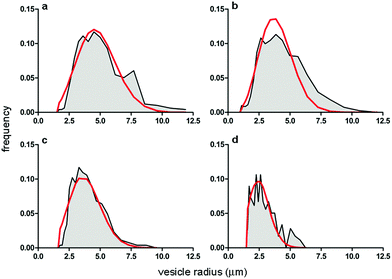 | ||
| Fig. 3 Comparison between the GV size distributions obtained experimentally (grey area) and by numerical modelling (Helfrich distribution, red curve). Size distributions refer to GVs filled with (a) pyranine; (b) calcein; (c) BSA–FITC; and (d) dextran–FITC. Population statistics are reported in Table 1. | ||
According to H0,I (a purely stochastic entrapment scenario), when GVs form by natural swelling the expectation is that the concentration of the solutes initially present in the solution is also found inside the vesicles. This scenario purposely neglects, at least on average, the potential attractive/repulsive solute–solute and solute–lipid interactions which may play a role in the entrapment process. It simply corresponds to a random sampling, with the number of entrapped molecules only determined by the vesicle volume. We expect that, due to the very large size of GVs, the intra-GV solute concentration is equal (or very near) to the bulk solute concentration.
The internal fluorescence of individual GVs was measured by image analysis, and a distribution of concentration was obtained for each population thanks to calibration curves. Fig. 4 (top line) shows the concentration vs. radius dot-plots referring to the four GV populations, one for each fluorescent solute. Most of the GVs containing pyranine, calcein, and BSA–FITC have internal solute concentrations near the expected bulk values of, respectively, 5, 10 and 10 μM (indicated by the dashed blue lines in Fig. 4). The average intra-GV concentrations of these solutes are, respectively, 5.4 ± 0.7 μM, 8.9 ± 1.3 μM, and 8.5 ± 2.1 μM. In contrast, the average intra-vesicle dextran–FITC concentration is 0.79 ± 0.17 μM, much less than the expected value (1.75 μM). This might be due to the considerably high molecular weight of dextran (150 kDa) which could lead to solute exclusion during lipid swelling and vesicle closure.
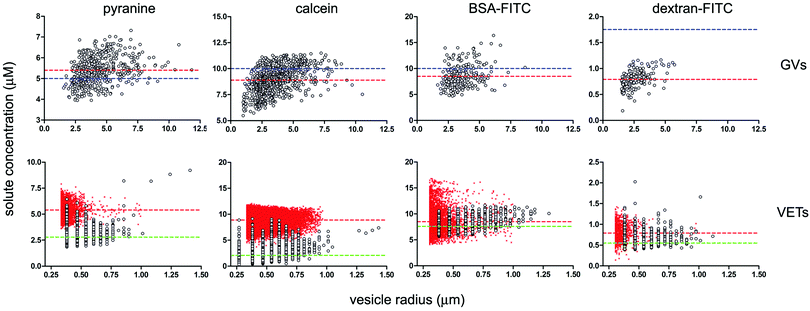 | ||
| Fig. 4 Dependence of solute intra-vesicle concentration on vesicle radius given as bivariate dot-plots. GV data are presented in the top line, VET data in the bottom line; each column refers to a solute (pyranine, calcein, BSA–FITC, dextran–FITC). Experimental data indicated as grey circles; simulated data indicated as red crosses. In the four GV plots on the top, the solute concentrations in bulk solution (referring to the solution used for GV formation) are indicated by dashed blue lines (corresponding to 5, 10, 10 and 1.75 μM for the four above-mentioned solutes). The measured intra-GV solute average concentrations are instead reported as red dashed lines. For the four VET plots on the bottom, the expected solute concentrations inside the VETs (obtained after an ‘ideal’ extrusion) are indicated as red dashed lines (corresponding to the value found inside GVs, namely 5.4, 8.9, 8.5 and 0.79 μM). The average concentration values as obtained by the simulated extrusion are very close to these values (see Table 2). The measured intra-VET average concentrations are indicated as green dashed lines (corresponding to 2.8, 2.1, 7.6 and 0.55 μM). The size cut-off in the case of VETs is due to the optical resolution limit. | ||
The GV data in Fig. 4 (top line) also point to two other facts. First, the solute concentration distribution is quite broad. This is a noteworthy fact, not consistent with random fluctuations around an average value. Fluctuations are proportional to 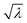 , where λ is the expected average number of entrapped solutes, that scales with the vesicle volume. In our conditions n is typically very large (105–106), so that the relative variability
, where λ is the expected average number of entrapped solutes, that scales with the vesicle volume. In our conditions n is typically very large (105–106), so that the relative variability 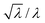 should be below 1%. A much larger variation among intra-GV solute concentrations is observed, suggesting more complex (and heterogeneous) mechanisms of GV formation and solute capture. Second, there is a weak dependence of inner solute concentration on the GV size (this is particularly evident in the case of small GVs). Again, this can be due to different coexisting mechanisms of vesicle formation (larger and smaller GVs originating in different ways). As the deeper investigation about these patterns lies outside the scope of the present paper, we postpone it to future work.
should be below 1%. A much larger variation among intra-GV solute concentrations is observed, suggesting more complex (and heterogeneous) mechanisms of GV formation and solute capture. Second, there is a weak dependence of inner solute concentration on the GV size (this is particularly evident in the case of small GVs). Again, this can be due to different coexisting mechanisms of vesicle formation (larger and smaller GVs originating in different ways). As the deeper investigation about these patterns lies outside the scope of the present paper, we postpone it to future work.
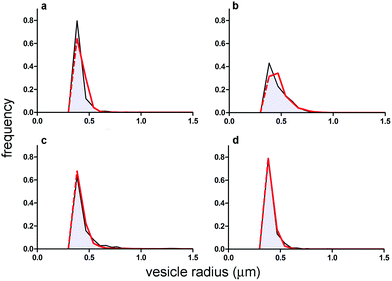 | ||
| Fig. 5 Comparison between VET size distribution as obtained experimentally (grey area) and by numerical modelling (negative exponential distribution, red curve). Size distributions refer to GVs filled with (a) pyranine; (b) calcein; (c) BSA–FITC; and (d) dextran–FITC. Population statistics are reported in Table 1. Note that both experimental and simulated size distributions (the latter being based on the exponential distribution) have been truncated at the resolution limit of the microscope (a red dashed line has been added to the simulated exponential distribution just for the sake of comparison). | ||
As in the GV case, the internal solute concentration has been measured for each vesicle and plotted in Fig. 4 (bottom line). The distribution, in terms of solute concentration (y-axis) is again quite broad, and the dispersion of concentration around the mean increases as the size decreases (the average values are reported as green dashed lines in Fig. 4). This qualitatively fits with the expectations, as the smaller vesicles are expected to be highly diverse with respect to the number of encapsulated solutes. Indeed the term  increases as n decreases (n being proportional to the vesicle volume). From the quantitative viewpoint, however, these intra-VET solute distributions are broader than expected. The reason is that they originate from GVs which are already quite dispersed in terms of internal solute concentration.
increases as n decreases (n being proportional to the vesicle volume). From the quantitative viewpoint, however, these intra-VET solute distributions are broader than expected. The reason is that they originate from GVs which are already quite dispersed in terms of internal solute concentration.
When averaged over the whole VET population, the mean solute concentrations in the case of pyranine, calcein, BSA–FITC, and dextran–FITC are 2.8 ± 0.7, 2.1 ± 1.4, 7.6 ± 1.0 and 0.55 ± 0.1 μM, respectively (Table 2). The comparison between such values and those referring to GVs (compare the dashed green and red lines in Fig. 4), shows that for pyranine and calcein there is a large concentration decrease, whereas for BSA–FITC and dextran–FITC there is a minor decrease. Solutes have been lost during extrusion. Note that the missing number of solute molecules mentioned here is not referring to the well-known volume loss when a large vesicle fragments into many small ones. The intra-VET concentration is reduced because the local composition (per unit of volume) changes during the membrane rupture-and-resealing occurring during the vesicle extrusion.
| Solute | Bulk | Intra-GVs (measured) | Δ(GVs–bulk) | Intra-VET (simulated) | Intra-VET (measured) | Δ(VETs–GVs) | Normalized loss (%) |
|---|---|---|---|---|---|---|---|
| Pyranine | 5 | 5.4 ± 0.7 (496) | +0.4* | 5.4 ± 0.7 (4075) | 2.8 ± 0.7 (4394) | −2.6** | −48 |
| Calcein | 10 | 8.9 ± 1.3 (814) | −1.1* | 9.0 ± 1.2 (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299) 299) |
2.1 ± 1.4 (7554) | −6.8** | −76 |
| BSA–FITC | 10 | 8.5 ± 2.1 (265) | −1.5* | 8.6 ± 2.2 (6103) | 7.6 ± 1.0 (4400) | −0.9* | −11 |
| Dextran–FITC | 1.75 | 0.79 ± 2.1 (179) | −0.96** | 0.82 ± 0.20 (1191) | 0.55 ± 0.11 (9634) | −0.24* | −30 |
| CA | 2 | 1.7 ± 1.0 (233) | −0.3 | 1.7 ± 0.3 (4837) | 1.0 ± 0.6 (368) | −0.7* | −41 |
2.2 Modelling
Intrigued by these observations, we set up a mathematical model that reproduces in all details the processes under investigation, asking whether the retention and the partition of solutes in the crucial moment of vesicle division (here substituted by forced extrusion through a narrow pore) follow theoretical expectations or not.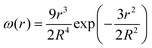 | (1) |
As shown in Fig. 3, there is an excellent agreement between the theoretical and experimental size distributions. The so-obtained in silico population of GVs was filled with solutes according to a Poisson process. The filling is the result of a pure stochastic process where the solute can accumulate randomly and without cooperative effects15 or other kinds of inter-molecular interactions. Like the Helfrich's distribution, also the Poisson probability (p(n) = e−λλn/n!) depends on a single parameter which is the average value λ (n being the number of entrapped molecules). In our simulation λ has been set as the number of molecules expected in the GVS volume, according to H0,I. The concentration of solutes inside GVs is equal, at least on average, to the solute concentration in the bulk (supposed uniform, as for a well-stirred environment). In other words, this is a simple space partition, that rules out any active contribution of the entrapment process. The Poisson process generates a random variability between the solute distribution in the in silico GVs (not shown). While this is a satisfactory procedure for pyranine-, calcein-, and BSA–FITC-containing GVs, it failed to model GVs prepared in the presence of dextran–FITC-containing GVs. For this reason, a new in silico GV population has been produced by setting λ as the average number of dextran–FITC molecules actually found in the vesicle's volume, as determined experimentally (0.79 μM instead of 1.75 μM). This was a mandatory change because in the next step (GV extrusion) the starting point should be a GV population that closely mimics the experimental data.
The comparison between the experimental and simulated size distribution reveals again an excellent agreement (Fig. 5). The simulated intra-VET solute concentrations are instead shown in Fig. 4 (bottom line). Here the small red crosses represent the expected concentrations of pyranine, calcein, BSA–FITC and dextran–FITC inside VETs. Their mean values are 5.4 ± 0.7, 9.0 ± 1.2, 8.6 ± 2.2, and 0.82 ± 0.20, respectively (Table 2). These values correspond to the expected values, namely the intra-GV concentrations, in agreement with H0,II. In other words, the GV fragmentation, when carried out in silico, gives ideal VET populations where the VETs have the same internal solute concentration as the parent GVs. However, intriguing discrepancies are found when the experimental and simulated values are compared (Table 2 and Fig. 4, 6). Low- and high-MW solutes behave differently. The stochastic model has generated in silico populations of VETs that can be compared quantitatively with experimentally determined distributions and provides more information than a mere comparison among means. Fig. 6 shows such a comparison. It is evident that low-MW solutes (pyranine and calcein) are mainly lost during extrusion. In contrast, high molecular weight ones (BSA–FITC, dextran–FITC) are essentially retained.
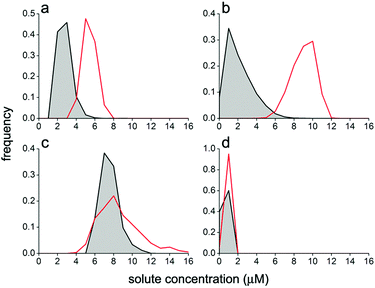 | ||
| Fig. 6 Comparison between VET solute occupancy distribution as obtained experimentally (grey area) and by numerical modelling (red lines). The distributions refer to VETs filled with (a) pyranine; (b) calcein; (c) BSA–FITC; and (d) dextran–FITC. Note that the same concentration bins have been used for all cases. Population statistics are reported in Table 2. | ||
2.3 The case of carbonic anhydrase
In addition to the four fluorescent solutes, we have studied the case of an enzyme entrapped in liposomes, aiming at modelling simple reactions occurring inside protocells. Carbonic anhydrase (CA) was employed, taking advantage of its esterase activity.36,37 The non-fluorescent 6-carboxyfluorescein diacetate (CFDA) is a substrate of CA, which converts it into the fluorescent 6-carboxyfluorescein (CF), whose concentration can be monitored by confocal microscopy. CA-Containing GVs were prepared as described; external CA is removed during GV fractionation by centrifugation. The GVs are then extruded in order to obtain CA-containing VETs. To start the reaction, CFDA is added to the GVs or to the VETs and the course of the enzymatic reaction is followed by measuring the green fluorescence which develops with time inside the vesicles. Non-fluorescent CFDA penetrates into the vesicles’ lumen by passive diffusion through the lipid membrane. Once inside, it is hydrolysed by CA to give the fluorescent product CF and acetate (Fig. 7).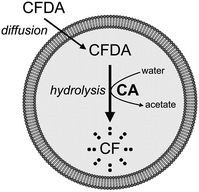 | ||
| Fig. 7 Schematic drawing of CA-containing vesicles and their reaction with externally added CFDA. Fluorescent CF is produced after hydrolysis. | ||
The size distribution of the CA-containing GVs resembles those obtained with the other solutes, but CA-containing VETs, being extruded through larger pores (radius 1 μm), are larger than the other cases, and their distribution is broader (see the bottom line of Table 1). The reason for this choice is that if the VETs are too small, it is difficult to measure the very weak intra-vesicle fluorescence that is generated in the initial period. This would result in a less reliable analysis. Starting from the experimental data, in silico CA-containing vesicles have been firstly generated using the Helfrich (GVs) and the exponential (VETs) functions to model their size distributions (not shown).
In order to proceed with the partition analysis, the intra-GV CA concentration is required, but this value cannot be measured experimentally because CA does not fluoresce in the visible region. Thus, we elaborated a kinetic model for calculating the CA concentration inside vesicles. Each vesicle has been modelled as a CA-containing spherical microreactor with a semipermeable membrane. As a known amount of substrate CFDA is added to the vesicle suspension, it is possible to calculate the internal CF concentration, at any time and for any vesicle with radius r, by combining the CFDA passive diffusion equation and CA enzyme kinetics. Here, the reverse calculation is carried out, namely, determining the intra-vesicle CA concentration that leads to the measured CF concentration (details in Section 5.3). The model has been applied both to GVs and VETs. Such an approach allowed us to estimate, with a certain approximation, the intra-vesicle CA concentrations by a backward kinetic extrapolation.
Internal CA concentrations have been calculated after discrete time intervals from the addition of CFDA, up to 10 minutes. The average CA concentration inside GVs is 1.7 ± 1.0 μM. The mean value is below the bulk CA concentration used for the GV preparation (2 μM), but the quite large variations among vesicles makes this difference not statistically significant. In turn, we ascribe the large standard deviation to the indirect determination of CA concentration, which is limited by the accuracy of r and CF fluorescence measurements. Using the experimental value (1.7 μM), the partition of CA has been simulated by creating firstly in silico GVs and then in silico VETs, as described above. Random and volume-based partition of CA in the daughter VETs, brings about a population with a mean CA concentration of 1.7 ± 0.3 μM. Such an in silico population was then compared with the experimental one, determined by calculating the CA content via the kinetic model. The intra-vesicle CA concentration was found to be 1.0 ± 0.6 μM. As for the other high-MW compounds, this comparison suggests that CA molecules are essentially retained during vesicle extrusion.
2.4 Solute occupancy distribution and ‘super-filled’ vesicles
One of the motivations of this study was the investigation of the possible formation of ‘super-filled’ vesicles from the fragmentation of larger mother vesicles. These special vesicles would derive from an uneven accumulation of solutes according to a specific mechanism. In this respect, it is useful to investigate in more detail the shape and the features of the solute concentration distributions, especially looking at their high-concentration tails. In the past, we have reported that under certain experimental conditions ferritin-15 and ribosome-containing40 conventional vesicles formed by natural swelling (25 nm ≤ r ≤ 100 nm) display a power law distribution of the solute concentration.In this study none of the investigated solutes has a power law occupancy distribution inside VETs. In particular, the distributions are all bell-shaped (Fig. 6). A small but measurable fraction of vesicles is however found on the high-concentration tail of the distributions. In particular, for the five solutes pyranine, calcein, BSA–FITC, dextran–FITC, and CA, the vesicles whose internal solute concentration is higher than the average concentration plus three standard deviations are 1.2%, 0.8%, 1.1%, 0%, and 0.6% of the whole population, respectively (cf. with the expected 0.3% of a Gaussian distribution).
3 Discussion
The two processes depicted in Fig. 1 have been scrutinized against four null hypotheses, H0,I and h0,I for the vesicle formation step/solute encapsulation, and H0,II and h0,II for the vesicle extrusion step/solute partition. Table 2 summarizes the results of this analysis (statistical details in Section 5.4 and Table 3).| # | Hypotheses under scrutiny | Pyranine | Calcein | BSA–FITC | Dextran–FITC | CA |
|---|---|---|---|---|---|---|
| 1 | Normality of intra-GVs solute distribution | >0.20 | <0.10 | <0.01* | >0.20 | <0.01* |
| 2 | Normality of intra-VETs solute distribution | <0.001* | <0.001* | <0.001* | <0.001* | <0.001* |
| 3 | H 0,I, i.e., Cbulk = 〈CGVs〉 | <0.001* | <0.001* | <0.001* | <0.001* | 0.3848 |
| 4 | h 0,I, i.e., Cbulk ∈ {CGVs} | 0.692 | 0.204 | 0.211 | <0.001* | 0.248 |
| 5 | H 0,II, i.e., 〈CVETs〉 = 〈CGVs〉 | <0.001* | <0.001* | <0.001* | <0.001* | <0.001* |
| 6 | h 0,II, i.e., 〈CVETs〉 ∈ {CGVs} | <0.001* | <0.001* | 0.628 | 0.081 | 0.486 |
3.1 Process 1. Vesicle formation and solute entrapment
When the difference between Cbulk and 〈CGVs〉 is strictly considered, it results that H0,I should be rejected for all solutes but CA (this latter result, probably, derives from the quite broad intra-GV solute concentration distribution, which has been obtained by numerical methods, rather than to a true qualitatively different behaviour). A large difference, however, is observed only in the case of dextran–FITC, where in addition to H0,I also h0,I is rejected. This is well evident in Fig. 4 where a large distance between the blue and red dashed lines is present only in the dextran–FITC panel. The reduced entrapment efficiency for high-MW dextran was already observed.41 The average values of the intra-GV concentrations of pyranin and calcein, both negatively charged at the experimental pH, are unexpectedly above and below the corresponding Cbulk, suggesting either fine-tuned molecular effects or a very cautious use of average values, also in view of the sample high dispersity. Our results suggest that sampling a vesicle population to obtain an average behaviour is per se not a trivial process, due to the very heterogeneous nature of vesicle samples (when prepared by the natural swelling) and that the concept of mean concentration should be utilized cautiously. The encapsulation of macromolecules, and in particular of proteins (enzymes) is known to be dependent on several factors, such as the operative procedure, pH, ionic strength, and nature of the lipids.42–44 Here we have shown that working on similar conditions, MW plays a major role in encapsulation. With respect to dispersion around the mean value, it is well known, but not studied in detail, that the formation of vesicles brings about a heterogeneous population in terms of solute content. A previous report indicates that 5–20 kDa poly(ethylene glycol)- and 4–2000 kDa dextran-containing GVs prepared by the natural swelling method have solute distribution widths of ±50% around the average concentration.41 Numerous flow cytometry studies28,29,45 carried out on GVs prepared both by the natural swelling method and by droplet transfer have also evidenced similar trends. Here we have shown that, for GVs prepared by the natural swelling method, and for all investigated solutes, such GV heterogeneity (or ‘diversity’46) is normally present, and that it is higher than expected. The physics behind the large dispersion around the mean concentration value is not well known and should be investigated separately for each preparation method.3.2 Process 2. Vesicle division (here, fragmentation) simulated by extrusion
We have inquired as to what happens to encapsulated solutes during extrusion – intended as an artificial model of vesicle division. This is an important point as the small vesicles deriving from division (or fragmentation) of a parent one must inherit the solutes therein contained, in order to be able to perform similar functions (imagine the fragmentation of primitive cells containing dozens of different molecular species). In the past, the fate of solutes during vesicle self-reproduction was firstly studied by employing ferritin-containing oleic acid/oleate vesicles (radius of about 45 nm), which spontaneously undergo self-reproduction when fed with oleate micelles.19,20 The daughter vesicles (ca. 30 nm) contained ferritin with a similar distribution to the parent one, but the average ferritin number inside the daughter vesicles was less than the initial value due to the co-presence of several new empty vesicles. Subsequent studies showed that the extrusion of calcein-containing myristoleate vesicles (radius reduction from 70 to 44 nm) brings about a calcein loss (−55%) that could not be explained by the decrease of the vesicle volume (−38%).38 The spontaneous division of lecithin-stabilized water-in-oil droplets (3.5 μm) wherein the green fluorescent protein was being produced led to smaller droplets (ca. 2 μm) without interruption of protein synthesis.22 Here we have studied the solute partition pattern following the extrusion of GVs (radius around 3.5 μm) to 0.4 μm VETs in the presence of encapsulated low- and high-MW solutes. With respect to the previous studies, which focused on small volume reduction, the volume difference among the GVs and VETs is remarkable. It is expected that the extrusion of one GV typically yields 70–80 VETs, and about 90% of GV content is lost. We investigated whether the remaining 10% is homogeneously partitioned in the daughter VETs or not. The last two columns of Table 2 show absolute and relative differences between the intra-VET and intra-GV solute concentrations. All differences are statistically significant (i.e., H0,II must be rejected for all solutes). However, when the less restrictive h0,II is considered, the solute retention appears to be a function of MW (h0,II is rejected only for pyranine and calcein). Pyranine and calcein are largely released during GV extrusion, and the intra-VET solution becomes sensitively different (solute-depleted) when compared to the GV one. Vice versa, macromolecules like BSA, dextran and CA (the latter to a minor extent) appear to be less sensitive to solute loss during extrusion, and are therefore more retained than low-MW solutes. The last column of Table 2 indicates the percent decrease of intra-VET solute concentration. Pyranine and calcein show high solute loss (−48 to 76%), whereas the corresponding values for BSA–FITC, dextran–FITC and CA lie in the −11 to 41% range. These trends partially overlap, also considering inter-experiment reproducibility (∼5%), but reveal an interesting and potentially important effect that deserves further attention.3.3 Physical mechanism
As mentioned, vesicle extrusion consists in the forced passage of large vesicles through narrow channels of a thin polycarbonate sheet.47 The vesicle membrane is deformed when it enters into the channel, forced by the pressure exerted above the membrane, and fragments into smaller vesicles with diameters approximately equal to the diameter of the pore. The effect of applied pressure on the size of the extruded vesicles has been studied in detail for a number of pore sizes (up to diameters of 200 nm), lipids, concentrations, and temperatures.48–50 In particular, it has been shown that the threshold pressure should be overcome to extrude vesicles, and that vesicle size inversely depends on the square root of applied pressure (see also a short discussion on the pressure exerted for extruding GVs in this study in Section 5.2.1). The mechanism of vesicle formation is not well understood, but it is clear that the membrane of the mother vesicle must break, and only afterwards do its membrane fragments reseal to form new small vesicles. Whether this occurs via an extended membrane fragmentation (and then resealing) or budding of small membrane portions48,49,51 it is evident that solutes can escape from the broken mother compartment before ending up (re-captured) in the in situ-formed smaller vesicles. In the absence of strong solute–membrane interaction, the fate of solutes will be determined essentially by their diffusion coefficient D, which depends on molecular size and shape. Considering the solutes under study as spherical particles, D is estimated to be around 500 μm2 s−1 (low-MW) and 100 μm2 s−1 (high-MW) by the Stokes–Einstein relation. The three-dimensional mean displacement ρ of these solutes in the typical time required for vesicle closure (ca. 1 ms)52 is 1.73 μm (low-MW) and 0.77 μm (high-MW), calculated according to eqn (2)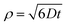 | (2) |
Thus, considering that VETs have typical diameters of 0.8 μm (or ca. 1.5 μm in the case of CA-containing vesicles), small molecules have lower chances of being entrapped inside the incipient vesicles, whereas for macromolecules the opposite is true. Although this analysis does not allow the discrimination between the two possible extrusion mechanisms, it identifies molecular size and thus diffusion as the primary factors that explain the observations.
It is interesting to note – at least for pyranine, calcein, BSA–FITC and dextran–FITC cases – that the VET mean sizes and dispersions around the mean are comparable (see Table 1), suggesting that the extrusion of these four different samples occurred at similar pressure (and plausibly quite low, of the order of a few bars). This implies that the mechanisms underlying the extrusion of solute-filled GVs, in the four above-mentioned cases, was not dramatically different. In fact, previous studies have shown that the vesicle mean size depends on applied extrusion pressure (but accurate measurements have been carried out only for membrane pores of diameter 200 nm, or smaller).48–50 Moreover, there is no correlation between mean VET size and solute retention, implying that even if minor pressure differences were applied for extruding these samples, this did not invalidate the conclusions of this study. Such considerations allow us to conclude that the observed variations of intra-vesicle solute concentrations are due to solute size, and not to different mechanisms of membrane breakage and resealing. Unfortunately, CA-containing VETs cannot be directly compared with the other cases, because they have been extruded through a membrane with larger pores.
4 Concluding remarks
Although this work has shown an interesting tendency, i.e., that macromolecules could be preferentially retained inside daughter vesicles derived from fragmentation (and, by extrapolation, from division) of a mother vesicle, it should not be considered conclusive. There are several open questions not covered by our investigation. The first one is whether the observed behaviour is really general or whether it can be observed only for the five types of solutes studied here. This knowledge gap should be covered by extending this kind of study to many more low- and high-MW solutes, including nucleic acids for instance. Second, POPC GVs have been used as protocellular models, but other kinds of membranes should be explored. In the field of phospholipids, an interesting question refers to changing the chain length (e.g., DMPC) or the membrane fluidity (e.g., DOPC, POPC, DPPC and their mixtures), as well as the effect of cholesterol. Maybe more importantly, fatty acid vesicles, which are generally considered realistic protocell models,53 should be investigated. Third, it should be kept in mind that our results are based on a mechanical fragmentation, whereas the final goal refers to spontaneous vesicle division, following a growth–division mechanism.4–6 A more stringent control of extrusion pressure, is however required to corroborate our observations. Thus, we hope for future studies that address all these aspects.With the aim of extending the relevance of our study also outside origin-of-life research, we noted that the physical mechanisms at the basis of VET formation from GVs could be of interest for research on exosomes.54–56 In particular, it is an open question whether physical factors could act in synergy with highly regulated control bio-mechanisms operating when exosomes stem from large cells. In this respect it should also be mentioned that recently reported ‘super-filled’ vesicles, whose diameter lies in the 60–200 nm range,15,40 can be considered intriguing models of exosomes, as they contain closely packed biomacromolecules (proteins, ribosomes).
Returning to an origin-of-life scenario, this study suggests – albeit with the due caution – that very basic biophysical mechanisms (based on solute size) could have been a source of selective pressure in prebiotic times, before the onset of sophisticated control mechanisms of cell reproduction, favouring the vertical transfer of macromolecules (information-carrying and/or catalytic polymers) through generations of primitive cells.
5 Materials and methods
5.1 Materials
8-Hydroxypyrene-1,3,6-trisulfonic acid trisodium salt (pyranine, #H1529, 524 Da), calcein disodium salt (#21030, 667 Da), bovine serum albumin–fluorescein isothiocyanate conjugate (BSA–FITC, #A9771, 66 kDa), dextran–fluorescein isothiocyanate conjugate (dextran–FITC, #FD150S, 150 kDa), carbonic anhydrase (CA, #C4396, 60 kDa), and 6-carboxyfluorescein diacetate (CFDA, #C5041, 460 Da) were all from Sigma-Aldrich, as well as all solvents and buffers used in the study. POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine) was bought from Avanti (Alabaster, AL, USA). DMSO stands for dimethyl sulfoxide.5.2 Methods
Preliminary tests and optimizations showed good inter-experiment reproducibility (average values within ∼5%) provided that extensive vesicle sampling is carried out.In order to separate GVs from non-entrapped solutes and isolate small-sized GVs, 3 volumes of GVs were diluted with 1 volume of dilution buffer (200 mM glucose, 5 mM Na-bicine pH 8.5). This creates an isotonic density gradient that allows facile GV centrifugation. The raw GV samples were centrifuged and washed at increasing rates (700, 1000 and 5000 rpm on a Eppendorf desktop centrifuge). The final GV pellet was suspended in 200 μL of working buffer (150 mM sucrose, 50 mM glucose, 5 mM Na-bicine pH 8.5). Due to material loss during the centrifugation procedure, it was convenient to prepare a large volume of GVs (4 × 1 mL). The final POPC concentration was 1.1 mM as estimated by the Stewart assay.57 The centrifugation allows the removal of non-entrapped solutes and brings about the isolation of GVs whose radius lies in the 1–10 μm range.
Solute-containing GVs (0.5 mL) were extruded (seven passages) in order to prepare sub-micrometer extruded vesicles with a nominal radius of 0.4 μm (Vesicles by the Extrusion Technique, VETs). Extrusion was carried out by means of a hand-extruder (Liposofast, Avestin, Canada), whereby two 0.4 μm-pore (radius) polycarbonate membranes (Corning Nuclepore Track-Etch Membranes) were sandwiched between three support drain discs. In the case of CA-containing vesicles, membranes with 1 μm-pores (nominal radius) have been used.
It is known that the radius of extruded vesicles tend to the radius of extrusion pores as the exerted pressure increases.50 However, as the membrane pore diameter (0.8 or 2 μm) used in this study is quite large when compared with the case of well-studied extrusion through pores whose diameter is 200 nm or less,48–50 the available knowledge does not allow a quantitative discussion on the effect of pressure on extrusion. A tentative approach can be based on the following considerations. According to the available hand-extruder technical specifications (from Genizer, San Gabriel, CA), the maximal pressure that can be exerted on the hand-extruder is ca. 150 psi (ca. 10 bar), whereas the minimal pressure for extrusion of 1.1 mM POPC through 800 nm (diameter) pores is difficult to estimate (cf. the threshold pressure for extruding 0.13 mM POPC vesicles on 100 nm (diameter) pores is ca. 2.8 bar50). Thus, even if the extrusion pressure has not been controlled in this study, it realistically lies in the 3–10 bar range. However, as the mean VET sizes, and the dispersions around the mean are very similar (see Table 1), it can be cautiously concluded that the occasional pressure variations unavoidably associated with hand extrusion have not been decisive to determine different vesicle sizes and different vesicle extrusion mechanisms.
The Michaelis–Menten parameters of the CA-catalysed CFDA-hydrolysis were determined for the reaction in bulk by adding 13 to 665 μM CFDA (the final DMSO concentration was kept constant at 5% v/v) to 1 μM CA in 200 mM sucrose, 5 mM Tris–HCl (pH 7.5) and measuring the initial reaction rate by recording the absorbance at 491 nm, where the product of the reaction, CF, has an absorption peak (ε491 = 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 M−1, measured at pH 7.5). The apparent turnover number (kcat) and the apparent Michaelis–Menten constant (KM) have been determined by non-linear and linear fittings of experimental data, giving consistently the values of 3.0 ± 0.2 s−1 and 4.0 ± 0.3 mM, respectively.17
300 cm−1 M−1, measured at pH 7.5). The apparent turnover number (kcat) and the apparent Michaelis–Menten constant (KM) have been determined by non-linear and linear fittings of experimental data, giving consistently the values of 3.0 ± 0.2 s−1 and 4.0 ± 0.3 mM, respectively.17
Vesicles observation by confocal laser scanning microscopy and image acquisition. GVs and VETs have been observed by means of a Leica TCS SP5 confocal microscope. Images were acquired at 1024 × 1024 resolution, 8-bit depth. All fluorochromes used in this study can be excited by the 488 nm Argon laser line; fluorescence was collected in the 500–550 nm range. Vesicles (30 μL) have been diluted using 70 μL of isotonic isopycnic buffer (150 mM sucrose; 50 mM glucose; and 5 mM Na-bicine pH 8.5 or 5 mM Tris–HCl pH 7.5) and directly visualized without any pre-treatment. Visualization chambers have been created by overlapping a microscope glass slide and a 0.17 mm cover slip above each other, using as a spacer two layers of suitably shaped and molten Parafilm M (which holds together the glass slide and the cover slip). Due to the complete removal of non-entrapped solutes, the GV background was not fluorescent, whereas the VET background was partly fluorescent, as expected, because of solute loss during GV extrusion. In the case of CA-containing vesicles, CFDA (as DMSO solution) was added to the vesicle sample and thoroughly mixed just before placing the sample in the visualization chamber; images were recorded at regular time intervals, for a total time of 40 minutes.
Image analysis. Quantitative image analysis was carried out by using ImageJ (http://imagej.nih.gov/ij). The background average fluorescence (F0) and standard deviation (ΔF) of the 8-bit green-channel images were firstly measured, in order to set the threshold at the F0 + 3ΔF fluorescence value. In the resulting 1-bit images, the vesicles were recognized by the built-in ImageJ algorithm. The ROI map was then applied to the original 8-bit images and vesicle parameters were measured (projected area, fluorescence, shape). Shape descriptors (circularity and solidity) were used to discard bad-quality vesicles. Vesicle projected areas have been assumed to be the vesicle great circle, and from this, vesicle radius was calculated. This assumption is accurate for VETs but can lead to GV size underestimation (because the confocal optical slice under our experimental conditions is about 0.7 μm). Intra-vesicle fluorescence values were converted to solute concentrations by means of calibration lines. Care was taken to image free-solute samples at the same optical depth (along the z-direction) of the vesicle samples.
5.3 Kinetic analysis of CA-catalyzed CFDA hydrolysis
The external addition of CFDA to CA-containing spherical unilamellar vesicles triggers two processes, namely, the passive diffusion of CFDA from the external solution to the vesicle lumen, and its CA-catalysed hydrolysis to give CF and acetate. In order to model these processes the required physico-chemical parameters are the CFDA permeability coefficient across the phosphatidylcholine membrane58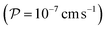 , and the CFDA/CA Michaelis–Menten kinetic parameters (kcat and KM).
, and the CFDA/CA Michaelis–Menten kinetic parameters (kcat and KM).
Given the vesicle radius r, the initial external CFDA concentration [CFDA]0,out and the intra-vesicle CA concentration Ein (which is supposed not to change with time), it is possible to calculate, under certain approximations and by numerical integration, the internal CF concentration at any time [CF]t,in. Similarly, it is possible to carry out the inverse calculations, namely determining [CA]in from r, [CFDA]0,out, and [CF]t,in. The reaction can be summarized as follows:
The time evolution of all species has been obtained by numerical integration of the ordinary differential equations shown in eqn (3)–(5):
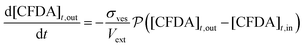 | (3) |
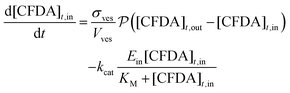 | (4) |
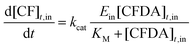 | (5) |
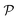 is the CFDA permeability through the lipid bilayer. In order to determine the unknown enzyme concentration inside the vesicles (Ein), the evolution of the product concentration [CF]t,in (whose value was recorded by confocal microscopy after known amounts of time tm) was simulated by the numerical solution of eqn (3)–(5) for each measured vesicle. In particular, Ein was varied by a binary search approach until the difference between the experimental and calculated [CF]tm,in was less than the desired accuracy ε = 10−6 μM. Note that a numerical solution was found for the majority of vesicles, however in some cases the routine did not converge.
is the CFDA permeability through the lipid bilayer. In order to determine the unknown enzyme concentration inside the vesicles (Ein), the evolution of the product concentration [CF]t,in (whose value was recorded by confocal microscopy after known amounts of time tm) was simulated by the numerical solution of eqn (3)–(5) for each measured vesicle. In particular, Ein was varied by a binary search approach until the difference between the experimental and calculated [CF]tm,in was less than the desired accuracy ε = 10−6 μM. Note that a numerical solution was found for the majority of vesicles, however in some cases the routine did not converge.
5.4 Statistical analysis
Statistical tests were applied to draw conclusions with respect to the hypotheses under scrutiny. For all tests, statistical significance was attributed when p < 0.05. In addition to H0,I and H0,II, specified at the beginning of Section 2, the following hypotheses were also statistically tested:| h0,I, that Cbulk belongs to the population of intra-GV concentrations; i.e., Cbulk ∈ {CGVs}; |
| h0,II, that 〈CVETs〉 belongs to the population of intra-GV concentrations; i.e., 〈CVETs〉 ∈ {CGVs}; |
The normality of the GV and VET solute occupancy distribution (internal solute concentration, μM) was assessed by the Kolmogorov–Smirnov test, as reported in Table 3, entries 1 and 2. Similar but not identical conclusions were obtained by the Shapiro–Wilk W-test and by the Lilliefors test (only pyranine- and calcein-containing GVs gave contrasting results). H0,I compares an individual value with a mean, and it was assessed by a one-sample t-test (two-tailed). H0,II compares two means that derive from two non-normal populations, and it was assessed by the Mann–Whitney nonparametric test (two-tiled). The two additional hypotheses h0,I and h0,II compare an individual value with a population (i.e., with a distribution function, which is non necessarily normal). In order to proceed, the experimental distribution was best-fitted to give either a normal distribution (when the normality test was passed) or a log-normal distribution (when the normality test was not passed); the resulting probability density function was used to compute the p-value (one-tailed).
5.5 In silico GVs and VETs, and solute partition
The simulations of GV and VET size and solutes distributions were performed by using lab-made Python routines. In particular, pseudo-random number generations and Poisson random variables where managed thanks to the Numpy and MatPlotLib open source scientific libraries. Due to the very large number of substrate molecules involved, the dynamical simulation of a CA reaction has been implemented in a deterministic way, by calculating the standard Michaelis–Menten enzyme kinetics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Pier Luisi Luisi (ETH Zürich, Switzerland and Roma Tre University, Italy) for inspiring discussions on the open questions about vesicle roles in primitive origin-of-life scenarios. Collaboration among the authors has been fostered by the European COST Action CM1304 “Emergence and Evolution of Complex Chemical Systems”.References
- P. L. Luisi, F. Ferri and P. Stano, Naturwissenschaften, 2006, 93, 1–13 CrossRef CAS PubMed.
- V. de Lorenzo and A. Danchin, EMBO Rep., 2008, 9, 822–827 CrossRef CAS PubMed.
- J. C. Blain and J. W. Szostak, Annu. Rev. Biochem., 2014, 83, 615–640 CrossRef CAS PubMed.
- P. Walde, R. Wick, M. Fresta, A. Mangone and P. Luisi, J. Am. Chem. Soc., 1994, 116, 11649–11654 CrossRef CAS.
- P. Stano, E. Wehrli and P. L. Luisi, J. Phys.: Condens. Matter, 2006, 18, S2231 CrossRef CAS.
- T. F. Zhu and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 5705–5713 CrossRef CAS PubMed.
- W. Yu, K. Sato, M. Wakabayashi, T. Nakaishi, E. P. Ko-Mitamura, Y. Shima, I. Urabe and T. Yomo, J. Biosci. Bioeng., 2001, 92, 590–593 CrossRef CAS PubMed.
- S. Nomura, K. Tsumoto, T. Hamada, K. Akiyoshi, Y. Nakatani and K. Yoshikawa, ChemBioChem, 2003, 4, 1172–1175 CrossRef CAS PubMed.
- V. Noireaux and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17669–17674 CrossRef CAS PubMed.
- G. Murtas, Y. Kuruma, P. Bianchini, A. Diaspro and P. L. Luisi, Biochem. Biophys. Res. Commun., 2007, 363, 12–17 CrossRef CAS PubMed.
- Y. Kuruma, P. Stano, T. Ueda and P. L. Luisi, Biochim. Biophys. Acta, 2009, 1788, 567–574 CrossRef CAS PubMed.
- G. Sessa and G. Weissmann, J. Biol. Chem., 1970, 245, 3295–3301 CAS.
- D. W. Deamer and G. L. Barchfeld, J. Mol. Evol., 1982, 18, 203–206 CrossRef CAS PubMed.
- P. Walde and S. Ichikawa, Biomol. Eng., 2001, 18, 143–177 CrossRef CAS PubMed.
- P. L. Luisi, M. Allegretti, T. P. de Souza, F. Steiniger, A. Fahr and P. Stano, ChemBioChem, 2010, 11, 1989–1992 CrossRef CAS PubMed.
- P. Stano, E. D’Aguanno, J. Bolz, A. Fahr and P. L. Luisi, Angew. Chem., Int. Ed., 2013, 52, 13397–13400 CrossRef CAS PubMed.
- E. D’Aguanno, E. Altamura, F. Mavelli, A. Fahr, P. Stano and P. L. Luisi, Life, 2015, 5, 969–996 CrossRef PubMed.
- F. Mavelli and P. Stano, Artif. Life, 2015, 21, 445–463 CrossRef PubMed.
- N. Berclaz, M. Müller, P. Walde and P. L. Luisi, J. Phys. Chem. B, 2001, 105, 1056–1064 CrossRef CAS.
- N. Berclaz, E. Blöchliger, M. Müller and P. L. Luisi, J. Phys. Chem. B, 2001, 105, 1065–1071 CrossRef CAS.
- M. M. Hanczyc, S. M. Fujikawa and J. W. Szostak, Science, 2003, 302, 618–622 CrossRef CAS PubMed.
- D. Fiordemondo and P. Stano, ChemBioChem, 2007, 8, 1965–1973 CrossRef CAS PubMed.
- F. Mavelli, BMC Bioinf., 2012, 13(Suppl 4), S10 CrossRef CAS PubMed.
- Y. P. Patil, A. K. Ahluwalia and S. Jadhav, Chem. Phys. Lipids, 2013, 167–168, 1–8 CrossRef CAS PubMed.
- P. Walde, R. Wick, M. Fresta, A. Mangone and P. Luisi, J. Am. Chem. Soc., 1994, 116, 11649–11654 CrossRef CAS.
- P. Stano and P. L. Luisi, Chem. Commun., 2010, 46, 3639–3653 RSC.
- K. Kurihara, M. Tamura, K.-I. Shohda, T. Toyota, K. Suzuki and T. Sugawara, Nat. Chem., 2011, 3, 775–781 CrossRef CAS PubMed.
- T. Sunami, K. Sato, T. Matsuura, K. Tsukada, I. Urabe and T. Yomo, Anal. Biochem., 2006, 357, 128–136 CrossRef CAS PubMed.
- K. Nishimura, T. Hosoi, T. Sunami, T. Toyota, M. Fujinami, K. Oguma, T. Matsuura, H. Suzuki and T. Yomo, Langmuir, 2009, 25, 10439–10443 CrossRef CAS PubMed.
- L. Lazzerini-Ospri, P. Stano, P. Luisi and R. Marangoni, BMC Bioinf., 2012, 13, S9 CrossRef CAS PubMed.
- K. Nishimura, T. Matsuura, K. Nishimura, T. Sunami, H. Suzuki and T. Yomo, Langmuir, 2012, 28, 8426–8432 CrossRef CAS PubMed.
- L. Calviello, P. Stano, F. Mavelli, P. L. Luisi and R. Marangoni, BMC Bioinf., 2013, 14, S7 Search PubMed.
- E. Altamura, F. Milano, R. R. Tangorra, M. Trotta, O. H. Omar, P. Stano and F. Mavelli, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3837–3842 CrossRef CAS PubMed.
- A. C. Chakrabarti, R. R. Breaker, G. F. Joyce and D. W. Deamer, J. Mol. Evol., 1994, 39, 555–559 CrossRef CAS PubMed.
- P. A. Monnard and D. W. Deamer, Origins Life Evol. Biospheres, 2001, 31, 147–155 CrossRef CAS.
- R. E. Tashian, D. P. Douglas and Y. S. Yu, Biochem. Biophys. Res. Commun., 1964, 14, 256–261 CrossRef CAS PubMed.
- J. A. Verpoorte, S. Mehta and J. T. Edsall, J. Biol. Chem., 1967, 242, 4221–4229 CAS.
- M. M. Hanczyc, S. M. Fujikawa and J. W. Szostak, Science, 2003, 302, 618–622 CrossRef CAS PubMed.
- W. Helfrich, J. Phys., 1986, 47, 321–329 Search PubMed.
- T. Pereira de Souza, F. Steiniger, P. Stano, A. Fahr and P. L. Luisi, ChemBioChem, 2011, 12, 2325–2330 CrossRef CAS PubMed.
- L. M. Dominak and C. D. Keating, Langmuir, 2007, 23, 7148–7154 CrossRef CAS PubMed.
- R. L. Shew and D. W. Deamer, Biochim. Biophys. Acta, 1985, 816, 1–8 CrossRef CAS.
- J.-P. Colletier, B. Chaize, M. Winterhalter and D. Fournier, BMC Biotechnol., 2002, 2, 9 CrossRef PubMed.
- S. Y. Hwang, H. K. Kim, J. Choo, G. H. Seong, T. B. D. Hien and E. K. Lee, Colloids Surf., B, 2012, 94, 296–303 CrossRef CAS PubMed.
- T. Sakakura, K. Nishimura, H. Suzuki and T. Yomo, Anal. Methods, 2012, 4, 1648–1655 RSC.
- P. Stano, T. Souza, P. Carrara, E. Altamura, E. D’Aguanno, M. Caputo, P. L. Luisi and F. Mavelli, Mech. Adv. Mater. Struct., 2015, 22, 748–759 CrossRef.
- P. Walde, in Encyclopedia of Nanoscience and Nanotechnology, ed. H. S. Nalwa, American Scientific Publishers edn, 2004, vol. 9, pp. 43–79 Search PubMed.
- D. G. Hunter and B. J. Frisken, Biophys. J., 1998, 74, 2996–3002 CrossRef CAS PubMed.
- B. J. Frisken, C. Asman and P. J. Patty, Langmuir, 2000, 16, 928–933 CrossRef CAS.
- P. J. Patty and B. J. Frisken, Biophys. J., 2003, 85, 996–1004 CrossRef CAS PubMed.
- S. G. Clerc and T. E. Thompson, Biophys. J., 1994, 67, 475–476 CrossRef CAS PubMed.
- E. Hernández-Zapata, L. Martínez-Balbuena and I. Santamaría-Holek, J. Biol. Phys., 2009, 35, 297–308 CrossRef PubMed.
- P.-A. Monnard and D. W. Deamer, Anat. Rec., 2002, 268, 196–207 CrossRef CAS PubMed.
- K. Denzer, M. J. Kleijmeer, H. F. Heijnen, W. Stoorvogel and H. J. Geuze, J. Cell Sci., 2000, 113(Pt 19), 3365–3374 CAS.
- N. Yi, J. Kim, D. Jeong, M. Lee, S. C. Jang, J. Kim, Y. Gho and J. Park, Proceedings of the 16th International Conference on Miniaturized Systems for Chemistry and Life Sciences, MicroTAS 2012, 2012, pp. 1861–1863.
- M. Colombo, G. Raposo and C. Théry, Annu. Rev. Cell Dev. Biol., 2014, 30, 255–289 CrossRef CAS PubMed.
- J. C. Stewart, Anal. Biochem., 1980, 104, 10–14 CrossRef CAS PubMed.
- A. V. Thomae, Experimental and Theoretical Investigations on Lipid Bilayer Permeation, PhD thesis, No. 16989, Eidgenössische Technische Hochschule (ETH), Zürich, 2007 Search PubMed.
Footnotes |
| † These authors contributed equally to this work. |
| ‡ Current address: DiSTeBA, University of Salento, Ecotekne, I-73100 Lecce, Italy. E-mail: pasquale.stano@unisalento.it; Fax: +39 0832 298732; Tel: +39 0832 298709. |
| This journal is © The Royal Society of Chemistry 2018 |