Data-driven learning and prediction of inorganic crystal structures

Abstract

Crystal structure prediction algorithms, including ab initio random structure searching (AIRSS), are intrinsically limited by the huge computational cost of the underlying quantum-mechanical methods. We have recently shown that a novel class of machine learning (ML) based interatomic potentials can provide a way out: by performing a high-dimensional fit to the ab initio energy landscape, these potentials reach comparable accuracy but are orders of magnitude faster. In this paper, we develop our approach, dubbed Gaussian approximation potential-based random structure searching (GAP-RSS), towards a more general tool for exploring configuration spaces and predicting structures. We present a GAP-RSS interatomic potential model for elemental phosphorus, which identifies and correctly “learns” the orthorhombic black phosphorus (A17) structure without prior knowledge of any crystalline allotropes. Using the tubular structure of fibrous phosphorus as an example, we then discuss the limits of free searching, and discuss a possible way forward that combines a recently proposed fragment analysis with GAP-RSS. Examples of possible tubular (1D) and extended (3D) hypothetical allotropes of phosphorus as found by GAP-RSS are discussed. We believe that in the future, ML potentials could become versatile and routine computational tools for materials discovery and design.

---

Introduction

Exploring and cataloguing new crystal structures is one of the principal tasks in chemistry. Decades of careful experimental work are collected in the Inorganic Crystal Structure Database (ICSD)¹ and the Cambridge Structural Database (CSD),² which have been impressive examples of “big data” since long before the phrase became fashionable. While structural space has traditionally been explored by synthesis, more recent work has shown that ab initio structure searching can play an important and complementary role in this regard. Computational tools, including genetic algorithms,^3–5 particle swarm optimisation,^6,7 or ab initio random structure searching (AIRSS),^8,9 can predict structures that are (sometimes) far from what chemical intuition would suggest. Many of these predictions have subsequently been validated by experiments^10–14 or have given rise to databases of their own.¹⁵ We only mention in passing the prediction of organic molecular crystal structures, which has likewise seen fundamental breakthroughs.^16–19

Despite their predictive power, these structure searching methods are normally driven by quantum-mechanical density-functional theory (DFT) computations, and therefore they are limited to systems with relatively small unit cells. The allotropes of elemental phosphorus,^20–22 which are the topic of the present paper, directly illustrate the problem at hand. The thermodynamically stable “black” (orthorhombic) form, as well as the high-pressure As-type (rhombohedral) allotrope, exhibit simple crystal structures with only one symmetry-independent atom each (Table 1). Such systems are easily amenable to ab initio crystal structure prediction, and various, especially layered, hypothetical allotropes have been proposed in recent years.^23–32 On the other hand, “violet” (Hittorf’s) phosphorus³³ has a notoriously complex structure that was solved more than 100 years after the initial synthesis³⁴ and contains no fewer than 21 symmetry-independent atoms in the unit cell. Systems of this size have hitherto been out of reach for ab initio crystal structure prediction.

Table 1 Experimentally known crystal structures of phosphorus.²⁰Z is the number of atoms in the conventional unit cell; Z′ gives the number of symmetry-inequivalent atoms in the cell, and is therefore a measure of structural complexity. The molecular (“white”) and amorphous (“red”) forms are omitted from this study for simplicity^b

	Space group	Z	Z′	Source	Ref.
a Occasionally referred to as “blue P” in recent literature,^46 especially in the monolayer form. b To explore whether our GAP would be able to find molecular (“white”) P, we carried out a set of preliminary searches at low density (1.0 g cm^−3). The resulting structures did include distorted P4 units, but also other small fragments, and we expect that the GAP will need to have “seen” these in iterative training to distinguish them more clearly. We also expect that fully capturing the intricate structural details of white P, including its packing variants,^74 will require additional reference data; this is the topic of ongoing work. Regarding amorphous forms, our searches are restricted to relatively small periodic unit cells which cannot fully represent the amorphous allotrope(s).
Black P	Cmca	8	1	High-pressure synthesis	43
As-type P^a	R3̄m	2	1	From black P (p > 5 GPa)	44
Simple cubic P	Pm3̄m	1	1	From black P (p > 11 GPa)	44
Hittorf’s P	P2/c	84	21	Slow cooling from Pb melt	34
Fibrous P	P1̄	42	21	Resublimation with I catalyst	45

---

It has recently been suggested that machine learning (ML) based interatomic potentials could help with this long-standing issue.^35–38 Such potentials are fitted to reference databases of DFT energies and forces and, once generated, they allow one to perform atomistic simulations with close to DFT quality but at a computational cost that is orders of magnitude lower.³⁹ Indeed, we have recently shown that an ML-based Gaussian approximation potential (GAP), initially developed for amorphous carbon,⁴⁰ can be used to identify crystalline allotropes.³⁶ This has added around 150 entries to the Samara Carbon Allotrope Database (SACADA, ref. 15). Very recently, the use of ML to speed up global searching and crystal structure optimization itself has been reported,^41,42 but we focus here on the use of explicit interatomic potentials (“force fields”) for this purpose. What is more, in recent work,³⁷ we have argued that RSS can be used to construct the interatomic potential from scratch, exploring and fitting a complex potential energy surface (PES) at the same time. This points towards a more general “data-driven” strategy for atomistic materials modelling.

In this Discussion paper, we aim to take new steps in this direction and further develop our emerging method (which we call “GAP-RSS”). After briefly summarising its components, we present results for elemental phosphorus, generating and applying the first GAP-RSS potential for this material. Our protocol “discovers” the crystal structure of black P during the iterations and, by construction, adds it to the reference database without prior knowledge of any existing allotropes. We then use this potential for some exercises in crystal structure prediction: we show that a fibrous allotrope of P (Table 1) appears to be prohibitively hard to find in free searches, and we outline the use of an alternative approach, showing exemplary predicted structures in 1D and 3D. We also discuss open questions and expected future directions.

Methodology

The protocol for GAP-RSS potential fitting and structure searching consists of three components: single-point DFT computations, GAP fitting to an updated reference database, and structural optimisation using GAP. We give details of these in sequence, and an overview is provided in Fig. 1.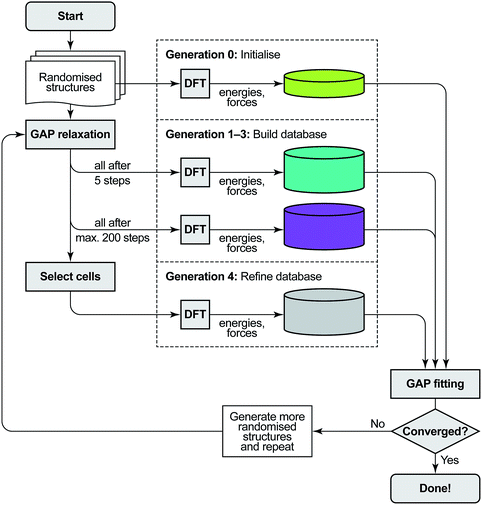

Fig. 1 Overview of the GAP-RSS protocol as introduced in ref. 37 and extended here by a selection step. We start from a set of randomised seed structures for a given chemical composition (in generations 0–3, 250 each; in generation 4, 5000). The reference database of energies and forces is then built by single-point DFT computations: first, for unrelaxed structures (generation 0), later, at various stages of structural relaxation (1–4), performed by fitting interim GAPs to the evolving database. Initially, we feed all structures back into the training (up to generation 3); later, we only add selected structures. As a criterion to select cells, here we use coordination numbers, demanding that all atoms in a candidate structure must have three nearest neighbours, and discarding any structures which do not comply. The GAP-RSS iterations are deemed “converged” when the resulting potential shows satisfactory performance. Here, we do so after generation 4, as that version of the potential has “found” black P from scratch (see Fig. 3 and 4).

DFT computations

These provide the input data for GAP fitting: initially, single-point DFT computations are done for randomised atomic configurations, later, for intermediates or local minima of GAP-RSS searches. We obtain these data using standard DFT procedures, with high numerical accuracy to minimise noise in the input for fitting. In this work, we used the PBEsol functional,⁴⁷ which has been validated for black P before,⁴⁸ and on-the-fly ultra-soft pseudopotentials as implemented in CASTEP.⁴⁹ Reciprocal space was sampled on dense k-point meshes (maximum spacing 0.02 Å⁻¹). The cut-off energy for plane-wave expansions was 600 eV, and an extrapolation scheme was used to counteract finite-basis errors.⁵⁰ In Fig. 1, all parts that involve single-point DFT computations (viz. the construction of the reference database) are enclosed by dashed lines.

GAP fitting

With reference data available, an interatomic potential is fitted to these using GAP. The framework was introduced in 2010 (ref. 51) and has since been used to generate potentials for diverse molecular and solid-state materials.^40,52–54 A high-dimensional fit to reference energy and force data is performed based on structural similarity or kernel functions, comparing atomic environments one by one. The initial choice for these have been many-body descriptors, most importantly the Smooth Overlap of Atomic Positions (SOAP), which includes all neighbours of an atom up to a cut-off radius.⁵⁵ To improve the stability of the fit, similar to our previous work on amorphous materials modelling⁴⁰ and structure searching,^36,37 we combine the many-body SOAP expansion with non-parametric two-body (“2b”) and three-body (“3b”) terms that encode interatomic distances and bond angles, respectively. The 2b and SOAP descriptors have radial cut-offs of 5.0 Å, whereas that for the 3b term is 2.6 Å (to include only “true” bond angles involving nearest-neighbour contacts). The final GAP uses 10 sparse points (that is, fitting coefficients) for the 2b term, 100 for the 3b term, and 3000 for SOAP. The convergence and smoothness parameters for the SOAP expansion are n_max = l_max = 8 and σ_at. = 0.75 Å, respectively, which were found to be suitable for GAP-RSS in ref. 37. For a more detailed walk-through of the underlying ML framework, we refer the reader to ref. 56.

GAP-RSS relaxation

This is the heart of the technique: structural space is explored by optimising random structures, akin to the well-established AIRSS technique, but now using GAP. In AIRSS (and consequently in GAP-RSS), it is important to make a sensible choice of randomised initial structures. For example, a reasonable minimum interatomic distance (“hard-sphere” criterion) is imposed. Furthermore, exploiting space-group symmetry can significantly reduce the number of attempts required. Here we search with 2–16 atoms in the unit cell, allowing for either 1, 2, 4, or 8 symmetry operations to be present. To some extent, this penalises rhombohedral space groups and their subgroups, but our data below show that the rhombohedral A7 structure is found by our protocol nonetheless. We choose the initial densities to be distributed around 2.5 g cm⁻³, in between the black and red forms of phosphorus, and we constrain the P–P distances in the initial structures to at least 1.8 Å. An independent set of randomised input structures is generated for initialisation and for each new generation of the potential.

Results and discussion

Exploring the potential energy surface of elemental phosphorus

To showcase the principle of GAP-RSS, in this paper we explore the potential energy surface (PES) of elemental phosphorus. This is summarised in Fig. 2, where we show the energy–volume data for the reference database that is built during construction of the potential. We start with randomised input structures, the data for which are added to the database without relaxation (light green points in Fig. 2; generation 0). We then extend the database by three rounds (generations 1–3), where snapshots of both intermediate (teal) and relaxed (purple) structures are added; finally, in generation 4, we perform a larger search and keep only the unique structures with all-threefold coordinated atoms (“3c”, determined using a 2.4 Å bond-length cut-off; light grey points). After this, we deem the database “converged” for the purpose of the present study, by the (subjectively chosen) criterion that the GAP has “learned” black P; see below. Future work will be concerned with less heuristic criteria for convergence. The distributions shown on the right-hand side of Fig. 2 illustrate how the different parts of the database, and thus of the PES, comprise progressively lower-lying structures.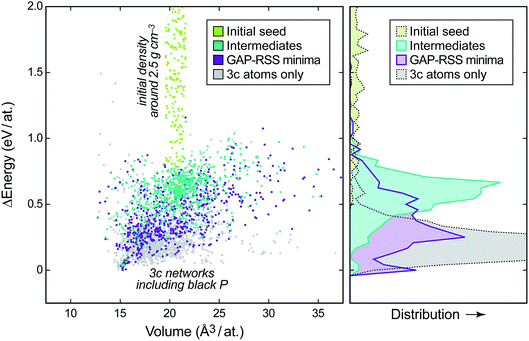

Fig. 2 Left: energy–volume plot of single-point DFT data during the generation of a GAP-RSS model for phosphorus, given relative to the most stable structure. The different stages of building the database (cf.Fig. 1) are highlighted in different colours. Right: binned distribution for energies in these datasets, drawn on the same vertical axis.

We will show in the following that, concomitant with increasing exploration of the phase space, the GAP-RSS interatomic potential becomes more accurate, ultimately describing crystal structures without prior knowledge. We stress that in most of the previous literature on fitting ML potentials, reference databases are constructed by including known crystal structures (and distorted variants thereof).^39,40,53

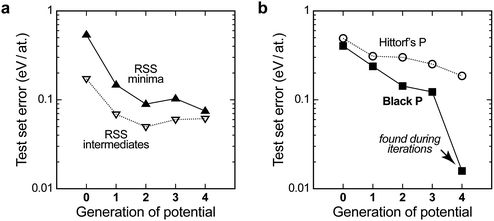
To assess the quality of the potential, we use it to compute energies for independent test sets of structures not included in the training, for which the DFT energies are known. The results are shown in Fig. 3a. The description of the higher-energy regions (“RSS intermediates”, open symbols) appears to converge quite early on, but it carries a residual root-mean-square prediction error of the order of 0.05–0.10 eV per at. that does not improve with further iterations. The same is observed, and is even more pronounced, for a test set of randomised seed structures, where the error is practically constant at ≈0.10 eV per at. for all the GAP generations (not shown in Fig. 3a for clarity). This is intuitively understandable: the PES is smooth, and since the high-energy structures are so diverse, only a handful of them are required for acceptable sampling. A similar observation was made for liquid carbon in our earlier work: the high-temperature liquid contains many different environments and is thus straightforward to “learn” from a single ab initio MD trajectory. In contrast, the amorphous regions of the PES required several rounds of GAP-driven MD and iterative refinement of the potential.⁴⁰

Fig. 3 Quality of the evolving interatomic potential, assessed by computing the energies for independent test sets (configurations outside the database) with different generations of the GAP, and reporting the root-mean-square error against the DFT data. (a) Errors for sets of structures from an independent GAP-RSS run without symmetry, taken after 5 CG steps (“intermediates”) and 200 CG steps (“minima”); (b) the same for sets of distorted unit cells of known allotropes, viz. Hittorf’s and black P. In generation 4, our GAP has “seen” black P and therefore the predicted error for this allotrope falls close to zero (see the arrow).

For the purposes of GAP-RSS, these findings are encouraging: the early steps of relaxation appear to be easily “learned” by the potential, and even a notable degree of residual error can be tolerated if the potential is successful in navigating the high-energy region of the PES (say, the green data points in Fig. 2). In contrast, a growing database is needed for the relaxed minima. Indeed, testing for a set of local RSS minima outside the database initially leads to a significant prediction error above 0.5 eV per at. (filled symbols in Fig. 3a), but this gradually improves and falls below 0.1 eV per at. with increasing quality of the potential.

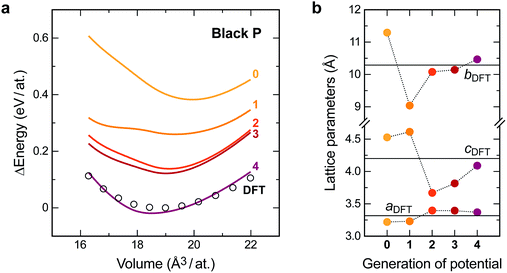
The latter accuracy turns out to be acceptable for exploratory searches, but it is still worse than what one would expect from an ML potential for the stable allotropes. Our long-term vision for GAP-RSS is therefore to find stable minima (such as black or orthorhombic P) during the iterations and automatically include them in the reference database. We expect this to improve the accuracy substantially, which is supported by the following result. Fig. 3b shows test set errors as before, but now for ensembles of distorted unit cells of two experimentally known allotropes. The orthorhombic structure of black P is a particularly interesting test, as it competes with other, more highly symmetric structures that are very close in energy on the PES.²² Our potential, during generation 4, did succeed in finding black P, and hence includes this structure type in the final reference database. This is reflected in Fig. 3b: the energy errors for black P get progressively lower, but only in generation 4 do they drop to very close to zero.

Likewise, the computed energy–volume scans for black P (Fig. 4a) progressively improve during the GAP-RSS iterations, but the structure needs to have been “seen” and included in the fitting (in generation 4) to achieve an accurate result. The same is true for computed structural properties (Fig. 4b): for this test, we fully relaxed the black P structure with each version of our potential, as well as with DFT. In generation 4, all three GAP-computed lattice parameters come very close to the DFT benchmark.

Fig. 4 Quality of the evolving interatomic potential, assessed by computing properties of black P. (a) Energy–volume scans for the orthorhombic unit cell (scaling lattice vectors and atomic coordinates without further relaxation), comparing progressive GAP generations (lines) to DFT reference data (circles). (b) Lattice parameters, obtained by fully relaxing the crystal structure of black P with each generation of the GAP. DFT results, obtained at the same computational settings as for the reference database, are given as horizontal lines.

“Learning” high-pressure structures

Two important phosphorus allotropes, As-type and simple-cubic, are obtained from the black form at high pressure (Table 1).⁴⁴ With this in mind, we decided to explore what effect external pressure would have on the result of GAP-RSS for this element; doing so has already been suggested and proven to be beneficial for exploring the PES of elemental boron.³⁷ To sample higher-pressure structures, we apply hydrostatic external pressure during the GAP-RSS relaxation runs, with a randomised value in each run. The values are drawn from an exponential distribution with the probability density P of finding a given pressure p,³⁷

P(p) = λ exp(−λp) × p₀

where λ is the rate parameter (we chose λ = 5, a narrower distribution, to sample more around the low-pressure region but still include some high-pressure points), and p₀ is an arbitrarily chosen reference. In this work, we tested the settings of p₀ = 10 GPa and p₀ = 100 GPa, respectively. For both, we generated new sets of potentials through iterative GAP-RSS fitting, starting with the same ensembles of seed structures as used in the pressure-free searches reported above (p₀ = 0 GPa).

The results are easily rationalised by looking at the evolving energy–volume scans again, but now for the high-pressure forms (Fig. 5). For reference, our pressure-free search (p₀ = 0 GPa) already yields an acceptable description of both allotropes in generation 4 (purple lines), but it fails to reach quantitative accuracy, especially for the simple cubic form. Searching with moderate external pressure (p₀ = 10 GPa) visibly improves the description of both high-pressure forms: the GAP and DFT data are now in better agreement. Note that due to the nature of the exponential distribution, most of the pressure values drawn are significantly smaller than p₀, and thus correspond to typical experimental conditions. When using external pressures that are an order of magnitude higher (p₀ = 100 GPa), the description of the As-type form deteriorates visibly, whereas the simple cubic form is already “learned” very easily in generation 2 (bottom right panel in Fig. 5). All this is intuitively understood, as the experimentally observed sequence of pressure-induced phase transitions is black → As-type → simple cubic, with transition pressures around 5 GPa and 11 GPa, respectively.^44,57

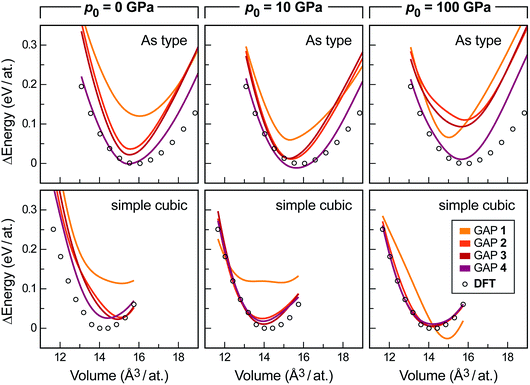Fig. 5 Energy–volume scans similar to those in Fig. 4a, but now assessing the high-pressure forms, As-type (top) and simple cubic P (bottom). Data were obtained with three separate sets of GAP-RSS iterations that utilise, from left to right: no external pressure (i.e. the main dataset), 10 GPa, or 100 GPa of reference pressure p₀, as defined in the text. In all cases, the respective lowest DFT energy point is set as zero. The data for generation 0 are outside the range of the energy axis.

Fibrous phosphorus

“Fibrous” P, described by Ruck et al. in 2005,⁴⁵ is structurally reminiscent of Hittorf’s P: both allotropes exhibit characteristic tubes built from covalently bonded cage motifs, reminiscent of organophosphorus compounds.^58,59 The difference between the two allotropes is in the arrangement of the tubes, which is simpler (all tubes parallel) in fibrous P. Both allotropes contain 21 independent atomic positions (Table 1), which are repeated by space-group symmetry two and four times, respectively.

We performed 100 000 attempts to find the structure of fibrous P using GAP-RSS, seeding with 21 independent, randomised atomic positions in space group P1̄. However, this search was unsuccessful, and none of the attempts led to the known structure after minimisation. We show three of the resulting structures, as mere examples, in Fig. 6. This reflects the more general problem that in global structure determination, the searching task becomes exponentially more complex with system size (and each independent atom adds three structural degrees of freedom), as discussed by Stillinger⁶⁰ and in ref. 9. While the GAP still provides an approximation of the DFT potential energy surface, and therefore some care must be taken when transferring conclusions from GAP-RSS to (DFT-based) AIRSS, we take the present findings as clear evidence that the structure of fibrous P (and, by extension, Hittorf’s P) is too complex to find in free random searches.

Fig. 6 Unsuccessful attempts to find fibrous P in free searches. Exemplarily, we show three low-energy, DFT-relaxed structures resulting from 100 000 GAP-RSS attempts (21 symmetry-independent atoms in space group P1̄). One of these structures is a stacking variant of As-type phosphorus (left); the two other are low-symmetry configurations that are clearly different from the tubular structure of fibrous (and Hittorf’s) P.

Merging modular decomposition and GAP-RSS: towards fully data-driven crystal structure prediction

Inevitably, a fully unconstrained random search for more and more complex structures will fail at some point, as discussed above. Very recent work has shown that molecular network analysis can be used to great effect in this regard.⁶¹ Inspired by Pauling’s iconic rule of parsimony, stating that the number of constituents in a crystal structure tends to be small,⁶² it was proposed in ref. 61 to decompose a crystal structure into building blocks such as to minimise the (mathematically quantifiable) information content. Here we combine this with GAP-RSS searching, and argue that both together provide a useful way forward for the prediction of complex crystal structures.

Fig. 7a summarises the procedure and illustrates how the structure of fibrous P is decomposed into two fragments using the approach of ref. 61. While this is a purely automated, data-driven procedure, its outcome is often in line with chemical intuition.⁶¹ Indeed, in the original publication on fibrous P, the structure was described as a sequence of alternating [P₈] and [P₉] cages, interspersed with P₂ dumbbells.⁴⁵ Similar fragments have been identified by Thurn and Krebs in the crystal structure of Hittorf’s P;³⁴ they have been discussed in Baudler’s seminal work on the nomenclature of phosphorus cages,⁵⁸ and have been the topic of comprehensive theoretical analyses both in the gas phase and in the bulk.^22,59,64 Without chemical knowledge, but with an algorithm to find the most simple and representative building units, the network analysis likewise “cut” the chains into fragments.⁶¹ In these, the well-known [P₉] cage was combined with P₂ dumbbells on either side, forming a [P₁₃] unit (“Fragment A”), whereas the [P₈] cage was recovered directly (“Fragment B”). We believe that alternative ways of decomposition, e.g. isolating the [P₉] cage, may also be useful as starting points for structure searches—as will combinations of different fragments. We also note the advantage of a chemically “agnostic” approach: while there is an extensive body of literature on the building blocks of P allotropes,^22,58,59 future work might be concerned with new materials where the local atomic structure is a priori unknown.

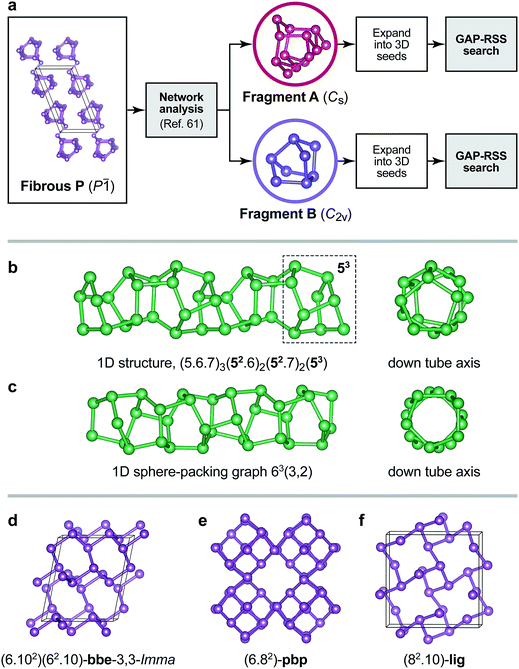Fig. 7 (a) Overview of the fragment-based approach to structure analysis and structure searching introduced in ref. 61 that we combine here with GAP-RSS. Two fragments have previously been identified in the structure of fibrous P (see text),⁶¹ and here we use both separately to generate seed structures for GAP-RSS structure searches. (b) Example of a 1D-periodic structure identified by this procedure. The tube “inherits” some of the structural information from Fragment B, namely, fused five-membered rings (dashed box). Full topology information is given in the text. (c) The same for a 1D structure composed of six-membered rings only. (d–f) Examples of 3D-periodic structures from the same search, labelled according to their network topologies.⁶³

Even with an exemplary and simplified approach that uses only one fragment or the other (Fig. 7a), our GAP-RSS searches readily identified several hypothetical phosphorus allotropes with different dimensionalities. We filtered the output with more stringent criteria than in the preceding GAP-RSS generations, enforcing a minimum “non-bonded” (beyond-nearest-neighbour) distance of 2.9 Å, removing any structures that contain three- or four-membered rings (which are expected to be under significant strain), and post-relaxing selected structures using dispersion-corrected DFT.^65–67 We explored the effect of feeding structural data back into the GAP as before, but now for the more ordered structures coming from fragment-based searches, and generated two additional generations of the potential. An intermediate generation was used to find the structures shown in Fig. 7 (generation 5a); another, final one additionally contains all the minima found in that search (5b). We observed that this reduces the energy error for distorted unit cells of Hittorf’s P (cf.Fig. 3b) from 0.19 eV per at. (generation 4) to 0.16 eV per at. (5a), and further to 0.13 eV per at. (5b); note that in none of these generations has our GAP-RSS potential “seen” the actual crystal structure of Hittorf’s P. A full account of this, including the results of much more diverse searches, will be published elsewhere, and for the sake of brevity we present only a few salient examples here.

As expected, several 1D tubular motifs were found in our GAP-RSS searches, packed in different ways to form extended structures. One of these tubes, shown in Fig. 7b, retains some features of the [P₈] cage from which the initial seed is constructed: namely, fused five-membered rings, of which there are four in the [P₈] cage (topology symbol [5⁴]), and up to three in the chain structure (dashed box in Fig. 7b). Another structure found by GAP-RSS, shown in Fig. 7c, breaks up the initial seed fragment, forming a tube that consists of only six-membered rings. This corresponds to a sphere-packing graph for a hexagonal net (6³) with coincidence vectors (m, n) = (3, 2).⁶⁸ In this, it is also equivalent to one of the smallest theoretically possible carbon nanotubes.

The same protocol also identified fully three-dimensional structures. One of them is a rare binodal net, bbe-3,3-Imma (Fig. 7d), which has occasionally been observed in MOFs.⁶⁹ We find another structure with a uninodal pbp net containing six- and eight-membered rings (Fig. 7e) that had originally been proposed for a hypothetical carbon structure dubbed “6.8²P” (ref. 70) and also investigated as a hypothetical allotrope of P.²⁷ We finally find the uninodal lig net (Fig. 7f), which corresponds to the anion network in the Zintl phase LiGe.⁷¹ Such a structure has not been proposed for P thus far, but it is in conceptual agreement with the Zintl–Klemm–Busmann framework (in which the group-14 element is viewed as “Ge⁻”, and thus takes the structural signature of a group-15 element due to its excess electron).⁷² The computed dispersion-corrected DFT energies^65–67 for the structures shown in Fig. 7d–f are ≈+2 kJ mol⁻¹ (bbe-3,3-Imma) and ≈+8 kJ mol⁻¹ (pbp and lig) above that of black P, placing them well within the experimentally and computationally derived stability range of known allotropes.²²

In ongoing work, beyond the scope of this paper, we are performing much larger-scale searches, including attempts to find “fibrous” P and possible related structures using GAP-RSS, and trying to understand the observed preference for the experimentally known form. It seems especially interesting to study such tubular forms since some of these structural units can be chemically extracted from phosphorus-rich compounds.⁷³

Conclusions

Machine learning-based interatomic potentials can speed up random structure searching by orders of magnitude. Therefore, they seem well poised to become useful tools for crystal structure prediction and materials discovery. We expect them not to replace DFT-driven searching, but to provide a valuable complement, especially for very large and complex structures that are outside the reach of DFT. In this paper, we have discussed and further developed our recently introduced technique, dubbed Gaussian approximation potential-driven random structure searching (GAP-RSS), which combines ideas from the fields of potential fitting and structure prediction. We believe that this technique will be of interest not only for finding new structures, but also for the automated generation of fast, flexible, and accurate interatomic potentials for diverse materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Noam Bernstein for ongoing valuable discussions. V. L. D. gratefully acknowledges a Feodor Lynen fellowship from the Alexander von Humboldt Foundation, a Leverhulme Early Career Fellowship, and support from the Isaac Newton Trust. C. J. P. is supported by the Royal Society through a Royal Society Wolfson Research Merit award. This work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) via EPSRC grant EP/P022596/1. Data access statement: original data supporting this publication are available at https://doi.org/10.17863/CAM.25572.

Notes and references

1. A. Belkly, M. Helderman, V. L. Karen and P. Ulkch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369.
2. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., 2016, 72, 171–179.
3. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
4. A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237.
5. D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 372–387.
6. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
7. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
8. C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504.
9. C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
10. Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182–185.
11. M. Marqués, M. I. McMahon, E. Gregoryanz, M. Hanfland, C. L. Guillaume, C. J. Pickard, G. J. Ackland and R. J. Nelmes, Phys. Rev. Lett., 2011, 106, 095502.
12. H. Wang, J. S. Tse, K. Tanaka, T. Iitaka and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6463–6466.
13. W. Zhang, A. R. Oganov, A. F. Goncharov, Q. Zhu, S. E. Boulfelfel, A. O. Lyakhov, E. Stavrou, M. Somayazulu, V. B. Prakapenka and Z. Konôpková, Science, 2013, 342, 1502–1505.
14. M. Jansen, Adv. Mater., 2015, 27, 3229–3242.
15. R. Hoffmann, A. A. Kabanov, A. A. Golov and D. M. Proserpio, Angew. Chem., Int. Ed., 2016, 55, 10962–10976.
16. S. L. Price, Acc. Chem. Res., 2009, 42, 117–126.
17. A. M. Reilly, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2016, 72, 439–459.
18. A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664.
19. F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Chem. Sci., 2018, 9, 1289–1300.
20. J. Donohue, The Structures of the Elements, John Wiley & Sons, New York, 1974.
21. A. Pfitzner, Angew. Chem., Int. Ed., 2006, 45, 699–700.
22. F. Bachhuber, J. von Appen, R. Dronskowski, P. Schmidt, T. Nilges, A. Pfitzner and R. Weihrich, Angew. Chem., Int. Ed., 2014, 53, 11629–11633.
23. A. J. Karttunen, M. Linnolahti and T. A. Pakkanen, Chem.–Eur. J., 2007, 13, 5232–5237.
24. M. Wu, H. Fu, L. Zhou, K. Yao and X. C. Zeng, Nano Lett., 2015, 15, 3557–3562.
25. T. Zhao, C. Y. He, S. Y. Ma, K. W. Zhang, X. Y. Peng, G. F. Xie and J. X. Zhong, J. Phys.: Condens. Matter, 2015, 27, 265301.
26. J.-R. Feng and G.-C. Wang, RSC Adv., 2016, 6, 22277–22284.
27. J. Liu, S. Zhang, Y. Guo and Q. Wang, Sci. Rep., 2016, 6, 37528.
28. D. Liu, J. Guan, J. Jiang and D. Tománek, Nano Lett., 2016, 16, 7865–7869.
29. Z. Zhuo, X. Wu and J. Yang, J. Am. Chem. Soc., 2016, 138, 7091–7098.
30. W. H. Han, S. Kim, I.-H. Lee and K. J. Chang, J. Phys. Chem. Lett., 2017, 8, 4627–4632.
31. H. Wang, X. Li, Z. Liu and J. Yang, Phys. Chem. Chem. Phys., 2017, 19, 2402–2408.
32. G. Sansone, L. Maschio and A. J. Karttunen, Chem.–Eur. J., 2017, 23, 15884–15888.
33. W. Hittorf, Ann. Phys. Chem., 1865, 202, 193–228.
34. H. Thurn and H. Krebs, Acta Crystallogr., Sect. B: Struct. Sci., 1969, 25, 125–135.
35. P. E. Dolgirev, I. A. Kruglov and A. R. Oganov, AIP Adv., 2016, 6, 085318.
36. V. L. Deringer, G. Csányi and D. M. Proserpio, ChemPhysChem, 2017, 18, 873–877.
37. V. L. Deringer, C. J. Pickard and G. Csányi, Phys. Rev. Lett., 2018, 120, 156001.
38. Q. Tong, L. Xue, J. Lv, Y. Wang and Y. Ma, Faraday Discuss., 2018 10.1039/c8fd00055g.
39. J. Behler, J. Chem. Phys., 2016, 145, 170901.
40. V. L. Deringer and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 094203.
41. T. L. Jacobsen, M. S. Jørgensen and B. Hammer, Phys. Rev. Lett., 2018, 120, 026102.
42. T. Yamashita, N. Sato, H. Kino, T. Miyake, K. Tsuda and T. Oguchi, Phys. Rev. Mater., 2018, 2, 013803.
43. A. Brown and S. Rundqvist, Acta Crystallogr., 1965, 19, 684–685.
44. J. C. Jamieson, Science, 1963, 139, 1291–1292.
45. M. Ruck, D. Hoppe, B. Wahl, P. Simon, Y. Wang and G. Seifert, Angew. Chem., Int. Ed., 2005, 44, 7616–7619.
46. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
47. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
48. A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2014, 112, 176801.
49. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
50. G. P. Francis and M. C. Payne, J. Phys.: Condens. Matter, 1990, 2, 4395–4404.
51. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403.
52. A. P. Bartók, M. J. Gillan, F. R. Manby and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054104.
53. W. J. Szlachta, A. P. Bartók and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104108.
54. A. P. Bartók, S. De, C. Poelking, N. Bernstein, J. R. Kermode, G. Csányi and M. Ceriotti, Sci. Adv., 2017, 3, e1701816.
55. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
56. A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057.
57. P. W. Bridgman, Proc. Am. Acad. Arts Sci., 1948, 76, 55–70.
58. M. Baudler, Angew. Chem., Int. Ed. Engl., 1982, 21, 492–512.
59. S. Böcker and M. Häser, Z. Anorg. Allg. Chem., 1995, 621, 258–286.
60. F. H. Stillinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 59, 48–51.
61. S. E. Ahnert, W. P. Grant and C. J. Pickard, npj Comput. Mater., 2017, 3, 35.
62. L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026.
63. M. O’Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
64. F. Bachhuber, J. von Appen, R. Dronskowski, P. Schmidt, P. Nilges, A. Pfitzner and R. Weihrich, Z. Kristallogr., 2015, 230, 107–115.
65. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
66. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
67. E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
68. E. Koch and W. Fischer, Z. Kristallogr., 1978, 148, 107–152.
69. V. A. Blatov and D. M. Proserpio, Acta Crystallogr., Sect. A: Found. Crystallogr., 2009, 65, 202–212.
70. M. O’Keeffe, G. B. Adams and O. F. Sankey, Phys. Rev. Lett., 1992, 68, 2325–2328.
71. E. Menges, V. Hopf, H. Schäfer and A. Weiss, Z. Naturforsch. B Chem. Sci., 1969, 24, 1351–1352.
72. R. Nesper, Z. Anorg. Allg. Chem., 2014, 640, 2639–2648.
73. A. Pfitzner, M. F. Bräu, J. Zweck, G. Brunklaus and H. Eckert, Angew. Chem., Int. Ed., 2004, 43, 4228–4231.
74. A. Simon, H. Borrmann and J. Horakh, Chem. Ber., 1997, 130, 1235–1240.

---