Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The application of hierarchical structures in energy devices: new insights into the design of solid oxide fuel cells with enhanced mass transport†
Xuekun
Lu‡
 a,
Tao
Li‡
b,
Antonio
Bertei
a,
Tao
Li‡
b,
Antonio
Bertei
 cd,
Jason I. S.
Cho
a,
Thomas M. M.
Heenan
cd,
Jason I. S.
Cho
a,
Thomas M. M.
Heenan
 a,
Mohamad F.
Rabuni
b,
Kang
Li
a,
Mohamad F.
Rabuni
b,
Kang
Li
 b,
Dan J. L.
Brett
b,
Dan J. L.
Brett
 a and
Paul R.
Shearing
a and
Paul R.
Shearing
 *a
*a
aElectrochemical Innovation Lab, Department of Chemical Engineering, University College London, London, WC1E 7JE, UK. E-mail: p.shearing@ucl.ac.uk
bBarrer Center, Department of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK
cDepartment of Earth Science and Engineering, Imperial College London, London, SW7 2AZ, UK
dDepartment of Civil and Industrial Engineering, University of Pisa, Pisa, 56122, Italy
First published on 8th May 2018
Abstract
Mass transport can significantly limit the rate of reaction and lead to concentration polarisation in electrochemical devices, especially under the conditions of high operating current density. In this study we investigate hierarchically structured micro-tubular solid oxide fuel cells (MT-SOFC) fabricated by a phase inversion technique and quantitatively assess the mass transport and electrochemical performance improvement compared to a conventional tubular SOFC. We present pioneering work to characterise the effective mass transport parameters for the hierarchically porous microstructures by an integrated computed fluid dynamics simulation, assisted by multi-length scale 3D X-ray tomography. This has been historically challenging because either imaging resolution or field of view has to be sacrificed to compensate for the wide pore size distribution, which supports different transport mechanisms, especially Knudsen flow. Results show that the incorporation of radially-grown micro-channels helps to decrease the tortuosity factor by approximately 50% compared to the conventional design consisting of a sponge-like structure, and the permeability is also improved by two orders of magnitude. When accounting for the influence of Knudsen diffusion, the molecule/wall collisions yield an increase of the tortuosity factor from 11.5 (continuum flow) to 23.4 (Knudsen flow), but the addition of micro-channels helps to reduce it down to 5.3. Electrochemical performance simulations using the measured microstructural and mass transport parameters show good agreement with the experimental results at elevated temperatures. The MT-SOFC anode displays 70% lower concentration overpotential, 60% higher power density (0.98 vs. 0.61 W cm−2) and wider current density window for maximum power density than the conventional design.
Broader contextHierarchical materials are a popular choice not only for electrochemical energy devices such as fuel cells and batteries, but also for a range of functional materials including catalysts, diffusion media and membranes for waste processing. This study qualitatively and quantitatively illustrates the effectiveness of hierarchically structured pores in reducing gas transport resistance, providing new insights into advanced microstructure optimisation. Moreover, it is a common mistake in the modelling of hierarchical materials to assume the flow to be governed by continuum physics irrespective of the length scale, whereas in the region of finest structure, the molecule/wall collisions become dominant, which cannot be addressed by continuum physics. It is also impossible to define a relevant average pore size to describe the mass transport in these materials due to the wide pore size distribution. The integrated computed fluid dynamics (I-CFD) technique proposed by us for the first time herein, aims to overcome this problem and accurately characterise the effective mass transport in these complex hierarchical structures. The concept and techniques used in this study are believed to be of wide interest across an increasingly broad range of functional applications in respect of advanced electrode design, 3D characterization and performance prediction of gas and multi-phase flow. |
1. Introduction
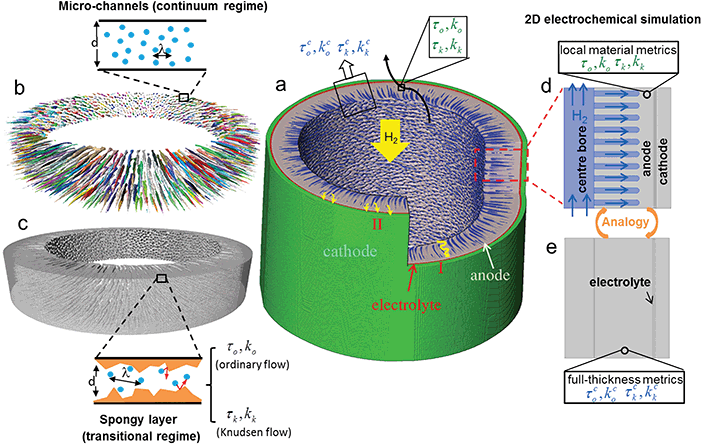
Solid Oxide Fuel Cells (SOFCs) are one of the most promising electrochemical devices for the efficient co-generation of heat and electricity with fuel flexibility.1,2 Mass transport in the electrodes is one of the critical problems that limits the electrochemical performance.3 Electrodes fabricated with a large pore size have outstanding mass transport properties at the expense of active reaction sites (i.e. triple phase boundary)4 and mechanical strength; conversely smaller pore sizes improve the mechanical integrity, especially in long-term operation, but prohibit the mass transport thus yielding high concentration polarisation. Three-dimensional hierarchical porous structures have been proved to be a promising solution to tackle this problem. This strategy has been widely used not only in catalysis, and energy generation and storage,5–7 but also for wastewater filtration8–10 and gas separation using Knudsen selectivity.11,12 In fuel cells, the incorporation of macro-pores into meso- and micro-porous architectures not only provides reduced diffusion resistance for the gaseous species, but also helps to maintain high specific surface area and improve distribution of active sites. Various approaches have been attempted to introduce macro-pores in micro-porous SOFC electrodes, such as multi-layer electrode design with graded composition,13–16 and novel manufacturing routes like freeze-casting.17–19 However, multi-layered electrodes that are stacked sequentially may cause problems in structural integrity during long-term operation or under conditions of thermal shock. Moreover, most of the strategies attempted are only suitable for planar cell design and cannot be applied to tubular design due to its structural complexity. Meanwhile, tubular SOFCs offer a number of advantages over the planar counterparts, including low fabrication cost, ease of gas sealing, higher thermal resilience and long-term stability.20Further advancements have been developed to improve the mass transport of tubular SOFCs. This study introduces an innovative application of hierarchical structure in tubular SOFCs manufactured using a phase inversion (PI) technique. Compared to the conventional tubular design fabricated by ram extrusion, which consists of a homogeneous sponge-like porous structure (pore diameter dp ≈ 0.2 μm), the phase inversion process introduces radially aligned micro-channels (Dp = 10 to 25 μm) that considerably facilitate mass transport (Fig. 1a), which is critical to mitigate concentration polarisation.21 Compared to multi-layer graded electrodes for planar SOFCs, hierarchical structures fabricated by this method in a single step have superior structural integrity. Electrochemical performance also shows that this micro-tubular SOFC (MT-SOFC) can provide 25–40% higher power density than those reported for conventional tubular SOFCs of full-sponge structure.22,23
Accordingly, comprehensive understanding of transport properties of the hierarchical microstructures is required for the design and synthesis of high performance fuel cells. The void space within the porous solids consists of labyrinths of interconnected paths with varying geometric factors such as pore diameter (dp), constriction and tortuosity factor (τ).24–26 The pore size distribution causes local variations in diffusion rates thereby introducing inaccuracies in the diffusive flux estimation as it could result in a 200% aberration of diffusive flux using an average diffusivity in the pore phase,27 making the electrochemical performance simulation invalid. Moreover, as the Knudsen number of the typical SOFC anodes falls within the range of transitional diffusion regime,27 molecule/wall collisions and slippage effects become significant, but are often neglected in models using Fick's law and Stefan–Maxwell equations.28,29 Direct simulation of the molecule/wall collisions is often averted by using the analytical model, known as Dusty Gas Model (DGM)30,31 in continuum flow. However, this application neglects the geometrical details of the pore phase, such as constrictions, random distortions and tortuosity, which are critical in the gas transport as the Knudsen tortuosity factor obtained by numerical method with the consideration of molecule/wall collision can be 1.5–3 times larger than the ones obtained by continuum physics.32,33 Furthermore, neglecting permeation flux in the DGM can result in an inaccurate prediction of concentration losses with errors as large as 20–60%.31,34 To address the molecules–surface interaction, numerical studies were used to study the diffusive processes using random packing sphere models33,35,36 which concluded that the tortuosity factors increase as a function of the Knudsen number. Again, these idealized morphologies cannot provide a faithful description of the typical pore structures.
In order to address the aforementioned problems in the mass transport in porous media, in this paper we use a molecule-based method, Direct Simulation Monte Carlo (DSMC) on 3D reconstructed electrode microstructures from X-ray computed tomography, to compute the Knudsen tortuosity factor and permeability in the spongy layer of the anode and then validate using experimental permeation tests. DSMC is a numerical method for approximating the Boltzmann equation which describes the kinetics of gas molecules in thermally dynamic systems. The motion of neutral flows is tracked using simulation molecules instead of solving fluid conservation equations, the accuracy of which is often in doubt for rarefied and Knudsen flows.37 The method has been well validated by comparing the numerical simulation either with the experimental permeability38 or the established analytical solution.39 DSMC has been widely applied to the permeability study for Knudsen gas flows in various structures such as fibrous materials,39,40 channels filled with packed spheres41,42 and ablative materials.38 Previous application of the DSMC method on a 3D nano-particle model claimed that the empirical equation for the estimation of the tortuosity factor τ = (ε1/3)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 could cause aberrations in concentration distribution.44 However, to our knowledge, few studies apply numerical methods like DSMC to extract the Knudsen tortuosity factor based on 3D reconstructed electrode microstructures obtained from X-ray computed tomography (X-ray CT), which provides a faithful description of the pore structures. The simulated Knudsen tortuosity factor at the pore-scale makes it possible to relate macroscopic transport properties to the underlying pore-scale physical process, which will be a breakthrough benefiting the study of multi-scale gas transport in porous media.
43 could cause aberrations in concentration distribution.44 However, to our knowledge, few studies apply numerical methods like DSMC to extract the Knudsen tortuosity factor based on 3D reconstructed electrode microstructures obtained from X-ray computed tomography (X-ray CT), which provides a faithful description of the pore structures. The simulated Knudsen tortuosity factor at the pore-scale makes it possible to relate macroscopic transport properties to the underlying pore-scale physical process, which will be a breakthrough benefiting the study of multi-scale gas transport in porous media.
Different from the conventional tubular SOFCs, in which the mass transport can be described using the strategy discussed above, in a hierarchical MT-SOFC anode, the pore size spans over two orders of magnitude. The trajectories of the fuel gas are different in each region. For conventional tubular SOFCs, the fuel gas travels in the tortuous spongy layer (i.e. the electrochemically active region), displayed as trajectory I (yellow-curved lines, Fig. 1a). On the contrary, introduction of the micro-channels in the MT-SOFC greatly mitigates the resistance of the gas flow from the centre-bore to the anode/electrolyte interface as the gas molecules preferentially flow through the micro-channels first and then access the interface by diffusion, shown as trajectory II (yellow arrows at the tip of the micro-channels, Fig. 1a). The reactant gas flow in macro pores is governed by continuum physics (Fig. 1b) whereas Knudsen gas flow applies to the microporous region (Fig. 1c). However, the voids in the spongy anode cannot be captured by full cell imaging. As a consequence, measurement of the characteristic mass transport parameters of the entire electrode using image-based techniques remains challenging due to the complex fluid dynamics and also the trade-off between imaging resolution and field of view, which impedes the assessment of the structural design and further electrochemical performance prediction.45,46
This work aims to (1) introduce the advantage of hierarchical porous materials applied to MT-SOFC electrode design; (2) solve the problem of hierarchical porous materials simulation stemming from the trade-off between imaging resolution and field of view; (3) explore the solution for gas flow in these materials governed by both continuum and non-continuum (Knudsen) fluid physics.
Our previous work presented an initial attempt to characterise the effective mass transport parameters of a hierarchical porous material using continuum-based CFD simulation,47 which is regarded as a precursor of this study as it structurally tackled the problem by length-scale decoupling, but did not account for the distinct fluid dynamics in the macro and microporous regions. Here we propose a significant advancement through the development and application of an integrated computed fluid dynamics (I-CFD) simulation framework to emphasise the coupling of molecular-continuum fluid dynamics in the hierarchical porous structure. The upgraded technique is used in this study for advanced electrode design by linking the mass transport in hierarchical structure with the electrochemical performance.
Characteristic transport parameters on two distinct types of hierarchical MT-SOFC anodes plus the conventional design are investigated. With the assistance of multi-length scale X-ray CT, the I-CFD technique makes it possible to relate macroscopic transport properties of the spongy layer (mass transport parameters in blue, top of Fig. 1a) to the underlying molecule–wall interactions (mass transport parameters in green, top of Fig. 1a) and furthermore integrates molecular dynamics into a continuum flow. This solves the problem of multi-scale pores and multi-physics fluid at the same time, and also significantly reduces the computation load. Electrochemical simulation models defined based on the local material parameters (Fig. 1d) and full-thickness characteristic parameters (Fig. 1e) are then compared with the experimental measurements. We expect this methodology will be useful not just for advanced electrode characterization and design in fuel cells and batteries, but also for performance prediction for the hierarchical porous membranes in the application of water treatment and gas separation.
2. Experimental
2.1 Cell fabrication
Anodes with distinct microstructures were fabricated by a phase inversion-assisted extrusion technique, as described elsewhere.48–52 Commercially available powders of yttria-stabilized zirconia (8YSZ, mean particle size 0.1–0.4 μm) and nickel oxide (NiO, mean particle size 0.5–1.5 μm) were purchased from Inframat Advanced Materials and used as supplied. Polyethersulfone (PESf) (Radal A300, Ameco Performance, USA), 30-dipolyhydroxystearate (Arlacel P135, Uniqema), and N-methyl-2-pyrrolidone (NMP, HPLC grade, VWR) were used as the polymer binder, dispersant, and solvent, respectively. Detailed composition information is listed out in the ESI† (see Table S3). The milling of the suspension was conducted for 4 days using a planetary miller (SFM-1 Desk-top Miller, MTI Corporation, USA) to assure homogeneity. Prior to the fabrication, the suspension was degassed under vacuum to fully eliminate air bubbles trapped inside.The fabrication process is illustrated in Fig. 2a. Two different bore fluids were used during the extrusion of the suspension, including solvent (NMP, denoted as BF-S) and aqueous solution of polyvinyl alcohol (PVA, M.W. approx. 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Merck Schuchardt OHG, Germany, denoted as BF-P). The suspension and bore fluid were extruded simultaneously throughout the spinneret (Fig. 2b) to a bath filled with external coagulant (i.e. H2O). For BF-P, short finger-like micro-channels are formed when the suspension is in contact with the bore fluid (PVA) during co-extrusion process as a consequence of solvent/non-solvent exchange, resulting in a rapid increase in the local suspension viscosity and final precipitation of the polymer binder.53 In contrast, the external coagulant penetrates the radial thickness of the fiber (200–300 μm), forming percolated micro-channels. A YSZ electrolyte (layer thickness of 5 μm) was subsequently dip-coated onto the anode substrate precursor. After drying, a co-sintering step was undertaken at 1450 °C for 6 hours to densify the electrolyte. Finally the dual-layer cathode was dip-coated onto the sintered micro-tube, with the first layer composed of YSZ/LSM mixture (YSZ
000, Merck Schuchardt OHG, Germany, denoted as BF-P). The suspension and bore fluid were extruded simultaneously throughout the spinneret (Fig. 2b) to a bath filled with external coagulant (i.e. H2O). For BF-P, short finger-like micro-channels are formed when the suspension is in contact with the bore fluid (PVA) during co-extrusion process as a consequence of solvent/non-solvent exchange, resulting in a rapid increase in the local suspension viscosity and final precipitation of the polymer binder.53 In contrast, the external coagulant penetrates the radial thickness of the fiber (200–300 μm), forming percolated micro-channels. A YSZ electrolyte (layer thickness of 5 μm) was subsequently dip-coated onto the anode substrate precursor. After drying, a co-sintering step was undertaken at 1450 °C for 6 hours to densify the electrolyte. Finally the dual-layer cathode was dip-coated onto the sintered micro-tube, with the first layer composed of YSZ/LSM mixture (YSZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LSM = 50
LSM = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%) and second layer of pure LSM. After both layers were dried, a sintering process at 1100 °C was undertaken for 1 hour to deliver a complete single cell (Fig. 2c). The total thickness of cathode is approximately 50 μm.
50 wt%) and second layer of pure LSM. After both layers were dried, a sintering process at 1100 °C was undertaken for 1 hour to deliver a complete single cell (Fig. 2c). The total thickness of cathode is approximately 50 μm.
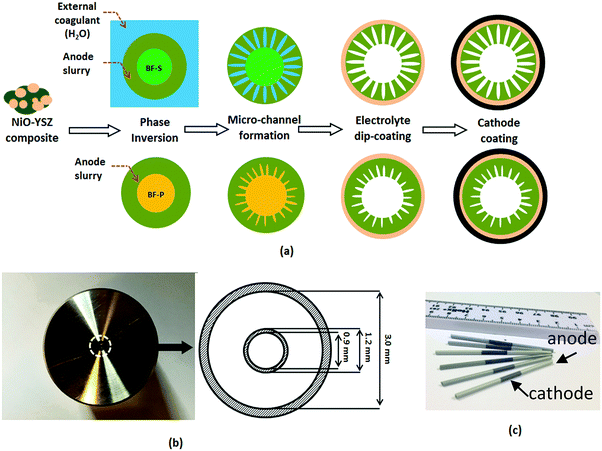 | ||
| Fig. 2 (a) Schematic diagram of the fabrication process of MT-SOFC; (b) photographic image of spinneret from bottom and detailed dimensions; (c) as-prepared MT-SOFCs. | ||
2.2 Electrochemical performance test
Silver wires of 0.2 mm diameter (99.99% purity, Advent Materials Ltd, UK) were wrapped along the cathode and on the exposed anode for current collection and secured using silver paste. Wires from both electrodes were connected to a potentiostat/galvanostat (Iviumstat, Netherlands). Cells were reduced in situ at 700 °C for 2.5 hours. Voltage–current (V–I) curves were recorded with 30 ml min−1 of nominally pure H2 fed to anode as the fuel and 50 ml min−1 of air fed to cathode as oxidant.2.3 Multi-length scale X-ray computed tomography (X-ray CT)
The two distinct types of full cells were imaged in 3D using a Versa 520 X-ray microscope (micro-CT), followed by high resolution imaging on the spongy layer of the anodes using an Ultra 810 X-ray microscope (nano-CT; both Zeiss Xradia, Carl Zeiss, CA, USA).54 Detailed scanning parameters are shown in Table 1. Proprietary Feldkamp–Davis–Kress (FDK) and filtered-back projection algorithms were used for the reconstruction of the full SOFC and the spongy layer scans respectively.55,56 The reconstructed sample volumes were segmented using Avizo V9.0 software (Avizo, Thermo Fisher Scientific, Waltham, Massachusetts, U.S.) package. The triple-phase boundary (TPB) densities were measured using a 3D imaging-based algorithm explained thoroughly elsewhere.4 The binary image stacks of the spongy layer were imported into Fiji Software57 for the pore diameter and porosity measurement using Local Thickness plug-in.| Sample | Voxel size (μm) | Field of view (μm2) | Projections | Exposure time (s) | Camera binning | |
|---|---|---|---|---|---|---|
| BF-S | Spongy | 0.032 | 16 × 16 | 1201 | 60 | 2 |
| Tube | 1.070 | 2140 × 2140 | 2001 | 18 | 1 | |
| BF-P | Spongy | 0.064 | 16 × 16 | 1201 | 40 | 4 |
| Tube | 1.080 | 2160 × 2160 | 2001 | 18 | 1 | |
2.4 Ordinary mass transport parameters by continuum model
In the continuum flow regime, tortuosity factor τ is a parameter reflecting the effect of convoluted gas pathways on mass transport in porous media. Here it was measured by H2 ordinary diffusion flux: the H2 molar concentration was set as c = 1 mol m−3 at the inlet and c = 0 at the outlet. The H2 diffusion flux driven by a concentration gradient in a fully porous volume is described by Fick's law as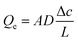 | (1) |
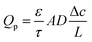 | (2) |
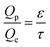 | (3) |
For mass transport in porous electrodes under operating conditions, the viscous forces dominate over inertial forces and a fluid is said to be in the creeping flow regime according to the low Reynolds number,58,59 which suggests that the permeability can be obtained according to Darcy's law,60
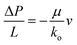 | (4) |
2.5 Knudsen mass transport parameters by DSMC (non-continuum)
The Stochastic PArallel Rarefied-gas Time-accurate Analyzer (SPARTA)61 DSMC code developed at Sandia National Laboratory is used in this work to evaluate transport properties by considering Knudsen effects. In the DSMC algorithm, molecular processes include molecular advection and collisions and each simulation molecule represents a large number of real molecules so that the computational load is significantly reduced.The surface mesh (i.e. .stl file) of the spongy anode from Avizo was imported into the SPARTA software such that it was embedded in the simulation domain consisting of an array of 3D Cartesian grids, the size of which is only a fraction of the mean free path of the simulating gas. Molecule/surface collisions were performed in each grid following a no-time-counter (NTC) procedure.37 Parameters such as temperature, pressure and density can be computed by sampling the molecule properties in the grids.
In this study, the simulation was conducted on the datasets with the volume of approximately 260 μm3 embedded within 3.5 million grids. H2/H2O counter-diffusion was achieved by setting subsonic boundary conditions at the inlet (H2, 800 °C, 1 bar) and outlet (H2O, 800 °C, 1 bar) at each side. Buffer zones of at least 10% total flow domain were added at inlet and outlet. A total of 20 million simulation molecules were generated so that the average molecule number in each cell was above 20 to avoid statistical scattering.62 The mass transport in the simulated domain is composed of ordinary diffusion, Knudsen diffusion and permeation. The ordinary diffusivity Do and Knudsen diffusivity Dk are calculated as,
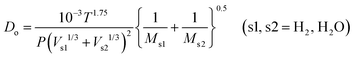 | (5) |
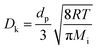 | (6) |
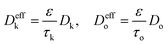 | (7) |
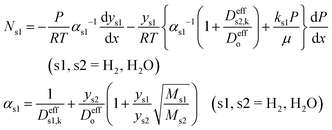 | (8) |
The Knudsen permeability (kk) is obtained by eqn (9) as a combination of the ideal gas law, conservation of mass and the differential form of Darcy's law. J denotes the permeation mass flux by DSMC. The simulation was run at P = 1 bar with a pressure drop ΔP = 0.02 bar at 800 °C,
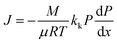 | (9) |
It should be noted that the Knudsen tortuosity factor and Knudsen permeability discussed here do not necessarily mean that DSMC simulation was performed in Knudsen regime (Kn ≫ 1). Instead, they refer to the values obtained by taking into account Knudsen effects via DSMC in transitional flow regime according to the operating conditions of SOFCs.
2.6 Characteristic mass transport parameters for full anode by integrated computed fluid dynamics (I-CFD) simulation
The obtained continuum (τo, ko) and Knudsen (τk, kk) mass transport parameters from high resolution imaging and simulation can then be directly used to define the material property of the spongy layer (Table 2). A full anode continuum-based CFD simulation is then conducted to extract the characteristic mass transport parameters in the continuum flow regime (τco, kco) and Knudsen flow regime (τck, kck), with the macroscopic mass transport properties of the spongy layer related to the underlying molecule–wall interactions in the microporous phase. This integrated simulation technique enables to tackle the mass transport problem of multi-scale pores and multi-fluid dynamics at the same time. The flux obtained by integrated CFD simulation is then divided by the flux simulated on the empty volume (ε = 1) to obtain the characteristic tortuosity factors (τco, τck) according to eqn (3), and the characteristic permeabilities (kco, kck) are obtained using eqn (4). It should be noted that the permeabilities are calculated based on pure permeation flux. The reconstructed volumes of the anodes with an axial depth of 70 μm and 90° arc angle were imported into the commercial CFD software Star-CCM+ 11.06 (CD-adapco Inc., Siemens PLM Software, London) for meshing and image-based simulation. The simulation domain was meshed with 5 million polyhedral cells. The simulation parameters are shown in Table 2.| Simulating parameter | Micro-channels | Spongy layer | Boundary conditions |
|---|---|---|---|
| τ co | 1 | ε/τo (continuum) | c = 1 mol m−3 (inlet) c = 0 (outlet) |
| τ ck | ε/τk (Knudsen) | ||
| k co | Open pore | k o (continuum) | ΔP = 50 Pa, T = 1073 K |
| k ck | k k (Knudsen) | ||
2.7 Electrochemical performance simulations
In this study, two different electrochemical simulations were conducted for the validation and application of the DSMC and I-CFD techniques: (1) micro-channel geometry (Fig. 1d): model with the spongy layer defined based on the local material parameters (i.e. λTPB, ordinary, Knudsen tortuosity factor τo and τk, Knudsen permeability kk of the spongy layer); (2) no-microchannel geometry (Fig. 1e): model is defined as a homogeneous anode using the full-thickness characteristic parameters τco, τck and kck measured by the I-CFD technique. The former case allows the possibility for further parametric study on the geometrical effect of the micro-channels. The latter case provides the convenience for 3D electrochemical simulation on complex hierarchical structures with just a simple geometry using the full anode characteristic parameters. The results of both cases are compared with the experiment data in Section 3.4.Mass balance, species balance, charge balance and momentum conservation were ensured in the whole simulation domain. Laminar gas flow in the centre-bore and micro-channels were solved by the Navier–Stokes equation using Maxwell–Stefan diffusivity; the mass transport in the spongy electrode was solved by the DGM, which needs both the ordinary and Knudsen diffusivities as input parameters. The continuity of mole fraction, pressure, velocity and flux were ensured at the boundary between channels and spongy layer. The electrochemical current generation was described using the Butler–Volmer equation,64,65 in which the exchange current density and the activation overpotential must be evaluated locally. More details of the simulation including the input parameters and physics models can be found in the ESI.†
3. Results & discussion
3.1 Macro-scale structure characterizations (micro-CT)
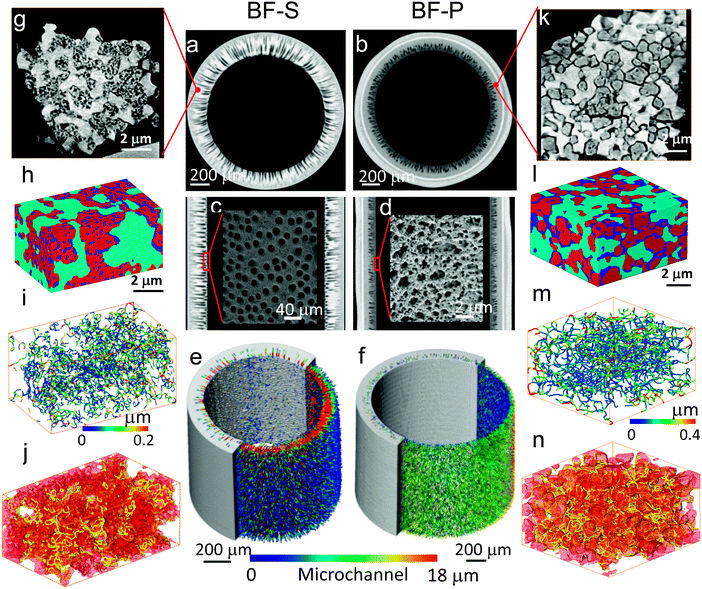
Although the microstructure of BF-S was briefly introduced previously,47 a more comprehensive structural characterisation from macro-scale to micro-scale is presented here (for both BF-S and BF-P). This highlights the effect of the different fabrication parameters on morphological optimisation, and the interplay between microstructure and electrochemical performance. The macroscopic morphologies of the two types of cells were firstly imaged using micro-CT and the virtual slices of the reconstructed 3D volumes are shown in Fig. 3. When solvent was used as the bore fluid (sample BF-S), solidification of the hollow fiber precursor, as a result of the exchange between the solvent in the suspension and the external coagulant, was markedly arrested. Therefore, the micro-channels initiated from the exterior surface were able to grow radially until they penetrated almost 85% of the anode thickness (Fig. 3a), leaving uniform and open entrances on the inner surface as illustrated in Fig. 3c. In contrast, when PVA aqueous solution was used as the bore fluid (sample BF-P), the solidification process at the inner surface region was fast, and as a consequence, the anode substrate displays a typical heterogeneous structure composed of teardrop-shaped micro-channels and sponge-like regions (Fig. 3b). The penetration length of the micro-channels is approx. 50% of the radial thickness, much lower compared to BF-S. In addition, as shown in Fig. 3d, the inner surface consists of loosely packed particles (Ni and YSZ). As measured in a previous study, such inter-granular packing pores have an average pore diameter ranging between 1–2 μm and span approx. 10 μm,66,67 much smaller than BF-S (Fig. 3c). Color-coded micro-channel diameter distribution (Fig. 3e and f) also confirms that BF-S has significantly larger average microchannel diameter (16 vs. 10 μm) and entrance diameter (20 vs. 2 μm) than BF-P.3.2 Micro-scale structure characterizations (nano-CT)
Micro-CT scans enable us to investigate the morphology of the full anode. However, due to the trade-off between resolution and field of view, it is impossible to image the full-thickness anode with sufficient resolution to explore the local microstructure, this is especially the case for the pore phase in the spongy layer, where the local mass transport (i.e. tortuosity factor, pore diameter) and reaction kinetics (i.e. TPB density) are largely determined.68 Accordingly, small pieces of the spongy layer were extracted from the anodes using a scalpel for high resolution tomography. The microstructures are significantly different between the two samples (Fig. 3g and k); the boundaries of the Ni particles in BF-S are not as clear as those in BF-P. In addition, the pore phase in BF-S appears mostly inside of the Ni particles; in contrast, in BF-P the Ni particles are dense and well separated from YSZ and pores. Three phases were subsequently segmented and visualized in Fig. 3h and l, from which it is clearer to see the different morphologies of three phases between BF-S and BF-P as described above. The spongy layer porosity of BF-S was measured to be 17.1 ± 3.1%, slightly lower than that in BF-P (18.4 ± 1.6%) and the pore connectivity was measured to be 99.1% for BF-S and 98.3% for BF-P. The pore phase was then skeletonized and colour coded to visualize the local pore diameter distribution (Fig. 3i and m).69 It displays that the pore size in BF-P is generally larger than that in BF-S and the average pore diameter dp is 0.16 and 0.23 μm for BF-S and BF-P respectively. Fig. 3j and n show the TPBs detected using the developed Matlab algorithm4 alongside the pore and Ni phases. The TPB density in BF-S is slightly lower than that in BF-P (5.3 ± 0.74 vs. 6.2 ± 0.51 μm−2). The materials statistics at different length scales are summarised in Table 3.| BF-S | BF-P | |
|---|---|---|
| Macro-scale parameters of the tube | ||
| Mc percentage (%) | 14.7 | 9.5 |
| Mc length (μm) | 170 ± 12 | 110 ± 7 |
| Mc Din (μm) | 20 ± 3.2 | 1–2 |
| Mc Dp (μm) | 15.9 ± 0.5 | 10.2 ± 0.3 |
| Mc Dmax (μm) | 22 ± 2.5 | 14 ± 1.8 |
| ε c (%) | 29.2 | 26.1 |
| Micro-scale parameters of the spongy layer | ||
| ε (%) | 17.1 ± 3.1 | 18.4 ± 1.6 |
| d p (μm) | 0.16 ± 0.05 | 0.23 ± 0.1 |
| Pore connectivity (%) | 99.1 | 98.6 |
| TPB density (μm−2) | 5.3 ± 0.74 | 6.2 ± 0.51 |
3.3 Characteristic mass transport parameters by I-CFD
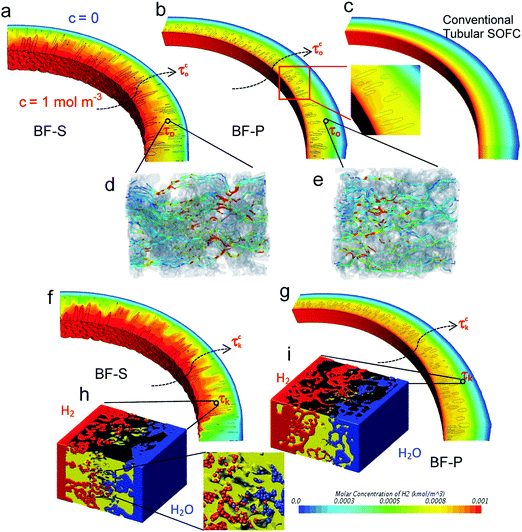
Our previous work demonstrated the feasibility of applying the multi-scale CFD simulation technique on the 3D reconstructed hierarchical SOFC anodes.47 However, the effective mass transport parameters were extracted using continuum-fluid dynamics (i.e. ordinary diffusion tortuosity factor τo), and the conclusions were made on the premise that it represents a species-independent microstructural parameter. As the gas flow in the SOFC electrodes is mainly governed by transition fluid dynamics, which is proved by the Knudsen number estimation based on the local pore diameter (see Section S1.2, ESI†), the molecule/wall collisions should be taken into account. Thus it is worth comparing the results between continuum-fluid simulation, as we did before, to the I-CFD simulation which couples the molecular-continuum fluid dynamics in hierarchical porous structure. Moreover, the direct comparison between BF-S, BF-P and conventional design will shed light on the dependence of mass transport on different microstructures, which provides new insights into the micro-tubular SOFC design.Gas flow simulated using continuum method is visualised by streamlines in Fig. 4d and e, with local maxima indicating the constriction of flux at pore necks which are more severe in BF-S. H2/H2O counter diffusion with the same pressure (1 bar) at both sides using DSMC is shown in Fig. 4h and i, which displays that the H2 molecules travel faster than H2O in both spongy layers, according to the larger pore volume filled by H2 molecules. This disparity is caused by the different values of mean molecular velocity, with H2 having a larger mean molecular velocity than H2O due to its lower molecular weight, thus resulting in a faster Knudsen diffusion rate. The different Knudsen diffusion rates of the species generate a pressure gradient in the fluid domain, thus the permeation flux develops, despite it is often neglected in the literature when using continuum methods.70
The Knudsen tortuosity factors τk are measured to be about twice larger than the ordinary ones τo (24.6 vs. 12.0 and 21.3 vs. 11.1 for BF-S and BF-P respectively). By defining the spongy layers using the values above, the full anode characteristic tortuosity factor τco and τck can be obtained, as is shown in Fig. 4a, b, f and g. The combination of molecule-based method (DSMC) and continuum physics on full anode scale (I-CFD) enables the simulation of multi-mechanism mass transport in these hierarchical materials for the first time. A referential sample of purely spongy layer (i.e. no micro-channels) is also compared here (Fig. 4c).
Fig. 4a and b clearly display that the micro-channels in BF-S yield a heterogeneous H2 concentration distribution with a small gradient in the micro-channel effective zone. This is reasonable since the gradient of H2 concentration is inversely proportional to the diffusivity of the material at a fixed boundary condition. In contrast, the isolated micro-channels in BF-P are less significant in mass transport as the H2 concentration drops sharply from 1 to 0.8 mol m−3 near the inner wall. This inefficient contribution of micro-channels in BF-P is attributed to their narrow entrance, which does not facilitate gas flow. However, the close-up image and the relatively uniform concentration distribution within the central micro-channel zones indicate superior diffusivity compared to the conventional design (Fig. 4c).
It should be noted that the Knudsen tortuosity factor and permeability discussed next do not necessarily mean that DSMC simulation was performed in Knudsen regime (Kn ≫ 1), in which these parameters approach asymptotic values and are independent of temperature and pressure. Instead, they refer to the values obtained by taking into account Knudsen effects via DSMC in the transitional flow regime, alongside ordinary diffusion, according to the operating conditions of SOFCs. When the Knudsen effects are taken into account, the concentration drops sharply at the end of micro-channel zone (Fig. 4f) because of the decreased diffusivity in the spongy layer. Similar phenomenon is also observed in BF-P (Fig. 4g), although the drop of concentration is less dramatic due to the larger difference in diffusivity between micro-channels and spongy layer when Knudsen properties are considered rather than continuum flow. Table 4 lists the obtained tortuosity factors for all the three types of samples.
| Parameters | Conventional | BF-P | BF-S | Units |
|---|---|---|---|---|
| τ o | 11.5 | 11.1 | 12.0 | — |
| τ k | 23.4 | 21.3 | 24.6 | |
| τ co | 11.5 | 9.8 | 5.3 | — |
| τ ck | 23.4 | 15.3 | 8.9 | |
| k o (×10−17) | 4.2 | 5.4 | 3.1 | m2 |
| k k (×10−16) | 6.4 | 6.8 | 5.7 | |
| k co (×10−17) | 4.2 | 28 | 170 | m2 |
| k ck (×10−14) | 6.4 | 0.39 | 4.6 |
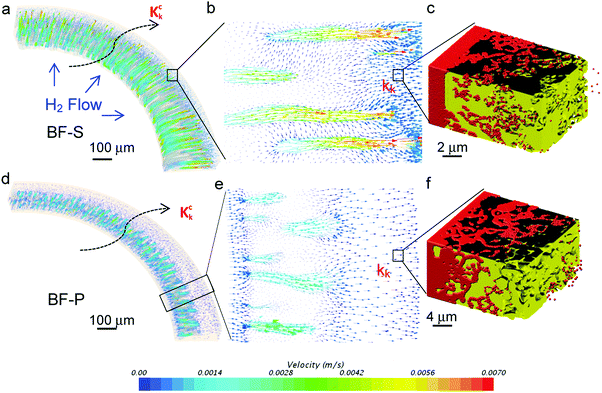
The Knudsen permeability of the full-thickness anode is also simulated by coupling the local Knudsen permeability obtained from DSMC (Fig. 5): significantly faster mass transport in the micro-channels is shown in BF-S compared to BF-P (Fig. 5a and d). The magnified images clearly display that the gas molecules are drawn into the micro-channels at the vicinity of the inner wall (Fig. 5e) and they can transfer from the neighbouring micro-channels and permeate outward at the micro-channels tip (Fig. 5b). The resultant Knudsen permeability values kk, kck are summarised and compared with the ones obtained from the continuum method (i.e. ko and kco) in Table 4. It needs to be emphasised that comparing each columns, BF-S shows significantly better characteristic mass transport parameters than BF-P and conventional design; for instance, the wide and long micro-channels in BF-S help to reduce the τco by more than 50% compared to the conventional design (5.3 vs. 11.5), more effective than BF-P (9.8). Comparing each row, BF-S also displays remarkable improvement relative to the spongy layer. Tortuosity factor drops by 56% for BF-S (12 (τo) vs. 5.3 (τco)) but only decreases by 10% for BF-P (11.1 (τo) vs. 9.8 (τco)), highlighting that the entrance diameter and the length of micro-channels are key factors in determining the effectiveness of the hierarchical design. It is also noted that the molecule/wall collisions increase the spongy layer tortuosity factor by ca. 2 times, which is consistent with what was reported in the literature.32,33 This indicates that the diffusion mass transport flux could be overestimated by 100% if the Knudsen effect is ignored using continuum-fluid dynamics simulation.47 The permeability is also improved more significantly in BF-S (from 3.1 × 10−17 to 17 × 10−16 m2) compared to BF-P (5.4 × 10−17 to 2.8 × 10−16 m2). An experimental gas permeation test was also conducted at different pressure levels using N2 and H2 at room temperature to validate the developed I-CFD technique (see ESI,† Fig. S2 and S3). Generally, the simulated gas permeances show good agreement with the experimental result. In particular, the H2 permeance is independent of the pressure levels, indicating the Knudsen flow; N2 permeance remains constant until the pressure reaches 4 bars and starts increasing, which suggests a transition to viscous flow.
3.4 Experimental performance and electrochemical simulation
The experimental performance tests (polarisation curves) were conducted at 700, 750 and 800 °C on the two types of samples as shown in Fig. 6a (BF-P) and Fig. 6b (BF-S). It is evident that BF-P displays fuel starvation towards the maximum current density (2.5 A cm−2) at 750 °C and this is more pronounced at 800 °C. This could be a consequence of faster exchange current density and oxygen ions transport with the increase in temperature. However, no sign of fuel depletion is observed for BF-S, which proves the effectiveness of micro-channels in mass transport optimisation. Although BF-S has a slightly smaller pore diameter, lower spongy layer porosity and more constrictions in the spongy layer, it is proved from this result that longer micro-channels and larger inner-wall entrance diameters can compensate for or even outweigh, to a certain extent, the spongy layer's inferiorities. As a consequence, the power density of BF-S is approx. 18% better than BF-P (0.98 vs. 0.83 W cm−2). The output current density of the BF-S is 100% higher than the ones at the same working condition obtained from conventional design.23,71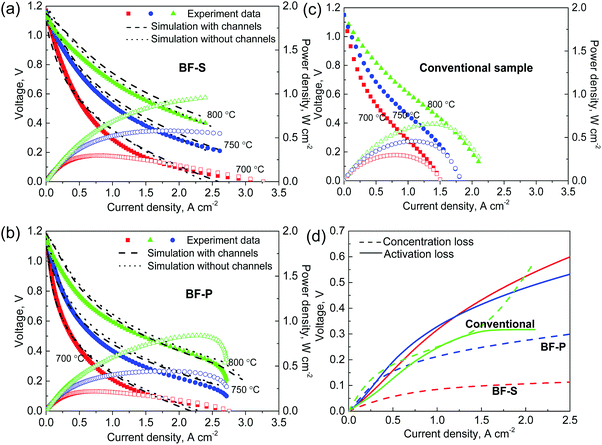 | ||
| Fig. 6 Electrochemical performance simulation using the materials parameters measured from multi-length scale tomography and simulation. Dashed lines and dotted lines in (a) BF-P and (b) BF-S correspond to simulations using Fig. 1(d and e) respectively; (c) conventional sample simulated based on the spongy layer of BF-P with no micro-channels is compared here as a reference; (d) comparisons of the activation and concentration overpotentials of different designs. | ||
The microstructural and mass transport parameters measured by multi-length scale X-ray CT and CFD simulations in Tables 3 and 4 are used to define the 2D electrochemical simulation models. The geometries with embedded micro-channels (Fig. 1d) were defined according to the local properties of the spongy layer only, and the geometries without micro-channels (Fig. 1e) were set up using the characteristic properties of the full anode. The former case is meaningful not only to validate the mass transport parameters obtained from CFD simulations, but also provide the possibility for further parametric study on the geometry of the micro-channels. The latter case could be viewed as a validation of the I-CFD technique when compared with the experimental result, and also provides the convenience for 3D electrochemical simulation in complex hierarchical structures with just a simple geometry using the full anode characteristic parameters.
Simulations of the polarisation curve were conducted at 700, 750 and 800 °C and compared with the experimental results in Fig. 6a (BF-P) and Fig. 6b (BF-S). Conductivity and exchange current density used in the model were adjusted according to the performance at 700 °C on the basis of the empirical formulas from literature (see ESI† for more details). The performance predictions using the two methods both display good agreement with the experimental data. Moreover, the electrochemical performance of the conventional sample, as a reference, is simulated using the same electrochemical parameters as BF-P. The predicted performance of the conventional design (Fig. 6c) matches the published results very well,22,23 displaying 39% lower power density (0.61 W cm−2) than BF-S (0.98 W cm−2). BF-S and BF-P display significantly wider current density window for maximum power density than the conventional design. This evidence confirms the significant performance improvement available when using the micro-channels design as used in BF-S and the validity of the I-CFD technique to estimate the material parameters at multiple length scales.
By using the electrochemical model the different polarisation mechanisms can also be differentiated: the contribution of the concentration loss was isolated by deactivating the mass transport physics; similarly the activation losses can be identified and removed by subsequently increasing the exchange current density i0 up to infinity. Due to the thin electrolyte (5 μm), the Ohmic loss is negligible compared to concentration and activation losses and is not discussed here. The predicted performance at 800 °C is plotted in Fig. 6d which shows that BF-P has approx. 20% lower concentration loss than conventional design, and BF-S decreases the concentration loss by 70%. H2 depletion occurs from the current density of 1.5 A cm−2 onward in the conventional design. The activation overpotential is still the main source of polarisation loss for BF-S and BF-P, but not for the conventional design due to the high local H2O partial pressure, which increases the exchange current density. Further improvement of TPB density was discussed in previous work4 in the aspects of phase content, sintering of Ni and surface area ratio. Also, impregnation of PdO particles grown by coalescence in the cathode has shown great potential to mitigate the activation loss.72
Fig. 7 compares the distributions of simulated field values for three different designs obtained at current density j = 1.3 A cm−2 at 800 °C. Same electrochemical parameters were used for all the three geometries so as to highlight the effect of the micro-channels exclusively. The reactant flux maps clearly show that the reactants are drawn from the centre-bore into the micro-channels and permeate through the spongy layer around them (Fig. 7a and b). These flux maps are consistent with the gas flow simulation in Fig. 5b and f. It is also noticed that the mass flux in the spongy layer ahead of the micro-channels in BF-S is lower than BF-P. This arises from the different diffusion path lengths from the micro-channels tip to the anode-electrolyte interface: the reaction active layer is less than 10 μm and the H2 gas delivered outside of this zone accumulates. The longer the micro-channels are, the higher the local H2 molar concentration will be, as is shown in Fig. 7d and e. The difference between the flux maps for the BF-P and the conventional design is quite small, which indicates that the large distance from the tip of the micro-channels to the reaction sites and the narrow entrance diameter undermine the effectiveness of micro-channels in BF-P. The larger inner-wall diameter of the micro-channels facilitates the permeation of the reactants through the spongy layer as little concentration loss is observed behind the micro-channels in BF-S compared to BF-P (Fig. 7g and h). Moreover, the concentration overpotential ahead of the micro-channels tip is significantly lower in BF-S than BF-P and this is related to the longer micro-channels in BF-S. In contrast, severe concentration polarisation exists in the conventional design in Fig. 7i. Compared with the anode, the concentration loss from cathode is negligible due to the shorter diffusion path and chemical stoichiometry. From the results and discussions above, the incorporation of micro-channels has been proved to be a promising solution to mitigate the mass transport resistance, therefore the electrochemical performance could be further improved by reducing the activation loss at the anode via TPB optimisation and at the cathode through catalyst impregnation.
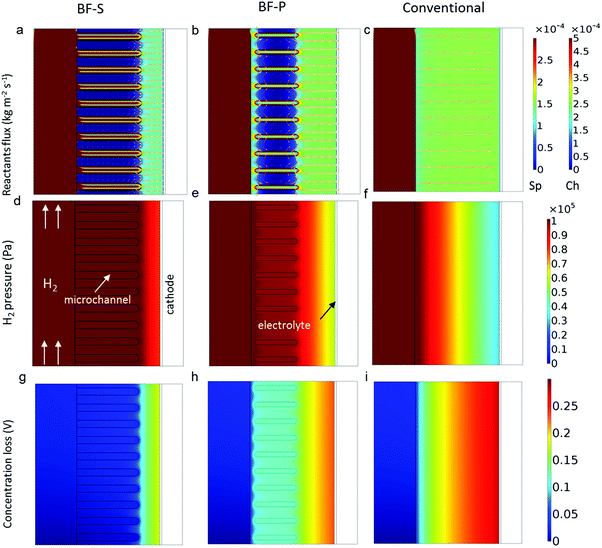 | ||
| Fig. 7 Comparisons of the 2D distributions of reactant fluxes, pressure and concentration overpotential for different designs (Sp: spongy layer; Ch: channels). | ||
4. Conclusion
This study has comprehensively characterised the hierarchically porous microstructure of micro-tubular SOFC (MT-SOFC) anodes and extracted the mass transport parameters for the localized spongy layer and full-thickness anode by using X-ray computed tomography and the integrated computed fluid dynamics (I-CFD) simulation. The I-CFD technique allows the integration of the spongy layer properties into the larger volume simulation and also integrates the Knudsen effect into a continuum flow simulation. The complexity of co-existing continuum and Knudsen flows at different regions of the anode has been decomposed by coupling the continuum flow and molecule-based Direct Simulation Monte Carlo method for the first time. For continuum flow, micro-channels with radial extension of 80% anode thickness and 20 microns inner wall diameter (BF-S) can help to decrease the tortuosity factor by approximately 50% compared to the conventional design. Poorly designed micro-channels (BF-P), spanning for only 50% of anode thickness and having narrow entrance diameter (1–2 μm), decrease the global tortuosity factor by 10% only. The permeability is also improved by approximately two orders of magnitude for BF-S but increases less than one order of magnitude for BF-P. When Knudsen effect is considered, the molecule-wall collisions increase the tortuosity factor by 1.8 to 2 times compared to the value in continuum regime. Electrochemical simulations using either local (with micro-channels) or global (without the micro-channels) measured microstructural and mass transport parameters display good agreement with the experimental measurements, which show that BF-S has 18% higher power density (0.98 W cm−2) than BF-P (0.83 W cm−2) and 60% larger than the conventional tubular design without micro-channels (0.61 W cm−2). The maximum current density has significantly improved compared to the conventional design. BF-P has approximately 20% lower concentration loss than conventional design, while micro-channels in BF-S allow for a decrease in the concentration loss by over 70%. All these results quantitatively prove the effectiveness of micro-channels incorporation in the tubular SOFC anode design. The proposed I-CFD technique in this study provides a unique solution to characterise the mass transport property not only for MT-SOFC anodes or batteries but also for a wider range of hierarchically porous materials such as membranes which could be used under either the continuum regime (water treatment) or the Knudsen regime (gas separation).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge support from the EPSRC under grants EP/N032888/1, EP/P009050/1 and EP/M014045/1, Paul R Shearing acknowledges funding from the Royal Academy of Engineering. Antonio Bertei acknowledges funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 654915.References
- Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602–1644 Search PubMed
.
- Y. Takagi, B.-K. Lai, K. Kerman and S. Ramanathan, Energy Environ. Sci., 2011, 4, 3473–3478 Search PubMed
.
- P. P. Mukherjee, Q. Kang and C.-Y. Wang, Energy Environ. Sci., 2011, 4, 346–369 Search PubMed
.
- X. Lu, T. M. M. Heenan, J. J. Bailey, T. Li, K. Li, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2017, 365, 210–219 CrossRef
.
- C. M. Parlett, K. Wilson and A. F. Lee, Chem. Soc. Rev., 2013, 42, 3876–3893 RSC
.
- Y. Li, Z. Y. Fu and B. L. Su, Adv. Funct. Mater., 2012, 22, 4634–4667 CrossRef
.
- M. Wang, X. Yu, Z. Wang, X. Gong, Z. Guo and L. Dai, J. Mater. Chem. A, 2017, 5, 9488–9513 Search PubMed
.
- G. Pearce, Filtrat. Separ., 2007, 44, 24–27 CrossRef
.
-
Y. Watanabe and K. Kimura, Treatise on Water Science, Elsevier, Oxford, 2011, pp. 23–61 DOI:10.1016/B978-0-444-53199-5.00072-5
.
- M. M. Pendergast and E. M. V. Hoek, Energy Environ. Sci., 2011, 4, 1946–1971 Search PubMed
.
- P. Pandey and R. S. Chauhan, Prog. Polym. Sci., 2001, 26, 853–893 CrossRef
.
- N. Du, H. B. Park, M. M. Dal-Cin and M. D. Guiver, Energy Environ. Sci., 2012, 5, 7306–7322 Search PubMed
.
- J. Kong, K. Sun, D. Zhou, N. Zhang, J. Mu and J. Qiao, J. Power Sources, 2007, 166, 337–342 CrossRef
.
- A. A. Hassan, N. H. Menzler, G. Blass, M. E. Ali, H. P. Buchkremer and D. Stöver, Adv. Eng. Mater., 2002, 4, 125–129 CrossRef
.
- A. C. Müller, D. Herbstritt and E. Ivers-Tiffée, Solid State Ionics, 2002, 152, 537–542 CrossRef
.
- Z. Wang, N. Zhang, J. Qiao, K. Sun and P. Xu, Electrochem. Commun., 2009, 11, 1120–1123 CrossRef
.
- C. Gaudillere and J. M. Serra, Bol. Soc. Esp. Ceram. Vidrio, 2016, 55, 45–54 CrossRef
.
- Y. Chen, Y. Lin, Y. Zhang, S. Wang, D. Su, Z. Yang, M. Han and F. Chen, Nano Energy, 2014, 8, 25–33 CrossRef
.
- S. W. Sofie, J. Am. Ceram. Soc., 2007, 90, 2024–2031 CrossRef
.
-
U. Doraswami, Modelling of Micro-tubular Hollow Fibre Solid Oxide Fuel Cells, PhD thesis, Department of Chemical Engineering, Imperial College London, 2010
.
- W. Lehnert, J. Meusinger and F. Thom, J. Power Sources, 2000, 87, 57–63 CrossRef
.
- D. Panthi and A. Tsutsumi, Sci. Rep., 2014, 4, 5754 CrossRef PubMed
.
- L. Zhou, M. Cheng, B. Yi, Y. Dong, Y. Cong and W. Yang, Electrochim. Acta, 2008, 53, 5195–5198 CrossRef
.
- B. Tjaden, J. Lane, P. J. Withers, R. S. Bradley, D. J. Brett and P. R. Shearing, Solid State Ionics, 2016, 288, 315–321 CrossRef
.
- T. C. Zhang and P. L. Bishop, Water Res., 1994, 28, 2279–2287 CrossRef
.
- N. Epstein, Chem. Eng. Sci., 1989, 44, 777–779 CrossRef
.
- X. Lu, B. Tjaden, A. Bertei, T. Li, K. Li, D. Brett and P. Shearing, J. Electrochem. Soc., 2017, 164, F188–F195 CrossRef
.
- Y. Fu, Y. Jiang, S. Poizeau, A. Dutta, A. Mohanram, J. D. Pietras and M. Z. Bazant, J. Electrochem. Soc., 2015, 162, F613–F621 CrossRef
.
- A. Leonide, Y. Apel and E. Ivers-Tiffee, ECS Trans., 2009, 19, 81–109 Search PubMed
.
- J. Veldsink, R. Van Damme, G. Versteeg and W. Van Swaaij, Chem. Eng. J. Biochem. Eng. J., 1995, 57, 115–125 CrossRef
.
- A. Bertei and C. Nicolella, ECS Trans., 2015, 68, 2887–2895 CrossRef
.
- R. Mueller, S. Zhang, M. Klink, M. Baumer and S. Vasenkov, Phys. Chem. Chem. Phys., 2015, 17, 27481–27487 RSC
.
- J. M. Zalc, S. C. Reyes and E. Iglesia, Chem. Eng. Sci., 2004, 59, 2947–2960 CrossRef
.
- M. Ni, D. Y. C. Leung and M. K. H. Leung, J. Power Sources, 2008, 183, 668–673 CrossRef
.
- Y. Nakano, S. Iwamoto, I. Yoshinaga and J. W. Evans, Chem. Eng. Sci., 1987, 42, 1577–1583 CrossRef
.
- A. Bertei, B. Nucci and C. Nicolella, Chem. Eng. Sci., 2013, 101, 175–190 CrossRef
.
-
G. A. Bird, NASA STI/Recon Technical Report A, 1976, vol. 76 Search PubMed
.
- C. White, T. J. Scanlon and R. E. Brown, J. Spacecr. Rockets, 2015, 53, 134–142 CrossRef
.
- A. Borner, F. Panerai and N. N. Mansour, Int. J. Heat Mass Transfer, 2017, 106, 1318–1326 CrossRef
.
- S. Jaganathan, H. Vahedi Tafreshi and B. Pourdeyhimi, Chem. Eng. Sci., 2008, 63, 244–252 CrossRef
.
- L. M. De Socio and L. Marino, J. Fluid Mech., 2006, 557, 119–133 CrossRef
.
- T. Oshima, S. Yonemura and T. Tokumasu, A numerical study for transport phenomena of nanoscale gas flow in porous media, 28th International symposium on rarefield gas dynamics, American Institute of Physics, 2012, pp. 809–815 Search PubMed.
- R. J. Millington, Science, 1959, 130, 100–102 Search PubMed
.
- J. A. Dreyer, N. Riefler, G. R. Pesch, M. Karamehmedović, U. Fritsching, W. Y. Teoh and L. Mädler, Chem. Eng. Sci., 2014, 105, 69–76 CrossRef
.
- M. Andersson, J. Yuan and B. Sundén, Appl. Energy, 2010, 87, 1461–1476 CrossRef
.
- A. Bertei, J. Mertens and C. Nicolella, Electrochim. Acta, 2014, 146, 151–163 CrossRef
.
- X. Lu, O. O. Taiwo, A. Bertei, T. Li, K. Li, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2017, 367, 177–186 CrossRef
.
- S. M. Jamil, M. H. D. Othman, M. A. Rahman, J. Jaafar, A. F. Ismail and K. Li, J. Eur. Ceram. Soc., 2015, 35, 1–22 CrossRef
.
-
K. Li, Ceramic membranes for separation and reaction, John Wiley & Sons Ltd, Chichester, UK, 2007 Search PubMed
.
- T. Li, Z. Wu and K. Li, J. Power Sources, 2015, 273, 999–1005 CrossRef
.
- H. Strathmann and K. Kock, Desalination, 1977, 21, 241–255 CrossRef
.
- S. Liu, Ceram. Int., 2003, 29, 875–881 CrossRef
.
- B. F. K. Kingsbury and K. Li, J. Membr. Sci., 2009, 328, 134–140 CrossRef
.
- R. Schurch, S. M. Rowland, R. S. Bradley and P. J. Withers, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 709–719 CrossRef
.
- Y. Sagara, A. K. Hara, W. Pavlicek, A. C. Silva, R. G. Paden and Q. Wu, Am. J. Roentgenol., 2010, 195, 713–719 CrossRef PubMed
.
- H. Scherl, M. Koerner, H. Hofmann, W. Eckert, M. Kowarschik and J. Hornegger, Proc. SPIE, 2007, 6510, 651058 CrossRef
.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, Nat. Methods, 2012, 9, 676–682 CrossRef PubMed
.
- S. Campanari and P. Iora, J. Power Sources, 2004, 132, 113–126 CrossRef
.
- M. Benzina, D. Mowla and G. Lacoste, Chem. Eng. J., 1983, 27, 1–7 CrossRef
.
-
H. Darcy, Les fontaines publiques de la ville de Dijon: exposition et application, Victor Dalmont, 1856 Search PubMed
.
- M. A. Gallis, J. R. Torczynski, S. J. Plimpton, D. J. Rader and T. Koehler, AIP Conf. Proc., 2014, 1628, 27–36 CrossRef
.
- Z.-X. Sun, Z. Tang, Y.-L. He and W.-Q. Tao, Comput. Fluids, 2011, 50, 1–9 CrossRef
.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, Ind. Eng. Chem., 1966, 58, 18–27 CrossRef
.
- D. G. Goodwin, H. Zhu, A. M. Colclasure and R. J. Kee, J. Electrochem. Soc., 2009, 156, B1004–B1021 CrossRef
.
-
B. Boer, SOFC anode: hydrogen oxidation at porous nickel and nickel/zirconia electrodes, Universiteit Twente, 1998 Search PubMed
.
- K. Kanawka, M. H. D. Othman, N. Droushiotis, Z. Wu, G. Kelsall and K. Li, Fuel Cells, 2011, 11, 690–696 CrossRef
.
- M. H. D. Othman, Z. Wu, N. Droushiotis, G. Kelsall and K. Li, J. Membr. Sci., 2010, 360, 410–417 CrossRef
.
- T. Heenan, J. Bailey, X. Lu, J. Robinson, F. Iacoviello, D. Finegan, D. Brett and P. Shearing, Fuel Cells, 2017, 17, 75–82 CrossRef
.
- C. Fouard, G. Malandain, S. Prohaska and M. Westerhoff, IEEE Trans. Med. Imaging, 2006, 25, 1319–1328 CrossRef PubMed
.
- A. Bertei and C. Nicolella, J. Power Sources, 2015, 279, 133–137 CrossRef
.
- Z. Yu, S. Liu, F. Zheng and Y. Ding, Int. J. Electrochem. Sci., 2016, 11, 10210–10222 CrossRef
.
- N.-Q. Duan, D. Yan, B. Chi, J. Pu and L. Jian, Sci. Rep., 2015, 5, 8174 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee01064a |
| ‡ The authors equally contributed to this study. |
| This journal is © The Royal Society of Chemistry 2018 |