Na11Sn2PS12: a new solid state sodium superionic conductor†
Z.
Zhang
a,
E.
Ramos‡
a,
F.
Lalère‡
a,
A.
Assoud‡
a,
K.
Kaup
a,
P.
Hartman
b and
Linda F.
Nazar
 *a
*a
aDepartment of Chemistry, Department of Chemical Engineering, and the Waterloo Institute of Nanotechnology, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. E-mail: lfnazar@uwaterloo.ca
bBASF SE, Ludwigshafen, Germany
First published on 4th December 2017
Abstract
We report a new sodium superionic conductor, Na11Sn2PS12, that crystallizes in an unprecedented three-dimensional structure type and exhibits an ionic conductivity of 1.4 mS cm−1, with a very low activation energy barrier for Na-ion mobility of 0.25 eV. A combination of structural elucidation via single crystal X-ray diffraction and ab initio molecular dynamics simulations show that Na+-ion conduction pathways flow through equi-energetic sodium–sulfur octahedra interconnected by partial vacancy cross-over sites in all crystallographic dimensions, providing an understanding of the underlying isotropic 3D fast-ion conduction in this material.
Broader contextLithium-ion technology has led the energy storage market in recent years, but if the electric vehicle market increases as widely anticipated, the growing demand combined with possible lithium resource availability may lead to prohibitive price increases. Low-cost sodium batteries may prove an excellent alternative for grid storage, especially for solid-state batteries where practical energy densities can be anticipated with high performance fast-ion conducting electrolytes. However, very few of the latter are known to date. We report here a new sodium superionic conductor, which crystallizes in a heretofore unprecedented structure, and exhibits amongst the highest conductivity reported for this class of materials. Our study provides an insight into its unique three-dimensional ion conductivity, which aids in the understanding and development of highly functional sodium ion conductors. |
All-solid state batteries (ASSBs) have emerged as very attractive alternatives to conventional liquid electrolyte cells, because of their enhanced safety and higher energy densities.1,2 While development of Li-ion ASSBs is well underway owing to major advances in Li-ion solid state sulfide-based electrolytes that exhibit good ductility,1,3–6 their sodium counterparts lag behind, in part due to a paucity of fast Na-ion conducting analogues.7–9 Amongst the various solid-state electrolytes that have considered for solid state Li-ion systems, the remarkably high ion conductivity of Li10GeP2S12 (“LGPS”, 12 mS cm−1) reported in 2011,3 has inspired growing interest in sulfide based ion-conductors and especially in lithium thiophosphates.4–6 These materials generally exhibit high conductivity and their ductile nature makes them relatively easy to process.4–6 While the aim is to obtain glass-ceramic compositions that can optimize or eliminate grain boundaries, a fundamental understanding of ion conduction in these materials must be founded in studies of single-phase crystalline materials,10 invaluable theoretical studies6,11 and/or studies of ion dynamics.5 Several substitutions in the LGPS family have been explored successfully using Sn4+, and Si4+ to replace (partially or completely)12–19 expensive and reducible Ge4+. Oxygen has partially replaced sulfur, thus potentially increasing the stability towards moisture, however this has been shown to lower the ion conductivity.20
To date, however, there have been very few reports published on replacing Li+ by Na+ in the thiophosphate-type conductors.13,21,22 In particular, although the potential existence of materials in the Na10MP2S12 system in the LGPS structure type (M = Ge, Si, Sn) was predicted by a seminal study involving first-principles calculations,9,23 only one material has been synthesized to date, with nominal formula Na10SnP2S12. Ab initio molecular dynamics (AIMD) simulations show it is a 1D ion conductor, with chains of NaS4 tetrahedra linked along the c-axis providing facile mobility. This material exhibits one of the highest Na+ conductivities ever reported (0.4 mS cm−1),9 in spite of a significant fraction of impurity phases. Materials with a higher degree of phase purity apparently exhibited surprisingly lower conductivity, but the science behind this behavior remains unclear as the structure was unfortunately not resolved by either powder or single crystal methods.
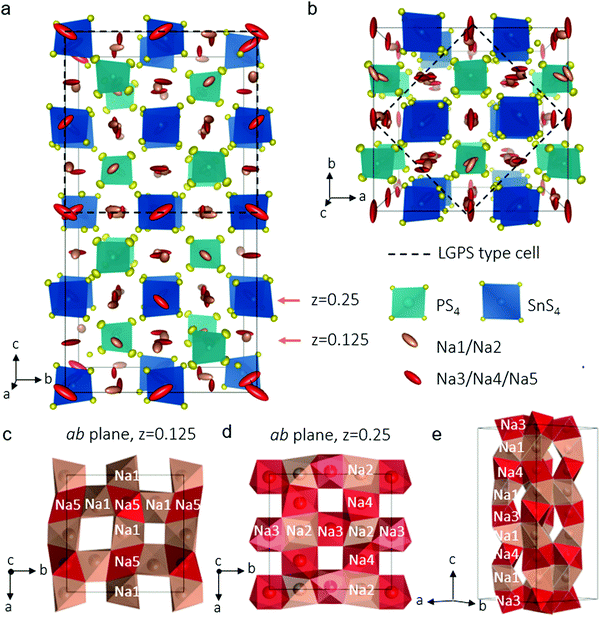
In our explorations of the Na–Sn–P–S phase diagram, we altered our synthesis protocols to favor single crystal growth. After the precursors were melted, slow cooling afforded an agglomerate containing well-defined colourless rectangular crystals about 200 μm long. Single crystal X-ray diffraction allowed us to unequivocally solve the structure of the new phase, Na11Sn2PS12 which is shown in Fig. 1a (see Table 1 and Table S1, ESI† for crystallographic details). The unit cell was indexed in the tetragonal space group I41/acd:2 with a = 13.6148(3) Å and c = 27.2244(7) Å. The structure is related to its LGPS lithium relative,3,10 being comprised of a characteristic 3D chessboard framework of SnS4 and PS4 tetrahedra that delimit wide Na+-ion channels along the c axis and within the ab planes. However, in distinct contrast to either the LGPS structure type, cubic Na3PS4,21 or Na3SbS4,22 the Na+ ions occupy only octahedral sites and the Na ion conductivity is completely three dimensional in nature as demonstrated by ab initio molecular dynamics (AIMD) simulations (see below). This makes it the first example of this structure type among fast ion conductors. The structure is likely not related to the high pressure composition Li11Si2PS12,15 as the latter's PXRD data were refined in a LGPS-type space group (P42/nmc) although the Li sites were not identified, nor their coordination. In Na11Sn2PS12, as expected and confirmed by bond length data (see Table S2, ESI†), Sn and P occupy two distinct sites (Wyckoff sites 16e and 8a, respectively). The relationship between this structure and LGPS is described in Fig. 1a and b. The Sn/P ordering results in quadrupling of the unit cell of Na11Sn2PS12 compared to Li10GeP2S12 (i.e., 5046.4(3) Å3vs. 965.47(9) Å3).3 The replacement of Li+ by Na+ widens the channels resulting in a 30% increase of the equivalent unit cell volume.
| Atom | Wyck site | x | y | z | Occ. | U(eq) (Å2) |
|---|---|---|---|---|---|---|
| Sn1 | 16e | 0.27463(5) | 0 | 1/4 | 1 | 0.0220(2) |
| S1 | 32g | 0.14789(10) | 0.37559(11) | 0.05036(5) | 1 | 0.0280(4) |
| S2 | 32g | 0.15089(10) | 0.07664(11) | 0.05119(5) | 1 | 0.0261(4) |
| S3 | 32g | 0.08891(13) | 0.16558(14) | 0.33188(7) | 1 | 0.0474(5) |
| P1 | 8a | 0 | 1/4 | 3/8 | 1 | 0.0242(7) |
| Na1 | 32g | 0.0099(3) | 0.0185(4) | 0.12519(14) | 0.868(18) | 0.0730(19) |
| Na2 | 16d | 0 | 1/4 | 0.0071(2) | 0.78(3) | 0.082(3) |
| Na3 | 16e | 0.0248(4) | 0 | 1/4 | 0.965(19) | 0.093(3) |
| Na4 | 16c | 0 | 0 | 0 | 0.97(2) | 0.162(5) |
| Na5 | 16f | 0.2383(3) | 0.4883(3) | 1/8 | 0.95(3) | 0.136(4) |
The chains of sodium ions running along the [010] and the [001] directions are shown in Fig. 1c–e by thermal ellipsoids in rose (partially occupied sites) and red (fully occupied sites), which also run along [100]. The sodium ions occupy five distinct octahedral sites, listed in Table 1. Three of these sites are almost, but not quite fully occupied (Na(3), occ. 0.96; Na(4), occ. 0.97 and Na(5), occ. 0.95). The two sites that are partially vacant (Na(1), occ. 0.87; Na(2), occ. 0.78) provide all-important cross-over points that enable the fast ion conduction that we observe by experiment (see below). The pathways are created by each NaS6 octahedron connecting by sharing faces to form networks in all directions. Fortuitously, the partially vacant sites are located at intersection points; Fig. 1(c–e) demonstrate these features. Examples of the 2D slabs in the ab planes are shown at z = 0.125 formed by intersecting Na(1)–Na(5) chains (Fig. 1c) and at z = 0.25 displaying the intersecting Na(3)–Na(2) or Na(4)–Na(2) chains (Fig. 1d). These slabs repeat and are joined along c to form chains of Na+ ions running along [100] (Fig. 1e).
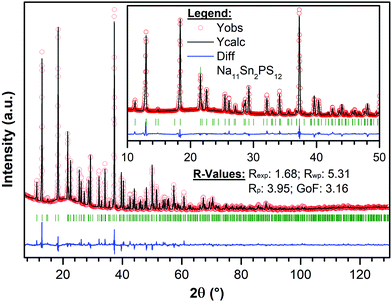
The targeted synthesis of stoichiometric Na11Sn2PS12 as a polycrystalline powder provided a pure phase material. The X-ray diffraction data (Fig. 2) were fit using the model determined by single crystal diffraction. Notably, when the same synthesis procedure (see Methods) was followed to target a stoichiometry of Na10SnP2S12, it resulted in a mixture of Na11Sn2PS12 (60 wt%) and Na3PS4 (40 wt%) with minor unknown impurities. This demonstrates that the Na11Sn2PS12 phase (with entirely NaS6 octahedral sites) is more thermodynamically stable than the Na10SnP2S12 phase. The latter ostensibly comprises a mixture of NaS4/NaS6 sites by analogy to the LGPS structure with which it is reported to be isostructural. Although the precise structure of the latter was not disclosed, the difference in stability revealed by our experiments is likely due to fundamental differences in the framework structure. Because the Na11Sn2PS12 composition melts congruently, we expect it is also more thermodynamically stable than cubic Na3PS4 (which easily converts to a low conductivity tetragonal phase).
The conductivity of a pressed pellet of Na11Sn2PS12 was studied over a broad temperature range (−20 °C to 50 °C). The AC impedance plot at −20 °C is shown in the inset of Fig. 3. The Nyquist plot was fit using an equivalent circuit (see inset) where the grain, grain boundary contribution and the Warburg impedance are represented by their respective elements.
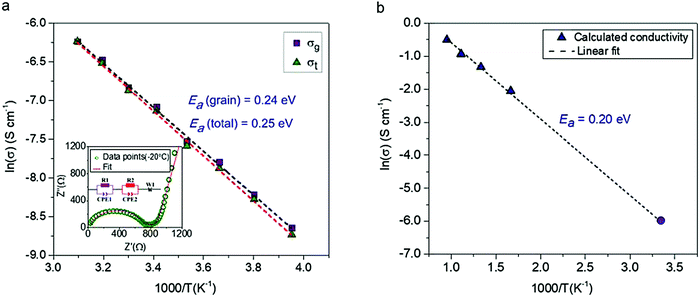 | ||
| Fig. 3 The conductivity and electrochemical stability of Na11Sn2PS12. (a) Activation energy calculated from experimentally measured ionic conductivity versus temperature. The dashed line is the Arrhenius fit to the data; data was collected on two different samples to check for reproducibility, with the other yielding an total Ea of 0.25 eV. (inset) Nyquist plot of the electrochemical impedance spectroscopy at 253 K along with the equivalent circuit employed to fit the data. purple (R1 and CPE1) = grain resistance; red (R2 and CPE2) = grain boundary resistance; W1 = Warburg impedance (electrode polarisation). σ300K = 1.4 × 10−3 S cm−1 @ 2 ton pressure; 1.1 × 10−3 S cm−1 @ 1 ton pressure; (b) Arrhenius plot of Na-ion diffusivity in Na11Sn2PS12 from AIMD simulations. The dotted line is the linear fit to the data (purple triangles), yielding an activation energy of 0.20 eV. The data point represented by the solid purple circle is derived from the extrapolated conductivity at 300 K from the plot of calculated diffusion coefficients shown in Fig. S1 (ESI†). | ||
The relevant fitting parameters are shown in Table S4 (ESI†). Unlike Na+ oxide conductors, the conductivity in cold pressed Na11Sn2PS12 is governed by Na ion mobility within the grains, and therefore the total conductivity is dominated by the grain conductivity. The total conductivity obtained from the sum of the grain boundary and bulk resistances −1.4 mS cm−1 at room temperature – is amongst the highest reported for sodium ion conductors. The overall activation energy for Na-ion hopping determined from the Arrhenius plot (Fig. 3a) is 0.25 eV, and the activation energy for ion transport within the grains is 0.24 eV, which is much lower than that of Na10SnP2S12 (0.35 eV).9 The ionic conductivity and activation energy data of Na11Sn2PS12 are compared to other Na-ion thiophosphate conductors in Table 2. Comparison with other materials is difficult since to date few other superionic conductors have been successfully synthesized for room temperature sodium based battery applications. The partial electronic conductivity of Na11Sn2PS12 measured by the DC polarization method is 6.0 × 10−9 S cm−1, similar to that of other sulfide-based fast ion conductors such as Na3SbS4 (1.9 × 10−10 S cm−1)22 and Li7P3S11 (8.0 × 10−9 S cm−1).24 It is about six orders of magnitude lower than the ionic conductivity, qualifying the material as a solid state electrolyte.
| Formula | Experimental | Predicted | Ref. | ||
|---|---|---|---|---|---|
| σ 25°C (mS cm−1) | E a (eV) | σ 25°C (mS cm−1) | E a (eV) | ||
| Na11Sn2PS12 | 1.4 | 0.25 | 2.4 | 0.20 | This work |
| Na10SnP2S12 | 0.4 | 0.356 | 0.94 | 0.317 | 9 |
| Na10GeP2S12 | — | — | 3.5; 4.7 | 0.27; 0.2 | 9 and 23 |
| Na3PS4 tetragonal | 0.004 | 0.416 | — | — | 21 |
| Na3PS4 cubic (glass-ceramic) | 0.2 | 0.28 | — | — | 7 |
| Na3PSe4 | 0.11 | 0.28 | — | — | 8 |
Aside from brittle crystalline materials such as NASICON that exhibit high ionic conductivity and excellent stability to Na metal,25,26 the electrochemical stabilities of most sodium phosphosulfides have not been reported. Their lithium counterparts such as Li10SnP2S12, and even Li7P3S11 typically are reduced in contact with metallic Li,24 but are quite oxidatively stable. Na3SbS4 is also stable up to 5 V,22 and similar oxidative stability of Na11Sn2PS12 was exhibited by our cyclic voltammogram studies. Na3SbS4 is also reported to be surprisingly stable to reduction. While Na metal has a higher potential than Li metal, and is thus less reducing, we still expect that decomposition products may form at the interface for these materials. These may providentially passivate the negative electrode. On the other hand, since Na10SnP2S12 has a predicted reduction potential of 1.25 V vs. Na,9,11 similar properties may govern Na11Sn2PS12. Incorporating an additional nanometric layer (i.e., ionic liquid or polymer) would further stabilize the interface, but this is beyond the scope of this work that focusses on the outstanding fast-ion conduction properties of the material.
To explore the Na-ion dynamics and diffusion in Na11Sn2PS12, we performed AIMD simulation. The MD simulations were carried out at elevated temperatures ranging from 600 K to 1050 K to speed up the diffusion and shorten the simulation time. The Na-ion probability density isosurface from the AIMD simulation at 1050 K is shown in Fig. 4. The results clearly demonstrate the 3D diffusion pathways in this structure and show the significant Na+ ion hopping both in the ab plane and along the c axis, consistent with that predicted from simple consideration of the single-crystal structure. Remarkably, all the Na atoms in the five distinct crystallographic sites take part in ion diffusion, owing to the strategic partial Na vacancies at the cross-over points. This suggests that increasing the Na vacancy content by aliovalent doping may further enhance the conductivity. The partially occupied Na(1) and Na(2) sites provide fast ion exchange sites for ion conduction as mentioned above. Na ion diffusion along the c axis involves –Na(4)–Na(1)–Na(3)–Na(1)– chains, as shown in Fig. 4a. Meanwhile, Na ions transport via 3-2-3 sites; 4-2-4 sites; or 5-1-5 sites along the a axis or b axis. Fig. 4b and c depict the ion migration pathway in two different ab planes at z = 0.125 and 0.25, respectively. The evenly distributed probability densities imply that the Na ions have a relatively flat landscape along these channels, which explains the high ionic conductivity and the low activation energy we observe. This is in accord with a concerted ionic migration mechanism recently proposed to account for fast ion diffusion in super-ionic conductors.27 The diffusivities can be calculated from the mean square displacement of the Na atoms from the AIMD calculations. Fig. S1 (ESI†) presents the Arrhenius plot for the diffusion coefficients at temperatures from 600 K to 1050 K. The extrapolated diffusion coefficient of 2.2 × 10−8 cm2 s−1 to room temperature (300 K) yields a theoretical conductivity of 2.4 mS cm−1. This is remarkably consistent with the experimental value of 1.4 mS cm−1.
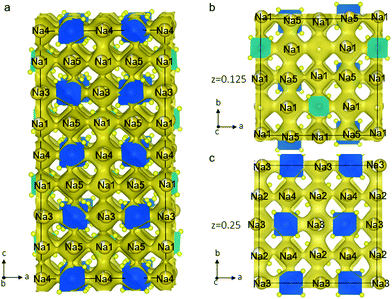 | ||
| Fig. 4 Na-ion probability density isosurface (yellow) obtained from ab initio molecular dynamics (AIMD) studies at 1050 K for 40 ps, confirming the nature of the 3D Na+ ion conduction paths suggested by the structure shown in Fig. 1. (a) Sodium diffusion along the c axis involves a pathway along –Na(4)–Na(1)–Na(3)–Na(1)– chains; (b) the Na-ion probability density obtained from the AIMD Na-ion trajectories in the ab plane shows the pathways at (b) z = 0.125 and (c) z = 0.25. | ||
The directional diffusivities are also obtained by fitting the mean square displacement in crystallographic directions as a function of time. Details of the calculations can be found in the ESI.† The diffusivities from 600 K to 1050 K in three different directions (along the a, b and c axes) are shown in Table S5 (ESI†). Na+ ion diffusion coefficients along these three directions are very close to each other, indicating that Na11Sn2PS12 is a quasi-isotropic conducting material, in contrast to the members of the LGPS family. The latter are primarily 1D conductors that exhibit additional 2D pathways of lower diffusivity. 3D conductors are clearly superior since they maintain good conductivity in all macroscopic dimensions and prohibit blocking effects that can plague 1D or 2D conductors. Fig. S2 (ESI†) shows the trigonal faces of the octahedra that Na+ ions hop through along the c axis, and a, b axes in the ab plane, which define a bottleneck for ion transport. The calculated diffusion coefficients at 750 K along these three directions are labeled. The bottleneck size for Na+ ion transport through these three directions (Table S6, ESI†) suggest that they are very similar, in accord with the calculated diffusion coefficients. Furthermore, the Na–Na atomic distances are almost the same along a, b, or c axis, as shown in Table S2 (ESI†). Therefore, the uniform diffusivity along the three directions of Na11Sn2PS12 can be attributed to the equivalent Na-Na atomic distances (3.41 ± 0.04 Å) and the similar bottleneck sizes for Na+ ion hopping along the three directions which results in an equipotential surface for ion transport.
The ionic conductivities at different temperatures were obtained from the calculated diffusion coefficients using the Nernst Einstein equation, and the Arrhenius plot of the calculated conductivity vs. reciprocal temperature is shown in Fig. 3(b). The fitted activation energy of 0.20 eV is in excellent agreement with the experimentally determined value (0.24 eV for the grains), giving us confidence in both values. We note that these values are fairly similar to those of LGPS (0.24 eV measured; 0.19 eV calculated).
In conclusion, Na11Sn2PS12 is a promising solid-state sulfide electrolyte with a high ionic conductivity, owing to a unique structure type with ordered Sn/P tetrahedra as determined by single crystal diffraction. Its Na+-ion transport channels present the first example of a totally 3D face-sharing octahedral site pathway in a solid state sulfide conductor. In materials where ions are trapped in very low-energy minima, activation energy for moving between these sites is increased, and thus diffusivity is reduced. In contrast, Na11Sn2PS12 presents an excellent example of a structure in which the diffusivity of alkali cations is determined by a smooth free-energy landscape: namely all Na+–Na+ distances are effectively equivalent, and all Na+ ions are in the same coordination environment. The energy of the Na ions in the c-axis chains, two dimensional ab planes and in the crossover sites that connect them (the partially occupied sites) is thus expected to be similar. This allows Na+ to migrate in three dimensions as shown by the AIMD simulations, with a very low barrier of 0.24 eV. Furthermore, the conductivity of the new Na11Sn2PS12 electrolyte, 1.4 mS cm−1, is higher than that of the best known phosphosulfide sodium conductors, with the potential to approach the conductivities of known Na-electrolytes such as NASICON (3.4–4.0 mS cm−1)25,26 by additional tweaking via substitution. Importantly, the sulfides are more compatible with all solid-state battery fabrication than oxide electrolytes owing to their highly ductile nature. Our study highlights the benefits that can be gained by using targeted synthesis approaches to guide material discovery, and represents a further understanding the dynamics of ion transport in solid electrolytes.
Methods
Single crystal synthesis
Na2S (99%, Sigma-Aldrich), P2S5 (99%, Sigma-Aldrich) and SnS2 (99.9%, Kojundo) were mixed together in a mortar at a molar ratio of 5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The mixture was pelletized and sealed in a carbon-coated quartz tube under vacuum. After a heat treatment at 700 °C for 2 h followed by a slow cooling step of 99 h from 700–250 °C, the sample was cooled to room temperature. The resultant material consisted of an agglomerate of crystals that were gently separated from each other to give single crystals.
2. The mixture was pelletized and sealed in a carbon-coated quartz tube under vacuum. After a heat treatment at 700 °C for 2 h followed by a slow cooling step of 99 h from 700–250 °C, the sample was cooled to room temperature. The resultant material consisted of an agglomerate of crystals that were gently separated from each other to give single crystals.
Single crystal diffraction and structure resolution
Several colourless block-shaped single crystals of Na11Sn2PS12 with dimensions of approximately 0.070 × 0.020 × 0.018 mm3 were scanned to determine their quality. Two data sets were collected and gave exactly the same results. The data were collected on BRUKER KAPPA diffractometer equipped with SMART APEX II CCD, utilizing graphite-monochromated Mo-Kα radiation. Since the crystals were moisture and air sensitive, they were protected by Paratone-N oil and liquid nitrogen flow using an OXFORD Cryostream controller 700 at 280 K. The data were collected by scanning ω and ϕ of 0.3° in couple of groups of frames at different ω and ϕ and an exposure time of 30 seconds per frame. The data were corrected for Lorentz and polarization effects. Absorption corrections were based on fitting a function to the empirical transmission surface as sampled by multiple equivalent measurements using SADABS (since the crystal did not exhibit well defined facets). The unit cells were indexed using the Bruker APEX II suite, Cell_Now software. Reciprocal space was checked since the crystals showed pseudo-merohedral twinning. The structure was solved using direct methods and was refined anisotropically using the least squares method incorporated in the SHELXTL package (see Table S3, ESI† for details). The program Tidy was used to standardize the atomic positions.Microcrystalline synthesis
Na2S (99%, Sigma-Aldrich), P2S5 (98%, Sigma-Aldrich) and SnS2 (99%, Kojundo) were mixed together in a mortar at a molar ratio of 5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The mixture was pelletized, sealed in a quartz tube under vacuum and heated at 700 °C for 5 h followed by two cooling steps at 0.2 °C min−1 from 700–400 °C and at 2 °C min−1 from 400 °C to room temperature. The sample resulted in an agglomerate of tiny crystals that were crushed into powder for further analysis.
2. The mixture was pelletized, sealed in a quartz tube under vacuum and heated at 700 °C for 5 h followed by two cooling steps at 0.2 °C min−1 from 700–400 °C and at 2 °C min−1 from 400 °C to room temperature. The sample resulted in an agglomerate of tiny crystals that were crushed into powder for further analysis.
Powder diffraction and refinement
X-ray powder diffraction data were collected on a PANalytical Empyrean instrument outfitted with a PIXcel two-dimensional detector using Cu-Kα radiation. In order to protect the sample from air exposure, it was loaded in a 0.3 mm diameter glass capillary in an argon filled glovebox. Rietveld quality patterns were recorded in Debye–Scherrer geometry using a parabolic X-ray mirror in the incident beam. All powder patterns were refined using the Rietveld method within the software package TOPAS 4 (Bruker-AXS).Conductivity measurements
The microcrystalline powder of Na11Sn2PS12 was pelletized at room temperature in a 10 mm diameter. The pellet was then placed between two In foils in a swagelok cell. The cell was placed in an ITS oven (Bio-Logic) for measurements at different temperatures and connected to a MTZ-35 impedance analyzer (Bio-Logic), both controlled by the software MT-LAB (Bio-Logic). The impedance was measured from 35 MHz to 1 Hz every 10° from −20 °C to 50 °C. For measurement of partial electronic conductivity, DC polarization experiments were conducted on a pellet of 1.08 mm thickness, using ion blocking electrodes (stainless steel).Density functional theory (DFT) calculations and ab initio molecular dynamics (AIMD) simulations
Geometry optimization was performed by DFT calculations with the Vienna ab initio simulation package,28 using the projector augmented-wave (PAW) method.29 The generalized gradient approximation (GGA) function parameterized by Perdew–Burke–Ernzerhof (PBE)30 was used to describe the exchange correlation potential. The plane wave energy cut-off was set to 550 eV. The geometry optimization was carried out using a 1a × 1b × 1c supercell with 208 atoms. The total energy was converged to within 10−5 eV, and the force on each atom was converged to within 0.01 eV Å−1.The Na+ ion diffusivity in Na11Sn2PS12 was studied by AIMD simulations in the canonical (NVT) ensemble at four elevated temperatures (600 K, 750 K, 900 K, 1050 K). The volume of the unit cell and the initial position of atoms were obtained from the fully relaxed cells. The samples are heated up to the targeted temperature (600 K, 750 K, 900 K, 1050 K) by velocity scaling over 2 ps, and then equilibrated at the desired temperature. The MD simulations were carried out for 40 ps at each temperature by a Nosé thermostat,31 and a time step of 1 fs was used to integrate the equation of motion. No melting or breaking of P–S or Sn–S bonds were observed during the simulations. To keep the computational time reasonable for the relatively large unit cell, integration in reciprocal space was only performed at the Γ-point.
Na+ ion probability densities were calculated from the atomic trajectories. The Na positions relative to the mass center of the framework atoms (Sn, P, S) were smoothed using a Gaussian kernel with s.d. of 0.2 Å.
The diffusion coefficient is defined as
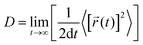 | (1) |
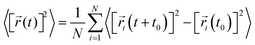 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) is the displacement of the i-th Na ion at time t and t0 is the initial time. D is obtained by linear fitting to the dependence of average mean square displacement over 2dt. The diffusivity in certain directions is obtained by fitting to the mean square displacement in these directions over time. For example, the diffusion coefficient in the c direction Dc can be defined as
i(t) is the displacement of the i-th Na ion at time t and t0 is the initial time. D is obtained by linear fitting to the dependence of average mean square displacement over 2dt. The diffusivity in certain directions is obtained by fitting to the mean square displacement in these directions over time. For example, the diffusion coefficient in the c direction Dc can be defined as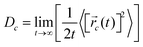 | (3) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) is the displacement of Na ions in the c directions at time t.
c(t) is the displacement of Na ions in the c directions at time t.
Ionic conductivity is obtained from the diffusivity according to the Nernst–Einstein relation (eqn (4)), in which zNae is the charge of a Na+ ion, cNa is the concentration of Na ions, T is the temperature, and kB is the Boltzmann's constant.
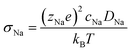 | (4) |
The extrapolation of results to room temperature and the calculation of the activation energy were performed based on the Arrhenius fit to the diffusion coefficient.
Conflicts of interest
There are no conflicts to declare.References
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631 CAS.
- D. A. Weber, A. Senyshyn, K. S. Weldert, S. Wenzel, W. Zhang, R. Kaiser, S. Berendts, J. Janek and W. G. Zeier, Chem. Mater., 2016, 28, 5905–5915 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- S.-H. Bo, Y. Wang, J. C. Kim, W. D. Richards and G. Ceder, Chem. Mater., 2016, 28, 252–258 CrossRef CAS.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef CAS PubMed.
- A. Kuhn, J. Köhler and B. V. Lotsch, Phys. Chem. Chem. Phys., 2013, 15, 11620–11622 RSC.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17 CrossRef CAS.
- P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697 CrossRef CAS PubMed.
- Y. Kato, R. Saito, M. Sakano, A. Mitsui, M. Hirayama and R. Kanno, J. Power Sources, 2014, 271, 60–64 CrossRef CAS.
- O. Kwon, M. Hirayama, K. Suzuki, Y. Kato, T. Saito, M. Yonemura, T. Kamiyama and R. Kanno, J. Mater. Chem. A, 2014, 3, 438–446 Search PubMed.
- A. Kuhn, O. Gerbig, C. Zhu, F. Falkenberg, J. Maier and B. V. Lotsch, Phys. Chem. Chem. Phys., 2014, 16, 14669–14674 RSC.
- S. Hori, K. Suzuki, M. Hirayama, Y. Kato, T. Saito, M. Yonemura and R. Kanno, Faraday Discuss., 2015, 176, 83–94 RSC.
- P. Bron, S. Dehnen and B. Roling, J. Power Sources, 2016, 329, 530–535 CrossRef CAS.
- P. Zhou, J. Wang, F. Cheng, F. Li and J. Chen, Chem. Commun., 2016, 52, 6091–6094 RSC.
- Y. Sun, K. Suzuki, S. Hori, M. Hirayama and R. Kanno, Chem. Mater., 2017, 29, 5858–5864 CrossRef CAS.
- Y. Sun, K. Suzuki, K. Hara, S. Hori, T. Yano, M. Hara, M. Hirayama and R. Kanno, J. Power Sources, 2016, 324, 798–803 CrossRef CAS.
- A. Hayashi, K. Noi, N. Tanibata, M. Nagao and M. Tatsumisago, J. Power Sources, 2014, 258, 420–423 CrossRef CAS.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, Angew. Chem., Int. Ed., 2016, 55, 8551–8555 CrossRef CAS PubMed.
- V. S. Kandagal, M. D. Bharadwaj and U. V. Waghmare, J. Mater. Chem. A, 2015, 3, 12992–12999 CAS.
- S. Wenzel, D. A. Weber, T. Leichtweiss, M. R. Busche, J. Sann and J. Janek, Solid State Ionics, 2016, 286, 24–33 CrossRef CAS.
- Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li, L. Gu, Y.-S. Hu, H. Li, X.-Q. Yang, L. Chen and X. Huang, Adv. Energy Mater., 2017, 7, 1601196 CrossRef.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Chem. Mater., 2016, 28, 4821–4828 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- A. Franceschetti, S.-H. Wei and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17797–17801 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee03083e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |