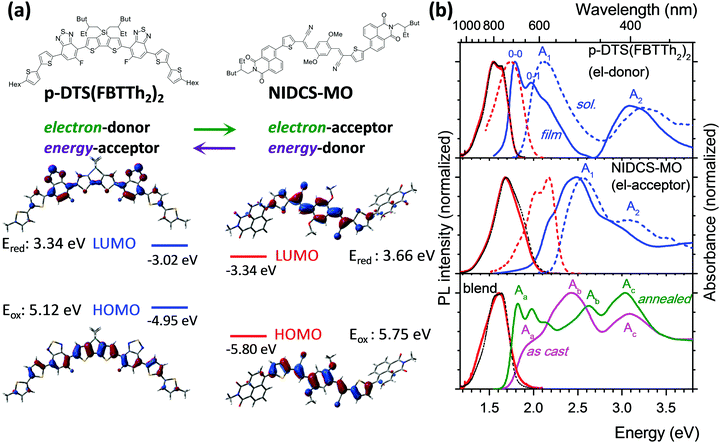
Designing high performance all-small-molecule solar cells with non-fullerene acceptors: comprehensive studies on photoexcitation dynamics and charge separation kinetics†
Junqing
Shi
 a,
Anna
Isakova
a,
Anna
Isakova
 a,
Abasi
Abudulimu
a,
Marius
van den Berg
b,
Oh Kyu
Kwon
c,
Alfred J.
Meixner
b,
Soo Young
Park
a,
Abasi
Abudulimu
a,
Marius
van den Berg
b,
Oh Kyu
Kwon
c,
Alfred J.
Meixner
b,
Soo Young
Park
 *c,
Dai
Zhang
*b,
Johannes
Gierschner
*c,
Dai
Zhang
*b,
Johannes
Gierschner
 *ab and
Larry
Lüer
*ab and
Larry
Lüer
 *a
*a
aMadrid Institute for Advanced Studies, IMDEA Nanoscience, Calle Faraday 9, Campus Cantoblanco, 28049 Madrid, Spain. E-mail: larry.luer@imdea.org; johannes.gierschner@imdea.org
bInstitute of Physical and Theoretical Chemistry, University of Tübingen, Auf der Morgenstelle 15, 72076 Tubingen, Germany. E-mail: dai.zhang@uni-tuebingen.de
cCenter for Supramolecular Optoelectronic Materials and WCU Hybrid Materials Program, Department of Materials Science and Engineering, Seoul National University, ENG 445, Seoul 151-744, Korea. E-mail: parksy@snu.ac.kr
First published on 12th December 2017
Abstract
Solution-processable all-small-molecule organic solar cells (OSCs) have shown dramatic progress in improving stability and photovoltaic efficiency. However, knowledge of photoexcitation dynamics in this novel class of materials is very limited. To fully exploit the design capacities inherent in small molecule chemistry, the elementary processes and branching yields must be known in detail. Here, we present a combined computational–experimental study of photoexcitation dynamics of a prototypical all-small-molecule photovoltaic blend, p-DTS(FBTTh2)2 as a donor and NIDCS-MO as an acceptor. Femtosecond spectroscopy data show that excitonic coupling is small and that the charge transfer states are localized, at first glance contradicting the high internal quantum efficiency (IQE) and open circuit voltage (VOC) of this material. A target analysis of the femtosecond spectra yields exciton dissociation rates of 1/(25 ps) and 1/(100 ps) for the as-deposited and annealed blend, respectively. These rates are far slower than in typical polymer based organic solar cells. Still, internal quantum yields are high because parasitic quenching processes are found to be even slower. In the framework of semiclassical Marcus theory, we demonstrate that our system shows near-optimum energy conversion and charge separation yields, due to negligible activation energy for charge generation but high activation energy for charge recombination, allowing enough time to separate localized charge transfer states. We thus justify both the high internal quantum yields and the high open circuit voltage found in this system. Finally, we predict that highly efficient and stable low-optical bandgap systems can be realized by reducing the electronic coupling between the donor and acceptor.
Broader contextOrganic solar cells (OSCs) contribute to a sustainable society because their salient properties – transparency, flexibility, large illumination acceptance angle – make them apt for applications close to the customer. Polymeric electron donor materials are easy to process but have intrinsically limited efficiencies and morphological stability. Small molecules allow for much better control than polymers but do not lend themselves to low-cost production. Therefore, a novel class of solution-processable all-small-molecule OSCs has been developed, combining high definition with ease of processing. High efficiencies have been reached in just a few years of research, which calls for a dedicated study of the specific bottlenecks and branching yields in the photovoltaic elementary processes in these materials. This is done here on a prototype cell, which is ideal for this purpose as the donor and acceptor can be excited independently due to complementary absorption spectra. We address the role played by delocalized states (a crucial factor in polymer based OSCs) and exciton diffusion, and we quantify dominant loss channels as a function of processing conditions. |
Introduction
Organic-based solar cells (OSCs) are a promising route to develop photovoltaic devices for novel low-cost applications such as light-weight, shape-adapted, large-area and semi-transparent devices.1 The main strategy during the past 15 years was focused on combining (co)polymers as electron donors (D) with fullerene derivatives (in particular [6,6]-phenyl-C61-butyric acid methyl ester; PCBM) as electron acceptors (A). The dominance of polymers over small molecules relied on their facile synthesis and high solubility which allows for easy processing, while the exceptional acceptor abilities of PCBM were unmatched by other materials. To compromise the typically small exciton diffusion length of about 10 nm in the polymers and sufficient light absorption, bulk heterojunction (BHJ) morphologies are used.2 Although copolymer:PCBM BHJ OSCs have surpassed 10% power conversion efficiency (PCE), their further improvement meets severe intrinsic limitations, significantly slowing down overall progress in the past few years.3The most important new trend of the last few years is high-efficiency non-fullerene OSCs4–10 which can be e.g. based solely on polymers.5 On the other hand, recently there have been large efforts to synthesize small molecules by simple chemistry and with high solubility4,6,10–18 so that such materials can be easily processed.13 In fact, efficient solution-processed mixed polymer/small-molecule OSCs have recently been achieved with 10–13% PCE13,14 and long-term stability.15 In particular, solution-processed all-small-molecule (i.e. polymer-free) non-fullerene OSCs have been increasingly reported in the last two years,10,16–18 and despite their very recent appearance, PCEs are now already at 9–10%.18
Despite the success of all-small-molecule OSC devices, the advantages of the concept against the classic polymer:PCBM type cells are not fully understood. It is expected that morphological16 and stability issues15 play important roles; however little information is available so far on the dynamics of exciton dissociation and of the rates and yields of competing processes.
Here we present a combined spectroscopic, morphological and computational study on the groundbreaking first example for solution-processed highly efficient all-small-molecule BHJ OSCs (PCE of 5.4%),16 based on p-DTS(FBTTh2)2 as a donor19 and NIDCS-MO as an acceptor (for the chemical structure see Fig. 1a). This material combination has shown phase separation into nanofibrils (under optimized annealing conditions; i.e. 110 °C),16 leading to efficient charge extraction. Due to the complementary absorption spectra of D and A, this system is ideal for quantitative photophysical studies. We recall that PCE is the product of the yields for light absorption, energy conversion, charge separation and charge extraction. The PCE values of more than 10%, published recently,18b have been achieved mainly by improvements in the light absorption and charge extraction yields. In contrast, the energy conversion and charge separation yields have already been very high in the material of ref. 16, as demonstrated by VOC values exceeding 0.9 V and by internal quantum efficiencies close to 50%, respectively. In our work, we quantify and rationalize the high energy conversion and charge separation yields of the blend of ref. 16, thus showing that the results are relevant also for the most recent high efficiency small molecule based OSC.
We use transient absorption (TA) and time-resolved photoluminescence (PL) spectroscopy as complementary techniques, allowing us to assess the properties and dynamics of both neutral and charged excited states in the relevant time scale from femtoseconds to microseconds. We obtain the delocalization lengths of singlet excited states and charged states, which we also calculate by time-dependent density functional theory (TD-DFT). Deploying a target analysis of the TA spectra, we obtain the rates of charge transfer and parasitic exciton quenching at defects. Our results suggest that the dynamics of charge generation in solution-processed all-small-molecule BHJ OSCs is drastically different from that in polymer-based OSCs. Finally, we use our results to predict reorganization energies and D–A coupling strengths giving maximum charge separation efficiency in the framework of the semiclassical model of Marcus electron transfer.
Experimental and computational details
Materials
The donor compound p-DTS(FBTTh2)2 was purchased from 1-Material Inc.;19 the synthesis of the acceptor compound NIDCS-MO has been described elsewhere;20 the chemical structures are given in Fig. 1a. Dilute solutions (optical density OD ≤ 0.05) of the compounds were prepared in chloroform (Sigma-Aldrich, spectroscopic grade) by stirring. Pure and blend films under different thermal conditions (as cast and annealed) were prepared by spin-coating from solutions of the pure compounds (10 mg mL−1 in chloroform) as well as their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture by stirring at 55 °C. Spin-coating (1800 rpm, 60 s) of these solutions was done on glass substrates (10 × 10 mm2) to give devices with a film thickness of 90–110 nm. Thermal annealing was done at 110 °C for 20 min, being the optimal procedure for high power conversion efficiency for this material mixture.16
1 mixture by stirring at 55 °C. Spin-coating (1800 rpm, 60 s) of these solutions was done on glass substrates (10 × 10 mm2) to give devices with a film thickness of 90–110 nm. Thermal annealing was done at 110 °C for 20 min, being the optimal procedure for high power conversion efficiency for this material mixture.16
Experimental details
Results and discussion
Optical spectra and photophysics of pure D and A
For ease of presentation, p-DTS(FBTTh2)2 and NIDCS-MO will be called D and A, respectively, for the remainder of this paper, referring to their respective roles as donor and acceptor. The optimized molecular structures of D and A are shown in Fig. 1a, together with the frontier orbital topologies and calculated energies. In agreement with the experimental results from ref. 16, given as dashed lines, this material combination shows an appealingly small offset of the LUMO energies, which is thought to be one reason for the high open circuit voltages reached in OSCs.16 Absorption and PL spectra of D and A in chloroform solutions are given as dashed blue and red lines, respectively, in Fig. 1b. Both D and A show two main absorption bands in the visible and near UV spectral region. A detailed discussion of the electronic transitions involved in the bands, based on (TD)DFT calculations, is given in the ESI,† part B.In the as-cast film of D, the absorption and PL spectra are strongly red-shifted against solution by 0.35 eV and 0.22 eV, respectively (solid lines in Fig. 1b, and Table 1), and well-resolved vibronic sidebands are observed in particular in the absorption spectrum (apparent 0–0, 0–1 bands in Fig. 1).22 The latter is a clear sign of the more rigid, well-ordered environment in the film as compared to fluid solution, which steepens the torsional potentials.23 In fact, in single crystal X-ray analysis, densely packed, planar, π-stacked molecules were observed which are considerably slipped along their long molecular axis.24 These structural properties and the molecule's rather extended conjugation25 significantly reduce excitonic coupling as indeed confirmed by TD-DFT calculations (see ESI,† part B, Table S2). The observed significant spectral red-shift against solution therefore arises mainly from polarizability effects observed in well-ordered solids.26 On the other hand, planarization effects are expected to be small as well due to the essentially planar molecular backbone in the equilibrium geometry (see also ESI,† part B). This is especially the case for the emission, which originates from a largely planarized S1 state also in solution (Scheme S1, ESI†). Annealing of the film at 110 °C hardly changes the absorption features,16 although X-ray diffraction (XRD) clearly indicates the transformation from an amorphous to a (poly)crystalline phase.16 The equivalence of the absorption spectra in the two phases proves that the formation of well-ordered nuclei (i.e. short-range order) is the initial step in the self-organization of D; however the main morphological change upon annealing is taking place in the long range. Compared to solution, the PL is strongly quenched in the films of p-DTS(FBTTh2)2 giving ΦF = 1% (Table 1), which is attributed to effective trapping typically found in polycrystalline films.27 Annealing of the film hardly changes the spectral characteristics.
| E abs/eV | E PL/eV | Φ F | τ F/ns | ||
|---|---|---|---|---|---|
| a As-cast/annealed. | |||||
| p-DTS(FBTTh2)2 | Solution | A1: 2.14 | 1.77 | 0.12 | 1.4 |
| A2: 3.23 | |||||
| Filma | A1: 1.79 | 1.55 | 0.01/0.01 | — | |
| A2: 3.08 | |||||
| NIDCS-MO | Solution | A1: 2.56 | 2.18 | 0.37 | 1.2 |
| A2: 3.09 | |||||
| Filma | A1: 2.49 | 1.70 | 0.04/0.04 | 1.3/1.5 | |
| A2: 2.90 | |||||
| Blend | As-cast | A1: 1.96 | 1.64 | <0.01 | — |
| A2: 2.43 | |||||
| A3: 3.08 | |||||
| Annealed | A1: 1.82 | 1.64 | <0.01 | — | |
| A2: 2.63 | |||||
| A3: 3.04 | |||||
The as-cast film of A exhibits only a moderate red-shift of 0.07 eV against solution (Fig. 1 and Table 1), with a pre-band at 2.22 eV (558 nm), giving the spectrum features of weak H-aggregates.28 The film is amorphous and does not change upon annealing at 110 °C,16 giving rise to the same absorption feature. At higher annealing temperatures (150 °C) a different phase is found,16 with a blue-shifted absorption band, which is indicative of stronger H-aggregation. As compared to the solution spectrum, the PL intensity of the as-cast and annealed film (110 °C) is largely reduced (ΦF = 4%) and the spectral profiles are unstructured, which points to non-negligible intermolecular vibronic contributions.29
Optical spectra and photophysics of blended films
The original report on the blended films of p-DTS(FBTTh2)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NIDCS-MO (1
NIDCS-MO (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
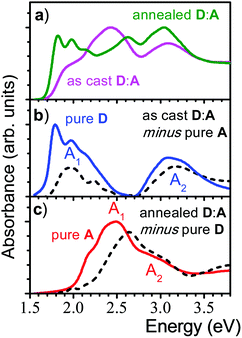
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) demonstrated a strong impact of annealing on the OSC device performance,16 which was correlated with a significant change in the absorption spectra as shown in Fig. 1. Comparing the as-cast and annealed blended films with pure films, it might be surprising that none of the absorption spectra of the blended films is a simple superposition of the single components, as one might expect from a BHJ film. Instead, the features of the as-cast film seem to be dominated by the electron acceptor (A; NIDCS-MO) spectrum, while the main features of the annealed film seem to originate from the donor (D; p-DTS(FBTTh2)2). To quantify this effect, we subtracted in the first step the pure A-spectrum from that of the as-cast blended film, see Fig. 2. The resulting spectrum shows a D-spectrum with significant differences compared to the pure film of D, i.e., less structured features and a blue-shift for both the low (A1) and high (A2) energy band. This indicates a less rigid and less ordered arrangement in the as-cast D-domains. Concomitantly, a completely amorphous structure was observed in the XRD experiment.16 The same strategy was applied to the annealed film, subtracting the pure D-spectrum from the absorption spectrum (Fig. 2). The resulting A-spectrum is again blue-shifted against pure A-film, quite similar to the high-temperature phase of A (i.e. annealing at 150 °C).16 The A-phase in the annealed blend is amorphous as no reflections were found in XRD, while the D-phase is of (poly)crystalline nature.16 An increase of order in both A and D phase is a prerequisite for high charge mobilities avoiding charge accumulation and recombination. The annealing -induced drastic increase of hole mobility in D has been rationalized by the formation of fibrils.16 Here we rationalize the concomitant increase of electron mobility in the A phase by the attainment of a more ordered structure upon annealing.
1) demonstrated a strong impact of annealing on the OSC device performance,16 which was correlated with a significant change in the absorption spectra as shown in Fig. 1. Comparing the as-cast and annealed blended films with pure films, it might be surprising that none of the absorption spectra of the blended films is a simple superposition of the single components, as one might expect from a BHJ film. Instead, the features of the as-cast film seem to be dominated by the electron acceptor (A; NIDCS-MO) spectrum, while the main features of the annealed film seem to originate from the donor (D; p-DTS(FBTTh2)2). To quantify this effect, we subtracted in the first step the pure A-spectrum from that of the as-cast blended film, see Fig. 2. The resulting spectrum shows a D-spectrum with significant differences compared to the pure film of D, i.e., less structured features and a blue-shift for both the low (A1) and high (A2) energy band. This indicates a less rigid and less ordered arrangement in the as-cast D-domains. Concomitantly, a completely amorphous structure was observed in the XRD experiment.16 The same strategy was applied to the annealed film, subtracting the pure D-spectrum from the absorption spectrum (Fig. 2). The resulting A-spectrum is again blue-shifted against pure A-film, quite similar to the high-temperature phase of A (i.e. annealing at 150 °C).16 The A-phase in the annealed blend is amorphous as no reflections were found in XRD, while the D-phase is of (poly)crystalline nature.16 An increase of order in both A and D phase is a prerequisite for high charge mobilities avoiding charge accumulation and recombination. The annealing -induced drastic increase of hole mobility in D has been rationalized by the formation of fibrils.16 Here we rationalize the concomitant increase of electron mobility in the A phase by the attainment of a more ordered structure upon annealing.
Photoluminescence after photoexcitation was observed also for the blended film (Fig. 1), where the PL features are in fact more similar to the donor emission, indicating energy transfer from the electron acceptor NIDCS-MO to the donor PL p-DTS(FBTTh2)2. In both as-deposited and annealed blends, PL quantum efficiencies are below our detection limit (ΦF < 1%) which is expected for donor–acceptor blends. In the ESI† (part D), we show PL microscopy images demonstrating lateral homogeneity of the PL spectral shapes on a 100 nm to 100 μm length scale, thus excluding any regions of D or A access which would lead to electrical performance loss. This demonstrates the good processability of these blends from solution.
Transient absorption (TA) spectroscopy
In Fig. 3, we show the TA spectra of pure D- and A-films (Fig. 3a and b, respectively), excited at 2.0 and 2.43 eV, respectively, into their respective S0 → S1 transitions; compare with Fig. 2. Under these conditions, both pure D- and A-films show TA spectra without any spectral evolution (symbols in Fig. 3a and b), which is confirmed by perfect global fits using only a single state undergoing two parallel reactions (lines in Fig. 3a and b, for details see Fig. S8–S11, ESI†). Therefore, it is safe to assign the strong and narrow band of photoinduced absorption (PASD) at 1.03 eV in Fig. 3a to an excited state transition of the singlet exciton in the D phase. A second, weaker PA band at 1.4 eV is probably due to a transition of the singlet exciton to a higher lying, more weakly coupled state. Bands of formally negative TA at 1.8, 2.0, and 2.2 eV coincide with the vibronically resolved ground state absorption spectrum (GSA, given as a dashed line) and can therefore be assigned to transient photobleach (PBD).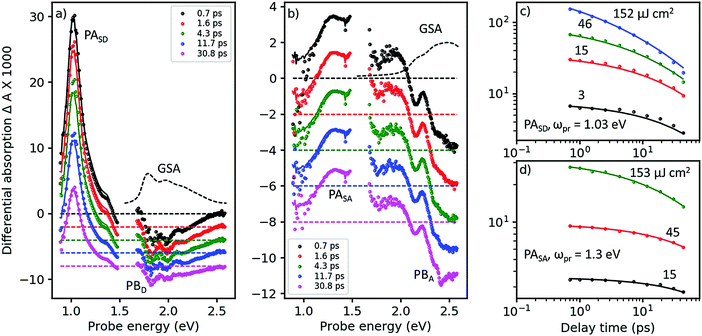 | ||
| Fig. 3 Femtosecond TA spectroscopy of (a) pure donor (D) film, pumped at 620 nm, and (b) pure acceptor (A) film pumped at 510 nm (symbols), at pump–probe delays as shown in the inset. Lines are fits from a target analysis (for details see ESI†). (c) TA dynamics at a probe energy of ωpr = 1.03 eV in the D-film at pump energies given next to the curves (symbols) and fits (lines) by the same target analysis as in panel a. (d) The same for the acceptor films probed at 1.3 eV, with the target analysis from panel b. | ||
In Fig. 3b, a similar picture emerges for the A-film. The singlet exciton produces a broad PA band at 1.3 eV possibly followed by a second transition in the spectral range around 1.6 eV which is not accessible to our TA setup. A third, weaker transition of the singlet exciton to a higher lying state is found at 1.9 eV. Negative TA bands at 2.1 and 2.5 eV coincide with the vibronic structure of the A GSA spectrum and therefore are assigned to PB bands. The stronger visibility of the vibronic structure in the TA spectra as compared to the GSA spectrum is probably due to a hole burning effect caused by the relatively narrowband pump pulse. Additionally, electroabsorption30 and dispersive motion31 might contribute at short and long time delays, respectively.
The good match across the whole spectral region of the lowest energetic GSA band and the PB bands for the pure D- and A-films allows us to quantify the amount of excited state delocalization Lexc by comparing the absorption cross-section of a single molecule, σmol, to that of an excited state, σexc. For the donor film, we find LDexc = σexc/σmol ≈ 0.7 which is close to unity given significant uncertainties in the evaluation of the cross-sections (for details see ESI,† part Eb). An analogous calculation for the acceptor phase gives LAexc = 0.4. Considering the fact that the PBA band is significantly superposed by a PA band around 2.2 eV, we predict that the apparent value of PBexc is reduced and therefore Lexc must be increased. We conclude that singlet excited states in both the donor and acceptor phases are confined on single molecules. This finding is confirmed by a TD-DFT calculation of the excitonic interaction in the donor phase based on a dimer picture, yielding an excitonic splitting of only 0.12 eV, which is half of the energy difference between the states carrying the highest and lowest oscillator strength; for details see ESI,† part B.
In Fig. 3c and d, we show TA dynamics, measured in the maxima of the singlet PA bands in the D- and A-film, respectively. Comparing the decay traces after pumping at three different pump intensities, we find a significant contribution of intensity dependent singlet–singlet annihilation (SSA) to the overall decay. SSA occurs only at high exciton densities and therefore is irrelevant under normal operational conditions of OSCs; here we use SSA as a probe for exciton mobility.32,33 Comparing Fig. 3c and d, it is obvious that under the same pumping conditions, SSA is stronger in the donor than in the acceptor film. Note also that in both D- and A-films, the TA dynamics at the lowest and second lowest intensities are very similar, suggesting the presence of an exciton quenching channel active on the picosecond time scale, in agreement with the observation of a strongly reduced ΦF in pure films compared to solution, see Table 1.
To quantify these observations, we have modeled singlet exciton dynamics by assuming diffusion-controlled exciton quenching at indestructible quenching sites at a concentration cQ, assumed homogeneous, in parallel with diffusion-enhanced exciton annihilation by a Förster resonance energy transfer mechanism with typical annihilation distance Ra. As a cross-check, we can use the resulting concentration-time dependence of singlet states, S(t), to predict the fluorescence quantum yield in the solid state for vanishing contribution of annihilation (for details see ESI†). In the case of the donor film we get a very good agreement between measured and calculated ΦF for predominantly one-dimensional exciton diffusion, which is in agreement with the crystal structure.24 The good match further justifies our assumption of dominance of diffusion in the annihilation process. Therefore, we consider the fitted diffusion constant of 0.09 cm2 s−1 and the resulting quencher molar fraction in the lower permille range as reliable. On the other hand, the best fits of the TA dynamics of the acceptor overestimate ΦF in the films: instead of the experimental 4% we obtain 14% (20%) for 3D (1D) diffusion. Although the fits at low intensity (see Fig. 3d, black curve) are perfect, the actual dynamics is very little so that a substantial error can be anticipated. The results are summarized in Table 2.
| Sample | R a/nm | D exc/cm2 s−1 | c Q/1018 cm−3 | Φ F,calc (%) | IQEcalc (%) | k diffCT/s−1 |
|---|---|---|---|---|---|---|
| D | 1* | 9.1 × 10−2 | 6.3 | 0.8 | 0 | 0 |
| A | 2.91 | 4.9 × 10−5 | 2.4 | 14 | 0 | 0 |
| D:A as cast | 1* | 9.1 × 10−2* | 2.16 | 48 | 4 × 1010 | |
| D:A annealed | 1* | 0.33 | 3.5 | 35 | 1 × 1010 |
The TA spectra of the as-cast blend, after pumping at 2.0 eV, are shown in Fig. 4a. Under these conditions, virtually only singlet excitons in the D-phase are excited but not in the A-phase; see absorption spectra in Fig. 2. Indeed, in the early TA spectra for times <2 ps, we observe the PASD band at 1.03 eV (compare black and red symbols in Fig. 4a to the red spectrum in Fig. 3a). However, even at a delay time of only 700 fs we already find the presence of a band around 1.2–1.3 eV. As exciton transfer from D to A is prohibited for energetic reasons (vide supra), we conclude that a large portion of the primarily excited singlet states in the D-phase have already dissociated into charge separated states in less than 700 fs. This notion is corroborated by the observation of PB features from both D and A already on the femtosecond time scale; compare visible range of Fig. 4a with Fig. 3b.
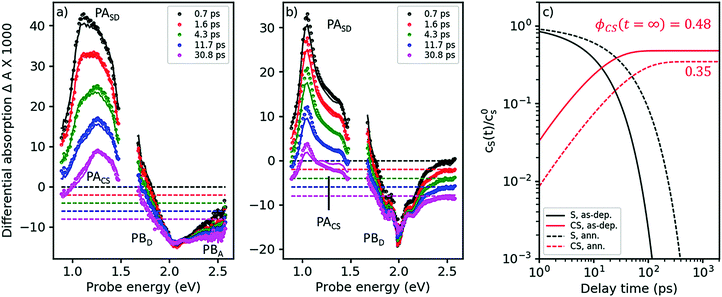 | ||
| Fig. 4 Femtosecond TA spectra for the as-cast and the annealed blend (panels a and b, respectively). Symbols: experimental data, lines: global fits from a target analysis with kCT as the only free kinetic parameter (for details see ESI†). (c) Dynamics of singlet states and charge separated states (black and red curves, respectively) at solar intensities for the as-cast and the annealed blend (solid and dashed curves, respectively), as obtained from a target analysis, globally fitting TA spectra at 3 different pump intensities and extrapolating to solar conditions. The asymptotic value for the charge carrier yield ϕCS after long times, disregarding geminate recombination. | ||
As Fig. 4a shows, singlet decay in the as-cast blend is active in the lower picosecond regime. This photophysical scenario – ultrafast polaron generation in parallel with a delayed, diffusion-induced process – is thus very similar to the one encountered in as-cast blends of the prototype polymer OSC material, P3HT:PCBM,34,35 caused by the absence of phase separation. Intimate mixing of D and A is indeed demonstrated in the TEM micrographs in ref. 16 and by the disorder-induced D spectrum found by decomposition of the absorption spectrum of the as-deposited blend (dashed line in Fig. 2b).
In the absence of phase separation, a large portion of resonantly excited singlet excitons in the donor phase have a certain wavefunction overlap with an acceptor molecule. Hence, charge transfer between nearest neighbor pairs can be achieved without prior exciton diffusion and thus occurs in the lower picosecond or femtosecond time domain (e.g.ref. 36). This scenario is confirmed at different excitation wavelengths where the primary excitation is the A singlet exciton, see ESI.†
In the annealed blend the scenario is drastically different, see Fig. 4b. For at least 50 ps, the singlet exciton remains the dominant photoexcitation. We have reproduced the TA spectra in both annealed and as-deposited blends by assuming a 2-state target model, see solid lines in Fig. 4a and b, using eqn (1), now setting the diffusion-limited interfacial charge transfer constant kdiffCT ≠ 0.
As explained in the ESI,† section Ec, a target analysis as performed here goes beyond a simple global fitting. Apart from a good fit between model and experiment, a successful target analysis requires the resulting characteristic spectra to be those of pure states. This additional requirement allows one to obtain branching ratios and yields of photophysical pathways, which is a priori impossible using only a global fit. The fits are shown in Fig. 4a and b as solid lines; note that both the region of PA and of PB are fitted nearly perfectly over the whole time, probe energy, and pump intensity range (only one intensity shown here, the others given in the ESI,† part Ec). As the fits yield characteristic spectra of pure singlet and charge separated states (see ESI†), we are able to quantify two exciton quenching processes occurring in parallel, namely parasitic exciton quenching at defects and diffusion-mediated exciton dissociation (charge transfer) at the D–A interface. For the as-cast film, we find that the diffusion constant for excitons in the D-phase does not significantly change upon blending. The charge transfer time is about 25 ps. In contrast, in the annealed blend, a clear increase of the diffusion constant was found, which can be explained by crystallite coalescence reducing the number of grain boundaries. At the same time, the quencher concentration is reduced. For the annealed blend, we find a charge transfer time of approximately 100 ps.
As a cross-check, we apply eqn (1) to predict the yield of charge separated states under solar conditions, which can be compared to the published value for the internal quantum efficiency (IQE), see Fig. 4c.16 For the as-deposited blend, we find a charge carrier yield of 48%, which has to be augmented by the amount of ultrafast carrier generation. Summarizing these channels yields a very high IQE strongly contrasting with the published low photovoltaic efficiency. This finding is however in agreement with studies in the prototype polymer-based solar cell, P3HT:PCBM, where the discrepancy between ultrafast charge carrier generation and low current output has been shown to be caused by geminate recombination.34 For the parameters in Table 2, we predict an IQE of 35%, not far from the published value of 45% at 620 nm. The discrepancy can arise from sample statistics. Nonetheless, considering that the calculated value refers only to charge generation while the measured one also considers geminate recombination, it seems to suggest that the experimental IQE value in the annealed blend is limited by defect quenching while geminate recombination plays only a minor role.
Discussion
High PCE values require good light absorption, as well as efficient exciton diffusion and charge generation, transport and extraction yields at the same time. The intense work on classic polymer:PCBM OSCs in the past now offers optimized absorption, charge transport and extraction; however, effective exciton transport and its subsequent breaking at the D:A interface minimizing losses due to recombination or bad level matching demands improved materials as now offered by (all) small molecule based devices. The BHJ blend of this work has previously shown VOC values up to 1.0 V, owing to the higher reduction potential (“LUMO level”) of the acceptor as compared to the standard acceptor PCBM, and thus conserving a larger fraction of the initial photon energy in the charge separated states.16 Increasing the reduction potential however reduces the driving force for exciton dissociation which might reduce the exciton dissociation yield. It is therefore clear that a balance must be sought between a high driving force and high VOC values. In the previous section, we have shown that owing to the high purity of the blend materials, parasitic quenching processes are slow enough to accommodate exciton dissociation times as long as 100 ps, slower than in any high efficiency polymer BHJ blend. This shows the potential of small-molecule based solar cells for efficient charge transfer even at low driving forces, thus allowing higher VOC values without penalizing exciton dissociation yields.Another critical aspect of organic solar cells is the formation of free carriers from the primary bound interfacial charge transfer states. In order to outperform geminate recombination, the Coulomb binding energy of the interfacial charge transfer state should not exceed the thermal energy. In polymer OSCs, there is an increasing body of literature showing that binding energies can be minimized by wavefunction delocalization,37 or by strong coupling allowing hot38 or coherent36,39 mechanisms. From the evaluation of the relative photobleach in Fig. 3, we have found that in our blends, both neutral and charged excited states are essentially localized on single molecules. In the absence of wavefunction delocalization, the Coulomb binding energy will be significant. As a consequence, charge separation will be thermally activated and very slow, thus requiring charge recombination to be even slower.
Given these specific properties of small-molecule OSCs, maximizing the PCE values requires reducing the driving force for exciton dissociation but making sure that exciton dissociation still outperforms parasitic exciton quenching. At the same time, charge recombination should be slow enough to allow for activated charge separation of the relatively strongly bound CT state. We will demonstrate now that these requirements can be fulfilled by choosing D–A systems that show only weak electronic coupling between D and A. We define the free carrier yield as
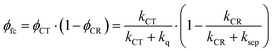 | (1) |
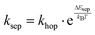 , where the hopping rate khop is obtained from the charge mobility given in ref. 16 assuming Langevin and Einstein relations, and the exponential term gives the probability for an attempt to hop to be successful, where ΔEsep is the energy difference for the first electron transfer (for details see ESI,† part G). The rates kCT and kCR are the Marcus rates for charge transfer and recombination, respectively, obtained with40,41
, where the hopping rate khop is obtained from the charge mobility given in ref. 16 assuming Langevin and Einstein relations, and the exponential term gives the probability for an attempt to hop to be successful, where ΔEsep is the energy difference for the first electron transfer (for details see ESI,† part G). The rates kCT and kCR are the Marcus rates for charge transfer and recombination, respectively, obtained with40,41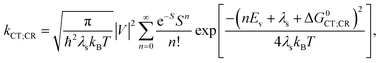 | (2) |
| ΔG0CT = [e(E0D,ox − E0A,red) − Eopt] − Ec; ΔG0CR = Eopt − ΔG0CT, | (3) |
Both λs and ΔEsep depend on the center-to center distance of the donor and acceptor charge density, Rcc, so that the D–A coupling V and Rcc are the only free parameters. In Fig. 5, we show the predicted rates for charge transfer and recombination as a function of Rcc and V (panels a and b, respectively). In Fig. 5a, we find that kCT depends strongly on V but only very weakly on Rcc. As Rcc is expected to change the contribution of the Coulomb attraction to the reorganization energy, this observation means in the Marcus picture that the crossing point between the respective potential energy parabola for the initial and final state is very close to the minimum of the initial state (see also ESI,† part G). Exciton breaking therefore proceeds with near-zero activation energy, showing the good choice of the frontier energy levels of D and A in our system. A blue bold line close to the left corner in Fig. 5a indicates the position where kCT = kq and thus ϕCT = 0.5. Improving ϕCT thus means going towards the right of the blue line. In contrast, the charge recombination rates kCR in Fig. 5b depend on both Rcc and V. The fact that kCR increases (and thus the activation energy for CR decreases) for decreasing Rcc shows that for CR the crossing point occurs in the Marcus inverted region, a favorable situation for photovoltaics. The blue line in Fig. 5b shows where kCR = ksep and thus ϕCR = 0.5; minimizing ϕCR means going to the left of the blue line. It follows that for the free charge carrier yield, there is an optimum range of Rcc/V combinations, as shown in Fig. 5c. With the parameters from this work and from ref. 16, we find that ϕfc increases for decreasing D–A coupling V, fully in agreement with our qualitative prediction. This finding constitutes a design rule for small-molecule based OSCs to match their salient properties: on the one hand, charge recombination must be very slow to allow for activated separation of the CT complex. On the other hand, the high structural definition of small molecules allows extended exciton lifetimes and low driving forces for exciton dissociation. Indeed, Fig. 5a suggests that even for a D–A coupling strength of only a few meV, the resulting (diffusion-free) values for kCT will still exceed the diffusion-limited experimental kdiffCT values. Hence, the D–A coupling can still be substantially reduced without penalizing charge transfer. This strategy can be used to counteract recombination losses in novel all – small molecule OSC with low optical bandgap.
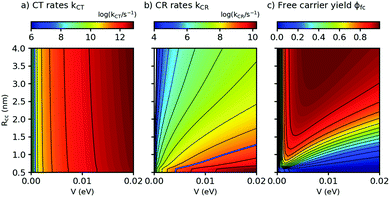 | ||
| Fig. 5 Charge transfer (CT) rates, charge recombination (CR) rates, and free carrier yields ϕfc, calculated using eqn (2) and (3), as a function of the center-to-center distance Rcc between donor D and acceptor A and the D–A coupling V (panels a, b, and c, respectively). Parameters: Eopt = 1.77 eV, λv = 0.12 eV, μe = μh = 10−4 cm2 V−1 s−1, kq = 1010 s−1, T = 298 K. For details of the calculation see ESI,† part G. | ||
Conclusions
Although intense research on classic polymer:PCBM based OSCs has generated devices with optimized absorption, charge transport and extraction, other factors have limited the further development of high PCE cells, in particular concerning the transport of the exciton and its subsequent breaking at the D:A interface. This has driven the development of small-molecule based OSCs, which are expected to outperform classic OSCs in only a short time. Despite the success of these cells, a mechanistic understanding of the relevant elementary processes was still missing. For this we have studied the photoexcitation dynamics in a prototype example for solution-processable all-small-molecule bulk heterojunction photovoltaic blends, offering an 'ideal' system due to its complementary D:A absorption spectra, so that D- and A-excitations can be independently studied. We found that both neutral and charged excited states are localized on single donor or acceptor molecules. Wavefunction delocalization, which is said to aid charge separation in polymer based OSCs, therefore does not play a significant role in this all-small-molecule system. By a target analysis of time-resolved transient absorption spectra, we obtained quencher concentrations and charge transfer rates for both as-deposited and annealed blends. In the annealed blends, which show superior photovoltaic efficiencies, we found a diffusion-limited exciton dissociation rate of ≈1/(100 ps), much slower than for typical polymer based OSCs. Thus, the high structural definition of small-molecule systems accommodates slow transfer rates without efficiency penalties. In the framework of the semiclassical Marcus theory for electron transfer, we show that weak electronic coupling between donor and acceptor moieties (with an optimum value close to 4 meV in our system) is the key to achieve efficient charge separation in small-molecule systems without wavefunction delocalization. These results pave the way for all-small-molecule OSCs with lower optical bandgaps.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Commission (FP7 ITN “POCAONTAS”, Nr. 316633), by the European COST Action Nanospectroscopy, MP1302. Financial support at IMDEA was provided by the Spanish Ministerio de Economía y Competitividad (MINECO-FEDER project CTQ2014-58801), by the 'Severo Ochoa' Programme for Centres of Excellence in R&D (MINECO, Grant SEV-2016-0686), by the Comunidad de Madrid (Project Mad2D, Grant No. S2013/MIT-3007) and by the Campus of International Excellence (CEI) UAM+CSIC. The work at Seoul National University was supported by the National Research Foundation of Korea (NRF) through a grant funded by the Korean Government (MSIP; No. 2009-0081571[RIAM0417-20150013]), by the Global Frontier R&D Program on Center for Multiscale Energy System funded by the NRF under the MSIP, Korea (2012M3A6A7055540), and by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No. 20173010012960). J. S. acknowledges a PhD grant of the Chinese Scholarship Council (CSC). M. van den Berg acknowledges the Landesgraduiertenförderung of the University of Tübingen for financial support. The authors thank H. Bolink (Valencia) for access to the integrating sphere.Notes and references
- L. Dou, J. You, Z. Hong, Z. Xu, G. Li, R. A. Street and Y. Yang, Adv. Mater., 2013, 25, 6642–6671 CrossRef CAS PubMed.
- For recent reviews see e.g. (a) I. Etxebarria, J. Ajuria and R. Pacios, Org. Electron., 2015, 19, 34–60 CrossRef CAS; (b) R. Volpi and M. Linares, Chem. Modell., 2017, 13, 1–26 Search PubMed; (c) J. Yu, Y. Zheng and J. Huang, Polymers, 2014, 6, 2473–2509 CrossRef; (d) L. Lu, T. Zheng, Q. Wu, A. M. Schneider, D. Zhao and L. Yu, Chem. Rev., 2015, 115, 12666–12731 CrossRef CAS PubMed.
- http://https://www.nrel.gov/pv/assets/images/efficiency-chart.png .
- Y. Lin, Y. Li and X. Zhan, Chem. Soc. Rev., 2012, 41, 4245–4272 RSC.
- A. Facchetti, Mater. Today, 2013, 16, 123–132 CrossRef CAS.
- A. F. Eftaiha, J.-P. Sun, I. G. Hill and G. C. Welch, J. Mater. Chem. A, 2014, 2, 1201–1213 CAS.
- Y. Lin and X. Zhan, Mater. Horiz., 2014, 1, 470–488 RSC.
- G. Sauv and R. Fernando, J. Phys. Chem. Lett., 2015, 6, 3770–3780 CrossRef PubMed.
- N. Liang, W. Jiang, J. Hou and Z. Wang, Mater. Chem. Front., 2017, 1, 1291–1303 RSC.
- W. Chen and Q. Zhang, J. Mater. Chem. C, 2017, 5, 1275–1302 RSC.
- A. Mishra and P. Bäerle, Angew. Chem., Int. Ed., 2012, 51, 2020–2067 CrossRef CAS PubMed.
- F. Fernádez-Láaro, N. Zink-Lorre and Á. Sastre-Santos, J. Mater. Chem. A, 2016, 4, 9336–9346 Search PubMed.
- S. D. Collins, N. A. Ran, M. C. Heiber and T.-Q. Nguyen, Adv. Energy Mater., 2017, 7, 1602242 CrossRef.
- (a) S. Chen, Y. Liu, L. Zhang, P. C. Y. Chow, Z. Wang, G. Zhang, W. Ma and H. Yan, J. Am. Chem. Soc., 2017, 139, 6298–6301 CrossRef CAS PubMed; (b) X. Li, X. Liu, W. Zhang, H.-Q. Wang and J. Fang, Chem. Mater., 2017, 29, 4176–4180 CrossRef CAS; (c) F. Zhao, S. Dai, Y. Wu, Q. Zhang, J. Wang, L. Jiang, Q. Ling, Z. Wei, W. Ma, W. You, C. Wang and X. Zhan, Adv. Mater., 2017, 1700144 CrossRef PubMed; (d) H. Bin, L. Gao, Z.-G. Zhang, Y. Yang, Y. Zhang, C. Zhang, S. Chen, L. Xue, C. Yang, M. Xiao and Y. Li, Nat. Commun., 2016, 7, 13651 CrossRef CAS PubMed; (e) Z. Li, K. Jiang, G. Yang, J. Y. L. Lai, T. Ma, J. Zhao, W. Ma and H. Yan, Nat. Commun., 2016, 7, 13094 CrossRef CAS PubMed; (f) R. Yu, S. Zhang, H. Yao, B. Guo, S. Li, H. Zhang, M. Zhang and J. Hou, Adv. Mater., 2017, 29, 1700437 CrossRef PubMed; (g) D. Baran, R. Shahid Ashraf, D. A. Hanifi, M. Abdelsamie, N. Gasparini, J. A. Rör, S. Holliday, A. Wadsworth, S. Lockett, M. Neophytou, C. J. M. Emmott, J. Nelson, C. J. Brabec, A. Amassian, A. Salleo, T. Kirchartz, J. R. Durrant and I. McCulloch, Nat. Mater., 2017, 16, 363–370 CrossRef CAS PubMed; (h) G. Zhang, G. Yang, H. Yan, J.-H. Kim, H. Ade, W. Wu, X. Xu, Y. Duan and Q. Peng, Adv. Mater., 2017, 29, 1606054 CrossRef PubMed; (i) B. Fan, K. Zhang, X.-F. Jiang, L. Ying, F. Huang and Y. Cao, Adv. Mater., 2017, 29, 1606396 CrossRef PubMed; (j) W. Wang, C. Yan, T.-K. Lau, J. Wang, K. Liu, Y. Fan, X. Lu and Z. Zhan, Adv. Mater., 2017, 29, 1701308 CrossRef PubMed; (k) S. Li, L. Ye, W. Zhao, S. Zhang, S. Mukherjee, H. Ade and J. Hou, Adv. Mater., 2016, 28, 9423–9429 CrossRef CAS PubMed; (l) W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, J. Am. Chem. Soc., 2017, 139, 7148–7151 CrossRef CAS PubMed.
- E. Y. Ko, G. E. Park, J. H. Lee, H. J. Kim, D. H. Lee, H. Ahn, M. A. Uddin, H. Y. Woo, M. J. Cho and D. H. Choi, ACS Appl. Mater. Interfaces, 2017, 9, 8838–8847 CAS.
- O. K. Kwon, J.-H. Park, D. W. Kim, S. K. Park and S. Y. Park, Adv. Mater., 2015, 27, 1951–1956 CrossRef CAS PubMed.
- (a) O. K. Kwon, J.-H. Park and S. Y. Park, Org. Electron., 2016, 30, 105–111 CrossRef CAS; (b) G. Feng, Y. Xu, J. Zhang, Z. Wang, Y. Zhou, Y. Li, Z. Wei, C. Li and W. Li, J. Mater. Chem. A, 2016, 4, 6056–6063 RSC; (c) J. Min, O. Kyu Kwon, C. Cui, J.-H. Park, Y. Wu, S. Y. Park, Y. Li and C. J. Brabec, J. Mater. Chem. A, 2016, 4, 14234–14240 RSC; (d) R. Xin, J. Feng, C. Zeng, W. Jiang, L. Zhang, D. Meng, Z. Ren, Z. Wang and S. Yan, ACS Appl. Mater. Interfaces, 2017, 9, 2739–2746 CrossRef CAS PubMed.
- (a) L. Yang, S. Zhang, C. He, J. Zhang, H. Yao, Y. Yang, Y. Zhang, W. Zhao and J. Hou, J. Am. Chem. Soc., 2017, 139, 1958–1966 CrossRef CAS PubMed; (b) H. Bin, Y. Yang, Z.-G. Zhang, L. Ye, M. Ghasemi, S. Chen, Y. Zhang, C. Zhang, C. Sun, L. Xue, C. Yang, H. Ade and Y. Li, J. Am. Chem. Soc., 2017, 139, 5085–5094 CrossRef CAS PubMed; (c) B. Qiu, L. Xue, Y. Yang, H. Bin, Y. Zhang, C. Zhang, M. Xiao, K. Park, W. Morrison, Z.-G. Zhang and Y. Li, Chem. Mater., 2017, 29, 7543–7553 CrossRef CAS.
- T. S. van der Poll, J. A. Love, T.-Q. Nguyen and G. C. Bazan, Adv. Mater., 2012, 24, 3646–3649 CrossRef CAS PubMed.
- O. K. Kwon, J.-H. Park, S. K. Park and S. Y. Park, Adv. Energy Mater., 2015, 5, 1400929 CrossRef.
- A. M. Brouwer, Pure Appl. Chem., 2011, 83, 2213–2228 CrossRef CAS.
- M. Reichenberger, J. A. Love, A. Rudnick, S. Bagnich, F. Panzer, A. Stradomska, G. C. Bazan, T.-Q. Nguyen and A. Köler, J. Chem. Phys., 2016, 144, 074904 CrossRef PubMed.
- G. Srinivasan, J. A. Villanueva-Garibay, K. Müler, D. Oelkrug, B. Milián-Medina, D. Beljonne, J. Cornil, M. Wykes, L. Viani, J. Gierschner, R. Martinez Alvarez, M. Jazdzyk, M. Hanack and H.-J. Egelhaaf, Phys. Chem. Chem. Phys., 2009, 11, 4996–5009 RSC.
- J. A. Love, C. M. Proctor, J. Liu, C. J. Takacs, A. Sharenko, T. S. van der Poll, A. J. Heeger, G. C. Bazan and T.-Q. Nguyen, Adv. Funct. Mater., 2013, 23, 5019–5026 CrossRef CAS.
- J. Gierschner, Y.-S. Huang, B. Van Averbeke, J. Cornil, R. H. Friend and D. Beljonne, J. Chem. Phys., 2009, 130, 044105 CrossRef PubMed.
- (a) H.-J. Egelhaaf, J. Gierschner and D. Oelkrug, Synth. Met., 2002, 127, 221–227 CrossRef CAS; (b) Y.-S. Huang, J. Gierschner, J. P. Schmidtke, R. H. Friend and D. Beljonne, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205311 CrossRef.
- J. Gierschner, L. Lür, B. Milán-Medina, D. Oelkrug and H.-J. Egelhaaf, J. Phys. Chem. Lett., 2013, 4, 2686–2697 CrossRef CAS.
- J. Gierschner and S. Y. Park, J. Mater. Chem. C, 2013, 1, 5818–5832 RSC.
- (a) J. Gierschner, H.-G. Mack, D. Oelkrug, I. Waldner and H. Rau, J. Phys. Chem. A, 2004, 108, 257–263 CrossRef CAS; (b) J. Gierschner, M. Ehni, H.-J. Egelhaaf, B. Milián-Medina, D. Beljonne, H. Benmansour and G. C. Bazan, J. Chem. Phys., 2005, 123, 144914 CrossRef PubMed; (c) M. Wykes, S. K. Park, S. Bhattacharyya, S. Varghese, J. E. Kwon, D. R. Whang, I. Cho, R. Wannemacher, L. Lüer, S. Y. Park and J. Gierschner, J. Phys. Chem. Lett., 2015, 6, 3682–3687 CrossRef CAS PubMed.
- A. Marsh, J. M. Hodgkiss, S. Albert-Seifried and R. H. Friend, Nano Lett., 2010, 10, 923–930, DOI:10.1021/nl9038289.
- P. J. Brown, H. Sirringhaus, M. Harrison, M. Shkunov and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125204 CrossRef.
- O. V. Mikhnenko, H. Azimi, M. Scharber, M. Morana, P. W. M. Blom and M. A. Loi, Energy Environ. Sci., 2012, 5, 6960–6965 CAS.
- P. E. Shaw, A. Ruseckas, J. Peet, G. C. Bazan and I. D. W. Samuel, Adv. Funct. Mater., 2010, 20, 155–161 CrossRef CAS.
- I. A. Howard, R. Mauer, M. Meister and F. Laquai, J. Am. Chem. Soc., 2010, 132, 14866–14876 CrossRef CAS PubMed.
- J. Guo, H. Ohkita, H. Benten and S. Ito, J. Am. Chem. Soc., 2010, 132, 6154–6164 CrossRef CAS PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef CAS PubMed.
- S. Few, J. M. Frost and J. Nelson, Phys. Chem. Chem. Phys., 2015, 17, 2311–2325 RSC.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H.-J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef CAS PubMed.
- E. Vella, H. Li, P. Gréoire, S. M. Tuladhar, M. S. Vezie, S. Few, C. M. Bazán, J. Nelson, C. Silva-Acuña and E. R. Bittner, Sci. Rep., 2016, 6, 29437 CrossRef CAS PubMed.
- D. Caruso and A. Troisi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13498–13502 CrossRef CAS PubMed.
- T. A. Reekie, M. Sekita, L. M. Urner, S. Bauroth, L. Ruhlmann, J.-P. Gisselbrecht, C. Boudon, N. Trapp, T. Clark, D. M. Guldi and F. Diederich, Chem. – Eur. J., 2017, 23, 6357–6369 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee02967e |
| This journal is © The Royal Society of Chemistry 2018 |