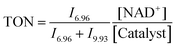Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of sulfonamidoethylenediamine substituents in RuII arene anticancer catalysts on transfer hydrogenation of coenzyme NAD+ by formate†
Feng
Chen
 a,
Joan J.
Soldevila-Barreda
a,
Joan J.
Soldevila-Barreda
 a,
Isolda
Romero-Canelón
a,
Isolda
Romero-Canelón
 ab,
James P. C.
Coverdale
ab,
James P. C.
Coverdale
 a,
Ji-Inn
Song
a,
Ji-Inn
Song
 a,
Guy J.
Clarkson
a,
Guy J.
Clarkson
 a,
Jana
Kasparkova
a,
Jana
Kasparkova
 c,
Abraha
Habtemariam
c,
Abraha
Habtemariam
 a,
Viktor
Brabec
a,
Viktor
Brabec
 c,
Juliusz A.
Wolny
c,
Juliusz A.
Wolny
 d,
Volker
Schünemann
d,
Volker
Schünemann
 d and
Peter J.
Sadler
d and
Peter J.
Sadler
 *a
*a
aDepartment of Chemistry, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK. E-mail: P.J.Sadler@warwick.ac.uk
bSchool of Pharmacy, University of Birmingham, Birmingham B15 2TT, UK
cDepartment of Biophysics, Faculty of Science, Palacky University, 17. listopadu 12, CZ-77146 Olomouc, Czech Republic
dDepartment of Physics, University of Kaiserslautern, Erwin-Schrödinger-Str. 46, 67663 Kaiserslautern, Germany
First published on 13th April 2018
Abstract
A series of neutral pseudo-octahedral RuII sulfonamidoethylenediamine complexes [(η6-p-cym)Ru(N,N′)Cl] where N,N′ is N-(2-(R1,R2-amino)ethyl)-4-toluenesulfonamide (TsEn(R1,R2)) R1,R2 = Me,H (1); Me,Me (2); Et,H (3); benzyl,H (Bz, 4); 4-fluorobenzyl,H (4-F-Bz, 5) or naphthalen-2-ylmethyl,H (Naph, 6), were synthesised and characterised including the X-ray crystal structure of 3. These complexes catalyse the reduction of NAD+ regioselectively to 1,4-NADH by using formate as the hydride source. The catalytic efficiency depends markedly on the steric and electronic effects of the N-substitutent, with turnover frequencies (TOFs) increasing in the order: 1 < 2 < 3, 6 < 4, 5, achieving a TOF of 7.7 h−1 for 4 with a 95% yield of 1,4-NADH. The reduction rate was highest between pH* (deuterated solvent) 6 and 7.5 and improved with an increase in formate concentration (TOF of 18.8 h−1, 140 mM formate). The calculations suggested initial substitution of an aqua ligand by formate, followed by hydride transfer to RuII and then to NAD+, and indicated specific interactions between the aqua complex and both NAD+ and NADH, the former allowing a preorganisation involving interaction between the aqua ligand, formate anion and the pyridine ring of NAD+. The complexes exhibited antiproliferative activity towards A2780 human ovarian cancer cells with IC50 values ranging from 1 to 31 μM, the most potent complex, [(η6-p-cym)Ru(TsEn(Bz,H))Cl] (4, IC50 = 1.0 ± 0.1 μM), having a potency similar to the anticancer drug cisplatin. Co-administration with sodium formate (2 mM), increased the potency of all complexes towards A2780 cells by 20–36%, with the greatest effect seen for complex 6.
1. Introduction
Nicotinamide adenine dinucleotide (NAD+) and its reduced form (NADH), as well as their phosphorylated derivatives, NADP+ and NADPH, play a vital role in biological systems as redox coenzymes.1 More than 400 enzymatic redox reactions rely on the action of nicotinamide enzymes, in which the transformation of NAD(P)+ to NAD(P)H is involved.2–4 The reduction of pyridinium salts (e.g. NAD+) to dihydropyridine compounds (e.g. NADH) is of critical importance for energy storage and release in cell metabolism.3,4 Transition metal-mediated catalytic reduction of NAD+ to NADH, using hydrogen,5 2-propanol,6,7 glycerol8 and sodium formate as hydride donors, has been intensively studied for the last three decades.9–13 Compared to reduction with H2 (hydrogenation), transfer hydrogenation (TH) reactions have the advantage of being simpler, without the need for any high external pressure and use readily available, safer-to-handle, hydride sources.14 Also, TH reduction of NAD(P)+ artificially has attracted wide interest as an in vitro mimic for enzymatic reactions performed under biologically relevant conditions.15The pathways of hydride transfer between pyridinium salts and dihydropyridine compounds are also of interest. The first mechanistic study of the TH reduction of BNA+ (1-benzylnicotinamide), as a model for NAD+ was reported by Steckhan and Fish et al. using [(η5-Cp*)Rh(bipy)Cl] as the catalyst and sodium formate as a hydride source in aqueous media in the 1990s.10–12,16,17 They proposed a catalytic cycle involving a ring-slippage η4-Cp* intermediate with Rh coordinated to the amide of the pyridine ring.18 Knör et al. reported a Rh-coordinated poly(arylene-ethynylene)-alt-poly(arylene-vinylene) polymer as photocatalyst for the reduction of NAD+; involving a possible photoexcited polymer chain being quenched and transferring an electron to the RhIII active centre.19 More recently, Yoon et al. described a mechanism involving hydride transfer to Cp* and formation of the RhI intermediate [(η4-Cp*-H)Rh((CH2OH)2-bipy)]+ followed by hydride transfer from the endo orientation of the C–H bond to maintain the 1,4-regioselectivity of NADH.20
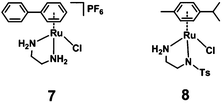
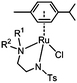
The half-sandwich ruthenium complex [(η6-p-cym)Ru(TsDPEN)Cl] (TsDPEN: N-((1S,2S)-2-amino-1,2-diphenylethyl)-4-methylbenzenesulfonamide) was first reported by Noyori and coworkers in 1995.21,22 Potent catalytic activity has been shown in asymmetric TH reduction of aromatic ketones. Most recently, the 16-electron Os analogues [(η6-arene)Os(TsDPEN)] of Noyori type complexes were reported to reduce pyruvate enantioselectively to (D- or L-) lactate via asymmetric transfer hydrogenation in human cancer cells.23 Nonetheless, the hydrophobic nature of the two phenyl groups on the ethylene backbone limits its application as a possible catalyst for TH reduction of NAD+ under biologically relevant conditions. Complexes with chelating diamine ligands such as complex 7 in Fig. 1, display good aqueous solubility but poor catalytic activity in TH reduction of NAD+.24 However, p-cymene (p-cym) complexes with functional sulfonyl substituents such as [(η6-p-cym)Ru(TsEn)Cl] (e.g. complex 8 in Fig. 1),25 exhibit good solubility in water and improved catalysis for NAD+ reduction to NADH in aqueous media. Moreover, co-administration of [(η6-p-cym)Ru(TsEn)Cl] with low non-cytotoxic doses of sodium formate led to an enhancement of the antiproliferative activity against A2780 human ovarian cancer cells by up to 50×.15,26
Here we investigate the effect on catalytic reduction of NAD+ using formate as a hydride source upon variation of substituents on the amino group of the N,N-chelating TsEn ligand in RuII complexes [(η6-p-cym)Ru(N,N′)Cl] where N,N′ is N-(2-(methylamino)ethyl)-4-toluenesulfonamide (TsEn(Me,H), 1), N-(2-(dimethylamino)ethyl)-4-toluenesulfonamide (TsEn(Me,Me), 2), N-(2-(ethylamino)ethyl)-4-toluene sulfonamide (TsEn(Et,H), 3), N-(2-(benzylamino)ethyl)-4-toluenesulfonamide (TsEn(Bz,H), 4), N-(2-((4-fluorobenzyl)amino) ethyl)-4-toluenesulfonamide (TsEn(4-F-Bz,H), 5) and N-(2-((naphthalen-2-ylmethyl)amino) ethyl)-4-toluenesulfonamide (TsEn(Naph,H), 6) (Table 1). In addition, the catalytic mechanism was investigated both experimentally and by density functional theory (DFT) calculations. We also explored the effect of co-administration of formate on the antiproliferative activity of these complexes against A2780 human ovarian cancer cells.
2. Experimental
2.1 Materials
Ruthenium(III) trichloride hydrate was purchased from Precious Metals Online (PMO Pty Ltd) and used as received. Toluenesulfonyl chloride, sodium formate and β-nicotinamide adenine dinucleotide hydrate (NAD+) were obtained from Sigma-Aldrich. Magnesium sulfate, potassium hydroxide, sodium chloride, and hydrochloric acid were obtained from Fisher Scientific. α-Phellandrene was purchased from SAFC. The RuII precursor dimer [(η6-p-cym)RuCl2]2 was prepared following literature methods,27 as were the ligands 4-methyl-N-(2-(methylamino)ethyl)benzene sulphonamide (TsEn(Me,H))28 and N-(2-(dimethylamino)ethyl)-4-methylbenzenesulfonamide (TsEn(Me,Me)).29 The solvents used for NMR spectroscopy were purchased from Sigma-Aldrich and Cambridge Isotope Laboratories Inc. Non-dried solvents used in synthesis were obtained from Fisher Scientific. Solvents were used as received, except in the case of ethanol, 2-propanol, and methanol, which were degassed prior to use by bubbling with nitrogen.A2780 human ovarian carcinoma cells were obtained from the European Collection of Cell Cultures. The cell line was grown in Roswell Park Memorial Institute medium (RPMI-1640) supplemented with 10% of foetal calf serum, 1% v/v of 2 mM glutamine and 1% v/v penicillin/streptomycin (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units). All cells were grown as adherent monolayers at 310 K in a 5% CO2-humidified atmosphere and passaged at ca. 70–80% confluency.
000 units). All cells were grown as adherent monolayers at 310 K in a 5% CO2-humidified atmosphere and passaged at ca. 70–80% confluency.
2.2 Instruments
NMR spectra were acquired on Bruker HD-300, HD-400, HD-500, and AV III 600 spectrometers. 1H NMR chemical shifts were internally referenced to TMS via 1,4-dioxane in D2O (δ = 3.75 ppm) or residual protiated d4-MeOD (δ = 3.31 ppm), or CDCl3 (δ = 7.26 ppm). 1D spectra were recorded using standard pulse sequences. Typically, data were acquired with 16 transients into 32k data points over a spectral width of 14 ppm and, for the kinetic experiment, 32 transients into 32k data points over a spectral width of 30 ppm using a relaxation delay of 2 s.Elemental analysis were performed by Warwick Analytical using an Exeter Analytical elemental analyzer (CE440).
Positive ion electrospray mass spectra were obtained on an Agilent 6130B ion mass spectrometer. High resolution mass spectrometry data were obtained on a Bruker Maxis Plus Q-TOF instrument.
X-ray crystallographic diffraction data were collected on an Oxford Diffraction Gemini four-circle system with a Ruby CCD area detector. The structure was refined by full-matrix least-squares against F2 using SHELXL 9735 and solved by direct methods using SHELXS36 (TREF) with additional light atoms found by Fourier methods. The atoms from the sulfonamide nitrogen to the end of the chain (C10 C11 N12 C13) were modelled as disordered over two positions related by a small ruffle in the chain. The occupancy of the two positions was linked to a free variable which refined to 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14. The minor component was refined isotropically. X-ray crystallographic data for complex 3 has been deposited in the Cambridge Crystallographic Data Center (CCDC) under the accession number CCDC 1571331.†
14. The minor component was refined isotropically. X-ray crystallographic data for complex 3 has been deposited in the Cambridge Crystallographic Data Center (CCDC) under the accession number CCDC 1571331.†
ICP-OES analysis were carried out on a PerkinElmer Optima 5300 DV series Optical Emission Spectrophotometer. The water used for ICP-OES analysis was doubly deionized (DDW) using a Millipore Milli-Q water purification system and a USF Elga UHQ water deionizer. The ruthenium Specupure plasma standard (ruthenium chloride, 1004 ± 5 μg mL−1 in 10% v/v hydrochloric acid) was diluted with 3.6% v/v HNO3 to freshly prepare calibrants at concentrations of 50–700 ppb. Calibration standards were adjusted to match the sample matrix by standard addition of sodium chloride (TraceSELECT®). Total dissolved solids did not exceed 0.2% w/v. Data were acquired and processed using WinLab32 V3.4.1 for Windows.
ICP-MS analysis were carried out on an Agilent Technologies 7500 series ICP-MS instrument. The water used for ICP-MS analysis was double-deionized (DDW) using a Millipore Milli-Q water purification system and a USF Elga UHQ water deionizer. The Ruthenium Specpure plasma standard (ruthenium chloride, 1004 ± 5 μg mL−1 in 10% v/v hydrochloric acid) was diluted with 3.6% v/v HNO3 to prepare calibrants freshly at concentrations of 0.1–1000 ppb. The ICP-MS instrument was set to detect 101Ru in no gas mode. Total dissolved solids did not exceed 0.1% w/v. An internal standard of 166Er (50 ppb) was used. Data were acquired using ICP-MS-TOP and proceeded using Offline Data Analysis (ChemStation version B.03.05, Agilent Technologies, Inc.).
pH values were measured using a Minilab IQ125 pH meter equipped with a ISFET silicon chip pH sensor and referenced in KCl gel. pH* values (pH meter reading without correction for the effect of deuterium on the sensor) of NMR samples in D2O were measured at 310 K. Relative hydrophobicity measurements were performed utilising the Agilent 1200 HPLC system with a VWD and 50 μL loop. The column was an Agilent Zorbax 300SB C18, 150 × 4.6 mm with a 5 μm pore size. The mobile phase was H2O (50 mM NaCl)/H2O/CH3CN 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (50 mM NaCl), with a flow of 1 mL min−1. The detection wavelength was set at 254 nm with the reference wavelength at 360 nm.
1 (50 mM NaCl), with a flow of 1 mL min−1. The detection wavelength was set at 254 nm with the reference wavelength at 360 nm.
2.3 Turnover frequency determination
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v, 102 mM sodium formate and 510 μM NAD+ in H2O) was added to a 1 mL cuvette, and the pH adjusted to 7.2, bringing the total volume to 1 mL (final concentrations: Ru complex 28 μM; NAD+ 170 μM; NaHCO2 34 mM; molar ratio 1
9 v/v, 102 mM sodium formate and 510 μM NAD+ in H2O) was added to a 1 mL cuvette, and the pH adjusted to 7.2, bringing the total volume to 1 mL (final concentrations: Ru complex 28 μM; NAD+ 170 μM; NaHCO2 34 mM; molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1200). UV spectra were recorded and the absorbance at 340 nm was monitored every 5 min until completion of the reaction.
1200). UV spectra were recorded and the absorbance at 340 nm was monitored every 5 min until completion of the reaction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, v/v) (1.4 mM) in a glass vial. Solutions of sodium formate (35 mM) and NAD+ (5.6 mM) in D2O were also prepared and then incubated at 310 K, pH* 7.2 ± 0.1. An aliquot of 200 μL from each solution was added to a 5 mm NMR tube, giving a final volume of 0.64 mL (Ru complex 0.44 mM; NAD+ 1.75 mM; NaHCO2 10.94 mM; molar ratio 1
4, v/v) (1.4 mM) in a glass vial. Solutions of sodium formate (35 mM) and NAD+ (5.6 mM) in D2O were also prepared and then incubated at 310 K, pH* 7.2 ± 0.1. An aliquot of 200 μL from each solution was added to a 5 mm NMR tube, giving a final volume of 0.64 mL (Ru complex 0.44 mM; NAD+ 1.75 mM; NaHCO2 10.94 mM; molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25). A 1H NMR spectrum was recorded at 310 K every 162 s until the completion of the reaction. Further experiments under similar conditions using different concentrations of sodium formate (complex 4, NAD+ and sodium formate in ratio of 1: 4: X, where X = 10, 25, 50, and 100 mol equiv.) and different concentrations of NAD+ (complex 4, NAD+ and sodium formate in ratio of 1
25). A 1H NMR spectrum was recorded at 310 K every 162 s until the completion of the reaction. Further experiments under similar conditions using different concentrations of sodium formate (complex 4, NAD+ and sodium formate in ratio of 1: 4: X, where X = 10, 25, 50, and 100 mol equiv.) and different concentrations of NAD+ (complex 4, NAD+ and sodium formate in ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y
Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, where Y = 2, 4, 6 and 10) were also studied. Another series of experiments using different pH* values of the reaction solutions (5, 6, 7, 8 and 9) were also performed. Molar ratios of NAD+ and NADH were determined by integrating 1H NMR peaks corresponding to NAD+ (9.33 ppm) and 1,4-NADH (6.96 ppm). The turnover number (TON) for the reaction was calculated as follows:
25, where Y = 2, 4, 6 and 10) were also studied. Another series of experiments using different pH* values of the reaction solutions (5, 6, 7, 8 and 9) were also performed. Molar ratios of NAD+ and NADH were determined by integrating 1H NMR peaks corresponding to NAD+ (9.33 ppm) and 1,4-NADH (6.96 ppm). The turnover number (TON) for the reaction was calculated as follows:where In is the integral of the signal at n ppm and [NAD+] is the concentration of NAD+ at the start of the reaction.
2.4 Cell growth inhibition assays
The antiproliferative activity of complexes 1–6 was determined in A2780 ovarian cancer cells. Briefly, 96-well plates were used to seed 5000 cells per well. Cells were incubated in drug-free medium at 310 K for 48 h before addition of tested compounds (prepared by serial dilution in culture medium containing 5% DMSO, typically 6 concentrations in the range: 0.01–100 μM). Exact Ru concentrations were determined by ICP-OES and the maximum concentration of DMSO to which cells were exposed never exceeded 0.5% v/v. A drug exposure period of 24 h was allowed. After this, supernatants were removed by suction and each well was washed with PBS. A further 72 h were allowed for the cells to recover in drug-free medium at 310 K. The sulforhodamine B (SRB) assay was used to determine cell viability.30 IC50 values, as the concentration that causes 50% cell death, were determined as duplicates of triplicates in two independent sets of experiments and their standard deviation were calculated. Data were processed using Microsoft Excel and sigmoidal curves fitted using Origin 9.1.2.5 Co-administration of Ru complexes with formate
Cell viability assays were carried out with complexes 1–6 with co-administration of sodium formate in A2780 ovarian cancer cells. These experiments were carried out as above (in vitro growth inhabitation assay) with the following modifications: a fixed equipotent concentration of each Ru complex equal to 1/3 × IC50 in that cell line was used in coadministration with three different concentrations of sodium formate (0.5, 1.0 and 2.0 mM). Drug stock solutions (ca. 100 μM) were prepared and they were further diluted using media until working concentrations were achieved. Separately, a stock solution of sodium formate was prepared in saline. The complex and formate solutions were added to each well independently, but within 5 minutes of each other. All other experiment conditions were kept unchanged (drug exposure and cell recovery time, as well as, end point assay used).2.6 Cellular accumulation
The accumulation studies for Ru complexes 1–6 were performed on A2780 ovarian cancer cells. 1.5 × 106 cells were seeded on a six-well plate using 2 mL of cell culture medium. After 24 h of pre-incubation in drug-free medium at 310 K, cells were exposed to complexes at equipotent IC50 concentrations for 24 h (prepared by serial dilution of a ca. 100 μM stock solution, prepared using culture medium containing 5% DMSO. This solution was analysed by ICP-OES to determine Ru concentration before treatment of cells with Ru complex). After this time, drug solutions were removed by suction, cells were washed with PBS and then treated with trypsin–EDTA. A suspension of single cells was counted, and cell pellets were collected. Each pellet was digested overnight in freshly-distilled concentrated nitric acid (200 μL, 72% v/v) at 353 K; the resulting solutions were diluted with double-distilled water to a final concentration of 3.6% v/v HNO3, and the amount of Ru in A2780 ovarian cells was determined by ICP-MS. These experiments did not include any cell recovery time in drug-free media; they were carried out in triplicate, and the standard deviations were calculated. Data were processed using Microsoft Excel and reported as ng Ru × 106 cells.2.7 ROS determination
Flow cytometry analysis of ROS/superoxide induction in A2780 cells caused by exposure to complexes 1 and 4 was carried out using the Total ROS/Superoxide detection kit (Enzo-Life Sciences) according to the manufacturer's instructions. Briefly, 1.0 × 106 A2780 cells per well were seeded in a six-well plate. Cells were preincubated in drug-free media at 310 K for 24 h in a 5% CO2 humidified atmosphere, and then drugs were added to triplicates wells at IC50 concentration. After 24 h of drug exposure, supernatants were removed by suction and cells were washed with PBS and harvested. Staining was achieved by re-suspending the cell pellets in buffer containing the orange/green fluorescent reagents. Cells were analysed in a Becton Dickinson FACScan flow cytometer using FL1 channel Ex/Em: 490/525 nm for the oxidative stress and FL2 channel Ex/Em: 550/620 nm for superoxide detection. Data were gated using positive-stained (pyocyanin positive control), untreated-stained and untreated-unstained control samples, acquired as instrumental triplicates, and were processed using FlowJo V10 for Windows. At all times, samples were kept under dark conditions to avoid light-induced ROS production.2.8 DFT calculations
The DFT calculations of electronic energy levels of the catalytic cycle were based on the crystal structure of complex 3. The method of the calculation was functional CAM-B3LYP31 with basis set CEP-31G,32–34 using Gaussian 16 software.35 Ultrafine grid of integration was used in each case. The starting geometry was taken from X-ray data for 3, with an appropriate change of substituents for other systems. All given energy values are the result of the full geometry optimisation with subsequent frequency calculations. Optimisations were performed with modelling of water as solvent, within the continuous polarisation model with integral equation formalism variant (IEFPCM keyword of Gaussian). Grimme empirical corrections for dispersion were applied (keyword GD3). The optimisations were performed using the solvent-accessible surface option and the final energy was calculated with using solvent-excluding surface options (keywords surface = sas and ses, respectively). NAD+ was modelled with an effective charge of −1, with two deprotonated phosphate groups; the same protonation of phosphate was used for NADH, giving an effective charge of −2.2.9 DNA binding
The reactions of complex 4 (ca. 2 mM) with nucleobases (9-EtG and 5′-AMP) were studied typically by addition of an aqueous solution of nucleobase (3 mM, 1.5 mol equiv.) in 10% of d4-MeOD and 90% of D2O, pH* 7.2 ± 0.1, and monitored by 1H NMR at 310 K. Solutions of double-helical calf thymus DNA (ct-DNA) at a concentration of 32 μg mL−1 were incubated with complex 4 at ri value of 0.1 in 10 mM NaClO4 at 310 K (ri is defined as the molar ratio of free ruthenium complex to nucleotide phosphates at the onset of incubation with DNA). The concentration of ruthenium associated with DNA in these samples was determined by flameless atomic absorption spectrometry (FAAS). The concentrations of DNA were determined by absorption spectrophotometry. Plasmid DNA pBR322 (28 μg mL−1) and complex 4 in various molar ratios (ri = 0.05–1) were incubated in 0.01 M NaClO4 at 310 K for 24 h in the dark. Then the samples were directly mixed with the loading buffer and loaded onto a 1% agarose gel running at 298 K in the dark with Tris-acetate-EDTA (TAE) buffer and the voltage set at 25 V. No separation step was included before loading the samples into the gel to allow detection of potential noncovalent binding (if any). The gels were then stained with EtBr, followed by photography with a transilluminator.3. Results and discussion
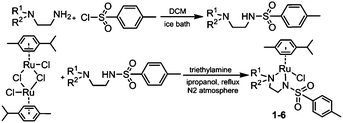
3.1 Synthesis and characterisation
RuII complexes 1–6 were synthesised using a similar procedure to that reported for related complexes (Scheme 1).25 Typically, triethylamine (4 mol equiv.) and ligands (ca. 2 mol equiv.) were added to a solution of [(η6-p-cym)RuCl2]2 in degassed isopropanol, and the reaction was stirred under a N2 atmosphere at 365 K for 12 h. All synthesised complexes were characterised by 1H and 13C NMR spectroscopy, mass spectrometry (ESI-MS) and elemental analysis (CHN). A crystal of complex 3 suitable for X-ray analysis was obtained by diffusion of diethyl ether into a solution of the complex in methanol at ambient temperature. Selected bond lengths and angles for complex 3 are listed in Table 2. Crystallographic data are presented in Table S1,† and the structure of complex 3 is shown in Fig. 2. Complex 3 adopts a pseudo-octahedral geometry with the η6-bonded aromatic ring occupying 3 coordination sites. The chelating ligand is deprotonated and bonded as a monoanionic bidentate ligand. The CH2CH2N-Et atoms from N,N′ chelated ligand (C10 C11 N12 C13) were modelled as disordered over two positions whose occupancy refined to 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14. Compared to reported ruthenium ethylenediamine complexes (either neutral or +1 charge),25,36,37 the Ru–N− bond length (N9, 2.126(9)) is within the expected range of 2.11–2.14 Å,37 but the Ru–N12 length (2.1702(11) Å) is longer than the neutral analogue [(η6-biph)Ru(TsEn)Cl] (2.122(3) Å),25 suggesting that the presence of N-ethyl substituent causes a slight weakening of this Ru–N bond. The remaining bond length and angles show no significant difference.
14. Compared to reported ruthenium ethylenediamine complexes (either neutral or +1 charge),25,36,37 the Ru–N− bond length (N9, 2.126(9)) is within the expected range of 2.11–2.14 Å,37 but the Ru–N12 length (2.1702(11) Å) is longer than the neutral analogue [(η6-biph)Ru(TsEn)Cl] (2.122(3) Å),25 suggesting that the presence of N-ethyl substituent causes a slight weakening of this Ru–N bond. The remaining bond length and angles show no significant difference.
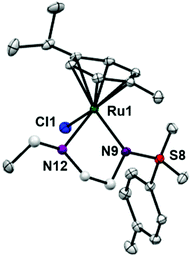 | ||
| Fig. 2 ORTEP diagrams for complex 3. Ellipsoids are shown at the 50% probability level. All hydrogen atoms have been omitted for clarity. | ||
| Bonds | Length/angle |
|---|---|
| Ru1–N9 | 2.1256(9) |
| Ru1–N12 | 2.1702(11) |
| Ru1–N12A | 2.157(8) |
| Ru1–Cl1 | 2.4173(3) |
| Ru1–arene (centroid) | 1.664 |
| N9–Ru1–N12 | 78.74(4) |
| N9–Ru1–N12A | 76.1(2) |
| N9–Ru1–Cl1 | 89.47(3) |
| N12–Ru1–Cl1 | 87.55(4) |
3.2 Hydrolysis and 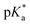 determination
determination
The hydrolysis of complex 4 was studied by dissolving the RuII complex in d4-MeOD/D2O (1.4 mM, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
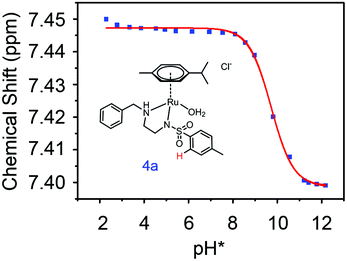
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (v/v)). The 1H NMR spectrum remained unchanged after 24 h and the hydrolysis was assumed to be rapid since the peaks could be assigned to the aqua RuII species (4a) by comparison to those from the aqua species generated in a reaction with silver nitrate in D2O (1 mol equiv.). The
9 (v/v)). The 1H NMR spectrum remained unchanged after 24 h and the hydrolysis was assumed to be rapid since the peaks could be assigned to the aqua RuII species (4a) by comparison to those from the aqua species generated in a reaction with silver nitrate in D2O (1 mol equiv.). The 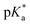 (pKa value determined in deuterated solvent) of complex 4a was determined by a pH* (meter reading) titration ranging from 2 to 12 by addition of NaOD or DNO3 solutions as appropriate. Changes in the chemical shift of a tosyl 1H NMR resonance were followed and the data were fitted to the Henderson–Hasselbalch equation, giving a
(pKa value determined in deuterated solvent) of complex 4a was determined by a pH* (meter reading) titration ranging from 2 to 12 by addition of NaOD or DNO3 solutions as appropriate. Changes in the chemical shift of a tosyl 1H NMR resonance were followed and the data were fitted to the Henderson–Hasselbalch equation, giving a 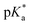 value of 9.73 ± 0.06 (Fig. 3).
value of 9.73 ± 0.06 (Fig. 3).
3.3 Kinetics of transfer hydrogenation reactions
The ratio of coenzyme NAD+/NADH greatly influences the intracellular potential and can drive many reactions in vivo.38 The reduction of coenzyme nicotinamide adenine dinucleotide (NAD+) to NADH was investigated in an aqueous medium using complexes 1–6 as catalysts and sodium formate as the hydride source. Initially, the TH reactions were studied by UV-visible spectroscopy under conditions of pH 7.2 ± 0.1, 310 K and MeOH/H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v, Table 3); in all the cases, an increase in intensity of the band at 340 nm was observed, which is assignable to formation of NADH (Fig. S1, ESI†). The kinetics of conversion were also monitored by 1H NMR at 310 K and pH* 7.2 ± 0.1. The reactions were performed in a mixed solvent d4-MeOD/D2O (1
9, v/v, Table 3); in all the cases, an increase in intensity of the band at 340 nm was observed, which is assignable to formation of NADH (Fig. S1, ESI†). The kinetics of conversion were also monitored by 1H NMR at 310 K and pH* 7.2 ± 0.1. The reactions were performed in a mixed solvent d4-MeOD/D2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, v/v), due to the poor aqueous solubility of complexes 5 and 6, although the presence of methanol in such reactions is known to enhance the reaction rate.25
4, v/v), due to the poor aqueous solubility of complexes 5 and 6, although the presence of methanol in such reactions is known to enhance the reaction rate.25
In general, the introduction of substituents on the terminal nitrogen improved the catalytic activity. The bulkier the substituents on the terminal nitrogen, the higher the TH reaction rate becomes. The turnover frequency reaches a maximum (ca. 7.54 h−1) when the substituent on the terminal N is benzyl (complex 4), making it as efficient as the RhIII complex [(η5-Cp*)Rh(bipy)Cl]PF6.16 Interestingly, the TOF decreases when the substituent is para-fluoro-benzyl (complex 5) or naphthalene (complex 6), probably, because these ligands hamper the approach of NAD+ to the Ru centre. Compared to the en complex with unsubstituted nitrogens [(η6-biph)Ru(en)Cl]PF6, the turnover frequency of complex 4 is 41× higher,24 and 2.7× higher compared to [(η6-p-cym)Ru(TsEn)Cl].25
The NH proton of the chelated diamine ligand appears to be essential for the TH reduction of ketones to alcohols;39 normally, RuII catalysts for TH of ketones form 16-e intermediates.40,41 It has been reported that a RuII complex with two N-alkyl groups (R,R)-[(η6-benzene)Ru(TsDPEN-Me2)Cl] exhibited poor catalytic reactivity in TH reaction of ketones.40 However, complex 2 [(η6-p-cym)Ru(TsEn(Me,Me))Cl] exhibited good catalytic activity towards the TH reduction of NAD+ to NADH (TOF = 4.1 h−1, Table 3), despite not having an NH proton, which suggests, as expected, that an N–H is not essential in the transfer reduction of NAD+ to NADH.
The dependence of the rate of catalysis on pH was determined. Six pH* values ranging from 5 to 9 were studied for complex 4 at a mol ratio complex 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NAD+
NAD+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formate of 1
formate of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, in the same mixed solvent at 310 K (Fig. S2, ESI†). The TOF was relatively insensitive to pH* over the range pH* 6–8 (ca. 7.5 h−1), but decreased slightly at lower and higher pH* (5.6 h−1 at pH* 5, 6.6 h−1 at pH* 9).
25, in the same mixed solvent at 310 K (Fig. S2, ESI†). The TOF was relatively insensitive to pH* over the range pH* 6–8 (ca. 7.5 h−1), but decreased slightly at lower and higher pH* (5.6 h−1 at pH* 5, 6.6 h−1 at pH* 9).
The dependence of turnover frequency on the concentrations of sodium formate and NAD+ was also investigated for complex 4 in d4-MeOD/D2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) at 310 K. The mol ratio of complex 4
4) at 310 K. The mol ratio of complex 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NAD+
NAD+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formate was 1
formate was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X, where X = 5, 10, 25, 50 and 100 (Fig. S3, ESI†). The TOF increased steadily from 2.2 h−1 to 18.8 h−1 as the concentration of formate was increased from 7 mM to 140 mM. Next the dependence of TOF on the NAD+ concentration was studied for mol ratio complex 4
X, where X = 5, 10, 25, 50 and 100 (Fig. S3, ESI†). The TOF increased steadily from 2.2 h−1 to 18.8 h−1 as the concentration of formate was increased from 7 mM to 140 mM. Next the dependence of TOF on the NAD+ concentration was studied for mol ratio complex 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NAD+
NAD+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formate = 1
formate = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y
Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, where Y = 2, 6 and 10. The TOF was found to be independent of NAD+ concentration (7.7 ± 0.5 h−1).
25, where Y = 2, 6 and 10. The TOF was found to be independent of NAD+ concentration (7.7 ± 0.5 h−1).
The Michaelis–Menten kinetic behaviour is apparent from a plot of turnover frequency versus formate concentration. A reciprocal plot of turnover frequency versus formate concentration gave a Michaelis constant of KM = 0.086 mM (Fig. S3 and S4, ESI†). The maximum turnover frequency TOFmax for complex 4 (30.3 h−1) is ca. 5× higher than for [(η6-p-cym)Ru(TsEn)Cl] (complex 8, TOFmax = 6.4 h−1)25 and 20× higher than for the complex [(η6-hmb)Ru(en)Cl]PF6 (TOFmax = 1.46 h−1).24 The much lower Michaelis–Menten constant (KM = 0.086 mM) for the N-benzyl complex 4 indicates a stronger affinity of the complex for formate compared to [(η6-p-cym)Ru(TsEn)Cl] (KM = 27.8 mM)25 and [(η6-hmb)Ru(en)Cl]PF6 (KM = 58 mM).24
The maximum turnover frequency was observed at pH* 6 (TOFmax = 7.7 h−1) (Fig. S2, ESI†). The TOF for complex 4 gradually decreased when the pH* was raised above 6. Transfer hydrogenation was halted below pH* 4 because of the decomposition of the complex.
3.4 Antiproliferative activity and anticancer activity with formate
Ruthenium complexes have shown promise for their activity against various types of cancer cells.42 The antiproliferative activity of complexes 1–6 towards A2780 human ovarian cancer cells was determined and compared with the clinically approved drug cisplatin, Fig. 4. The IC50 values (50% inhibition of cell growth) range from 1 to 6.5 μM for complexes containing aromatic R substituents (4–6), whereas those containing aliphatic R substituents were less potent with IC50 values of 12–31 μM. The complex [(η6-p-cym)Ru(TsEn(Bz,H))Cl] (4) (IC50, 1.0 μM) has a potency similar to cisplatin in this cell line (CDDP, 1.20 ± 0.02 μM). It is apparent that the presence of aromatic substituents on the chelated ligands of complexes 4–6 give rise to more potent cytotoxicity than aliphatic substituents in complexes 1–3, most probably due to their higher lipophilicity.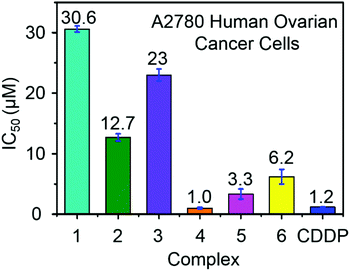 | ||
| Fig. 4 Antiproliferative activity of RuII complexes 1–6 and cisplatin towards A2780 human ovarian cancer cells. | ||
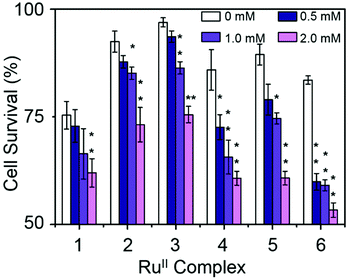
Combination treatment with formate can greatly increase the antiproliferative activity of RuII arene sulfonyl diamine complexes, which offers a potential new strategy for cancer treatment.15 In this work, the antiproliferative activity of RuII complexes in A2780 human ovarian cancer cells in the presence of sodium formate was studied (Fig. 5). Firstly, the cytotoxicity of sodium formate alone towards A2780 human ovarian cancer cells was investigated. No significant toxicity was found up to formate concentrations of 2 mM which is in agreement with the previous report.15 Then, A2780 human ovarian cancer cells were coincubated with equipotent concentrations of complexes 1–6 (1/3 × IC50) and three different concentrations of sodium formate (0.5, 1 and 2 mM) in order to observe the formate-concentration dependence of the cell viability. The antiproliferative activity of complexes 1–6 increased significantly upon coincubation with 2 mM formate. The formate-induced decrease in viability of A2780 cells ranged from 20% to 36% in the presence of complexes 1–6. Interestingly for complex 6, a 28% decrease in cell viability was observed with only 0.5 mM formate present (Fig. 5, for percentage of viability decrease see Table S3, ESI†). The largest decrease of cell survival was 31% for complex 6 in the presence of 2 mM sodium formate, followed by 29% and 32% for the other two complexes with aromatic substituents, complexes 4 and 5, respectively. Complexes 1–3 with aliphatic functional groups showed an increase in potency of 18%, 21% and 22%, respectively.
3.5 Cell accumulation and relative hydrophobicity
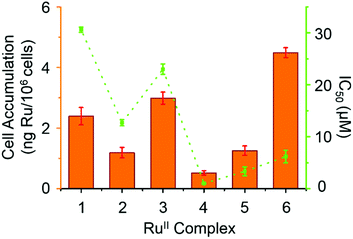
Hydrophobicity and cellular accumulation are often important factors that play key roles in the potency of organometallic and other anticancer drugs.43 The cellular accumulation, as an equilibrium between uptake and efflux, of ruthenium in A2780 human ovarian cancer cells after exposure to complexes 1–6 at their IC50 equipotent concentrations was determined by inductively coupled plasma mass spectrometry (ICP-MS) and is shown in Fig. 6.Complex 4 gave the lowest cellular accumulation (0.52 ± 0.08 ng of Ru per 106 cells), while complex 6 with moderate anticancer activity, exhibited the highest extent of cell accumulation with 4.5 ± 0.2 ng of Ru per 106 cells at IC50 concentration, 8.6× higher than complex 4. Complexes 1–3 and 5, gave rise to similar cell uptake 2.4 ± 0.3 ng, 1.2 ± 0.2 ng, 3.0 ± 0.2 ng and 1.3 ± 0.2 ng per 106 cells, respectively, following the order: 4 < 2, 5 < 1 < 3 < 6.
The relative hydrophobicity of complexes 1–6 was determined by RP-HPLC. The more hydrophobic complexes have longer retention times on a reverse-phase C18 column.44 To ensure solubility of the RuII complexes in water, methanol was used as co-solvent (MeOH/H2O, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) together with NaCl (50 mM) to suppress hydrolysis of the complexes. The HPLC solvents were also prepared with 50 mM NaCl (measurements see Fig. S5, ESI†). The resulting retention times are shown in Table 4, and follow the order: 1, 2, 3 < 4, 5 < 6. Complex 3 shows the shortest retention time (least hydrophobic) of 14.0 min, while complex 6 shows the longest retention time (most hydrophobic), 20.9 min.
9 v/v) together with NaCl (50 mM) to suppress hydrolysis of the complexes. The HPLC solvents were also prepared with 50 mM NaCl (measurements see Fig. S5, ESI†). The resulting retention times are shown in Table 4, and follow the order: 1, 2, 3 < 4, 5 < 6. Complex 3 shows the shortest retention time (least hydrophobic) of 14.0 min, while complex 6 shows the longest retention time (most hydrophobic), 20.9 min.
| Complex | t R (min) | Cellular-Ru (ng per 106 cells) |
|---|---|---|
| 1 | 15.4 ± 0.9 | 2.4 ± 0.3 |
| 2 | 14.5 ± 0.3 | 1.2 ± 0.2 |
| 3 | 14.0 ± 0.3 | 3.0 ± 0.2 |
| 4 | 17.4 ± 0.2 | 0.52 ± 0.08 |
| 5 | 17.27 ± 0.08 | 1.3 ± 0.2 |
| 6 | 20 ± 1 | 4.5 ± 0.2 |
It is evident from Table 4 that the RuII complexes with aromatic substituents (complexes 4–6) exhibit higher hydrophobicity than complexes with aliphatic substituents (complexes 1–3). The most hydrophobic complex (6) shows the highest cell accumulation. Nonetheless, there is no linear correlation between the hydrophobicity of complexes 1–6 and their cellular accumulation. This has been observed before.45 In these cases, the chemistry and the mechanism of action of each particular complex has a higher impact on the compound's anticancer activity than cellular accumulation per se. However, complex 4 has the lowest extent of cell uptake, but the most potent antiproliferative activity, suggesting that it is the chemical properties of the intracellular drug that are more important for activity than the total amount of Ru entering the cell. In general, a high hydrophobicity could facilitate interaction between the organometallic complex and cell membranes, and also correlate with the potency of the complex, but that is not always the case.43,45
3.6 ROS induction
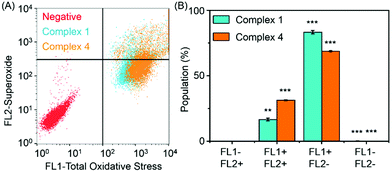
Reactive oxygen species (ROS) are metabolic byproducts of aerobic respiration and are responsible for maintaining redox homeostasis in cells.46 ROS also play a significant role in the mechanism of action of anticancer agents.47,48 Some organometallic complexes, e.g. Ir and Os,49–51 can generate high ROS levels or bursts of superoxide in cancer cells to induce cell apoptosis,49 but by comparison, other complexes are known to induce cell death by reductive stress.15 The levels of reactive oxygen species (ROS) were determined in A2780 human ovarian cancer cells for complexes 1 and 4 at IC50 concentrations by flow cytometry fluorescence analysis (Fig. 7). This included the monitoring of H2O2, peroxy and hydroxyl radicals using a green probe, and superoxide levels using the orange channel. Induction of total ROS and superoxide were determined in A2780 cells after 24 h exposure to complexes 1 and 4 when compared to the negative untreated control. The populations of cells that show high fluorescence in both FL-1 and FL-2 channels (both high total ROS and high superoxide generation) for complexes 1 and 4 are 16.5 ± 1.0% and 31.3 ± 0.3%, respectively, which indicates a higher induction of superoxide by complex 4. Remarkably, the total increase of the population in the high FL-1 green channel shows that the levels of total ROS are induced in the majority, if not in all, of the cell population. These ROS may play a major role in killing the cancer cells (Table S4, ESI†).3.7 DNA related binding for complex 4
The interaction of complex 4 with DNA nucleobase models: 9-ethylguanine (9-EtG) and adenosine 5′-monophosphate (5′-AMP) was studied by 1H NMR spectroscopy (Fig. S6, ESI†). The reactions were performed by adding nucleobase solution (3 mM in D2O) to RuII complex solution (2 mM in 10% d4-MeOD/90% D2O) at 310 K, to give a final 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol ratio. The formation of adduct 4-9-EtG was confirmed by following the new set of peaks, and up to 90% yield of adduct was obtained when 1.5 mol equiv. nucleobase solution was added. However, no adduct was found when 1.5 mol equiv. of 5′-AMP was added to complex 4, even after 24 h incubation at 310 K. Reactions of double-helical calf thymus DNA (ct-DNA, 32 μg mL−1) and plasmid DNA pBR322 (28 μg mL−1) with complex 4 in various molar ratios (ri = 0.05–1, ri = the molar ratio of free Ru complex to nucleotide phosphates at the onset of incubation with DNA) were studied. Very low amounts of ruthenium (5–7% of initial Ru) were found in the samples of DNA treated with complex 4 for 24 h. No significant changes in the mobilities of supercoiled (sc) or open circular (oc) form of plasmid DNA were observed even when incubated with high concentration of complex 4 (ri = 1, Fig. S7, ESI†). DNA is thought to be a cellular target for the en complex 7 (Fig. 1).52,53 However, for the substituted-en complex studied here, no obvious unwinding of DNA was observed after coincubation of ct-DNA with complex 4, suggesting that binding is weak, nor changes in the ratio of sc and oc forms of plasmid DNA, suggesting that complex 4 does not cleave DNA.
1 mol ratio. The formation of adduct 4-9-EtG was confirmed by following the new set of peaks, and up to 90% yield of adduct was obtained when 1.5 mol equiv. nucleobase solution was added. However, no adduct was found when 1.5 mol equiv. of 5′-AMP was added to complex 4, even after 24 h incubation at 310 K. Reactions of double-helical calf thymus DNA (ct-DNA, 32 μg mL−1) and plasmid DNA pBR322 (28 μg mL−1) with complex 4 in various molar ratios (ri = 0.05–1, ri = the molar ratio of free Ru complex to nucleotide phosphates at the onset of incubation with DNA) were studied. Very low amounts of ruthenium (5–7% of initial Ru) were found in the samples of DNA treated with complex 4 for 24 h. No significant changes in the mobilities of supercoiled (sc) or open circular (oc) form of plasmid DNA were observed even when incubated with high concentration of complex 4 (ri = 1, Fig. S7, ESI†). DNA is thought to be a cellular target for the en complex 7 (Fig. 1).52,53 However, for the substituted-en complex studied here, no obvious unwinding of DNA was observed after coincubation of ct-DNA with complex 4, suggesting that binding is weak, nor changes in the ratio of sc and oc forms of plasmid DNA, suggesting that complex 4 does not cleave DNA.
3.8 DFT calculations
We modelled the catalytic cycle by considering seven states of the reaction: (1) the initial aqua complex [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]+ and formate (with isolated NAD+); (2) [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]+ interacting intermolecularly with NAD+, and formate; (3) [(η6-p-cym)Ru(TsEn(R1,R2))(HCOO−)]·NAD+ and water; (4) [(η6-p-cym)Ru(TsEn(R1,R2))H] ·NAD+ and water and CO2; (5) [(η2-p-cym)Ru(TsEn(R1,R2))(OH2)NADH] and CO2; (6) [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]NADH and CO2; (7) [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]+, water and CO2, and isolated NADH (Fig. 8).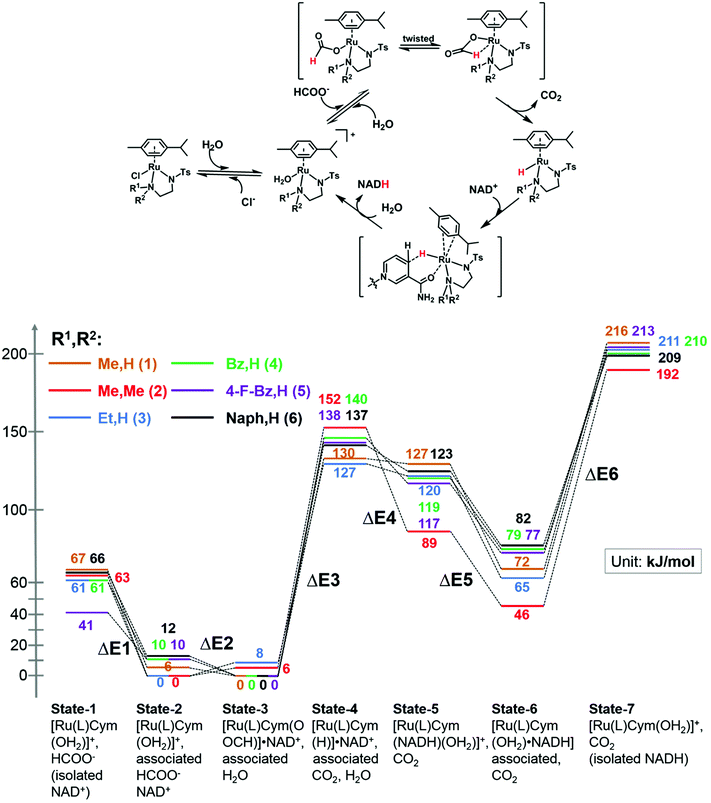 | ||
| Fig. 8 (Top) Reduction cycle for conversion of NAD+ to 1,4-NADH via transfer hydrogenation with formate as the hydride donor. (Bottom) DFT energy profile for the formation of Ru formate species, Ru hydride complex and hydride transfer from ruthenium; brown line, complex 1; red line, complex 2; blue line, complex 3; green line, complex 4; purple line, complex 5; black line, complex 6. Sets of calculated structures of states 1–7 are supplied in the ESI and illustrated graphically in Fig. S8† for complex 2. To calculate the energy of states 1 and 7, the energies of the states represented in pdb files 1 and 7 were added to the energies calculated for NAD+ and NADH. | ||
For state 5, with ring-slipped coordinated η2-p-cymene, the introduction of water into coordination sphere was necessary, while highly distorted complexes without coordinated water were found ca. 100 kJ mol−1 higher in energy. It is notable that the Ru atoms of all complexes in state 5 are coordinated to the amide oxygen atom of NADH, while only weakly bound to the (hydridic) CH2 of NADH, giving a Ru–H distance of 3.11–3.12 Å for R1,R2 = Me,H (1); Et,H (3); Naph,H (6) and 3.06–3.07 Å for R1,R2 = Bz,H (4) and 4-F-Bz,H (5). For R1,R2 = Me,Me (2) the calculations revealed a true bonding of the (hydridic) CH2, with a Ru–H distance of 1.99 Å. The results obtained are shown in Fig. 8. Four general conclusions can be drawn from these data: (a) there is a strong interaction between the [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]+ cation and NAD+ and NADH molecules, leading to a stabilisation of the cationic form by 60–70 kJ mol−1 for NAD+ (41 kJ mol−1 for R1,R2 = 4-F-Bz,H (5)) and 130–150 kJ mol−1 for NADH; (b) depending on the N-substituent, the species of the lowest energy is either [(η6-p-cym)Ru(TsEn(R1,R2))(HCOO−)]·NAD+ (R1,R2 = Me,H (1); Bz,H (4); 4-F-Bz,H (5) and Naph,H (6)) or [(η6-p-cym)Ru(TsEn(R1,R2))(OH2)]·NAD+ (R1,R2 = Et,H (3) and Me,Me (2)), the difference between them being only 6–12 kJ mol−1; (c) the effective NADH-hydride coordination for bulky R1,R2 = Me,Me (2) lowers the energy, relative to the state of lowest energy, of the species with coordinating NADH by 30–40 kJ mol−1, compared to other complexes; (d) the formation of the state with the Ru–H hydride bond, including the twist of formate and the elimination of carbon dioxide, corresponds to the highest energy step. These four factors seem all to influence the turnover. The energy barriers and optimized structures for the seven states of complex 2 in the cycle with NAD+ are listed in Table S5 and illustrated graphically in Fig. S8.† The structure files for the remaining complexes are supplied as ESI.†
4. Conclusions
In this work, we have synthesised a series of new RuII complexes of the type [(η6-p-cym)Ru(N,N′)Cl] where N,N′ are monosulfonamide chelating ligands derived from tosylethylenediamine, with either alkyl (Me,H (1); Me,Me (2); Et,H (3)) or aryl (Bz,H (4); 4-F-Bz,H (5); Naph,H (6)) substituents on the terminal N. These substituents have a significant effect on the rate of transfer hydrogenation of coenzyme NAD+ with formate as hydride donor as determined by NMR and UV-vis spectroscopy. In general, the bulkier aromatic substituents gave rise to faster hydrogenation rates (Table 3). DFT calculations provided insight into the mechanism of hydride transfer form formate to NAD+ involving initial coordination of formate followed by transfer of hydride to ruthenium and then to NAD+ with release of CO2. The calculations suggested a preorganization of the initial aqua complex, formate and NAD+ involving T-shaped adenosine NH-tosyl stacking, H-bonding of the NH of the chelated ligand and phosphate O of NAD+, H-bonding between formate and water, and between formate and the pyridine ring of NAD+. They also indicated strong interactions with NADH involving T-shaped adenosine NH-tosyl stacking, as well as H-bonds to phosphate and (hydridic) CH2-tosylate O (Fig. S8, ESI†).To investigate the possibility of achieving transfer hydrogenation mediated by formate in cells, we investigated the effect of formate on the antiproliferative activity of these complexes towards human ovarian cancer cells. In each case a dose-dependent increase in potency of the complexes (20–36%) was observed with increasing formate concentration over a range of non-toxic formate concentrations (0–2 mM). The complexes with aromatic substituents were the most potent, the benzyl complex 4 being as potent as the anticancer drug cisplatin (Fig. 6). In general, the most hydrophobic complexes were found to be the most biologically active. However, the activity does not correlate closely with total cell accumulation of Ru or with hydrophobicity (Table 3). Although DNA can be a target for related arene RuII diamine complexes, it does not appear to be a target for these sulfonyl-en RuII catalysts since we observe very weak binding to both calf thymus and plasmid DNA (Fig. S7, ESI†).
We showed that complexes 1 and 4 can generate high levels of ROS in A2780 human ovarian cancer cells, especially 4, the most potent complex. This is consistent with interference in cellular redox pathways and possible attack on NAD+ when sodium formate is present. The enhancement of anticancer activity by low non-toxic dose of formate might be clinically useful since it introduces a new mechanism of activity which does not involve DNA attack, unlike the clinical drug cisplatin. Such a regime might therefore avoid some unwanted side-effects. Formate itself is a natural biochemical molecule enriched in some cancer cells.54 However, more work remains to be done to investigate possible intracellular catalysis, especially since a range of metabolites might readily poison these catalysts in cells.
Author contributions
Feng Chen, Joan J. Soldevila-Barreda, Abraha Habtemariam and Peter J. Sadler designed the experiments and interpreted data.Feng Chen carried out synthesis and characterisation of ligands and complexes, investigated hydrolysis, determined the pKa value, and TH turnover frequencies.
Isolda Romero-Canelón and Ji-Inn Song carried out the cell antiproliferative screening and related biochemical assays.
Guy J. Clarkson carried out the X-ray crystallography.
Juliusz A. Wolny and Volker Schünemann carried out all the DFT calculations.
Jana Kasparkova and Viktor Brabec carried out DNA binding studies.
James P. C. Coverdale carried out metal analyses by ICP-OES and ICP-MS, and related biological and biochemical assays.
All authors contributed to the writing of the paper.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank ERDF/AWM (Science City), NWO (Rubicon grant), EPSRC (grant no. EP/F042159/1), and ERC (grant no. 247450) for support for this work, China Scholarship Council (CSC) for a scholarship for F. C., and Bruker Daltonics and Warwick Collaborative Postgraduate Research Scholarship (WCPRS, funding for J. P. C. C.); J. A. W. and V. S. acknowledge support of the research initiative NANOKAT and the German Federal Ministry of Education and Research (BMBF under 05K14UK1) and are grateful to the Allianz für Hochleistungsrechnen Rheinland-Pfalz (AHRP) for providing CPU-time within the project TUK-SPINPLUSVIB.We also thank Dr Ivan Prokes, Dr Lijiang Song, and Mr Philip Aston (University of Warwick) for their excellent assistance with the NMR and MS measurements.
References
- U. Eisner and J. Kuthan, Chem. Rev., 1972, 72, 1–42 CrossRef CAS.
- J. Gȩbicki, A. Marcinek and J. Zielonka, Acc. Chem. Res., 2004, 37, 379–386 CrossRef PubMed.
- A. McSkimming and S. B. Colbran, Chem. Soc. Rev., 2013, 42, 5439–5488 RSC.
- S. Fukuzumi and T. Suenobu, Dalton Trans., 2013, 42, 18–28 RSC.
- S. M. Barrett, C. L. Pitman, A. G. Walden and A. J. M. Miller, J. Am. Chem. Soc., 2014, 136, 14718–14721 CrossRef CAS PubMed.
- M. C. Carrión, F. Sepúlveda, F. A. Jalón, B. R. Manzano and A. M. Rodríguez, Organometallics, 2009, 28, 3822–3833 CrossRef.
- Y. Maenaka, T. Suenobu and S. Fukuzumi, J. Am. Chem. Soc., 2012, 134, 9417–9427 CrossRef CAS PubMed.
- A. Wolfson, C. Dlugy, Y. Shotland and D. Tavor, Tetrahedron Lett., 2009, 50, 5951–5953 CrossRef CAS.
- R. Ruppert, S. Herrmann and E. Steckhan, Tetrahedron Lett., 1987, 28, 6583–6586 CrossRef CAS.
- E. Steckhan, S. Herrmann, R. Ruppert, E. Dietz, M. Frede and E. Spika, Organometallics, 1991, 10, 1568–1577 CrossRef CAS.
- E. Steckhan, S. Herrmann, R. Ruppert, J. Thömmes and C. Wandrey, Angew. Chem., Int. Ed. Engl., 1990, 29, 388–390 CrossRef.
- V. D. Westerhausen, S. Herrmann, W. Hummel and E. Steckhan, Angew. Chem., Int. Ed. Engl., 1992, 31, 1529–1531 CrossRef.
- R. T. Hembre and S. McQueen, J. Am. Chem. Soc., 1994, 116, 2141–2142 CrossRef CAS.
- C. Wang, B. Villa-Marcos and J. Xiao, Chem. Commun., 2011, 47, 9773–9785 RSC.
- J. J. Soldevila-Barreda, I. Romero-Canelón, A. Habtemariam and P. J. Sadler, Nat. Commun., 2015, 6, 6582 CrossRef CAS PubMed.
- H. C. Lo, O. Buriez, J. B. Kerr and R. H. Fish, Angew. Chem., Int. Ed., 1999, 38, 1429–1432 CrossRef CAS.
- H. C. Lo, C. Leiva, O. Buriez, J. B. Kerr, M. M. Olmstead and R. H. Fish, Inorg. Chem., 2001, 40, 6705–6716 CrossRef CAS PubMed.
- J. M. O'Connor and C. P. Casey, Chem. Rev., 1987, 87, 307–318 CrossRef.
- K. T. Oppelt, J. Gasiorowski, D. A. M. Egbe, J. P. Kollender, M. Himmelsbach, A. W. Hassel, N. S. Sariciftci and G. Knör, J. Am. Chem. Soc., 2014, 136, 12721–12729 CrossRef CAS PubMed.
- V. Ganesan, D. Sivanesan and S. Yoon, Inorg. Chem., 2017, 56, 1366–1374 CrossRef CAS PubMed.
- S. Hashiguchi, A. Fujii, J. Takehara, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1995, 117, 7562–7563 CrossRef CAS.
- A. Fujii, S. Hashiguchi, N. Uematsu, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1996, 118, 2521–2522 CrossRef CAS.
- J. P. C. Coverdale, I. Romero-Canelón, C. Sanchez-Cano, G. J. Clarkson, A. Habtemariam, M. Wills and P. J. Sadler, Nat. Chem., 2018, 10, 347–354 CrossRef CAS PubMed.
- Y. K. Yan, M. Melchart, A. Habtemariam, A. F. A. Peacock and P. J. Sadler, J. Biol. Inorg. Chem., 2006, 11, 483–488 CrossRef CAS PubMed.
- J. J. Soldevila-Barreda, P. C. A. Bruijnincx, A. Habtemariam, G. J. Clarkson, R. J. Deeth and P. J. Sadler, Organometallics, 2012, 31, 5958–5967 CrossRef CAS.
- S. Betanzos-Lara, Z. Liu, A. Habtemariam, A. M. Pizarro, B. Qamar and P. J. Sadler, Angew. Chem., Int. Ed., 2012, 51, 3897–3900 CrossRef CAS PubMed.
- A. Habtemariam, M. Melchart, R. Fernández, S. Parsons, I. D. H. Oswald, A. Parkin, F. P. A. Fabbiani, J. E. Davidson, A. Dawson, R. E. Aird, D. I. Jodrell and P. J. Sadler, J. Med. Chem., 2006, 49, 6858–6868 CrossRef CAS PubMed.
- J. E. D. Martins, G. J. Clarkson and M. Wills, Org. Lett., 2009, 11, 847–850 CrossRef CAS PubMed.
- X. Li, L. Li, Y. Tang, L. Zhong, L. Cun, J. Zhu, J. Liao and J. Deng, J. Org. Chem., 2010, 75, 2981–2988 CrossRef CAS PubMed.
- V. Vichai and K. Kirtikara, Nat. Protoc., 2006, 1, 1112–1116 CrossRef CAS PubMed.
- D. T. T. Yanai and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- W. J. Stevens, H. Basch and M. Krauss, J. Phys. Chem., 1984, 81, 6026–6033 CrossRef.
- W. J. Stevens, M. Krauss, H. Basch and P. G. Jasien, Can. J. Chem., 1992, 70, 612–630 CrossRef CAS.
- T. R. S. Cundari, J. Chem. Phys., 1993, 98, 5555–5565 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A. 03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. E. Morris, R. E. Aird, M. P. Socorro, H. Chen, J. Cummings, N. D. Hughes, S. Parsons, A. Parkin, G. Boyd, D. I. Jodrell and P. J. Sadler, J. Med. Chem., 2001, 44, 3616–3621 CrossRef CAS PubMed.
- A. F. A. Peacock, A. Habtemariam, R. Fernández, V. Walland, F. P. A. Fabbiani, S. Parsons, R. E. Aird, D. I. Jodrell and P. J. Sadler, J. Am. Chem. Soc., 2006, 128, 1739–1748 CrossRef CAS PubMed.
- J. Zhang, A. Pierick, H. M. Rossum, R. M. Seifar, C. Ras, J. Daran, J. J. Heijnen and S. A. Wahl, Sci. Rep., 2015, 5, 12846 CrossRef CAS PubMed.
- M. Yamakawa, H. Ito and R. Noyori, J. Am. Chem. Soc., 2000, 122, 1466–1478 CrossRef CAS.
- R. Soni, F. K. Cheung, G. C. Clarkson, J. E. D. Martins, M. A. Graham and M. Wills, Org. Biomol. Chem., 2011, 9, 3290–3294 CAS.
- X. Wu, X. Li, W. Hems, F. King and J. Xiao, Org. Biomol. Chem., 2004, 2, 1818–1821 CAS.
- Z. Adhireksan, G. E. Davey, P. Campomanes, M. Groessl, C. M. Clavel, H. Yu, A. A. Nazarov, C. H. F. Yeo, W. H. Ang, P. Droge, U. Rothlisberger, P. J. Dyson and C. A. Davey, Nat. Commun., 2014, 5, 3462 Search PubMed.
- A. J. Millett, A. Habtemariam, I. Romero-Canelón, G. J. Clarkson and P. J. Sadler, Organometallics, 2015, 34, 2683–2694 CrossRef CAS PubMed.
- T. Bugarcic, O. Nováková, A. Halámiková, L. Zerzánková, O. Vrána, J. Kašpárková, A. Habtemariam, S. Parsons, P. J. Sadler and V. Brabec, J. Med. Chem., 2008, 51, 5310–5319 CrossRef CAS PubMed.
- M. Hanif, A. A. Nazarov, C. G. Hartinger, W. Kandioller, M. A. Jakupec, V. B. Arion, P. J. Dyson and B. K. Keppler, Dalton Trans., 2010, 39, 7345–7352 RSC.
- A. T. Dharmaraja, J. Med. Chem., 2017, 60, 3221–3240 CrossRef CAS PubMed.
- D. Trachootham, J. Alexandre and P. Huang, Nat. Rev. Drug Discovery, 2009, 8, 579–591 CrossRef CAS PubMed.
- J. Watson, Open Biol., 2013, 3, 120144 CrossRef PubMed.
- Z. Liu, I. Romero-Canelón, A. Habtemariam, G. J. Clarkson and P. J. Sadler, Organometallics, 2014, 33, 5324–5333 CrossRef CAS PubMed.
- Z. Liu, I. Romero-Canelón, B. Qamar, J. M. Hearn, A. Habtemariam, N. P. E. Barry, A. M. Pizarro, G. J. Clarkson and P. J. Sadler, Angew. Chem., Int. Ed., 2014, 53, 3941–3946 CrossRef CAS PubMed.
- Y. Fu, M. J. Romero, A. Habtemariam, M. E. Snowden, L. Song, G. J. Clarkson, B. Qamar, A. M. Pizarro, P. R. Unwin and P. J. Sadler, Chem. Sci., 2012, 3, 2485–2494 RSC.
- H. Chen, J. A. Parkinson, S. Parsons, R. A. Coxall, R. O. Gould and P. J. Sadler, J. Am. Chem. Soc., 2002, 124, 3064–3082 CrossRef CAS PubMed.
- G. Gasser, I. Ott and N. Metzler-Nolte, J. Med. Chem., 2010, 54, 3–25 CrossRef PubMed.
- P. M. Tedeschi, E. K. Markert, M. Gounder, H. Lin, D. Dvorzhinski, S. C. Dolfi, L. L. Y. Chan, J. Qiu, R. S. DiPaola, K. M. Hirshfield, L. G. Boros, J. R. Bertino, Z. N. Oltvai and A. Vazquez, Cell Death Dis., 2013, 4, 877 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1571331. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt00438b |
| This journal is © The Royal Society of Chemistry 2018 |