Mismatch in cation size causes rapid anion dynamics in solid electrolytes: the role of the Arrhenius pre-factor

Abstract

Crystalline ion conductors exhibiting fast ion dynamics are of utmost importance for the development of, e.g., sensors or rechargeable batteries. In some layer-structured or nanostructured compounds fluorine ions participate in remarkably fast self-diffusion processes. As has been shown earlier, F ion dynamics in nanocrystalline, defect-rich BaF₂ is much higher than that in the coarse-grained counterpart BaF₂. The thermally metastable fluoride (Ba,Ca)F₂, which can be prepared by joint high-energy ball milling of the binary fluorides, exhibits even better ion transport properties. While long-range ion dynamics has been studied recently, less information is known about local ion hopping processes to which ¹⁹F nuclear magnetic resonance (NMR) spin–lattice relaxation is sensitive. The present paper aims at understanding ion dynamics in metastable, nanocrystalline (Ba,Ca)F₂ by correlating short-range ion hopping with long-range transport properties. Variable-temperature NMR line shapes clearly indicate fast and slow F spin reservoirs. Surprisingly, from an atomic-scale point of view increased ion dynamics at intermediate values of composition is reflected by increased absolute spin–lattice relaxation rates rather than by a distinct minimum in activation energy. Hence, the pre-factor of the underlying Arrhenius relation, which is determined by the number of mobile spins, the attempt frequency and entropy effects, is identified as the parameter that directly enhances short-range ion dynamics in metastable (Ba,Ca)F₂. Concerted ion migration could also play an important role to explain the anomalies seen in NMR spin–lattice relaxation.

---

Introduction

The irregular movement of small anions and cations in crystalline and amorphous solids is a natural phenomenon that plays a key role in many devices as well as technological and geological processes. Extracting general rules from the existing amount of experimental data that control ionic transport and ionic diffusivity is, thus, of importance if we want to optimize devices, such as batteries,^1–4 relying on dynamic processes of ions. Nanostructured materials play a prominent role in these fields.^1,5,6

Although ion dynamics in a huge number of various nanomaterials have been studied over the last decades with a wide range of techniques,^7–11 our picture about ionic diffusivity is far from being completely understood. The introduction of defects, that is, in a more general sense describable with structural disorder, represents a powerful instrument with which we can control the chemical and physical properties of a material.^12–17 Ion dynamics sensitively depend on local arrangements. The present work is aimed at describing the interrelations between local disorder and short-range ion dynamics using a suitable model substance that may also be of interest as a fast ion conducting solid electrolyte.^4,18–23

The metastable (quasi) solid-solution (Ba,Ca)F₂ served as such model substance.^24,25 Recently, it has also attracted groups from theory to model ion conductivities.^26,27 Nanocrystalline Ba_1−xCa_xF₂ (0 < x < 1) can easily be prepared by mechanochemical reaction at low temperatures from the binary fluorides BaF₂ and CaF₂.^24,25 Joint milling the two fluorides forces the cations to mix at atomic scale while the symmetry of the educts remains the same; both BaF₂ and CaF₂ crystallize with antifluorite structure. Thus, over the entire compositional range the original crystal symmetry is preserved whereas local atomic arrangements do, however, differ.²⁸ At x = 0.5, and after sufficiently long mechanical treatment, the majority of the F anions are directly surrounded by both Ba and Ca ions without any heavy clustering of Ba- and Ca-rich regions.²⁸ These features, as well as the possibility to prepare incompletely mixed samples, render Ba_1−xCa_xF₂ a complex model system to study the influence of structural disorder on local ion dynamics.

Although the mixing effect on (i) atomic structure and (ii) long-range ion transport in Ba_1−xCa_xF₂ has recently been studied via DC conductivity measurements in detail,²⁸ less is known about the change of local hopping processes. Starting from x = 0 the ionic conductivity increases and passes through a maximum at approximately x = 0.5 before it decreases and reaches the value of pure CaF₂ (x = 1).²⁸ In turn, the associated activation energy runs through a minimum at x = 0.5 being the composition with maximum structural disorder with regard to intimate cation mixing. The specific conductivity of the solid solution Ba_0.5Ca_0.5F₂ prepared by ball milling exceeds even that of epitaxially grown BaF₂–CaF₂–BaF₂ layers.^28,29 This layered system²⁹ is one of the most famous examples of an artificial ion conductor whose transport properties are explained by non-trivial size effects, i.e., by overlapping space charge zones.^9,10,30,31 Such effects might also influence ion transport in mechanosynthesized (Ba,Ca)F₂.²⁸

While local strain, i.e., a strongly heterogeneous potential landscape, has been made responsible for the increase in conductivity of Ba_0.5Ca_0.5F₂,²⁸ short-range ion dynamics have so far not been probed. Shedding light on these hopping processes is expected to help identify the driving forces that control the increase in ionic diffusivity seen. Here, we took advantage of ¹⁹F NMR (spin-lock) relaxometry to extract mean activation barriers the ions are subjected to in Ba_1−xCa_xF₂. For heterogeneous nanocrystalline materials with disordered interfacial regions and crystalline grains NMR can, in ideal cases, differentiate the mobile ions in or near the (percolating) interfaces from those in the defect-rich interior of the nm-sized grains.^32–34 For Li₂O and the dispersed, nanocrystalline ion conductors Li₂O : X₂O₃ (X = Al, B) it was possible to draw conclusions about the location of the mobile ions responsible for fast macroscopic ion transport.^32,33

Experimental

Mechanochemical preparation and characterization of the samples

A series of nanocrystalline samples Ba_1−xCa_xF₂ with the compositions of x = 0, 0.1, 0.2, 0.5, 0.8, 1.0 were prepared by high-energy ball milling. Pure, microcrystalline BaF₂ (99.99%, Sigma-Aldrich) and CaF₂ (99.9%, ABCR) served as starting materials. We used of a Fritsch Pulverisette 7 (premium line) planetary mill. Two 45 mL grinding beakers, filled with the reactants (the total mass was 4 g) and 180 ZrO₂ milling balls (5 mm in diameter) in each case, were employed. The mixtures were mechanically treated for 10 h at a rotational speed of 600 rpm. To exclude contamination with moisture or oxygen during milling, the beakers were filled and emptied in a glovebox with dry argon atmosphere. The powders obtained were characterized by X-ray powder diffraction (XRPD) using a Bruker D8 Advance diffractometer that operates with Bragg Brentano geometry and Cu K_α radiation.

Conductivity measurements

For our conductivity measurements cylindrical pellets with 5 mm in diameter and ca. 1.5 mm in thickness were used. The pellets were uniaxially cold-pressed at a pressure of approximately 0.5 GPa. Blocking electrodes with a layer thickness of 100 nm were applied with a Leica EM SCD 050 evaporator. Impedance measurements were carried out with a Novocontrol Concept 80 broadband dielectric spectrometer. Our measurements covered a frequency range from 0.01 Hz to 10 MHz; temperatures (173 K–473 K) were adjusted with a QUATRO controller (Novocontrol). To avoid any contamination with water or oxygen during the measurements, the pellets were dried inside the impedance cell, which was permanently flushed with dry nitrogen gas.

NMR measurements

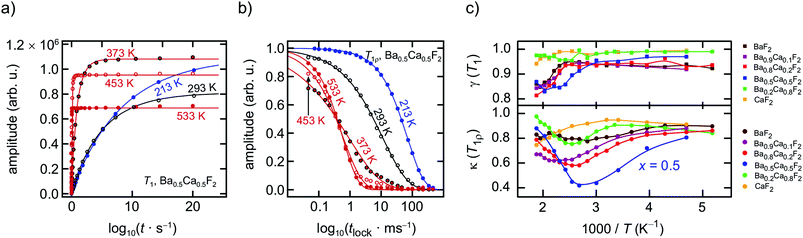
To assess the fluorine self-diffusion parameters ¹⁹F NMR spectroscopy and relaxometry were used to estimate jump rates and activation energies. Here, we took advantage of the saturation recovery and the spin-lock technique to record longitudinal (1/T₁) as well as transversal (1/T_1ρ) NMR spin–lattice relaxation (SLR) rates. For the NMR measurements the dry powders were fire-sealed in Duran glass tubes (ca. 4 cm in length and 3 mm in diameter) under vacuum to protect them from any impact of humidity. All measurements were carried out on a Bruker Avance III spectrometer that was connected to a shimmed cryomagnet with a nominal magnetic field of 7 T. This field corresponds to a ¹⁹F NMR Larmor frequency of ω₀/2π = 282.0 MHz. A home-built NMR probe, which is suitable to record NMR signals under static conditions in a temperature range from 193 K to 533 K, was used to record the SLR rates and the ¹⁹F NMR spectra. At 200 W the π/2 pulse length was approximately 1 μs. A Eurotherm temperature controller in combination with a type-T thermocouple was utilized for both temperature controlling and monitoring. The saturation recovery pulse sequence consisted of ten succeeding pulses that destroy any longitudinal magnetization M_z, after a delay time t_d the reading pulse was sent to detect the recovery of M_z as a free induction decay (FID): 10 × π/2-t_d − π/2-acquisition (acq.). To construct the magnetization transients M_z(t_d) we plotted the area under the FIDs vs. t_d. Additionally, rotating-frame ¹⁹F NMR SLRρ rates 1/T_1ρ were measured by means of the spin-lock technique, π/2 p(t_lock)-acq., using a locking frequency ω₁/2π of approximately 100 kHz.^18,35 We varied the locking pulse length from t_lock = 46 μs to t_lock = 460 ms. To guarantee full longitudinal relaxation between each scan the recycle delay was set to at least 5 × T₁. Both the 1/T₁ and 1/T_1ρ rates were obtained by parameterizing the resulting transients M_z(t_d) and M_ρ(t_lock) with stretched exponentials of the form M_z(t_d) ∝ 1 − exp(−(t_w/T₁)^γ) and M_ρ(t_lock) ∝ exp(−(t_lock/T_1ρ)^κ), respectively. While the stretching exponents γ varied from 1 to 0.8, the parameter κ ranged from 0.4 to 1.0 depending on temperature.

Static ¹⁹F NMR spectra were obtained with a single 90° pulse experiment via Fourier transformation of the FID. We employed a 500 MHz Avance spectrometer (Bruker) to record the spectra; the ¹⁹F Larmor frequency was 470.4 MHz. The NMR lines shown represent Fourier transforms recorded under static, i.e., non-rotating, conditions. ¹⁹F NMR spectra under magic angle spinning (MAS) were measured at a rotation speed of 60 kHz using 1.3 mm rotors. Spectra were referenced to crystalline CaF₂, which shows, as a secondary reference, an isotropic chemical shift δ_iso of 58 ppm; C₆F₆ served as primary reference.

Results and discussion

Characterization via X-ray powder diffraction and ¹⁹F MAS NMR

The phase purity of the samples and the formation of a mixed (Ba,Ca)F₂ phase with retained cubic symmetry (see Fig. 1) was verified with the help of XRPD. We collected diffraction patterns at room temperature and in air atmosphere. Exemplarily, Fig. 1(a) shows the pattern of the mixture with the composition Ba_0.2Ca_0.8F₂ which was milled for 10 h in the P7 planetary mill (see Fig. S1 in the ESI† for the characterization of the other samples studied). For comparison, in Fig. 1 the patterns of nanocrystalline BaF₂ and CaF₂ prepared under the same milling conditions are presented. The pure nanocrystalline samples feature reflections at exactly the same positions as their coarse-grained samples. A marked difference is, however, that the reflections of the powders ball-milled for 10 h show noticeable broadening. This broadening is attributed to the formation of nm-sized crystallites and the generation of strain upon mechanical treatment. As has been shown by earlier studies on nanocrystalline (Ba,Ca)F₂ as well as other fluorides and oxides prepared by high-energy ball milling the final average crystallite size reached after many hours of mechanical treatment is in the order of 10 to 17 nm for the mixed samples.³⁶ This result was obtained by evaluating the width of the reflections with the equation introduced by Scherrer³⁷ (see ESI (Table S1†) for the exact crystallite sizes calculated). These values are supported by high-resolution transmission electron microscopy carried out in early studies.^24,25 It is worth noting that abrasion of ZrO₂ on ion conductivities turned out to be negligible in our case; such effects have been discussed by some of us in earlier studies.^24,25,28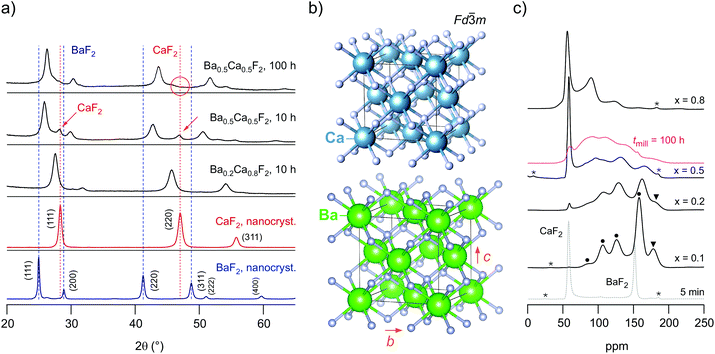

Fig. 1 (a) X-ray powder patterns of high-energy ball milled CaF₂, BaF₂ and a mixtures Ba_1−xCa_xF₂ with the compositions Ba_0.2Ca_0.8F₂ and Ba_0.5Ca_0.5F₂. From the point of view of XRPD, the pattern of the mixed phase with x = 0.8 reveals the formation of a nanocrystalline solid solution as all reflections refer to a cubic phase with shifts to lower diffraction angles. The same holds for x = 0.2. The samples were prepared in a planetary mill using a ZrO₂ vial set; the rotational speed was 600 rpm, the milling time was set to 10 h. To prepare Ba_0.5Ca_0.5F₂ free of any residuals of nanocrystalline Ca(Ba)F₂ longer milling times are needed. The conductivity response of the two samples is the same. (b) Crystal structure of cubic CaF₂ and BaF₂; the two materials only differ by the lattice constant a. (c) ¹⁹F MAS NMR spectra of Ba_1−xCa_xF₂ recorded at 470.4 MHz and a spinning frequency of 60 kHz. The asterisks mark spinning sidebands, the black dots (x = 0.1) indicate the different F environments. Note that signals arising from orthorhombic BaF₂, as also seen in X-ray diffraction (see Fig. 1(a)), are marked by red dots; these partly overlap with those from the mixed phases. If not stated otherwise, the milling time was 10 h. The spectrum, referring to a milling time of 5 min, shows a stochiometric mixture of BaF₂ and CaF₂ to highlight the initial δ_iso values of the starting materials, 58 ppm (CaF₂) and 152 ppm (BaF₂), respectively.

A close look at the pattern of the Ba_0.2Ca_0.8F₂ mixture reveals that the reflections shifted to smaller diffraction angles if compared with those of pure (nanocrystalline) CaF₂. The incorporation of the larger Ba²⁺ ions (ionic radius of 1.42) into the F-sublattice of CaF₂, the ionic radius of Ca²⁺ is 1.12, causes the original lattice to expand. According to Bragg's law this mismatch in size results in lower diffraction angles. The reverse process is observed when some Ca²⁺ ions are introduced into BaF₂. For Ba_1−xCa_xF₂ with x = 0.5 the final reflections are characterized by almost the arithmetic average.²⁸ The formation of mixed (Ba,Ca)F₂ and the discussion of the corresponding XRPD patterns is already well documented in literature.^24,25,28 Most important for us is the following aspect: after milling the educts for 10 h, the reflections originating from the non-mixed starting materials BaF₂ are no longer visible for most compositions. As an example, for Ba_0.2Ca_0.8F₂ the formation of a mixed phase with no significant amounts of crystalline educts is seen by XRPD.

Besides decreasing the crystallite size and introducing structural disorder, it cannot be ruled out that mechanical treatment also lead to the formation of some amorphous material. Although recent EXAFS studies by Chadwick and co-workers³⁸ did not point to large fractions of amorphous regions in mechanosynthesized Ba_1−xCa_xF₂, the XRPD pattern of Ba_0.2Ca_0.8F₂ revealed a shallow hump at low diffraction angles. This feature is frequently assigned to amorphous material.³⁹

For samples with x being close to 0.5, i.e., considering equimolar mixtures, longer milling times than 10 h are needed to ensure intimate mixing of the earth alkaline cations. As an example, in Fig. 1 the XRPD pattern of two samples of Ba_0.5Ca_0.5F₂ are shown that were obtained after milling for t_mill = 10 h and 100 h, respectively. After 10 h residual CaF₂ is still present and not all Ca²⁺ ions have been fully incorporated into the BaF₂ lattice, as can be seen by the small CaF₂ reflections visible (see the red arrows in Fig. 1(a)). After milling the mixture for 100 h these reflections disappear. Additionally, the more Ca²⁺ ions are introduced into the BaF₂ lattice the larger the lattice contraction of BaF₂ which in turn causes a shift of the reflections toward larger diffraction angles. Hence, only very long milling times ensured the absence of any (nanocrystalline) starting materials.

The positions of the final reflections of the sample obtained after 100 h suggest the formation of an almost fully mixed sample. Of course, the existence of both Ba-rich and Ca-rich regions cannot be excluded on the basis of XRPD. As seen by (high-resolution) ¹⁹F MAS NMR, which is sensitive to the local, atomic environments of the F nuclei, heavy clustering, however, seems to be negligible for x = 0.5. This conclusion is at least valid for mixtures obtained after sufficiently long periods of milling with t_mill = 100 h (see Fig. 1c). The ¹⁹F MAS NMR spectra of the fully mixed samples are composed of several overlapping lines revealing partly the magnetically inequivalent F anions in Ba_0.5Ca_0.5F₂. In general, since each F anion is directly surrounded by 4 cations, in an ideal solid solution the environments are [Ba]₃[Ca], [Ba]₂[Ca]₂, [Ba][Ca]₃ as well as [Ba]₄ and [Ca]₄ (see Fig. S2 in the ESI† for the assignment of the different atomic F environments in Ba-rich Ba_1−xCa_xF₂ including a deconvolution of the spectra).²⁸

The signals of [Ba]₄ and [Ca]₄ are the weakest in intensity for x = 0.5 and t_mill = 100 h. Keeping in mind that the NMR chemical shift for [Ba]₄ in completely mixed Ba_0.5Ca_0.5F₂ (182 ppm) is different compared to that in pure nanocrystalline BaF₂ (152 ppm), the NMR spectra point to mixing of the earth alkaline ions on atomic scale. For the sample milled only for 10 h (x = 0.5) we see that the sharp signal around 52 ppm points to Ca-rich regions that only vanish if t_mill is increased to 100 h. The reason for the disappearance of the [Ca]₄ signal is, that more and more CaF₂ gets incorporated into BaF₂ the longer the milling time is chosen. After 100 h of milling, the equimolar mixture forms a disordered phase with a large amount of mixed F environments: [Ba]₃[Ca], [Ba]₂[Ca]₂, [Ba][Ca]₃. The more effective the mixing process is, the less the probability to find Ba- and Ca-rich species [Ba]₄ and [Ca]₄ originating from the educts (see also the corresponding XRPD pattern in Fig. 1(a)).

When comparing the samples with x = 0.8 and x = 0.1 it is, however, evident that after a milling period of 10 h Ca-rich and Ba-rich regions are clearly present. The Ca-rich sample (x = 0.8) reveals the fastest ¹⁹F SLR rates, see below. ¹⁹F MAS NMR reveals further that mixing of the earth-alkaline ions seems to be easier for compositions x < 0.5, i.e., for Ba-rich samples. Mechanical treatment of cubic-BaF₂ always leads to the formation of some orthorhombic material (up to 20 wt% depending on the milling conditions). The orthorhombic form is a high-pressure phase of BaF₂; it is also seen in ¹⁹F MAS NMR. With increasing x the amount of orthorhombic BaF₂ decreases.

As outlined above, after the formation of the mixed phase, either completely or partially, the F anion conductivity σ_DC sharply increases when compared to the pure nanocrystalline starting materials. σ_DC passes through a maximum at intermediate compositions. Correspondingly, the activation energy takes a minimum at x = 0.5. While σ_DC refers to long-range ion transport, that is affected by grain boundaries, interfacial regions and porosity, NMR relaxometry, on the other hand, is primarily sensitive to bulk properties and, most importantly, to local F⁻ hopping processes. In ideal cases, NMR was able to differentiate between ions in the interfacial regions and those in the bulk. This separation was possible for some single- and two-phase nanocrystalline oxides as well as binary fluorides with a large number fraction of ions residing in the structurally disordered interfacial regions.

¹⁹F NMR relaxometry to evaluate short-range F anion hopping

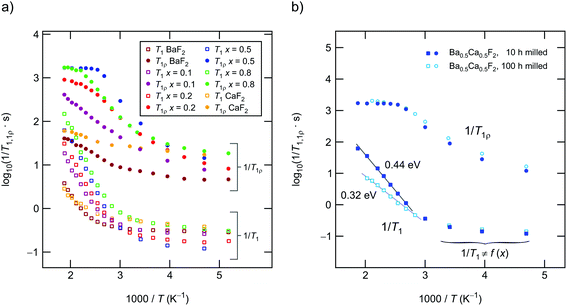
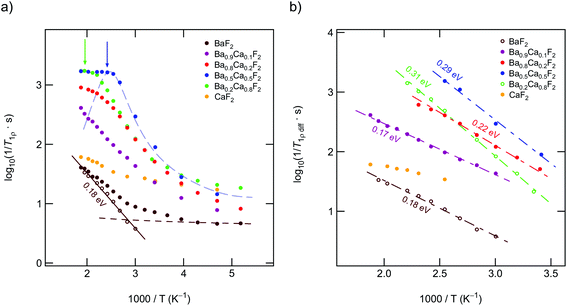
In Fig. 2 an overview of all variable-temperature ¹⁹F spin–lattice and spin-lock NMR relaxation rates is presented. To identify the thermally activated regions, from which hopping activation energies can be extracted, the rates were plotted in an Arrhenius representation. Stretched exponential functions served to parameterize the magnetization transients M_z(t_d) and M_ρ(t_lock), see Fig. 3(a) and (b) and section 2. The corresponding stretching exponents γ are illustrated in Fig. 3(c).

Fig. 2 (a) Temperature dependence of the ¹⁹F NMR SLR rates 1/T₁ (282.0 MHz) and 1/T_1ρ (100 kHz) for all nanocrystalline samples Ba_1−xCa_xF₂ prepared via high-energy ball milling. (b) ¹⁹F NMR SLR behavior of nanocrystalline Ba_0.5Ca_0.5F₂ obtained after t_mill = 10 h and t_mill = 100 h. While measurements in the kHz range (1/T_1ρ) are unaffected by t_mill, local jump processes, as seen by T₁ NMR, depend on the degree of cation mixing. The activation energies indicated refer to non-corrected rates; background correction to calculate 1/T_1diff changes E_a from 0.32 eV to 0.35 eV (100 h) and from 0.44 eV to 0.49 eV with no effect on the ratio of the two activation energies.

Fig. 3 (a) Selected variable-temperature ¹⁹F NMR T₁ transients of nanocrystalline Ba_0.5Ca_0.5F₂. The solid lines represent fits according to stretched exponentials: M_z(t_d) ∝ 1 − exp(−(t/T₁)^γ). (b) Spin-lock ¹⁹F NMR T_1ρ magnetization transients of the same sample shown in (a); the amplitude was scaled such that it ranges from 0 to 1. The solid lines represent fits according to M_ρ (t_lock) ∝ exp(−(t_lock/T_1ρ)^κ). (c) Change of γ and κ as a function of the inverse temperature 1/T.

The stretching factors of the M_z(t_d) transients, which contain the rate T₁, are almost exponential, except for few compositions deviations from γ = 1 show up at temperatures above 393 K. The κ values of the spin-lock transients reveal a more complex behavior and pass through minima at temperatures higher than 333 K; this feature is especially seen for the mixed sample Ba_0.5Ca_0.5F₂. The educts, which are characterized by lower ionic conductivities (see below), do not show such behavior. The Ba_0.5Ca_0.5F₂ sample features the lowest minimum with values of approximately κ = 0.4 at T = 360 K.

For all samples the ¹⁹F NMR SLR rates, measured in the laboratory frame of reference (1/T₁), show a non-diffusion induced regime below 330 K. In this T range the rates only marginally depend on temperature, see also Fig. 4(a). Background relaxation is in many cases driven by lattice vibrations or coupling of the spins to paramagnetic impurities.⁴⁰

Fig. 4 (a) Temperature dependence of the ¹⁹F NMR SLR rates 1/T₁ (282.0 MHz). A power law is used to extrapolate the background rates to higher T to obtain purely diffusion-induced relaxation rates 1/T_1diff. The dashed lines indicate possible positions of the peak maxima. (b) Diffusion induced ¹⁹F NMR rates after the correction procedure. The lines show linear fits to extract NMR activation energies, which range from 0.40 to 0.49 eV.

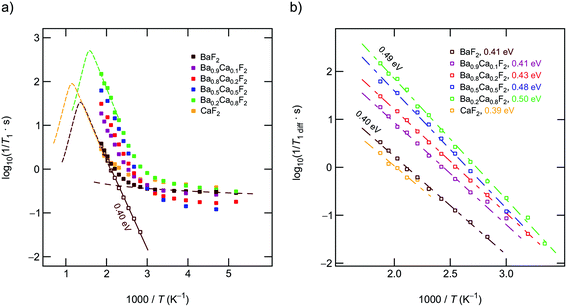
Above 330 K the rates start to increase because of F jumps on the time scale of the NMR experiment. We approximated the background rates with a power law, 1/T_1,bgr ∝ T^β, and extrapolated the rates to higher T to calculate background-free, diffusion-induced rates: 1/T_1diff = 1/T₁ − 1/T_1,bgr.⁴¹β values ranged from 0.3 (x = 0) to 1.5 (x = 0.5). For intermediate values of x we obtained β ≈ 1. In Fig. 4(a) this procedure is exemplarily shown for nanocrystalline BaF₂, see unfilled symbols. The rates 1/T_1diff follow Arrhenius behavior characterized by an activation energy of 0.4 eV.

As x in Ba_x−1Ca_xF₂ is increased, the beginning of the diffusion-induced flank is shifted toward lower T. This clearly indicates increased F self-diffusion in the partially or completely mixed phases. As can be already seen in Fig. 4(a), the slope of the different flanks do not vary much but run in parallel to each other. The diffusion induced rates, see Fig. 4(b), reveal measurable but by far not great differences in activation energies which range, disregarding the results of CaF₂, from 0.41 eV to 0.50 eV. These values are in good agreement with results from recently performed molecular dynamics studies.²⁷ For nanocrystalline CaF₂ background effects are predominant in the T range investigated; these effects do not allow the proper determination of an activation energy in the T range covered. Here, we estimated E_a after background correction to be approximately 0.39 eV. The better the flank is accessible the more precise the activation energy can be determined.

Fig. 4(b) entails two important information. First, the absolute rates 1/T_1diff increase with increasing x and sharply decrease if x exceeds 0.8. As a function of x, the diffusion-induced rates pass through a maximum that is similar, but not exactly the same, to that seen via DC conductivity spectroscopy. T₁ is most effective for Ca-rich samples, see the rates for x = 0.8. Apart from this small but important distinctions, the rates support the mixed earthy-alkaline effect observed in our earlier study.²⁸ Second, the activation energies from NMR turn out to be smaller than those seen by DC conductivity spectroscopy (see Table 1). Furthermore, their overall change with composition is less pronounced as seen for long-range ion transport.²⁸ In contrast to conductivity measurements, E_a from NMR pass through a very shallow maximum (ca. 0.5 eV at x = 0.5) rather than a minimum.

Table 1 Activation energies and ionic conductivities as derived from conductivity and NMR spectroscopy for the samples milled for 10 h in a high-energy planetary mill. Note that E_a from NMR, as well as E′_a, steadily increases from x = 0 to x = 0.8 although σ_DC and E_a(σ_DC) pass through a maximum and a minimum, respectively

	Conductivity spectroscopy			NMR relaxation
x	E a	σ DC (298 K) (S cm^−1)	log(σ0/S cm^−1 K)	E a (T1)^a (eV)	E′a(T1)^f (eV)	E a (T1ρ) (eV)	α
a Corrected values that take into account a non-diffusive background; the error for all values is ±0.01 eV. b Activation energy read off at 1 MHz: 0.50 eV. c 0.58 eV (1 MHz). d 0.55 eV (1 MHz). e After 100 h of milling a value of 5.44 is obtained; the largest increase for the pre-factor is seen when comparing nanocrystalline CaF2 with nanocrystalline BaF2. f E′a denotes values corrected using a joint fit of both diffusion and non-diffusive effects. g Values refer to Ea(T1); α = 2 would result for 3D (isotropic) uncorrelated motion. h For x = 0.5 and tmill = 100 h we obtained E′a = Ea = 0.35 eV. After 100 h of milling we obtain α = 1.54.
0	0.78	1.6 × 10^−11	5.17	0.41	0.43	0.19	1.51	Low-T flank not completely reached
0.1	—	—	—	0.41	0.45	0.17
0.2	0.64^b	4.6 × 10^−9	5.06	0.43	0.43	0.22	1.66
0.5	0.61^c	1.6 × 10^−8	5.23^e	0.49	0.46	0.29	1.80	E a(T1) = 0.35 eV,^a^,^h for tmill = 100 h.
0.8	0.71^d	8.7 × 10^−10	5.52	0.50	0.51	0.32	1.70
1.0	0.80	7.2 × 10^−14	3.41	0.39	0.35	0.09	1.39	Low-T flank only partly accessible below 500 K

---

To further support the activation energies obtained according the correction procedure sketched above, we also analyzed our T₁ data with an Arrhenius fit that directly takes into account the deviation at low temperatures with the help of a power law ansatz: 1/T₁ = c·exp(−E_a/(k_BT)) + a·(1/T)ⁿ. c and a denote fitting parameters. The exponent n (0.4 < n < 1.2) should agree with β. It characterizes the type of relaxation, e.g., driven by coupling of the spins to electrons or phonons, being responsible for the change in 1/T₁ at low T. The fitting results are shown in Fig. 5; the activation energies E′_a are listed also in Table 1. E′_a is, for all samples, closely comparable with E_a.

Fig. 5 (a) Temperature dependence of the ¹⁹F NMR SLR rates 1/T₁ (282.0 MHz) for nanocrystalline Ba_0.5Ca_0.5F₂ obtained after t_mill = 10 h and t_mill = 100 h. A joint fit of both diffusion and non-diffusive effects is used to obtain the activation energies. (b) Change of the low-T¹⁹F NMR 1/T₁ rates of Ba_1−xCa_xF₂ as a function of x. Solid and dashed lines show fits with the joint fit mentioned. The extracted NMR activation energies range from 0.35 to 0.51 eV.

Comparison with results from conductivity spectroscopy and ¹⁹F NMR line shapes

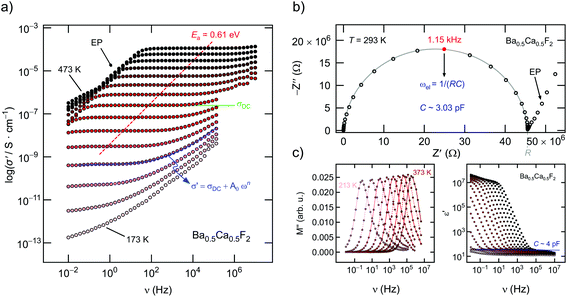
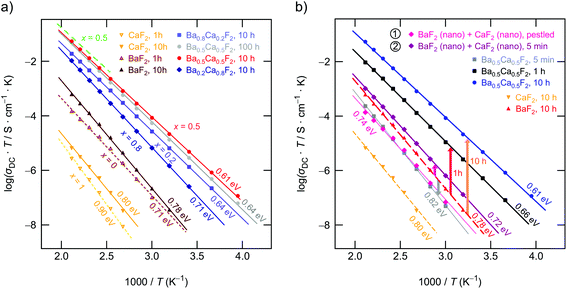
To characterize long-range F ion transport through impedance spectroscopy, in Fig. 6(a) the conductivity isotherms of Ba_0.5Ca_0.5F₂ are shown. While at low frequencies and sufficiently high T electrode polarization effects show up, the main parts of the spectra are dominated by the so-called DC plateau (ν → 0) from which σ_DC can be read off. Pronounced dispersion regions are only visible at sufficiently low T. The DC plateau transforms into a semi-circle when the Nyquist representation is used to analyze the impedance data. The semicircle shown in Fig. 6(b) is characterized by a capacity C of 3 pF which unequivocally points to a bulk electrical relaxation process. Blocking grain boundary resistances seem to be negligible. A value of 3 pF is also in perfect agreement with permittivities well below 10², see Fig. 6(c). The modulus representation, M′′(ν), reveals single peaks with a width (full width at half maximum) larger than that expected for a Debye process, cf.Fig. 6(c). Hence, the F ions are subjected to correlated motion in Ba_0.5Ca_0.5F₂ sensing a distribution of diffusion pathways in an irregularly shaped potential landscape. Such dynamics are usually described with non-exponential motional correlation functions.⁴²

Fig. 6 (a) Conductivity isotherms of nanocrystalline Ba_0.5Ca_0.5F₂. A Jonscher-type power law is used to parameterize the dependency on frequency. While electrode polarization (EP) shows up at high T and low frequencies, at low T dispersive regions dominate the spectra. DC conductivities were read off from the frequency independent plateau regions. (b) Complex plane plot of the conductivity isotherm recorded at 293 K. Only one depressed semicircle is seen which corresponds to a relaxation process characterized by a capacity expected for a bulk response. The electrical relaxation frequency ω_el at 293 K is 1.15 kHz. (c) Modulus spectra and change of the real part of the complex permittivity with frequency in a temperature range between 173 K and 473 K (spectra recorded in steps of 20 K).

Evaluating σ_DCT, see Fig. 7(a), illustrates that, depending on x, the activation energy for long-range ion transport varies from 0.80 eV (CaF₂, ball milled for 10 h) to 0.61 eV (Ba_0.5Ca_0.5F₂). Pure nanocrystalline BaF₂ (10 h) has to be characterized by 0.78 eV. These values perfectly agree with those published earlier.²⁸ In Fig. 7(b) we show the increase of σ_DCT for Ba_0.5Ca_0.5F₂ with increasing milling time. While for a mixture of BaF₂ and CaF₂ milled for only 5 min σ_DC is still affected by the low-conducting CaF₂, milling for 1 h already results in a significant increase of the DC ionic conductivity exceeding that of nanocrystalline BaF₂ (10 h) by one order of magnitude. After 10 h of mechanical treatment the upper limit of σ_DC is reached. Further increase of t_mill does not change σ_DC significantly.

Fig. 7 (a) Change of the DC conductivity of Ba_1−xCa_xF₂ as a function of inverse temperature. The highest conductivities are found for x = 0.5. While the solid lines show linear fits to extract activation energies for samples prepared by milling for t_mill = 10 h, dashed lines refer to samples milled for 1 h only. (b) Conductivity of Ba_0.5Ca_0.5F₂ samples prepared by high-energy ball milling and comparison to BaF₂ : CaF₂ mixtures, see text for further details. Samples 1 and 2 refer to compounds which have been prepared by mixing nanocrystalline BaF₂ (t_mill = 10 h) and CaF₂ (t_mill = 10 h) either by hand with mortar and pestle or by high-energy ball milling the two components for only 5 min. For the ball-milled sample even the 5 min milling procedure results in a measurable increase of σ_DCT.

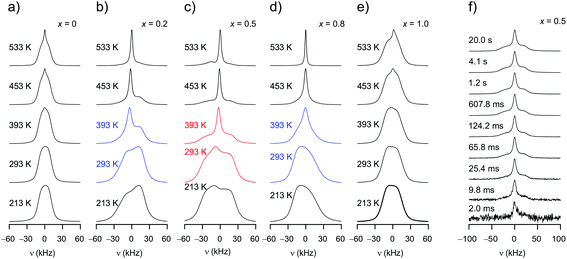
While for σ_DC the activation energy and the σ₀ in σ_DCT = σ₀ exp(−E_{a, DC}/k_BT) may vary with x, in ¹⁹F NMR relaxometry the change of the NMR pre-factor 1/τ_{0, NMR} (see below) seems to play a more significant role. This idea is illustrated in Fig. 4(a). The higher F anion conductivity in mixed samples is a proven fact. Indeed, ¹⁹F NMR line shape measurements also show enhanced F anion hopping in the mixed samples as compared to the pure end members. In contrast to BaF₂ and CaF₂ the corresponding NMR lines of the samples with 0.2 < x < 0.8 are composed of a clearly visible motionally narrowed contribution that is attributed to F anions being fast enough to average (homonuclear) dipole–dipole couplings (Fig. 8). As the rigid lattice ¹⁹F NMR line width of BaF₂ (and CaF₂) is at least 30 kHz, full narrowing, which is already seen slightly above 400 K, corresponds to F jump rates 1/τ_NMR in the order of 10⁶ s⁻¹, see also the estimation below via spin-lock NMR. Such a value will definitely affect the low-T regime of SLR NMR. The peak maximum of the 1/T₁ rate would be expected to show up if 1/τ_NMR reaches values in the order of 1.8 × 10⁹ s⁻¹.

Fig. 8 (a) to (e) Variable-temperature ¹⁹F NMR spectra of Ba_1−xCa_xF₂ (282.0 MHz, static conditions). At low T broad NMR lines are seen. Broadening is due to dipole–dipole couplings and the existence of a (partially) mixed F environments with distinct chemical shifts. Spectra are shown such that the centre of the NMR signal is located at 0 kHz. As T increases heterogeneous motional narrowing sets in. The narrowed line, which emerges with increasing temperature at the centre of the NMR signal, reflects the number fraction of mobile F anions with respect to the NMR time scale. For x = 0.5 and T = 393 K the area fraction of this NMR line is larger for x = 0.5 than for x = 0.2 and x = 0.8. (f) Evolution of the ¹⁹F NMR Fourier transforms in the frame of a T₁ saturation recovery experiment, that is, spectra obtained at different waiting times t. Strong spin-diffusion effects account for a single spin temperature with no differences in T₁ relaxation for both the narrow and the broad NMR spectral components.

As the rates of Ba_0.5Ca_0.5F₂ reveal the onset of the diffusion-induced low-T flank at lower temperatures we expect the corresponding rate peak, see dashed lines in Fig. 4(a), to show up at lower T as compared to BaF₂ and CaF₂, respectively. With the low-T activation energies being rather similar, especially if we consider the flanks of the samples with x = 0.2, x = 0.5 and x = 0.8, the only parameter that can further increase 1/τ_NMR is the pre-factor in 1/τ_NMR = 1/τ_{0, NMR} exp(−E_{a, high-T}/k_BT). Here, E_{a, high-T} denotes the activation energy of the high-T flank of the peaks indicated in Fig. 5(a). The flank is inaccessible as the nanocrystalline samples are sensitive to grain growth and decomposition if NMR experiments were performed at too high temperatures. E_{a, high-T} can be identified with E_{a, DC}. Although E_{a, DC} change from 0.61 eV to 0.71 eV for x ranging from 0.2 to 0.8 (cf.Table 1), the variation in E_{a, DC} alone could not explain the significant shift of the low-T flank. As for σ₀, also 1/τ₀ is, besides other factors, affected mainly by the attempt frequency v₀, the activation entropy ΔS as well as the number of spins effectively taking part in ¹⁹F NMR spin–lattice relaxation. The latter number is strongly associated to the concentration of available sites where the mobile ions can jump to. As has been shown recently, the softness of a lattice may influence v₀.⁴³ In the present case, besides such an influence, effects of migration entropy, affected by both vibrational or configurational contributions, is expected to control the pre-factor mostly. Frenkel defects show a considerable high migration entropy that may especially affect the samples with x = 0.5 and x = 0.8.

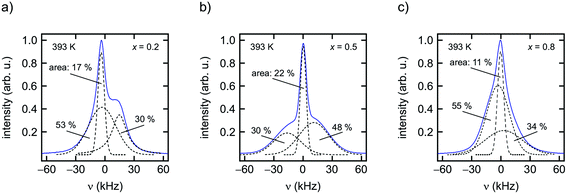
As can be clearly inferred from the ¹⁹F NMR spectra (Fig. 8(a)–(e)), the number fraction of mobile F anions, which are represented by the motionally narrowed lines for each sample, passes through a maximum at x = 0.5. This is best seen at T = 393 K. For the sake of clarity we deconvoluted the spectra with appropriate Voigt functions to estimate the area fraction A_f of the motionally narrowed NMR component (see Fig. 9).¹² The larger the number of mobile ions, performing net displacements as well as local jumps, the more effective spin fluctuations. Of course, the x-dependent number of effective charge carriers will, to some extent, also affect σ₀, which is related to long-range ion transport. It turned out, however, that its influence on localized jump processes is much larger.

Fig. 9 (a) to (c) ¹⁹F NMR spectra of Ba_1−xCa_xF₂ (x = 0.2, x = 0.5 and x = 0.8) recorded at 393 K (282.0 MHz). In order to estimate the area fraction of the narrow component several Gaussian curves were used to deconvolute the spectra. The narrowed lines at the centre of the NMR signals reflect the number fraction A_f of mobile F anions. For x = 0.5 approximately 20% participate in fast ion dynamics. Although the Ca-rich sample with x = 0.8, see also the corresponding XRD pattern, is characterised by A_f of only 11%, ¹⁹F relaxation is most effective for this sample. The mixed but Ca-rich regions seem to facilitate nuclear spin relaxation.

Although F anion dynamics is clearly heterogeneous in Ba_x−1Ca_xF₂, effective spin-diffusion, i.e., flip-flop processes without any mass transfer, ensures homogeneous relaxation of the spin system. Accordingly, the ¹⁹F NMR transients do not feature a two-step decay of fast and slowly relaxing components as it has been seen for other nanocrystalline core–shell model systems.^32–34 In the frame of a saturation recovery experiment ¹⁹F NMR spectra uniformly buildup with increasing waiting time (see Fig. 8(f)). Thus, there is fast communication between all ¹⁹F spins in mixed Ba_0.5Ca_0.5F₂.

Influence of correlated motion on activation energies

Understanding the slight increase in E_{a, low-T} when going from x = 0.2 (0.43 eV) to x = 0.5 (0.48 eV) and further to x = 0.8 (0.50 eV) also needs our attention. Although perhaps not applicable to our disordered system with relatively low barriers, the trend of both pre-factor and E_a from NMR resembles that of the Meyer–Neldel rule after which a higher activation energy is associated with a higher pre-factor.⁴⁴ In our case, however, we have to consider the following. In contrast to E_{a, high-T}, E_{a, low-T} is a so-called apparent activation energy that is additionally affected by correlation effects.⁴⁵ It is comparable to AC conductivity activation energies read off in the dispersive regions of the conductivity isotherms (see also Table 1).¹⁶ The larger the impact of correlation effects, such as structural disorder and Coulomb interactions of F⁻ interstitials and vacancies, the larger the difference between E_{a, high-T} and E_{a, low-T}. The two activation energies are linked according to the following relation E_{a, low-T} = (α − 1)E_{a, high-T}.⁴⁶ For 3D uncorrelated motion the parameter α equals 2. Correlated motion results in α < 2 and, thus, yields asymmetric NMR rate peaks.⁴⁵ Here it turned out that α pass through a maximum located near x = 0.5 (see Table 1). This result means less correlated motion for the samples with the highest diffusion-induced relaxation rates. To be clear, in all samples correlated motion is sensed by NMR; its extent, however, seems to be less for local ion dynamics in samples milled just for 10 h and x = 0.5 or x = 0.8. It is evident from XRPD and ¹⁹F MAS NMR that under these conditions mixing at atomic scale is incomplete; ¹⁹F MAS NMR revealed that the same is true for the sample with x = 0.8. Therefore, fast F anion diffusion might occur along or near Ca- and Ba-rich regions as mentioned above. Precisely speaking, diffusion induced T₁ relaxation is more effective for x = 0.8, i.e., for mixed but Ca-rich environments.

.Recently, we probed a very similar trend of α for Li ion diffusivity in layer-structured 2H-Li_yNbS₂.⁴⁷ Although in 2H-Li_yNbS₂ Li diffusivity decreases when y approaches y = 1, which is the maximum Li load, the low-T activation energy in deduced from T₁(T) measurements steadily decreases when going from y = 0.3 to y = 1.0. This effect has been ascribed to an increasing effect of correlated ion motion which is maximal when the van-der-Waals gap in NbS₂ is completely filled with Li ions. At the same time, also dipolar magnetic and electric quadrupolar interactions increase the larger the Li concentration.

Here, the origin of correlated motion in mixed Ba_x−1Ca_xF₂ is, however, definitely different from that seen for 2H-Li_yNbS₂. An increasing number fraction of mobile F spins, activation entropy contributions and lower long-range activation energies cause a sharp increase in Li diffusivity and ionic conductivity when mixed phases are formed. For all samples correlated motion is expected because the ions are subjected to a highly irregular potential landscape, including also metastable states. The extent and origins of correlation effects seem, however, change with composition. According to the NMR factor α the Ba-rich phases (x = 0.1, x = 0.2) provide an additional source of correlated motion leading to lower apparent activation energies than expected. Zahn et al. pointed out differences in the concentration of mobile charge carriers when Ca or Ba ions are introduced in BaF₂ and CaF₂, respectively. At very low levels of doping, the incorporation of Ca²⁺ ions resulted in trapped F interstitial sites and mobile F vacancies as the opponent defect.²⁶ The formation of such interstitial site next to a Ca²⁺ dopant in BaF₂ was promoted by 0.08 eV. On the other hand, the generation of Frenkel defects in Ba-doped CaF₂ is energetically disfavored by 0.14 eV.²⁶

In our case substitutional disorder is much larger than dopant concentrations and a direct comparison with results for extremely low levels of doping turns out to be difficult. At least we can say the following. Even if we consider complete and uniform mixing at atomic scale, we deal with samples that naturally have larger regions being rich in Ba²⁺. Segregation effects in interfacial regions or clustering on the nm scale will lead to even larger non-uniform areas. As has been shown recently for several types of ion conductors, concerted ion movements always cause the mean activation barrier to decrease.⁴⁸ Thus, concerted and, thus, highly correlated ion movements in the vicinity of Ca-doped Ba-rich regions or at the interface of Ba-rich and Ca-rich regions in non-intimately mixed samples could serve as an explanation for the unusual ¹⁹F NMR SLR behavior and the origin of additional correlation effects seen for the Ba-rich samples.

Obviously, on the angstrom length scale, to which ¹⁹F SLR NMR is sensitive, this effect levels off when the region 0.5 ≤ x ≤ 0.8 is reached. Note that also the activation energy of Ba_0.5Ca_0.5F₂ (0.58 eV, see Table 1), when determined from AC impedance spectroscopy at 1 MHz, is higher than that of Ba_0.2Ca_0.8F₂ (0.55 eV) and Ba_0.8Ca_0.2F₂ (0.50 eV). In this compositional range, the increase in mobile spins near non-uniformly mixed interfaces is more significant and leads to a further increase in diffusivity. Simultaneously, the impact of correlation effects on the low-T¹⁹F NMR T₁ measurements decreases, at least for samples milled for 10 h.

¹⁹F NMR spin-lock NMR and the effect of long-term milling

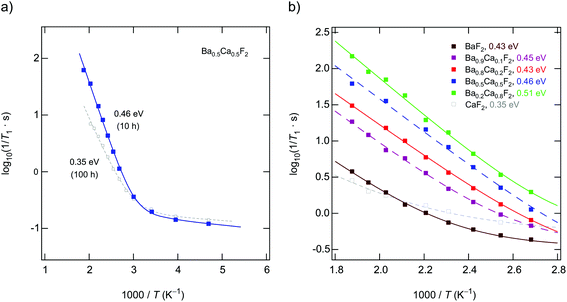
If we consider the corresponding rates measured in the kHz range through spin-lock NMR, see Fig. 10(a) and (b), the activation energies seem to reflect the same behavior. Regarding the absolute values for E_a suggests, however, that the temperature dependence of the ¹⁹F NMR SLR rates, see data for x = 0.1 and x = 0.2, are additionally influenced by other effects. Besides changes in the diffusion mechanisms, non-diffusive effects, such as spin-diffusion, presumably play the most important role. The characteristic spin-diffusion correlation times are expected to take values in the s to ms range, which fall into the time window of spin-lock NMR. Dipolarly coupled ¹⁹F spins with short distances to each other are prone to be affected by flip-flop effects. Hence, 1/T_1ρ NMR rates are expected to be much larger influenced by spin-diffusion as laboratory-frame SLR measurements performed in the MHz to GHz range. Apart from such interfering effects, spin-lock NMR relaxation is most effective for the sample with x = 0.5. This finding mirrors the change of long-range ion dynamics as seen by DC conductivity measurements.

Fig. 10 (a) Arrhenius representation of the spin-lock ¹⁹F MAS NMR rates 1/T_1ρ (100 kHz, 282.0 MHz) for Ba_1−xCa_xF₂. As for T₁, we used a power law ansatz to correct the measured rates for any non-diffusive background relaxation, as indicated for the data referring to nanocrystalline BaF₂. The dashed line drawn through the data points of the Ba_0.5Ca_0.5F₂ sample is to guide the eye. The peak is located at the lowest possible temperature. For x = 0.2 and x = 0.8 we see that the peaks shift toward higher T (see vertical arrows). These shifts fully agree with a lower F anion diffusivity and, consequently, a lower F ion conductivity as seen through conductivity spectroscopy. (b) Diffusion induced ¹⁹F NMR SLR rates 1/T_{1ρ diff} rates after background correction.

Up to here, we discussed results from samples prepared by milling the starting materials for 10 h. Except for Ba_0.5Ca_0.5F₂ our results from XRPD do not reveal any substantial amounts of the nanocrystalline binary parents. Increasing t_mill up to 100 h forces the earth alkaline ions to mix almost completely, as is also verified by ¹⁹F MAS NMR. Importantly, the 1/T_1ρ rates, as well as the DC conductivity values, do not change when t_mill is increased from 10 to 100 h. Hence, bulk long-range ion transport and spin-diffusion effects are already fully developed at shorter periods of mechanical treatment. In contrast, ¹⁹F NMR spectra and 1/T₁ do depend on t_mill. Although static line shapes reveal an increase of the number of mobile spins on the NMR time scale, this change does not cause an increase of σ_DC, see above (Table 1 and Fig. 7(a)). While the onset of the low-T¹⁹F NMR 1/T₁ flank remains unchanged (see Fig. 4(b)), the corresponding activation energy decreases from E_a = 0.49 eV to only 0.35 eV. We attribute this unusual change in E_a(T₁) to enhanced localized ion jump processes. Localized or caged jumps, including unsuccessful highly correlated forward–backward processes, will definitely affect the low-T 1/T_1diff rates but do not contribute to net charge transport, which is sensed by σ′ in the limit of low frequencies. This is the classical way to interpret differences between diffusion parameters derived from NMR and those from conductivity spectroscopy. In general, the two methods are sensitive to quite different kinds of motional (auto-)correlation functions, see above. The relationship between parameters from NMR and conductivity spectroscopy in disordered media, such as glasses, has been discussed in detail by Ngai and co-workers.^49–54

Careful inspection of Fig. 7(a) shows that the sample milled for 100 h shows even lower conductivities as compared to that milled for 10 h. We also see a slight increase of the corresponding activation energy E_a (0.64 eV vs. 0.61 eV). This finding supports our idea that long-time milling, i.e., the formation of solid-solution like environments, mainly lead to an increase of localized correlated motional processes. The corresponding factor α turned out to be 1.54. This value is lower than α ≈ 1.8 found for Ba_0.5Ca_0.5F₂, which was prepared using t_mill = 10 h. On the other hand, it resembles the behavior of nanocrystalline BaF₂. Obviously, the most favorable configurations for long-range ion transport are internal, heterogeneously intermixed interfaces between Ca-rich and Ba-rich regions, as discussed above. Complete mixing, or the formation of clusters with, e.g., diameters of 1 nm, as suggested recently,²⁶ seems to be not needed to ensure effective long-range ion transport. Here, we assume that these heterogeneous regions act as non-stopping or percolating pathways similar to those in dispersed ion conductors.^{32,33,55–58} Interestingly, these regions, acting as hosts for fast F anion diffusivity, have partly been formed already at shorter milling times of t_mill = 1 h (see Fig. 7(b)). As compared to nanocrystalline BaF₂ we see a considerable increase in σ_DC for such a sample. Even if we mix nanocrystalline BaF₂ and CaF₂, each separately milled for 10 h, for just 5 min in a planetary mill, we found a measurable increase in ionic conductivity. For these samples ¹⁹F MAS NMR also points to a very low, but detectable fraction of F anions residing in or near the earth-alkaline mixed environments.

Self-diffusion coefficient

In contrast to the T₁ measurements, the spin-lock data (see Fig. 10(a)) reveal the beginning of a peak maximum from which we can finally deduce an upper limit of a diffusion coefficient. Interestingly, at the temperature where 1/T_1ρ passes through a maximum, in many cases the corresponding stretching factor, κ, takes its minimal value (see Fig. 3(c)). At the 1/T_1ρ peak maximum the F anion jump rate τ_NMR should be in the order of the (effective) locking frequency. Using ω₁/2π = 100 kHz as a lower limit, via ω₁τ = 0.5 we estimate 1/τ_NMR to be in the order of 1.3 × 10⁶ s⁻¹ at 410 K (x = 0.5). This value translates into a self-diffusion coefficient of D_{410 K} = a²/(6τ_NMR) of 1.8 × 10⁻¹⁴ m² s⁻¹. Here, a denotes the average jump distance; for Ba_0.5Ca_0.5F₂ we used a = 2.92 Å as a good approximation of the mean F–F distance in Ba_0.5Ca_0.5F₂ (10 h). D_{410 K} is a typical value for a moderate ionic conductor. The diffusion coefficient determined at the rate maximum of a spin-lock experiment carried out at 100 kHz should be comparable to that which we obtain when DC conductivities are analyzed that probe successful ion displacements. With the ionic conductivity at 410 K we estimated a solid-state diffusion coefficient via the Nernst–Einstein relation, D_σ = σ_DCk_BT/(q²N) with q being the charge of the F anions and N the number density of charge carriers. From ¹⁹F NMR we know that approximately 20% of the ions take part in ionic conduction. In this case D_{σ, 410 K} amounts to 1.7 × 10⁻¹⁴ m² s⁻¹, which is very close to the Einstein–Smoluchowski diffusion coefficient. For x = 0.8 the corresponding 1/T_1ρ peak is shifted toward higher T, directly reflecting the decrease in σ_DC as seen in Fig. 7(a). For x = 0.2, i.e., Ba-rich samples, strongly correlated motions (see above) and spin-diffusion effects govern the low-T¹⁹F NMR spin-lock rates.

Summary and conclusions

Mechanical treatment of CaF₂ and BaF₂ in high-energy ball mills leads to the formation of metastable Ba_x−1Ca_xF₂. Long-range ion transport is maximized for equimolar compositions and E_a, determined from DC conductivity measurements, passes through a minimum value (0.61 eV) at this composition. Through ¹⁹F NMR relaxometry measurements, being in our case sensitive to short-range F anion dynamics, we tried to sharpen this picture. Here, we showed that ion dynamics on the angstrom length scale is characterized by very similar activation energies if x varies from 0.2 (0.43 eV) to 0.5 (0.50 eV). The increase of the absolute ¹⁹F SLR NMR rates can be explained by an increase of the pre-factor of the underlying Arrhenius equation, which is, besides other factors, governed by the activation entropy. For all samples we observed highly correlated ionic motion. While macroscopic properties, such as σ_DC, do not depend much on milling time; short-range order and motional correlation effects do. By comparing the various samples prepared we conclude that F anion diffusivity in earth-alkaline mixed interfacial regions, either rich in Ba or Ca, mainly boost long-range ion transport. Extensive mixing of the cations during long milling periods, on the other hand, primarily influences short-range ion dynamics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Veronika Pregartner for her help with sample preparation and characterization. Financial support by the Deutsche Forschungsgemeinschaft (DFG Research Unit 1277, grant no. WI3600/2-1(4-1) and WI3600/5-2 (SPP 1415)) as well as by the Austrian Federal Ministry of Science, Research and Economy, and the Austrian National Foundation for Research, Technology and Development (Christian Doppler Laboratory of Lithium Batteries: Ageing Effects, Technology and New Materials) is greatly appreciated.

References

1. P. G. Bruce, B. Scrosati and J. M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930–2946.
2. B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935.
3. J. B. Goodenough and K. S. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
4. J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
5. A. S. Arico, P. Bruce, B. Scrosati, J. M. Tarascon and W. Van Schalkwijk, Nat. Mater., 2005, 4, 366–377.
6. M. Anji Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059–17062.
7. P. Heitjans and S. Indris, J. Phys.: Condens. Matter, 2003, 15, R1257–R1289.
8. A. Chadwick and S. Savin, Solid State Ionics, 2006, 177, 3001–3008.
9. J. Maier, Chem. Mater., 2014, 26, 348–360.
10. J. Maier, Phys. Chem. Chem. Phys., 2009, 11, 3011–3022.
11. J. Maier, Z. Phys. Chem., 2003, 217, 415–436.
12. P. Heitjans, M. Masoud, A. Feldhoff and M. Wilkening, Faraday Discuss., 2007, 134, 67–82.
13. F. Preishuber-Pflügl, V. Epp, S. Nakhal, M. Lerch and M. Wilkening, Phys. Status Solidi C, 2015, 12, 10–14.
14. D. Wohlmuth, V. Epp, P. Bottke, I. Hanzu, B. Bitschnau, I. Letofsky-Papst, M. Kriechbaum, H. Amenitsch, F. Hofer and M. Wilkening, J. Mater. Chem. A, 2014, 2, 20295–20306.
15. V. Epp and M. Wilkening, ChemPhysChem, 2013, 14, 3706–3713.
16. M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291–9300.
17. F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590.
18. V. Epp and M. Wilkening, in Handbook of Solid State Batteries, World Scientific, Singapore, 2015, ch. Li dynamics in solids as seen via NMR relaxometry.
19. M. Heise, G. Scholz, A. Düvel, P. Heitjans and E. Kemnitz, Solid State Sci., 2016, 60, 65–74.
20. G. Scholz, S. Breitfeld, T. Krahl, A. Düvel, P. Heitjans and E. Kemnitz, Solid State Sci., 2015, 50, 32–41.
21. H. Bhatia, D. T. Thieu, A. H. Pohl, V. S. K. Chakravadhanula, M. H. Fawey, C. Kubel and M. Fichtner, ACS Appl. Mater. Interfaces, 2017, 9, 23707–23715.
22. C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, ACS Appl. Mater. Interfaces, 2014, 6, 2103–2110.
23. C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, J. Phys. Chem. C, 2013, 117, 4943–4950.
24. B. Ruprecht, M. Wilkening, A. Feldhoff, S. Steuernagel and P. Heitjans, Phys. Chem. Chem. Phys., 2009, 11, 3071–3081.
25. B. Ruprecht, M. Wilkening, S. Steuernagel and P. Heitjans, J. Mater. Chem., 2008, 18, 5412–5416.
26. D. Zahn, P. Heitjans and J. Maier, Chem. – Eur. J., 2012, 18, 6225–6229.
27. A. Düvel, P. Heitjans, P. Fedorov, G. Scholz, G. Cibin, A. V. Chadwick, D. M. Pickup, S. Ramos, L. W. L. Sayle, E. K. L. Sayle, T. X. T. Sayle and D. C. Sayle, J. Am. Chem. Soc., 2017, 139, 5842–5848.
28. A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789.
29. N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946–949.
30. J. Maier, Prog. Solid State Chem., 1995, 23, 171–263.
31. J. Maier, J. Phys. Chem. Solids, 1985, 46, 309–320.
32. M. Wilkening, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2003, 5, 2225–2231.
33. S. Indris and P. Heitjans, J. Non-Cryst. Solids, 2002, 307, 555–564.
34. P. Heitjans and M. Wilkening, Mater. Res. Bull., 2009, 34, 915–922.
35. D. C. Look and I. J. Lowe, J. Chem. Phys., 1966, 44, 2995–3000.
36. S. Indris, D. Bork and P. Heitjans, J. Mater. Synth. Process., 2000, 8, 245–250.
37. A. L. Patterson, Phys. Rev., 1939, 56, 978–982.
38. A. V. Chadwick, A. Düvel, P. Heitjans, D. M. Pickup, S. Ramos, D. C. Sayle and T. X. T. Sayle, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 80 , 012005.
39. D. Wohlmuth, V. Epp, B. Stanje, A. M. Welsch, H. Behrens and M. Wilkening, J. Am. Ceram. Soc., 2016, 99, 1687–1693.
40. M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77 , 024311.
41. M. Wilkening, D. Bork, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2002, 4, 3246–3251.
42. B. Ruprecht, H. Billetter, U. Ruschewitz and M. Wilkening, J. Phys.: Condens. Matter, 2010, 22 , 245901.
43. M. A. Kraft, S. P. Culver, M. Calderon, F. Bocher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918.
44. W. Meyer and H. Neldel, Phys. Z., 1937, 38, 1014–1019.
45. P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter – Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2005, pp. 367–415.
46. M. Uitz, V. Epp, P. Bottke and M. Wilkening, J. Electroceram., 2017, 38, 142.
47. B. Stanje, V. Epp, S. Nakhal, M. Lerch and M. Wilkening, ACS Appl. Mater. Interfaces, 2015, 7, 4089–4099.
48. X. F. He, Y. Z. Zhu and Y. F. Mo, Nat. Commun., 2017, 8 , 15893.
49. K. L. Ngai, Solid State Ionics, 1998, 105, 225–230.
50. K. L. Ngai, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13481–13485.
51. V. Blache, J. Forster, H. Jain, O. Kanert, R. Kuchler and K. L. Ngai, Solid State Ionics, 1998, 113, 723–731.
52. O. Kanert, R. Kuchler, K. L. Ngai and H. Jain, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 76–82.
53. K. L. Ngai and O. Kanert, Solid State Ionics, 1992, 53, 936–946.
54. O. Kanert, J. Steinert, H. Jain and K. L. Ngai, J. Non-Cryst. Solids, 1991, 131, 1001–1010.
55. C. C. Liang, J. Electrochem. Soc., 1973, 120, 1289–1292.
56. S. Indris, P. Heitjans, M. Ulrich and A. Bunde, Z. Phys. Chem., 2005, 219, 89–103.
57. M. Ulrich, A. Bunde, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2004, 6, 3680–3683.
58. S. Indris, P. Heitjans, H. E. Roman and A. Bunde, Phys. Rev. Lett., 2000, 84, 2889–2892.

---

Footnote

† Electronic supplementary information (ESI) available: XRPD patterns, crystallite sizes, deconvoluted ¹⁹F MAS NMR spectra. See DOI: 10.1039/c7dt04487a

---