Excited-state structural relaxation and exciton delocalization dynamics in linear and cyclic π-conjugated oligothiophenes
Kyu Hyung
Park
a,
Woojae
Kim
a,
Jaesung
Yang
b and
Dongho
Kim
 *a
*a
aDepartment of Chemistry and Spectroscopy Laboratory for Functional π-Electronic Systems, Yonsei University, Seoul 03722, Korea. E-mail: dongho@yonsei.ac.kr
bDepartment of Chemistry and Medical Chemistry, Yonsei University, Wonju, Gangwon 26493, Korea
First published on 8th May 2018
Abstract
π-Conjugated oligothiophene is considered a chain segment of its polymeric counterpart, whose size and shape can be precisely controlled. Because of its simplified structure, it is possible to understand complex excited-state dynamics of the π-conjugated polymers by employing a bottom-up approach. We review theoretical and experimental aspects of π-conjugated oligothiophenes by summarizing recent works employing time-resolved spectroscopy. The extent of exciton delocalization, which is a prerequisite to efficient charge generation at organic heterojunctions, is described sequentially in model linear and cyclic oligothiophenes, and their analogues. The heterogeneous nature of these systems is highlighted by illustrating the results at both ensemble and single-molecule levels. Exciton dynamics that arise in the polymers are also covered and the signifcance of exciton and charge delocalization in photovoltaic materials is highlighted.
Key learning points(1) Electronic structures of linear and cyclic π-conjugated oligomers.(2) Relationship between absorption/emission characteristics and the extent of exciton delocalization. (3) Excited-state dynamics in π-conjugated oligomers and accompanied change in the exciton delocalization. (4) Identification of cyclic and acyclic excitons at single-molecule level through multiparameter analysis. (5) Additional (in)coherent excited-state dynamics emerging from energetic and structural manifolds in π-conjugated polymers. |
1. Introduction
π-Conjugated polymers (CPs) have played a crucial role in the development of organic photovoltaic devices. Despite their low dielectric constant in organic frameworks, which preferentially generate Frenkel excitons,1 the charge photogeneration process has proven to be efficient, reaching power conversion efficiencies over 10%. The exact mechanism of charge photogeneration in CPs has remained a controversial issue, but recent studies employing ultrafast spectroscopy have demonstrated that exciton and charge delocalization are a prerequisite for the reduction of electron–hole binding energy.1–4 Therefore, understanding the delocalization phenomena in conjunction with the structural properties of polymeric systems is of utmost importance.CPs are inherently heterogeneous systems. The low torsional barrier between aromatic subunits and the flexibility along the chain allow for numerous isoenergetic conformers containing short π-conjugated segments.5 These chain segments couple to each other to create exciton manifolds that are similar to the band structures of semiconductors. Photogenerated high-energy excitons are initially delocalized over the electronically coupled conjugated segments.6 This state is coherently funneled to a lower-energy segment, where subsequent structural relaxation and incoherent energy transfer occur.
The complexity of excited-state dynamics can be reduced by employing model oligomeric systems. Ultrafast localization by a coherent energy transfer process and long-range energy migration can be excluded in short oligomers to exclusively investigate the vibration assisted self-trapping and structural relaxation dynamics. The size of the molecule can be systematically controlled to determine the extent of exciton delocalization at various timescales. Shape and conformational disorder can also be controlled to study the exemplary CP structures such as random coil, toroid, and rod. While excited-state dynamics in oligomeric systems can be studied in correspondence to the polymeric counterparts, the simplicity and controllability of oligomers facilitate the comprehensive understanding of the nature of CPs.
In this tutorial review, we aim to describe the excited-state structural relaxation dynamics and associated exciton localization and delocalization processes in model π-conjugated oligomers. Emphasis is placed on π-conjugated oligothiophenes, which have been recently studied by our group using fluorescence upconversion spectroscopy to explicitly monitor the evolution of exciton coherence using different spectral parameters. First, we introduce the Hamiltonian approach used to model the energy states and emission properties of linear and cyclic systems. The relationships between the exciton coherence length and fluorescence vibronic peak ratio with and without disorder are outlined. In the following sections, spectroscopic approaches for the characterization of excited-state dynamics of linear and cyclic oligomers are summarized. In the last section, the excited-state dynamics that only exist in polymer systems is introduced and the significance of exciton delocalization in photovoltaic devices is discussed.
2. Comparison of the electronic structures of linear and cyclic systems
π-Conjugated oligomers share common photophysical characteristics with H/J-aggregates because their constituent subunits are electronically coupled to generate delocalized excitons.7 Spano et al. and Barford et al. have conducted theoretical studies on the absorption and fluorescence properties of π-conjugated oligomers with different structures to show that it is possible to relate the extent of exciton delocalization to the spectral parameters as in H/J-aggregates.8–12 In this section, we briefly introduce the basis of the Hamiltonian approach to derive the relationship between the exciton coherence length and vibronic peak ratios in linear and cyclic π-conjugated oligomers. We also discuss the effect of conformational disorder on limiting the coherence length in these oligomeric systems and describe the concept of spectroscopic unit.2.1. Influence of geometry in the Frenkel–Holstein model
A Frenkel exciton is a tightly-bound electron–hole pair with a small interchange distance. Analogous to the particle-in-a-box model, the center-of-mass of a Frenkel exciton can be delocalized over a number of monomers that comprise the π-conjugated chains. They couple to the local vibrational modes, typically to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes (≈1400 cm−1) that are commonly found in organic chromophores. This coupling can be adequately described by the Frenkel–Holstein model. For a chain composed of N monomers, the Frenkel–Holstein Hamiltonian in the k,q space reads
C stretching modes (≈1400 cm−1) that are commonly found in organic chromophores. This coupling can be adequately described by the Frenkel–Holstein model. For a chain composed of N monomers, the Frenkel–Holstein Hamiltonian in the k,q space reads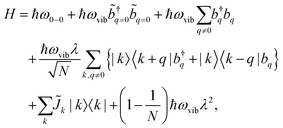 | (1) |
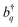 and their Hermitian conjugate, bq, respectively. q = 0 and q ≠ 0 indicate totally symmetric and non-totally symmetric phonons, respectively, and λ2 is the Huang-Rhys (HR) factor.
and their Hermitian conjugate, bq, respectively. q = 0 and q ≠ 0 indicate totally symmetric and non-totally symmetric phonons, respectively, and λ2 is the Huang-Rhys (HR) factor. ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) k is the exciton coupling given by
k is the exciton coupling given by![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) k = 2Jn,n+1 k = 2Jn,n+1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(k) cos(k) | (2) |
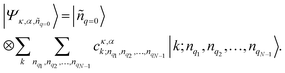 | (3) |
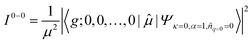 | (4) |
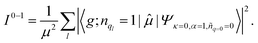 | (5) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b3.gif) , between the ground electronic state, |g〉, and exciton state, |k〉, for a straight chain, are
, between the ground electronic state, |g〉, and exciton state, |k〉, for a straight chain, are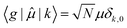 | (6) |
Then for a bent chain, where the angle between transition dipole moments of monomeric units is defined as θ,
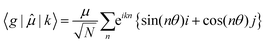 | (7) |
The ratio of the intensities of the 0–0 and the 0–1 emission bands can be reduced to a simple relationship in straight chains8
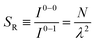 | (8) |
A similar relationship can also be approximated in bent chains9
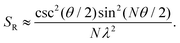 | (9) |
Since N is the number of constituent monomers, the emission intensity ratio in a straight chain, is proportional to the length of the chain as shown in Fig. 1a (inversely proportional to the HR factor and independent of the exciton bandwidth as shown in Fig. 1b and c). However, in a regularly bent chain, SR decreases as a function of θ and reaches SR = 0 when the geometry of the chain is circular at θ = 2π/N. This indicates a complete suppression of the 0–0 emission band (Fig. 2). In the circular chain, SR as a function of N manifests a deflection point that appears before N/2, indicating that the exciton delocalization over half of the circular chain reduces SR. The SR values in the two limiting cases have also been evaluated with open boundary conditions by Barford et al., who obtained qualitatively identical results.10–12
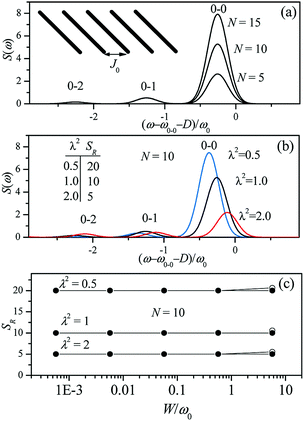 | ||
| Fig. 1 Changes in the fluorescence spectra as a function of (a) the number of subunits N and (b) Huang-Rhys factor λ2. Exciton bandwidth is set W = ω0 = 1400 cm−1 in (a) and (b). (c) Fluorescence vibronic peak ratio SR as a function of exciton bandwidth. Adapted from ref. 8 with permission. Copyright 2011 American Chemical Society. | ||
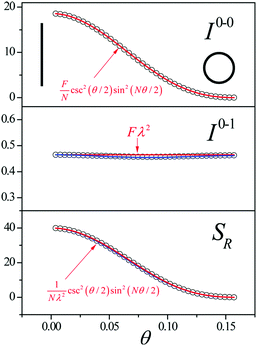 | ||
| Fig. 2 Change in the 0–0 (top) and 0–1 (middle) fluorescence vibronic peak intensities, and the ratio SR (bottom) as a function of curvature θ. N = 40 and Jn,n+1 = −200 cm−1 were used. Adapted from ref. 9 with permission. Copyright 2014 American Chemical Society. | ||
Although SR can be an indicator of the length and curvature of the exciton in uniform disorder-free π-conjugated chains, in most cases, static and dynamic conformational disorders are imposed on the system, for which the thermal effects and site energy disorder are required to be considered.
2.2. The role of disorder in electronic transitions
In the presence of thermal fluctuation or static disorder, the size of the exciton does not correspond to the number of constituent monomers. In many cases, excitons in actual systems are localized to a segment of a chain. The extent of delocalization is defined as coherence length, Ncoh. As thermal energy contributes to κ, the emission at T > 0 K is weighted by the Boltzmann distribution factor9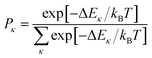 | (10) |
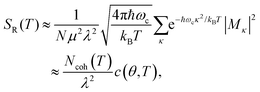 | (11) |
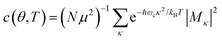 is the conformation factor, which accounts for the curvature of a chain. This shows that even in the presence of thermal fluctuation, SR can be a good indicator of the size and shape of an exciton.
is the conformation factor, which accounts for the curvature of a chain. This shows that even in the presence of thermal fluctuation, SR can be a good indicator of the size and shape of an exciton.
Torsional disorder is an omnipresent conformational disorder that induces off-diagonal disorder in π-conjugated chains. Theoretically, any amount of disorder can induce the localization of excitons in one-dimensional systems. This has carefully been investigated by Barford et al. Unlike the strict dipole–dipole approximation of Spano's approach, Barford incorporates superexchange interactions in the exciton coupling as
Jn,n+1 = JDD + JSE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2ϕn cos2ϕn | (12) |
3. Linear π-conjugated oligomers
3.1. Electronic structures of linear π-conjugated oligomers: general description
The electronic transitions of linear π-conjugated oligomers are located throughout the UV-Vis-NIR region where the position of the S1 transition strongly depends on the monomeric unit (e.g., phenylene, fluorene, thiophene, and porphyrin) and/or linkers (e.g., vinylene, ethynylene, and butadinylene). Assuming ideally linear geometry without torsional disorder, a transition from the ground state to the first singlet excited (S1) state corresponds to a one-photon allowed B transition (HOMO → LUMO transition, 1Ag → 1Bu for even-numbered and 1A1 → 1B2 for odd-numbered oligomers). This transition shows an oligomer-length-dependence, and thus can serve as a good indicator of an effective conjugation length, i.e., the length of light absorbing units or chromophores.15Moreover, π-conjugated oligomers have a strong correlation between electronic transitions and vibrational modes: electron–phonon coupling in which two vibrational modes are mainly involved (the high-frequency C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch at ≈1400 cm−1 and low-frequency inter-ring torsion at ≈100 cm−1).16 On account of the inherently strong electron–phonon coupling in π-conjugated systems, the manner in which these vibrational modes and molecular geometries affect the shape of the steady-state linear electronic spectra can be deduced. Typically, at room temperature, the absorption spectra of oligomers are quite broad, whereas the fluorescence spectra show structured vibronic bands that correspond to the break of the mirror image symmetry. These spectral characteristics can be easily understood from the curvatures of torsional potentials, which are closely related to different bond length alternations (BLA) between the ground and S1 states. On account of the benzoidal bond arrangement (a large BLA, single-bond character between monomeric units) in the ground state, the torsional potential is quite shallow. Therefore, at room temperature (kBT ∼ 200 cm−1) the broad distribution of conformers with nonplanar equilibrium induces an inhomogeneous broadening of the absorption spectra. In contrast, a quinoidal bond arrangement (a small BLA, double-bond character between monomeric units) is formed in the S1 state; thus, the torsional potential becomes sharper in comparison with the ground-state potential. Upon photoexcitation, the broadly distributed (torsionally disordered) Franck–Condon geometries undergo torsional relaxation along the steep excited-state potential, thus narrowing the torsional distribution near the planar equilibrium. This results in the narrower fluorescence spectra.
C stretch at ≈1400 cm−1 and low-frequency inter-ring torsion at ≈100 cm−1).16 On account of the inherently strong electron–phonon coupling in π-conjugated systems, the manner in which these vibrational modes and molecular geometries affect the shape of the steady-state linear electronic spectra can be deduced. Typically, at room temperature, the absorption spectra of oligomers are quite broad, whereas the fluorescence spectra show structured vibronic bands that correspond to the break of the mirror image symmetry. These spectral characteristics can be easily understood from the curvatures of torsional potentials, which are closely related to different bond length alternations (BLA) between the ground and S1 states. On account of the benzoidal bond arrangement (a large BLA, single-bond character between monomeric units) in the ground state, the torsional potential is quite shallow. Therefore, at room temperature (kBT ∼ 200 cm−1) the broad distribution of conformers with nonplanar equilibrium induces an inhomogeneous broadening of the absorption spectra. In contrast, a quinoidal bond arrangement (a small BLA, double-bond character between monomeric units) is formed in the S1 state; thus, the torsional potential becomes sharper in comparison with the ground-state potential. Upon photoexcitation, the broadly distributed (torsionally disordered) Franck–Condon geometries undergo torsional relaxation along the steep excited-state potential, thus narrowing the torsional distribution near the planar equilibrium. This results in the narrower fluorescence spectra.
Within the Franck–Condon approximation, the HR analysis for narrowed fluorescence spectra allows the measurement of the extent of electron–phonon coupling (HR factor), which is proportional to the square of the displacement between the potential minima of the ground and excited states for a certain vibrational mode.17 In π-conjugated oligomeric systems, a single vibrational mode, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch, is good enough to simulate vibronic progression in the solution-phase fluorescence spectra at room temperature because this vibrational mode is most strongly coupled to the electronic transition between the ground and S1 states. Furthermore, the HR factor generally decreases as the oligomer length increases, resulting in a relatively intense 0–0 band compared with a small 0–1 side band for longer oligomers. Since π-conjugated oligomers (coupled by through-bond interaction) share similar photophysical properties with linear J-aggregates (coupled by through-space interaction),7 three spectroscopic parameters are relevant for the length of the exciton delocalization along the oligomer chain. These parameters are the peak position of the 0–0 band (E0–0), radiative decay rate (kr), and fluorescence intensity ratio between the 0–0 and 0–1 bands (I0–0/I0–1). As the oligomer length increases, (1) the 0–0 peak position red-shifts, (2) the radiative decay rate increases, and (3) the vibronic peak ratio between the 0–0 and 0–1 bands increases.
C stretch, is good enough to simulate vibronic progression in the solution-phase fluorescence spectra at room temperature because this vibrational mode is most strongly coupled to the electronic transition between the ground and S1 states. Furthermore, the HR factor generally decreases as the oligomer length increases, resulting in a relatively intense 0–0 band compared with a small 0–1 side band for longer oligomers. Since π-conjugated oligomers (coupled by through-bond interaction) share similar photophysical properties with linear J-aggregates (coupled by through-space interaction),7 three spectroscopic parameters are relevant for the length of the exciton delocalization along the oligomer chain. These parameters are the peak position of the 0–0 band (E0–0), radiative decay rate (kr), and fluorescence intensity ratio between the 0–0 and 0–1 bands (I0–0/I0–1). As the oligomer length increases, (1) the 0–0 peak position red-shifts, (2) the radiative decay rate increases, and (3) the vibronic peak ratio between the 0–0 and 0–1 bands increases.
3.2. Exciton localization processes: the experimental evidence of exciton self-trapping
When conjugated oligomers absorb light, excitons are widely delocalized throughout the oligomer backbone, but within 200 fs, the excitons rapidly localize on conjugated segments of the chain; this is the exciton localization process. This ultrafast relaxation process has been extensively characterized and discussed by several theoretical and experimental approaches in the field of CPs.6,18 The following three processes are generally accepted to be important in the exciton localization:19 (1) electronic relaxation through the slightly delocalized states formed by several coupled chromophoric units, (2) coherent excitation energy transfer (EET) processes among partially delocalized states in the intermediate coupling regime, and (3) self-trapping of delocalized excitons via nuclear vibrational modes. Among these, there is still a controversy over which is the most deeply involved in the exciton localization process. However, it has been proposed that the relative contribution of each of the possible processes may vary depending on the type of polymers and the polymer's surrounding environment. For oligomers, the first two processes have little effect on the localization because of their inherently short chain lengths. Therefore, self-trapping through molecular vibrations is the dominant process for the localization of an initially delocalized exciton. Similar to CPs, this ultrafast relaxation process in oligomers is governed by two vibrational modes: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching (∼25–30 fs period) and inter-ring torsion (∼160–250 fs period), which again reflects the strong nature of the electron–phonon coupling in π-conjugated systems.
C stretching (∼25–30 fs period) and inter-ring torsion (∼160–250 fs period), which again reflects the strong nature of the electron–phonon coupling in π-conjugated systems.
There is spectroscopic evidence of exciton localization dynamics in conjugated oligomers occurring at the sub-200 fs time scale. The first evidence is the time-resolved fluorescence spectra at early time delay, usually with a 200–300 fs decay that is the earliest measurable spectrum considering the instrumental response function of typical fluorescence upconversion experiments. This can provide indirect but important information on the sub-200 fs relaxation processes. Kim et al. reported the reconstructed time-resolved fluorescence spectra of a linear oligothiophene 10-mer (L-10T) in which monomeric thiophenes are linked by ethynylene bridges.20 Certainly, the time-resolved fluorescence spectra at a few hundred femtoseconds are already similar to the steady-state fluorescence spectra and are also narrower than the mirror-image of the absorption spectra. This implies that by the time we observe the fluorescence spectra of the linear oligothiophenes, the exciton localization via self-trapping has already finished and the broad distribution of torsionally disordered conformers in the Franck–Condon state is relaxed along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch and inter-ring torsional coordinates. Similar spectral behaviors were also observed in time-resolved fluorescence measurements of shorter oligothiophenes with the same ethynylene linkers,21 directly-linked oligothiophenes,22 oligofluorenes,23 and porphyrin oligomers.24
C stretch and inter-ring torsional coordinates. Similar spectral behaviors were also observed in time-resolved fluorescence measurements of shorter oligothiophenes with the same ethynylene linkers,21 directly-linked oligothiophenes,22 oligofluorenes,23 and porphyrin oligomers.24
Then the polarization memory loss (anisotropy decay), which can be measured by both transient fluorescence and absorption techniques, provides additional evidence. In these experiments, two parameters may provide a direct insight into the ultrafast exciton localization process via self-trapping: the initial anisotropy value and the time constants of ultrafast depolarization. It must be considered that an ideal anisotropy value is theoretically 0.4 when there is no relaxation process in the exciton transition dipole. In particular, the initial anisotropy value also provides indirect but valuable information, although a rapid anisotropy drop from 0.4 cannot be directly observed due to the temporal resolution limit of the spectroscopic apparatus. Kim et al. performed this experiment on linear oligothiophenes 4-, 6- and 10-mers (L-4T, L-6T, and L-10T) with ethynylene linkers after photoexcitation at the S1 state using fluorescence upconversion spectroscopy (Fig. 3).20 The initial anisotropy value of the shortest L-4T is around 0.38, and it does not show any ultrafast depolarization components, implying that the exciton localization process is not so prominent for the short oligomer. As the chain length increases, the initial values gradually decrease (∼0.36 and ∼0.28 for L-6T and L-10T, respectively). This suggests an important characteristic regarding molecular structures; in solution, long chains do not exist as a straight structure, but rather in a bent geometry such as a worm-like structure. Therefore, when the initially delocalized exciton is localized through the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretches, the loss of polarization memory should be more prominent in the longer oligomer.25 Furthermore, for L-6T and L-10T additional ultrafast depolarization components were detected with time constants of ∼200 and ∼400 fs, respectively. These were assigned to the self-trapping process through inter-ring torsion, which leads to not only exciton localization but also local planarization. For butadiyne-bridged porphyrin tetra-, hexa-, and octamers, Chang et al. reported an oligomer-length-dependent decline of the initial fluorescence anisotropy values.24 The authors synthesized a double-stranded octamer ladder as a reference for the isolated octamer. This ladder-like structure has a rigid backbone and suppressed torsion; they observed a much higher initial anisotropy value (∼0.34) compared with the worm-like octamer chain (∼0.24). This is in strong agreement with the fact that the ultrafast depolarization originates from the exciton self-trapping process and is greatly influenced by molecular conformation. Based on transient absorption anisotropy measurements, Dykstra et al. studied oligo-para-phenylenevinylene 4-, 6-, and 8-mers and observed a slightly lower initial anisotropy value only for the 8-mer.14 In this study, they suggested that the entropy due to the relatively large conformational disorder of the 8-mer presumably has significant implications for the ultrafast depolarization.
C stretches, the loss of polarization memory should be more prominent in the longer oligomer.25 Furthermore, for L-6T and L-10T additional ultrafast depolarization components were detected with time constants of ∼200 and ∼400 fs, respectively. These were assigned to the self-trapping process through inter-ring torsion, which leads to not only exciton localization but also local planarization. For butadiyne-bridged porphyrin tetra-, hexa-, and octamers, Chang et al. reported an oligomer-length-dependent decline of the initial fluorescence anisotropy values.24 The authors synthesized a double-stranded octamer ladder as a reference for the isolated octamer. This ladder-like structure has a rigid backbone and suppressed torsion; they observed a much higher initial anisotropy value (∼0.34) compared with the worm-like octamer chain (∼0.24). This is in strong agreement with the fact that the ultrafast depolarization originates from the exciton self-trapping process and is greatly influenced by molecular conformation. Based on transient absorption anisotropy measurements, Dykstra et al. studied oligo-para-phenylenevinylene 4-, 6-, and 8-mers and observed a slightly lower initial anisotropy value only for the 8-mer.14 In this study, they suggested that the entropy due to the relatively large conformational disorder of the 8-mer presumably has significant implications for the ultrafast depolarization.
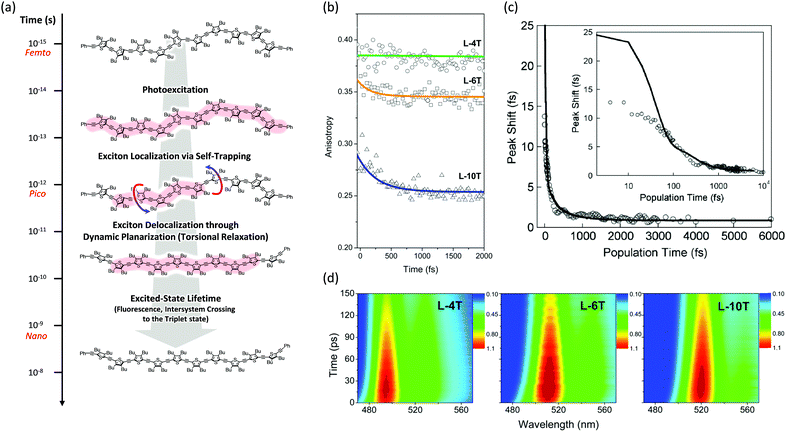 | ||
| Fig. 3 (a) Schematic representation of excited-state dynamics of linear oligothiophenes from femto- to nanosecond timescales. Image modified from ref. 25 with permission. Copyright 2015 American Chemical Society. (b) Fluorescence anisotropy decays of linear oligothiophene 4- (green), 6- (yellow), and 10-mers (blue). Adapted from ref. 21 with permission. Copyright 2016 American Chemical Society. (c) Three-pulse photon echo peak shift (3PEPS) of the MEH-PPV pentamer (inset: the same data in log-x scale). Adapted from ref. 26 with permission. Copyright 2005 American Physical Society. (d) Transient fluorescence spectra of oligothiophene 4- (left), 6- (middle), and 10-mers (right). Adapted from ref. 21 with permission. Copyright 2016 American Chemical Society. | ||
Finally, additional evidence of the exciton localization in conjugated oligomers was experimentally observed by Dykstra et al. using three-pulse photon echo peak shift (3PEPS) spectroscopy.26 This tool is known to be useful for probing the early time dynamics hidden by ensemble averaging in linear spectroscopy. The authors directly observed a rapid peak-shift decay on a time scale of ∼25 fs for a pentameric analog of MEH-PPV, which corresponds to the rapid exciton localization via self-trapping with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch (Fig. 3). Furthermore, as compared to the MEH-PPV polymer, the pentamer shows a lower asymptotic offset as well as longer damped oscillation. These results clearly reflect the lower degree of conformational disorder and structural defects in conjugated oligomers.
C stretch (Fig. 3). Furthermore, as compared to the MEH-PPV polymer, the pentamer shows a lower asymptotic offset as well as longer damped oscillation. These results clearly reflect the lower degree of conformational disorder and structural defects in conjugated oligomers.
3.3. Exciton delocalization processes through dynamic planarization
After the ultrafast localization process of the initially delocalized exciton in linear conjugated oligomers at a sub-ps regime, an additional relaxation process occurs with time constants of a few picoseconds to a few tens of picoseconds. This is known as the dynamic planarization process, which is also called torsional relaxation. Through this process, the torsional angle between the monomeric units becomes small, thereby planarizing the molecular backbone and reducing the inhomogeneous broadening. Moreover, the process induces exciton delocalization along the oligomer chain, which further lowers the excited-state energy. Until the early 1990s, the origin of the intraband relaxation dynamics of oligothiophenes was unclear. In 1996, by measuring the transient stimulated emission using a pump–probe technique, Lanzani et al. firstly suggested this dynamics showing a 4 ps time constant as a torsional relaxation process, which involves inter-ring torsional motion.27 Two years later, Wong et al. directly measured the dynamic red-shift occurring in a few picoseconds in the time-resolved fluorescence spectra of hexamethylsexithiophene using a fluorescence upconversion technique.28 This experimentally proved that the intraband relaxation process is a redistribution dynamics of excess excitation energy through torsional relaxation that enhances π-electron delocalization in the excited state. Furthermore, by applying coherent vibrational spectroscopy for a substituted quinquethiophene molecule, Cirmi et al. directly observed torsional wavepackets (∼140 cm−1) which consequently lead to the excited-state planarization.29 Chain-length-dependent conformational relaxation dynamics in oligofluorenes was investigated by Hintschich et al. By using picosecond single photon counting and a streak camera, they found that in contrast to a polyfluorene derivative, the relaxation in oligofluorenes involves entirely conformational dynamics with time constants ranging between 10 and 300 ps, which decreases with decreasing oligomer length and viscosity of the solvents or increasing temperature.23 Furthermore, Chang et al. suggested that the vibronic peak ratio between the purely electronic 0–0 band and higher vibronic peaks is an indicator of torsional relaxation dynamics.24 This is because of the strong electron–phonon coupling in conjugated oligomers. Therefore, the HR factor (along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch coordinate) can be estimated when analysing the vibronic peak ratio from the time-resolved fluorescence spectra. The time-dependent variation of this factor suggests that the exciton delocalization process occurs through dynamic planarization. Moreover, the same authors suggested that the rise of total emission intensity indicates dynamic planarization because the exciton delocalization causes a growth in the emitting oscillator strength. The similar spectral behaviors were also revealed in oligothiophenes with ethynylene linkers reported by Kim et al.20,21 They found that the time scale of rise dynamics in total emission intensity profiles is in line with the dynamic red shift and spectral narrowing, proving that indeed all the spectral dynamics occurring on picosecond time scales are related with exciton delocalization through dynamic planarization. In particular, the shorter time constants of planarization processes of oligothiophenes, where the thiophene units are directly linked, were reported by Gallaher et al.22 This is due to the result that different force constants (stiffness) of excited-state torsional potential arise from the possession of conjugated linkers.16
C stretch coordinate) can be estimated when analysing the vibronic peak ratio from the time-resolved fluorescence spectra. The time-dependent variation of this factor suggests that the exciton delocalization process occurs through dynamic planarization. Moreover, the same authors suggested that the rise of total emission intensity indicates dynamic planarization because the exciton delocalization causes a growth in the emitting oscillator strength. The similar spectral behaviors were also revealed in oligothiophenes with ethynylene linkers reported by Kim et al.20,21 They found that the time scale of rise dynamics in total emission intensity profiles is in line with the dynamic red shift and spectral narrowing, proving that indeed all the spectral dynamics occurring on picosecond time scales are related with exciton delocalization through dynamic planarization. In particular, the shorter time constants of planarization processes of oligothiophenes, where the thiophene units are directly linked, were reported by Gallaher et al.22 This is due to the result that different force constants (stiffness) of excited-state torsional potential arise from the possession of conjugated linkers.16
4. Cyclic π-conjugated oligomers
Cyclic geometry has two major differences when compared with its linear counterpart: (1) the symmetry of the system which alters the electronic transition between the ground and emitting states and (2) the reduced degree of freedom, i.e., conformational disorder, of the two termini due to the formation of a closed loop.20 The former has a direct impact on the spectroscopic parameters such as extinction coefficient, fluorescence quantum yield and lifetime, and fluorescence vibronic peak ratios. The latter influences the extent of exciton delocalization, which is a function of torsional disorder, as suggested by Barford et al.11,124.1. Extent of exciton delocalization in π-conjugated cyclic oligomers
Unlike the optically allowed B transition of the linear π-conjugated systems, the lowest-energy transition of the cyclic counterpart has A symmetry, which is optically forbidden. The characteristics of the electronic transitions of cyclic systems have been extensively investigated with the light harvesting complex (LH) of Rhodopseudomonas acidophila, an ideal noncovalently constructed assembly. Despite the fundamental difference in the interchromophore coupling mode, the description of electronic structures of the LH complex is identical to that of π-conjugated cyclic oligomers.30 The impact of disorder parameters, such as site energy disorder, elliptical deformation, and symmetry-breaking gap, on the electronic structures of the LH complex can also be applied to π-conjugated cyclic oligomers with conformational disorder.31 Again, this suggests that the electronic structures of CPs can be reasonably described by considering only dipole–dipole coupling and diagonal disorder, as suggested by Spano et al.8,9The electronic structure of a cyclic system comprising n monomeric units comprises 2n states, which are rearranged by the nearest neighbor coupling (V ≠ 0) of two nondegenerate states of each monomer, as shown in Fig. 4. For the cyclic structure with no disorder (Δ = 0), the lowest-energy excited-state, k = 0, is optically forbidden. Higher energy states form doubly-degenerate states (k = ±1, ±2, ±3,…), where only k = ±1 states carry oscillator strength. The transition dipole moments of k = ±1 are in plane and perpendicular to each other. The k = 0 state gains a small oscillator strength through Herzberg–Teller (HT) coupling to non-totally symmetric vibrational modes, which dynamically deform the cyclic structure to transiently produce a localized deformation. The effect of HT coupling on electronic transitions in cyclic systems has been carefully investigated by Sprafke et al. in a six-porphyrin nanoring, which is rigidly held by a hexapod template molecule.32 Through simulation of steady-state fluorescence spectra, the authors showed that excitons generated in the nanorings weakly fluoresce through HT coupling to a non-totally symmetric vibrational mode, which is the stretching motion of butadiyne linkers at 2244 cm−1. This vibrational mode significantly alters the bond lengths of that part of the rim, developing localized transition densities that resemble those of the optically allowed S0–S2 and S0–S3 transitions.
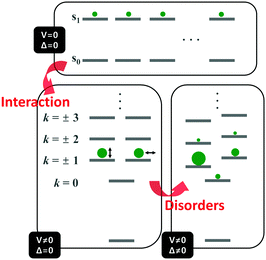 | ||
| Fig. 4 Energy diagram of the electronically excited states of cyclic π-conjugated oligomers. Top panel indicates the nondegenerate energy levels of n monomeric units and bottom left panel shows the rearranged energy levels upon nearest-neighbor interaction. Size of the green circles and direction of the double-headed arrow indicate oscillator strength and direction of transition dipole moment of a given state, respectively. Bottom right panel shows the change in the energy levels and oscillator strength upon addition of disorder. Image modified from ref. 30 with permission. Copyright 2001 Cell Press. | ||
Aside from this dynamic symmetry-lowering motion, the lowest energy transition is influenced by static disorder. Addition of disorder (Δ ≠ 0) lifts the pairwise degeneracy and redistributes the oscillator strength. The k = 0 state, which is optically forbidden in the absence of disorder, gains appreciable oscillator strength. The gradual increase in the conformational disorder is evident in size-dependent changes in the steady-state absorption spectra of cyclic oligothiophenes, as investigated by Park et al.33 The lowest energy transition of the smallest cyclic oligothiophene composed of 6 thienylene-ethynylene subunits (C-6T), corresponding to the tailing band from 450 to 550 nm in Fig. 6, is weakly allowed by the HT mechanism. As the size of the cyclic system increases, this band gradually intensifies. For the largest cyclic oligothiophene with 12 subunits (C-12T), the absorption spectrum is structureless, indicating that large conformational heterogeneity similar to that of linear systems is present. The effect of increasing conformational disorder is also observed in other fluorescence parameters, such as fluorescence quantum yields and fluorescence lifetimes, yet it is most noticeable in the ratio of 0–0 to 0–1 fluorescence vibronic bands. In the smallest cyclic oligothiophene, C-6T, the 0–0 vibronic band is greatly suppressed compared to the 0–1 one, whereas in the largest cyclic oligothiophene, C-12T, the 0–0 is more intense than the 0–1 vibronic band, similar to typical fluorescence spectra of linear systems. The decrease in I0–1/I0–0 when the size of the system increases indicates that based on the model by Spano et al., the extent of exciton delocalization is limited. Thus, the size of the exciton relative to the size of the conjugation pathway of cyclic oligothiophenes decreases when the size of the system is increased. Such a trend is also observed for other π-conjugated cyclic oligomers, for example, cycloparaphenylenes,34 porphyrin nanorings,35 and cyclothiophenes,36 but systematic analyses on the extent of exciton delocalization have seldom been reported.
In cycloparaphenylene systems, the size of exciton delocalization was investigated by Adamska et al.34 Quantum mechanical calculations of the excited-state geometry including the solvent have shown that cycloparaphenylenes with less than 8 subunits generate fully delocalized excitons, whereas those composed of more than 8 subunits develop localized excitons upon relaxation to the lowest excited-state geometry, S1′ (Fig. 5). Nonadiabatic excited-state dynamics (NA-ESMD) simulations suggest that the self-trapping of excitons in these systems is an ultrafast process that occurs within 50 fs. Exciton localization in porphyrin nanorings has been studied in detail by Parkinson et al.35 The initial fluorescence anisotropy value of 0.1 in porphyrin nanorings comprising 20 or less subunits indicates that initially formed excitons are fully delocalized. However, those with more than 20 subunits exhibit initial anisotropy values over 0.1, followed by additional picosecond depolarization. Combined with Monte Carlo simulations, it was shown that in the 40-porphyrin nanoring, both initial and final excitons behave as linear excitons, and this behavior is similar to that in linear porphyrin arrays.
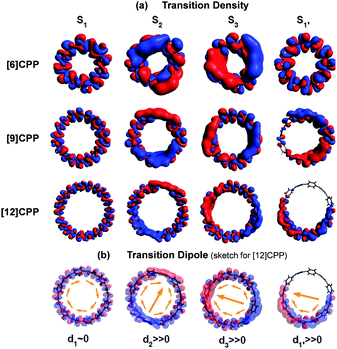 | ||
| Fig. 5 (a) Transition density and (b) transition dipole moment of cycloparaphenylene 6-, 9-, and 12-mers at S1, S2, S3, and relaxed S1′ states. Adapted from ref. 34 with permission. Copyright 2014 American Chemical Society. | ||
There is a clear dependence between the size of the initial excitons generated upon photoexcitation and the following self-trapping process, as demonstrated in cycloparaphenylenes and porphyrin nanorings. In a picosecond timescale, the slower planarization of the backbone chain re-extends the localized exciton. This has been studied in the transient fluorescence spectra of cyclic oligothiophenes and analyzed in terms of spectral red-shift, total fluorescence intensity (Total IFL), and 0–1 to 0–0 vibronic peak ratio (I0–1/I0–0).33 As shown in the transient fluorescence spectra (Fig. 6c–f), the cyclic oligothiophenes comprising 6 and 8 subunits (C-6T and C-8T) present no apparent spectral red-shift, but those with 10 and 12 subunits (C-10T and C-12T) display a distinct red-shift. This indicates that the excitons are effectively delocalized in 10- and 12-mers, whereas excitons are already fully delocalized along the whole cyclic framework in 6- and 8-mers. Nonetheless, the total fluorescence intensity abruptly drops in 6- and 8-mers with an exponential decay time constant (amplitude) of 11 (47.3%) and 26 (48.8%) ps, respectively, which coincide with the typical time constants of the dynamic planarization process. Comparable picosecond decay components were found in the total fluorescence decays of 10- and 12-mers with time constants of 49 (33.4%) and 66 (29.5%) ps, respectively. A similar size-dependent trend was observed in the rise dynamics of I0–1/I0–0 indicating that this picosecond dynamics is a consequence of the exciton delocalization that regenerates the cyclic symmetry. The large amplitude and short time constant in 6- and 8-mers suggest that dynamic planarization is the process that removes marginal conformational disorder in these systems to attain the ideal cyclic geometry. Then, the large red-shift along with the long time constant and small amplitude of dynamics planarization in 10- and 12-mers suggest that localized excitons are inefficiently delocalized through the dynamic planarization motion, due to the large conformational disorder of the system. Small I0–1/I0–0 values of 10- and 12-mers indicate that excitons are not fully delocalized over the whole conjugated backbone and remain as acyclic excitons after the dynamic planarization dynamics.
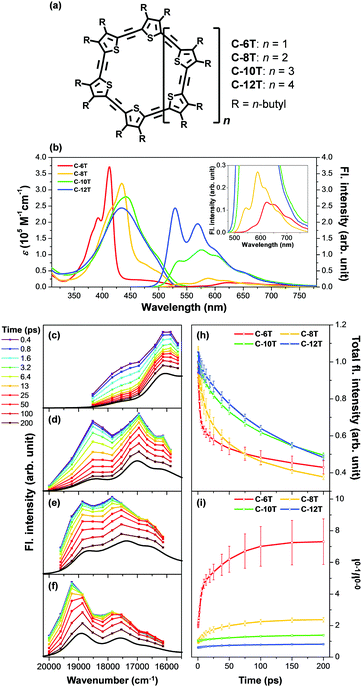 | ||
| Fig. 6 (a) Molecular structure of cyclic oligothiophenes and their (b) steady-state absorption and fluorescence spectra and (c–f) transient fluorescence spectra. Transient fluorescence spectra are analysed with two to three Gaussian-shaped vibronic peaks and their (h) total fluorescence intensity and (i) 0–1 to 0–0 vibronic peak ratios are plotted against time. Adapted from ref. 33 with permission. Copyright 2015 Wiley-VCH. | ||
4.2. Subpopulations of cyclic and acyclic excitons
Fluorescence parameters in ensemble measurements are averaged quantities from various conformers that oligomers can adopt in the given environment. Therefore, the limits of exciton delocalization described in the previous section may not be applicable to the entire population of π-conjugated oligomers when conformational heterogeneity is considered. Single-molecule spectroscopy is the optimal technique to discriminate and identify the behaviors of conformationally heterogeneous systems at the sub-ensemble level. Especially in cyclic systems, where severe conformational disorder such as torsional defects can significantly alter the excitonic nature, a statistical treatment of the fluorescence parameters can be used to identify the subpopulations elusive in the ensemble measurements.In an exemplary work by Yang et al., the authors studied a cyclic oligothiophene comprising 10 thienylenes with ethynylene and vinylene linkers (C-10T2V).37 In contrast to the previous ensemble measurements,20 a subpopulation of linear-like excitons at the single-molecule level was additionally found.43 To identify the excitonic features of the molecule, two parameters that have a direct correlation to the structure of the cyclic system, fluorescence lifetime and peak position, were used to construct two-dimensional correlation maps. As shown in Fig. 7a, the initial step displays a single population dispersed along the map. The negative slope of the distribution indicates that fluorescence lifetime and fluorescence peak position are anticorrelated parameters, which are modulated by the torsional disorder of the system. In the following step (Fig. 7b), consecutive laser excitation perturbs the initial conformation to induce torsional disorder into the system. This generates a higher energy domain that does not exhibit the linear correlation shown in the initial step.
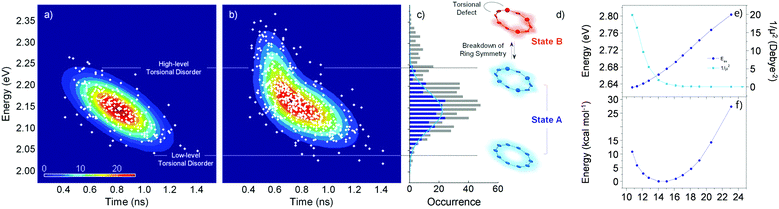 | ||
| Fig. 7 Two-dimensional correlation maps between fluorescence lifetime and 0–1 fluorescence vibronic peak position from (a) the initial and (b) subsequent steps before photobleaching. (c) Distribution of peak positions in the first (blue) and subsequent (grey) steps, which correspond to (d) two different excitonic states. (e) Energies and inverse of the square of dipole moments for the transition to the lowest excited state as a function of average torsional angle. (f) Relative ground-state stability as a function of the same parameter is shown to provide information on the thermal distribution. Adapted from ref. 37 with permission. Copyright 2015 American Chemical Society. | ||
To account for the different behaviors of the two subpopulations, the lowest-energy transition energy and 1/μ2, which is inversely proportional to the radiative decay rate, are calculated as a function of increasing average torsional angle of the cyclic oligothiophene. As presented in Fig. 7e and f, while the transition energy shows monotonic increase, 1/μ2 displays a deflection point and then remains constant. This deflection point corresponds to the conjugation cut-off angle, as evidenced by the electron density difference map. The generation of a new domain with no transition-energy-responsive fluorescence lifetimes indicates that this subpopulation has a linear character due to the torsional defects generated via conformational fluctuations.
Two-dimensional correlation maps can be used when a single fluorescence parameter does not sufficiently support the formation of cyclic excitons. When unambiguous characteristics of cyclic excitons appear, such as long fluorescence lifetime and large I0–1/I0–0, it can be concluded that the system exclusively generates cyclic excitons.38 This is the case for small cyclic oligothiophenes comprising 6 and 8 subunits. Extremely long fluorescence lifetimes (over 2 ns), along with low fluorescence intensity indicate that cyclic excitons with small torsional disorder are generated. Fluorescence lifetimes longer than 1 ns are not found in larger systems with 10 and 12 subunits. Their average fluorescence lifetimes are respectively 590 and 540 ps, which are similar to those of typical linear oligomers. The determination of the extent of the exciton delocalization in the vicinity of the ring-to-linear behavioral turning point again requires two-dimensional correlation maps.
Fig. 8 shows the correlation distribution of fluorescence lifetimes and fluorescence peak positions extracted from the first and the following steps. It is worth noting that new domains at higher energies arise in both the cyclic oligothiophenes. If this change is associated with the generation of torsional defects in cyclic excitons, according to the discussion provided by Yang et al., the fluorescence lifetime should be significantly decreased. In cyclic oligothiophenes with 10 subunits, the conformational fluctuation modifies the fluorescence lifetime from 620 to 590 ps; this supports that the conformational fluctuations in this system induce a cyclic–acyclic transition of excitons. In cyclic oligothiophenes with 12 subunits, the fluorescence lifetimes remain unaltered upon conformational fluctuation. This suggests that the torsional disorder of this system is positioned beyond the deflection point in Fig. 7e. Excitons generated in this system are initially acyclic due to a large degree of torsional disorder, and subsequent conformation fluctuation only induces a reduction of the delocalization length.
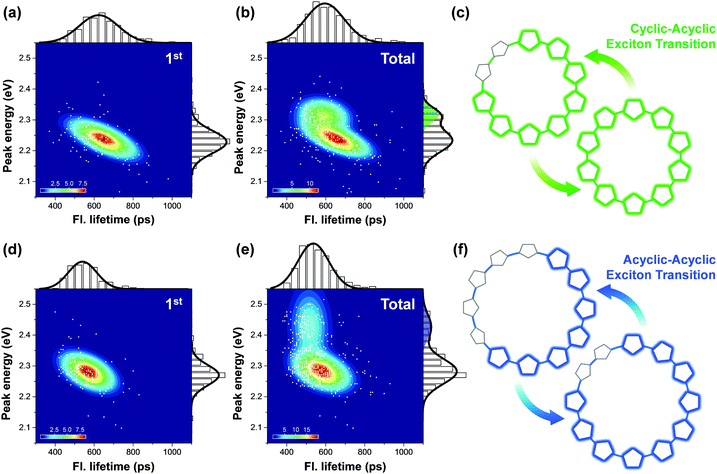 | ||
| Fig. 8 Two-dimensional correlation maps between fluorescence lifetimes and peak positions of 0–1 vibronic transition of the initial (panel a for 10-mer and panel d for 12-mer) and all the subsequent molecular states (panel b for 10-mer and panel e for 12-mer). The corresponding fluorescence lifetime histogram and spectral distribution are respectively depicted at the top and right side of each panel. (c and f) Schematic illustrations of the change in excitonic states from the first to the next steps. Adapted from ref. 38 with permission. Copyright 2016 American Chemical Society. | ||
Excitons in much larger systems are not fully delocalized over the whole molecular framework, but their dynamics are still influenced by the geometry of the system. Aggarwal et al. studied the exciton dynamics of a giant macrocycle using single-molecule spectroscopy.39 The macrocycle, comprising 6 carbazole-bridged phenylene-ethynylene-butadiynylene subunits, generates localized excitons which span over the size of two subunits. To study the localization dynamics, they measured the excitation and emission linear dichroism, Dex(em) = (IV − IH)/(IV + IH). Dex uses polarized excitation and monitors the emission intensity to determine the anisotropy of the absorption. On account of the rigid cyclic geometry, Dex of the giant macrocycle exhibits a narrow distribution centered at Dex = 0. In comparison to the broad Dex peaks near ±1, this indicates that the absorption of the giant macrocycle is ideally isotropic. Dem compares the emission intensity of horizontal and vertical polarization to measure the orientation of the emitting state. Again, unlike the broad distribution in the dimer and hexamer, the Dem is centered at 0. If the localization dynamics were a deterministic process, which delivers excitons in an identical position for every excitation, the distribution of Dem should resemble that of a linear system. This suggests that in a well-defined cyclic system, even acyclic excitons are influenced by the geometry of the cyclic conjugation pathway.
4.3. Enhancing exciton delocalization: the effect of π-linkers
Cyclic geometry is certainly advantageous over its linear counterpart to achieve superior exciton delocalization. However, it is not the best approach because π-orbital overlap can be greatly enhanced by chemically restraining the torsional motions.40 Such synthetic strategies were proven successful in extending the π-conjugation in polymers. However, they are not applicable in cyclic systems because an increase of ring strain, which is already high in small rings, can hamper the attainment of the ideal structure.A mild approach that does not impose stress on the structure is the incorporation of rigidifying π-linkers. Liu et al. tested single bond, vinylene, and ethynylene linkers between bipyridyl and fluorene moieties in alternating copolymers and found that the ones with vinylene linkers exhibit the most red-shifted absorption and fluorescence spectra.41 This suggests that vinylene linkers enhance the π-conjugation by planarizing the backbone structure. Kim et al. applied this method in cyclic oligothiophenes comprising 12 thienylene-ethynylene subunits, that produce acyclic excitons exclusively.42 Upon addition of two and three vinylene linkers, the steady-state absorption and fluorescence spectra are systematically red-shifted. Concomitantly, the I0–1/I0–0 ratio increases from 0.781 to 0.915 and radiative rate decreases from 7.23 × 108 to 5.89 × 108 s−1, indicating that the extent of exciton delocalization is enhanced when the number of vinylene linkers is increased. The nonradiative decay displays a decreasing trend from 14.0 × 108 to 7.81 × 108 s−1 upon increasing the number of vinylene linkers. This suggests that vinylene linkers make the backbone structures rigid, which in turn can affect the dynamic planarization process in the excited state.
To study the exciton delocalization process during dynamic planarization, the transient fluorescence spectra were analyzed. Initial spectral positions at 300 fs of 12-mers with two and three vinylene linkers are red-shifted with respect to those without vinylene linkers, indicating that the Franck–Condon geometry is already planar. Since the exciton size in these systems is clearly larger than half of the ring, the center of mass of the spectrum (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/char_e0ce.gif) COM) is more red-shifted in 12-mers with three vinylene linkers. Exponential decays of
COM) is more red-shifted in 12-mers with three vinylene linkers. Exponential decays of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/char_e0ce.gif) COM have time constants of 32.4, 25.2, and 25.5 ps for 12-mers without and with two and three vinylene linkers, respectively. Associated indicative I0–1/I0–0 ratios have an identical trend of 51.2, 31.4, and 30.7 ps with increasing order of the number of vinylene linkers. Faster dynamic planarization processes for both the fluorescence parameters suggest that vinylene linkers are more rigid bridges and thus reduce the torsional disorder in both the initial Franck–Condon geometry and the final structure obtained after the dynamic planarization process. This demonstrates that the manipulation of π-linkers in strained circular structures can be a promising synthetic strategy to obtain cyclic excitons with superior coherence lengths.
COM have time constants of 32.4, 25.2, and 25.5 ps for 12-mers without and with two and three vinylene linkers, respectively. Associated indicative I0–1/I0–0 ratios have an identical trend of 51.2, 31.4, and 30.7 ps with increasing order of the number of vinylene linkers. Faster dynamic planarization processes for both the fluorescence parameters suggest that vinylene linkers are more rigid bridges and thus reduce the torsional disorder in both the initial Franck–Condon geometry and the final structure obtained after the dynamic planarization process. This demonstrates that the manipulation of π-linkers in strained circular structures can be a promising synthetic strategy to obtain cyclic excitons with superior coherence lengths.
5. Implications on polymeric counterparts
Structurally, a polymer is a chain of interconnected oligomeric duplicates. Thus the main differences between a polymer and its oligomer are the size and additional degree of freedom, which give rise to the long-range inter- and intrachain interactions. The relative strength of inter- and intrachain coupling is modulated by the structure of the polymer chain. In a good solvent, polymers are preferentially in an extended chain structure, whereas in a bad solvent, they collapse into random coils, molten globules, or rod-like structures to minimize the solvent–polymer interactions. In the solid phase, where most optoelectronic applications are conceived, interchain interactions dominate the photoinduced dynamics of the polymer.43 The Coulombic interaction between the electron and hole in exciton or charge transfer states is dramatically reduced by efficient interchain delocalization, and free charge carriers can be generated. We first examine the polymers in solution that adopt stretched conformations. Coherent and incoherent EET processes will be discussed.5.1. Polymers in solution phase: weak interchain coupling
Unlike a small number of countable monomers in short oligomeric systems, polymers contain numerous subunits that interact to form exciton manifold. In the absence of conformational disorder, their electronic structures can be best described by the band model of semiconductors. However, when pervasive torsional defects or kinks induce inhomogeneous broadening of energy states, as in typical polymers, a sum of interacting chromophores is an adequate description.44 On account of numerous energy levels and degrees of inter-chromophore coupling, exciton dynamics in the energy landscape of CPs inevitably includes EET processes.In an ultrafast timescale (<200 fs), the initial photoexcitation undergoes a coherent EET process. The coherent intrachain EET process has been studied by Collini et al. in poly[2-methoxy,5-(2′-ethyl-hexoxy)-1,4-phenylenevinylene] (MEH-PPV).45 In CPs, this process occurs in the donor and acceptor segments quantum mechanically entangled by intermediate coupling strength (U ∼ γ, where U is the resonance coupling between the donor and acceptor and γ is the dephasing strength).46 Coherence between the energy donor and acceptor chromophores and its phase information are preserved before dephasing. Since EET between the randomly oriented spectroscopic subunits is accompanied by a loss of polarization memory, anisotropy can be a good indicator. By monitoring the time evolution of anisotropy of EET dynamics as a function of coherence time (τ) and population time (T), known as the two-time anisotropy decay (TTAD), it is possible to identify the coherent EET process.
Fig. 9A and B are the TTAD maps of the MEH-PPV nanoparticle in water and MEH-PPV in chloroform. Fig. 9C is the simulated map assuming the empirically obtained finite coherence and population times. The main difference is the TTAD decay along the τ axis. MEH-PPV in chloroform displays τ-dependent variation in the anisotropy, indicating that the transition dipole moment coherently changes direction. In nanoparticles, however, the τ-dependence is negligible as in rhodamine 6G, where EET is unviable (Fig. 9D). Coherent EET dynamics of MEH-PPV was reconfirmed by two-dimensional photon echo (2DPE) spectroscopy. In 2DPE, the two-dimensional electronic spectra along the coherence frequency, ωτ and rephasing frequency, ωt are measured at a population time T. Spectra along the diagonal line in the 2DPE map, which is related to the linear absorption spectrum of MEH-PPV, oscillate along T, as shown in Fig. 9E. The peak amplitude and diagonal-to-antidiagonal peak width ratio were analyzed to show the anticorrelation, which is manifested in electronic coherence, between these parameters. This electronic coherence persists for more than 250 fs, which is surprisingly long considering the ambient conditions for the measurements. This means that the long-lived coherence can significantly enhance the EET process of CPs.
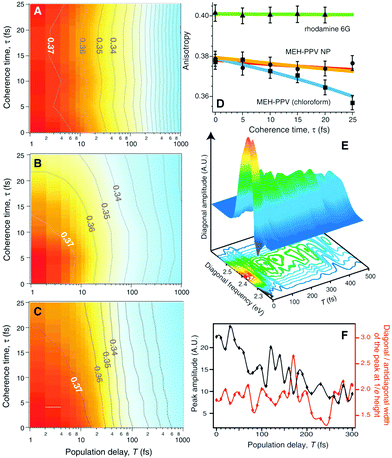 | ||
| Fig. 9 Two-time anisotropy decay plots for (A) MEH-PPV nanoparticles in water and (B) MEH-PPV in chloroform. (C) Two-time anisotropy decay plots simulated by a multi-exponential model based on experimentally obtained time constants. (D) Initial anisotropy values as a function of coherence time τ for rhodamine 6G (green), MEH-PPV nanoparticles in water (orange), and MEH-PPV in chloroform (blue). (E) Three-dimensional plot of the diagonal amplitude as a function of diagonal frequency and population time T. (F) Peak amplitude of diagonal line (black) and the ratio between the diagonal and antidiagonal widths of the peak at 1/e height (red). Adapted from ref. 45 with permission. Copyright 2009 American Association for the Advancement of Science. | ||
Incoherent EET is a process occurring between chromophores that are spatially separated over 5 Å, and are weakly coupled (U ≪ γ).44 The process in this regime is best described by Förster energy transfer (FET), or resonance energy transfer (RET). The successive FET processes that deliver excitons to lower or isoenergetic states is known as exciton diffusion. Since the directionality of EET can stochastically change depending on mutual orientation and coupling between chromophores in the polymer chain, one-dimensional random walk models are often employed to evaluate the exciton diffusion constants. In poly(3-hexylthiophene) (P3HT), the intrachain exciton diffusion constant was calculated by Healy et al. using P3HT chains of controlled lengths.47 Two chain ends were functionalized with C60 fullerenes and quenching efficiencies were analyzed with one-dimensional random walk exciton diffusion and RET-mediated quenching. The exciton diffusion coefficient and length were 9.8 × 10−4 cm2 s−1 and 7.0 nm, respectively. These values are comparable to those of C60-functionalized oligofluorenes and are also similar to those reported for P3HT films, where exciton diffusion takes place in the chain-stacked aggregated domains. This implies that the incoherent EET process in P3HT, as well as in other π-conjugated polymer analogues, allows for long-range transportation of excitons to the heterojunctions in photovoltaic materials where the charge transfer reaction takes place, as discussed in the following section.
5.2 Polymers in solid phase: strong intermolecular coupling
CP films are semicrystalline, indicating that their morphologies can be divided into two parts: amorphous and crystalline domains. The former is composed of weakly interacting polymer chains with large conformational disorder. Their structures can be regarded as direct projections of the heterogeneous conformations in the solution phase.48 The crystalline domain is composed of cofacial π-stacks of polymer chains. Chain aggregates have greatly reduced conformational heterogeneity because intermolecular interactions between π-conjugated segments and between pendent alkyl chains greatly suppress the torsional degree of freedom in a polymer chain. Typical interchain distances in the π-stacking direction lie in a narrow range of 3.3–3.6 Å, where interchain electronic coupling becomes viable. The features of interchain vibronic coupling in the absorption and fluorescence spectra have been modeled by Spano et al. by employing a Hamiltonian approach similar to the one outlined in Section 2.49 In both the absorption and fluorescence spectra, suppressed 0–0 vibronic transitions indicate interchain coupling. The relative strength of 0–0 to 0–1 vibronic transitions in the absorption spectra is associated with the strength of interchain coupling J, and that in the fluorescence spectra is associated with interchain exciton delocalization.Recent studies have demonstrated that charge photogeneration in organic photovoltaic devices employs interchain exciton and charge delocalization in the crystalline domains. On account of the low dielectric constant in organic systems (εr ≈ 2–4), the exciton binding energy in CPs is as large as ∼1 eV, which cannot be compensated by thermal energy at room temperature.1 However, when the electron and hole of a charge transfer exciton are delocalized, the separation between the two charge centers effectively reduces the Coulombic interaction between them and the free charges can be readily generated. Similar to the coherent EET process, which benefits from the coherence superposition state between the energy donor and acceptor moieties, charge separation processes at heterojunctions benefit from coherent dynamics in an ultrafast timescale. Bakulin et al. employed pump-push spectroscopy to access hot charge-delocalized states in various CPs (Fig. 10A).2Fig. 10B shows the differences in photocurrent obtained after a pump pulse above the bandgap energy and the subsequent push pulse in the IR region. All the polymer-based heterojunction materials exhibited an increase in photocurrent except for the PCDTBT:PC70BM blend, which displayed a slight decrease possibly resulting from bimolecular recombination. The increase in photocurrent was monitored using a sub-band gap pump and optical probe. The charge density distributions in higher charge transfer states of molecular heterojunctions were simulated by quantum mechanical calculations, which revealed a drastic increase in the distance between charge centers associated with intrachain charge delocalization (Fig. 10C–F).
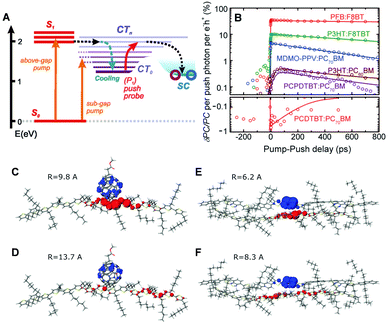 | ||
| Fig. 10 (A) Energy level diagram of the typical organic photovoltaic (OPV) system. (CT0, lowest-lying charge transfer state; CTn, higher-lying charge transfer states; SC, separated-charges states). (B) Time-resolved pump-push photocurrent data for a series of OPVs after photoexcitation at the higher singlet excited state. Computational results of the charge distribution at (C and D) the P3HT/PCBM and (E and F) P3HT/F8TBT heterojunctions. Blue and red lobes indicate electron and hole densities, respectively. (C and E) Simulated charge distribution in the lowest CT-state configuration, and (D and F) in the higher CT state configuration after irradiation of IR-push pulse. Adapted from ref. 2 with permission. Copyright 2012 American Association for the Advancement of Science. | ||
The same technique was utilized by Gélinas and Jakowetz et al. to measure the electron–hole distance in the charge separation process.3,4 The studies focused on the microscopic Stark effect arising from the electric field between loosely bound electron–hole pairs, which cause a red-shift in the absorption spectra, i.e., electroabsorption (Fig. 11B). Gélinas et al. prepared blend films with different donor, p-DTS(FBTTh2)2, and acceptor, PC71BM, ratios. For the 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 blend ratio, both molecules form a crystalline phase, whereas at 90
40 blend ratio, both molecules form a crystalline phase, whereas at 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, the acceptor is intercalated between the donor molecules.3Fig. 11C presents the pump–probe spectra of films with different blend ratios; the steady-state electroabsorption spectrum is shown for comparison. While the 90
10, the acceptor is intercalated between the donor molecules.3Fig. 11C presents the pump–probe spectra of films with different blend ratios; the steady-state electroabsorption spectrum is shown for comparison. While the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 blend film displays only a reduced stimulated emission, the 60
10 blend film displays only a reduced stimulated emission, the 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 blend film manifests a clear negative band near 700 nm that matches the position of electroabsorption of the donor molecule. Similar results were obtained using a PCDTBT polymer donor, suggesting that the formation of delocalized states is a prerequisite for an efficient charge separation process. Jakowetz et al. investigated this further by utilizing push pulse as an energy input for electron–hole separation.4 Pump–probe spectra were measured with and without push pulse, which were subtracted to yield only the signal from electroabsorption. They compared the PCDTBT donor and PC71BM acceptor at 4
40 blend film manifests a clear negative band near 700 nm that matches the position of electroabsorption of the donor molecule. Similar results were obtained using a PCDTBT polymer donor, suggesting that the formation of delocalized states is a prerequisite for an efficient charge separation process. Jakowetz et al. investigated this further by utilizing push pulse as an energy input for electron–hole separation.4 Pump–probe spectra were measured with and without push pulse, which were subtracted to yield only the signal from electroabsorption. They compared the PCDTBT donor and PC71BM acceptor at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratios, which are respectively characterized by crystalline and disordered phases. The positions of the electroabsorption indicative of the electron–hole separation were plotted as a function of time (Fig. 11D). In the 1
4 ratios, which are respectively characterized by crystalline and disordered phases. The positions of the electroabsorption indicative of the electron–hole separation were plotted as a function of time (Fig. 11D). In the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 blend film, charge separation is an energetically uphill process, unfavorable for long-range charge separation. For the 4
4 blend film, charge separation is an energetically uphill process, unfavorable for long-range charge separation. For the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend film, the electron and hole move to highly ordered lower-energy sites within 150 fs. Since this ultrafast coherent process delocalizes charges over large distances, estimated at 5 nm, charges can be easily separated afterwards.
1 blend film, the electron and hole move to highly ordered lower-energy sites within 150 fs. Since this ultrafast coherent process delocalizes charges over large distances, estimated at 5 nm, charges can be easily separated afterwards.
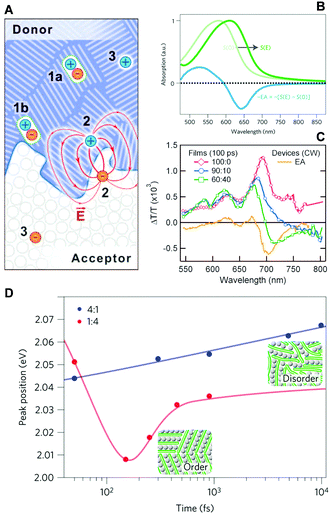 | ||
Fig. 11 (A) Schematic illustration of photogenerated species at a donor/acceptor interface (1a, excitons in the bulk; 1b, excitons at the interface; 2, electron–hole pairs generating a dipole-like electric field; 3, free charge carriers). (B) Stark shift of absorption spectrum due to an electric field, S(E), and electro-absorption characteristic, EA. (C) Transient absorption spectra of the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 90 0, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and 60 10, and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 films normalized at 640 nm. The steady-state EA spectra are shown for comparison. (D) Peak positions of integrated EA signals of 4 40 films normalized at 640 nm. The steady-state EA spectra are shown for comparison. (D) Peak positions of integrated EA signals of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (blue) and 1 1 (blue) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (red) PCDTBT/mPCBM blends as a function of pump–push delays. Adapted from ref. 3 and 4 with permission. Copyright 2014 American Association for the Advancement of Science and 2017 Nature Publishing Group. 4 (red) PCDTBT/mPCBM blends as a function of pump–push delays. Adapted from ref. 3 and 4 with permission. Copyright 2014 American Association for the Advancement of Science and 2017 Nature Publishing Group. | ||
The role of exciton and charge delocalization in the charge separation process has been extensively studied using a number of different techniques and is presented in a number of excellent review articles.1,50 The oligomer approach in this review shows that exciton dynamics, especially exciton (de)localization processes, can ideally be described in controlled model systems. Such ideality is partially blurred out in the polymeric part; nonetheless, at the microscopic level identical excited-state dynamics are still attained. Concerning this, we found that a careful control and examination of oligomeric model systems will further broaden and deepen the knowledge on complex excited-state dynamics of CPs, which have great potential in organic optoelectronics applications.
6. Conclusions
In this review, excited-state dynamics of π-conjugated oligomers have been illustrated. Special focus was put on the oligothiophenes, which can be considered as model systems for polythiophenes exploited in modern organic photovoltaic devices. We took a bottom-up approach to understand the complex photophysics of CPs. First, general description on the electronic structures and associated absorption and fluorescence characteristics of oligomers was introduced using the Hamiltonian approach by Spano and Barford et al. Important relationship between the extent of exciton delocalization and the vibronic peak intensity ratio in the fluorescence spectra was derived. Extent of exciton delocalization was described in chronological order from exciton self-trapping, dynamic planarization, and to the relaxation to the ground state, which occur in femto-, pico-, and nanosecond timescales, respectively. These exciton dynamics were studied in both linear and cyclic oligothiophenes at both ensemble and single-molecule levels. Other analogous oligomeric systems such as oligoparaphenyeles, porphyrin arrays, and oligo(phenylene vinylene) have also been introduced. Finally, excited-state dynamics unique in CPs was outlined in the solution and solid phases. In the solution phase, where interchain interaction is weak, exciton migration processes by coherent and incoherent processes were introduced. In the solid phase, the role of interchain exciton and charge delocalization in the charge generation process was illustrated with recent works employing ultrafast time-resolved spectroscopy. Theoretical and experimental aspects of π-conjugated oligomer and polymer systems reviewed herein will provide a general overview on the excited-state dynamics of these systems crucial in understanding the charge photogeneration processes in organic photovoltaic materials currently studied in related fields.Conflicts of interest
There are no conflicts to declare.Acknowledgements
First, we thank the colleagues with whom we have been collaborating on this subject, in particular Prof. Masahiko Iyoda (Tokyo Metropolitan University) and his research fellows. The work at Yonsei University was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (2016R1E1A1A01943379).Notes and references
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef PubMed.
- A. C. Jakowetz, M. L. Böhm, A. Sadhanala, S. Huettner, A. Rao and R. H. Friend, Nat. Mater., 2017, 16, 551–557 CrossRef CAS PubMed.
- W. Barford, D. G. Lidzey, D. V. Makhov and A. J. H. Meijer, J. Chem. Phys., 2010, 133, 044504 CrossRef PubMed.
- O. R. Tozer and W. Barford, J. Phys. Chem. A, 2012, 116, 10310–10318 CrossRef CAS PubMed.
- H. Yamagata and F. C. Spano, J. Phys. Chem. Lett., 2014, 5, 622–632 CrossRef CAS PubMed.
- F. C. Spano and H. Yamagata, J. Phys. Chem. B, 2011, 115, 5133–5143 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, J. Phys. Chem. B, 2014, 118, 8352–8363 CrossRef CAS PubMed.
- W. Barford and M. Marcus, J. Chem. Phys., 2014, 141, 164101 CrossRef PubMed.
- W. Barford and M. Marcus, J. Chem. Phys., 2016, 145, 124111 CrossRef PubMed.
- M. Marcus, J. Coonjobeeharry and W. Barford, J. Chem. Phys., 2016, 144, 154102 CrossRef PubMed.
- B. Van Averbeke and D. Beljonne, J. Phys. Chem. A, 2009, 113, 2677–2682 CrossRef CAS PubMed.
- T. E. Dykstra, E. Hennebicq, D. Beljonne, J. Gierschner, G. Claudio, E. R. Bittner, J. Knoester and G. D. Scholes, J. Phys. Chem. B, 2009, 113, 656–667 CrossRef CAS PubMed.
- H. Meier, Angew. Chem., Int. Ed., 2005, 44, 2482–2506 CrossRef CAS PubMed.
- S. Karabunarliev, J. Phys. Chem. A, 2000, 104, 8236–8243 CrossRef CAS.
- A. Yang, M. Kuroda, Y. Shiraishi and T. Kobayashi, J. Phys. Chem. B, 1998, 102, 3706–3711 CrossRef CAS.
- N. Banerji, S. Cowan, E. Vauthey and A. J. Heeger, J. Phys. Chem. C, 2011, 115, 9726–9739 CAS.
- N. Banerji, J. Mater. Chem. C, 2013, 1, 3052–3066 RSC.
- P. Kim, K. H. Park, W. Kim, T. Tamachi, M. Iyoda and D. Kim, J. Phys. Chem. Lett., 2015, 6, 451–456 CrossRef CAS PubMed.
- T.-W. Kim, W. Kim, K. H. Park, P. Kim, J.-W. Cho, H. Shimizu, M. Iyoda and D. Kim, J. Phys. Chem. Lett., 2016, 7, 452–458 CrossRef CAS PubMed.
- J. K. Gallaher, K. Chen, G. S. Huff, S. K. K. Prasad, K. C. Gordon and J. M. Hodgkiss, J. Phys. Chem. Lett., 2016, 7, 3307–3312 CrossRef CAS PubMed.
- S. I. Hintschich, F. B. Dias and A. P. Monkman, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045210 CrossRef.
- M. H. Chang, M. Hoffmann, H. L. Anderson and L. M. Herz, J. Am. Chem. Soc., 2008, 130, 10171–10178 CrossRef CAS PubMed.
- A. Thiessen, D. Würsch, S.-S. Jester, A. V. Aggarwal, S. Bange, J. Vogelsang, S. Höger and J. M. Lupton, J. Phys. Chem. B, 2015, 119, 9949–9958 CrossRef CAS PubMed.
- X. Yang, T. E. Dykstra and G. D. Scholes, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 045203 CrossRef.
- G. Lanzani, M. Nisoli, S. De Silvestri and R. Tubino, Chem. Phys. Lett., 1996, 251, 339–345 CrossRef CAS.
- K. S. Wong, H. Wang and G. Lanzani, Chem. Phys. Lett., 1998, 288, 59–64 CrossRef CAS.
- G. Cirmi, D. Brida, A. Gambetta, M. Piacenza, F. Della Sala, L. Favaretto, G. Cerullo and G. Lanzani, Phys. Chem. Chem. Phys., 2010, 12, 7917–7923 RSC.
- M. Matsushita, M. Ketelaars, A. M. van Oijen, J. Köhler, T. J. Aartsma and J. Schmidt, Biophys. J., 2001, 80, 1604–1614 CrossRef CAS PubMed.
- M. F. Richter, J. Baier, T. Prem, S. Oellerich, F. Francia, G. Venturoli, D. Oesterhelt, J. Southall, R. J. Cogdell and J. Köhler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6661–6665 CrossRef CAS PubMed.
- J. K. Sprafke, D. V. Kondratuk, M. Wykes, A. L. Thompson, M. Hoffmann, R. Drevinskas, W.-H. Chen, C. K. Yong, J. Kärnbratt, J. E. Bullock, M. Malfois, M. R. Wasielewski, B. Albinsson, L. M. Herz, D. Zigmantas, D. Beljonne and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 17262–17273 CrossRef CAS PubMed.
- K. H. Park, P. Kim, W. Kim, H. Shimizu, M. Han, E. Sim, M. Iyoda and D. Kim, Angew. Chem., Int. Ed., 2015, 54, 12711–12715 CrossRef CAS PubMed.
- L. Adamska, I. Nayyar, H. Chen, A. K. Swan, N. Oldani, S. Fernandez-Alberti, M. R. Golder, R. Jasti, S. K. Doorn and S. Tretiak, Nano Lett., 2014, 14, 6539–6546 CrossRef CAS PubMed.
- P. Parkinson, D. V. Kondratuk, C. Menelaou, J. Q. Gong, H. L. Anderson and L. M. Herz, J. Phys. Chem. Lett., 2014, 5, 4356–4361 CrossRef CAS PubMed.
- E. Mena-Osteritz, F. Zhang, G. Götz, P. Reineker and P. Bäuerle, Beilstein J. Nanotechnol., 2011, 2, 720–726 CrossRef CAS PubMed.
- J. Yang, S. Ham, T.-W. Kim, K. H. Park, K. Nakao, H. Shimizu, M. Iyoda and D. Kim, J. Phys. Chem. B, 2015, 119, 4116–4126 CrossRef CAS PubMed.
- K. H. Park, J.-W. Cho, T.-W. Kim, H. Shimizu, K. Nakao, M. Iyoda and D. Kim, J. Phys. Chem. Lett., 2016, 7, 1260–1266 CrossRef CAS PubMed.
- A. V. Aggarwal, A. Thiessen, A. Idelson, D. Kalle, D. Würsch, T. Stangl, F. Steiner, S.-S. Jester, J. Vogelsang, S. Höger and J. M. Lupton, Nat. Chem., 2013, 5, 964–970 CrossRef CAS PubMed.
- T. Lei, X. Xia, J.-Y. Wang, C.-J. Liu and J. Pei, J. Am. Chem. Soc., 2014, 136, 2135–2141 CrossRef CAS PubMed.
- B. Liu, W.-L. Yu, J. Pei, S.-Y. Liu, Y.-H. Lai and W. Huang, Macromolecules, 2001, 34, 7932–7940 CrossRef CAS.
- W. Kim, J. Sung, K. H. Park, H. Shimizu, M. Imamura, M. Han, E. Sim, M. Iyoda and D. Kim, J. Phys. Chem. Lett., 2015, 6, 4444–4450 CrossRef CAS PubMed.
- J. Vogelsang, T. Adachi, J. Brazard, D. A. Vanden Bout and P. F. Barbara, Nat. Mater., 2011, 10, 942–946 CrossRef CAS PubMed.
- I. Hwang and G. D. Scholes, Chem. Mater., 2011, 23, 610–620 CrossRef CAS.
- E. Collini and G. D. Scholes, Science, 2009, 323, 369–373 CrossRef CAS PubMed.
- E. Collini and G. D. Scholes, J. Phys. Chem. A, 2009, 113, 4223–4241 CrossRef CAS PubMed.
- A. T. Healy, B. W. Boudouris, C. D. Frisbie, M. A. Hillmyer and D. A. Blank, J. Phys. Chem. Lett., 2013, 4, 3445–3449 CrossRef CAS.
- H. Sirringhaus, P. J. Brown, R. H. Friend, M. M. Nielen, K. Bechgaard, B. M. W. Langeveld-Voss, A. J. H. Spiering, R. A. J. Janssen, E. W. Meijer, P. Herwig and D. M. de Leeuw, Nature, 1999, 401, 685–688 CrossRef CAS.
- F. C. Spano and C. Silva, Annu. Rev. Phys. Chem., 2014, 65, 477–500 CrossRef CAS PubMed.
- O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2018 |




