Assigning a structural motif using spontaneous molecular dipole orientation in thin films†
Abstract
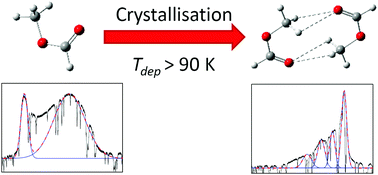
Spontaneous orientation of molecular dipoles has been observed to produce bulk electric fields, termed ‘spontelectric’ fields, in a broad variety of molecular solid thin films formed by condensation from the gas phase. Such spontelectric fields are found in cis-methyl formate (cis-MF) and the present work combines observation of these fields with high quality ab initio studies of cis-MF monomers and dimers. This enables a prediction of the structural motif within the unit cell of the crystalline phase of solid cis-MF, showing it to be a non-polar dimer. Dimer formation at deposition temperatures of >90 K is therefore cited to contribute to the observed collapse of the spontelectric field at these temperatures. This is the first time that such a structural prediction has been made using observations of spontelectric behaviour as a key indicator.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...
