Viscoelastic subdiffusion in a random Gaussian environment

Abstract

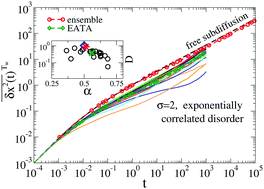
Viscoelastic subdiffusion governed by a fractional Langevin equation is studied numerically in a random Gaussian environment modeled by stationary Gaussian potentials with decaying spatial correlations. This anomalous diffusion is archetypal for living cells, where cytoplasm is known to be viscoelastic and a spatial disorder also naturally emerges. We obtain some first important insights into it within a model one-dimensional study. Two basic types of potential correlations are studied: short-range exponentially decaying and algebraically slow decaying with an infinite correlation length, both for a moderate (several k_BT, in the units of thermal energy), and strong (5–10k_BT) disorder. For a moderate disorder, it is shown that on the ensemble level viscoelastic subdiffusion can easily overcome the medium's disorder. Asymptotically, it is not distinguishable from the disorder-free subdiffusion. However, a strong scatter in single-trajectory averages is nevertheless seen even for a moderate disorder. It features a weak ergodicity breaking, which occurs on a very long yet transient time scale. Furthermore, for a strong disorder, a very long transient regime of logarithmic, Sinai-type diffusion emerges. It can last longer and be faster in the absolute terms for weakly decaying correlations as compared with the short-range correlations. Residence time distributions in a finite spatial domain are of a generalized log-normal type and are reminiscent also of a stretched exponential distribution. They can be easily confused for power-law distributions in view of the observed weak ergodicity breaking. This suggests a revision of some experimental data and their interpretation.