Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum-classical dynamics of the capture of neon atoms by superfluid helium nanodroplets†
Miquel
Blancafort-Jorquera
 ,
Arnau
Vilà
,
Arnau
Vilà
 and
Miguel
González
and
Miguel
González
 *
*
Departament de Ciència de Materials i Química Física and IQTC, Universitat de Barcelona, c. Martí i Franquès, 1-11, 08028, Barcelona, Spain. E-mail: miguel.gonzalez@ub.edu; Fax: +34-934021231
First published on 6th November 2018
Abstract
The capture of a Ne atom by a superfluid helium nanodroplet, Ne + (4He)N → Ne@(4He)N′ + (N − N′) 4He, was studied using a hybrid quantum (helium)–classical (Ne) approach and taking into account the angular momentum. The atom is captured by (4He)N and follows elliptical rotating trajectories, and large energy and angular momentum transfer from the atom to the nanodroplet occur. Evaporation of helium atoms from (4He)N allows removal of the excess energy and angular momentum of the doped nanodroplet. The behaviours observed for angular momentum different from zero are similar to the zero angular momentum case. The angular momentum of the Ne atom can induce vortex nucleation for high enough initial angular momentum values (∼176.3–220.3 ℏ). Vortices arise from collapse of the surface excitations (ripplons) and are long-lived under some initial conditions. Comparison with our own previous quantum dynamics study at zero angular momentum shows that quantum effects are not important under the initial conditions examined here. Besides, a comparison with the scarce information available on other systems has been performed, showing the rich variety of behaviours that can be observed in the solvation of impurities by superfluid helium. More efforts are welcome in order to obtain a deeper insight into the dynamics of the capture process, especially in the vortex formation context.
1. Introduction
The study of superfluid helium nanodroplets (structure, energy and dynamics), (4He)N, T = 0.37 K, is an already rooted research area in physics.1–3 Their intermediate size allows researchers to investigate the properties of quantum fluids and how they change with the size of the system, from clusters to bulk liquids. Besides, one of the features attracting more attention is the fact that, due to the inert character of He and the superfluidity of liquid 4He below T = 2.17 K, 4He nanodroplets can be used as low temperature matrices for high resolution spectroscopy.4–6From the initial study of chemical reactivity in helium nanodroplets,7 the evolution of this field of study has been significant.8–16 Interest in chemistry has increased in recent times due to the possibility of synthesizing new chemical species using these nanodroplets, as they are able to stabilize species which are not stable in the gas phase such as metallic nanoclusters17–19 and nanowires.20,21 In terms of chemical reaction dynamics in the (4He)N quantum fluid several reactions have been studied,1,22 experimentally (photodissociation of alkyl iodides,23–25 bimolecular reactions involving metals, Mg + O2,26 Al + O2, H2O,9 Ba + N2O,7etc.) and theoretically (photodissociation of Cl2(B) in superfluid11,12 and non-superfluid27 helium nanodroplets; and Ne2 formation16).
Even though our group is mainly interested in the study of reaction11,12,15,16 and relaxation14,28 dynamics inside helium nanodroplets, the pickup (capture) process of atomic or molecular species by (4He)N is, of course, an important and related process as it precedes any chemical reactions and other processes that may occur inside the nanodroplets (see, e.g., ref. 13 and 16). On the other hand, the impurities (atomic or molecular) can be considered as probes to investigate (4He)N.
The first time helium clusters were proved to have the ability to capture chemical species was in molecular beam experiments with neon atoms.29 There is a wide variety of atomic and molecular species that can be captured by helium nanodroplets: Ar, Kr, Xe, H2O, and SF6,30 Arn,31 Krn,32 transition metal atoms (Crn,33 Cun34), organic radicals (ethyl radicals),35 aromatic organic molecules and related species (anthracene, pyrromethene, and porphyrin derivatives),36 fullerene with small molecules (C60(H2O)n, C60(NH3)n and C60(CO2)n),37etc.
Even though a lot of experimental effort has been made (see, e.g., ref. 29, 28 and 38), information about the dynamics of the pickup process is still limited. The first attempt to study the quantum scattering dynamics of helium nanodroplets dates back to 1988,39 and the first quantum analysis of the motion of particles inside nanodroplets was made in the late 1990s.40,41 Further detailed many-body quantum studies of the scattering of atoms from helium nanodroplets and surfaces have been performed lately.42–44 But it has not been until very recently that a few realistic theoretical studies of the pickup process and motion of the impurity inside the nanodroplet have been reported.12,45–48
In the present work we have theoretically investigated, using a quantum (helium)–classical (neon atom) hybrid approach, the dynamics of the pickup process of a Ne atom by a superfluid helium nanodroplet of 500 atoms, Ne + (4He)N → Ne@(4He)N′ + (N − N′)4He (N = 500). To do this we have considered four representative velocities of those typical in a pickup experimental chamber (T ≈ 300 K) and a wide set of atom impact parameters, in order to take into account the angular momentum. Particular attention has been paid to the dynamics of the pickup microscopic mechanism and to the energy and angular momentum exchange processes. This quantum-classical study complements and extends a previous quantum dynamics investigation on the Ne + (4He)N pickup process at zero angular momentum carried out by our group.13
This paper has the following structure: the theoretical methods are explained in Section 2; the description and analysis of the most important results are given in Section 3; and finally the summary and conclusions are reported in Section 4. Additional useful information is provided in the ESI.†
2. Theoretical methods
The theoretical study of the Ne + (4He)N pickup dynamics has been carried out following a “divide and conquer” (hybrid) strategy. Thus, the superfluid helium nanodroplet has been modelled using one of the main procedures employed to describe large systems of bosonic liquid 4He (time dependent density functional theory (TDDFT)) and the Ne atom has been described using classical mechanics (CM). In this case, differing from ref. 13, where a similar approach was used but the Ne atom was treated quantum mechanically, the angular momentum of the attacking atom has been taken into account. The quantum-classical treatment of the pickup dynamics used here has also been applied to other atom + (4He)N systems (see, e.g., ref. 45 and 46).To describe the helium system we have used the Orsay-Trento (OT) phenomenological density functional.49 The non-local contributions to the helium correlation energy and the back-flow term have been neglected for computational reasons and the major numerical complications arising from the second term. Besides, a modification has been added to the OT density functional that avoids unphysical helium density values, when the interaction between the impurity and helium is strong.50 The theoretical investigation of the dynamics of chemical and physical processes involving (4He)N has only been possible recently11–16,28,45,46,51,52 and in all cases the approach indicated above has been used. On the other hand, when it has been possible to make the comparison between theory and experiment, a satisfactory agreement has been obtained by using such simplification in the OT functional51–53 and, in addition, some satisfactory tests have been reported in the context of the (4He)N relaxation.14
The helium wave function is propagated in time using the TDDFT method. Here we will only show the main equations used in the present study. To model the helium the quantum-classical action, in terms of the effective complex wave function of (4He)N, |ΨHe(RHe,t)|2 ≡ ρHe(RHe,t), reads:
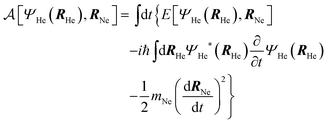 | (1a) |
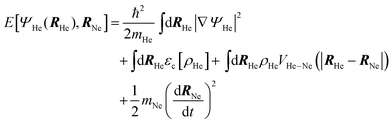 | (1b) |
To obtain the equations for the time evolution of the Ne + (4He)N system, where N = 500 has been used, the quantum-classical action must be minimised by making variations in ΨHe(RHe) and RNe. The resulting expressions correspond to a non-linear time-dependent Schrödinger-like equation for the helium and to the classical laws of motion for the propagation of the position and the velocity of the Ne atom (that occurs in the xy-plane):
 | (2a) |
 | (2b) |
Eqn (2a) has been solved using a discretization procedure (Cartesian grid) while no grid has been used for eqn (2b). The helium grid depends on the initial Ne velocity, the grids being denser the higher the velocity (Table S1, ESI†). The numerical integration (time propagation) of these equations has been performed using a fourth order Adams predictor–corrector–modifier method,55 initialised by a fourth order Runge–Kutta method.56 The time step used in the numerical integration also depends on the initial velocity of Ne considered (Table S1, ESI†). The derivatives involved in the calculations have been calculated in momentum space using a Fourier transform as implemented in the FFTW package.57 To avoid possible unphysical reflections of the helium effective wave function at the edges of the grids, a quartic negative imaginary potential (NIP)58 has been placed 1 Å before the minimum and maximum limits of the x, y, and z axes (Table S1, ESI†), employing the same absorption strength and length as in ref. 13 (3315.0 K Å4 and 1 Å, respectively).
The initial positions of the Ne atom considered in order to explore the influence of angular momentum on the pickup process are the following: −25.0 Å for the x-axis and 0, 7, 14, 17, 20, 27 and 34 Å for the y-axis. Moreover, the Ne and (4He)N initial energies, considering a nanodroplet of 500 helium atoms, are given in Table 1 and the total simulation times are reported in Table S2 (ESI†).
| v 0 Ne (m s−1) | E kin Ne (K) |
|---|---|
| a E kin, Epot+corr and Etot helium are equal to 79.99, −2552.4 and −2472.3 K, respectively. | |
| 90.0 | 9.74 |
| 210.0 | 53.02 |
| 500.0 | 300.6 |
| 800.0 | 769.4 |
3. Results and discussion
The process of capturing a neon atom by a superfluid helium nanodroplet, Ne + (4He)N → Ne@(4He)N′ + (N − N′) 4He with N = 500 has been studied at several initial velocities of Ne (v0 = 90, 210, 500 and 800 m s−1 (along the x-axis)) and several impact parameters to account for several angular momenta (b = 0, 7, 14, 17, 20, 27 and 34 Å). These velocities have been chosen in order to have a good representation of the Maxwell–Boltzmann velocity distribution of the Ne atoms at T = 300 K (Fig. S1, ESI†), which is the typical experimental condition in pickup chambers. The selected impact parameters allow us to examine the different possible situations that can be found (captured, tangential to the nanodroplet surface and non-captured trajectories).Before carrying out the dynamics calculations and in order to define the initial conditions, the helium density of (4He)N=500 has been optimised using static DFT calculations with different grids, depending on the Ne atom initial velocity considered (Table S1, ESI†). The radial distribution of the helium density obtained can be seen in Fig. S2 (ESI†). The helium density strongly decreases near its surface and near its centre the density is constant (a saturation density value (ρ0) of 0.0224 Å−3; where the helium DFT functional has been fitted in order to reproduce the experimental value of 0.02184 Å−3). Surface atoms have the tendency to migrate to the centre of the nanodroplet in order to minimise their energy, and this leads to the strong decrease of density observed at the HeND surface. The surface thickness is defined as the distance at which the density varies from 90% to 10% of ρ0 and a value of 5.2 Å has been obtained. The initial energies of the dynamic calculation are gathered in Table 1.
3.1. Case 1: zero angular momentum
Here we present the main results obtained from the calculations with b = 0 Å and v0 = 90, 210, 500, 800 m s−1. In addition to the figures given here, additional material can be found in the ESI† and, in particular, in Movies 1 and 2 (ESI†) the time evolution of the helium density and helium wave function phase in the xy-plane for v0 = 500 m s−1 and two representative cases (b = 0 and 14 Å, respectively) is shown. This initial velocity corresponds to the most probable velocity of neon at T = 300 K. Snapshots of the helium density in the xy-plane and in the x- and y-axes for v0 = 500 m s−1 and b = 0 Å at illustrative times are shown in Fig. 1. Moreover, the evolution of the position and velocity of the Ne atom in the x-axis as a function of time and the velocity as a function of the position (i.e., phase-space like diagram) are shown in Fig. 2. | ||
| Fig. 1 Time evolution of the helium density in the xy-plane and in the x- and y-axes for v0 = 500 m s−1 and b = 0 Å at representative times. | ||
 | ||
| Fig. 2 Kinematic properties of the Ne atom (x-axis) for b = 0 Å vs. time: (a) position; (b) velocity; (c) velocity at short times; (d) phase-space like diagram. | ||
These figures and Movie 1 (ESI†) allow us to elucidate the capture process mechanism, which can be described considering three steps. Firstly, during the Ne atom approach a deformation of the helium nanodroplet density towards the Ne atom appears, due to the Ne–helium interaction potential energy. At this point, a waving pattern in the approaching direction appears in the HeND density, due to the excitation introduced by the atom and its velocity is increased. Secondly, once the Ne atom reaches the surface of the nanodroplet its velocity rapidly (∼5 ps) decreases and, in some cases, it reaches negative values (the atom bounces back at some extent, as it can be seen in the position evolution; Fig. 2). In addition, the waves formed due to the collision have already reached the opposite surface of the nanodroplet, colliding against it and going backwards. Finally, the helium density surrounds the Ne atom and drags it to the inside of the nanodroplet (leading to capture), where the returning waves create interference patterns with the newly created ones.
Once the Ne atom is located inside the HeND and the perturbation in the helium density is weaker, a solvation layer is formed around the atom. Then, in the bulk-like region of the HeND the atom reaches the Landau's critical velocity (vL ≈ 58 m s−1 in superfluid liquid helium (bulk)).59,60 This velocity has been reported experimentally and theoretically (TDDFT (helium) + classical mechanics (Ag)) in HeNDs with a thousand or more helium atoms.51 We have also found the existence of this critical velocity in quantum dynamics studies (TDDFT (helium) + quantum mechanics (dopants); angular momentum equal to zero) on the Ne + (4He)1000 capture13 and Ne + Ne@(4He)500 reaction16 processes. Probably, this behaviour should be expected in superfluid helium nanodroplets that include a bulk-like zone.
This critical velocity reached by the atom, that when using the present method to describe the helium is ≈90 m s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 [due to the reasonable approximations made in the helium functional (the non-local contributions to the helium correlation energy and the back-flow term have been neglected), in order to make possible the dynamic calculations; cf. Section 2], remains constant unless the atom approaches the surface of the HeND, where it bounces back. The asymmetric helium density distribution pushes the atom back and forward preventing it from staying in the centre of the nanodroplet, even though this is the most stable geometrical arrangement. Under these conditions the Ne atom moves inside the HeND without friction, due to the superfluid character of helium below 2.17 K. In all cases examined the behaviour of the Ne atom inside the nanodroplet is similar, showing the great efficiency of the nanodroplet to accommodate the atom, even at the higher initial velocities studied.
51 [due to the reasonable approximations made in the helium functional (the non-local contributions to the helium correlation energy and the back-flow term have been neglected), in order to make possible the dynamic calculations; cf. Section 2], remains constant unless the atom approaches the surface of the HeND, where it bounces back. The asymmetric helium density distribution pushes the atom back and forward preventing it from staying in the centre of the nanodroplet, even though this is the most stable geometrical arrangement. Under these conditions the Ne atom moves inside the HeND without friction, due to the superfluid character of helium below 2.17 K. In all cases examined the behaviour of the Ne atom inside the nanodroplet is similar, showing the great efficiency of the nanodroplet to accommodate the atom, even at the higher initial velocities studied.
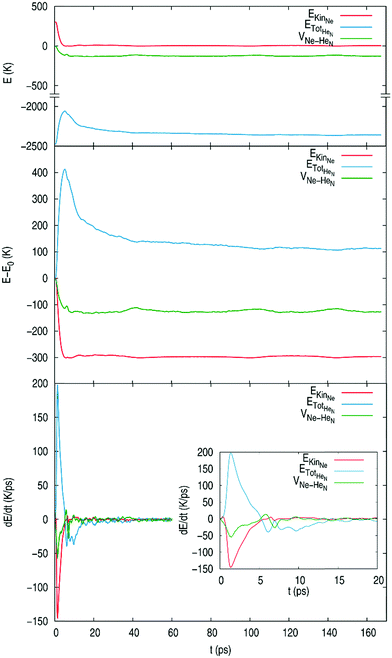
The Ne atom kinetic, potential (Ne–helium) and total (kinetic + potential) energies as a function of time are given in Fig. 3 for all the initial velocities investigated. In general terms, all energies experience a decrease when the atom is captured by the nanodroplet, i.e., the atom is stabilised by the capture. Then, there are oscillations arising from the collisions of the atom against the nanodroplet surface. Besides, for all initial velocities there is a small increase in the Ne kinetic energy at initial times, due to the Ne atom–helium interaction potential energy, and it sharply decreases as the atom reaches the inside of the HeND. There is a clear correspondence between the kinetic energy of Ne and the Ne–helium potential energy: the minima in the kinetic energy correspond to maxima in the potential energy and vice versa.
 | ||
| Fig. 3 Neon kinetic energy (top), Ne–helium potential energy (middle) and the sum of both energies (bottom) for b = 0 Å vs. time. | ||
The kinetic energy of Ne, the Ne–helium potential energy and the total energy of the HeND (without considering the previous term) vs. time are given in Fig. 4 for the v0 = 500 m s−1 case. The larger variations in the energies arise within the first 15 ps, the changes that occur below t ≈ 5 ps being particularly strong, when the capture takes place. At first, the kinetic energy of the atom strongly decreases and is mainly transformed into the excitation energy of the nanodroplet.
After around 20 ps only small oscillations of the energies occur. When the Ne atom is well inside the nanodroplet, its kinetic energy and the Ne–helium interaction energy are almost constant and the HeND total energy has a slightly decreasing tendency. The HeND decreases its energy by evaporation of some density (helium atoms) in order to reach the ground state density of the doped nanodroplet, Ne@(4He)N′, according to the process Ne + (4He)N → Ne@(4He)N′ + (N − N′)4He.
The helium density is considered to correspond to evaporated density, i.e., it is not a part of the nanodroplet, when it is absorbed by the NIPs placed at the edges of the Cartesian grid of helium (cf. Section 2), as we have also considered in other studies.11–16,28 Moreover, the evaporated helium density is integrated in time in order to obtain the number of evaporated He atoms, as usual.
In terms of the time derivatives of the energies, three strong peaks are evident at about 1.4 ps, when the atom reaches the surface of the nanodroplet, which are followed by small peaks and oscillations that show the existence of small energy exchanges between the atom and the HeND, with the system being not far from stability (cf.Fig. 4).
The time evolution of the total energy of the system (without considering the energy of the evaporated He atoms) is shown in Fig. 5. The energy is constant at the initial times and then it monotonically decreases with an asymptotic tendency (approx. −2480 K). This decrease does not occur until the Ne atom has been captured (t ≈ 5 ps for v0 = 500 m s−1; and at t = 6.0 ps the neon velocity is equal to zero for the first time) and it arises from the evaporation of some helium density, which allows the system to evolve towards the ground state structure of the resulting doped nanodroplet.
 | ||
| Fig. 5 Total energy of the system vs. time for b = 0 Å. The total energy changes due to the evaporation of some He atoms until the resulting doped HeND stabilizes. | ||
The number of helium atoms of the HeND and the corresponding energy per helium atom vs. time are given in Fig. 6. The initial decrease of both properties is close to the moment when the neon velocity is equal to zero for the first time. Indeed, thanks to helium evaporation, the nanodroplet energy per helium atom decreases to reach similar values in all cases (≈−4.8 K), even though the perturbation induced by the impurity is stronger for higher velocities.
 | ||
| Fig. 6 Number of helium atoms (left) and energy per helium atom of the HeND (right) for b = 0 Å vs. time. | ||
Fig. 7 shows how the evaporation of He atoms releases the excitation energy introduced in the HeND by collision with the Ne atom, presenting both the time interval (Δt) and energy released during each atomic evaporation. The initial evaporations are the faster ones and it is increasingly more difficult for the system to evaporate atoms, as the HeND becomes gradually less excited. Besides, the initial evaporated atoms take substantially more energy of the HeND with them than the others and the energy released per atom diminishes as the HeND becomes less excited. Hence, at the beginning the HeND relaxation through He evaporation is particularly efficient, because the atoms evaporate in a faster way and remove significantly more excitation energy of the nanodroplet than the remaining evaporated atoms.
 | ||
| Fig. 7 He atom evaporation for b = 0 Å: time interval needed (left) and energy released (right) during each atomic evaporation. | ||
The comparison of the present quantum-classical results for b = 0 Å with the quantum results at zero angular momentum previously obtained for Ne + (4He)100013 shows that they are quite similar. Regarding the properties involving helium, we should be aware than the present nanodroplet, (4He)500, has half helium atoms that the nanodroplet used in ref. 13. Thus, e.g., if we consider the main peaks of the energy per He atom representation for v0 = 500 and 800 m s−1, increments of ≈1.53 and 0.68 K have been obtained here (Fig. 6) with respect to the corresponding asymptotic values (final simulation times). The quantum values are ≈0.79 and 0.34 K, respectively, and this is consistent with the ratio of He atoms of the two nanodroplets. Also, if we consider the number of evaporated He atoms very close results have been obtained here and in the quantum study,13 showing that this number only depends on the HeND excitation energy. Hence, we can conclude that for the initial conditions explored quantum effects are not important in the Ne + HeND system, which is the lighter one of the Rg + HeND family (Rg: He, Ne, Ar, Kr, Xe, Rn), with the only exception of the Rg = He case.
Some theoretical information has been provided on the capture of a Xe or an Ar atom by (4He)1000 (for Xe: v0 = 200, 300, 400 and 600 m s−1 with b = 0 Å, and v0 = 200 m s−1 with b = 20.3 and 22.2 Å; for Ar: v0 = 360 m s−1 and b = 0 Å), in a TDFFT-CM study that was mostly centred on the capture of Xe and Ar atoms by HeNDs hosting quantized vortices.47 These results are in qualitative agreement with the results obtained here for Ne, where these and other issues have been investigated in much more detail than in the previous reference: (a) most of the energy is transferred from the atom to the nanodroplet in the initial times of the collision; (b) the nanodroplet experiences large deformations; and (c) at low-moderate initial velocities of the atom it moves back and forth inside the nanodroplet. Analogous trends have also been observed in the quantum dynamics studies at zero angular momentum carried out for the Ne atom capture by (4He)100013 and by the Ne@(4He)500 doped nanodroplet,16 in the last case leading to the formation of the Ne2 dimer.
Although strictly speaking it does not correspond to a capture process (as capture has really occurred previously, once the heliophobic species Rb, Cs and Ba have been captured by the HeND and located on its surface forming a dimple), it is interesting to consider here the solvation process that occurs after photoionization of the Rb, Cs and Ba atoms, producing the Rb+, Cs+ and Ba+ cations, respectively;61 although the initial conditions are, of course, very different from those of the Ne capture. Even though at the beginning the cations move towards the center of the nanodroplet they exhibit a large variety of behaviors. The TDDFT-CM comparative study of ref. 61 shows that after forming the Rb+ snowball (i.e., a solid-like helium solvation structure) the cation remains essentially stationary and the helium rearranges around it; while after the formation of the Cs+ snowball it does not penetrate the nanodroplet and, in around 90 ps, it desorbs from the HeND. The solvation of the cations initially located in the nanodroplet surface not only depends on the energy balance but also on the finer details of these systems.
In the case of Ba+, once the snowball has been formed, it performs an almost undamped oscillating motion inside the nanodroplet. That is to say, the Ne atom (for which solvation does not lead to the formation of snowballs) presents an oscillating behavior inside the HeND that is similar to that of Ba+, and this also happens for the capture of a Xe atom (with the exception of the highest initial velocity reported, 600 m s−1, which is well above the velocity range of Xe encountered in the experiments).46 Related to the study developed in ref. 61 is the experimental research on the desorption of an electronically excited Na atom, initially attached to the HeND surface, reported in ref. 62, where the behavior of several excited states has been analyzed. The alkali metal atoms and small alkali clusters, which are classical heliophobes, can be induced to immerse into HeND when a highly polarizable co-solute (C60) is added to the nanodroplet.63
Regarding the solvation of the Ne atom in the HeND, it is worth noting that around half of the time the atom oscillates inside the nanodroplet it is well immersed, with the first and second solvation shells well defined. However, when the atom approaches the surface of the nanodroplet the second solvation layer is partly lost (typically ∼1/3 to 1/2 of the second solvation layer is lost, on the side of it which is closer to the surface). Because when the impurity is completely immersed in the HeND its electronic spectrum of excitation moves towards the blue,64 certain differences are expected to appear in the atomic spectrum, depending on whether the Ne atom is well immersed or not. On the other hand, in the case of neon the formation of the first solvation shell occurs for the first time at ∼15 ps, taking as a reference the moment the atom hits the nanodroplet surface. In the case of Rb+, Cs+ and Ba+ the snowball structure is formed at about 20, 30 and 10 ps, respectively.61
What has been indicated here on the Ne atom oscillating motion inside the HeND and solvation also applies when the angular momentum is different from zero. Furthermore, the formation of vortices in two of the three cationic systems considered above will be taken into account at the end of the next section.
3.2. Case 2: angular momentum different from zero
Here we will analyse the influence of angular momentum on the pickup process. The initial velocity of the Ne atom for all the results presented in this sub-section is v0 = 500 m s−1 (which corresponds to the most probable value at T = 300 K) and the impact parameters examined are b = 0, 7, 14, 17, 20, 27 and 34 Å. The results obtained for the other initial velocities are similar.Snapshots, at representative times, of the movie prepared for v0 = 500 m s−1 and b = 14 Å (Movie 2 in the ESI†) are shown in Fig. S3 (ESI†), where the helium density in the xy-plane and in the x- and y-axes are presented. The capture mechanism is similar to the case without angular momentum (b = 0 Å; cf.Fig. 1) but in the present situation, of course, the y-axis component also affects the motion of the Ne atom and helium density.
The trajectories of the Ne atom for the studied cases are depicted in Fig. 8. The dotted lines correspond to the x- and y-axes, which are centred in the HeND, and to the HeND surface circumference (R ≈ 20 Å). From these results it comes out that the Ne atom is captured when it has an impact parameter between zero and a value that is somewhat smaller than the radius of the nanodroplet. For the impact parameters leading to capture, once the Ne atom is inside the nanodroplet, it describes rotating elliptical-like trajectories. In the other situations, the motion of the non-captured Ne atom is affected by the Ne–HeND interaction that is weaker when the impact parameter is larger. The trajectories for v0 = 500 m s−1 and b = 7, 14 and 17 Å show a kink that results from the fact that, a little after the Ne atom enters into the nanodroplet, the atom stops or even moves back due to the helium (the atom experiences the effect of a potential barrier due to the helium density), before the first solvation layer is formed around the Ne atom and then it is able to move inside the nanodroplet.
 | ||
| Fig. 8 Ne atom trajectories for v0 = 500 m s−1 and impact parameters b = 0 (red), 7 (blue), 14 (green), 17 (magenta), 20 (black), 27 (orange) and 34 (yellow) Å. | ||
Qualitatively similar trajectories were found in ref. 48 (using a related but simpler theoretical approach), considering very different systems. The formation of metal dimers (M + M → M2; M: Cu, Ag and Au) in HeNDs was studied with the two metal atoms (M) initially placed, randomly distributed, in the nanodroplet, and only small velocities were considered (v0: 0–56 m s−1, where the largest value corresponds to the experimental Landau's critical velocity). The time values required to form the M2 dimers obtained in ref. 48 are expected to be reasonably good for “soft” initial reaction conditions, i.e., when the atoms have small velocities and are captured by the HeND. However, under the ordinary conditions of the pickup chambers (T ≈ 300 K), the most probable velocity is substantially larger (281, 215 and 159 m s−1 for Cu, Ag and Au, respectively) than the values indicated before. These higher velocities will probably yield a substantial excitation of the nanodroplet, after the collision with the two atoms, and the helium density waves produced will probably lead to different formation times than in the previous case. Of course, in order to determine in a quantitative way the degree of validity of the interesting model applied in ref. 48, it would be desirable to compare with the M2 formation times obtained from the TDDFT-CM method, considering initially the capture of both M atoms and following their evolution inside the nanodroplet.
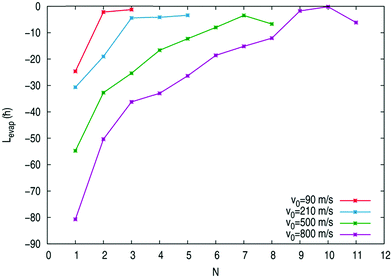
For a captured Ne atom trajectory, the deflection angle has been taken as equal to the angle defined by the initial direction of the Ne atom motion and the direction of the trajectory of this atom during the first approach to the surface of the nanodroplet (once the atom is inside the nanodroplet). For a non-captured Ne atom trajectory, the deflection angle has the usual definition. These deflection angles, αd, have been found to be 0, −19, −59, −82, −13, 0 and 0° for b = 0, 7, 14, 17, 20, 27 and 34 Å, respectively (Fig. S4, ESI†). Further short-time calculations, considering some additional impact parameter values, have been performed in order to find the maximum impact parameter for capture (bmax) and it has been found to be about 25, 23, 18 and 16 Å for v0 = 90, 210, 500 and 800 m s−1, respectively. The decrease of bmax with v0 suggests that the capture process has no energy theshold65 (see at the end of this section the comparison with the Xe atom capture).
Velocities evolve over time following similar behaviours as for b = 0 Å, the only difference is that the velocity decrease, due to the atom collision against the HeND surface, occurs at larger times for larger impact parameters (Fig. S5, ESI†), as it takes longer for the atom to reach the HeND surface when b increases. The phase-space like diagrams for Ne (v0 = 500 m s−1) are plotted in Fig. 9, where it can also be seen that the atom with an impact parameter slightly smaller than the radius of the nanodroplet is indeed captured (elliptical-like trajectories).
 | ||
| Fig. 9 Phase-space like diagram of the Ne atom for v0 = 500 m s−1 at several impact parameters: x component (left); y component (right). | ||
The evolution of the energies and the time derivatives of the energies vs. time is also similar to the b = 0 Å case. Higher Ne atom impact parameters (i.e., higher angular momentum values) only introduce smoothness in the whole process, i.e., the pickup process is ‘softer’ the bigger the impact parameter is (cf. Fig. S6 and S7, ESI†). Moreover, the kinetic energy transferred by the Ne atom to the HeND is essentially constant (≈300 K) and corresponds to its initial kinetic energy, until the b value is not far from bmax, where a strong decrease occurs (Fig. S8, ESI†).
The time evolution of the total energy of the system (Ne + HeND), the number of helium atoms of the HeND, and the energy per helium atom of the HeND are given in Fig. S9 and S10 (ESI†), and the required time to evaporate helium atoms is reported in Fig. S11 (ESI†). These properties also show similar behaviours to those reported for b = 0 Å.
The most important difference found between the b ≠ 0 and b = 0 results comes from the fact that, in some cases, shortly after the Ne atom has been captured, vortices (vortex lines) are formed in the nanodroplet, as a result of the surface perturbations created by the atom impact. Moreover, the examination of the angular momentum exchange between the Ne atom and the HeND and the distribution of angular momentum in the HeND is also of great interest. These issues are considered below.
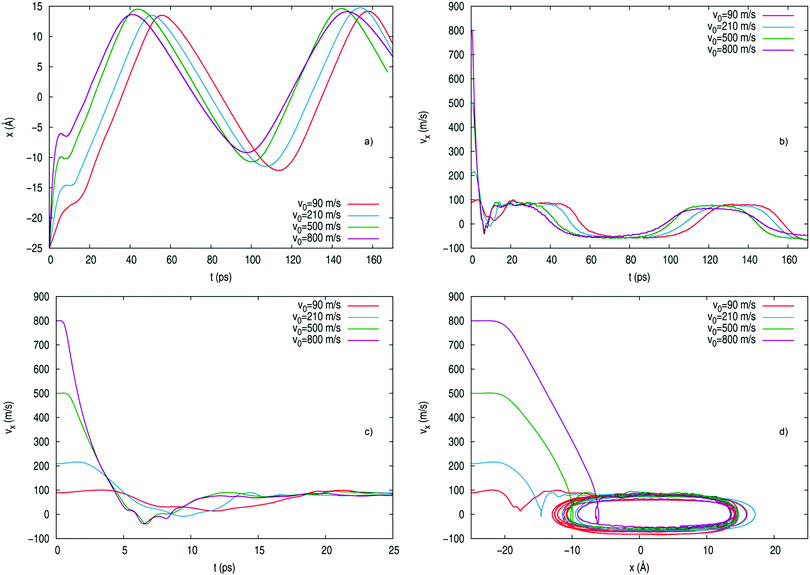
The vortices have been found to travel along with the Ne atom inside the nanodroplet and vortex formation only occurs when the initial angular momentum of neon is high enough (see, e.g., Fig. 10 and 11 and Movies 2–4, ESI†). A long-lived vortex (which is close or very close to the HeND surface), i.e., a vortex initially lasting several Ne atom rebounds with the HeND surface and showing subsequent and sequential temporary disappearances and reappearances approximately between the atom rebounds during the whole simulation time, has been found for the v0 = 500 m s−1, b = 14 and 17 Å and v0 = 800 m s−1, b = 14 Å initial conditions. From this information, we have estimated that the minimum initial angular momentum of neon (LNe; z-component only) leading to the formation of long-lived vortices is within the interval between −176.3 and −220.3 ℏ, where these values correspond to LNe for v0 = 800 m s−1, b = 7 Å and v0 = 500 m s−1, b = 14 Å, respectively. The formation of a short-lived vortex, i.e., lasting as long as a Ne atom rebound with the HeND surface has been found in other cases. The different situations observed, including those where no vortex has been formed, are collected in Table 2, as a function of the initial conditions (v0, b).
| a Vortex cases: not formed (red); short-lived (yellow); long-lived (green). b Numbers represent the number of rebounds of the atom against the HeND surface that the vortex survives. “6…” means that six is the maximum number of rebounds the simulation time allows us to find. The vortices indicated in green are expected to last longer. c b max is around 25, 23, 18 and 16 Å for v0 = 90, 210, 500 and 800 m s−1, respectively. d This vortex is formed in the second atom rebound which differs from the other cases indicated in yellow, which are formed in the first rebound. |
|---|
|
The complexity of the dynamics of the vortex formation/disappearance process can be understood better after examination of Movies 2–4 (ESI†). Thus, for v0 = 500 m s−1 and b = 14 Å the vortex is formed shortly after the atom enters inside the HeND and exists during the time it takes the Ne atom to make the first three rebounds on the HeND surface. Then, the vortex reappears in the fourth atom rebound, disappears in the fifth and reappears in the sixth one (a bit after the simulation finishes). In addition, an ephemeral (very short-lived) new vortex is observed in the first rebound of the Ne atom on the HeND surface. The behaviours observed for v0 = 500 m s−1, b = 17 Å and v0 = 800 m s−1, b = 14 Å are similar to the previous one, particularly for the last condition. Thus, for v0 = 500 m s−1 and b = 17 Å the initial period of existence of the vortex corresponds to four Ne atom rebounds, the ephemeral vortex occurs before the first rebound and the evolution after the fourth rebound is somewhat more complex (ephemeral reappearance and reappearance of the vortex at the fifth and sixth rebounds, respectively), while for v0 = 800 m s−1 and b = 14 Å no ephemeral vortex around the first rebound has been found.
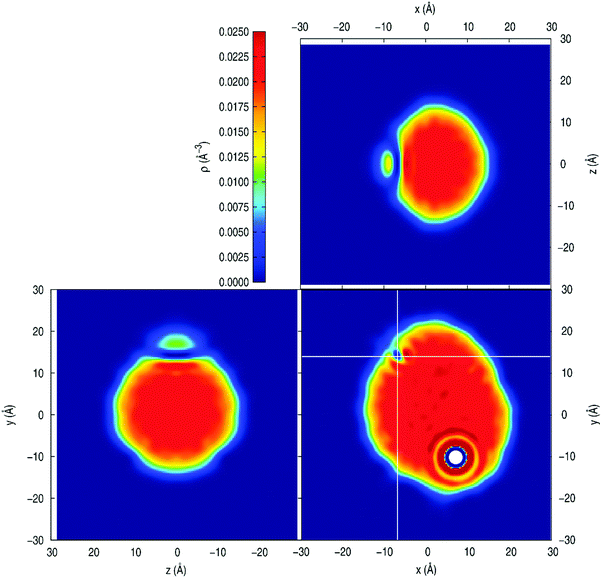
The helium density in the xy-plane and in the perpendicular planes cutting along the centre of the long-lived vortex found for v0 = 500 m s−1 and b = 17 Å is shown in Fig. 10. Besides, the helium velocity field, the helium wave function phase, and the volume occupied by the vortex for the situation reported in the previous figure are presented in Fig. 11. Also, several snapshots of the time evolution of the helium density, velocity field and wave function phase are shown in Fig. S12 (ESI†); and the time evolution of the helium density and helium wave function phase for v0 = 500 m s−1 and b = 14 and 17 Å and v0 = 800 m s−1 and b = 14 Å can be seen in Movies 2–4 (ESI†), respectively.
The helium density plot shows that the vortex line has a slightly curved tube shape perpendicular to the xy-plane (where the Ne atom moves), in which there is little or no helium density (Fig. 10); and the helium velocity field plot indicates that the helium density moves in circles around the centre of the vortex (Fig. 11). The bigger helium velocities are found around the vortex, the velocity in the rest of the points of the nanodroplet being small. The helium wave function phase (ϕ) diagram shows that the phase changes in a substantial way (from π to −π) for the points around the vortex (Fig. 11). The calculation of the circulation of the velocity of the helium fluid  in a closed path around the centre of the vortex
in a closed path around the centre of the vortex  (ref. 66) yields
(ref. 66) yields  , which means that the circulation is quantised (
, which means that the circulation is quantised ( , n ∈ integer) with n = 1. All these facts confirm that, in fact, the initial condition v0 = 500 m s−1 and b = 17 Å case shows a quantised vortex line.
, n ∈ integer) with n = 1. All these facts confirm that, in fact, the initial condition v0 = 500 m s−1 and b = 17 Å case shows a quantised vortex line.
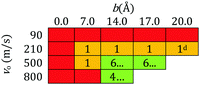
Regarding the angular momentum (L) and as a representative example, the neon (LNe), helium nanodroplet (LHeND), and total (Ltot) angular momenta, as a function of time, are plotted in Fig. 12 for v0 = 500 m s−1 and b = 14 Å, where it becomes clear that an important angular momenta exchange process occurs in the system. Initially the HeND has no angular momentum, but once the Ne atom reaches the nanodroplet surface (t ≈ 2.4 ps) it begins to transfer in a fast way its angular momentum to the nanodroplet, which leads to HeND rotational excitation. The maximum angular momentum transfer occurs in about 5 ps after the Ne atom collision, where 92.5% of the initial LNe (LNe,0) appears as LHeND (≈−203.4 ℏ). The correlation between LHeND and LNe,0 for v0 = 500 m s−1 can be seen in Fig. S13 (ESI†).
 | ||
| Fig. 12 Ne atom, HeND and total (without considering the evaporated He atoms) angular momenta vs. time for v0 = 500 m s−1 and b = 14 Å. | ||
A bit after the collision (≈2.4 ps) the Ne to HeND kinetic energy transfer leads to the evaporation of some He atoms and then the HeND angular momentum is reduced in a substantial way. LHeND evolves from around −203.4 to −109.9 ℏ in about 7.2 ps and reaches a value of ≈−62.3 ℏ in around 32.7 ps. Therefore, a high percentage of LNe,0 is removed by the evaporated He atoms (62.5% of LNe,0 at t ≈ 30 ps and smaller changes at higher times; 70 and 75% of LNe,0 at t = 60 and 170 ps, respectively). The angular momentum carried out by each evaporated helium atom is shown in Fig. 13 for the four initial velocities studied and for b = 14 Å. The atoms evaporated at smaller values of time are produced with a greater amount of angular momentum than those formed later, analogously to what happens for the energy.
In the doped nanodroplet most of the angular momentum is carried out by the helium and some smooth oscillations occur in the Ne atom and HeND angular momenta time evolution (Fig. 12), due to the collisions of the atom with the nanodroplet surface. These oscillations are in anti-phase, i.e., when the Ne atom angular momentum modulus decreases the HeND angular momentum modulus increases and vice versa.
The velocity of the change in angular momenta (dL/dt) vs. time is given in Fig. 14. The major changes are observed in the initial times (the most intense peak appears at ≈3.2 ps), when the Ne atom reaches the HeND surface and enters into the nanodroplet, as expected. Three main peaks are found, due to similar reasons to the ones driving the variation of the Ne atom kinetic energy (Fig. 4). At larger times (t above ≈15 ps), variations are small and only occur when the Ne atom rebounds against the surface of HeND, where the corresponding angular momenta are reduced or increased. These variations are more important as the impact parameter value leading to capture increases, due to the larger amount of angular momentum involved.
 | ||
| Fig. 14 Ne atom, HeND and total (without considering the evaporated He atoms) angular momenta vs. time for v0 = 500 m s−1 and b = 14 Å. The results for the initial times are shown on the right. | ||
The angular momentum of the nanodroplet is not evenly stored in all points, as it can be seen for v0 = 500 m s−1 in Fig. 15. In this figure the end of simulation radial distribution of LHeND for all impact parameters leading to capture is presented (the final simulation times are shown in Table S2, ESI†). The angular momentum transferred by the Ne atom to the nanodroplet is mainly placed near the HeND surface, due to the irrotational character of superfluid 4He.67,68 This corresponds to surface excitations of the helium density (ripplons) and, in some cases, they can collapse into vortices, as we have already detailed (v0 = 500 m s−1 and b = 14 and 17 Å and v0 = 800 m s−1 and b = 14 Å). The wider peak observed for b = 17 Å results from the existence of a long-lived vortex, in addition to the surface excitations. As opposed to the surface excitation peaks, which are narrow due to the small value of the surface thickness, the b = 17 Å vortex peak is wider as the vortex occupies a wider radial thickness. The angular momentum peaks within the nanodroplet are explained by helium circulations due to the Ne atom motion. For the final simulation time of b = 14 Å (177 ps) the long-lived vortex does not exist, in contrast to what happens for b = 17 Å (171 ps). In Fig. S14 (ESI†) the results obtained for the other initial velocities of neon are given.
 | ||
| Fig. 15 Angular momentum radial distribution of the HeND for the final simulation times (cf. Table S2, ESI†) and as a function of the impact parameter, for v0 = 500 m s−1. It should be noted that for the final simulation time of b = 14 Å (177 ps) the long-lived vortex does not exist, in contrast to what happens for b = 17 Å (171 ps). | ||
The angular momentum carried by the HeND (LHeND) can be divided into three components corresponding to the centre of mass (displacement of the entire nanodroplet; Lcm), vortex line (Lvor) and other excitations (Lother). The contribution of each one of these components to the angular momentum of the doped nanodroplet with respect to the origin of coordinates is reported in Table S3 (ESI†), including the angular momentum of the vortex with respect to its centre (Lvor,centre). All angular momenta have been calculated using the quantum operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z except Lcm that has been calculated classically using the helium velocity field (both approaches lead to the same results; see the Appendix).
z except Lcm that has been calculated classically using the helium velocity field (both approaches lead to the same results; see the Appendix).
L cm and Lother show a non-monotonic complex dependence with the initial conditions (v0, b) even though, for a given initial velocity, Lother increases its modulus with b (Table S3, ESI†). Besides, Lother plays a dominant role with the only exception of what happens for v0 = 210 m s−1 and b = 7 and 17 Å. Regarding the case where a long-lived vortex is present at the end of the simulation (v0 = 500 m s−1 and b = 17 Å), the angular momentum of HeND referred to the origin of coordinates (−84.9 ℏ) is distributed as follows: centre of mass 9.5% (−8.1 ℏ), vortex line 19.2% (−16.3 ℏ) and other excitations 71.3% (−60.5 ℏ). ‘Other excitations’ mostly refer to surface excitations, as there are no relevant peaks in regions near the centre of the HeND.
One would think that the fraction of total angular momentum a vortex line carries should be larger considering the heavy helium circulation it creates (Fig. 11). The fact is that the angular momentum stored in a vortex line comes from surface excitations that are transformed into vortex rotation. The angular momentum calculated before (Lvor) is due to the circulation of the whole vortex as a body around the origin. To better compare the surface angular momentum and the vortex circulation angular momentum, the last one should be calculated with respect to its centre. Doing so, it is seen that the vortex circulation and surface angular momenta are more similar than before (−30.9 ℏ and −60.5 ℏ, respectively).
In the context of the capture process when angular momentum is different from zero it is interesting to consider two initial conditions reported for the Xe capture in ref. 47: v0 = 200 m s−1 and b = 20.3 and 22.2 Å. This velocity was selected in order to simulate the thermal conditions of the pickup chamber and the first b value corresponds to the largest impact parameter value (among the ones calculated in that reference) that leads to capture. It is worth noting that the Ne and Xe atoms at v0 = 500 and 200 m s−1, respectively, have practically the same kinetic energy.
Although bmax for Xe capture (20.3 Å) is similar to the geometric HeND radius (22.2 Å), it should be noted that in general, even for the simpler capture process (i.e., that occurring in the gas phase),65bmax depends on the collision energy, the degree of dependence being a function of the interaction potential energy. Consistently with this, we have found that bmax clearly depends on the initial velocity of the Ne atom (bmax ≈ 25, 23, 18 and 16 Å for v0 = 90, 210, 500 and 800 m s−1, respectively). Besides, considering as in ref. 47 the radius of the HeND defined by R = r0N1/3, where r0 = 2.22 Å, we get for 4He500 a radius of 17.6 Å; i.e., bmax values significantly higher than the nanodroplet radius can be obtained for low initial velocities.
Regarding the collision of Xe with the HeND reported in ref. 47 for which some information is provided on the angular momentum (v0 = 200 m s−1 and b = 22.2 Å), it should be noted that this initial condition does not lead to Xe atom capture, i.e., corresponds to a situation that differs from the main initial conditions examined here (i.e., the set of conditions leading to atomic capture). Anyway, we have also found that a large amount of the Ne atom initial angular momentum is transferred to the evaporated helium atoms: e.g., 66.0, 74.6, 36.4 and 66.9% of LNe,0 at v0 = 90 m s−1 (b = 20.0 Å), 210 m s−1 (b = 20.0 Å), 500 m s−1 (b = 17.0 Å) and 800 m s−1 (b = 14.0 Å), respectively; while a transference of 32.7% of LXe,0 was observed for Xe at v0 = 200 m s−1 (b = 22.2 Å).
The final angular momentum of Ne (e.g., 3.9, 15.7, 1.7 and 2.2% of LNe,0 at v0 = 90 m s−1 (b = 20.0 Å), 210 m s−1 (b = 20.0 Å), 500 m s−1 (b = 17.0 Å) and 800 m s−1 (b = 14.0 Å), respectively), however, is small in comparison with the final angular momentum of the non-captured Xe(4He)5 complex reported in ref. 47 for Xe (v0 = 200 m s−1 and b = 22.2 Å), which carries 56.9% of LXe,0. For the final angular momentum of HeND we have, e.g., the following values for the Ne case: 17.0, 12.7, 31.8 and 16.5% of LNe,0 at v0 = 90 m s−1 (b = 20.0 Å), 210 m s−1 (b = 20.0 Å), 500 m s−1 (b = 17.0 Å) and 800 m s−1 (b = 14.0 Å), respectively; while 10.4% of LXe,0 was found for Xe under the initial conditions mentioned above.47
In what refers to the vortex formation, it is worth noting that for the collision of Xe with the HeND (v0 = 200 m s−1; b = 20.3 and 22.2 Å) vortex loops appear at the latest stages of the simulation,47 in contrast to what happens in the Ne atom case. Concerning the solvation processes mentioned in Section 3.1 (zero angular momentum initial conditions), the large helium density fluctuations involved in the Rb+ solvation process lead to the nucleation of quantized vortices, which can be either loop or ring vortices; while no vortices are found for the Cs+ solvation,61 and the solvation of the Ba+ cation leads to the nucleation of a ring vortex.64 This differs from what has been observed for the Ne capture at zero angular momentum, where no vortices have been found.
The diversity of behaviours described here results from the different properties of the dopants (interaction potential energy dopant-helium and dopant mass) and the different initial conditions (v0, b).
4. Summary and conclusions
The capture process of a neon atom by a superfluid helium nanodroplet ((4He)N=500; T = 0.37 K), i.e., the Ne + (4He)N → Ne@(4He)N′ + (N − N′) 4He process, has been investigated in detail using a quantum-classical approach (quantum treatment (TDDFT method) for helium and classical mechanics description of the Ne atom) and taking into account the angular momentum. This work complements and extends a previous quantum dynamics work of our group on this capture process at zero angular momentum and particular attention has been paid to the capture mechanism and the energy and angular momentum exchange between the Ne atom and the helium nanodroplet.The atom is captured by the HeND below a certain maximum impact parameter, which decreases with increasing velocities, following elliptical rotating trajectories inside the HeND. Major energy exchanges occur when the atom collides with the nanodroplet and the excitation energy of (4He)N=500 is released by evaporation of helium atoms through the excitation of the surface modes of the HeND. Angular momentum introduces smoothness into the overall process, but the general trends are similar to the zero angular momentum case (b = 0). Energy exchange and variations are softer with increasing impact parameter, while angular momentum exchange and variations are stronger when the angular momentum is higher (for b values leading to capture). The neon atom with angular momentum induces a certain amount of angular momentum to the HeND surface so both the atom and the surface tend to rotate solidarily when the atom is captured. Besides, helium density evaporation leads to the decrease of the angular momentum of the doped nanodroplet. The angular momentum of neon can induce vortex nucleation if the initial angular momentum is high enough (in the interval of ∼176.3–220.3 ℏ) and the vortex (vortex line) can be long-lived. Thus, the vortex, which arises from the collapse of surface excitations (ripplons), can exist during three–four initial Ne atom rebounds against the HeND surface and then be successively created and destructed during the following rebounds. Finally, it is worth noting that at zero angular momentum quantum effects are not important under the initial pickup conditions explored in this work.
In spite of the limited information available, it has also been possible to carry out a comparative analysis on the solvation of impurities by superfluid helium. In this analysis the Ne, Ar, Xe, Rb+, Cs+ and Ba+ dopant species have been considered, under different initial conditions, and the large diversity of behaviours that can be found in the solvation process has been shown.
More theoretical and experimental efforts are desirable in order to obtain a deeper insight into the dynamics of the capture process of atomic/molecular species by superfluid helium nanodroplets, particularly in order to better understand the vortex formation process.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
The comparison between the angular momentum results calculated using the quantum operator![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z acting on the helium wave function and the classical expression considering the helium “quantum velocity” field is carried out below.
z acting on the helium wave function and the classical expression considering the helium “quantum velocity” field is carried out below.
The expected value of the k-component of the angular momentum is given by
 | (a1) |
Then, introducing the “quantum velocity” definition from a hydrodynamic analogy (as it was calculated the helium velocity field), it follows that the velocity is equal to
 | (a2) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the flux, and introducing
) is the flux, and introducing  into eqn (a1) we get
into eqn (a1) we get | (a3) |
And since the angular momentum operator is Hermitian:
 | (a4) |
 | (a5) |
Acknowledgements
This work has been supported by the Spanish Ministry of Science and Innovation (projects ref. CTQ2011-27857-C02-01 and MDM-2017-0767) and by the University of Barcelona (Theoretical Chemistry Institute (IQTC) and Faculty of Chemistry). M. B.-J. acknowledges the University of Barcelona for a PhD research grant. We also want to acknowledge some support from the Autonomous Government of Catalonia (projects ref. 2014SGR 25, 2017SGR 348 and XRQTC).References
- J. P. Toennies and A. F. Vilesov, Superfluid helium droplets: a uniquely cold nanomatrix for molecules and molecular complexes, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- M. Barranco, R. Guardiola, S. Hernández, J. Navarro, M. Pi and R. Mayol, Helium nanodroplets: an overview, J. Low Temp. Phys., 2006, 142, 1–81 CrossRef CAS.
- F. Ancilotto, M. Barranco, F. Coppens, J. Eloranta, N. Halberstadt, A. Hernando, D. Mateo and M. Pi, Density functional theory of doped superfluid liquid helium and nanodroplets, Int. Rev. Phys. Chem., 2017, 36, 621–707 Search PubMed.
- S. Goyal, D. L. Schutt and G. Scoles, Vibrational spectroscopy of sulfur hexafluoride attached to helium clusters, Phys. Rev. Lett., 1992, 69, 933–936 CrossRef CAS PubMed.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. F. Vilesov, High-resolution molecular spectroscopy of van der Waals clusters in liquid helium droplets, Science, 1996, 272, 1631–1634 CrossRef CAS PubMed.
- A. Vilà, M. González, R. Mayol and M. Paniagua, Theoretical approach to the structure, energy and electronic spectroscopy of O@(4He)N doped nanodroplets, RSC Adv., 2014, 4, 44972–44979 RSC.
- E. Lugovoj, J. P. Toennies and A. F. Vilesov, Manipulating and enhancing chemical reactions in helium droplets, J. Chem. Phys., 2000, 112, 8217–8220 CrossRef CAS.
- G. E. Douberly and R. E. Miller, The growth of HF polymers in helium nanodroplets:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) probing the barriers to ring insertion, J. Phys. Chem. B, 2003, 107, 4500–4507 CrossRef CAS.
probing the barriers to ring insertion, J. Phys. Chem. B, 2003, 107, 4500–4507 CrossRef CAS. - S. A. Krasnokutski and F. Huisken, Low-temperature chemistry in helium droplets: reactions of aluminum atoms with O2 and H2O, J. Phys. Chem. A, 2011, 115, 7120–7126 CrossRef CAS PubMed.
- S. Yang and A. M. Ellis, Helium droplets: a chemistry perspective, Chem. Soc. Rev., 2013, 42, 472–484 RSC.
- A. Vilà, M. González and R. Mayol, Photodissociation dynamics of homonuclear diatomic molecules in helium nanodroplets. The case of Cl2@(4He)N, J. Chem. Theory Comput., 2015, 11, 899–906 CrossRef PubMed.
- A. Vilà, M. González and R. Mayol, Quantum interferences in the photodissociation of Cl2(B) in superfluid helium nanodroplets (4He)N, Phys. Chem. Chem. Phys., 2015, 17, 32241–32250 RSC.
- A. Vilà, M. González and R. Mayol, Quantum dynamics of the pick up process of atoms by superfluid helium nanodroplets: the Ne + (4He)1000 system, Phys. Chem. Chem. Phys., 2016, 18, 2006–2014 RSC.
- A. Vilà, M. González and R. Mayol, Relaxation dynamics of helium nanodroplets after photodissociation of a dopant homonuclear diatomic molecule. The case of Cl2@(4He)N, Phys. Chem. Chem. Phys., 2016, 18, 2409–2416 RSC.
- A. Vilà and M. González, Mass effects in the photodissociation of homonuclear diatomic molecules in helium nanodroplets: inelastic collision and viscous flow energy exchange regimes, Phys. Chem. Chem. Phys., 2016, 18, 27630–27638 RSC.
- A. Vilà and M. González, Reaction dynamics inside superfluid helium nanodroplets: the formation of the Ne2 molecule from Ne + Ne@(4He)N, Phys. Chem. Chem. Phys., 2016, 18, 31869–31880 RSC.
- J. Tiggesbäumker and F. Stienkemeier, Formation and properties of metal clusters isolated in helium droplets, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC.
- T. Döppner, T. Diederich, S. Göde, A. Przystawik, J. Tiggesbäumer and K. H. Meiwes-Broer, Ion induced snowballs as a diagnostic tool to investigate the caging of metal clusters in large helium droplets, J. Chem. Phys., 2007, 126, 244513 CrossRef PubMed.
- S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binnis, Growing metal nanoparticles in superfluid helium, Nanoscale, 2013, 5, 11545–11553 RSC.
- L. F. Gomez, E. Loginov and A. F. Vilesov, Traces of vortices in superfluid helium droplets, Phys. Rev. Lett., 2012, 108, 155302 CrossRef PubMed.
- E. Latimer, D. Spence, C. Feng, A. Boarwright, A. M. Ellis and S. Yang, Preparation of ultrathin nanowires using superfluid helium droplets, Nano Lett., 2014, 14, 2902–2906 CrossRef CAS PubMed.
- A. Slenczka and J. P. Toennies, in Low Temperature and Cold Molecules, ed. I. W. M. Smith, Imperial College Press, London, 2008, pp. 345–392 Search PubMed.
- A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets I: kinetic energy transfer, J. Chem. Phys., 2007, 127, 114303 CrossRef PubMed.
- A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets. II. solvation dynamics, J. Chem. Phys., 2007, 127, 114304 CrossRef PubMed.
- A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets. III. recombination, J. Chem. Phys., 2007, 127, 114305 CrossRef PubMed.
- S. A. Krasnokutski and F. Huisken, Ultra-low-temperature reactions of Mg atoms with O2 molecules in helium droplets, J. Phys. Chem. A, 2010, 114, 7292–7300 CrossRef CAS PubMed.
- T. Takayanagi and M. Shiga, Photodissociation of Cl2 in helium clusters: an application of hybrid method of quantum wavepacket dynamics and path integral centroid molecular dynamics, Chem. Phys. Lett., 2003, 372, 90–96 CrossRef CAS.
- A. Vilà, M. Paniagua and M. González, Vibrational energy relaxation dynamics of diatomic molecules inside superfluid helium nanodroplets. The case of the I2 molecule, Phys. Chem. Chem. Phys., 2018, 20, 118–130 RSC.
- A. Scheidemann, J. P. Toennies and J. A. Northby, Capture of neon atoms by 4He clusters, Phys. Rev. Lett., 1990, 64, 1899–1902 CrossRef CAS PubMed.
- M. Lewerenz, B. Schilling and J. P. Toennies, Successive capture and coagulation of atoms and molecules to small clusters in large liquid helium clusters, J. Chem. Phys., 1995, 102, 8191–8207 CrossRef CAS.
- F. F. Da Silva, P. Bartl, S. Denifl, O. Echt, T. D. Märk and P. Scheier, Argon clusters embedded in helium nanodroplets, Phys. Chem. Chem. Phys., 2009, 11, 9791–9797 RSC.
- H. Schoebel, P. Bartl, C. Leidlmair, S. Denifl, O. Echt, T. D. Maerk and P. Scheier, High-resolution mass spectrometric study of pure helium droplets, and droplets doped with krypton, Eur. Phys. J. D, 2011, 63, 209–214 CrossRef CAS.
- M. Ratschek, M. Koch and W. E. Ernst, Doping helium nanodroplets with high temperature metals: formation of chromium clusters, J. Chem. Phys., 2012, 136, 104201 CrossRef PubMed.
- F. Lindebner, A. Kautsch, M. Koch and W. E. Ernst, Laser ionization and spectroscopy of Cu in superfluid helium nanodroplets, Int. J. Mass Spectrom., 2014, 365–366, 255–259 CrossRef CAS PubMed.
- P. L. Raston, J. Agarwal, J. M. Turney, H. F. Schaefer III and G. E. Douberly, The ethyl radical in superfluid helium nanodroplets: rovibrational spectroscopy and ab initio computations, J. Chem. Phys., 2013, 138, 194303 CrossRef PubMed.
- T. Premke, E.-M. Wirths, D. Pentlehner, R. Riechers, R. Lehnig, A. Vdovin and A. Slenczka, Microsolvation of molecules in superfluid helium nanodroplets revealed by means of electronic spectroscopy, Front. Chem., 2014, 2, 51 Search PubMed.
- H. Schöbel, C. Leidlmair, P. Bartl, S. Denifl, T. D. Märk, O. Echt and P. Scheier, Electron ionization of superfluid helium nanodroplets doped with C60 and small molecules, J. Phys.: Conf. Ser., 2012, 388, 012044 CrossRef.
- A. Scheidmann, B. Shilling, J. P. Toennies and J. A. Northby, Capture of foreign atoms by helium clusters, Phys. B, 1990, 165, 135–136 CrossRef.
- D. Eichenauer, A. Scheidemann and J. P. Toennies, Liquid drop and optical model calculations of elastic, vibrationally inelastic and absorptive scattering of 4He atoms from 4Hen-clusters, Z. Phys. D: At., Mol. Clusters, 1988, 8, 295–304 CrossRef CAS.
- J. P. Toennies and A. F. Vilesov, Novel low-energy vibrational states of foreign particles in fluid 4He clusters, Chem. Phys. Lett., 1995, 235, 596–603 CrossRef CAS.
- K. K. Lehmann, Potential of a neutral impurity in a large 4He cluster, Mol. Phys., 1999, 97, 645–666 CrossRef CAS.
- E. Krotscheck and R. Zillich, Scattering of 3He atoms from 4He surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 5707–5718 CrossRef CAS.
- E. Krotscheck and R. Zillich, Dynamics of atom scattering from 4He nanoclusters, Eur. Phys. J. D, 2007, 43, 113–116 CrossRef CAS.
- E. Krotscheck and R. Zillich, Hydrogen and 3He atoms on 4He surfaces: bound states and scattering features, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094507 CrossRef.
- A. Leal, D. Mateo, A. Hernando, M. Pi and M. Barranco, Capture of heliophobic atoms by 4He nanodroplets: the case of cesium, Phys. Chem. Chem. Phys., 2014, 16, 23206–23213 RSC.
- F. Coppens, A. Leal, M. Barranco, N. Halberstadt and M. Pi, Head-on collisions of Xe atoms against superfluid 4He nanodroplets, J. Low Temp. Phys., 2017, 187, 439–445 CrossRef CAS.
- F. Coppens, F. Ancilotto, M. Barranco, N. Halberstadt and M. Pi, Capture of Xe and Ar atoms by quantized vortices in 4He nanodroplets, Phys. Chem. Chem. Phys., 2017, 19, 24805–24818 RSC.
- A. W. Hauser, A. Volk, P. Thaler and W. E. Ernst, Atomic collisions in suprafluid helium-nanodroplets: timescales for metal-cluster formation derived from He-density functional theory, Phys. Chem. Chem. Phys., 2015, 17, 10805–10812 RSC.
- F. Dalfovo, A. Lastri, L. Pricaupenko, S. Stringari and J. Treiner, Structural and dynamical properties of superfluid helium: a density-functional approach, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1193–1209 CrossRef CAS.
- F. Ancilotto, M. Barranco, F. Caupin, R. Mayol and M. Pi, Freezing of 4He and its liquid–solid interface from density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214522 CrossRef.
- N. B. Brauer, S. Smolarek, E. Loginov, D. Mateo, A. Hernando, M. Pi, M. Barranco, W. J. Buma and M. Drabbles, Critical Landau velocity in helium nanodroplets, Phys. Rev. Lett., 2013, 111, 153002 CrossRef PubMed.
- D. Mateo, A. Hernando, M. Barranco, E. Loginov, M. Drabbels and M. Pi, Translational dynamics of photoexcited atoms in 4He nanodroplets: the case of silver, Phys. Chem. Chem. Phys., 2013, 15, 18388–18400 RSC.
- D. Mateo, F. Gonzalez and J. Eloranta, Rotational superfluidity in small helium droplets, J. Phys. Chem. A, 2015, 119, 2262–2270 CrossRef CAS PubMed.
- S. M. Cybulski and R. R. Toczylowski, Ground state potential energy curves for He2, Ne2, Ar2, He–Ne, He–Ar, and Ne–Ar: a coupled-cluster study, J. Chem. Phys., 1999, 111, 10520–10528 CrossRef CAS.
- A. Ralston, in Mathematical methods for digital computers, ed. A. Ralston and H. S. Wilf, John Wiley & Sons, New York, 1960, vol. 1, pp. 95–109 Search PubMed.
- R. J. Thompson, Improving round-off in Runge–Kutta computations with Gill's method, Commun. ACM, 1970, 13, 739–740 CrossRef.
- M. Frigo and S. G. Johnson, The design and implementation of FFTW3, Proc. IEEE, 2005, 93, 216–231 Search PubMed.
- Á. Vibók and G. G. Balint-Kurti, Parametrization of complex absorbing potentials for time-dependent quantum dynamics, J. Phys. Chem., 1992, 96, 8712–8719 CrossRef.
- D. R. Tilley and J. Tilley, Condensates and excitations. Superfluidity and superconductivity, Institut of Physics Publishing, Bristol, 1990, pp. 41–53 Search PubMed.
- J. F. Annet, Superfluid helium-4. Superconductivity, superfluids and condensates, Oxford University Press, Oxford, 2004, pp. 38–43 Search PubMed.
- A. Leal, D. Mateo, A. Hernando, M. Pi, M. Barranco, A. Ponti, F. Cargnoni and M. Drabbels, Picosecond solvation dynamics of alkali cations in superfluid 4He nanodroplets, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224518 CrossRef.
- E. Loginov and M. Drabbels, Dynamics of excited sodium atoms attached to helium nanodroplets, J. Phys. Chem. A, 2014, 118, 2738–2748 CrossRef CAS PubMed.
- M. Renzler, M. Daxner, L. Kranabetter, A. Kaiser, A. W. Hauser, W. E. Ernst, A. Lindinger, R. Zillich, P. Scheier and A. M. Ellis, Dopant-induced solvation of alkalis in liquid helium nanodroplets, J. Chem. Phys., 2016, 145, 181101 CrossRef PubMed.
- D. Mateo, A. Leal, A. Hernando, M. Barranco, M. Pi, F. Cargnoni, M. Mella, X. Zhang and M. Drabbels, Nucleation of quantized vortex rings in 4He nanodroplets, J. Chem. Phys., 2014, 140, 131101 CrossRef PubMed.
- R. D. Levine, Molecular reaction dynamics, Cambridge University Press, Cambridge, 2005, pp. 91–94 Search PubMed.
- R. J. Donnelly, Quantized vortices in helium II, Cambridge University Press, Cambridge, 1991 Search PubMed.
- A. Bohr and B. R. Mottelson, Nuclear structure, W. A. Benjamin, INC., Advanced Book Program, Reading, Massachussets, USA, 1975, pp. 674–676 Search PubMed.
- G. M. Seidel and H. J. Maris, Morphology of superfluid drops with angular momentum, Phys. B, 1994, 194–196, 577–578 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1: Helium grids. Table S2: Propagation data. Table S3: HeND final ang. momenta. Fig. S1: Ne v0-distrib. at 300 K. Fig. S2: HeND radial density distrib. Fig. S3: He density vs. t (v0 = 500 m s−1, b = 14 Å). Fig. S4: αdvs. b and incidence angle (v0 = 500 m s−1). Fig. S5: Ne vx, vyvs. t (v0 = 500 m s−1). Fig. S6: Ne energies vs. t (v0 = 500 m s−1). Fig. S7: Energies and their time derivatives vs. t (v0 = 500 m s−1). Fig. S8: Kinetic energy transf. to HeND vs. b (v0 = 500 m s−1). Fig. S9: ENe + EHeNDvs. t (v0 = 500 m s−1). Fig. S10: Norm of HeND and E per He atom vs. t (v0 = 500 m s−1). Fig. S11: Time required to evaporate He atoms (v0 = 500 m s−1). Fig. S12: He density, velocity and wave function phase vs. t (v0 = 500 m s−1, b = 17 Å). Fig. S13: Angular momentum transferred to HeND vs. b and vs. LNe,0 and Ltrans/LNe,0vs. b (v0 = 500 m s−1). Fig. S14: HeND final ang. momentum radial distrib. vs. v0 and b. Movies 1–4: Helium density and wave function phase in the xy-plane vs. t (v0 = 500 m s−1, b = 0, 14 and 17 Å, and v0 = 800 m s−1, b = 14 Å, respectively). See DOI: 10.1039/c8cp05140b |
| This journal is © the Owner Societies 2018 |