Core electron binding energies of adsorbates on Cu(111) from first-principles calculations

Abstract

Core-level X-ray Photoelectron Spectroscopy (XPS) is often used to study the surfaces of heterogeneous copper-based catalysts, but the interpretation of measured spectra, in particular the assignment of peaks to adsorbed species, can be extremely challenging. In this study we present a computational scheme which combines the use of slab models of the surface for geometry optimization with cluster models for core electron binding energy calculation. We demonstrate that by following this modelling strategy first principles calculations can be used to guide the analysis of experimental core level spectra of complex surfaces relevant to heterogeneous catalysis. The all-electron ΔSCF method is used for the binding energy calculations. Specifically, we calculate core-level binding energy shifts for a series of adsorbates on Cu(111) and show that the resulting C1s and O1s binding energy shifts for adsorbed CO, CO₂, C₂H₄, HCOO, CH₃O, H₂O, OH, and a surface oxide on Cu(111) are in good overall agreement with the experimental literature.

---

1 Introduction

Metallic copper and copper nanoparticles play an important role in industrially relevant catalytic processes, such as the low-temperature water gas shift reaction^1–3 and the synthesis of methanol from CO₂ and H₂.^4–6 Considerable efforts have been directed towards understanding the mechanisms that operate in these systems and X-ray photoemission spectroscopy (XPS) has been the tool of choice in many experimental studies.^7–17 XPS is particularly attractive for the characterization of surfaces because it provides information about the elemental composition of the surface as well as the chemical states of the elements.

However, despite nearly forty years of research, many gaps remain in our understanding of the correspondence between features in the experimental XPS spectra and the composition of the sample surface. For example, O1s peaks at binding energies of 531.4 eV, 533.4 eV, 534.2 eV and 535.5 eV have been assigned to physisorbed CO₂ on Cu(111), polycrystalline Cu, Cu(211) and Cu(100), respectively.^12,18–20 It is surprising that the reported values differ by as much as 4 eV as physisorbed CO₂ is expected to interact only weakly with any of these surfaces. The situation is similar for many other species: for HCOO⁻ (formate) on Cu(111), C1s binding energies ranging from 287.3 eV to 289.8 eV have been reported,^13–15,21 and values between 288.2 eV and 291.0 eV have been assigned to the C1s peak of “surface carbonates” on various copper surfaces.^8,20,21 Importantly, the reported binding energy ranges for these species also overlap with reported binding energies of “chemisorbed CO₂” which range from 287.9 eV to 289.8 eV.^8,9,12,15,19 This clearly shows that there is a need for additional insights to analyze and interpret experimental photoemission spectra of adsorbed species on Cu surfaces.

First-principles calculations based on density-functional theory (DFT) or the GW approach are routinely used to guide the interpretation of valence electron photoemission spectra.^22–27 In contrast, the vast majority of experimental core-level photoemission spectra are currently interpreted without the aid of computational simulation of the spectroscopic process. For example, none of the twenty experimental XPS studies of Cu surfaces that we reviewed when writing the manuscript used comparisons to theoretical core level binding energies to guide peak fitting.^{7–21,28–32} However, a number of approaches for calculating core level bindings energies have been developed over the years, including the frozen-orbital method,³³ the Z + 1 approximation,³⁴ the Slater–Janak transition state method,^35–39 the GW method⁴⁰ and the ΔSCF scheme.^41–44

In the ΔSCF scheme, the core-level binding energy is calculated as the total energy difference between the ground state and the fully screened final state. Benchmark calculations on molecular systems indicate that ΔSCF calculations based on DFT yield binding energies shifts within 0.3 eV of the experimental values.^41–43 This accuracy is significantly higher than reported binding energy ranges for many adsorbates on Cu surfaces and therefore insights from theoretical calculations should be very useful for the interpretation of experimental core level spectra.

To calculate core-level binding energies of adsorbates on surfaces, ΔSCF calculations have been performed on clusters containing the adsorbate and a number of surface atoms.^45–49 Importantly, the cluster size in such a calculation must be sufficiently large to adequately capture the bonding of the adsorbate to the surface as well as the screening of the core hole in the final state. Because of the rapid increase of the computational expense with cluster size, previous calculations often employed very small clusters containing only a few atoms,⁴⁹ or slightly larger clusters containing up to 30 atoms.^46–48

In this paper we use the ΔSCF method to calculate core–electron binding energies of various adsorbed species on Cu(111), which is the lowest energy surface of metallic copper. The calculations are performed in two stages: firstly, the geometries of the adsorbates are relaxed using a slab model of the Cu(111) surface. Secondly, a cluster comprising 88 Cu atoms and the adsorbate is cut from the slab, and the core electron binding energy is calculated using the all-electron ΔSCF method. The use of a cluster model for the ΔSCF calculation, in contrast to a periodic model of the surface, avoids the need to introduce a compensating background charge in the calculation of the total energy of the final state. We pay particular attention to the convergence of our results and carry out a series of tests to establish that the chosen cluster size, basis set and exchange–correlation functional are appropriate to obtain binding energy shifts with an accuracy of ∼0.3 eV or better. We compare our calculated C1s and O1s binding energy shifts for CO, CO₂, ethene, formate, methoxy, water, OH, and a surface oxide on Cu(111) in detail with the available experimental literature and discuss the implications of our theoretical results on the interpretation of experimental spectra.

2 Computational details

The results of previously published experimental and theoretical studies of the adsorption of CO,^50,51 CO₂,^52–54 C₂H₄,⁵⁵ H₂O,^56–59 HCOO⁻,^13,29 CH₃O^−30,60,61 and OH⁻⁵⁶ on Cu(111), as well as the study of Lian et al. on the formation of surface oxides on low-index Cu surfaces,⁶² were used to build the structural models of the adsorbates on a Cu(111) slab used for geometry relaxation. For the case of adsorbed water, we have considered two distinct models: an isolated H₂O molecule on Cu(111) and an H₂O molecule hydrogen bonded to two other surface H₂O molecules, with a similar local environment to what is found in water hexamers on Cu(111).^58,59 For the case of adsorbed CO, we have considered two distinct adsorption sites: the “top” site, directly above a surface Cu atom, and the “three-fold” site, in the valley between three surface Cu atoms (see Fig. 1 and ESI† Fig. S2). The Cu slabs were cut with the (111) faces exposed and are four atomic layers thick. In order to minimize the interactions between periodic images, the slabs were built from orthorhombic supercells with a total of 64 Cu atoms per cell, except for the case of the surface oxide for which a 4 × 4 supercell of the hexagonal Cu(111) surface unit cell was used.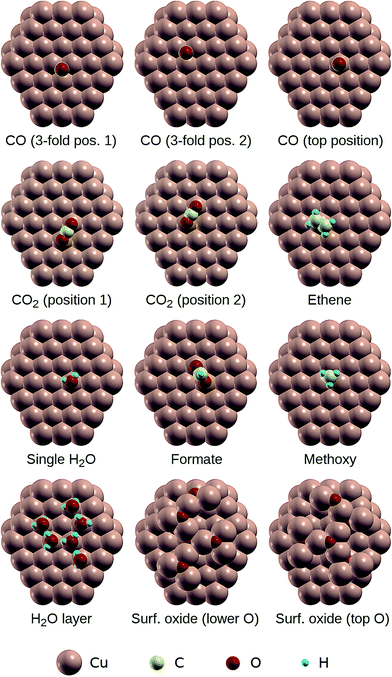

Fig. 1 The clusters used for the calculation of core level binding energies of adsorbates on Cu(111).

The structures were relaxed until the forces on the atoms were less than 10⁻³ Ry bohr⁻¹ and the total energy change between the last two optimization steps was less than 10⁻⁴ Ry. These calculations were carried out using DFT as implemented in the Quantum Espresso software package,⁶³ which employs a plane-wave basis set. Cut-off energies of 40 Ry and 200 Ry were used for the wavefunctions and the charge density, respectively, and the interaction between core and valence electrons is described via ultrasoft pseudopotentials from the Garrity–Bennett–Rabe–Vanderbilt (GBRV) Pseudopotential Library.⁶⁴ The slabs were separated by ∼14 Å of vacuum and a dipole correction⁶⁵ was used to minimize spurious interactions between adjacent layers. We employed the PBE exchange–correlation functional⁶⁶ with the Grimme-D2 correction to capture the effect of van der Waals interactions.⁶⁷ The relaxed geometries are shown in ESI† Fig. S2 and the corresponding atomic positions are also provided in the ESI.†

Using the relaxed structures, photoelectron binding energies were calculated using the ΔSCF approach, i.e. as the total energy difference between the ground state and the ionized state where one electron is removed from a core orbital. This corresponds to the assumption of a fully screened core hole. For these calculations, clusters comprising 88 Cu atoms and the adsorbate were cut from the slabs, such that the adsorbed species sits approximately at the centre of the top (111) face. The geometries of the adsorbed species on the clusters are illustrated in Fig. 1 and the corresponding atomic positions are provided in ESI.†

The total energies of the clusters were calculated using DFT with a Gaussian orbital basis set as implemented in the all-electron quantum chemistry code NWChem.⁶⁸ For simulating the final states, an explicit core hole was generated by constraining the occupancy of one of the core orbitals, whilst all other electrons were allowed to relax in the presence of the core hole. The basis sets used in the cluster calculations are provided in the ESI.† Briefly, effective core potentials with the associated basis sets from ref. 69 were used for the Cu atoms with the following modifications: for the Cu atoms in the top layer, the exponents of the two most diffuse sp-type basis functions were increased to 0.1619 and 0.074, respectively; for the Cu atoms which are not in the top layer, the sp-type basis function with the smallest exponent was removed and the exponent of the sp-type basis function with the second smallest exponent was reduced to 0.1119. These changes were required to prevent numerical instabilities during the self-consistent field procedure. The pcseg-2 all-electron basis sets developed by Jensen⁷⁰ were used for the light elements H, C and O, except for the atoms with a core hole, for which a special basis set with uncontracted core orbitals was used (derived from the pcJ-3_2006 basis sets from ref. 71), in order to allow full relaxation of the other electrons on the same atom in the presence of a core hole. All ΔSCF calculations of Cu(111) clusters with adsorbates were carried out using the PBE exchange–correlation functional.

The UK national supercomputer ARCHER was used for the geometry optimizations as well as the cluster calculations. The geometry optimization runs took approximately 6 hours per adsorbate on 8 nodes with two 12-core Intel Xeon E5-2697 v2 processors per node. For each core hole the total energy calculations of the ground state and the final state took approximately 9 hours on 16 nodes each.

In order to assess the accuracy of our calculations, additional C1s binding energy calculations were carried out for the free molecules CH₄, C₂H₆, CO, CO₂, CCl₄, and CF₄, and the O1s binding energy was calculated for H₂O, CO, CO₂, CH₃OH, and HCOOH (both O sites). In these calculations both the initial structure relaxation as well as the subsequent ΔSCF calculation were carried out using both the M06 hybrid functional⁷² as well as PBE.⁶⁶

When there are equivalent atoms in the molecule, it is necessary to manually break the symmetry in order to localize the core hole at one of them.⁷³ In this work, this was achieved by introducing a fictitious additional atomic charge of +0.1 e (with e being the proton charge) at that site only for the initialization of the Kohn–Sham wavefunctions (the additional charge was removed immediately afterwards). The same procedure was used to guide the core hole to the desired site in molecules with multiple inequivalent atoms of the same element. A basis set with uncontracted core wavefunctions was only used for the atom with a core hole.

3 Results: tests

To assess the accuracy of our calculations for core-level binding energies of adsorbates on Cu(111) surfaces, we have carried out test calculations of (i) core–electron binding energies of free molecules, (ii) core–electron binding energies of adsorbed small molecules at different quasi-equivalent adsorption sites on the Cu₈₈ cluster, (iii) core–electron binding energies of adsorbed small molecules ona smaller Cu₄₂ cluster, and (iv) the density of states (DOS) of the Cu₈₈ cluster and bulk Cu metal.

The results of the calculations on free molecules are summarized in Table 1 and Fig. 2. The theoretical binding energy shifts (referenced to methane for the C1s core level and methanol for the O1s core level) have been compared to experimental values compiled by Cavigliasso.⁴¹ Good agreement between theory and experiment is found for both functionals, with M06 performing somewhat better than PBE: the mean unsigned errors are 0.08 eV and 0.13 eV for M06 and PBE, respectively, and the maximum errors are 0.23 eV (C1s binding energy of CO) for M06 and 0.79 eV (C1s binding energy of CF4) for PBE. Despite the small quantitative difference with the M06 results, the results obtained with PBE are sufficiently accurate to interpret experimental spectra. It is also possible to compare the absolute values of the theoretical binding energies to the experimental data for the free molecules, and for the C1s and O1s core levels considered in this work, we find that the values agree to within ∼0.3% for M06 and ∼0.5% for PBE. These results are in line with previous DFT-ΔSCF calculations of core electron binding energies in free molecules.^41–44

Table 1 A comparison between experimental and theoretical core level binding energy shifts in free molecules

Atom^a	Exp. B.E.^b	Exp. shift	M06 shift	M06 error	PBE shift	PBE error
a Bold typeface is used to indicate the position of the core hole. b All experimental values are taken from ref. 41. All energies are given in eV.
C 2H6	290.72	−0.12	−0.13	−0.01	−0.13	−0.01
CH4	290.84	0	0	0	0	0
CO	296.21	5.37	5.60	0.23	5.37	0.00
CCl4	296.36	5.52	5.58	0.06	5.48	−0.04
CO2	297.69	6.85	6.97	0.12	6.35	−0.50
CF4	301.89	11.05	11.04	−0.01	10.26	−0.79
HCO(OH)	538.97	−0.14	−0.28	−0.14	−0.25	−0.11
CH3OH	539.11	0	0	0	0	0
H2O	539.90	0.79	0.64	−0.15	0.77	−0.02
HCO(OH)	540.63	1.52	1.66	0.14	1.58	0.06
CO2	541.28	2.17	2.22	0.05	2.19	0.02
CO	542.55	3.44	3.37	−0.07	3.49	0.05

---

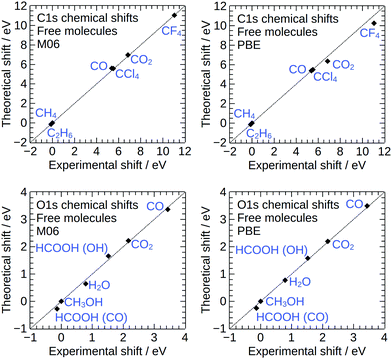Fig. 2 Theoretical core level binding energy shifts for free molecules, plotted against the corresponding experimental shifts from gas phase measurements.⁴¹

Next, we calculated the C1s and O1s binding energies for the CO and CO₂ molecules adsorbed at two different adsorption sites on the top surface of the Cu₈₈ cluster that are equivalent with respect to the underlying lattice, but distinguishable by their position relative to the finite sized cluster, see Fig. 1. Large differences in the obtained binding energies at different quasi-equivalent sites on the cluster surface would indicate that the calculated values are strongly affected by finite size effects. The results of these tests are shown in Table 2. Amongst the tested positions, the calculated binding energies vary by less than 0.05 eV indicating that finite-size effects are small.

Table 2 Theoretical C1s and O1s core-level binding energies of CO and CO₂ molecules adsorbed on different quasi-equivalent sites of a Cu₈₈ cluster (see Fig. 1)

Species	C1s ΔSCF (eV)	O1s ΔSCF (eV)
CO (3-fold pos. 1)	289.32	534.81
CO (3-fold pos. 2)	289.32	534.80
CO2 (pos. 1)	292.85	537.53 (O1)
		537.51 (O2)
CO2 (pos. 2)	292.83	537.53 (O1)
		537.52 (O2)

---

To further probe the magnitude of finite size effects, we also calculated the C1s and O1s binding energies for adsorbed CO and CO₂ on a smaller Cu₄₂ cluster shown in Fig. 3. The results are shown in Table 3. The absolute values of the binding energies obtained on Cu₄₂ are approximately 0.25–0.5 eV higher than for Cu₈₈, most likely due to the poorer screening of the core hole in the final state by the conduction electrons of the smaller metal cluster. This effect is partly cancelled out when binding energy shifts are considered, which differ by no more than 0.2 eV in the tested cases.

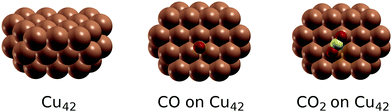Fig. 3 The Cu₄₂ cluster used to test the dependence of calculated core electron binding energies on cluster size, and the adsorption geometries of CO and CO₂ on Cu₄₂.

Table 3 Theoretical C1s and O1s core-level binding energies of CO and CO₂ molecules adsorbed on different sized Cu clusters

Core level	Cluster	CO2 ΔSCF (eV)	CO ΔSCF (eV)	CO2–CO shift (eV)
C1s	Cu88	292.84	289.32	3.52
C1s	Cu42	293.11	289.79	3.32
O1s	Cu88	537.52	534.80	2.72
O1s	Cu42	537.78	535.09	2.69

---

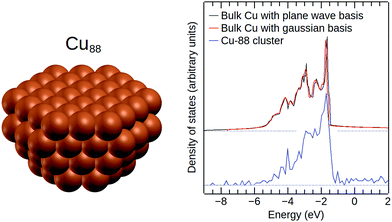
Finally, in order to verify that the effective core potential and the Gaussian basis set from ref. 69 are suitable for simulations of metallic Cu, we calculated the DOS of bulk Cu using this basis set and the CRYSTAL14 software package.⁷⁴Fig. 4 shows that the resulting DOS is in excellent agreement with the DOS of bulk Cu obtained from plane-wave DFT. For comparison, we have also included the DOS of the bare Cu₈₈ cluster in Fig. 4.

Fig. 4 Left: The Cu₈₈ cluster used for the ΔSCF calculations. Right: The density of states of bulk Cu calculated using a plane-wave basis set, bulk Cu calculated using a Gaussian basis set and of the Cu₈₈ cluster. The curve of Cu₈₈ has been offset for clarity. The energies are referenced to the respective calculated Fermi energies.

4 Results: adsorbates on Cu(111)

The results of the C1s and O1s binding energy calculations for the various adsorbed species on Cu(111) are compared to experimental data in Fig. 5 and 6 and in Tables 4 and 5. Whenever possible, we compare our results to measured binding energies of adsorbates on Cu(111). However, because of the limited availability of experimental data for this surface, we also compare to results obtained on other Cu surfaces as well as polycrystalline Cu.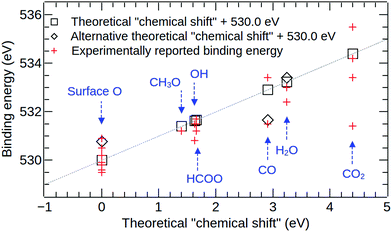

Fig. 5 A comparison of calculated and experimental O1s binding energy shifts for various surface species on copper. For the surface oxide, the square indicates the theoretical value obtained for the higher (surface) oxygen site, and the diamond shows the value for the lower (buried) oxygen site. For CO, the square indicates the theoretical value obtained for the “top” adsorption site, and the diamond shows the value for the “3-fold” site. For water, the square indicates the theoretical value obtained for a surface water molecule hydrogen bonded to two other water molecules, and the diamond shows the value for an isolated water molecule on Cu(111). Full details and references for the experimental datapoints are given in Table 4.

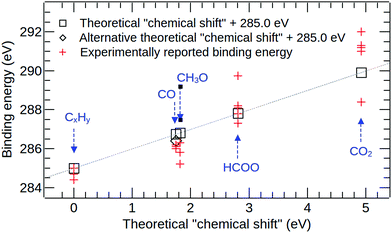Fig. 6 A comparison of calculated and experimental C1s binding energy shifts for various surface species on copper. For CO, the square indicates the theoretical value obtained for the “top” adsorption site, and the diamond gives the value for the “3-fold” site. Full details and references for the experimental datapoints are given in Table 5.

Table 4 A summary of the results of O1s binding energy shift calculations of various adsorbates on Cu(111), as well as the surface oxide

Exp. species	Ref.	Exp. B.E.^a	Exp. shift	Theor. species	Theor. shift
a All energies are given in eV.
Subsurface O on Cu(111)	12	529.80	−0.20	Surf-ox./Cu88	0.0 (top O)
Oxide on Cu(111)	32	530.50	0.50
Surface O on Cu(111)	16	530.90	0.90
Surface O on Cu(111)	12	531.00	1.00
Chemisorbed oxygen on Cu(211)	19	529.50	−0.50
Adsorbed oxygen on Cu(110)	21	529.60	−0.40		0.78 (lower O)
Surface O on suboxidic CuxO	12	529.60	−0.40
Chemisorbed O on Cu(poly)	8	529.80	−0.20
Cu2O	16	529.90	−0.10
Cu2O	8	530.20	0.20
Methoxy on Cu(110)	21	531.20	1.20	CH3O/Cu88	1.40
OH on Cu(111)	9	531.50	1.50	OH/Cu88	1.63
OH on Cu(poly)	8	530.80	0.80
Formate on Cu(111)	13 and 14	531.5	1.50	HCOO/Cu88	1.66
Formate on Cu(110)	21	531.20	1.20
HCOO^− on cold deposited Cu film	15	531.7	1.70
CO on Cu(111)	7	531.50	1.50	CO/Cu88	1.67 (3-fold site)
CO on Cu(111)	9	533.40	3.40		2.91 (top site)
Adsorbed H2O on Cu(111)	32	533.00	3.00	H2O/Cu88	3.41
H2O on Cu(111)	12	532.40	2.40
H2O on Cu(poly)	8	533.00	3.00	H2O-layer/Cu88	3.24
Physisorbed CO2 on Cu(111)	12	531.40	1.40	CO2/Cu88	4.39
Physisorbed CO2 on Cu(poly)	18	533.40	3.40
Monolayer physisorbed CO2 on Cu(211)	19	534.20	4.20
Physisorbed CO2 on Cu(100)	20	535.50	5.50

---

Table 5 A summary of the results of C1s binding energy shift calculations of various adsorbates on Cu(111)

Exp. species	Ref.	Exp. B.E.^a	Exp. shift	Theor. species	Theor. shift
a All energies are given in eV.
Graphitic carbon on Cu(111)	12	284.50	−0.50	C2H4/Cu88	0.00
sp^3 carbon on Cu(111)	12	285.20	0.20
CxHy on Cu(111)	9	285.00	0.00
C^0 species on Cu(poly)	8	284.40	−0.60
Carbon contamination on Cu(poly)	8	284.70	−0.30
C^0 on Cu(poly)	19	285.00	0.00
Graphitic carbon on Cu(100)	20	285.00	0.00
CO on Cu(111)	7	286.10	1.10	CO/Cu88	1.40 (3-fold site)
CO on Cu(111)	9	286.20	1.20
Carbonyl carbon	19	286.00	1.00		1.75 (top site)
C–O(H) bonds on Cu(111)	12	286.30	1.30	CH3O/Cu88	1.82
Methoxy on Cu(110)	21	285.80	0.80
Methoxy on Cu(poly)	8	285.20	0.20
HCOO^− on Cu(111)	12	287.30	2.30	HCOO/Cu88	2.81
Formate on Cu(111)	13 and 14	288.20	3.20
HCOO on Cu(111)	29	289.75	4.75
Formate on Cu(poly)	8	287.30	2.30
Formate on Cu(110)	21	287.80	2.80
HCOO^− on cold deposited Cu film	15	288.10	3.10
Physisorbed CO2 on Cu(111)	12	288.40	3.40	CO2/Cu88	4.92
Monolayer physisorbed CO2 on Cu(poly)	19	291.00	6.00
Physisorbed CO2 on Cu(poly)	18	291.30	6.30
Monolayer physisorbed CO2 on Cu(211)	19	291.50	6.50
Physisorbed CO2 on Cu(100)	20	292.00	7.00

---

Fig. 5 and Table 4 show good overall agreement between the calculated O1s binding energy shifts and experimental measurements. In our calculations, the top O atoms in the surface oxide structure, see Fig. 1, exhibit the smallest binding energy and we use this energy as reference for all O1s binding energy shifts. The binding energy shift of the lower O atom in the surface oxide is 0.78 eV. To compare this result to experimental data, we have grouped together all peak assignments that are referred to as “adsorbed oxygen”, “oxygen adatom” or “surface oxide” in the experimental literature, see Table 4. The corresponding experimental binding energy shifts are calculated relative to a reference energy of 530.0 eV and range from −0.50 to +1.00 eV.^{8,12,16,19,21,32} For an adsorbed methoxy (CH₃O) group we obtain a binding energy shift of 1.40 eV in good agreement with the experimental result of 1.20 eV for methoxy on Cu(110).²¹ The calculated binding energy shifts of adsorbed hydroxyl (OH) and formate (HCOO) are 1.63 eV and 1.66 eV, respectively, in very good agreement with the measured values of 1.50 eV for OH on Cu(111)⁹ and 1.50 eV for formate on Cu(111).^13,14

For the case of CO on Cu(111), it is important to note that the top adsorption site is found to be the most favourable one by experiment⁷⁵ and also in calculations using the DFT+U method,⁵¹ hybrid functionals⁷⁶ and the Random Phase Approximation (RPA).⁷⁷ In contrast, standard functionals based on the Generalized Gradient Approximation (GGA) predict adsorption at the 3-fold site to be most stable.^78,79 In our calculations, a core level binding energy shift of 2.91 eV is obtained for the molecule on the top site, whereas a value of 1.67 eV is obtained for the molecule at the three-fold site. The value obtained for the top site is in reasonable agreement with the experimental value of 3.40 eV reported in ref. 9 for CO on the Cu(111) surface. In contrast, a much smaller binding energy shift of 1.5 eV has been reported in ref. 7, also for CO on Cu(111), and this value is similar to our calculated result for the three-fold site. Whilst this result might be interpreted to mean that both adsorption sites can be occupied under the measurement conditions, further work on this matter is desirable. In particular, we note that in addition to the aforementioned limitations of GGA functionals which we employ in our ΔSCF calculations in describing the adsorption of CO on Cu(111), Bagus et al. have recently shown that the limited ability of most exchange–correlation functionals to capture non-dynamic correlation effects is also manifested in ΔSCF calculations of the free CO molecule.^80,81

For H₂O on Cu(111), both the isolated molecule and the monolayer have similar binding energy shifts of 3.41 eV and 3.24 eV, respectively. Both of these values are in good agreement with the experimental studies that report a binding energy shift of 3.0 eV for adsorbed water on Cu.^8,32 Finally, CO₂ on Cu(111) exhibits the largest binding energy shift of 4.39 eV of all oxygen-containing molecules in our study. We find that this molecule is not chemically bonded to the surface. Experimental findings for O1s binding energies of physisorbed CO₂ on Cu surfaces range from 1.40 eV to 5.50 eV,^12,18–20 making it difficult to assess the agreement between theory and experiment. It is interesting to compare our results also to experimental measurements for physisorbed CO₂ on different metals as the binding energy shifts which are dominated by electrostatic image charge effects should only weakly depend on the chemical composition of the metal. In particular, O1s binding energy shifts of 4.7 eV and 5.0 eV have been reported for physisorbed CO₂ on Ni(110) and polycrystalline Fe, respectively.⁸² This, combined with the theoretical results, suggests that the peaks at much lower binding energies that have been assigned to physisorbed CO₂ on Cu may actually correspond to some other chemical environments.

The calculated C1s binding energy shifts are compared against the available experimental data in Fig. 6 and Table 5. In our calculations, adsorbed ethene is used as a model of “adventitious carbon”, and we use the C1s binding energy of this species as the reference for all theoretical C1s binding energy shifts. Experimental C1s binding energy shifts are calculated relative to a reference energy of 285.0 eV. In Fig. 6 and Table 5, we have grouped together all peak assignments that are referred to as “adventitious carbon”, “carbon contamination”, “graphitic carbon”, “C⁰” or “C_xH_y” in the experimental literature. The corresponding experimental binding energy shifts range from −0.6 eV to 0.2 eV.^8,9,12,19,20

For CO on Cu(111), the theoretical binding energy shift obtained for the 3-fold adsorption site (1.40 eV) is slightly closer to the experimental values reported for the (111) surface (1.1–1.2 eV)^7,9 than the theoretical value for the top site (1.75 eV). However, as discussed before, further work is required to assess the influence of the choice of exchange–correlation functional in the ΔSCF calculation on the core-level binding energy of CO on Cu(111). For the formate species, the theoretical binding energy of 2.81 eV agrees well with the majority of the published experimental values for formate on various Cu surfaces that range from 2.3 eV to 3.2 eV.^8,12–15,21 The outlier amongst the experimental datapoints (at 4.75 eV²⁹) is also the one that lies furthest from the calculated value. For methoxy on Cu(111), we note that unfortunately neither of the detailed photoelectron diffraction studies of this species^30,83 report the experimental C1s binding energy. The binding energy shift that has been reported for C–O(H) environments on Cu(111) (1.3 eV) is relatively similar to our calculated value for methoxy on Cu(111) (1.82 eV), whereas the shifts that have been reported for the methoxy species on Cu(110) and polycrystalline Cu (0.8 eV and 0.2 eV^8,21) are much smaller. However, we believe that all of these experimental values should be taken with a note of caution, because they come from studies where complex surface chemical processes were investigated,^8,12,21 making the interpretation of the experimental spectra extremely challenging.

For physisorbed CO₂ on Cu(111), we have obtained a theoretical C1s binding energy shift of 4.92 eV. Favaro et al.¹² have reported a binding energy shift of 3.4 eV for CO₂ on Cu(111), but the binding energy shifts reported for physisorbed CO₂ on other Cu surfaces and polycrystalline copper are significantly larger and range from 6.0 eV to 7.0 eV.^18–20 Similarly large shifts of 6.2 eV and 6.5 eV have been reported for physisorbed CO₂ on Ni(110) and polycrystalline iron,⁸² respectively. This suggests that the theoretical binding energy shift value of 4.92 eV is probably too low by approximately 1–2 eV. We note that in the calculations of free molecules, the C1s binding energy shift in CO₂ is also underestimated by ∼0.5 eV when using the PBE functional, but this is not sufficient to explain the discrepancy of more than 1 eV for the adsorbed species. In order to account for the remaining part of the disagreement, we hypothesize that CO₂ molecules may not physisorb onto Cu as a uniform monolayer. In particular, since the adsorption energy for CO₂ on Cu (∼24 kJ mol^−1 53) is similar to the enthalpy of sublimation of solid CO₂ (∼26 kJ mol^−1 84), the formation of three-dimensional adsorbed clusters may be favourable even at monolayer or sub-monolayer coverage. For CO₂ molecules in adsorbed clusters, it is reasonable to expect that the O1s binding energy is higher than for a single adsorbed molecule because the screening of the core hole in the final state is weaker when the molecule is located further away from the metal surface. Alternatively, it is possible that physisorption at step or kink sites dominates under realistic conditions and that adsorbed molecules at these sites exhibit a different binding energy.

Finally, we note that we have not been able to calculate theoretical photoelectron binding energies for chemisorbed CO₂. In agreement with previous experimental^10,53,85,86 and theoretical^52,53 investigations we have found that CO₂ does not chemisorb on defect-free Cu(111), which is the surface that has been considered throughout this work. In fact, the theoretical calculations of Muttaqien et al. suggest that the chemisorption of CO₂ is also unfavourable on ideal stepped and kinked Cu surfaces that expose the Cu(111) face,⁸⁷ and very recently it has been proposed that the chemisorbed state can only occur on Cu(111) in the presence of sub-surface oxygen atoms.¹²

5 Conclusions

In this work, we have presented a computational scheme for the calculation of core level binding energy shifts in which a slab model of the surface is first used for optimizing the geometry of the adsorbate, and then the all electron ΔSCF method is applied to a cluster cut from the slab for the binding energy calculation. We have applied this scheme to the calculation of core-level binding energy shifts for various adsorbed molecules on Cu(111). For the majority of the studied adsorbates (H₂O, OH, HCOO, C₂H₄ and CO), the calculated binding energy shifts agree well with published experimental data. In the few cases where the agreement is less good (CH₃O, CO₂), further work is required to establish the origin of the discrepancy between the theoretical and the experimental results.

The ability to calculate core-level binding energy shifts from first principles is highly desirable due to the commonly encountered difficulties in the interpretation of experimental spectra. In particular, theoretical modelling may be the only practical way for estimating core-level binding energies of atoms in complex chemical environments, such as those that are formed under non-UHV conditions, under irradiation or in electrochemical setups.

On the other hand, the results presented in this work also highlight the difficulty of assessing the accuracy of a method for calculating XPS binding energy shifts for surface species which stems from the scarcity of reliable reference data. To make progress in this direction, it would be highly desirable to combine XPS measurements with other experimental techniques, such as scanning tunnelling microscopy or surface X-ray diffraction, to establish detailed structural models for several adsorbed species which could then inform first-principles calculations of core-level binding energies.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

J. M. K. and J. L. acknowledge support from EPRSC under Grant No. EP/R002010/1 and also from the Thomas Young Centre under Grant No. TYC-101. Via J. L.'s membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service.

References

1. D. Newsome, Catal. Rev.: Sci. Eng., 1980, 21, 275.
2. Z. Zhang, S.-S. Wang, R. Song, T. Cao, L. Luo, X. Chen, Y. Gao, J. Lu, W.-X. Li and W. Huang, Nat. Commun., 2017, 8, 488.
3. D. Nielsen, X.-M. Hu, K. Daasbjerg and T. Skrydstrup, Nat. Catal., 2018, 1, 244.
4. S. Kattel, B. Yan, Y. Yang, J. G. Chen and P. Liu, J. Am. Chem. Soc., 2016, 138, 12440–12450.
5. M. Behrens, Angew. Chem., Int. Ed., 2014, 53, 12022–12024.
6. F. C. Meunier, Angew. Chem., Int. Ed., 2011, 50, 4053–4054.
7. B. Eren, C. Heine, H. Bluhm, G. A. Somorjai and M. Salmeron, J. Am. Chem. Soc., 2015, 137, 11186–11190.
8. X. Deng, A. Verdaguer, T. Herranz, C. Weis, H. Bluhm and M. Salmeron, Langmuir, 2008, 24, 9474.
9. K. Mudiyanselage, S. D. Senanayake, L. Feria, S. Kundu, A. E. Baber, J. Graciani, A. B. Vidal, S. Agnoli, J. Evans, R. Chang, S. Axnanda, Z. Liu, J. F. Sanz, P. Liu, J. A. Rodriguez and D. J. Stacchiola, Angew. Chem., Int. Ed., 2013, 52, 5101–5105.
10. J. Graciani, K. Mudiyanselage, F. Xu, A. E. Baber, J. Evans, S. D. Senanayake, D. J. Stacchiola, P. Liu, J. Hrbek, J. F. Sanz and J. A. Rodriguez, Science, 2014, 345, 546–550.
11. J. A. Rodriguez, P. Liu, J. Hrbek, J. Evans and M. Pérez, Angew. Chem., Int. Ed., 2007, 46, 1329–1332.
12. M. Favaro, H. Xiao, T. Cheng, W. Goddard III, J. Yano and E. Crumlin, PNAS, 2017, 114, 6706.
13. J. Nakamura, Y. Kushida, Y. Choi and T. Uchijima, J. Vac. Sci. Technol., A, 1997, 15, 1568.
14. H. Nishimura, T. Yatsu, T. Fujitani, T. Uchijima and J. Nakamura, J. Mol. Catal. A: Chem., 2000, 155, 3.
15. M. Pohl and A. Otto, Surf. Sci., 1998, 406, 125–137.
16. D. J. Stacchiola, Acc. Chem. Res., 2015, 48, 2151–2158.
17. A. Carley, M. Roberts and A. Strutt, Catal. Lett., 1994, 29, 169.
18. W. Shuai and X. Guoqin, Chin. J. Catal., 2013, 34, 865.
19. R. G. Copperthwaite, P. R. Davies, M. A. Morris, M. W. Roberts and R. A. Ryder, Catal. Lett., 1988, 1, 11–19.
20. V. M. Browne, A. F. Carley, R. G. Copperthwaite, P. R. Davies, E. M. Moser and M. W. Roberts, Appl. Surf. Sci., 1991, 47, 375–379.
21. A. Carley, A. Chambers, P. Davies, G. Mariotti, R. Kurian and M. Roberts, Faraday Discuss., 1996, 105, 225.
22. J. Minar, J. Braun, S. Mankovsky and H. Ebert, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 91.
23. M. W. Haverkort, I. S. Elfimov, L. H. Tjeng, G. A. Sawatzky and A. Damascelli, Phys. Rev. Lett., 2008, 101, 026406.
24. W. Jin, P.-C. Yeh, N. Zaki, D. Zhang, J. T. Sadowski, A. Al-Mahboob, A. M. van der Zande, D. A. Chenet, J. I. Dadap, I. P. Herman, P. Sutter, J. Hone, J. Osgood and M. Richard, Phys. Rev. Lett., 2013, 111, 106801.
25. D. J. Payne, M. D. M. Robinson, R. G. Egdell, A. Walsh, J. McNulty, K. E. Smith and L. F. J. Piper, Appl. Phys. Lett., 2011, 98, 212110.
26. J. M. Kahk, C. G. Poll, F. E. Oropeza, J. M. Ablett, D. Céolin, J.-P. Rueff, S. Agrestini, Y. Utsumi, K. D. Tsuei, Y. F. Liao, F. Borgatti, G. Panaccione, A. Regoutz, R. G. Egdell, B. J. Morgan, D. O. Scanlon and D. J. Payne, Phys. Rev. Lett., 2014, 112, 117601.
27. J. Lischner, G. K. Pálsson, D. Vigil-Fowler, S. Nemsak, J. Avila, M. C. Asensio, C. S. Fadley and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205113.
28. M. Bowker and R. Madix, Surf. Sci., 1980, 95, 190.
29. Y. Yang, J. Evans, J. A. Rodriguez, M. G. White and P. Liu, Phys. Chem. Chem. Phys., 2010, 12, 9909–9917.
30. P. Hofmann, K.-M. Schindler, S. Bao, V. Fritzsche, D. E. Ricken, A. M. Bradshaw and D. P. Woodruff, Surf. Sci., 1994, 304, 74–84.
31. C. T. Au and M. W. Roberts, Chem. Phys. Lett., 1980, 74, 472–474.
32. M. Roberts, Catal. Lett., 2014, 144, 767.
33. J. Zhao, F. Gao, S. P. Pujari, H. Zuilhof and A. V. Teplyakov, Langmuir, 2017, 33, 10792–10799.
34. F. A. Delesma, M. Van den Bossche, H. Grönbeck, P. Calaminici, A. M. Köster and L. G. M. Pettersson, ChemPhysChem, 2018, 19, 169–174.
35. C. Kunkel, F. Viñes, P. Ramírez, J. Rodriguez and F. Illas, J. Phys. Chem. C, 2018 DOI:10.1021/acs.jpcc.7b12227.
36. K. Artyushkova, I. Matanovic, B. Halevi and P. Atanassov, J. Phys. Chem. C, 2017, 121, 2836.
37. N. Pueyo Bellafont, F. Vines, W. Hieringer and F. Illas, J. Comput. Chem., 2017, 28, 518.
38. K. Artyushkova, B. Kiefer, B. Halevi, A. Knop-Gericke, R. Schlogl and P. Atanassov, Chem. Commun., 2013, 49, 2539–2541.
39. T. Aizawa, S. Suehara, S. Hishita, S. Otani and M. Arai, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165405.
40. M. J. van Setten, R. Costa, F. Viñes and F. Illas, J. Chem. Theory Comput., 2018, 14, 877–883.
41. G. Cavigliasso, PhD thesis, The University of British Columbia, Vancouver, Canada, 1999.
42. G. Cavigliasso and D. P. Chong, J. Chem. Phys., 1999, 111, 9485–9492.
43. N. Pueyo Bellafont, G. Alvarez Saiz, F. Vines and F. Illas, Theor. Chem. Acc., 2016, 135, 35.
44. N. Pueyo Bellafont, F. Viñes and F. Illas, J. Chem. Theory Comput., 2016, 12, 324.
45. P. S. Bagus, E. S. Ilton and C. J. Nelin, Surf. Sci. Rep., 2013, 68, 273.
46. P. S. Bagus, C. Wöll and A. Wieckowski, Surf. Sci., 2009, 603, 273–283.
47. K. Weiss, H. Ostrom, L. Triguero, H. Ogasawara, M. Garnier, L. Pettersson and A. Nilsson, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 179.
48. L. Triguero, O. Plashkevych, L. Pettersson and H. Agren, J. Electron Spectrosc. Relat. Phenom., 1999, 104, 195.
49. C. Bureau and D. Chong, J. Electron Spectrosc. Relat. Phenom., 1998, 88, 657.
50. Y.-J. Zhang, V. Sethuraman, R. Michalsky and A. Peterson, ACS Catal., 2014, 4, 3742.
51. M. Gajdoš and J. Hafner, Surf. Sci., 2005, 590, 117–126.
52. S.-G. Wang, X.-Y. Liao, D.-B. Cao, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. C, 2007, 111, 16934.
53. F. Muttaqien, Y. Hamamoto, I. Hamada, K. Inagaki, Y. Shiozawa, K. Mukai, T. Koitaya, S. Yoshimoto, J. Yoshinobu and Y. Morikawa, J. Chem. Phys., 2017, 147, 094702.
54. F. Muttaqien, PhD thesis, Department of Precision Science and Technology, Osaka University, 2017.
55. G. W. Watson, R. P. K. Wells, D. J. Willock and G. J. Hutchings, Surf. Sci., 2000, 459, 93–103.
56. A. Phatak, W. Delgass, F. Ribeiro and W. Schneider, J. Phys. Chem. C, 2009, 113, 7269.
57. A. Michaelides, Appl. Phys. A: Mater. Sci. Process., 2006, 85, 415–425.
58. A. Michaelides and K. Morgenstern, Nat. Mater., 2007, 6, 597–601.
59. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
60. J. Greeley and M. Mavrikakis, J. Catal., 2002, 208, 291.
61. W.-K. Chen, S.-H. Liu, M.-J. Cao, C.-H. Lu, Y. Xu and J.-Q. Li, Chin. J. Chem., 2006, 24, 872.
62. X. Lian, P. Xiao, S.-C. Yang, R. Liu and G. Henkelman, J. Chem. Phys., 2016, 145, 044711.
63. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
64. K. Garrity, J. Bennett, K. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446.
65. L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
67. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
68. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
69. W. Stevens, M. Krauss, H. Basch and P. Jasien, Can. J. Chem., 1992, 70, 612.
70. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085.
71. F. Jensen, J. Chem. Theory Comput., 2006, 2, 1360–1369.
72. Y. Zhano and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
73. P. S. Bagus, I. Schaefer and F. Henry, J. Chem. Phys., 1972, 56, 224–226.
74. R. Dovesi, R. Orlando, A. Erba, C. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noel, M. Causa, M. Rerat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287.
75. R. Raval, S. F. Parker, M. E. Pemble, P. Hollins, J. Pritchard and M. A. Chesters, Surf. Sci., 1988, 203, 353–377.
76. A. Stroppa, K. Termentzidis, J. Paier, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195440.
77. X. Ren, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045402.
78. N. Lopez and J. K. Nørskov, Surf. Sci., 2001, 477, 59–75.
79. M. Gajdos, A. Eichler and J. Hafner, J. Phys.: Condens. Matter, 2004, 16, 1141–1164.
80. P. S. Bagus, C. Sousa and F. Illas, J. Chem. Phys., 2016, 145, 144303.
81. N. Pueyo Bellafont, P. S. Bagus, C. Sousa and F. Illas, J. Chem. Phys., 2017, 147, 024106.
82. G. Illing, D. Heskett, E. W. Plummer, H.-J. Freund, J. Somers, T. Lindner, A. M. Bradshaw, U. Buskotte, M. Neumann, U. Starke, K. Heinz, P. L. De Andres, D. Saldin and J. B. Pendry, Surf. Sci., 1988, 206, 1–19.
83. A. V. de Carvalho, M. C. Asensio and D. P. Woodruff, Surf. Sci., 1992, 273, 381–384.
84. J. S. Chickos, J. Acree and E. William, J. Phys. Chem. Ref. Data, 2002, 31, 537–698.
85. F. Solymosi and J. Kiss, Surf. Sci., 1981, 104, 181–198.
86. F. Solymosi, J. Mol. Catal., 1991, 65, 337.
87. F. Muttaqien, Y. Hamamoto, K. Inagaki and Y. Morikawa, J. Chem. Phys., 2014, 141, 034702.

---

Footnote

† Electronic supplementary information (ESI) available: The geometries of the relaxed slabs (figure and atomic positions), the clusters (atomic positions) and the molecules (figure). The basis sets and effective core potentials used in the calculations of the free molecules and the clusters with adsorbates. See DOI: 10.1039/c8cp04955f

---