The nature of frontier orbitals under systematic ligand exchange in (pseudo-)octahedral Fe(II) complexes

Abstract

Understanding and controlling properties of transition metal complexes is a crucial step towards tailoring materials for sustainable energy applications. In a systematic approach, we use resonant inelastic X-ray scattering to study the influence of ligand substitution on the valence electronic structure around an aqueous iron(II) center. Exchanging cyanide with 2-2′-bipyridine ligands reshapes frontier orbitals in a way that reduces metal 3d charge delocalization onto the ligands. This net decrease of metal–ligand covalency results in lower metal-centered excited state energies in agreement with previously reported excited state dynamics. Furthermore, traces of solvent-effects were found indicating a varying interaction strength of the solvent with ligands of different character. Our results demonstrate how ligand exchange can be exploited to shape frontier orbitals of transition metal complexes in solution-phase chemistry; insights upon which future efforts can built when tailoring the functionality of photoactive systems for light-harvesting applications.

---

1 Introduction

Due to the variety of occurring stable oxidation states and the resulting charge and spin distributions, transition metal complexes exhibit properties relevant for catalysis and solar energy materials.¹ For the development of cheap and sustainable light-harvesting applications tremendous efforts are therefore being made to replace complexes involving scarce 4d and 5d transition metals with complexes based on more abundant 3d metals like iron (Fe).² Particularly polypyridyl complexes such as [Fe(bpy)₃]²⁺ with their strong metal-to-ligand charge-transfer (MLCT) bands in the visible spectrum have been intensively studied in that regard.^3–7 However, as internal conversion and intersystem crossing channels efficiently depopulate the primary charge-transfer excited state, MLCT lifetimes in Fe-based complexes are usually on the femtosecond timescale. Finding concepts that inhibit the ultrafast depopulation of MLCT states and instead stabilize the photo-induced charge-separation therefore constitutes a crucial step towards cost-efficient complexes that still serve the specific needs of solar energy applications.

In a recent series of studies, Gaffney and coworkers demonstrated how exchanging and combining different kinds of ligands allows to manipulate rates and pathways of MLCT state decay in Fe(II) complexes.^8–11 By varying the ligands coordinated towards the metal center within a suitable solvent environment, the relative energies between MLCT and metal-centered (MC) states could be manipulated in a way that intersystem crossing channels were quenched. Specifically, it was found that the MLCT lifetime can be increased by a factor of 100 compared to [Fe(bpy)₃]²⁺ by substituting two 2-2′-bipyridine (bpy) ligands with four cyanide (CN) ligands and dissolving the compound in dimethyl sulfoxide.⁹ By combining time-resolved Kβ X-ray emission and transient absorption spectroscopy, MLCT and MC states could be distinguished, providing a robust description of how molecular structure varies the dynamics following a charge-transfer excitation.

In this study, we demonstrate how these differences can be traced back to the varying nature of frontier orbitals induced by ligand substitution. Along the series [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺, we systematically study changes in the ground state valence electronic structure and deduce trends in the valence excited state landscape. We use resonant inelastic X-ray scattering¹² (RIXS) in the soft X-ray regime, that, due to its local and element-specific access to valence excited final states, is a probe particularly suited for such investigations. Through the Fe 2p → 3d core-excitation, the method is sensitive to occupied as well as unoccupied orbitals around the central metal,^13–18 while the nitrogen (N) 1s → 2p core-excitation probes the analogue ligand orbitals.^19–21 Thus, our approach allows to experimentally access frontier orbitals that contribute to the metal–ligand bond as well as participate in solute–solvent interaction. By independently investigating local charge densities and orbital character of Fe 3d as well as CN and bpy derived orbitals, trends in ligand field strength, metal–ligand bonding and solvation are observed that are directly linked to the varying excited-state landscape of charge-transfer Fe complexes with different ligand cages.

2 Experimental and computational details

K₄Fe(CN)₆·3H₂O was purchased from Sigma-Aldrich and dissolved in deionized water at a concentration of 300 mM. K₂Fe(bpy)(CN)₄·3H₂O and Fe(bpy)₃Cl₂ were purchased from HetCat and prepared in 60 mM aqueous solutions. The experimental data were acquired at the U49-2/PGM-1 beamline²² of the synchrotron BESSY II using the LiquidFlexRIXS endstation.²³ The sample was sprayed into the experimental chamber by a 20 μm in-vacuum liquid jet and excited with horizontally polarized X-rays. The bandwidth of the incident energy was 250 meV at the N K-edge and 580 meV at the Fe L-edge. The calibration of the X-ray excitation energy was performed by using the data reported by Kunnus et al.¹⁶ The emitted photons were detected by a Rowland spectrometer operated in slitless mode at a 90° scattering angle in the plane of the polarization of the incident beam.

The quantum chemical simulations were for the most part performed within the same density functional theory (DFT) framework as by Van Kuiken et al.²⁴ For the discussion of orbitals and charges, the molecular structure of each sample was optimized with the ORCA software²⁵ at the B3LYP level^26,27 using the all-electron def2-TZVP(-f) basis set²⁸ for all atoms. All calculations have been additionally performed with the reparametrized B3LYP* functional;²⁹ results for this functional showed a sightly worse agreement with the experimental data, but were in overall good agreement with ones presented here for B3LYP. To simulate the solvent-effects of water the conductor-like polarizable continuum model COSMO³⁰ was employed for all calculations. Additionally, the RIJCOSX method³¹ was used with the def2-TZV/J as auxiliary basis set³² to speed up calculations. Based on the optimized structures, X-ray absorption and emission spectra at the N K-edge were obtained using time-dependent DFT. Core-excitations were simulated individually for N sites of different chemical environment by using the Pipek–Mezey orbital localization scheme.³³ The X-ray absorption spectra were generated by convolution of each transition with a Gaussian function of 0.5 eV FWHM for bpy ligands and 0.9 eV FWHM for CN ligands. A shift of 12.3 eV was applied to the X-ray absorption spectrum of [Fe(bpy)₃]²⁺ to match the experimental partial fluorescence yield. All other absorption spectra were shifted equally. For the X-ray emission spectra, all transitions were convolved with a Gaussian function of 1.5 eV FWHM. The spectra were shifted individually to match the energy transfer of the experimental data.

3 Results and discussion

3.1 Fe L-edge

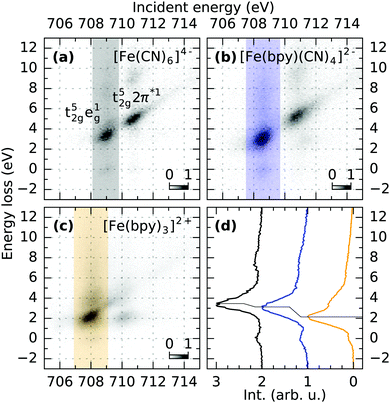
The molecular structures of [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ are displayed in Fig. 1a. The different ligand cages all nominally provide 12 electrons to the formal Fe(II) center. This results in a closed-shell configuration obeying the 18-electron rule for all three complexes. While only [Fe(CN)₆]⁴⁻ exhibits a perfectly octahedral structure, from a metal perspective, the other two complexes can also be classified as six-fold coordinated. The low spin and the high symmetry therefore allow the most dominant spectral effects to be discussed within a molecular orbital picture and within the nomenclature of octahedral symmetry.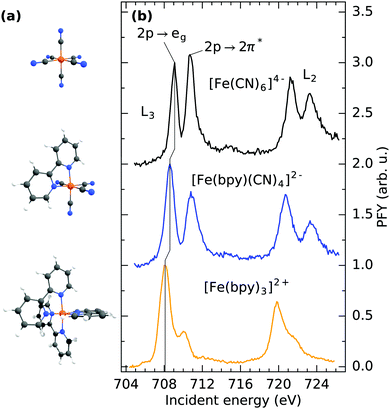

Fig. 1 (a) Molecular structure and (b) Fe L_3/2-edge partial fluorescence yield absorption spectra of [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ in aqueous solution.

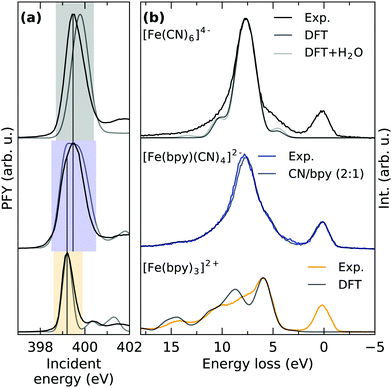
Fig. 1b shows the Fe L_3/2-edge partial fluorescence yield (PFY) of the three samples under investigation. The spectra are acquired by integrating over all detected L-edge X-ray emission channels and are normalized to the maximum of the first resonance. By comparison of the detected transitions, the implications of ligand exchange on the local valence electronic structure can be observed, exemplified by two major trends visible in the spectra. By gradually exchanging CN with bpy ligands, a drastic decrease in relative intensity of the second absorption feature at ∼710.5 eV incident energy can be observed. In [Fe(CN)₆]⁴⁻, this feature has been identified to originate from a mixing of metal t_2g MOs with the anti-bonding CN 2π* MOs of equal symmetry. Thereby, metal electron density is delocalized onto the ligands. As the Fe 2p → 2π* core-excitation probes the Fe content of the CN 2π* MO, the resulting feature has been postulated to be a “direct probe of back-bonding”.³⁴ Consequently, the gradually lowered intensity of the feature in [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ is reflective of the reduced ability of bpy ligands to accept metal t_2g electron density. The remaining absorption in [Fe(bpy)₃]²⁺ at 710 eV incident energy can therefore be rationalized as a combination of remaining Fe 2p → 2π* excitation and multiplet effects that previously have been observed in complexes with similar ligand cages.^35–37 Additional multiplet-effects caused by the simultaneous presence of CN and bpy ligands and the resulting deviation from octahedrality could therefore explain the broadened second resonance in [Fe(bpy)(CN)₄]²⁻ compared to [Fe(CN)₆]⁴⁻.

Besides the decrease of Fe 2p → 2π* intensity upon ligand-exchange, the onset of the lowest lying Fe 2p → 3d excitation at the L₃-edge (corresponding to a Fe 2p → e_g excitation) shifts to lower incident energy. Shifts of the L-edge absorption onset have traditionally been interpreted to reflect the local charge at the metal center, where an increase in electron density enhances the ability to screen the Fe 2p core-hole in the core-excited state.³⁸ This has been proven to be a useful tool to determine the oxidation state of the central metal.³⁹ As previously stated, exclusively Fe(II) complexes are compared within this study. The shift of the absorption onset is thus directly reflective of a change in covalent metal–ligand interaction. The shift to lower incident energy can therefore be interpreted as a reduced delocalization of metal electron density onto the ligands (i.e. backbonding) and subsequent increase of electron density at the metal center, in agreement with the decrease of Fe 2p → 2π* intensity.

For a discussion of the RIXS final states of the three complexes we turn to Fig. 2. The displayed range of incident energy is restricted to the L₃-edge as the interpretation of the L₂-edge is complicated by the presence of Coster–Kronig features.⁴⁰ Similarly to the discussion of the L-edge PFY, the RIXS plane of [Fe(CN)₆]⁴⁻ displayed in (a) can serve as a reference, as a detailed assignment of final states has been performed by Kunnus et al.¹⁶ The two most intense features can be identified as t⁵_2ge¹_g (709.1 eV incident energy, 3.5 eV energy loss) and t⁵_2g2π*¹ final states (710.8 eV incident energy, 5 eV energy loss). The decrease in intensity of the latter final state in [Fe(bpy)(CN)₄]²⁻ and almost complete disappearance in [Fe(bpy)₃]²⁺ (compare (b) and (c)) is the cause for the trend of decreasing integrated Fe 2p → 2π* intensity observed in the PFYs.

Fig. 2 (a–c) RIXS maps of [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ measured at the Fe L₃-edge. The integration along the incident energy over the t⁵_2ge¹_g feature is marked in the respective maps and displayed in (d). The shift of the main loss feature to lower energy losses reflects the decrease of 10Dq upon ligand exchange.

The t⁵_2ge¹_g final state allows for a more quantitative analysis. In octahedral symmetry, the position of the feature in terms of energy loss effectively probes the difference between the t_2g and e_g levels and can therefore measure trends in 10Dq.⁴¹Fig. 2d shows intensities integrated over the respective marked incident energy ranges in the RIXS maps. The final state energy loss therefore decreases from 3.5 eV in [Fe(CN)₆]⁴⁻ to 3.1 eV in [Fe(bpy)(CN)₄]²⁻ and 2.2 eV in [Fe(bpy)₃]²⁺. This trend is consistent with the field strength of the two different ligands predicted by the spectrochemical series.⁴² Furthermore, it agrees with the mechanistic explanation of the extended MLCT lifetime of [Fe(bpy)(CN)₄]²⁻ dissolved in dimethyl sulfoxide. There, spin crossover decay channels were successfully quenched by destabilizing MC states through an exchange of bpy with CN ligands, while simultaneously stabilizing MLCT energies by solvents of low Lewis-acidity.^9,11

To substantiate the interpretations of the observed spectral trends we performed DFT and time-dependent (TD) DFT calculations. TD-DFT provides a natural link between experimental X-ray spectra and the ground state electronic structure of the complexes, as both the electronic ground state and the X-ray excitations are here described within the same basis of (Kohn–Sham) molecular orbitals. This approach further provides a framework in which the different complexes under investigation can be similarly described, besides their different ligand structures; in contrast to restricted active space approaches,^16,43–45 where comparability is only guaranteed if the orbitals within the respective active spaces are the same for all complexes.

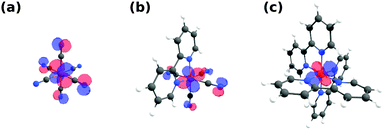
As previously stated, the Fe L-edge PFY measurements suggest reduced delocalization of electron density, i.e. a reduced π-backbonding, onto the ligands upon exchanging CN with bpy ligands. This trend is reproduced by our calculations, as can be seen in Fig. 3, where the highest occupied molecular orbitals (HOMOs) for [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ are displayed. In [Fe(CN)₆]⁴⁻ (a), there is significant amplitude visible at the N sites in plane with the Fe 3d MOs. This mixing of metal and ligand orbitals is reduced in [Fe(bpy)(CN)₄]²⁻ (b), with smaller contribution on the CN ligands and no contribution visible on the bpy ligand. Consequently, no amplitude can be observed on any of the bpy ligands in [Fe(bpy)₃]²⁺ (c). This degree of mixing is quantified in Table 1 by the average Fe 3d character of the HOMO, HOMO(−1), HOMO(−2) orbitals (representing the Fe t_2g orbitals in octahedral symmetry). The Fe 3d character increases as a result of exchanging CN with bpy ligands. This is in agreement with the gradually vanishing Fe 2p → 2π* resonance in the Fe L-edge PFY (compare Fig. 1b), as it measures the mixing of the Fe 3d and ligand 2π* orbitals.

Fig. 3 Highest occupied molecular orbitals (HOMO) of (a) [Fe(CN)₆]⁴⁻, (b) [Fe(bpy)(CN)₄]²⁻ and (c) [Fe(bpy)₃]²⁺ exhibiting amplitude on the CN but not bpy ligands. All orbitals are plotted with an isovalue of 0.04.

Table 1 Simulated HOMO Fe 3d character (%) and Mulliken, Hirshfeld and Loewdin charges of the Fe sites in units of the elementary charge e

	HOMO Fe 3d character	Mulliken	Hirshfeld	Loewdin
[Fe(CN)6]^4−	75.6	−0.01	−1.01	−0.83
[Fe(bpy)(CN)4]^2−	78.0	−0.15	−1.12	−0.62
[Fe(bpy)3]^2+	83.7	−0.23	−1.14	−0.26

---

The trend of reduced delocalization of metal electron density can also be expected to be reflected by a varying local charge of the Fe centers in different ligand cages. Table 1 therefore additionally shows the Mulliken, Hirshfeld and Loewdin charge analysis of the respective Fe sites in the three complexes. Consistent with our interpretation, the Mulliken and Hirshfeld charges are indeed turning more negative in the order [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻, [Fe(bpy)₃]²⁺ as a result of incremental concentration of electronic density at the metal site. This potentially causes the experimentally observed shift of the L-edge PFY absorption onset to lower incident energy (compare Fig. 1b) as a result of increased electronic screening of the Fe 2p core-hole. However, a recent study by Kubin et al.⁴⁶ suggests that such a picture might be an oversimplification. The Loewdin charges also presented in Table 1, in fact, show the opposite trend. This exemplifies the known difficulty of unambiguously and accurately defining atomic charges from electronic structure calculations. Future in-depth theoretical studies, possibly based on higher level quantum chemical methods, may therefore be necessary to derive a mechanistic explanation also for the observed onset shifts resulting from changes in metal–ligand covalency, similarly as for varying oxidation states.

3.2 N K-edge

Fig. 4a shows the N K-edge PFYs of [Fe(CN)₆]⁴⁻, [Fe(bpy)(CN)₄]²⁻ and [Fe(bpy)₃]²⁺ normalized to their respective absorption maximum. On top, X-ray absorption spectrum simulations are displayed that are acquired with TD-DFT from the earlier discussed electronic structure calculations. The calculation of [Fe(bpy)₃]²⁺ is shifted to match the experimental spectrum. The same shift was applied to the other absorption spectra. The simulations allow to assign the dominant transitions in the spectra to be of N 1s → 2π* character. Due to the different chemical environment of the CN and bpy N sites, the excitation energy of the corresponding main absorption feature is slightly lower in [Fe(bpy)₃]²⁺ than in [Fe(CN)₆]⁴⁻. This difference in excitation energy is reproduced, but slightly overestimated by the calculations. The chemical shift between the two N sites therefore explains the shoulder to lower incident energy in [Fe(bpy)(CN)₄]²⁻ as the complex contains N atoms in both, a CN and bpy environment. For a better agreement with the measurement, the calculated X-ray transitions involving core-holes located at a CN site were convolved with Gaussian functions of 0.9 eV FWHM, while for bpy N sites a 0.5 eV FWHM broadening was used. This could be due to varying Franck-Condon factors between the respective ground and core-excited states of the respective N sites. However, the difference in broadening could also be caused by the local environments of two different N sites in their respective ligands. While the N atoms of the bpy ligands are located close to the metal and surrounded by an extensive ligand structure, interaction with solvent molecules can be expected to be minimal. The CN ligands however, are directly involved in solute–solvent interaction, where hydrogen bonding has been reported to withdraw electron density from the ligand.^11,47,48 This interaction with a highly fluctuating solvent structure can therefore be expected to generate an ensemble of different configurations that are responsible for the increased broadening of CN N sites, an interaction that cannot be explicitly treated within the theoretical framework used for the calculations in Fig. 4a.

Fig. 4 (a) Partial fluorescence yield N 1s → 2π* absorption resonance of [Fe(CN)₆]⁴⁻ (black), [Fe(bpy)(CN)₄]²⁻ (blue) and [Fe(bpy)₃]²⁺ (orange) compared to DFT calculations. The spectrum calculations reproduce the experimentally observed shift between the CN and bpy ligands. (b) Emission spectra of the three compounds integrated over their respective main absorption resonances marked in (a). All spectra are normalized to the intensity of their elastic line. For [Fe(CN)₆]⁴⁻ and [Fe(bpy)₃]²⁺, non-resonant XES simulations are plotted in addition. The gray spectrum superimposing the data of [Fe(bpy)(CN)₄]²⁻ is a weighted sum (2 : 1) of the experimental spectra of [Fe(CN)₆]⁴⁻ and [Fe(bpy)₃]²⁺.

Fig. 4b shows RIXS spectra of the three compounds gathered by integration over their respective main resonance in the PFY (compare Fig. 4a). To facilitate some degree of comparability between spectra generated by integration over different energy ranges, they are normalized to their elastic peak maximum at 0 eV energy loss. For [Fe(CN)₆]⁴⁻ and [Fe(bpy)₃]²⁺, non-resonant X-ray emission (XES) calculations are additionally shown. Intensity from elastic scattering (0 eV energy loss) is not accounted for by non-resonant XES calculations, where the core-excited electron is ignored. The calculations are normalized and energetically shifted to the experimental emission maximum. The main features of [Fe(CN)₆]⁴⁻ can now be assigned to dominantly result from inelastic scattering from the Fe t_2g (4.6 eV energy loss) and CN 1π MOs (8.3 eV energy loss) in agreement with the final state assignment by Kunnus et al.¹⁶ The biggest difference between experiment and theory here is the underestimation of the emission signal from the Fe t_2g orbitals at 4.6 eV energy loss. Similar to the broadening of the absorption resonance observed in the N K-edge PFY, this could be due to an insufficient treatment of the solvent environment. The earlier mentioned withdrawal of electron density from the CN ligand in an aqueous environment has been reported to subsequently increase π-backdonation in Fe cyanides.^11,47,48 Due to its sensitivity to the overlap of the N 1s core-hole with the Fe t_2g orbitals, this emission line is a direct probe thereof. Within a simple model similar to Kjær et al.,¹¹ we simulated the solute–solvent interaction by explicitly adding one water molecule to each N site of the six CN ligands. This calculation is additionally shown and indeed exhibits an increase of emission from the t_2g orbitals, however to a very small degree. While strict solvent-treatment can therefore be expected to increase accuracy, the remaining disagreement illustrates the limits of DFT to simultaneously and with high accuracy account for metal-, ligand- and solvent structure within the same framework of basis sets and exchange correlation potentials.

When comparing the RIXS of [Fe(CN)₆]⁴⁻ with [Fe(bpy)₃]²⁺, the latter one exhibits significantly more features, directly reflective of the more complicated bpy ring structure. This is confirmed by our calculations, where emission from a variety of orbitals with predominant π character can be assigned to the dominant spectral features. Within the applied normalization the individual emission lines have less intensity than the main feature in [Fe(CN)₆]⁴⁻. This can be explained by the fact that the bpy π* orbitals are distributed across the pyridine rings and therefore have less overlap with the N core-hole than in a CN ligand.

Having established the characteristic RIXS signatures of the N sites in a CN and a bpy ligand, the signature of [Fe(bpy)(CN)₄]²⁻ can be understood as well. Analogously to the N 1s PFYs, the RIXS spectrum of [Fe(bpy)(CN)₄]²⁻ is a superposition of the different N sites. By adding the spectra of [Fe(CN)₆]⁴⁻ and [Fe(bpy)₃]²⁺ weighted by the ratio of N sites in CN and bpy ligands (2 : 1), the spectrum of [Fe(bpy)(CN)₄]²⁻ can be reproduced with high accuracy, as can be seen by the gray spectrum superimposed onto the measured spectrum. Different ligands in [Fe(bpy)(CN)₄]²⁻ are thus seen as independent moieties from a N 1s spectroscopic perspective. Furthermore, the excellent agreement also justifies the applied normalization on the elastic line.

4 Conclusions

In summary, we establish how ligand substitution in transition metal complexes predominantly induces characteristic changes of frontier orbital interactions with significant consequences for tailored excited state lifetimes. In particular, reduced π-backbonding in complexes involving bpy ligands over CN ligands reduces metal–ligand covalency and lowers MC state energies. Furthermore, indications of solute–solvent interaction could be observed for the CN ligands that agree with previous observations of solvent-effects on Fe cyanides. We were able to experimentally observe these trends in covalency, energy levels of dd transitions, local charge densities as well as solvent-interaction trough a combination of metal L-edge and ligand K-edge X-ray spectroscopy. Our findings are corroborated by DFT calculations that substantiate the derived orbital-based description of the observed spectral trends and how frontier orbitals are reshaped by a varying ligand field. These conclusions appear to be valid beyond the class of (pseudo-)octahedral closed-shell complexes, as our findings emphasize the universal role of local charge distributions as a determining property of photo-absorbers. Our results can therefore serve as general principles when manipulating the excited-state behavior in futures approaches of precisely tailoring the functionality of transition metal complexes.

Conflicts of interest

The authors have no conflict of interest to declare.

Acknowledgements

We thank HZB for the allocation of synchrotron radiation beamtime and Christian Weniger for technical support during the measurements. R. M. J., S. E. and A. F. acknowledge funding from the ERC-ADG-2014 – Advanced Investigator Grant No. 669531 EDAX under the Horizon 2020 EU Framework Program for Research and Innovation.

References

1. H. B. Gray and A. W. Maverick, Science, 1981, 214, 1201–1205.
2. Y. Liu, P. Persson, V. Sundström and K. Wärnmark, Acc. Chem. Res., 2016, 49, 1477–1485.
3. W. Gawelda, V.-t. Pham, M. Benfatto, Y. Zaushitsyn, M. Kaiser, D. Grolimund, S. L. Johnson, R. Abela, A. Hauser, C. Bressler and M. Chergui, Phys. Rev. Lett., 2007, 98, 057401.
4. C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492.
5. N. Huse, H. Cho, K. Hong, L. Jamula, F. M. F. de Groot, T. K. Kim, J. K. McCusker and R. W. Schoenlein, J. Phys. Lett., 2011, 2, 880–884.
6. H. Cho, M. L. Strader, K. Hong, L. Jamula, E. M. Gullikson, T. K. Kim, F. M. F. de Groot, J. K. McCusker, R. W. Schoenlein and N. Huse, Faraday Discuss., 2012, 157, 463.
7. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
8. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348.
9. W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T.-C. Weng, D. Zhu, K. Wärnmark, V. Sundström and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523.
10. K. S. Kjær, W. Zhang, R. Alonso-Mori, U. Bergmann, M. Chollet, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, J. S. Robinson, E. I. Solomon, D. Sokaras, T. B. van Driel, T.-C. Weng, D. Zhu, P. Persson, K. Wärnmark, V. Sundström and K. J. Gaffney, Struct. Dyn., 2017, 4, 044030.
11. K. S. Kjær, K. Kunnus, T. C. B. Harlang, T. B. Van Driel, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, E. Biasin, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, J. Uhlig, V. Sundstöm, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. Wärnmark, P. Persson, A. A. Cordones and K. J. Gaffney, Phys. Chem. Chem. Phys., 2018, 20, 4238–4249.
12. L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767.
13. K. Kunnus, I. Josefsson, S. Schreck, W. Quevedo, P. S. Miedema, S. Techert, F. M. F. De Groot, M. Odelius, P. Wernet and A. Föhlisch, J. Phys. Chem. B, 2013, 117, 16512–16521.
14. P. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81.
15. B. Liu, R.-P. Wang, E. N. Glass, C. L. Hill, T. Cuk, J. Okamoto, D.-J. Huang, M. M. van Schooneveld and F. M. F. de Groot, Inorg. Chem., 2016, 55, 10152–10160.
16. K. Kunnus, W. Zhang, M. G. Delcey, R. V. Pinjari, P. S. Miedema, S. Schreck, W. Quevedo, H. Schröder, A. Föhlisch, K. J. Gaffney, M. Lundberg, M. Odelius and P. Wernet, J. Phys. Chem. B, 2016, 120, 7182–7194.
17. A. W. Hahn, B. E. Van Kuiken, M. Al Samarai, M. Atanasov, T. Weyhermüller, Y. T. Cui, J. Miyawaki, Y. Harada, A. Nicolaou and S. DeBeer, Inorg. Chem., 2017, 56, 8203–8211.
18. R. M. Jay, J. Norell, S. Eckert, M. Hantschmann, M. Beye, B. Kennedy, W. Quevedo, W. F. Schlotter, G. L. Dakovski, M. P. Minitti, M. C. Hoffmann, A. Mitra, S. P. Moeller, D. Nordlund, W. Zhang, H. W. Liang, K. Kunnus, K. Kubiček, S. A. Techert, M. Lundberg, P. Wernet, K. Gaffney, M. Odelius and A. Föhlisch, J. Phys. Chem. Lett., 2018, 9, 3538–3543.
19. L. Weinhardt, M. Blum, O. Fuchs, A. Benkert, F. Meyer, M. Bär, J. Denlinger, W. Yang, F. Reinert and C. Heske, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 111–120.
20. S. Eckert, J. Norell, P. S. Miedema, M. Beye, M. Fondell, W. Quevedo, B. Kennedy, M. Hantschmann, A. Pietzsch, B. E. Van Kuiken, M. Ross, M. P. Minitti, S. P. Moeller, W. F. Schlotter, M. Khalil, M. Odelius and A. Föhlisch, Angew. Chem., Int. Ed., 2017, 56, 6088–6092.
21. S. Eckert, J. Niskanen, R. M. Jay, P. S. Miedema, M. Fondell, B. Kennedy, W. Quevedo, M. Iannuzzi and A. Föhlisch, Phys. Chem. Chem. Phys., 2017, 19, 32091–32098.
22. T. Kachel, J. Large-Scale Res. Facil., 2016, 2, A72.
23. K. Kunnus, I. Rajkovic, S. Schreck, W. Quevedo, S. Eckert, M. Beye, E. Suljoti, C. Weniger, C. Kalus, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, S. Techert, P. Wernet and A. Föhlisch, Rev. Sci. Instrum., 2012, 83, 123109.
24. B. E. Van Kuiken, H. Cho, K. Hong, M. Khalil, R. W. Schoenlein, T. K. Kim and N. Huse, J. Phys. Chem. Lett., 2016, 7, 465–470.
25. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
26. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55.
30. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
31. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
32. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
33. J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926.
34. R. K. Hocking, E. C. Wasinger, F. M. F. de Groot, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 10442–10451.
35. E. C. Wasinger, F. M. F. de Groot, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2003, 125, 12894–12906.
36. R. K. Hocking, E. C. Wasinger, Y.-l. Yan, F. M. F. DeGroot, F. A. Walker, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 113–125.
37. N. Huse, T. K. Kim, L. Jamula, J. K. McCusker, F. M. F. de Groot and R. W. Schoenlein, J. Am. Chem. Soc., 2010, 132, 6809–6816.
38. K. Godehusen, T. Richter, P. Zimmermann and P. Wernet, J. Phys. Chem. A, 2017, 121, 66–72.
39. S. P. Cramer, F. M. F. DeGroot, Y. Ma, C. T. Chen, F. Sette, C. A. Kipke, D. M. Eichhorn, M. K. Chan and W. H. Armstrong, J. Am. Chem. Soc., 1991, 113, 7937–7940.
40. D. Coster and R. D. L. Kronig, Physica, 1935, 2, 13–24.
41. M. M. van Schooneveld, R. W. Gosselink, T. M. Eggenhuisen, M. Al Samarai, C. Monney, K. J. Zhou, T. Schmitt and F. M. F. de Groot, Angew. Chem., Int. Ed., 2013, 52, 1170–1174.
42. D. Shriver, M. Weller, T. Overton, J. Rourke and F. Armstrong, Inorganic Chemsitry, W.H. Freeman and Company, New York, 6th edn, 2014.
43. R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116.
44. J. Norell, R. M. Jay, M. Hantschmann, S. Eckert, M. Guo, K. J. Gaffney, P. Wernet, M. Lundberg, A. Föhlisch and M. Odelius, Phys. Chem. Chem. Phys., 2018, 20, 7243–7253.
45. M. Kubin, M. Guo, M. Ekimova, M. L. Baker, T. Kroll, E. Källman, J. Kern, V. K. Yachandra, J. Yano, E. T. J. Nibbering, M. Lundberg and P. Wernet, Inorg. Chem., 2018, 57, 5449–5462.
46. M. Kubin, M. Guo, T. Kroll, H. Löchel, E. Källman, M. L. Baker, R. Mitzner, S. Gul, J. Kern, A. Föhlisch, A. Erko, U. Bergmann, V. Yachandra, J. Yano, M. Lundberg and P. Wernet, Chem. Sci., 2018, 9, 6813–6829.
47. H. E. Toma and M. S. Takasugi, J. Solution Chem., 1983, 12, 547–561.
48. T. J. Penfold, M. Reinhard, M. H. Rittmann-Frank, I. Tavernelli, U. Rothlisberger, C. J. Milne, P. Glatzel and M. Chergui, J. Phys. Chem. A, 2014, 118, 9411–9418.

---

Footnotes

† Present address: Deutsches Elektronen-Synchrotron DESY, Photon Science, 22607 Hamburg, Germany.

‡ Present address: University of Turku, Department of Physics and Astronomy, FI-20014, Finland.

---