Group-VIII transition metal boride as promising hydrogen evolution reaction catalysts†
Abstract
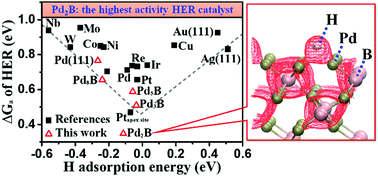
Searching for alternative catalysts for hydrogen evolution reaction (HER) under acidic conditions has been a major challenge in chemistry. Herein, we demonstrate that it is now feasible to identify unprecedented transition metal boride phases that are both stable and active for HER via stochastic global potential energy surface scanning. We show that B alloying alters the most stable crystal phase from face-centered (fcc) to hexagonal close packing (hcp) for both Pd and Rh. In particular, Pd2B, the thermodynamically most stable Pd boride with the highest B content, is predicted to exhibit an ultra-high intrinsic HER activity, ∼2 orders of magnitude higher than that of Pt nanoparticles at 0 V vs. NHE. The group VIII transition metal boride thus represents a promising HER catalyst to replace conventional Pt catalysts.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...