Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rotationally resolved electronic spectroscopy of 3-cyanoindole and the 3-cyanoindole–water complex†
Michael
Schneider
 a,
Marie-Luise
Hebestreit
a,
Marie-Luise
Hebestreit
 a,
Mirko Matthias
Lindic
a,
Mirko Matthias
Lindic
 a,
Hilda
Parsian
a,
América Yareth
Torres-Boy
b,
Leonardo
Álvarez-Valtierra
a,
Hilda
Parsian
a,
América Yareth
Torres-Boy
b,
Leonardo
Álvarez-Valtierra
 b,
W. Leo
Meerts
b,
W. Leo
Meerts
 c,
Ralf
Kühnemuth
d and
Michael
Schmitt
c,
Ralf
Kühnemuth
d and
Michael
Schmitt
 *a
*a
aHeinrich-Heine-Universität, Institut für Physikalische Chemie I, D-40225 Düsseldorf, Germany. E-mail: mschmitt@uni-duesseldorf.de; Fax: +49 211 8113689; Tel: +49 211 8112100
bDivisión de Ciencias e Ingenierías, Universidad de Guanajuato-Campus León, León, Guanajuato 37150, Mexico
cRadboud University, Institute for Molecules and Materials, Felix Laboratory, Toernooiveld 7c, 6525 ED Nijmegen, The Netherlands
dHeinrich-Heine-Universität, Lehrstuhl für Molekulare Physikalische Chemie, D-40225 Düsseldorf, Germany
First published on 27th August 2018
Abstract
The rotationally resolved electronic spectra of the origin bands of 3-cyanoindole, 3-cyanoindole(d1), and the 3-cyanoindole–(H2O)1 cluster have been measured and analyzed using evolutionary algorithms. For the monomer, permanent dipole moments of 5.90 D for the ground state, and of 5.35 D for the lowest excited singlet state have been obtained from electronic Stark spectroscopy. The orientation of the transition dipole moment is that of an 1Lb state for the monomer. The water moiety in the water cluster could be determined to be trans-linearly bound to the NH group of 3-cyanoindole, with an NH⋯O hydrogen bond length of 201.9 pm in the electronic ground state. Like the 3-cyanoindole monomer, the 3-cyanoindole–water cluster also shows an 1Lb-like excited singlet state. The excited state lifetime of isolate 3-cyanoindole in the gas phase has been determined to be 9.8 ns, and that of 3-cyanoindole(d1) has been found to be 14.8 ns, while that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water cluster is considerably shorter (3.6 ns). The excited state lifetime of 3-cyanoindole(d1) in D2O solution has been found to be smaller than 20 ps.
1 water cluster is considerably shorter (3.6 ns). The excited state lifetime of 3-cyanoindole(d1) in D2O solution has been found to be smaller than 20 ps.
1 Introduction
Understanding solvent reorganization processes at a molecular level is key to the determination of dipole moments of electronically excited molecules in solution. Beforehand, the driving forces which determine the solvent orientation in both electronic states have to be investigated on a molecular level. Indole derivatives are especially interesting in this respect, since they have two energetically close-lying excited singlet states, which have considerably different dipole moments. Dipole–dipole interactions with polar solvent molecules lead to different stabilization of the electronically excited states. Depending on the dipole moments, even the energetic order of the lowest excited singlet states might switch upon cluster formation or solvation in polar solvents. These states are called 1La and 1Lb in the nomenclature of Platt,1 adapted to indole by Weber.2 The 1Lb state has a small dipole moment and is lower in energy in apolar surroundings, while the 1La state on the other hand has a comparatively large dipole moment, leading to an inversion of the electronic state ordering in polar solvents. Some molecular systems change the energetic order of the excited states already upon addition of the first water molecules to the chromophore like azaindole.3Indole, as the chromophore of the aromatic amino acid tryptophane, has been extensively studied, mainly regarding the location of the higher electronically excited 1La state relative to the lowest 1Lb state, both experimentally4–12 as well as theoretically.13–18
Exchange of one hydrogen atom in the chromophore for the highly polar cyano group, changes the fluorescence properties of the indole chromophore considerably.19,20 5-Cyanotryptophane is used as a fluorescence probe of protein hydration.21 Its chromophore, 5-cyanoindole, has been studied using rotationally resolved electronic spectroscopy and fluorescence emission spectroscopy in our group.22–24 For 5-cyanoindole, we found that the lowest electronically excited singlet state is of 1La character. The question arises, if for other substitution positions, the cyano group has the same stabilizing effect on the 1La state. Therefore, we varied the position from the 5-position, which is located in the benzene ring of the chromophore, to the 3-position within the pyrrolic ring, in the present study. The 3-cyanoindole system is of general interest, since differently cyano-substituted indole derivatives find increasing interest as small fluorescence reporters in fluorescent proteins.19,20
Considerably less work has been performed on hydrogen bonded clusters of indole or indole derivatives. Korter et al.25 could show that the binary indole–water complex undergoes considerable solvent reorientation upon excitation to the lowest excited singlet state. The lowest excited singlet states of both the monomer and the water cluster, in which the water is bound linearly to the pyrrolic NH group, have been shown to be of 1Lb character. The dipole moment of the indole–water complex was determined by Kang and Pratt using rotationally resolved electronic Stark spectroscopy.9 They found that the dipole of the water molecule induces a dipole moment in the indole moiety, which amounts to a substantial fraction of 30–40% of the total dipole moment of the cluster. Azaindole–water clusters have been examined using high resolution laser induced fluorescence (HRLIF) spectroscopy. It could be shown that the lowest excited singlet state has 1Lb character, while the excitation in the n = 1 and n = 2 water clusters is to the 1La state.3
Ahn et al.26 investigated 3-cyanoindole and several 3-cyanoindole–water clusters, using mass-selected resonant two-photon ionization (R2PI) and UV–UV hole-burning (UVHB) spectroscopy. Assignments of the different cluster structures were made on the basis of a Franck–Condon analysis of the vibronic spectra. From the comparison of experiment and FC simulation they concluded that only the most stable conformer is present in the molecular beam. According to ab initio calculations, this is the linear N–H⋯O hydrogen bond complex.
In the present study, we investigate the electronic nature of the lowest excited state of 3-cyanoindole, its dipole moments in both ground and excited singlet states and the geometry and electronic nature of the binary 3-cyanoindole–water cluster using a combination of rotationally resolved fluorescence spectroscopy, rotationally resolved electronic Stark spectroscopy, time-correlated single photon counting, and ab initio quantum chemical calculations for a deeper understanding of the photophysics of electronically excited 3-cyanoindole.
2 Experimental section
2.1 Experimental procedures
2.2 Quantum chemical calculations
Structure optimizations were performed employing Dunning's correlation-consistent polarized valence triple zeta (cc-pVTZ) basis set from the Turbomole library.32,33 The equilibrium geometries of the electronic ground and the lowest excited singlet states were optimized using the approximate coupled cluster singles and doubles model (CC2) employing the resolution-of-the-identity approximation (RI).34–36 For the structure optimizations spin-component scaling (SCS) modifications to CC2 were taken into account.37 Vibrational frequencies and zero-point corrections to the adiabatic excitation energies were obtained from numerical second derivatives using the NumForce script.38 For the cluster stabilization energies, the basis set superposition errors (BSSE) have been accounted for, using the counterpoise corrections described by Boys and Bernardi39 and implemented in the JOBBSSE jobscript of turbomole. Additionally, the equilibrium geometries of the lowest electronically excited singlet states were geometry optimized by means of a time-dependent density functional theory (TD-DFT) gradient40,41 using the Becke, three-parameter, Lee–Yang–Parr (B3-LYP) density functional.422.3 Fits of the rovibronic spectra using evolutionary algorithms
Evolutionary algorithms allow us to make a quick and successful automatic assignment of the rotationally resolved spectra, even for large molecules and dense spectra.43–46 Beside a correct Hamiltonian to describe the spectrum and reliable intensities inside the spectrum, an appropriate search method is needed. Evolutionary strategies are a powerful tool to handle complex multi-parameter optimizations and find the global optimum. For the analysis of the presented high-resolution spectra, we used the covariance matrix adaptation evolution strategy (CMA-ES), which is described in detail elsewhere.47,48 In this variant of global optimizers mutations are adapted via a CMA mechanism to find the global minimum, even on rugged search landscapes that are additionally complicated due to noise, local minima and/or sharp bends.3 Results
3.1 Computational results
| Theory SCS-CC2 | Experiment | |||
|---|---|---|---|---|
| 3-CI | 3-CI(d1) | 3-CI | 3-CI(d1) | |
| A′′/MHz | 2255 | 2171 | 2258.53(48) | 2180.09(17) |
| B′′/MHz | 943 | 942 | 947.38(3) | 950.80(2) |
| C′′/MHz | 665 | 657 | 667.44(3) | 660.88(1) |
| ΔI′′/amu Å2 | 0 | 0 | −0.02 | −0.02 |
| μ a′′/D | +3.94 | +3.96 | ±4.15(1) | — |
| μ b′′/D | −4.38 | −4.34 | ±4.20(1) | — |
| μ′′/D | 5.89 | 5.89 | 5.90(1) | — |
| θ D′′/° | +48.0 | +47.53 | ±45.3 | — |
| A′/MHz | 2221 | 2140 | 2227.15(49) | 2150.84(18) |
| B′/MHz | 931 | 931 | 937.46(4) | 938.81(3) |
| C′/MHz | 656 | 649 | 659.83(4) | 653.59(2) |
| ΔI′/amu Å2 | 0 | 0 | −0.08 | −0.06 |
| μ a′/D | +3.71 | +3.75 | ±4.14(1) | — |
| μ b′/D | −3.91 | −3.87 | ±3.39(1) | — |
| μ′/D | 5.39 | 5.39 | 5.35(1) | — |
| θ D′/° | +46.5 | +45.92 | ±39.3 | — |
| ΔA/MHz | −34 | −31 | −31.38(1) | −27.90(1) |
| ΔB/MHz | −12 | −12 | −9.93(1) | −9.64(1) |
| ΔC/MHz | −9 | −9 | −7.61(1) | −7.71(1) |
| ΔνLorentz/MHz | — | — | 16.31(1) | 10.72(1) |
| τ/ns | — | — | 9.8(1) | 14.8(1) |
| θ/° | +4 | +4 | ±15.3(1) | ±3.16(73) |
| θ T/° | −0.45 | −0.45 | 00.52(5) | — |
| ν 0/cm−1 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 045 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299.36(12) 299.36(12) |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.58(15) 306.58(15) |
The inertial defects of 3-cyanoindole in both states are exactly zero for the equilibrium structures which immediately shows the planarity of the molecule.
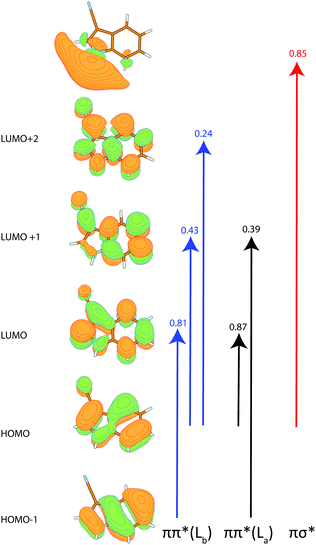
The calculated angle of the transition dipole moment with the inertial a-axis is +4°, cf.Fig. 1. To compare this value better with the transition dipole moment vector of bare indole, the transition dipole moment (TDM) is rotated into the inertial axis frame of indole. This yields an angle of +52° with the inertial a-axis of indole. The respective values in indole (Lb) and 5-cyanoindole (La) are +38° and −12°, respectively. Thus, the orientation of the TDM in 3-cyanoindole, is clearly that of an 1Lb state. The main contributions to the excitation to the lowest excited singlet state are 0.81(LUMO ← HOMO−1) + 0.43(LUMO+1 ← HOMO) + 0.24(LUMO+2 ← HOMO), cf.Fig. 3, which are also representative for a transition to a 1Lb state. The zero-point corrected adiabatic excitation energy amounts to 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 cm−1 (36
156 cm−1 (36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 cm−1) at the CC2 (SCS-CC2) level of theory. The permanent dipole moment in the ground state amounts to 5.95 D and to 5.51 D in the electronically excited 1Lb state.
045 cm−1) at the CC2 (SCS-CC2) level of theory. The permanent dipole moment in the ground state amounts to 5.95 D and to 5.51 D in the electronically excited 1Lb state.
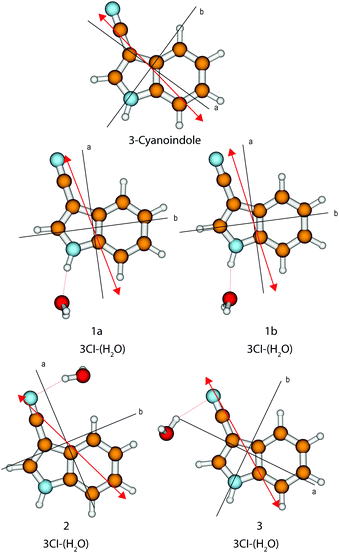 | ||
| Fig. 1 Calculated structures, inertial axes and transition dipole moments of 3-cyanoindole and the 3-cyanoindole water cluster. | ||
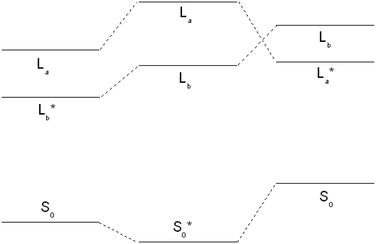
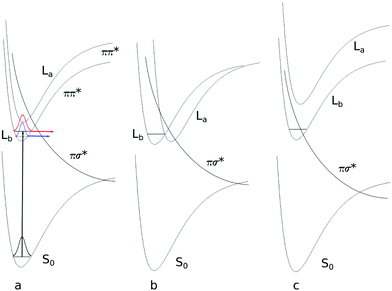
An explicit caveat has to be given for the 1La state optimization. This state is vertically the second excited singlet state at the SCS-CC2 level of theory. Optimization of this state leads, independently of the starting geometry, into a conical intersection with the lowest excited state. However, it is well-known, that the order of 1La and 1Lb states is reversed for time-dependent density functional theory (TD-DFT).49–52 Therefore, we changed the level of theory to TD-DFT using the B3-LYP functional and the cc-pVTZ basis set. As expected, at the TD-DFT level, the vertically lowest state is the 1La state, well below 1Lb. Geometry optimization led to the lowest excited state, which remained the 1La state. Thus, 1La is also adiabatically the lowest excited singlet state at the TD-DFT level. The fact that TD-DFT employing the B3-LYP functional reverses the order of 1La and 1Lb states has been observed before in tryptamine.52
For tryptamine, the correct energetic order of the excited states could be obtained using density functional multi-reference configuration interaction (DFT-MRCI), which correctly takes dynamic and static electron correlation into account, at the TD-DFT optimized geometries. For 3-cyanoindole, the SCS-CC2 energy of the 1La state, which constitutes the second electronically excited singlet state, was calculated at the geometry of the 1Lb state at the TD-DFT level, where it is the lowest electronically excited singlet state. In this geometry, 1La is adiabatically also at the SCS-CC2 level the lowest excited singlet state. These findings are summarized in Fig. 2. However, further optimization starting from this geometry again led to the conical intersection with the 1Lb state.
Using the SCS-CC2 energy at the TD-B3-LYP optimized structure for the 1La state an angle of the TDM with the inertial a axis of −80° is calculated. The leading contributions to the excitation are: 0.87(LUMO ← HOMO) + 0.39(LUMO−1 ← HOMO+1). The zero-point corrected adiabatic excitation energy amounts to 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392 cm−1 and the permanent dipole moment to 5.18 D in the electronically excited 1La state, with an angle of +31° to the inertial a-axis.
392 cm−1 and the permanent dipole moment to 5.18 D in the electronically excited 1La state, with an angle of +31° to the inertial a-axis.
Apart from the two lowest excited ππ* states, the photophysics of indoles is governed by the repulsive πσ* state (Table 2). We calculated the vertical excitation to all three states at the SCS-CC2/cc-pVTZ level of theory. While the two lowest ππ* states are relatively close at the ground state geometry, there is a larger gap to the πσ* state, cf.Table 2. The coefficients for this transition are shown in Fig. 3. The σ* orbital at the hydrogen atom of the NH is diffuse and collapses into the hydrogen 1s orbital upon distortion along the NH coordinate, as has been shown by Sobolewski and Domcke.17,53–55 For 3-cyanoindole, the πσ*–ππ* difference is by more than 1000 cm−1 smaller compared to indole. The dipole moment of the πσ* state in indole is more than 5 D higher than in the ground state, while for 3-cyanoindole only an increase of 2 D is found. The oscillator strengths of the respective states of indole and 3-cyanoindole are of comparable size, with the 1La oscillator strength between 2 and 3 times larger than for the 1Lb state.
| Indole | 3-Cyanoindole | |||||
|---|---|---|---|---|---|---|
| E (cm−1) | μ (D) | f | E (cm−1) | μ (D) | f | |
| ππ* (Lb) | 0 | 2.2 | 0.04 | 0 | 5.4 | 0.05 |
| ππ* (La) | 3534 | 5.0 | 0.09 | 1828 | 6.3 | 0.12 |
| πσ* | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
7.3 | 0.00 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 552 |
7.6 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 3-cyanoindole–water complexes. For details see text
1 3-cyanoindole–water complexes. For details see text
| SCS CC2/cc-pVTZ | Experiment | ||||||
|---|---|---|---|---|---|---|---|
| 1a | 1b | 2 | 3 | σ = 1 | σ = 0 | Δσ | |
| A′′/MHz | 1083 | 1093 | 1292 | 2015 | 1104.10 | 1100.04 | −4.06 |
| B′′/MHz | 745 | 743 | 739 | 559 | 728.29 | 728.01 | −0.28 |
| C′′/MHz | 442 | 443 | 471 | 439 | 439.07 | 438.99 | −0.08 |
| ΔI′′/amu Å2 | −2.33 | −2.33 | −1.92 | −2.06 | −0.6380 | −2.3774 | |
| A′/MHz | 1091 | 1092 | 1279 | 1979 | 1099.63 | 1096.97 | −2.66 |
| B′/MHz | 734 | 734 | 731 | 554 | 724.63 | 724.33 | −0.30 |
| C′/MHz | 440 | 440 | 466 | 434 | 437.28 | 437.20 | 0.00 |
| ΔI′/amu Å2 | −2.56 | −3.25 | −1.90 | −2.46 | −1.2938 | −2.0979 | |
| ΔA/MHz | 8.10 | −2.33 | −12.85 | −36.19 | −4.47 | −3.07 | |
| ΔB/MHz | −10.95 | −8.79 | −7.70 | −5.44 | −3.65 | −3.68 | |
| ΔC/MHz | −2.56 | −3.25 | −4.84 | −4.92 | −1.79 | −1.79 | |
| ΔνLor./MHz | — | — | — | — | 43.51 | 43.51 | |
| τ/ns | — | — | — | — | 3.66 | 3.66 | |
| θ/° | −39 | −39 | −26 | +13 | ±48.26 | ±48.26 | |
| ν 0/cm−1 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 029 029 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024 024 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 140 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.2 262.2 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.9 261.9 |
|
| Δν0/MHz | — | — | — | — | −8977.46 | ||
The stabilization energies, including zero-point energy (ZPE) corrections and considering the BSSE, are given in Table 4. Both NH⋯O hydrogen bond structures are by about 7 and 6 kJ mol−1 more stable than the CN⋯H hydrogen bond structures. The stabilization energies of 1a and 1b are too close to make a definite statement as to which of the two cluster structures is the more stable one. Both cluster structures show a slightly larger stabilization in the excited state and slight red shifts of their adiabatic excitation energies relative to that of the monomer. The origin of conformer 1a is red-shifted by 16 cm−1, and 1b shows a red-shift of 21 cm−1. The experimental value is 51 cm−1, cf. Section 4.1.
| 1a | 1b | 2 | 3 | |
|---|---|---|---|---|
| ΔEstab.(S0)/kJ mol−1 | −28.46 | −28.35 | −20.41 | −21.86 |
| ΔEstab.(S0)/cm−1 | −2378.7 | −2370.2 | −1706.4 | −2122.01 |
| ΔEstab.(S1)/kJ mol−1 | −28.64 | −28.61 | −21.18 | −20.71 |
| ΔEstab.(S1)/cm−1 | −2379.9 | −2391.3 | −1770.7 | −1731.2 |
| ΔEadiabatic/cm−1 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 029 029 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024 024 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 140 |
| ΔEvertical@opt. S0 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 832 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
| ΔEvertical@opt. S1 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 843 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009 009 |
The orientation of the transition dipole moment (Fig. 1), as well as the main contributions to the excitation to the lowest excited singlet state of 0.81(LUMO ← HOMO−1) + 0.41(LUMO+1 ← HOMO) − 0.27(LUMO+2 ← HOMO), cf. Fig. S1 of the ESI†, are indicative for a transition to the 1Lb state also for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water cluster.
1 water cluster.
3.2 Experimental results
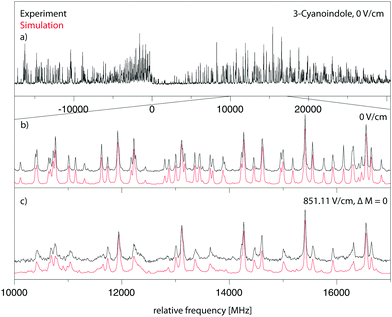
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299.36 cm−1 (0 on the scale of the figure) along with the best fit at zero field (trace (b)) and at a field strength of 851.11 V cm−1 (trace (c)). The electric field in the chosen set-up is parallel to the polarization of the plane of the exciting light, thus ΔM = 0 selection rules for the Stark spectrum hold. The spectrum was fit using a CMA-ES; the molecular parameters from the fit are summarized in Table 1 and are compared to the results of the SCS-CC2/cc-pVTZ calculations.
299.36 cm−1 (0 on the scale of the figure) along with the best fit at zero field (trace (b)) and at a field strength of 851.11 V cm−1 (trace (c)). The electric field in the chosen set-up is parallel to the polarization of the plane of the exciting light, thus ΔM = 0 selection rules for the Stark spectrum hold. The spectrum was fit using a CMA-ES; the molecular parameters from the fit are summarized in Table 1 and are compared to the results of the SCS-CC2/cc-pVTZ calculations.
The origin band is an ab-hybrid with predominant a-type character. The exact analysis yields an angle of ±15.3°. The indeterminacy of the TDM orientation can be resolved by comparison to the ab initio computed value of +4°. Thus, the orientation as shown in Fig. 1 seems to be the experimentally observed one. A more reliable determination can be performed on the basis of the TDM angle in the deuterated isotopologue of 3-cyanoindole, and on the basis of the relative orientation of the transition moment and axis reorientation angle, which will be presented in Section 4.1.
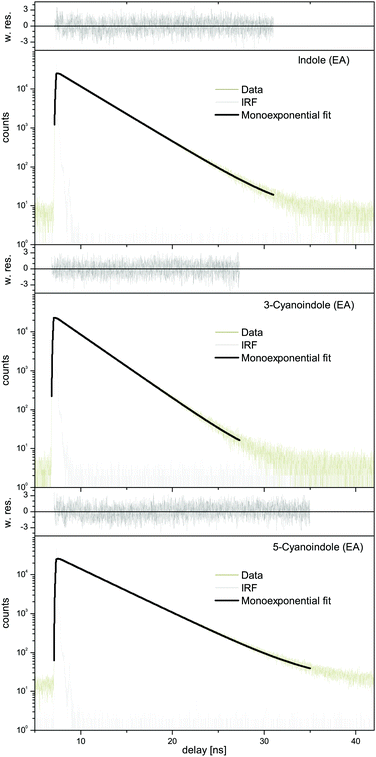
A Lorentzian linewidth of 16.31 MHz corresponds to an excited state lifetime of 9.8 ns.
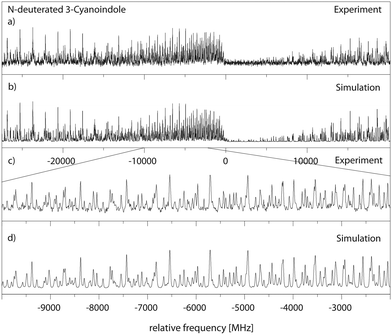
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.58 cm−1 (0 on the scale of the figure). The spectrum is composed mainly of a-type bands similar to the undeuterated species. The results of the CMA-ES fit of the spectrum are summarized in Table 1, where they are compared to the results of the SCS-CC2/cc-pVTZ calculations. The excited state lifetime of 14.8 ns is considerably longer than that of undeuterated 3-cyanoindole.
306.58 cm−1 (0 on the scale of the figure). The spectrum is composed mainly of a-type bands similar to the undeuterated species. The results of the CMA-ES fit of the spectrum are summarized in Table 1, where they are compared to the results of the SCS-CC2/cc-pVTZ calculations. The excited state lifetime of 14.8 ns is considerably longer than that of undeuterated 3-cyanoindole.
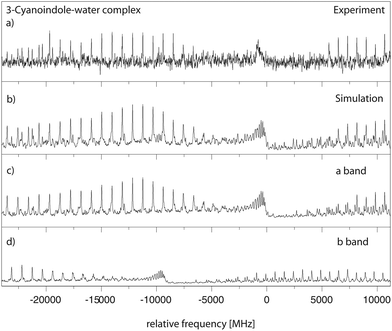
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.2 cm−1. This origin band is redshifted by 51 cm−1 relative to the origin of 3-cyanoindole at 35
262.2 cm−1. This origin band is redshifted by 51 cm−1 relative to the origin of 3-cyanoindole at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299.36 cm−1. The spectrum is split into two subbands due to the large amplitude internal motion of the water moiety. The molecular symmetry group which takes this motion into account is G4, isomorphic with the point group C2v. The lowest torsional state (with σ = 0) is of A1 symmetry, and the energetically following (with σ = 1) of B2 symmetry. Both subbands are fit using rigid asymmetric rotor selection rules, with the difference of the vibronic origins as an additional parameter. Trace (a) of Fig. 6 shows the experimental spectrum, and trace (b) the simulation using the best fit parameters from Table 3. The following traces (c) and (d) give the individual simulations for the two torsional subbands, due to the internal rotation of the water moiety. The resulting molecular parameters are given in Table 3. The spectrum is an ab-hybrid band with 56% b-type and 44% a-type character, and is split into two subbands by the internal rotation of the water moiety. The splitting between the origins of the two sub-bands amounts to 8977 MHz. The Lorentzian linewidth was determined to be 43 MHz, leading to an excited state lifetime of 3.6 ns.
299.36 cm−1. The spectrum is split into two subbands due to the large amplitude internal motion of the water moiety. The molecular symmetry group which takes this motion into account is G4, isomorphic with the point group C2v. The lowest torsional state (with σ = 0) is of A1 symmetry, and the energetically following (with σ = 1) of B2 symmetry. Both subbands are fit using rigid asymmetric rotor selection rules, with the difference of the vibronic origins as an additional parameter. Trace (a) of Fig. 6 shows the experimental spectrum, and trace (b) the simulation using the best fit parameters from Table 3. The following traces (c) and (d) give the individual simulations for the two torsional subbands, due to the internal rotation of the water moiety. The resulting molecular parameters are given in Table 3. The spectrum is an ab-hybrid band with 56% b-type and 44% a-type character, and is split into two subbands by the internal rotation of the water moiety. The splitting between the origins of the two sub-bands amounts to 8977 MHz. The Lorentzian linewidth was determined to be 43 MHz, leading to an excited state lifetime of 3.6 ns.
| Indole | 3-CI | 3-CI(d1) | 5-CI | 3-CI–H2O | |
|---|---|---|---|---|---|
| a Excitation of 3-cyanoindole and 3-cyanoindole(d1) in ethyl acetate (EA) at 283 nm. b 3-CI(d1) has been measured in D2O with excitation at 283 nm. c Excitation of indole in EA at 284 nm. d Excitation of 5-cyanoindole in EA at 295 nm. | |||||
| θ/° | +3812 | +35 | +36 | −1222 | +51 |
| τ/ns | 17.612 | 9.8 | 14.8 | 1222 | 3.9 |
| τ(EA)solv./ns | 3.1c | 2.6a | 2.7a | 3.6d | — |
| τ(H2O)solv./ns | 4.519 | <0.0519 | <0.02b | 0.319 | — |
4 Discussion
4.1 3-Cyanoindole
The angle of the TDM with the inertial a-axis was determined experimentally to be ±15.3°. In the following we will show two independent determinations of the sign of the TDM angle, which do rely on the comparison to the calculated TDM orientation.
The geometry change upon electronic excitation causes a reorientation of the inertial axes of a molecule if its symmetry is sufficiently low.56 The molecule fixed coordinate system, which rotates with the molecule, and the space fixed coordinate system can be interconverted by the Euler rotation matrix. In the case of different geometries of the two states, which are connected by the spectroscopic transition, two moving axis systems, and consequently two sets of Eulerian angles θ, ϕ, and χ are needed, one for each state. In this way, the rotational selection rules, which are valid only for unchanged geometries, have to be modified. Hougen and Watson's approach to this problem is the diagonalization of the rotational Hamiltonian for each state separately, and a rotation of the eigenvectors through a rotation matrix containing the axis reorientation angles θT, ϕT, and χT. Pratt and coworkers introduced a different procedure.57 In spite of rotating the wave functions, they express the Hamiltonian of the excited state in the coordinates of the ground state. Thus, the rotation of the eigenvectors is replaced by a rotation of the Hamiltonian about the axis reorientation angles θT, ϕT, and χT. This approach has the big advantage that the similarity transformation has to be applied only once, while in the Hougen–Watson approach, each J block has to be rotated by means of a (2J + 1) × (2J + 1) rotation matrix. When rotated, the excited state Hamiltonian has no longer the four group symmetry of the ground state. Thus, the effect of axis reorientation is a change of the intensities of several rovibronic lines. The line positions however are not altered, since the rotated and unrotated eigenfunctions are related though a similarity transformation. Thus, the eigenvalues of the rotated and unrotated Hamiltonian are the same.57
Pratt and coworkers have shown how the relative orientation of the transition dipole moment θ and the axis reorientation θT can be used to remove the indeterminacy of the sign of θ. The combinations of +θ/+θT and −θ/−θT have the same intensity pattern, which in turn is different for the +θ/−θT and −θ/+θT combinations. From a fit of the rovibronic intensities to the signed value of the axis reorientation angle, it can be deduced if TDM and axis reorientation have the same or opposite signs.
From the SCS-CC2 optimized structures, the axis reorientation angle of the inertial axis system upon electronic excitation θT can be determined using the relation for planar molecules given by Hougen and Watson:56
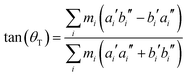 | (1) |
Since axis reorientation has no effect on the eigenvalues, i.e. the energies of the rovibrational levels, the only quantity to be fit is the axis reorientation angle θT, leaving all other parameters at their before determined values. However, only a few lines are considerably affected by axis reorientation. Improvement of the cost function in the course of the optimization might therefore be concealed by the majority of lines whose intensities do change. In order to circumvent this problem, we included only sections of the spectrum in the fit, which show, guided by a preliminary simulation, strong intensity variations. Two kinds of solutions were obtained. The combination of θ positive and θT negative as well as θ negative and θT positive had a better cost function than the combination of both angles positive or both angles negative. Therefore, we know θT and θ must have different signs. Using the fact that θT is negative from the above considerations, θ must be positive.
To facilitate the comparison to other indoles, we transform the angle of the TDM to refer to the pseudo C2-axis of indole. The results are shown in Table 5. Clearly, the orientation of the TDM is the same as in indole, and the lowest excited singlet state of 3-cyanoindole can be assigned to an 1Lb like state, in contrast to 5-cyanoindole in which the opposite sign of the TDM points to an 1La state.
The fact that no stable minimum at the SCS-CC2 level could be located for the 1La state might arise from two different reasons. (i) The 1La minimum might be so far outside the Franck–Condon region, that our searches just missed the minimum structure and followed instead the falling 1La potential right into the conical intersection (CI) with 1Lb. Although we tried a plethora of starting geometries, which were constructed from the known 1La geometries of indole and 5-cyanoindole, we cannot completely exclude this reason. (ii) A much more probable explanation for this finding is a very shallow 1La minimum in the coordinate, which connects 1La and 1Lb through the CI. Such a case was found for tryptamine.58 The slightest deviations from the correct 1La geometry at the chosen level of theory will then cause the optimization to run into the CI.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water complex the shortest lifetime of 3.9 ns has been measured, cf.Table 5. Interestingly, also the lifetime of 3-cyanoindole in water solution is the shortest (<0.05 ns),19 followed by the aqueous solution of 5-cyanoindole (0.3 ns)19 and indole (4.5 ns).19 The lifetime of deuterated 3-cyanoindole in the gas phase is longer than that of the undeuterated isotopologue (14.8 vs. 9.8 ns). A similar trend has been found for phenol (13.3 ns vs. 2.4 ns). Sobolewski and Domcke have shown, that along with the lowest two excited singlet 1La and 1Lb states, which are of ππ* character, a third state of πσ* character plays a crucial role in the photophysics of these chromophores.17,53–55 This πσ* state is repulsive along the OH coordinate for phenol and along the NH coordinate for indole and forms conical intersections with the directly excited state and subsequently with the electronic ground state. For excitations above the threshold, a rapid decay channel is open, which connects the primarily excited ππ* state through a conical intersection (CI) with the πσ* state, and subsequently through a second CI with the ground state. The ππ*–πσ* CI induces a barrier on the S1 potential energy surfaces, through which a wave packet prepared at the zero-point level of the primarily excited state can tunnel. This causes the S1 state lifetime of phenol to be as short as 2.4 ns, while the lifetime of deuterated phenol is considerably longer (13.3 ns) due to the lower zero-point energy. The same behavior is found for 3-cyanoindole and its ND-deuterated isotopologue (Fig. 8a). The isotope effect on the excited state lifetime of indole is negligible (17.6 ns vs. 17.2 ns for the deuterated isotopologue59), a consequence of the larger barrier formed by the ππ*–πσ* CI in indole. We therefore claim a lower barrier, formed on the S1 potential energy surface, to be responsible for the shorter lifetime of 3-cyanoindol compared to indole and 5-cyanoindole. The calculation of the vertically excited ππ* and πσ* states in Section 3.1 strongly supports this suggestion.
1 water complex the shortest lifetime of 3.9 ns has been measured, cf.Table 5. Interestingly, also the lifetime of 3-cyanoindole in water solution is the shortest (<0.05 ns),19 followed by the aqueous solution of 5-cyanoindole (0.3 ns)19 and indole (4.5 ns).19 The lifetime of deuterated 3-cyanoindole in the gas phase is longer than that of the undeuterated isotopologue (14.8 vs. 9.8 ns). A similar trend has been found for phenol (13.3 ns vs. 2.4 ns). Sobolewski and Domcke have shown, that along with the lowest two excited singlet 1La and 1Lb states, which are of ππ* character, a third state of πσ* character plays a crucial role in the photophysics of these chromophores.17,53–55 This πσ* state is repulsive along the OH coordinate for phenol and along the NH coordinate for indole and forms conical intersections with the directly excited state and subsequently with the electronic ground state. For excitations above the threshold, a rapid decay channel is open, which connects the primarily excited ππ* state through a conical intersection (CI) with the πσ* state, and subsequently through a second CI with the ground state. The ππ*–πσ* CI induces a barrier on the S1 potential energy surfaces, through which a wave packet prepared at the zero-point level of the primarily excited state can tunnel. This causes the S1 state lifetime of phenol to be as short as 2.4 ns, while the lifetime of deuterated phenol is considerably longer (13.3 ns) due to the lower zero-point energy. The same behavior is found for 3-cyanoindole and its ND-deuterated isotopologue (Fig. 8a). The isotope effect on the excited state lifetime of indole is negligible (17.6 ns vs. 17.2 ns for the deuterated isotopologue59), a consequence of the larger barrier formed by the ππ*–πσ* CI in indole. We therefore claim a lower barrier, formed on the S1 potential energy surface, to be responsible for the shorter lifetime of 3-cyanoindol compared to indole and 5-cyanoindole. The calculation of the vertically excited ππ* and πσ* states in Section 3.1 strongly supports this suggestion.
For the water clusters in the gas phase, only lifetimes for indole–H2O and 3-cyanoindole–H2O (3.6 ns) are known experimentally. Indole–H2O however, is hard to compare, because two very different values are reported. Korter et al. determined a value of 5 ns from the Lorentz component to the full linewidth in a rotationally resolved electronic spectrum of the origin band.25 Arnold and Sulkes found a value of 21 ns using time-correlated single photon counting after excitation of the electronic origin.60 What is then the reason for the short lifetime in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cluster and the ultrashort lifetime in the aqueous solution of 3-cyanoindole? The answer to this problem is further complicated by the fact that depending on the relative stabilization of the different excited states, conical intersections not only between the ππ* and the πσ* states develop, but also between the lowest ππ* 1La and 1Lb states58 (cf.Fig. 8b). Regarding the fact that the ππ*–πσ* barrier of 3-cyanoindole is lower than that of indole (vide supra), it seems plausible that the πσ* potential is lowered even further through stabilization via the water dipole (Fig. 8c). The short lifetime would then originate from the increase of the nonradiative decay rate. A conclusive answer, however, can only be given if the oscillator strengths to the fully adiabatically optimized excited states along the dissociative NH coordinate are known. These calculations are currently under way.
1 cluster and the ultrashort lifetime in the aqueous solution of 3-cyanoindole? The answer to this problem is further complicated by the fact that depending on the relative stabilization of the different excited states, conical intersections not only between the ππ* and the πσ* states develop, but also between the lowest ππ* 1La and 1Lb states58 (cf.Fig. 8b). Regarding the fact that the ππ*–πσ* barrier of 3-cyanoindole is lower than that of indole (vide supra), it seems plausible that the πσ* potential is lowered even further through stabilization via the water dipole (Fig. 8c). The short lifetime would then originate from the increase of the nonradiative decay rate. A conclusive answer, however, can only be given if the oscillator strengths to the fully adiabatically optimized excited states along the dissociative NH coordinate are known. These calculations are currently under way.
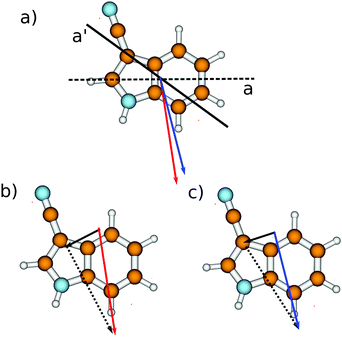
For 5-cyanoindole we found a good additivity of the dipole moments of indole and of the cyano fragment in the electronic ground state.61 In this molecule, the indole dipole and the dipole of the cyano fragment which is attached to the benzenoid ring are nearly aligned. For 3-cyanoindole, the individual dipoles form a large angle, and the cyano fragment is attached to the pyrrolic ring. Fig. 9b shows the experimental dipole moment vector of 3-cyanoindole (red, straight vector) and of indole (black, straight vector). Subtracting the experimentally determined dipole moment vector of 3-cyanoindole from that of indole9 should lead to the dipole moment vector of the substituent (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) CN =
CN = ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) 3CN–indole −
3CN–indole − ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) indole). If the dipole moments of indole and the cyano fragment are additive like in 5-cyanoindole, the difference vector will point in the direction of the fragment dipole with the corresponding length of the fragment dipole, cf.Fig. 9b and c. The most appropriate dipole moments to mimic the fragment dipole of the cyano group, attached to the pyrrole ring, are those of methyl cyanide CH3CN, isopropyl cyanide (CH3)CHCN and benzonitrile C6H5CN. The ground state dipole moment of methyl cyanide was determined by Steiner and Gordy to be 3.913 D,62 and the dipole moment of isopropyl cyanide has been determined to be 4.07 D by Müller et al.63 The most exact value of the benzonitrile dipole moment was reported by Wohlfahrt et al. to be 4.5152 D.31 Thus, a value of around 4 D for the cyano fragment, colinear with the CN bond, can be expected. Inspection of Fig. 9b shows that the fragment dipole indeed points in the same direction as the cyano fragment dipole. From the vectorial difference of the ground state dipoles a fragment dipole moment of 5.5 D is predicted, which is more than 1 D larger than expected from a simple additivity model. Using the excited state dipole moments of indole and 3-cyanoindole, a value of 5.6 D results, in agreement with the fragment dipole determined from the ground state values. Inspection of the direction of the fragment dipole in Fig. 9c however shows that in the excited state, even the direction of the dipole moment deviates from that of the fragment.
indole). If the dipole moments of indole and the cyano fragment are additive like in 5-cyanoindole, the difference vector will point in the direction of the fragment dipole with the corresponding length of the fragment dipole, cf.Fig. 9b and c. The most appropriate dipole moments to mimic the fragment dipole of the cyano group, attached to the pyrrole ring, are those of methyl cyanide CH3CN, isopropyl cyanide (CH3)CHCN and benzonitrile C6H5CN. The ground state dipole moment of methyl cyanide was determined by Steiner and Gordy to be 3.913 D,62 and the dipole moment of isopropyl cyanide has been determined to be 4.07 D by Müller et al.63 The most exact value of the benzonitrile dipole moment was reported by Wohlfahrt et al. to be 4.5152 D.31 Thus, a value of around 4 D for the cyano fragment, colinear with the CN bond, can be expected. Inspection of Fig. 9b shows that the fragment dipole indeed points in the same direction as the cyano fragment dipole. From the vectorial difference of the ground state dipoles a fragment dipole moment of 5.5 D is predicted, which is more than 1 D larger than expected from a simple additivity model. Using the excited state dipole moments of indole and 3-cyanoindole, a value of 5.6 D results, in agreement with the fragment dipole determined from the ground state values. Inspection of the direction of the fragment dipole in Fig. 9c however shows that in the excited state, even the direction of the dipole moment deviates from that of the fragment.
4.2 3-Cyanoindole–water
Further information is contained in the difference of the rotational constants between the σ = 0 and σ = 1 bands. Table 3 shows that in the electronic ground state mainly A changes, while B and C are nearly the same for the subtorsional levels. Thus, the torsional axis is mostly parallel to the a inertial axis in the cluster. The difference of the rotational constants between σ = 0 and σ = 1 bands (ΔBg = Bσ=0g − Bσ=1g) contains the second order perturbation terms, which can be used for an independent determination of the torsional barrier. A Levenberg–Marquart fit of the subtorsional splitting and the differences of the rotational constants yield barriers of 148 cm−1 for the S0 and of 125 cm−1 for the S1 state, respectively, for a torsional constant of 15.2 cm−1.
The position of the water molecule in the 3-cyanoindole–water cluster can be determined from the rotational constants of the water cluster and the monomer without further knowledge of the monomer structure using a Kraitchman66 analysis. The only assumption which is made therein is that the structure of the monomer moiety does not change upon cluster formation. While the original intention in using the Kraitchman equations is the determination of the Cartesian coordinates of an isotopically substituted atom in a molecule, it is also applicable in determining the center-of-mass (COM) distance of the two constituents of binary clusters. This procedure has first been applied to noble gas clusters of organic molecules,67 which directly yields the position of the noble gas atom in the inertial frame of the uncomplexed monomer. Later, it was extended to molecular clusters of hydrogen donors with water, in which the distance of the water COM from the COM of the organic molecule was determined. From the known structure of the water moiety, and the position of the oxygen (phenol) or nitrogen (indole) in the inertial frame of the monomer, also the heavy atom distance in hydrogen bonded clusters like N–H⋯O or O–H⋯O could be determined.
Using this method, we determined the distance between the COMs of the 3-cyanoindole monomer and of the water moiety in the ground state to be 494.1 pm and in the electronically excited state to be 492.1 pm. The Kraitchman analysis for the amino hydrogen position in both the ground and excited states of 3-cyanoindole has been performed using the rotational constants of 3-cyanoindole and of the N-deuterated 3-cyanoindole isotopologue from Table 1. The r0 coordinates of the H-atom along with the r0 coordinates of the water COM in the same reference frame are shown in Table 6.
| State | S0 | S1 | ||
|---|---|---|---|---|
| NH | Water | NH | Water | |
| a | 7.4 | 155.3 | 7.6 | 157.2 |
| b | 285.3 | 469.1 | 283.9 | 466.3 |
| R | 285.4 | 494.1 | 284.0 | 492.1 |
| NH⋯O(exp.) | 201.9 | 201.7 | ||
| NH⋯O(theo.) | 192.6 | 192.3 | ||
From the so determined distance of the water COM from the amino hydrogen and the known distance of the COM of the water moiety from the water oxygen atom, the NH⋯O distance can be determined to be 201.9 pm in the ground state and 201.7 in the excited state. This is the lower limit under the assumption that the amino hydrogen, water COM and oxygen atom are located on a straight line. If there is an angle α between the HOH plane and the hydrogen bond, the resulting bond length would be smaller by a factor of cos(α). For both conformers 1a and 1b this angle is smaller than 10°, equivalent to a reduction of less than 3 pm. The obvious difference between the experimental and the ab initio value for the hydrogen bond length results from zero-point vibrational averaging of the hydrogen bond along its very shallow stretching coordinate.
5 Conclusions
The dipole moment of 3-cyanoindole and its orientation in the ground and the lowest electronically excited state could be determined to be very similar. The excited state lifetime of 3-cyanoindole is considerably shorter than that of indole and 5-cyanoindole with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water cluster of 3-cyanoindole being especially short-lived. The electronic nature of the lowest excited state is a locally excited (LE) state with strong 1Lb character. The adiabatically higher lying 1La state has, in contrast to indole and 5-cyanoindole (and many other indole derivatives), a smaller permanent dipole moment. Therefore, the 1Lb state is stabilized more strongly upon attachment of the polar water molecule than the 1La state. This causes the 1
1 water cluster of 3-cyanoindole being especially short-lived. The electronic nature of the lowest excited state is a locally excited (LE) state with strong 1Lb character. The adiabatically higher lying 1La state has, in contrast to indole and 5-cyanoindole (and many other indole derivatives), a smaller permanent dipole moment. Therefore, the 1Lb state is stabilized more strongly upon attachment of the polar water molecule than the 1La state. This causes the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water cluster to be also of 1Lb character. Although we can confirm the above statement only for the binary water cluster, one might speculate that the exceptionally short lifetime of 3-cyanoindole in water solution might be due to the fact that the emitting state is the 1Lb which is different from the other cyanoindoles and indole in which 1La emission is observed.14
1 water cluster to be also of 1Lb character. Although we can confirm the above statement only for the binary water cluster, one might speculate that the exceptionally short lifetime of 3-cyanoindole in water solution might be due to the fact that the emitting state is the 1Lb which is different from the other cyanoindoles and indole in which 1La emission is observed.14
The characterization of the emitting state could be performed using high resolution (Stark) spectroscopy for the first time. Permanent dipole moments, transition dipoles, fluorescence lifetimes and structures of the isolated molecule, as well as of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water cluster (with the exception of the permanent dipole moments) could be obtained for the first time. These investigations show that already the first solvating water molecule opens the way to the unusually short life time of 3-cyanoindole in water solution. One might ask why we omitted the measurement of the Stark spectrum for the water cluster. Certainly, this would have added extremely important information about the function of the water moiety in the photophysics of the monomer. Unfortunately, 3-cyanoindole behaves differently than other cyanoindoles. Upon heating in the source chamber, 3-cyanoindole sublimates into an extremely fine powder, which clogs the orifice of the nozzle after a few minutes even at strongly elevated temperatures of the nozzle. Since the time for optimization of the cluster conditions was too short to get a better signal to noise ratio, we were unable to record the Stark spectrum.
1 water cluster (with the exception of the permanent dipole moments) could be obtained for the first time. These investigations show that already the first solvating water molecule opens the way to the unusually short life time of 3-cyanoindole in water solution. One might ask why we omitted the measurement of the Stark spectrum for the water cluster. Certainly, this would have added extremely important information about the function of the water moiety in the photophysics of the monomer. Unfortunately, 3-cyanoindole behaves differently than other cyanoindoles. Upon heating in the source chamber, 3-cyanoindole sublimates into an extremely fine powder, which clogs the orifice of the nozzle after a few minutes even at strongly elevated temperatures of the nozzle. Since the time for optimization of the cluster conditions was too short to get a better signal to noise ratio, we were unable to record the Stark spectrum.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support of the Deutsche Forschungsgemeinschaft via grant SCHM1043/12-3 is gratefully acknowledged. Computational support and infrastructure was provided by the “Center for Information and Media Technology” (ZIM) at the Heinrich-Heine-University Düsseldorf (Germany). We furthermore thank the Regional Computing Center of the University of Cologne (RRZK) for providing computing time on the DFG-funded High Performance Computing (HPC) system CHEOPS as well as support. Financial support provided by CONACYT under the grant 277871 is greatly appreciated.References
- J. R. Platt, J. Chem. Phys., 1949, 17, 484–495 CrossRef.
- G. Weber, Biochem. J., 1960, 75, 335–345 CrossRef PubMed.
- T. B. C. Vu, I. Kalkman, W. L. Meerts, Y. N. Svartsov, C. Jacoby and M. Schmitt, J. Chem. Phys., 2008, 128, 214311 CrossRef PubMed.
- B. Albinsson and B. Nordén, J. Phys. Chem., 1992, 96, 6204 CrossRef.
- D. M. Sammeth, S. Yan, L. H. Spangler and P. R. Callis, J. Phys. Chem., 1990, 94, 7340 CrossRef.
- T. L. O. Barstis, L. I. Grace, T. M. Dunn and D. L. Lubman, J. Phys. Chem., 1993, 97, 5820 CrossRef.
- L. A. Philips and D. H. Levy, J. Chem. Phys., 1986, 85, 1327–1332 CrossRef.
- G. Berden, W. L. Meerts and E. Jalviste, J. Chem. Phys., 1995, 103, 9596–9606 CrossRef.
- C. Kang, T. M. Korter and D. W. Pratt, J. Chem. Phys., 2005, 122, 174301 CrossRef PubMed.
- J. Zuclich, J. U. von Schütz and A. H. Maki, J. Am. Chem. Soc., 1974, 96, 710–714 CrossRef PubMed.
- B. J. Fender, K. W. Short, D. K. Hahn and P. R. Callis, Int. J. Quantum Chem., 1999, 72, 347–356 CrossRef.
- J. Küpper, D. W. Pratt, W. L. Meerts, C. Brand, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4980–4988 RSC.
- P. R. Callis, J. T. Vivian and L. S. Slater, Chem. Phys. Lett., 1995, 244, 53 CrossRef.
- L. Serrano-Andrés and B. O. Roos, J. Am. Chem. Soc., 1996, 118, 185–195 CrossRef.
- A. C. Borin and L. Serrano-Andrés, Chem. Phys., 2000, 262, 253–265 CrossRef.
- L. Serrano-Andrés and A. C. Borin, Chem. Phys., 2000, 262, 267–283 CrossRef.
- A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 1999, 315, 293–298 CrossRef.
- C. Brand, J. Küpper, D. W. Pratt, W. L. Meerts, D. Krügler, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4968–4997 RSC.
- M. R. Hilaire, D. Mukherjee, T. Troxler and F. Gai, Chem. Phys. Lett., 2017, 685, 133–138 CrossRef PubMed.
- M. R. Hilaire, I. A. Ahmed, C.-W. Lin, H. Jo, W. F. DeGrado and F. Gai, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6005–6009 CrossRef PubMed.
- B. N. Markiewicz, D. Mukherjee, T. Troxler and F. Gai, J. Phys. Chem. B, 2016, 210, 936–944 CrossRef PubMed.
- O. Oeltermann, C. Brand, B. Engels, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2012, 14, 10266–10270 RSC.
- C. Brand, B. Happe, O. Oeltermann, M. Wilke and M. Schmitt, J. Mol. Struct., 2013, 1044, 21–25 CrossRef.
- B. Stuhlmann, A. Gräßle and M. Schmitt, Phys. Chem. Chem. Phys., 2014, 16, 899–905 RSC.
- T. M. Korter, D. W. Pratt and J. Küpper, J. Phys. Chem. A, 1998, 102, 7211–7216 CrossRef.
- A. Ahn, A. Min, C. J. Moon, J. H. Lee and M. Y. Choi, Chem. Phys. Lett., 2014, 616–617, 55–60 CrossRef.
-
S. Gerstenkorn and P. Luc, Atlas du spectre d'absorption de la molécule d'iode 14
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–20
800–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, CNRS, Paris, 1986 Search PubMed.
000 cm−1, CNRS, Paris, 1986 Search PubMed. - M. Schmitt, Habilitation, Heinrich-Heine-Universität, Math. Nat. Fakultät, Düsseldorf, 2000 Search PubMed.
- M. Schmitt, J. Küpper, D. Spangenberg and A. Westphal, Chem. Phys., 2000, 254, 349–361 CrossRef.
- J. Wilke, M. Wilke, W. L. Meerts and M. Schmitt, J. Chem. Phys., 2016, 144, 044201 CrossRef PubMed.
- K. Wohlfart, M. Schnell, J. U. Grabow and J. Küpper, J. Mol. Spectrosc., 2014, 247, 119–121 CrossRef.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef.
- J. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951 CrossRef.
- C. Hättig, J. Chem. Phys., 2002, 118, 7751–7761 CrossRef.
- A. Hellweg, S. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 1159–1169 RSC.
- P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518 CrossRef.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 117, 7433 CrossRef.
- W. L. Meerts, M. Schmitt and G. Groenenboom, Can. J. Chem., 2004, 82, 804–819 CrossRef.
- W. L. Meerts and M. Schmitt, Phys. Scr., 2005, 73, C47–C52 CrossRef.
- W. L. Meerts and M. Schmitt, Int. Rev. Phys. Chem., 2006, 25, 353–406 Search PubMed.
- M. Schmitt and W. L. Meerts, Handbook of High Resolution Spectroscopy, John Wiley and Sons, 2011 Search PubMed.
- A. Ostenmeier, A. Gawelcyk and N. Hansen, Parallel Problem Solving from Nature, PPSN III, Springer, Berlin/Heidelberg, 1994 Search PubMed.
- N. Hansen and A. Ostermeier, Evol. Comput., 2001, 9, 159–195 CrossRef PubMed.
- S. Grimme and M. Parac, ChemPhysChem, 2003, 4, 292–295 CrossRef PubMed.
- M. Parac and S. Grimme, Chem. Phys., 2003, 292, 11–21 CrossRef.
- S. Arulmozhiraja and M. L. Coote, J. Chem. Theory Comput., 2011, 8, 575–584 CrossRef PubMed.
- M. Schmitt, R. Brause, C. Marian, S. Salzmann and W. L. Meerts, J. Chem. Phys., 2006, 125, 124309 CrossRef PubMed.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- W. Domcke and A. L. Sobolewski, Science, 2003, 302, 1693–1694 CrossRef PubMed.
- J. T. Hougen and J. K. G. Watson, Can. J. Phys., 1965, 43, 298–320 CrossRef.
- A. Held, B. B. Champagne and D. W. Pratt, J. Chem. Phys., 1991, 95, 8732 CrossRef.
- M. Böhm, J. Tatchen, D. Krügler, K. Kleinermanns, M. G. D. Nix, T. A. LeGreve, T. S. Zwier and M. Schmitt, J. Phys. Chem. A, 2009, 113, 2456–2466 CrossRef PubMed.
- G. A. Bickel, D. R. Demmer, E. A. Outhouse and S. C. Wallace, J. Chem. Phys., 1989, 91, 6013 CrossRef.
- S. Arnold and M. Sulkes, J. Phys. Chem., 1992, 96, 4768 CrossRef.
- J. Wilke, M. Wilke, C. Brand, W. L. Meerts and M. Schmitt, ChemPhysChem, 2016, 17, 2736–2743 CrossRef PubMed.
- P. A. Steiner and W. Gordy, J. Mol. Struct., 1966, 21, 291–301 Search PubMed.
- H. S. Müller, A. Coutens, A. Walters, J.-U. Grabow and S. Schlemmer, J. Mol. Spectrosc., 2011, 267, 100–107 CrossRef.
- G. Berden, W. L. Meerts, M. Schmitt and K. Kleinermanns, J. Chem. Phys., 1996, 104, 972–982 CrossRef.
- C. Jacoby and M. Schmitt, Chem. Phys. Chem., 2004, 5, 1686–1694 CrossRef PubMed.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17 CrossRef.
- W. L. Meerts, W. A. Majewski and W. M. van Herpen, Can. J. Phys., 1984, 62, 1293–1299 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp04020f |
| This journal is © the Owner Societies 2018 |