 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fragment motion in motor molecules: basic concepts and application to intra-molecular rotations
Klaus E.
Hermann
 *a,
Fei
Qi
*a,
Fei
Qi
 b,
Rundong
Zhao
b,
Rundong
Zhao
 b,
Rui-Qin
Zhang
b,
Rui-Qin
Zhang
 cd and
Michel A.
Van Hove
cd and
Michel A.
Van Hove
 b
b
aInorg. Chem. Dept., Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: hermann@fhi-berlin.mpg.de
bInstitute of Computational and Theoretical Studies & Department of Physics, Hong Kong Baptist University, Hong Kong SAR, China
cDepartment of Physics, City University of Hong Kong, Hong Kong SAR, China
dBeijing Computational Science Research Center, Beijing, China
First published on 2nd August 2018
Abstract
The complex motion of atoms inside large molecules can be analyzed by considering translation, rotation, and flexibility of corresponding molecular fragments and by applying classical mechanics based on Pulay forces on the atoms, as in molecular dynamics. We propose a fragment motion analysis that provides a basic qualitative understanding of the motion of the different molecular components. Further, it can help to describe or design simplified fragment motions, e.g. the rotation of a rotator with respect to its stator counterpart in a rotor molecule, despite the higher actual complexity due to flexibility of rotator and stator or due to a variable rotation axis. The formal aspects of the fragment motion analysis are discussed in detail. Its application is illustrated by the rotational motion inside the BTP-BCO molecule and by rotational transitions between cis- and trans-stilbene isomers.
1. Introduction
All molecules have internal degrees of freedom that allow many types of internal motion, such as vibration, bending and rotation of individual atoms or of subgroups of atoms. Normally, motions within molecules are complex combinations of such elementary motions: for example, a rotating fragment is never totally rigid, but actually is itself flexible, allowing vibration, bending and even internal differential rotation and other types of distortion within itself. While humans can easily recognize in a movie, for example, a rotating fragment even when it is not rigid, this is a more difficult task to program for a computer: to that end, we need a general formalism to decompose the complex real motion into its simpler superposed constituents – translation for stretching vibrations, rotation for back and forth swinging as well as for spinning, and flexing for all other distortions. Our aim here is to describe such a decomposition for an arbitrary molecule, with particular application to rotor molecules, i.e. molecules that contain rotating parts.Macromolecules, in particular large rotor molecules with 100 and more atoms, have attracted considerable attention due to their exciting physical and chemical properties,1 which have, for example, been acknowledged by the award of the 2017 Nobel Prize in Chemistry for molecular machines.2 Their complex rotational behavior manifested by the motion of atom groups inside the molecules has been examined in numerous studies, both experimentally and theoretically. Examples are molecular rotors with chiral rotators sticking out on one end,1,3 molecules with internal rotators, such as BTP-BCO,4–6 or large molecules combining internal rotation with translation, such as [c2]daisy chain supramolecules.7,8 In addition, rotational motion can also appear in conformation changes of larger molecules. An example is given by the rotational modes of the isomer transitions between cis- and trans-stilbene.9–14
Theoretical work on the time evolution of large molecules is often based on molecular dynamics methods using classical equations of motion15 to account for atom motion. The atoms are represented by point masses moving under the influence of external forces and of forces between them, which are either given by model potentials (force field methods16) or obtained from quantum calculations (e.g. Pulay forces17). These studies yield geometric conformations as well as transitions between them described by classical paths and physical parameters, such as energies, atom positions and velocities, linear and angular momenta, or torques. Appropriate ensemble averages can then provide information about statistical and thermodynamic quantities, such as free energy, entropy, and chemical potentials. However, the atom based molecular dynamics approach makes it difficult to highlight and visualize concerted motions of groups of atoms within molecules, such as relative rotations and translations/vibrations of comparatively rigid but movable parts of the molecules.
We therefore propose an approach that is often conceptually simpler to describe the internal motion within large molecules. We focus our attention on the concerted motion of those relatively rigid parts of the molecules, which we will call “fragments” in this work. In this approach, the complex motion of the set of individual atoms inside the molecule is approximated by that of relatively rigid fragments which allow also some internal flexibility during their rotation and vibration. Then the rotation and translation/vibration of the fragments can be obtained by applying classical mechanics to the whole fragments, based on Pulay forces on the atoms as obtained from quantum mechanical calculations. Our resulting fragment motion analysis, applied to the rigid approximant of each fragment, provides a qualitative but realistic understanding of the motion of the different molecular components. It also helps us to predict and design simplified fragment paths in the multi-dimensional configuration space, such as those of the motion of a rotator fragment relative to a stator fragment in a rotor molecule.
Clearly, the assumption of a fragment as a rigid subset of a molecule that can translate and rotate by coupled motions of the fragment atoms can only be approximate. We therefore include individual atom motion beyond cooperative effects in our detailed quantitative description of fragment dynamics. This can be connected with local flexibility or elasticity of a fragment and has to be evaluated on an individual basis where explicit atom forces are taken into account. If flexibility makes a major contribution to the motion of a fragment, the concept of fragment motion becomes questionable. Thus, our fragment motion analysis relies on the assumption of a relatively rigid fragment where flexibility can be treated as a minor perturbation or ignored in a qualitative analysis. This assumption can often be easily evaluated intuitively for a given system.
Section 2 discusses formal aspects of the fragment motion analysis in detail, while Section 3 illustrates the importance of the three different contributions – fragment rotation, translation, and flexibility – for the molecular rotor BTP-BCO4–6 and for rotational isomer transitions between cis- and trans-stilbene.9–14 Finally, Section 4 summarizes our conclusions.
2. Theoretical details
2.1 Basic concepts of fragment motion in molecules
In the present approach the atoms of a molecule are described by classical point masses at given positions, with velocities, and experiencing forces due to interatomic coupling as well as due to external fields. Details of this description on an individual atom basis can be rather complex and difficult to grasp. However, in large molecules one can often identify distinct fragments, whose atoms move together in a similar fashion, e.g. rotating, shifting, or vibrating as a more or less rigid fragment.The motion of a fragment becomes particularly simple and easy to describe if its N atoms are rigidly interconnected with fixed interatomic distances and angles. Then the motion of each constituent atom is determined by the global motion of the rigid fragment. Rigid fragment motion can only be translation (as in vibration or isomeric transitions) and/or rotation (as in back and forth swinging or continuous spinning about a fixed point on the static part18 of the molecule). Here a formal description of translation is based on a reference point ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref representing the fragment, which can be, for example, its center of mass (CoM) given by
ref representing the fragment, which can be, for example, its center of mass (CoM) given by
 | (1) |
![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) ref shifting all fragment atoms (including the CoM) equally determines the translational motion.
ref shifting all fragment atoms (including the CoM) equally determines the translational motion.
The fragment atoms of a molecule may experience forces ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) i that are partly internal forces due to other atoms in the molecule and possibly external forces originating e.g. from external charges or from other force fields. These forces, evaluated in the present work as quantum mechanical Pulay forces between atoms of the molecule,17,19 accelerate the atoms. Assuming a rigid fragment, the total force
i that are partly internal forces due to other atoms in the molecule and possibly external forces originating e.g. from external charges or from other force fields. These forces, evaluated in the present work as quantum mechanical Pulay forces between atoms of the molecule,17,19 accelerate the atoms. Assuming a rigid fragment, the total force ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) tot acting on it is given by the sum of forces on all fragment atoms and, if the fragment does not rotate, the total force will accelerate all atoms equally, giving rise to a linear translational fragment motion.
tot acting on it is given by the sum of forces on all fragment atoms and, if the fragment does not rotate, the total force will accelerate all atoms equally, giving rise to a linear translational fragment motion.
Rigid fragment rotation is described by its atoms rotating with the same angular velocity ω about a common rotational axis through a pivot point ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref. Thus, the velocity of each rotating fragment atom at position
ref. Thus, the velocity of each rotating fragment atom at position ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) i can be described as
i can be described as
 | (2) |
 defines the direction of the rotational axis and its length denotes the angular velocity of the rotation. The rotation can be further characterized by the angular momentum of the fragment with respect to its pivot
defines the direction of the rotational axis and its length denotes the angular velocity of the rotation. The rotation can be further characterized by the angular momentum of the fragment with respect to its pivot ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref which, for a rigid fragment, is given by
ref which, for a rigid fragment, is given by | (3) |
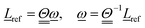 | (4) |
 is the moment of inertia of the fragment. Assuming Cartesian coordinates,
is the moment of inertia of the fragment. Assuming Cartesian coordinates, ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) i = (xi1, xi2, xi3) and
i = (xi1, xi2, xi3) and ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref = (Xref1, Xref2, Xref3), the moment of inertia is given by a 3 × 3 matrix with elements
ref = (Xref1, Xref2, Xref3), the moment of inertia is given by a 3 × 3 matrix with elements | (5) |
 and the fragment angular momentum
and the fragment angular momentum ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref, and one quantity can be evaluated from the other according to (4) and (5). Further, from relations (2)–(4) it can be shown that the scalar product
ref, and one quantity can be evaluated from the other according to (4) and (5). Further, from relations (2)–(4) it can be shown that the scalar product  is always positive (or zero). Thus, allowing unrestricted rotation about
is always positive (or zero). Thus, allowing unrestricted rotation about ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref, the rotation vector
ref, the rotation vector  and the fragment angular momentum
and the fragment angular momentum ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref always form an angle less than or equal to 90°. In looser language, this means that
ref always form an angle less than or equal to 90°. In looser language, this means that 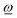 and
and ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref rotate essentially in the same direction since a right-handed angular momentum will favor a right-handed rotation, and a left-handed angular momentum will favor a left-handed rotation. Therefore, the direction of
ref rotate essentially in the same direction since a right-handed angular momentum will favor a right-handed rotation, and a left-handed angular momentum will favor a left-handed rotation. Therefore, the direction of ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref can be used to qualitatively indicate possible directions of fragment rotation axes and their rotational sense (right- vs. left-handed) without having to evaluate
ref can be used to qualitatively indicate possible directions of fragment rotation axes and their rotational sense (right- vs. left-handed) without having to evaluate  explicitly, a useful simplification that provides a very helpful guide to understand the rotational behavior of fragments.
explicitly, a useful simplification that provides a very helpful guide to understand the rotational behavior of fragments.
If, on the other hand, the direction of the rotation axis parallel to 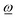 through
through ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref is fixed and predefined (examples are attached fragment rotations restricted to rotating about an interatomic bond), the acting angular momentum is forced to be collinear with
ref is fixed and predefined (examples are attached fragment rotations restricted to rotating about an interatomic bond), the acting angular momentum is forced to be collinear with  and is determined by the projection of
and is determined by the projection of ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref onto
ref onto  , yielding
, yielding ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) effref according to
effref according to
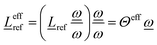 | (6) |
 | (7) |
In addition to linear acceleration of the rigid fragment discussed above, atom forces ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) i may also lead to a rotational acceleration about a pivot
i may also lead to a rotational acceleration about a pivot ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref which is induced by a torque
ref which is induced by a torque ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref with respect to the pivot given by
ref with respect to the pivot given by
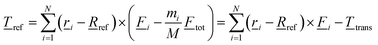 | (8) |
![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) trans = ( trans = (![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) CoM − CoM − ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref) × ref) × ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) tot tot | (8a) |
![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) trans, has been removed.20 This can also be written as the time derivative of the angular momentum, i.e.
trans, has been removed.20 This can also be written as the time derivative of the angular momentum, i.e.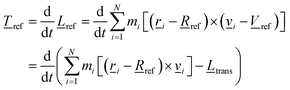 | (9) |
![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) trans = ( trans = (![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) CoM − CoM − ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref) × ref) × ![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) ref ref | (9a) |
![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) trans, has been removed. Thus, while a finite angular momentum
trans, has been removed. Thus, while a finite angular momentum ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref implies a rotational motion of the rigid fragment with an angular velocity according to the rotation vector
ref implies a rotational motion of the rigid fragment with an angular velocity according to the rotation vector 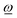 , a non-zero torque yields an angular acceleration of the fragment.
, a non-zero torque yields an angular acceleration of the fragment.
In reality, molecular fragments will not be exactly rigid, but exhibit flexibility, including rapid individual atomic vibrations and elasticity. The atoms thus can have individual velocity contributions ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) flexi beyond rigid fragment translation and rotation. Here we limit flexibility to motions that maintain the integrity and identifiability of the fragments. In particular we do not consider bond breaking and bond making between different fragments. In the simplest case, flexibility makes only a small contribution to the atom displacement inside the fragment and can be treated as a perturbation of the approximately rigid fragment; small organic components inside larger hydrocarbons can serve as examples. Altogether, the absolute velocities of the fragment atoms are described by contributions due to fragment translation, rotation about the pivot, and flexibility according to
flexi beyond rigid fragment translation and rotation. Here we limit flexibility to motions that maintain the integrity and identifiability of the fragments. In particular we do not consider bond breaking and bond making between different fragments. In the simplest case, flexibility makes only a small contribution to the atom displacement inside the fragment and can be treated as a perturbation of the approximately rigid fragment; small organic components inside larger hydrocarbons can serve as examples. Altogether, the absolute velocities of the fragment atoms are described by contributions due to fragment translation, rotation about the pivot, and flexibility according to
![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i = i = ![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) ref + ref + ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) roti + roti + ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) flexi flexi | (10) |
![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) flexi includes both slow deformations of the fragment changing its shape and rapid atomic vibrations about given fragment positions. Relations (1)–(10) will be the basis of the fragment motion analysis described in the following.
flexi includes both slow deformations of the fragment changing its shape and rapid atomic vibrations about given fragment positions. Relations (1)–(10) will be the basis of the fragment motion analysis described in the following.
2.2 Mechanical analysis applied to fragments
Our fragment motion analysis starts with a quasi-static approach which assumes that initially all N atoms of the fragment are at rest with positions![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) i and velocities
i and velocities ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i =
i = ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . Then forces
. Then forces ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) i are applied to the atoms for a short time τ, leading to finite velocities
i are applied to the atoms for a short time τ, leading to finite velocities ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i which can be described in linear approximation, by using the impulse-momentum equivalence, as
i which can be described in linear approximation, by using the impulse-momentum equivalence, as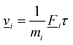 | (11) |
![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) ref given approximately by that of the fragment CoM, i.e. by
ref given approximately by that of the fragment CoM, i.e. by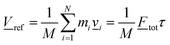 | (12) |
![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) tot denotes the sum of the N fragment atom forces
tot denotes the sum of the N fragment atom forces ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) i. Now we can estimate an approximate translation Δ
i. Now we can estimate an approximate translation Δ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref of the fragment, by using the average speed
ref of the fragment, by using the average speed  during the acceleration, which yields
during the acceleration, which yields | (13) |
This result allows us to estimate the displacement of the fragment as a whole along the direction of ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) tot. Further, the fragment torque
tot. Further, the fragment torque ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref defined by (8) and (9) leads to a fragment angular momentum
ref defined by (8) and (9) leads to a fragment angular momentum ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref which, in linear approximation after a short time τ, becomes
ref which, in linear approximation after a short time τ, becomes
![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ref = ref = ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) refτ refτ | (14) |
 for unconstrained rotation about
for unconstrained rotation about ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref according to (4) and (5), which helps to describe rotational details of a fragment that is only constrained to rotate around a pivot without a predefined axis. However, in real molecules, internal binding of a fragment with its neighborhood may restrict rotations to specific axes given by fixed directions parallel to
ref according to (4) and (5), which helps to describe rotational details of a fragment that is only constrained to rotate around a pivot without a predefined axis. However, in real molecules, internal binding of a fragment with its neighborhood may restrict rotations to specific axes given by fixed directions parallel to 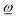 through the pivot
through the pivot ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref. Then, starting from a resting fragment, the acting angular momentum
ref. Then, starting from a resting fragment, the acting angular momentum ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) effref, collinear with
effref, collinear with  and pointing in the same direction, can be evaluated using relations (6) and (7) from which the magnitude of the angular velocity,
and pointing in the same direction, can be evaluated using relations (6) and (7) from which the magnitude of the angular velocity,  , is obtained as
, is obtained as | (15) |
In addition, the degree of flexibility for the individual atom motion and, thus, the quality of the assumption of an approximately rigid rotating/translating fragment, can be estimated by comparing the rigid-fragment motion with that of the flexible fragment. This is achieved by comparing the absolute velocities ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i of the individual atoms at time τ according to (11) with their flexibility contributions
i of the individual atoms at time τ according to (11) with their flexibility contributions ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) flexi, where the difference is given, according to (2) and (10), by
flexi, where the difference is given, according to (2) and (10), by
 | (16) |
![[V with combining low line]](https://www.rsc.org/images/entities/i_char_0056_0332.gif) ref with rotational atom velocities
ref with rotational atom velocities ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) roti relative to the pivot
roti relative to the pivot ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) ref.
ref.
The mechanical analysis discussed so far considers only an initial short time step where the approximation of a relatively rigid fragment with forces on initially resting atoms is justified. As each atom moves, the fragment can change both its orientation and internal structure, so that the forces ![[F with combining low line]](https://www.rsc.org/images/entities/i_char_0046_0332.gif) i will also change over time and have to be recalculated at each subsequent time step if we want to accurately follow complete trajectories. However, if we limit our interest to the qualitative behavior of the fragment (such as approximate direction of the axis of rotation and right- vs. left-handed sense of rotation), there is no need to go beyond the initial time step, thus making the analysis very efficient.
i will also change over time and have to be recalculated at each subsequent time step if we want to accurately follow complete trajectories. However, if we limit our interest to the qualitative behavior of the fragment (such as approximate direction of the axis of rotation and right- vs. left-handed sense of rotation), there is no need to go beyond the initial time step, thus making the analysis very efficient.
In the following, we will discuss results of two example systems where the fragment motion analysis can give additional information in the evaluation of internal motion details. The first example deals with the BTP-BCO molecule,4–6 in which the kinetic behavior of the internal rotating C2(C2H4)3 fragment is studied. In the second example, the rotational isomer transition between cis- and trans-stilbene is examined, in which possible transition paths induced by light can be identified.9–14 Clearly, the two example applications can also be dealt with by direct analytical methods based on simple algebra. It can be shown that in both examples the torque component along the rotational axis equals the negative angle derivative of the total energy. However, a comparison with results from our fragment motion analysis can serve as a useful double check.
The two applications in Section 3 deal only with the analysis of rotational motion of rigid fragments of the corresponding molecules. However, the theoretical details of the fragment motion analysis discussed in the present section are more general and can lay the groundwork for detailed studies of more complex molecules in the future. In these systems a discrimination between fragment translation and rotation starts by treating the fragments as rigid subunits, which has to be followed by considering their flexibility according to atom motion described by eqn (10). This will assist the classification of complex collective motions inside the complex molecule.
It must be emphasized that the concept of fragment motion can only be based on a meaningful selection of fragments where chemical intuition as well as physical insight is of paramount importance. An automated fragment search considering many (mathematically) possible fragmentations of a molecule (in trial-and-error strategies) may not yield chemically/physically meaningful fragments and may not be feasible computationally.
3. Applications
3.1 Random rotor inside BTP-BCO
This example refers to a large hydrocarbon molecule named (4′,4′′′′-(bicyclo[2,2,2]octane-1,4-diyldi-4,1-phenylene)-bis-2,2′:6′,2′′-terpyridine) or BTP-BCO for short,5,6 with a sum formula C50H40N6. It contains a bicyclo[2,2,2]octane (BCO) group connected to one phenylene group on each side, each of which in turn binds to terminal terpyridine groups, see Fig. 1. Scanning tunneling microscopy (STM) experiments for BTP-BCO molecules adsorbed at the Cu(111) surface have shown5 that the BCO group of approximately 3-fold rotational symmetry can be stimulated by tunneling electrons to rotate about its symmetry axis, which is parallel to the substrate surface. Theoretical studies6 indicate that the five groups – the central BCO, the two phenylenes, and the terminal terpyridines – form quite rigid subunits which, in the gas phase, can rotate relative to each other about the connecting C–C bonds between the subunits. On a surface, the phenylene and terpyridine groups tend to stick flat to the surface, while the internal BCO rotor can still be excited to make rapid jumps between four non-equivalent rotational orientations that are stabilized by the substrate–molecule interactions.Here we examine details of the rotational motion of the BCO group, C2(C2H4)3, inside free BTP-BCO by using a symmetrized model structure where the BCO rotor itself is assumed to exhibit exact D3h symmetry with its three C2H4 flaps forming 120° angles with each other and the two outer carbons positioned at the 3-fold symmetry axis, see Fig. 2a. Further, we assume that the two phenylene and two terpyridine groups form a fixed planar BTP framework in which the BCO can rotate. (For comparison, no planarity of the BTP framework was imposed in earlier gas-phase molecular-dynamics simulations,6 which allowed complete freedom of motion.) With these geometric constraints, density-functional theory calculations are performed to obtain optimized electronic and geometric structures analogous to those of an earlier study.6 In the calculations, the B3LYP exchange–correlation functional21,22 is used together with extended 6-31G# and 6-31G* basis sets23 as implemented in the GAUSSIAN 03 code.24
With the above symmetry constraints, the geometric optimization of BTP-BCO yields interatomic distances and bond angles defining the structure shown in Fig. 1. Here one of the three C2H4 flaps (emphasized by a blue C–C bond in Fig. 2a) of BCO is parallel to the planar BTP framework while the other two protrude on both sides, each forming dihedral angles of 60° with the framework. Keeping the planar geometry of the BTP framework and the 3-fold symmetry of BCO with the common symmetry axis fixed allows us to describe a rotation of BCO by just one dihedral angle φ, the torsion angle defined by four carbon atoms as indicated in Fig. 2a–c.
Clearly, due to the 3-fold symmetry of BCO, its rotation by φ = 120° inside the symmetrized BTP-BCO must reproduce the initial molecular geometry. This leads to a total energy of the molecule Etot(φ) having an angular periodicity Δφ = 120°. In fact, the additional 2-fold rotational symmetry of the BTP framework reduces the periodicity to Δφ = 60° as shown in Fig. 3a. As a consequence, the energy minimum at φ = 0° is reproduced at φ = 60°. However, the equilibrium structures corresponding to the two angles differ by a mirror operation perpendicular to the planar BTP framework such that the C2H4 flaps of BCO point in opposite directions. This becomes evident when comparing Fig. 2a with Fig. 2c. Between the energy minima at φ = 0° and 60°, the total energy varies smoothly with φ going over a maximum at 30°, see Fig. 2b, which corresponds to an energy barrier of only 1.68 kcal mol−1 (0.07 eV). Thus, the barrier can be easily overcome by thermal excitations, which confirms the results obtained previously.6 Further, the symmetry of the total energy Etot(φ) allows rotation in both positive and negative angular directions with equal angular acceleration. This characterizes the BCO rotor as a random rotor without directional preference (vibrations can break the symmetry but are themselves equally probable in both directions).
 | ||
| Fig. 3 (a) Total energy Etot(φ) of the symmetrized BTP-BCO molecule as a function of the BCO rotation angle φ. (b) Torque component TCoM(φ) acting along the symmetry axis of the BCO rotor as a function of the rotation angle φ. For the definition of dihedral angle φ see Fig. 2. Positive TCoM(φ) favors accelerated rotation (labeled “with”) while negative TCoM(φ) indicates decelerated rotation (labeled “against”). | ||
The atoms of the BCO fragment rotating away from equilibrium inside BTP-BCO experience forces which result in a torque on the BCO rotor as defined by (8) and (9), where the CoM coincides with the symmetry center of the rotor. Clearly, this torque ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) CoM(φ) depends on the rotation angle φ and, due to the symmetry constraints, its direction points always along the rotation axis of the BCO rotor (if we neglect vibrations). If vector
CoM(φ) depends on the rotation angle φ and, due to the symmetry constraints, its direction points always along the rotation axis of the BCO rotor (if we neglect vibrations). If vector ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) CoM(φ) is parallel to the rotation vector
CoM(φ) is parallel to the rotation vector 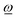 , described by a positive scalar TCoM(φ) = |
, described by a positive scalar TCoM(φ) = |![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) CoM(φ)| in the following, the torque favors the rotation by increasing its angular velocity ω. In contrast,
CoM(φ)| in the following, the torque favors the rotation by increasing its angular velocity ω. In contrast, ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) CoM(φ) antiparallel to
CoM(φ) antiparallel to 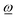 will be denoted by a negative scalar TCoM(φ) = −|
will be denoted by a negative scalar TCoM(φ) = −|![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) CoM(φ)| working against the rotation by decreasing ω. Fig. 3b shows the variation of the torque component TCoM(φ) with the rotation angle φ which, as for the total energy Etot(φ), is periodic with an angular periodicity of Δφ = 60°. In fact, due to the functional form of Etot(φ) (i.e. depending on angle φ only) it can be shown by simple algebra that the torque component TCoM(φ) equals the negative derivative of the total energy. For angles between φ = 0° and 30°, negative values of TCoM(φ) are obtained, which indicates decelerated rotation (labeled “against” in Fig. 3b) and accompanies increasing total energy towards the energy barrier at φ = 30°, see Fig. 3a. On the other hand, angles between φ = 30° and 60° yield positive TCoM(φ), suggesting accelerated rotation (labeled “with” in Fig. 3b) which characterizes the motion from the energy barrier towards the equilibrium at φ = 60°. Thus, the results of the torque analysis are consistent with those of the total energy and confirm the general behavior anticipated by the geometry of the symmetrized BTP-BCO.
CoM(φ)| working against the rotation by decreasing ω. Fig. 3b shows the variation of the torque component TCoM(φ) with the rotation angle φ which, as for the total energy Etot(φ), is periodic with an angular periodicity of Δφ = 60°. In fact, due to the functional form of Etot(φ) (i.e. depending on angle φ only) it can be shown by simple algebra that the torque component TCoM(φ) equals the negative derivative of the total energy. For angles between φ = 0° and 30°, negative values of TCoM(φ) are obtained, which indicates decelerated rotation (labeled “against” in Fig. 3b) and accompanies increasing total energy towards the energy barrier at φ = 30°, see Fig. 3a. On the other hand, angles between φ = 30° and 60° yield positive TCoM(φ), suggesting accelerated rotation (labeled “with” in Fig. 3b) which characterizes the motion from the energy barrier towards the equilibrium at φ = 60°. Thus, the results of the torque analysis are consistent with those of the total energy and confirm the general behavior anticipated by the geometry of the symmetrized BTP-BCO.
While the symmetrized BTP-BCO model gives a good qualitative understanding of the rotational motion of the inner BCO rotor, it will not be sufficient to describe all details of the dynamical behavior of the BTP-BCO molecule in reality. This is evident from molecular dynamics studies of BTP-BCO6 which yield rather complex motions of the complete molecule. The simulations reveal coupled rotations of the two phenylene groups adjacent to the inner BCO as well as of the outer terpyridine groups in addition to flexing and inner vibrations in all fragments. These couplings will distort the BCO rotor, changing its rotational axis with time, and, thus, affect its rotational symmetry. As a result, a prediction of the detailed BCO rotation in the real BTP-BCO molecule based on the present symmetrized and constrained model, chosen to double check rotational aspects of our fragment motion analysis, may become unreliable quantitatively. Clearly, fine details of the molecular motion require conventional quantum calculations which are expensive computationally while our approach gives a quick and inexpensive way to describe the general rotational behavior of the inner BCO rotor.
3.2 Isomer transition in stilbene
The stilbene molecule, C14H12, can be described structurally as (C6H5)–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C6H5), being composed of two phenyl rings connected by a C
C–(C6H5), being composed of two phenyl rings connected by a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone; the phenyls form very stable and almost rigid entities. It allows two isomers which can be distinguished by the relative positions of the phenyls in the molecule. In the trans-stilbene isomer the C6H5 groups reside on opposite sides of a plane through the C
C backbone; the phenyls form very stable and almost rigid entities. It allows two isomers which can be distinguished by the relative positions of the phenyls in the molecule. In the trans-stilbene isomer the C6H5 groups reside on opposite sides of a plane through the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone whereas the cis-stilbene isomer contains the C6H5 groups on the same side of the plane as shown in Fig. 4a and b (both planes are perpendicular to those of the figures).
C backbone whereas the cis-stilbene isomer contains the C6H5 groups on the same side of the plane as shown in Fig. 4a and b (both planes are perpendicular to those of the figures).
These isomers have been extensively studied both by experiment9,25–28 and theory10,11,14 as model systems for photochemical trans–cis isomerization. They have also been proposed for possible applications in molecular electronics where light-driven transitions between the isomers can provide mechanisms for molecular switching devices.29,30 The more stable of the two isomers is trans-stilbene10 which has been suggested by experiment to be planar in its ground state25 with slight torsions of the two C6H5 groups about their C-phenyl axes.14,31 The geometric structure of the cis isomer in its ground state, as obtained by quantum chemical calculations,11 can be obtained qualitatively by rotating the upper phenyl of trans-stilbene about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis by a twist angle of nearly 180°. In addition, the phenyl groups are rotated equally about their C-phenyl axes by a rotation angle close to 40° in order to minimize steric repulsion.
C backbone axis by a twist angle of nearly 180°. In addition, the phenyl groups are rotated equally about their C-phenyl axes by a rotation angle close to 40° in order to minimize steric repulsion.
Transitions between the two isomers, both trans to cis and cis to trans, have been observed by photoexcitation.12,32,33 The basic mechanism of the isomerization starts from one of the isomers, e.g. trans-stilbene, in its ground state (GS) which is transferred by photon absorption to an electronically excited state (ES) resulting in forces on the stilbene atoms. This drives the molecule along the ES potential energy surface until it reaches a point where the ES energy surface gets close to that of the GS. At this point, called conical intersection (CI), a transition to the GS is most probable and after the transition the molecule deexcites on the GS energy surface to the alternative isomer conformation, e.g. that of cis-stilbene.
As to details of the isomer transition, different geometric paths have been postulated.9,13 In the simplest approach, these paths assume that the stilbene consists of two rigid phenyl groups joined by a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone where only three types of internal rotations are allowed. The twist rotation about the backbone is quantified by a tetrahedral angle Θ (twist angle), illustrated in Fig. 5a. Internal rotations of each of the two phenyls about their corresponding C-phenyl axes are defined by dihedral angles α1 and α2 (C-phenyl angles) as shown in Fig. 5b and c. Thus, the total energy of the molecule along the isomerization path depends only on three parameters, i.e. Etot = Etot(Θ, α1, α2) where the GS geometry of the trans-stilbene is given by Θ = 180°, α1 = α2 = 0° while cis-stilbene is described by Θ near 0°, α1 and α2 finite.
C backbone where only three types of internal rotations are allowed. The twist rotation about the backbone is quantified by a tetrahedral angle Θ (twist angle), illustrated in Fig. 5a. Internal rotations of each of the two phenyls about their corresponding C-phenyl axes are defined by dihedral angles α1 and α2 (C-phenyl angles) as shown in Fig. 5b and c. Thus, the total energy of the molecule along the isomerization path depends only on three parameters, i.e. Etot = Etot(Θ, α1, α2) where the GS geometry of the trans-stilbene is given by Θ = 180°, α1 = α2 = 0° while cis-stilbene is described by Θ near 0°, α1 and α2 finite.
Considering the trans to cis isomerization, one model transition path, denoted as one-bond flip (OBF),9 is described by a twist rotation only without C-phenyl rotations such that, setting α1 = α2 = 0°, the total energy varies only with angle Θ ranging from 180° (trans) to near 0° (cis). As a consequence, the relative orientation of the normal vectors of the two phenyl planes is inverted by the backbone rotation. Along a different model transition path, denoted as hula-twist (HT),9 one of the C-phenyl angles, for example α1, is allowed to vary from 0° to near 180° (keeping α2 = 0°) while Θ changes from 180° to near 0°. This guarantees that the relative orientation of the normal vectors of the two phenyl planes remains similar during the backbone rotation. In the present work, we examine an alternative model path for trans to cis isomerization which can be described as relaxed one-bond flip (rOBF). Here both the backbone angle and the two C-phenyl angles are allowed to vary such that the stilbene keeps its two-fold symmetry C2 normal to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis. This constrains the C-phenyl angles to α1 = α2 = α and the total energy of the molecule along the isomerization path depends only on two parameters, i.e. Etot = Etot(Θ, α). The rOBF path can minimize the steric repulsion of the two phenyl rings in the vicinity of the cis geometry, Θ near 0°, better than the OBF or HT model paths. Interestingly, the rOBF path includes also the geometry of the conical intersection (CI) very near Θ = 90°, α = 0° considered to be essential for the isomerization as will be discussed below.
C backbone axis. This constrains the C-phenyl angles to α1 = α2 = α and the total energy of the molecule along the isomerization path depends only on two parameters, i.e. Etot = Etot(Θ, α). The rOBF path can minimize the steric repulsion of the two phenyl rings in the vicinity of the cis geometry, Θ near 0°, better than the OBF or HT model paths. Interestingly, the rOBF path includes also the geometry of the conical intersection (CI) very near Θ = 90°, α = 0° considered to be essential for the isomerization as will be discussed below.
Total energy surfaces as well as details of the rOBF path and corresponding physical parameters, discussed in Section 2, are evaluated using density-functional theory (DFT) together with the CAM-B3LYP exchange–correlation functional34 and extended 6-311g(d) basis sets as implemented in the GAUSSIAN 03 code.24 The isomerization process involves also electronically excitated states of the molecule. Therefore, potential energy surfaces and derived quantities of both the ground and the lowest excited state are considered, where the latter are calculated applying time-dependent DFT.24
First, we evaluate total energies Etot(Θ, α) of the molecular ground state for a range of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone and C-phenyl angles, 0° ≤ Θ ≤ 180°, −30° ≤ α ≤ 60° to obtain potential energy surfaces (PES) from which the equilibrium geometries of the trans and cis isomers are determined by energy minimization, see Fig. 6. As a result, trans-stilbene at equilibrium is found to be fairly close to planar, Θ = 175°, α = −12° with the PES being extremely flat for Θ between 175° and 180°. We have further verified the equilibrium geometry by unconstrained energy minimizations starting from the constrained equilibrium corresponding to Θ = 175°, α = −12° which yields good agreement concerning both geometry and total energies. This is consistent with previous quantum chemical studies on the isomer suggesting a planar C2h symmetry10 but also slight α deviations from zero.10,14 The cis-stilbene of C2 symmetry stabilizes at Θ = 5.5°, α = 41.2° which is also quite close to results from our corresponding unconstrained minimizations and agrees with published quantum chemical calculations.11,14 Further, the ground state PES shows a sharp barrier of 75 and 80 kcal mol−1 above the equilibrium energies of cis- and trans-stilbene, respectively, at a C
C backbone and C-phenyl angles, 0° ≤ Θ ≤ 180°, −30° ≤ α ≤ 60° to obtain potential energy surfaces (PES) from which the equilibrium geometries of the trans and cis isomers are determined by energy minimization, see Fig. 6. As a result, trans-stilbene at equilibrium is found to be fairly close to planar, Θ = 175°, α = −12° with the PES being extremely flat for Θ between 175° and 180°. We have further verified the equilibrium geometry by unconstrained energy minimizations starting from the constrained equilibrium corresponding to Θ = 175°, α = −12° which yields good agreement concerning both geometry and total energies. This is consistent with previous quantum chemical studies on the isomer suggesting a planar C2h symmetry10 but also slight α deviations from zero.10,14 The cis-stilbene of C2 symmetry stabilizes at Θ = 5.5°, α = 41.2° which is also quite close to results from our corresponding unconstrained minimizations and agrees with published quantum chemical calculations.11,14 Further, the ground state PES shows a sharp barrier of 75 and 80 kcal mol−1 above the equilibrium energies of cis- and trans-stilbene, respectively, at a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone angle close to Θ = 90° where one phenyl group stands perpendicular to the other, see Fig. 4c, separating between cis-like and trans-like stilbene isomer geometries. Additional optimizations, fixing the backbone angle at Θ = 90° and relaxing the atoms of the (initially planar) phenylene groups, yield an optimized total energy quite close to that with (constrained) planar phenylenes and only very minor geometry differences.
C backbone angle close to Θ = 90° where one phenyl group stands perpendicular to the other, see Fig. 4c, separating between cis-like and trans-like stilbene isomer geometries. Additional optimizations, fixing the backbone angle at Θ = 90° and relaxing the atoms of the (initially planar) phenylene groups, yield an optimized total energy quite close to that with (constrained) planar phenylenes and only very minor geometry differences.
The PES of the lowest excited state of stilbene Etot′(Θ, α) is also included in Fig. 6. It exhibits a pronounced dip for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C twist angles Θ close to 90° such that it gets very close to the ground state PES barrier for the same angles. In fact, for Θ = 90°, α = 0° the energy difference between the GS and ES surfaces is below 2 kcal mol−1. Thus, the two states are almost degenerate, suggesting an energetically very easy transition between them. This defines a conical intersection (CI) available for possible isomerization paths.
C twist angles Θ close to 90° such that it gets very close to the ground state PES barrier for the same angles. In fact, for Θ = 90°, α = 0° the energy difference between the GS and ES surfaces is below 2 kcal mol−1. Thus, the two states are almost degenerate, suggesting an energetically very easy transition between them. This defines a conical intersection (CI) available for possible isomerization paths.
The examination of a possible isomerization path between the cis and trans ground states via the transition state at the CI within the rOBF scheme starts from an optimized path on the ground state energy surface Etot(Θ, α). Here, for given C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone angles Θ, between 0° and 180° the C-phenyl angle α is optimized according to lowest total energy. This yields a path shown in Fig. 7a with the CI transition state near Θ = 90°, α = 0°. The color coded total energy map evidences the sharp ridge with energy barriers of about 80 kcal mol−1 near Θ = 90°, as mentioned above. This ridge has to be overcome by the isomerization path if a path exclusively along the GS energy surface is assumed. Fig. 7b shows a color coded map of the energy surface Etot′(Θ, α) of the lowest excited state with an approximate rOBF isomerization path which is assumed to be geometrically identical with that of the ground state, see Fig. 7a. This assumption is reasonable as evidenced by the behavior of Etot′(Θ, α) near the isomerization path shown in Fig. 7b. The approximate excited state path crosses the energy dip at the conical intersection near Θ = 90° with energies that are very close to those of the ground state path; this is also clear from the ground and excited state total energies along the transition path shown in Fig. 8a.
C backbone angles Θ, between 0° and 180° the C-phenyl angle α is optimized according to lowest total energy. This yields a path shown in Fig. 7a with the CI transition state near Θ = 90°, α = 0°. The color coded total energy map evidences the sharp ridge with energy barriers of about 80 kcal mol−1 near Θ = 90°, as mentioned above. This ridge has to be overcome by the isomerization path if a path exclusively along the GS energy surface is assumed. Fig. 7b shows a color coded map of the energy surface Etot′(Θ, α) of the lowest excited state with an approximate rOBF isomerization path which is assumed to be geometrically identical with that of the ground state, see Fig. 7a. This assumption is reasonable as evidenced by the behavior of Etot′(Θ, α) near the isomerization path shown in Fig. 7b. The approximate excited state path crosses the energy dip at the conical intersection near Θ = 90° with energies that are very close to those of the ground state path; this is also clear from the ground and excited state total energies along the transition path shown in Fig. 8a.
 | ||
Fig. 8 (a) Total energies Etot(Θ, α) of stilbene along the rOBF transition path, assumed to be the ground state path. For each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C twist angle 0° ≤ Θ ≤ 180°, the C-phenyl angle α has been optimized (cis isomer at Θ = 5.5°, α = 41.2°, CI near Θ = 90°, α = 0°, trans isomer at Θ = 175°, α = −12°), see text. The energies are given as blue circles for the ground state and as red diamonds for the excited state. (b) Fragment torque Tref(Θ, α) along the rOBF transition path as for (a), see text. The torque values refer to projections of the torque vector onto the C C twist angle 0° ≤ Θ ≤ 180°, the C-phenyl angle α has been optimized (cis isomer at Θ = 5.5°, α = 41.2°, CI near Θ = 90°, α = 0°, trans isomer at Θ = 175°, α = −12°), see text. The energies are given as blue circles for the ground state and as red diamonds for the excited state. (b) Fragment torque Tref(Θ, α) along the rOBF transition path as for (a), see text. The torque values refer to projections of the torque vector onto the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis. For cis to trans isomerization positive Tref values denote the torque pointing opposite to the sense of rotation (“against”) while for negative Tref values the torque coincides with the sense of rotation (“with”). For trans to cis isomerization the correlation between torque and sense of rotation is reversed, see also Fig. 9. C backbone axis. For cis to trans isomerization positive Tref values denote the torque pointing opposite to the sense of rotation (“against”) while for negative Tref values the torque coincides with the sense of rotation (“with”). For trans to cis isomerization the correlation between torque and sense of rotation is reversed, see also Fig. 9. | ||
Altogether, this suggests an isomerization transition between cis- and trans-stilbene based on an rOBF model path which combines the ground and lowest excited state energy surfaces. Here the cis isomer at equilibrium is initially excited from its ground to the lowest electronically excited state. This can be achieved by absorption of light in a photochemical process9,32 where the excitation energy from the present calculations amounts to 105 kcal mol−1 corresponding to soft UV light. This is consistent with the experimental findings.9 In a subsequent step, the cis isomer is distorted by rotation about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis combined with O-phenyl rotations descending on the excited state PES until it reaches the CI where its two phenyl groups are perpendicular to each other. At the CI the stilbene can easily switch to the ground state PES after which it descends further to become an almost planar trans isomer in the ground state. Due to the approximate symmetry of the energy curves w.r.t. the CI in Fig. 8a, the inverse isomerization transition between trans- and cis-stilbene can be described in a completely analogous way within the rOBF concept. For the trans isomer the initial excitation energy from the present calculations amounts to 100 kcal mol−1, only slightly smaller than for the cis isomer.
C backbone axis combined with O-phenyl rotations descending on the excited state PES until it reaches the CI where its two phenyl groups are perpendicular to each other. At the CI the stilbene can easily switch to the ground state PES after which it descends further to become an almost planar trans isomer in the ground state. Due to the approximate symmetry of the energy curves w.r.t. the CI in Fig. 8a, the inverse isomerization transition between trans- and cis-stilbene can be described in a completely analogous way within the rOBF concept. For the trans isomer the initial excitation energy from the present calculations amounts to 100 kcal mol−1, only slightly smaller than for the cis isomer.
The initial electronic excitation of the cis- to trans-stilbene isomerization transfers the cis isomer from its ground state to the lowest excited state, where the former reflects an equilibrium geometry while the latter does not. As a consequence, the atoms experience forces in the excited state which gives rise to torques of the phenyl fragments with respect to each other. The calculated torque on one of the fragments projected onto the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis,
C backbone axis, ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref, is given as a function of the C
ref, is given as a function of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C twist angle Θ in Fig. 8b. Here positive
C twist angle Θ in Fig. 8b. Here positive ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref values denote torques pointing against the sense of the cis to trans rotation, thus, hindering the isomerization, while negative Tref values point along the sense of rotation and support the isomerization. This is also sketched in Fig. 9 for the upper phenyl fragment. A comparison of Fig. 8a with b illustrates that along the chosen transition path the torque component parallel to the C
ref values denote torques pointing against the sense of the cis to trans rotation, thus, hindering the isomerization, while negative Tref values point along the sense of rotation and support the isomerization. This is also sketched in Fig. 9 for the upper phenyl fragment. A comparison of Fig. 8a with b illustrates that along the chosen transition path the torque component parallel to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis equals the derivative of the total energy with respect to angle Θ which can also be proven analytically. Fig. 8b evidences that for the rOBF path along the ground state PES (blue circles)
C axis equals the derivative of the total energy with respect to angle Θ which can also be proven analytically. Fig. 8b evidences that for the rOBF path along the ground state PES (blue circles) ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref values are positive between the cis-stilbene equilibrium, at Θ = 5.5°, and the CI, near Θ = 90°. Thus, the fragment torque in the ground state works against the isomer rotation for Θ ≤ 90°, which is compatible with the isomer climbing toward the energetic transition barrier. At the CI
ref values are positive between the cis-stilbene equilibrium, at Θ = 5.5°, and the CI, near Θ = 90°. Thus, the fragment torque in the ground state works against the isomer rotation for Θ ≤ 90°, which is compatible with the isomer climbing toward the energetic transition barrier. At the CI ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref jumps to negative values, decreasing to zero at the trans-stilbene equilibrium, at Θ = 175°. This means that the fragment torque favors the isomer rotation along the ground state PES for Θ ≥ 90°, which is understood as the isomer going down in energy from the transition barrier along the path.
ref jumps to negative values, decreasing to zero at the trans-stilbene equilibrium, at Θ = 175°. This means that the fragment torque favors the isomer rotation along the ground state PES for Θ ≥ 90°, which is understood as the isomer going down in energy from the transition barrier along the path.
Fig. 8b includes also the rOBF path along the excited state PES (red diamonds). Here ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref shows an opposite behavior compared with that of the ground state. For rotation angles between the cis-stilbene equilibrium and the CI, i.e. below Θ = 90°, the
ref shows an opposite behavior compared with that of the ground state. For rotation angles between the cis-stilbene equilibrium and the CI, i.e. below Θ = 90°, the ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref values are always negative. Thus, the fragment torque supports the isomer rotation for Θ ≤ 90°. This is compatible with the isomer approaching the energetic dip of the excited state PES along the path near the CI. At the CI
ref values are always negative. Thus, the fragment torque supports the isomer rotation for Θ ≤ 90°. This is compatible with the isomer approaching the energetic dip of the excited state PES along the path near the CI. At the CI ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref switches to strongly positive values, decreasing to zero at the trans-stilbene equilibrium. Thus, the fragment torque hinders the isomer rotation along the excited state PES for Θ ≥ 90°, again in tune with the isomer increasing its energy from the transition barrier along the path. The absolute torque values close to the CI increase by much more along the excited state path than along the ground state path. This is connected with the fact that the dip in the excited state PES near the CI is much sharper than the corresponding ridge of the ground state PES. However, some of this difference may be attributed to numerical inaccuracies due to convergence problems of the excited state wavefunctions very close to the CI. Altogether, the torque results are consistent with the total energy behavior along the cis- to trans-stilbene isomerization path within the rOBF model and confirm the combination of ground and lowest excited state energy paths supporting the photochemical process discussed above.
ref switches to strongly positive values, decreasing to zero at the trans-stilbene equilibrium. Thus, the fragment torque hinders the isomer rotation along the excited state PES for Θ ≥ 90°, again in tune with the isomer increasing its energy from the transition barrier along the path. The absolute torque values close to the CI increase by much more along the excited state path than along the ground state path. This is connected with the fact that the dip in the excited state PES near the CI is much sharper than the corresponding ridge of the ground state PES. However, some of this difference may be attributed to numerical inaccuracies due to convergence problems of the excited state wavefunctions very close to the CI. Altogether, the torque results are consistent with the total energy behavior along the cis- to trans-stilbene isomerization path within the rOBF model and confirm the combination of ground and lowest excited state energy paths supporting the photochemical process discussed above.
The inverse trans- to cis-stilbene isomerization (going from right to left in Fig. 7 and 8 along a reversed rOBF path) can be understood by the same energetic and torque behavior as for cis to trans isomerization. Due to the reversed variation of Θ, positive ![[T with combining low line]](https://www.rsc.org/images/entities/i_char_0054_0332.gif) ref values in Fig. 8b refer to torques pointing along the sense of trans to cis rotation, thus, supporting the isomerization; negative Tref values point against the sense of rotation and hinder the isomerization. Fig. 9a, b evidence that, starting from the trans-stilbene ground state, at Θ = 175°, and after excitation to the lowest excited state, the total energy decreases along the transition path towards the CI at Θ = 90°, which is supported by the torque along the C
ref values in Fig. 8b refer to torques pointing along the sense of trans to cis rotation, thus, supporting the isomerization; negative Tref values point against the sense of rotation and hinder the isomerization. Fig. 9a, b evidence that, starting from the trans-stilbene ground state, at Θ = 175°, and after excitation to the lowest excited state, the total energy decreases along the transition path towards the CI at Θ = 90°, which is supported by the torque along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis. After switching to the ground state PES at the CI, the total energy decreases further towards the cis-stilbene equilibrium at 5.5°, which is again confirmed by the torque along the C
C backbone axis. After switching to the ground state PES at the CI, the total energy decreases further towards the cis-stilbene equilibrium at 5.5°, which is again confirmed by the torque along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis.
C backbone axis.
4. Conclusions
The complex motion of atoms inside large molecules can be analyzed by considering translation, rotation, and flexibility of molecular fragments within the molecule and by applying classical mechanics based on quantum mechanical Pulay forces on the atoms. In this work we propose a simple fragment motion analysis which provides a basic qualitative understanding of the motion of the different molecular components with emphasis on fragment rotation. This allows us to efficiently predict motion paths and can help design simplified fragment paths in the multi-dimensional configuration space. Examples are rotations of a flexible rotator with respect to its flexible stator counterpart in a rotor molecule, but also rotational isomerization paths inside a large molecule.After dealing in detail with formal aspects of the fragment motion analysis, we have discussed two example applications where the analysis of fragment torques can give additional insight into the mechanism of rotational motion beyond total energy considerations. In the symmetrized model of the BTP-BCO molecule, the rotation of the inner BCO rotator is well described by the periodic variation of the total energy as a function of the rotation angle φ. Here the results of the torque analysis are confirmed to be consistent with those of the total energy and efficiently predict the general behavior anticipated by the geometry of the molecule. Further, model paths describing the photochemical isomerization between cis- and trans-stilbene by a relaxed one-bond flip (rOBF) scheme are examined in detail and verify the mechanism proposed earlier. After an initial excitation of the isomer from its equilibrium ground state to its lowest excited state (which is induced experimentally by UV light absorption) the molecule relaxes by rotating about its C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C backbone axis with additional rotation of the phenyl groups about their C-phenyl axes. This allows stilbene to reach a conical intersection where it can easily switch from the excited state energy surface to the ground state surface, after which it can relax further to the equilibrium of the alternative isomer. The torque analysis for the molecule confirms and illustrates the isomerization mechanism suggested by the rOBF model paths along the different potential energy surfaces and supports the photochemical process.
C backbone axis with additional rotation of the phenyl groups about their C-phenyl axes. This allows stilbene to reach a conical intersection where it can easily switch from the excited state energy surface to the ground state surface, after which it can relax further to the equilibrium of the alternative isomer. The torque analysis for the molecule confirms and illustrates the isomerization mechanism suggested by the rOBF model paths along the different potential energy surfaces and supports the photochemical process.
The mechanical analysis together with the concept of fragment motion will prove its usefulness in subsequent studies which include more complex types of motion. Examples are combinations of fragment translation and rotation as found in [c2]daisy chain supramolecules7,8 or the influence of fragment flexibility as identified in molecular dynamics calculations on BTP-BCO. Also details of interlocking rotor molecules, such as those examined recently,35,36 will be interesting as candidates for the mechanical analysis. Studies along these lines are currently under way.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Group Research Fund of the Hong Kong Research Grants Council (Project No. 12301814). Klaus E. Hermann is grateful for support by the ICTS at HKBU; ICTS is supported by the Institute of Creativity, which is sponsored by Hung Hin Shiu Charitable Foundation ( ). Fei Qi would like to acknowledge support by the Hong Kong Research Grants Council (Project No. 12324716). Open Access funding provided by the Max Planck Society.
). Fei Qi would like to acknowledge support by the Hong Kong Research Grants Council (Project No. 12324716). Open Access funding provided by the Max Planck Society.
References
- J. C. M. Kistemaker, P. Štacko, J. Visser and B. L. Feringa, Nat. Chem., 2015, 7, 890–896 CrossRef PubMed.
- See https://www.nobelprize.org/nobel_prizes/chemistry/laureates/2016/press.html.
- A. Kazaryan, J. C. M. Kistemaker, L. V. Schäfer, W. R. Browne, B. L. Feringa and M. Filatov, J. Phys. Chem. A, 2010, 114, 5058–5067 CrossRef PubMed.
- F. Barigelletti, L. Flamigni, V. Balzani, J.-P. Collin, J.-P. Sauvage and A. Sour, New J. Chem., 1995, 19, 793–798 Search PubMed.
- H. W. Wang, X. Q. Shi, M. Jin, C. Minot, M. A. Van Hove, J.-P. Collin and N. Lin, ACS Nano, 2010, 4, 4929–4935 CrossRef PubMed.
- Y. Li, R. Q. Zhang, X. Q. Shi, Z. Lin and M. A. Van Hove, J. Chem. Phys., 2012, 137, 234302 CrossRef PubMed.
- Y. L. Zhao, R. Q. Zhang, C. Minot, K. Hermann and M. A. Van Hove, Phys. Chem. Chem. Phys., 2015, 17, 18318–18326 RSC.
- Y. L. Zhao, R. Q. Zhang, C. Minot, K. Hermann and M. A. Van Hove, Phys. Chem. Chem. Phys., 2016, 18, 7419–7426 RSC.
- W. Fuß, C. Kosmidis, W. E. Schmid and S. A. Trushin, Angew. Chem., 2004, 116, 4273–4277 CrossRef.
- V. Molina, M. Merchán and B. O. Roos, J. Phys. Chem. A, 1997, 101, 3478–3487 CrossRef.
- V. Molina, M. Merchán and B. O. Roos, Spectrochim. Acta, Part A, 1999, 55, 433–446 CrossRef.
- R. Püttner, P. Schmidt-Weber, T. Kampen, C. Kolczewski, K. Hermann and K. Horn, J. Electron Spectrosc. Relat. Phenom., 2016, 215, 16–21 CrossRef.
- F. Qi, Light-driven molecular rotary motors, PhD thesis, Dept. of Physics, Hong Kong Baptist University, 2017, Open Access Theses and Dissertations 434.
- R. K. Chaudhuri, K. F. Freed, S. Chattopadhyay and U. S. Mahapatra, J. Phys. Chem. A, 2013, 117, 9424–9434 CrossRef PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef.
- A. R. Leach, Molecular Modelling, Principles and Applications, Prentice Hall, London, 2nd edn, 1996 Search PubMed.
- P. Pulay, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 169–181 Search PubMed.
- Here we use the terms “static fragments” and “stators” loosely to contrast them with more mobile fragments whose relative translations and rotations are being studied. In reality, all parts of a free molecule can move simultaneously, if only to conserve linear and angular momentum.
- The combination of classical Newtonian mechanics with quantum-based forces is common to concepts applied in ab initio geometric optimization and in molecular dynamics.
- R. Q. Zhang, Y. L. Zhao, F. Qi, K. Hermann and M. A. Van Hove, Phys. Chem. Chem. Phys., 2016, 18, 29665–29672 RSC.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- R. Q. Zhang, N. B. Wong, S. T. Lee, R. S. Zhu and K. L. Han, Chem. Phys. Lett., 2000, 319, 213–219 CrossRef.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., GAUSSIAN 03, Revision C.02, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- B. B. Champagne, J. P. Pfansfiel, D. F. Plusquellic, D. W. Pratt, W. M. Van Herpen and W. L. Meerts, J. Phys. Chem., 1990, 94, 6–8 CrossRef.
- J. A. Syage, P. M. Felker and A. H. Zewail, J. Chem. Phys., 1984, 81, 4706–4723 CrossRef.
- J. A. Bouwstra, A. Schouten and J. Kroon, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 428–431 CrossRef.
- M. Traetteberg and E. B. Frantsen, J. Mol. Struct., 1975, 26, 69–76 CrossRef.
- B. L. Feringa, Molecular Switches, Wiley Online Library, 2001 Search PubMed.
- J. K. Gimzewski and C. Joachim, Science, 1999, 283, 1683–1688 CrossRef PubMed.
- J. F. Arenas, I. López-Tocón, J. C. Otero and J. I. Marcos, J. Phys. Chem., 1995, 99, 11392–11398 CrossRef.
- M. Klessinger and J. Michl, Excited states and photochemistry of organic molecules, VCH, Weinheim, 1995 Search PubMed.
- T. R. Rizzo, Y. D. Park, L. A. Peteanu and D. H. Levy, J. Chem. Phys., 1986, 84, 2534–2541 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- R. Zhao, Y. L. Zhao, F. Qi, K. Hermann, R. Q. Zhang and M. A. Van Hove, ACS Nano, 2018, 12, 3020–3029 CrossRef PubMed.
- R. Zhao, F. Qi, Y. L. Zhao, K. Hermann, R. Q. Zhan and M. A. Van Hove, J. Phys. Chem. Lett., 2018, 9, 2611–2619 CrossRef PubMed.
| This journal is © the Owner Societies 2018 |







