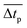Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predictability of the onset of spiking and bursting in complex chemical reactions
Marcus W.
Beims
 abc and
Jason A. C.
Gallas
abc and
Jason A. C.
Gallas
 bcd
bcd
aDepartamento de Física, Universidade Federal do Paraná, 81531-980 Curitiba, Brazil. E-mail: mbeims@fisica.ufpr.br; Tel: +55 41 3361 3349
bMax-Planck Institute for the Physics of Complex Systems, Nöthnitzer Str. 38, 01187 Dresden, Germany
cComplexity Sciences Center, 9225 Collins Avenue Suite 1208, Surfside, FL 33154-3001, USA. E-mail: jason.gallas@gmail.com; Tel: +1 786 843 8860
dInstituto de Altos Estudos da Paraíba, Rua Silvino Lopes 419-2502, 58039-190 João Pessoa, Brazil
First published on 18th June 2018
Abstract
For three complex chemical reactions displaying intricate dynamics, we assess the effectiveness of a recently proposed quantitative method to forecast bursting and large spikes, i.e. extreme events. Specifically, we consider predicting extreme events in (i) a copper dissolution model where Bassett and Hudson experimentally observed homoclinic (Shilnikov) chaos, (ii) a model derived from the mass action law of chemical kinetics, and (iii) an autocatalator model. For these systems, we describe how the alignment of Lyapunov vectors can be used to predict the imminence of large-amplitude events and the onset of complex dynamics in chaotic time-series of observables.
1. Introduction
The prediction of catastrophic events, outliers, is an enduring problem that continues to attract attention in virtually all scientific disciplines.1–3 Such extreme events are usually quite disruptive and manifest themselves as large-amplitude fluctuations in time-series of observables, either measured or computed. A plethora of methods to anticipate the onset of catastrophic events exist. Recently, we proposed a quantitative criterion to predict larger-amplitude events in chaotic systems.4,5 The criterion is obtained by studying the alignment of Lyapunov vectors (LVs), sometimes referred to as “covariant” Lyapunov vectors. The norms of the LVs, called Lyapunov exponents (LEs), measure the temporal expansion (or contraction) of the distance between two initially very close trajectories. Positive LEs are the signature of chaotic trajectories. We observed empirically4,5 that a tangency between LVs occurs every time that an observable under consideration tends towards its maximum. This tangency is an alignment of Lyapunov vectors. In some cases the value of the maximum is inversely proportional to the degree of the vector alignment.In the present paper, as a further application of the proposed criterion,4,5 we investigate the reliability of the alignment between Lyapunov vectors as a predictive tool in the context of complex chemical phenomena. Specifically, we use Lyapunov vectors to predict the onset of bursting and spiking in three familiar reactions. The first reaction was considered in pioneering work in 1988 by Bassett and Hudson6 to reproduce aspects of the experimental electrodissolution of a copper rotating disk in a H2SO4/NaCl solution. The second reaction is a mass-action model used to study the interplay of three interacting chemical species.7,8 The third reaction is a popular autocatalator model used to study complex oscillations in isothermal chemical systems.9 In all three examples, we find the alignment between Lyapunov vectors to be an effective predictor of extreme events. In addition, we point out some pitfalls of the method and discuss how to apply it effectively.
Lyapunov vectors provide a detailed step-by-step record of what exactly happens with the angles between stable and unstable manifolds during the whole evolution of a given dynamical process. The computation of Lyapunov vectors is no more complicated than the computation of standard Lyapunov exponents and is well-described in the literature.4,5,10–15 In an Appendix, we summarize the steps involved in their computation. As discussed below, it was observed heuristically4,5 that the onset of large peaks in a given physical variable corresponds to the alignment of LVs along the flow direction. Therefore, since Lyapunov vector alignment precedes large peaks, it can be used to predict the latter. It has been shown4 that predictability using LVs is closely related to alignment conditions, obtained by defining thresholds of how close LVs become tangent to the flow direction. When the alignment conditions are satisfied at a given time, called the prediction time, an extreme spike is expected to occur. The appropriate definition of the alignment conditions depends sensitively on the specific dynamics of the system.
For systems with long quiescent intervals between large spikes, the alignment conditions are very useful to anticipate unexpected large spikes. However, when numerous smaller spikes occur between large spikes, the choice of the appropriate alignment conditions can be tricky and some preparatory trial-error checks may be needed. In general, while small and large spikes can be predicted by the alignment of LVs, large spikes correspond to the prediction times where LVs are strongly parallel to the flow direction. Thus, the amplitude of the predicted peaks is related to how close the LV direction aligns along the flow direction.4
Apart from the chemical phenomena described by the models, complex chemical reactions are governed by sets of differential equations which are significantly different from the equations so far considered and no knowledge concerning the interplay of their Lyapunov vectors exists. Thus, it is of interest to verify the predictive power of Lyapunov vectors in foretelling the imminence of large-amplitude events in chemical time-series. Here, we check predictions for three typical systems governed by nonlinear differential equations involving different combinations of polynomial terms. We computed LVs using the methodology explained in detail in ref. 4 and 5. See also ref. 10–14 and the survey in ref. 15.
2. Electrodissolution of copper
In 1988, Bassett and Hudson6 performed a series of experiments on the electrodissolution of a copper rotating disk in a H2SO4/NaCl solution. They reported evidence of homoclinic (Shilnikov) chaos in their experimental time-series. Among this evidence, they presented a comparison of their time-series with those obtained from a mathematical model considered previously by Argoul et al.,16 in a discussion concerning homoclinic chaos in the Belousov–Zhabotinski reaction. The model is defined by the following three-dimensional flow| ẋ = y, | (1) |
| ẏ = z, | (2) |
| ż = −z − 1.3y − μx + x2 − 1.425y2 + 0.2xz − 0.01x2z. | (3) |
Fig. 1 shows the chaotic attractor for μ = 1.4 and initial conditions (−0.1, −0.1, 1.0). The attractor is obtained by solving eqn (1)–(3) numerically with the standard fourth-order Runge–Kutta algorithm and a fixed time-step h = 0.005. The first 107 steps were discarded as transient, with LVs computed subsequently for approximately 9.6 × 106 steps. The Lyapunov exponents λi (i = 1, 2, 3) are λ1 = 0.234, λ2 = −0.0013, and λ3 = −2.739, where the subindex i = 1 refers to the unstable direction, i = 2 to the flow direction and i = 3 to the stable direction. Accordingly, θ12, represented in colors in Fig. 1, is the angle between the unstable manifold and the flow direction. We observe that along the attractor the angle θ12 can change substantially.
 | ||
| Fig. 1 Representative attractor for the model of dissolution of copper, eqn (1)–(3), with colors representing the values of the angle θ12 between the unstable invariant manifold and the flow direction. | ||
In order to get a more quantitative insight concerning the ability of the alignment of LVs to anticipate spikes, Table 1 summarizes some statistical results. For this end, we consider the chaotic trajectory from Fig. 1 which has 2192 spikes over the integrated times, and say that there is a spike whenever x < −9.0 and an extreme spike when x < −15.0. To explain the quantities in Table 1, let us start by discussing the third line, which is the alignment condition displayed in Fig. 2. From the sample of 2192 spikes, Npp = 1693 of them were predicted, which is around 76.3% of the total number of spikes. However, Nfa = 686 (41.0%) from the 1693 predicted spikes are false alarms, meaning that 1007 spikes are not extreme. False alarms are those alarms which predicted spikes with small amplitudes, i.e. predicted non-extreme spikes. From the total number 2192 − 1693 = 499 of non-predicted spikes, Next = 181 of them were extreme spikes. Thus, for this alignment condition the method did not predict 181 extreme spikes. Such a large value of non-predicted extreme spikes has to be avoided. All predicted extreme spikes have an associated prediction time interval Δtp, which can be large or short. The prediction time interval is defined as the absolute value between the prediction time and the time for which the extreme spike occurs. While large prediction time intervals are most welcome to allow preparation to meet the extreme events, short prediction time intervals can bring difficulties for such preparations. In other words, for very short prediction time intervals there may not be enough time to prepare for the impingent extreme events. To quantify this, the last row displays the mean prediction time interval  .
.
 , the average prediction time interval
, the average prediction time interval
| θ (min)12 | θ (max)12 | N pp | N fa | N ext | |
|---|---|---|---|---|---|
| 0.05 | 3.09 | 759 (35%) | 315 (41%) | 725 | 19.1 |
| 0.10 | 3.04 | 1205 (55%) | 484 (40%) | 447 | 17.4 |
| 0.14 | 3.0 | 1693 (76%) | 686 (41%) | 181 | 15.2 |
| 0.20 | 2.94 | 1933 (88%) | 795 (41%) | 30 | 14.1 |
| 0.30 | 2.84 | 2146 (98%) | 982 (45%) | 4 | 15.1 |
| 0.50 | 2.64 | 2186 (99%) | 1022 (47%) | 4 | 18.2 |
| 0.70 | 2.44 | 2187 (99%) | 1022 (47%) | 3 | 20.4 |
 | ||
| Fig. 2 A time window displaying the evolution of x (black curve), of θ12 (red), and two straight lines (blue) indicating the values of θ(min)12 = 0.14 and θ(max)12 = 3.0 for the alignment condition. | ||
To better understand the relevance of θ12, Fig. 2 shows a time-window displaying the variable x (black curve) from the chaotic attractor from Fig. 1. The angle θ12 is plotted in the red color. Apart from some small amplitude oscillations, θ12 tends to 0 or π before spikes appear in variable x. This means that the peaks in x can be predicted in time if we define thresholds for θ12, namely θ(min)12 and θ(max)12. The two horizontal blue lines in Fig. 2 are illustrative thresholds for this trajectory, namely θ(min)12 = 0.14 and θ(max)12 = 3.0. Instants of time where θ12 crosses these thresholds (i.e., θ12 < 0.14 or θ12 > 3.0) are called prediction times and a large spike in x is expected to occur. Three such examples are indicated with black arrows in Fig. 2, the arrows chosen subjectively, for illustration purposes. For the first two arrows on the left we have θ12 > 3.0 and for the arrow on the right θ12 < 0.14, and they precede the large spikes with x < −15. The thresholds define the alignment condition for the LV along the flow direction and allows us to predict the spikes. The effectiveness to predict spikes may change for different alignment conditions, as discussed below in more detail.
The overall message from Table 1 is that for stronger alignment conditions the number of non-predicted spikes increases, specially the extreme spikes, Next. If the alignment conditions are relaxed, the number of predicted peaks increases but the number of false alarms also increases. Comparing the stronger alignment conditions with the more relaxed condition, Npp increases by around 65.2% but Nfa increases by only 5.2%. In fact, more relaxed alignment conditions lead to longer prediction time intervals. The selection of a suitable threshold depends very much on what is needed for practical purposes. For example, if we want to avoid all extreme spikes, we should chose an alignment condition consistent with Next → 0. In this case the appropriate alignment condition would be θ(min)12 = 0.7 and θ(max)12 = 2.44. On the other hand, if the large peaks provoke no major damage, one may accept some such peaks together with the condition to prevent a repetition of false alarms. This means, a compromise must be found between allowing some large peaks while at the same time not allowing the number of false alarms to dominate. To find such a compromise, one may consult Table 1 and select the suitable alignment condition providing an adequate balance. In such case, an adequate alignment condition would be θ(min)12 = 0.20 and θ(max)12 = 2.94.
3. Mass-action kinetics
In the next example, we revisit a chemical model introduced by Gaspard and Nicolis7,8 to study homoclinic phenomena. The dimensionless governing equations are| ẋ = (βx − fy − z + g)x, | (4) |
| ẏ = (x + sz − α)y, | (5) |
| εż = x − az3 + bz2 − cz. | (6) |
 | ||
| Fig. 3 Chaotic attractor governed by the mass-action kinetics, eqn (4)–(6), with colors representing the angle θ12 as indicated by the colorbar. | ||
The trajectory forming the attractor in Fig. 3 starts parallel to the xy plane with a chaotic spiraling-out motion, with the angles θ12 oscillating between π/4 (cyan) and π/2 (green), while the reinjection loops are shown in black and red, associated with θ12 approaching either 0 or π, respectively.
To better understand the time evolution of θ12, Fig. 4 presents the evolution of z (black lines) and the associated LV angle θ12 (red lines) for a regular trajectory in Fig. 4(a) and for a chaotic trajectory in Fig. 4(b). By ‘regular’ trajectory we mean a trajectory which has no positive Lyapunov exponent. In both cases, regular and chaotic, the LV angle θ12 oscillates fast in time but tends to approach 0 or π before the spikes in z are observed. This means that the peaks in z can be predicted in time when introducing suitable thresholds for θ12, namely θ(min)12 and θ(max)12. As exemplified in Fig. 4, the two horizontal blue lines indicate thresholds for these trajectories, namely θ(min)12 = 0.1 and θ(max)12 = 3.04 for the regular case and θ(min)12 = 0.5 and θ(max)12 = 2.64 for the chaotic case.
 | ||
| Fig. 4 Time window showing the variable z (black lines) and θ12 (red lines) for part of (a) a regular trajectory with parameters α = 0.7825 and β = 0.39213 and (b) the chaotic trajectory from Fig. 1. Two horizontal blue lines indicate thresholds to predict spikes and the two black arrows show two prediction times where θ12 crosses the thresholds. | ||
In order to choose adequate thresholds for these trajectories, a statistical analysis of the spikes must be performed, as done in the next paragraph. When θ12 crosses these thresholds, spikes in z are to be expected. We note that θ12 tends to approach 0 or π not only before the large spikes, but also before the small spikes. The crucial distinction is that, preceding large spikes, the angle comes closer to 0 or π than before the small spikes. From a physical point of view, our results show that each time the unstable (chaotic case) and the stable (regular case) manifolds align along the direction of motion, a spike in the z concentration is expected.
Fig. 4 also shows that, far from spikes, the angle θ12 oscillates in time. Such oscillations occur when the eigenvalues of the Jacobian matrix are complex and no invariant manifolds exist. In fact, manifolds rotate and the angles oscillate in time. This oscillatory behavior was observed and explained for specific parameter values of the Hénon map.5 Analogous angle oscillations were reported recently for interesting critical transition problems,17 although no explanation concerning the origin of the oscillations was given there.
The results above suggest that for times called prediction times, as exemplified in Fig. 4 by black arrows, it is possible to anticipate the imminent occurrence of a spike. It also becomes clear that prediction time intervals, defined as the absolute values between the prediction times and the times for which the extreme spike occurs, depend on the thresholds chosen.
Similar to before, Table 2 summarizes some statistical results. For this we consider the chaotic trajectory which has 549 spikes during the integration interval. We say that there is a spike when z > 0.9 and an extreme spike when z > 3.0. Let us start to discuss the first line, which has a very strong alignment condition. From the total of 549 spikes, Npp = 526 of them were predicted. However, Nfa = 33 from the predicted spikes are false alarms, meaning that the 33 spikes are not extreme (z < 3.0). From the 549 − 526 = 23 non-predicted spikes, Next = 16 are extreme spikes. The last row displays the mean prediction time intervals 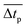 .
.
 , the average prediction time interval
, the average prediction time interval
The general behavior presented in Table 2 is similar to the one in Table 1. For strong alignment conditions the number of non-predicted spikes increases, especially the number Next of extreme spikes. If the alignment conditions are relaxed, there is an increase in the number of predicted peaks as well as in the number of false alarms. However, the percentage of false alarms is much smaller here. Comparing the stronger alignment conditions with the more relaxed condition, one sees that Npp increases by 4.2% while Nfa increases by only 1.0%. More relaxed alignment conditions require longer prediction time intervals, excluding almost all shorter (<1.0) prediction time intervals.
As discussed in the previous section, the appropriate alignment condition depends on what is sought in practical situations. If we again want to find a compromise between allowing some large peaks while at the same time not allowing the number of false alarms to dominate, consulting Table 2 the suitable alignment condition providing an adequate balance is θ(min)12 = 0.03 and θ(max)12 = 3.11.
4. The autocatalator model
Next, we consider the use of LVs to predict outliers in the complex oscillations generated by the isothermal chemical system governed by the following four-parameter autonomous polynomial model9 | (7) |
 | (8) |
 | (9) |
Fig. 5 displays the attractor for the typical parameters κ = 2.5, δ = 1, μ = 0.2983 and σ = 0.013 using the initial condition (α, β, γ) = (0.5, 2.5599, 0.5). As before, colors represent the values of the angle θ12 for each point on the attractor. The attractor is formed by a chaotic trajectory with Lyapunov exponents λ1 ∼ 0.755, λ2 ∼ 0.002 and λ3 ∼ −11.117. The attractor in Fig. 5 and in subsequent simulations was obtained by solving eqn (7)–(9) numerically with the standard fourth-order Runge–Kutta algorithm and a fixed time-step h = 0.05. The first 107 steps were discarded as transient, with LVs computed during the next 6 × 106 steps. For better visualization, only 12% of these points were plotted in Fig. 5. The angle θ12 changes along the attractor. The rightmost green ridge clearly visible in Fig. 5 is related to angles close to π/2 and corresponds to strong hyperbolic motion.
 | ||
| Fig. 5 Attractor for the autocatalator, eqn (7)–(9), with colors representing the angle θ23. | ||
Fig. 6 presents a time-window of the evolution of β (black lines) and associated LVs for the chaotic trajectory from Fig. 5. Fig. 6(a) presents the angle θ12 between the unstable manifold and flow direction, while Fig. 6(b) displays the angle θ23 between the stable manifold and flow direction. Besides the very fast variations of these angles, they assume values close to 0 and π for almost all integrated times.
 | ||
| Fig. 6 Time evolution of the concentration β (×3) (black lines) for a chaotic trajectory and (a) the angle θ12 (red line) and (b) θ23 (green line). | ||
Next, we consider a regular trajectory obtained for κ = 2.5, δ = 1, μ = 0.29776 and σ = 0.013 and initial conditions (α, β, γ) = (0.5, 0.25599, 0.5). The Lyapunov exponents for this case are λ1 ∼ 0.003, λ2 ∼ −0.914 and λ3 ∼ −16.16. Therefore the angles θ12 and θ13 are the angles between stable manifolds along the flow direction. The time evolution of the concentration β is shown in Fig. 7 (black lines) with colors representing the angle θ12 obtained along the trajectory. Results are analogous to the chaotic case discussed above, also for θ23. Since for the autocatalator the variables θ12 and θ23 show essentially the same behavior, we use θ23 to show that the prediction method also works when using angles between other manifolds.
 | ||
| Fig. 7 Time evolution of the concentration β (black lines) for a regular trajectory and (a) the angle θ12 (red line) and (b) θ13 (green line). | ||
In sharp contrast to the reaction considered in Sections 2 and 3, here the variable of interest, namely the concentration β, never relaxes to random quiescent intervals. It always increases towards a peak (large or not) and decreases very fast to a minimum. After each minimum, β promptly starts to increase towards the next maximum, while θ12 and θ13 tend to approach 0 or π, usually right after the minimum. This is the alignment of both stable and unstable manifolds along the direction of motion and precedes the appearance of a peak. This is in agreement with our recent proposal4 that the alignment of LVs along the flow direction precedes peaks in a chaotic dynamical system. Therefore all peaks in the concentration β can be easily predicted by the angles θ12 and θ13. However, since the concentration β always goes, after the minima, towards the peaks, the alignment of LVs to predict peaks is not necessary in this case. In fact, the dynamics is apparently strongly non-hyperbolic for all the duration of the integration.
For all three models considered here, the alignment of LVs is able to predict all peaks during the time evolution, large or not. Therefore, while the comparatively large number of false alarms found in Section 2 (∼46.7%) is compatible with this detection power, false alarms found in Section 3 (∼7.3%) are acceptable. However, this seemingly negative aspect of the method can be essential to predict spikes in systems where the quiescent motion does not give any indication that a spike will appear. For example, in the quiescent intervals shown in Fig. 2 and 4, the plotted quantities x and z, respectively, present some smaller spikes with increasing amplitudes which indicate that an extreme spike might appear. All these smaller spikes are detected by the alignment of LVs and lead to false alarms. Sometimes, the time evolution of the observed quantities x, z and β in the examples above provides clues that a large spike will appear. But the difficult situation is when such clues are not found in the time evolution. In this circumstance, LV alignment is quite helpful to predict large spikes. Comparing results for the two systems in Sections 2 and 3, one sees that when the alignment conditions are relaxed, the number of predicted peaks increases much more than the number of false alarms. In addition, the number of unpredicted extreme spikes tends to zero very fast. All in all, for the reactions considered, the LV alignment is able to foretell the imminence of spikes.
5. Conclusions and outlook
This work assessed the alignment of LVs as a quantitative tool to predict large-amplitude spikes in three chemical models governed by distinct polynomial dynamics. For the models in Section 2 and 3, the time evolution of the concentrations presents random intervals of quiescent motion. In these cases, large events are unpredictable by analyzing just the time evolution of the concentrations. Here, LVs are very helpful to predict spikes. In the model presented in Section 4 the concentrations oscillate continuously between minima and maxima. There is no relaxation and the arrival of spikes can be recognized by the time evolution of the concentrations. The three examples considered show that the alignment of Lyapunov vectors along the flow direction provides a straightforward and reliable quantity to predict small and large events for typical chemical reactions.The LV alignment as a spike prediction method is expected to be very general since it is able to detect all spikes. It is particularly useful when random intervals of quiescent motion are present in the time evolution of the concentrations. Due to the lack of analytical results, the relationship between the LV alignment and extreme events in dynamical systems must be tested for each particular case. An open challenge is to devise a way to apply LVs (i) to observational data, namely, for data which lack an underlying mathematical framework, and (ii) to realistic systems where the presence of noise is inevitable.
Conflicts of interest
There are no conflicts to declare.Appendix – numerical procedure
The most unstable direction of a chaotic trajectory can be determined from the direction of the eigenvector related to the largest LE, obtained as an eigenvalue of the Jacobian matrix of the system. The procedure for obtaining it is well known and widely used in the nonlinear and complex systems community and an explicit numerical code for the determination of Lyapunov exponents is given by Wolf et al.18 It involves a Gramm–Schmidt (GS) orthonormalization procedure which, unfortunately, destroys the information about the direction of all eigenvectors not related to the largest Lyapunov exponent. To compensate for this loss, a method proposed by Ginelli et al.,14 based on forward and backward time integrations, allows one to recover the direction of all unstable and stable invariant manifolds. This procedure is somewhat time consuming but very precise. In order to obtain stable and unstable directions in phase space we need to perform (i) forward and (ii) backward time evolutions:(i) The procedure summarized here is well known and uses ordinary differential equation (ODE) integrators and the aforementioned numerical code,18 based on the GS orthonormalization procedure. For the forward time evolution we integrate the equations of motion for variables (ẋ, ẏ, ż) (eqn (1)–(3), for example), together with their corresponding linearized equations
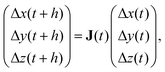 | (10) |
 | (11) |
Eqn (10) governs the time evolution in the tangent space. Choosing Δx(0) = a(1)0, Δy(0) = a(2)0 and Δz(0) = a(3)0, as an initially orthonormal basis G0 = (a(1)0,a(2)0,a(3)0), the evolution in tangent space up to a time t = nh (n = 0, 1, 2, 3,…) is then obtained from
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) n = JnG0, n = JnG0, | (12) |
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) n is renormalized for each step. As usual, this can be done by the QR decomposition
n is renormalized for each step. As usual, this can be done by the QR decomposition![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) n = GnRn. n = GnRn. | (13) |
The matrix Rn is upper-triangular
 | (14) |
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) n. Here, Gn = (a(1)n,a(2)n,a(3)n) are the GS vectors before the orthonormalization at iteration n and (g(1)n,g(2)n,g(3)n) are the GS vectors after the orthonormalization. Since g(1)n, g(2)n and g(3)n are orthonormal by construction, they can only provide information about the local rates of expansion (contraction) of the vectors, stored in the diagonal elements of Rn, from which the standard Lyapunov vectors can be obtained. The correct direction of the eigenvectors of the Jacobian matrix were corrupted by the orthonormalization procedure. They can be recovered by the backward integration, as shown below.
n. Here, Gn = (a(1)n,a(2)n,a(3)n) are the GS vectors before the orthonormalization at iteration n and (g(1)n,g(2)n,g(3)n) are the GS vectors after the orthonormalization. Since g(1)n, g(2)n and g(3)n are orthonormal by construction, they can only provide information about the local rates of expansion (contraction) of the vectors, stored in the diagonal elements of Rn, from which the standard Lyapunov vectors can be obtained. The correct direction of the eigenvectors of the Jacobian matrix were corrupted by the orthonormalization procedure. They can be recovered by the backward integration, as shown below.
(ii) The essential property is that for the backward time evolution the unstable direction is the stable direction from the forward time evolution. Thus, in the backward evolution the Lyapunov vector related to the largest Lyapunov exponent points along the stable direction from the forward evolution. In this way we define the Lyapunov vectors as
| v(1)n = c(1,1)ng(1)n, | (15) |
| v(2)n = c(1,2)ng(1)n + c(2,2)ng(2)n, | (16) |
| v(3)n = c(1,3)ng(1)n + c(2,3)ng(2)n + c(3,3)ng(3)n. | (17) |
Since in this work we use a fourth-order Runge–Kutta integrator, the error in the variables is around h5, which is negligible for the time steps h that we use. As convenient rules of thumb, one has to chose time steps small enough compared to the relevant oscillations of the system. For example, the peaks in Fig. 4 occur for small intervals of time, around Δt ∼ 0.4. Thus, to compute many points along such a short peak, we used h = 5 × 10−5 so to have around 8000 for each peak (not all plotted here). Once the above compromises are satisfied, the predictions are independent of the time step. On the other hand, the number of steps is more related to how much computational time is available or, in our case, how many peaks are needed to have a reliable statistical analysis. The precision of Lyapunov vectors is more dependent on the transient times than on other parameters.
It is worth mentioning that in general there is no need to realize the backward time evolution. It is enough to determine the unstable direction from the forward evolution and compare it to the flow evolution direction. Below, we present in schematic form the main steps used to determine Lyapunov vectors.
Acknowledgements
The authors were supported by CNPq, Brazil. Open Access funding provided by the Max Planck Society.References
- For a survey see, e.g., N. Akhmediev, et al., Roadmap on optical rogue waves and extreme events, J. Opt., 2016, 18, 063001 CrossRef and references therein.
- E. Mercier, A. Even, E. Mirisola, D. Wolfersberger and M. Sciamanna, Numerical study of extreme events in a laser diode with optical feedback, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042914 CrossRef PubMed.
- Extreme Events in Nature and Society, ed. S. Albeverio, V. Jentsch, and H. Kantz, Springer, New York, 2006 Search PubMed.
- M. W. Beims and J. A. C. Gallas, Alignment of Lyapunov Vectors: A Quantitative Criterion to Predict Catastrophes?, Sci. Rep., 2016, 6, 37102 CrossRef PubMed.
- M. W. Beims and J. A. C. Gallas, Manifold angles, the concept of self-similarity, and angle-enhanced bifurcation diagrams, Sci. Rep., 2016, 6, 18859 CrossRef PubMed.
- M. R. Bassett and J. L. Hudson, Shilnikov chaos during copper electrodissolution, J. Phys. Chem., 1988, 92, 6963–6966 CrossRef.
- P. Gaspard and G. Nicolis, What can we learn from homoclinic orbits in chaotic dynamics?, J. Stat. Phys., 1983, 31, 499 CrossRef.
- J. A. C. Gallas, The structure of infinite periodic and chaotic hub cascades in phase diagrams of simple autonomous flows, Int. J. Bifurcation Chaos Appl. Sci. Eng., 2010, 20, 197–211 CrossRef.
- V. Petrov, S. K. Scott and K. Showalter, Mixed-mode oscillations in chemical systems, J. Chem. Phys., 1992, 97, 6191 CrossRef.
- Y. Pomeau, A. Pumir and P. Pelce, Intrinsic stochasticity with many degrees of freedom, J. Stat. Phys., 1984, 37, 39 CrossRef.
- C. L. Wolfe and R. M. Samelson, An efficient method for recovering Lyapunov vectors from singular vectors, Tellus A, 2007, 59, 355 CrossRef.
- D. Pazó, J. M. López and M. A. Rodriguez, On the angle between the first and the second Lyapunov vectors in spatio-temporal chaos, J. Phys. A: Math. Theor., 2013, 46, 254014 CrossRef.
- A. Norwood, E. Kalnay, K. Ide, S. C. Yang and C. Wolfe, Lyapunov, singular and bred vectors in a multi-scale system an empirical exploration of vectors related to instabilities, J. Phys. A: Math. Theor., 2013, 46, 254021 CrossRef.
- F. Ginelli, H. Chaté, R. Livi and A. Politi, Covariant Lyapunov vectors, J. Phys. A: Math. Theor., 2013, 46, 254005 CrossRef , and references therein.
- P. V. Kuptsov and U. Parlitz, Theory and computation of covariant Lyapunov vectors, J. Nonlinear Sci., 2012, 22, 727–762 CrossRef.
- F. Argoul, A. Arneodo and P. Richetti, Experimental evidence for homoclinic chaos in the Belousov-Zhabotinsky reaction, Phys. Lett. A, 1987, 120, 269–275 CrossRef.
- N. Sharafi, M. Timme and S. Hallerberg, Critical transitions and perturbation growth directions, Phys. Rev. E, 2017, 96, 032220 CrossRef PubMed.
- A. Wolf, J. B. Swift, H. L. Swinney and J. A. Vastano, Determining Lyapunov exponents from a time series, Phys. D, 1985, 16, 285 CrossRef.
| This journal is © the Owner Societies 2018 |