Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anisotropic magnetic nanoparticles for biomedicine: bridging frequency separated AC-field controlled domains of actuation
David
Serantes
 *ab,
Roy
Chantrell
*ab,
Roy
Chantrell
 b,
Helena
Gavilán
c,
María del Puerto
Morales
b,
Helena
Gavilán
c,
María del Puerto
Morales
 c,
Oksana
Chubykalo-Fesenko
c,
Daniel
Baldomir
c,
Oksana
Chubykalo-Fesenko
c,
Daniel
Baldomir
 a and
Akira
Satoh
d
a and
Akira
Satoh
d
aApplied Physics Department and Instituto de Investigacións Tecnolóxicas, Universidade de Santiago de Compostela, 15782, Spain. E-mail: david.serantes@usc.es
bDepartment of Physics, University of York, Heslington, York YO10 5DD, UK
cInstituto de Ciencia de Materiales de Madrid, CSIC, Cantoblanco, ES-28049 Madrid, Spain
dFaculty of System Science and Technology, Akita Prefecture University, Yuri-Honjo 015-0055, Japan
First published on 3rd December 2018
Abstract
Magnetic nanoparticles (MNPs) constitute promising nanomedicine tools based on the possibility of obtaining different actuations (for example, heating or mechanical response) triggered by safe remote stimuli. Particularly, the possibility of performing different tasks using the same entity constitutes a main research target towards optimizing the treatment. But such a goal represents, in general, a very difficult step because the requisites for achieving efficient responses for separate actuations are often disparate – if not completely incompatible. An example of this is the response of MNPs to external AC fields, which could in principle be exploited for either magneto-mechanical actuation (MMA) at low frequencies (tens of Hz); or heat release at high frequency (0.1–1 MHz range) for magnetic fluid hyperthermia (MFH). The problem is that efficient MMA involves large torque, the required material parameters for which are detrimental to high heating, thus hindering the possibility of effective alternation between both responses. To overcome such apparent incompatibility, we propose a simple approach based on the use of anisotropic MNPs. The key idea is that the AC-frequency change must be concurrent with a field-amplitude variation able to promote – or impede – the reversal over the shape-determined anisotropy energy barrier. This way it is possible to switch the particle response between an efficient (magnetically dissipationless) rotation regime at low-f, for MMA, and a “frozen” (non-rotatable) high-energy-dissipation regime at high-f, for MFH. Furthermore, we show that such an alternation can also be achieved within the same high-f MFH regime. We use combined Brownian dynamics and micromagnetic simulations, based on real experimental samples, to show how such a field threshold can be tuned to working conditions with hexagonal-disk shape anisotropy.
1. Introduction
Magnetic nanoparticles are promising biomedical agents due to their versatile response to different external stimuli, with a number of potential applications ranging from drug delivery, imaging, hyperthermia cancer treatment or purely magneto-mechanically actuated responses (e.g. for breaking blood clots).1 Based on their differentiated actuation requirements and the inherent complexities, such different applications have been traditionally treated as separate research areas by the related communities.Nevertheless, in recent years increasing attention has been paid to the development of nanoentities with different properties, such that various functionalities could be achieved within the biological tissue by using the very same system. The main example is theranostics, where the same agent can be used for both detection and treatment.2 Such multiple fields of actuation by the same entity require an accurate control of the triggered responses. This is straightforwardly achieved if the required actions are promoted by different types of fields, as e.g. drug delivery and release (large homogeneous field gradients vs. AC-field triggered thermal release of the drug cargo).3 Similarly, very attractive physical responses for alternation would be heating, for magnetic fluid hyperthermia (MFH); and mechanical torque, for magneto-mechanical actuation (MMA). The working principle is the same (excitation by an external AC magnetic field), the differentiation arising from the different time domains of the phenomena:4 in principle, simply by changing the frequency of the AC field it would be possible to disentangle both responses, obtaining either magnetic actuation (Brownian regime, at low frequencies) or heating (Néel reversal regime, at high frequency). However, the switching between responses in this case of having different timescales of actuation becomes much more complicated than for example in theranostics, where the driving stimuli are of different types. Perusal of the literature rapidly shows how the – in principle incompatible – actuation requisites apparently restrict them to separated domains:5 the complementary high torque for low-frequency MMA requires large anisotropy, to avoid decoupling between magnetization and lattice; whereas for achieving high heating power it is necessary to overcome the anisotropy energy, thus losing the strong magnetization – lattice coupling (i.e. negligible Brownian rotation in the high-frequency MFH regime). At this point it is important to emphasize that, although some works still try to distinguish the contribution of Brownian reversal to hyperthermia (in the context of fitting to the linear response theory, whose limited applicability to MFH has been well documented6), it has been repeatedly shown that Brownian rotation plays a negligible role in heat dissipation under biological conditions.7–9 Also, neither has the mechanical response of the Brownian rotation in the high-frequency MFH regime proved to cause significant cell damage,10 in agreement with the observation that cellular internalisation can disable Brownian relaxation.9
In this context, we have recently shown that even if the Brownian contribution can be discarded as a heating mechanism, it may still play a role in tuning the heat dissipation by Néel reversal in chains of spherical particles11 and nanorods.12 This occurs because there is a progressive reorientation of the elongated structures during the AC treatment (parallel to the field in the case of the chains; orthogonal in the case of the rods) that allows for the enhanced performance of Néel-type heating.13 Therefore the question is; is such reorientation really accompanied by negligible losses? Understanding the heat losses of anisotropic nanomagnets over a wide range of frequencies (from the MMA regime to the purely MFH one) itself constitutes a crucial aspect to solve for the possible use of anisotropic nanomagnets for combined mechanical actuation and heating, either sequentially or simultaneously: large hysteresis losses are required for MFH, but are detrimental to MMA.
In order to shed some light on this question, we have theoretically investigated what would be the heating properties of anisotropic nanomagnets in a viscous environment, if the Néel contribution is quenched, for example in large (>20–50 nm) nanoparticles with high anisotropy. By using a Brownian dynamics (BD) technique14 we have simulated the AC field response of magnetic disks of large (>2–4) aspect ratios, able to provide large mechanical action. The interest in the disk shape is due to the similarity to the blood cells freely travelling within the vessels, hence constituting a very interesting morphology for the colloidal properties for intravenous injection. Particle magnetization is assumed to lie in the plane of the disks, and to be strongly coupled to the lattice so that particle reorientation is directly linked to magnetization rotation (see the Computational details section). This negligible thermal diffusion is due to the large particle size, which also prevents superparamagnetic fluctuations, hence ensuring the delivery of a large magnetic torque.15 The particle properties are those of magnetite, based on the suitability of iron oxides for biomedicine in comparison with other nanoparticles.16 Particularly, as a reference we have used disks of the same dimensions and composition as those recently reported by Gavilán et al.17 obtained by dry reduction of an antiferromagnetic precursor, i.e. uniform magnetite particles of hexagonal shape with average dimensions of 22 nm thickness and 140 nm diameter with a standard deviation of 10%. The experimental hexagonal shape is not the same as assumed in the BD simulations because of the difficulty of taking into account irregular shapes in the BD treatment; however, we note that the experimental samples are coated with a silica shell that softens the edges of the hexagons (regarding the viscous interaction with the environment) and hence the disk shape constitutes a rather good approximation to the experimental one. Sketches illustrating the shape of the disks assumed in the BD simulations are shown in Fig. 1, together with the TEM image of the experimental samples from ref. 17, both the as-prepared (A) and silica-coated (B) with smooth shapes. Importantly, those particles have a large in-plane magnetic moment, suitable for the BD description, as will be discussed later.
 | ||
| Fig. 1 (A) Schematics of the simulated particles (in red), together with some SEM examples of the experimental samples taken as a reference, either as-prepared (A) or silica-coated (B).17 The scheme on the right aims to illustrate the effect of the AC field in promoting the physical reorientation. | ||
It is known that not only large static fields, but also small alternating fields can cause aggregation,18 consequently enhancing the role of interactions. Nevertheless, since in this work we are interested in the pure Brownian interaction of the anisotropic particles with the environment, interactions with other particles will not be considered here (neither magnetic nor mechanical effects). Thus, the investigation procedure is to simulate the magnetization vs. field hysteresis loops, M(H(t)), of a random distribution of disks under the influence of an alternating AC field. Parameters to investigate are; the role of the medium viscosity (η), the amplitude (Hmax) and frequency (f) of the AC field, given as HAC(t) = Hmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft); and the size and aspect ratio of the particles. We consider first the purely Brownian rotation mechanism, which will be followed by a micromagnetic investigation of the Néel mechanism in the high frequency regime. The aim is to demonstrate that the applications of hexagonal particles, with close to coherent reversal, have strong but contrasting functionalities: mechanical actuation at low frequencies and magnetic hyperthermia at high frequencies and fields, and that such particles facilitate the intriguing possibility of alternating treatments for optimal therapeutic results.
sin(2πft); and the size and aspect ratio of the particles. We consider first the purely Brownian rotation mechanism, which will be followed by a micromagnetic investigation of the Néel mechanism in the high frequency regime. The aim is to demonstrate that the applications of hexagonal particles, with close to coherent reversal, have strong but contrasting functionalities: mechanical actuation at low frequencies and magnetic hyperthermia at high frequencies and fields, and that such particles facilitate the intriguing possibility of alternating treatments for optimal therapeutic results.
2. Computational details
Brownian dynamics simulations
We used the same model as in ref. 14, i.e. disk-like particles as schematically drawn in Fig. 1 which, in addition to the usual translational and rotational Brownian motion, considers the spin dynamical motion about the particle axis. For the characteristic parameters, we used the experimental value of MS = 415 emu cm−3 (300 K), and for the anisotropy we used the bulk value K = −1.1 × 104 erg cm−3. In the following we briefly summarize the basic equations for the present Brownian dynamics simulations; since there are no interactions and the AC field is homogeneous in space, only the rotational motion needs to be taken into account.The rotational motion about a line normal to the particle axis and the spin rotational motion about the particle axis are expressed, respectively, as
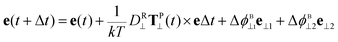 | (1) |
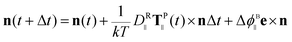 | (2) |
Expressions (1) and (2) show the equations providing the particle direction e and the magnetic moment direction n, respectively (note the simplification regarding the same expressions in ref. 14, since no shear flow is considered in the present work). The components normal and parallel to the particle axis are denoted by the subscripts ⊥ and ||, respectively; and Δt, k and T are the time interval, Boltzmann's constant and liquid temperature, respectively. It is noted that DR is the rotational diffusion coefficient of the disk-like particle which contains the viscosity (η), given by 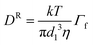 , where d1 defines the absolute particle size (see Fig. 1), and Γf is a geometric factor that takes into account the aspect ratio of the oblate spheroid, different for the normal and parallel components, expressed as14,19
, where d1 defines the absolute particle size (see Fig. 1), and Γf is a geometric factor that takes into account the aspect ratio of the oblate spheroid, different for the normal and parallel components, expressed as14,19
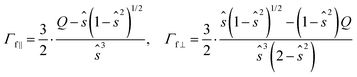 | (3) |
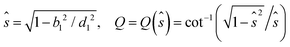 | (4) |
The dipole–field interaction torque is given by TP = MSVHmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πf·t)n × h, where V is the particle volume and h stands for the unit vector along the field direction. Moreover, e⊥1 and e⊥2 are the unit vectors normal to each other in the plane normal to the particle axis. The rotational Brownian motion is induced by the random angular displacements ΔϕB||, ΔϕB⊥1 and ΔϕB⊥2. These quantities have the following stochastic characteristics:
sin(2πf·t)n × h, where V is the particle volume and h stands for the unit vector along the field direction. Moreover, e⊥1 and e⊥2 are the unit vectors normal to each other in the plane normal to the particle axis. The rotational Brownian motion is induced by the random angular displacements ΔϕB||, ΔϕB⊥1 and ΔϕB⊥2. These quantities have the following stochastic characteristics:
| 〈ΔϕB‖〉 = 〈ΔϕB⊥1〉 = 〈ΔϕB⊥2〉 = 0, 〈(ΔϕB‖)2〉 = 2DR‖Δt, 〈(ΔϕB⊥1)2〉 = 〈(ΔϕB⊥2)2〉 = 2DR⊥Δt | (5) |
Finally, it is noted that the employment of an appropriate time interval is significantly important for obtaining physically reasonable results independent of the time interval from Brownian dynamics simulations. From preliminary simulations, we adopted a sufficiently small time-interval Δt as Δt = 5 × 10−4/f, 2 × 10−4/f, 1 × 10−4/f, etc. so that the results are Δt-independent, where f is the frequency of the applied alternating magnetic field. On the other hand, note that an extraordinary small time-interval such as Δt = 1 × 10−7/f cannot be employed since it would lead to the loss of precision in the calculation on the computer.
Micromagnetic simulations
We used the OOMMF software package24 to simulate the quasistatic hysteresis properties of the hexagonal disk-shape particles. The material parameters are those of the magnetite (cubic anisotropy, K = −0.011 × 105 erg cm−3; exchange stiffness Aexch = 1.0 × 10−6 erg cm−1), and the saturation magnetisation MS = 415 emu cm−3 which was taken from ref. 17. The easy axis directions are (1 0 0) and (0 1 0), and the applied field was varied at small intervals by energy minimization, until the torque criteria m × H × m = 0.1 is met (m is the reduced magnetization, m = M/MS).3. Results and discussion
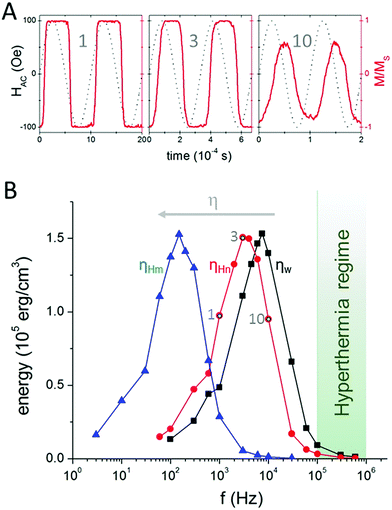
For the Brownian rotation mechanism, some examples of the time evolution of the magnetization with the varying field are shown in Fig. 2A for different frequencies, for a viscosity η = 2.0 × 10−3 Pa s (at room temperature) corresponding to that within HeLa cells (commonly used in cancer investigations). At this point it is worth emphasizing, however, that when dealing with nanosized dimensions the viscosity is not just defined by the solution properties, but also by the probe size, leading to definitions of “nano” viscosities for small hydrodynamic radius of the probes (order of tens of nanometres) and “macro” viscosity for larger sizes.20 While this factor is not the main aim of our current work, it is clearly of crucial importance for the related results and hence we decided to reflect it in our investigation. Therefore we have considered both the “nano” and “macro” viscosities of HeLa cells, which according to T. Kalwarczyk et al.20 have values of ηnano = 2.0 × 10−3 and ηmacroo = 4.4 × 10−2 Pa s, respectively. The systematic analysis of the energy losses of the studied disks for those viscosity values is shown in Fig. 2B, together with that of water, included as a reference.The results displayed in Fig. 2B show a common trend for the 3 viscosities investigated: a Gaussian-like shape whose peak shifts towards smaller frequencies for higher viscosities. Notably, the rotational losses (HL) become very small at high frequencies, supporting the negligible role of the Brownian contribution for MFH.7–9 In addition we clearly observe, for large anisotropies, the detrimental effect of increasing viscosity on the heating.21 On the opposite side of the peak, at low frequencies, the losses also become negligible when reaching values as low as tens of Hz, i.e. the values reported as efficient for causing membrane integrity loss by MMA using magnetic microdisks.22 Note that for efficient MMA a large magnetic torque is required, and such values are achieved for a strong coupling between magnetization and the lattice (condition equivalent to the infinitely strong coupling between moment and the lattice assumed in the BD simulations). Then, depending on the viscosity of the environment and field conditions, that torque can lead to two divergent cases in the ideal case of no phase lag between the magnetisation and field: a complete reorientation of the magnetisation with the field, at low-f; or just to a small oscillation amplitude at large frequency (magnetization unable to switch, leading to small rotations). Intermediate cases – i.e. relevant hysteresis – reflect a relevant interaction of the particle with the viscous environment; both the high- and intermediate-frequency scenario would be unsuitable for accurate mechanical action. Finally, it is important to note that the maximum HL values reached are of the order of the particle anisotropy, emphasizing that both Néel and Brown relaxation processes could potentially lead to similar heating performance (note that the Néel hyperthermia performance is directly proportional to the particle anisotropy, as illustrated by the magnetic hyperthermia trilemma23). Regarding attainable energy losses, the role played by the viscosity seems to be to shift the peak to lower frequencies, without changing the maximum value.
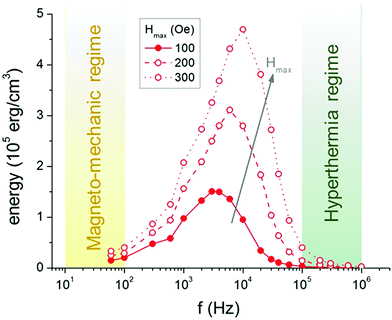
The results in Fig. 2 were obtained for a particular value of the AC field amplitude (Hmax = 100 Oe), but it is reasonable to expect that increasing its value could increase the Brownian heating at larger frequencies. To check whether such an increase could lead to the attainment of a more significant fraction of the maximum achievable value, we have investigated the role of the field amplitude. Values of the energy losses for various values of Hmax (of the same order as those used in the MFH experiments) are plotted in Fig. 3, for the case of “nano” viscosity of HeLa cells.
The results shown in Fig. 3 clearly indicate an overall growth of the energy losses with larger fields for all frequencies, but not significantly in the hyperthermia regime. Nevertheless, while such values remain quite low in comparison with the maximum possible values, it is important to keep in mind that they needed to be compared with the energy that could be obtained by Néel reversal in case the latter would be the preferred mechanism, as explained below.
To achieve an adequate understanding of the physical mechanism occurring in the system, it is important to consider not only the relative performance of both Brownian and Néel contributions (separately), but their possible coexistence: this is to say, is the Néel reversal achievable under the given experimental conditions? This requires knowing the field that would trigger the Néel switching, what will determine whether under given field and viscosity conditions both mechanisms are coexisting, or which one dominates over the other. In this context it is important to note the different nature of both mechanisms regarding heating: while the Brownian contribution continuously increases with Hmax, Néel reversal has a significant threshold related to the anisotropy field, and larger AC field amplitudes do not provide additional heating.11,13 Hence, it can be anticipated that the Brownian reorientation as the physical response of the magnetic nanoentities will be crucially limited by the onset of Néel reversal. This is a key element to consider in the context of the Brown vs. Néel scenario that has not been considered so far in the related literature (despite being critical in delimiting the applicability of the LRT). In the following the Néel heating properties will be studied and related to the Brownian ones.
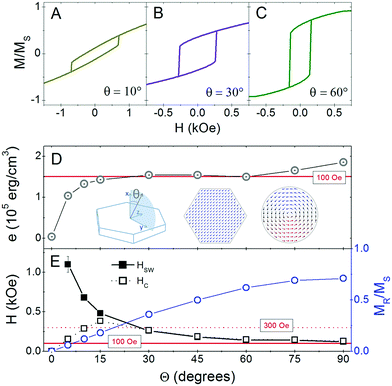
The large aspect ratio of the disks, which suggests a strong role of the shape anisotropy in the reversal of the magnetisation, could however be detrimental if it results in strongly non-coherent reversal modes. This does not seem to be the case with the hexagonal particles taken as a reference, which show a rather uniform magnetization state.17 In order to confirm such coherent-like behaviour and evaluate the corresponding hysteresis losses due to Néel reversal, we have used micromagnetic simulations (using the OOMMF software package24). Since a random dispersion is expected to exist in the crowded biological matrices, we considered different directions of application of the field over the particle and studied how the energy losses depend on the angle θ, as illustrated in Fig. 4D as a reference system. Note that while for the BD modeling we used the rounded-edge shape described in Fig. 1, which would resemble the magnetic particle with the silica coating (the TEM image in Fig. 1B), for the simulation of the reversal process only the magnetic part is relevant. Therefore, it is necessary to take into account the exact hexagonal shape of the nanomagnets (the TEM image in Fig. 1A), as will be shown below. The simulation values used correspond to those of the magnetite disks of ref. 17 (see the Computational details section). The micromagnetic results are summarized in Fig. 4.
The M(H) hysteresis loops shown in Fig. 4A–C illustrate the change in magnetic behaviour depending on the angle between the applied field and particle direction, θ. Importantly, the magnetic moment of the particle remains essentially unchanged throughout the entire loop (less than 1% decrease for all values of θ and field values), in agreement with the experimental observations on the uniformity of the magnetization.17 Such quasi-coherent behaviour is indicative of a large torque for MMA, which will promote Brownian rotation of the particles unless the field amplitude is large enough to lead to field-driven (Néel) switching over the internal energy barrier (note that the large sizes ensure a robust stability against thermal fluctuations, i.e. the anisotropy energy barrier is rather large so thermally induced decoupling of the magnetisation from the anisotropy easy magnetisation axis is negligible). In this regard, the overall shape of the loops is quite similar for all values of θ, with an abrupt jump that corresponds to the irreversible switching of the magnetisation (HSW) and suggests uniaxial symmetry for the anisotropy barrier. The variation of both HSW and remanence (MR) with θ suggests different hysteresis losses, as systematically analysed in Fig. 4D. Interestingly, the energy loss follows a rapid increase from low angles and then becomes essentially constant (angle-independent), which could be interesting for diminishing the dispersion in local heating.25 This behaviour reinforces the interest of such magnetic nanostructures for MFH; however, this is not the main objective of the current work so for the moment we focus our attention on the competition with the Brownian-origin heating performance. In this regard, it is worth noting that the red horizontal line in Fig. 4D indicates the peak of the hysteresis loss vs. frequency due to Brownian relaxation (Fig. 3), pointing out the similarity in the maximum achievable heating performances from both Néel and Brownian relaxation. While the Néel losses cannot be further increased (being defined by the particle anisotropy), the Brownian losses in principle can be continuously increased with larger field amplitudes, as illustrated in Fig. 3. Yet, it is important to emphasize that in the MFH regime, by comparison with Fig. 2 and 3, the Brownian energy losses only reach a small fraction of the peak value, thus anticipating a negligible contribution in relation to the Néel losses, as expected.7–9Fig. 4D also shows the disk-shape particle and the typical magnetisation at remanence, which corresponds to a rather uniform magnetisation (in agreement with panels A–C, as well as to the experimental observation). For comparison, also the snapshot of a particle of similar size but a rounded-shape disk (as assumed in the BD simulations) is shown, which clearly corresponds to a completely different magnetisation: a vortex-like structure of very small magnetic moment. The shown snapshots emphasize the importance of the shape of the nanomagnet in determining its magnetic response: the rounded disk would be rendered useless for MMA due to the associated negligible torque; hence, it is important to keep in mind that while the viscous interaction may correspond to that shape (due to the silica coating), the hexagonal-shape magnetic core is needed to provide the desired response under the external field. We note that a vortex configuration may exist in the hexagonal-like geometry if initialised specifically in the vortex state, but it is rapidly erased by an applied magnetic field and turned into the more stable saturated state. This is typical for small dots and for ultra-thin dots. Complementary, frequency-dependent simulations (not shown) also confirm the robust character of the saturated magnetic state, which is key for the alternation between magneto-mechanical actuation and heating actuation that will be discussed in detail later. Finally, it is worth mentioning that the usual parameters to distinguish likely coherent or non-coherent reversal behaviour through the correlation length (defined either as lexch1 = sqrt(2 × μ0A/MS2) or lexch2 = sqrt(A/K)) cannot be applied for the present geometry. Although the corresponding values indicate lexch1 = 9.6 nm and lexch2 = 30.2 nm, which in principle would indicate suitable conditions for non-coherent reversal, it should be noted that the large shape anisotropy of the hexagonal particles induces such a large in-plane magnetisation that these values are not appropriate for the geometry investigated here.
In order to further investigate the heating performance of either Brownian or Néel reversal, in Fig. 4E the evolution of HSWvs. θ is shown, since the switching field represents, to a first approximation, the minimum threshold for Néel-type magnetization reversal. Interestingly, plotting also the coercive field, HC, we observe a correlation of the angle-independent hysteresis loss range with the overlapping of HSW and HC, for values θ > 15°. Regarding the HSW(θ) evolution, this shows a monotonic decrease starting from θ = 5° (no switching is observed for the anhysteretic θ = 0° case), approaching asymptotically the value of 100 Oe (solid horizontal red line) with increasing angle. This suggests that Néel reversal could be negligible for fields of the order of or smaller than 100 Oe, resulting in the domination of Brownian rotation (i.e. the field is not able to activate the inner-magnetisation reversal path). This is a key result for interpreting not only our case, but in general experimental data involving Néel and Brown mechanisms: if the particles have a large inner (anisotropy) energy barrier, then the response will be magneto-mechanical if the amplitude of the external field is smaller than the switching field; otherwise, the magnetisation will be field-induced internally reversed over the anisotropy energy barrier. The former is the desired case for MMA, while the latter for MFH; achieving the alternation between both responses within the same experimental conditions would have huge potential for applications. This is what we will investigate from now on. It is important to note, however, that this is a simplified interpretation to the problem, since thermal effects could help in promoting the reversal at smaller fields: an effect which will become increasingly important for small particle size.26 In our current approximation, these results suggest that at larger fields (300 Oe is also depicted as a horizontal dotted red line) Néel reversal could dominate over Brownian rotation, depending on the relative orientation with respect to the applied field. Since the choice of either path would be decided by energy costs, this demonstrates the importance of checking the energy dissipated by particles at different orientations either by Néel or Brown reversal, for different Hmax values.
Comparing Néel and Brownian contributions to heating may be complicated, since both processes are expected to coexist. Furthermore, the progressive reorientation via Brownian rotation would dynamically change the Néel contribution, leading to the possibility that eventually all particles could reorientate up to a point at which Néel reversal is more favourable. While these arguments are sound, it is also important to take into account that the time scales of Brownian reorientation and Néel reversal are very different (orders of magnitude), particularly with the current particle sizes.27 Furthermore, we have previously shown that while the Brownian relaxation time would be at most of the order of milliseconds, its effects may be macroscopically observed in MFH experiments – indirectly, through the change in the Néel heating – in the timescale of minutes due to the rotation of the easy axes.12 Hence, for a system initially at random, it makes sense to evaluate both contributions independently. Therefore, and for the sake of simplicity, we have decided to consider a random distribution of particles and assume that the fraction of those dissipating by Néel reversal is that for which Hmax > HSW. This is illustrated in Fig. 5, where the MFH frequency regime from Fig. 3 is reproduced and augmented, to be taken as a reference for the hyperthermia performance.
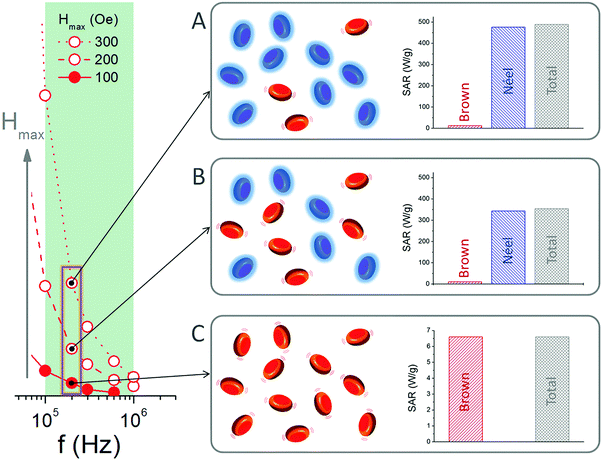 | ||
| Fig. 5 Estimation of the Specific Absorption Rate (SAR), for the f =200 kHz case of Fig. 3, for 3 different field amplitudes (A = 300 Oe; B = 200 Oe, C = 100 Oe); note the scale difference between A and B (the same) with respect to C (much smaller). The drawings illustrate heating via Brownian or Néel reversal (red and blue disks, respectively). | ||
Fig. 5 illustrates the relative importance of Brownian or Néel reversal contributions to the heating, using the simple approach described above: if the AC field is not able to switch the magnetization via Néel reversal, then Brownian reorientation is the heating source. Since the switching field is defined by the relative angle between the AC field and particle, then in this simple picture it is possible to estimate the fraction of particles that prefer Néel reorientation (nNéel) by correlating Hmax and HSW (as shown in Fig. 4E), so that 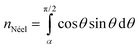 , where α is the angle at which Hmax = HSW. From Fig. 4E it can be estimated that α ≈ 41° (200 Oe) and 27° (300 Oe), so that the fraction of particles that may reverse by Néel switching increases from no contribution (at Hmax = 100 Oe), to 0.57 and 0.79 for Hmax = 200 and 300 Oe. Then, taking into account the heating performance of each type of particle, it is possible to estimate the total performance of each type of reversal for the entire system. This calculation is performed in terms of the Specific Absorption Rate (SAR), SAR = HL × frequency, the standard parameter for MFH. For the Brownian contribution, SARB, this value depends on Hmax (as shown in Fig. 3), estimated in average for a single particle SARB = 7, 25 and 60 W g−1; for Hmax = 100, 200 and 300 Oe, respectively. The Néel part, SARN, is taken as the average constant value shown in Fig. 4D, estimated as SARN = 603 W g−1 (as explained above, independently of Hmax). Then, taking into account also the relative fraction of each type of reversal (illustrated in the sketches with red or blue colours for Brownian and Néel reorientation, respectively), it is possible to estimate their contributions to heating as a function of Hmax. The results are shown as histograms in Fig. 5, which shows a large difference in the SAR value depending on the field amplitude. For Hmax = 100 Oe, when only Brownian rotation contributes to heating, the SAR values reached are very small (a few watts per gram); in contrast, when Néel reversal becomes the main contribution to heating (for larger Hmax values) a much larger SAR is reached. These results clearly demonstrate the negligible role of Brownian reversal in heat dissipation, in agreement with ref. 7–9, except for the very specific (inefficient) low-Hmax conditions. In addition, our work could help to understand results in different systems as for example those reported in ref. 28 with magnetic nanocubes, which show preference for the Brownian or Néel reversal mechanism not only depending on the field amplitude but also on the cube size. Thus, for the larger cubes (20 nm side), small field amplitude prompts dominance of Brownian reversal, while large fields promote the much more dissipative Néel switching; however, for the smaller particles the response is dominated by Néel reversal for either field amplitude. The latter behaviour can be understood based on the fact that for small particles the thermal energy may help induce the reversal over the anisotropy energy barrier, which is much faster than the physical particle reorientation (see later the discussion regarding the reversal times).
, where α is the angle at which Hmax = HSW. From Fig. 4E it can be estimated that α ≈ 41° (200 Oe) and 27° (300 Oe), so that the fraction of particles that may reverse by Néel switching increases from no contribution (at Hmax = 100 Oe), to 0.57 and 0.79 for Hmax = 200 and 300 Oe. Then, taking into account the heating performance of each type of particle, it is possible to estimate the total performance of each type of reversal for the entire system. This calculation is performed in terms of the Specific Absorption Rate (SAR), SAR = HL × frequency, the standard parameter for MFH. For the Brownian contribution, SARB, this value depends on Hmax (as shown in Fig. 3), estimated in average for a single particle SARB = 7, 25 and 60 W g−1; for Hmax = 100, 200 and 300 Oe, respectively. The Néel part, SARN, is taken as the average constant value shown in Fig. 4D, estimated as SARN = 603 W g−1 (as explained above, independently of Hmax). Then, taking into account also the relative fraction of each type of reversal (illustrated in the sketches with red or blue colours for Brownian and Néel reorientation, respectively), it is possible to estimate their contributions to heating as a function of Hmax. The results are shown as histograms in Fig. 5, which shows a large difference in the SAR value depending on the field amplitude. For Hmax = 100 Oe, when only Brownian rotation contributes to heating, the SAR values reached are very small (a few watts per gram); in contrast, when Néel reversal becomes the main contribution to heating (for larger Hmax values) a much larger SAR is reached. These results clearly demonstrate the negligible role of Brownian reversal in heat dissipation, in agreement with ref. 7–9, except for the very specific (inefficient) low-Hmax conditions. In addition, our work could help to understand results in different systems as for example those reported in ref. 28 with magnetic nanocubes, which show preference for the Brownian or Néel reversal mechanism not only depending on the field amplitude but also on the cube size. Thus, for the larger cubes (20 nm side), small field amplitude prompts dominance of Brownian reversal, while large fields promote the much more dissipative Néel switching; however, for the smaller particles the response is dominated by Néel reversal for either field amplitude. The latter behaviour can be understood based on the fact that for small particles the thermal energy may help induce the reversal over the anisotropy energy barrier, which is much faster than the physical particle reorientation (see later the discussion regarding the reversal times).
Furthermore, it is worth emphasizing that the SAR values predicted (of the order of 500 W g−1 for Hmax = 300 Oe and f = 200 kHz) are quite significant, pointing to a potential use of the investigated disks as heat generators for MFH. In addition, the clear separation of their performance into specific frequency regimes, together with their robust magnetic behaviour, suggests also the possibility of mechanical actuation. This suggests the intriguing possibility of alternating between purely magnetic and mechanical actuations to optimize the therapeutic results. As an additional comment we would like to point out that the large timescale difference between Néel and Brownian processes may have important implications for other aspects such as, for example, when estimating the SAR value from the initial slope of the temperature increase vs. time curve. Particles initially oriented at non-dissipation fields will likely slowly reorient (Brownian-rotation mediated) such that they may progressively join the fraction of particles contributing to heating. Thus, in moving towards fine-tuned MFH applications it is important to consider not only the heating mechanism, but also the fraction of the system actually dissipating significant energy.
The above considerations are strongly dependent on the fact that the internal magnetization processes behave coherently, which based on the micromagnetic simulations seems to be strongly determined by the hexagonal shape. Therefore, for additional studies it would be interesting to perform similar analyses as a function of particle size/aspect ratio, and for other shapes. While such systematic analysis is not the objective of the current work, it may still be worth investigating the role of size in the Brownian dynamics results. The reason is that we assumed a highly symmetrical shape for the disks (Fig. 1), despite the hexagonal magnetic part (as-prepared disks, TEM images of the experimental samples, Fig. 1A), under the assumption that the silica coating would smoothen the sharp edges of the hexagons (the TEM images of the experimental samples, Fig. 1B). But, if a silica shell is present, then the absolute size to compare the Brownian and Néel contributions should not be the same. To have some insight into the role of the absolute size in the BD results, in Fig. 6A the hysteresis loss vs. f data is shown (similar to that in Fig. 2 and 3), for the “nano” viscosity and Hmax = 100 Oe, for 2 different sizes ranging from 100 to 200 nm in diameter, smaller and larger than the used one, 140 nm. The effect of the disc size is clearly negligible, which gives additional support to our interpretation. Such a negligible role of size could be anticipated in view of eqn (1) and (2), where the size dependence of the diffusion coefficient and that of the torque are counterbalanced. The only size-dependence effect that could be anticipated for the non-interacting conditions assumed in this work would correspond to different response against thermal fluctuations; nevertheless, the large sizes considered in Fig. 6 make thermal effects play a secondary role. For the sake of completeness, the role of particle shape is shown in Fig. 6B, for particles with the same dimensions as those of particles 22/140 in panel A but different aspect ratios. In this case it is clearly observed that a different shape leads to a completely different response. It must be emphasized that these results are shown just for illustrative purposes; for the possible alternation between magneto-mechanical response and heating, a detailed study on the reversal mechanism – as in Fig. 4 – should be carried out.
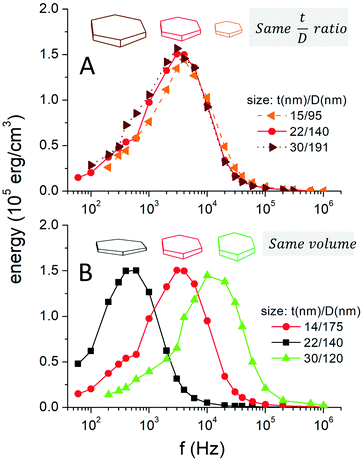 | ||
| Fig. 6 Energy losses vs. frequency, for the same field and viscosity conditions as in Fig. 3 (Hmax = 100 Oe case), for different absolute sizes of the particles but the same aspect ratio (top A panel), and for particles with the same volume but different aspect ratios (bottom B panel). The drawings are shown to illustrate the differences between cases. | ||
Our combined Brownian dynamics/micromagnetic study indicates a negligible role of Brownian rotation in heat dissipation in the magnetic hyperthermia range of frequencies, in agreement with some experiments.7–9 Furthermore, the fact that we have focused on highly anisotropic particles (to maximize the viscous interaction with the environment and hence maximize the losses) suggests that for most experimental samples – usually with spherical particles – the Brownian contribution to heating is even smaller, at least for coherent-like magnetization reversal process. At this point we consider, based on our calculations, the effective relaxation time approach followed by several insightful works29 for the description of the particle behaviour, under the assumption that both Brown and Néel reorientations would coexist. Such an approach is usually applied to particles in the 10–20 nm size, where both relaxation times can be of the same order of magnitude. However, a quick estimation of the Néel relaxation time for the large sizes considered in the current work yields values of the order of years, hence ensuring a complete inhibition of Néel relaxation and giving additional support to our approach for the separation of the heating contributions. Thus, while the complete separation between Brownian and Néel reversal mechanisms both would only be possible in the ideal case of infinite-coupling between magnetisation and the easy axis, the fact is that the large size of our hexagonal particles and their coherent-like Néel reversal – which corresponds to a negligible thermal decoupling – is a clear indicative that both mechanisms are essentially separated, as we have assumed in our analysis. Nevertheless, it is still necessary to keep in mind the need for further refinements, since the timescale of minutes for easy-axis reorientation should certainly be taken into account. It is also important to mention here that while the Brownian process has taken into account appropriate dynamics and thermal effects, the micromagnetic simulations did not consider thermal fluctuations, leading to the possibility that in the real system the Néel reversal could take place at smaller fields (thermally assisted switching). Further studies should take into account such considerations, which were however secondary to the current work, dealing with the study of the heating performance of Brownian rotation in a wide range of frequencies, and comparison with the purely magnetic dissipative contribution.
4. Conclusions
Our Brownian dynamics simulation results indicate a clear separation of two negligible hysteresis-loss regimes for disk-shape particles, corresponding to the high-frequency magnetic fluid hyperthermia regime (0.1–1 MHz range), and to the low-frequency (tens of Hz) magneto-mechanical actuation regime, respectively. The low-frequency anhysteretic regime points to suitable use of those particles as medical nanorobots,30 for a broad range of therapies based on pure nano-mechanical actuation.5 Interestingly, the complementary micromagnetic simulations predict very significant heating properties of the investigated hexagonal disks in the magnetic fluid hyperthermia regime (which, in addition to the large heating power, also display an essentially angle-independent performance strongly promising for homogenous local heat generation). Thus, while at low frequencies the absorbed energy is transformed into particle rotational energy, at high frequencies the behaviour will depend on the amplitude of the applied field: for large field amplitudes (greater than the switching field) the energy goes into internal energy (heating), whereas for small field amplitudes the energy goes into rotational motion. This is the key aspect that allows for alternation between magneto-mechanical response and heating not only with changing field frequency, but also at the same frequency by just changing the field amplitude. This important finding leads to the observation that the hyperthermia and the magneto-mechanical actuation regimes belong to well differentiated domains. The resulting easy alternation between both modalities not only with changing field frequency, but also at the same frequency just by changing the field amplitude, strongly suggests the use of the magnetic nanodisks for multimodal therapeutic purposes.Author contributions
Based on an original idea by M. P. M., the research plan of the present theoretical work was designed by D. S., R. C. and A. S. The simulations were performed by D. S., with the assistance of A. S. (Brownian dynamics) and O. C.-F. (micromagnetics). The magnetic particles used as a reference were synthesized by H. G. and M. P. M. Discussions and interpretations of the results were done by all authors. D. S. and R. C. wrote the core of the manuscript, with input and corrections from all co-authors.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was partially supported by the EU project NanoMag 604448; the Spanish Ministry of Economy and Competitiveness (MAT2016-76824-C3-1-R); the Royal Society International Exchanges Scheme (IE160535); and Xunta de Galicia (GRC 2014/013; and financial support of D. S. under Plan I2C). This work made use of the facilities of N8 HPC provided and funded by the N8 consortium and EPSRC (Grant No. EP/K000225/1) coordinated by the Universities of Leeds and Manchester and the EPSRC Small Items of Research Equipment at the University of York ENERGY (Grant No. EP/K031589/1).References
- M. Colombo, S. Carregal-Romero, M. F. Casula, L. Gutiérrez, M. P. Morales, I. B. Böhm, J. T. Heverhagen, D. Prosperi and W. J. Parak, Biological applications of magnetic nanoparticles, Chem. Soc. Rev., 2012, 41, 4306–4334 RSC.
- Y. X. J. Wáng, J.-M. Idéeb and C. Corot, Scientific and industrial challenges of developing nanoparticle-based theranostics and multiple-modality contrast agents for clinical application, Nanoscale, 2015, 7, 16146–16150 RSC.
- V. S. Kalambur, E. K. Longmire and J. C. Bischof, Cellular Level Loading and Heating of Superparamagnetic Iron Oxide Nanoparticles, Langmuir, 2007, 23, 12329–12336 CrossRef CAS PubMed.
- Y. I. Golovin, S. L. Gribanovsky, D. Y. Golovin, N. L. Klyachko, A. G. Majouga, A. M. Master, M. Sokolsky and A. V. Kabanov, Towards nanomedicines of the future: Remote magneto-mechanical actuation of nanomedicines by alternating magnetic fields, J. Controlled Release, 2015, 10, 43–60 CrossRef PubMed.
- Y. I. Golovin, N. L. Klyachko, A. G. Majouga, M. Sokolsky and A. V. Kabanov, Theranostic multimodal potential of magnetic nanoparticles actuated by non-heating low frequency magnetic field in the new-generation nanomedicine, J. Nanopart. Res., 2017, 19, 63 CrossRef.
- C. L. Dennis and R. Ivkov, Physics of heat generation using magnetic nanoparticles for hyperthermia, Int. J. Hyperthermia, 2013, 29, 715–729 CrossRef PubMed.
- R. Di Corato, A. Espinosa, L. Lartigue, M. Tharaud, S. Chat, T. Pellegrino, C. Ménagere, F. Gazeau and C. Wilhelm, “Magnetic hyperthermia efficiency in the cellular environment for different nanoparticle designs”, Biomaterials, 2014, 35, 6400–6411 CrossRef CAS PubMed.
- G. Vallejo-Fernandez, O. Whear, A. G. Roca, S. Hussain, J. Timmis, V. Patel and K. O'Grady, “Mechanisms of hyperthermia in magnetic nanoparticles”, J. Phys. D: Appl. Phys., 2013, 46, 312001 CrossRef.
- D. Soukup, S. Moise, E. Céspedes, J. Dobson and N. D. Telling, In Situ Measurement of Magnetization Relaxation of Internalized Nanoparticles in Live Cells, ACS Nano, 2015, 9, 231–240 CrossRef CAS PubMed.
- N. Hallali, P. Clerc, D. Fourmy, V. Gigoux and J. Carrey, Influence on cell death of high frequency motion of magnetic nanoparticles during magnetic hyperthermia experiments, Appl. Phys. Lett., 2016, 109, 032402 CrossRef.
- D. Serantes, K. Simeonidis, M. Angelakeris, O. Chubykalo-Fesenko, M. Marciello, M. P. Morales, D. Baldomir and C. Martinez-Boubeta, Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling, J. Phys. Chem. C, 2014, 118, 5927–5934 CrossRef CAS.
- K. Simeonidis, M. P. Morales, M. Marciello, M. Angelakeris, P. de la Presa, A. Lazaro-Carrillo, A. Tabero, A. Villanueva, O. Chubykalo-Fesenko and D. Serantes, In situ particles reorientation during magnetic hyperthermia application: Shape matters twice, Sci. Rep., 2016, 6, 38382 CrossRef CAS PubMed.
- I. Conde-Leborán, D. Serantes and D. Baldomir, Orientation of the magnetization easy axes of interacting nanoparticles: Influence on the hyperthermia properties, J. Magn. Magn. Mater., 2015, 380, 321–324 CrossRef.
- A. Satoh, Brownian dynamics simulation of a dispersion composed of disk-like hematite particles regarding the orientational distribution and the magneto-rheological properties, Colloids Surf., A, 2015, 483, 341–351 CrossRef CAS.
- Note that the requirement of strong coupling between magnetization and the lattice implies that the particle size must be large but not as much as to allow multidomain configurations or non-coherent reversal modes, since those would be detrimental to an efficient magnetic torque.
- D. Ling and T. Hyeon, Chemical Design of Biocompatible Iron Oxide Nanoparticles for Medical Applications, Small, 2012, 9, 1450–1466 CrossRef PubMed.
- H. Gavilán, O. Posth, L. K. Bogart, U. Steinhoff, L. Gutiérrez and M. P. Morales, How shape and internal structure affect the magnetic properties of anisometric magnetite nanoparticles, Acta Mater., 2017, 125, 416–424 CrossRef.
- P. C. Fannin, C. N. Marin, I. Malaescu, K. Raj and C. Popoiu, Local arrangement of particles in magnetic fluids due to the measurement alternating field, J. Magn. Magn. Mater., 2017, 438, 116–120 CrossRef CAS.
- S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Butterworth-Heinemann, Stoneham, 1991 Search PubMed.
- T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymański, A. Wilk, A. Patkowski, J. Gapiński, H.-J. Butt and R. Hołyst, Comparative Analysis of Viscosity of Complex Liquids and Cytoplasm of Mammalian Cells at the Nanoscale, Nano Lett., 2011, 11, 2157–2163 CrossRef CAS PubMed.
- P. T. Phong, L. H. Nguyen, L. T. H. Phong, P. H. Nam, D. H. Manh, I.-J. Lee and N. X. Phuc, Study of specific loss power of magnetic fluids with various viscosities, J. Magn. Magn. Mater., 2017, 428, 36–42 CrossRef CAS.
- D. H. Kim, E. A. Rozhkova, I. V. Ulasov, S. D. Bader, T. Rajh, M. S. Lesniak and V. Novosad, Biofunctionalized magnetic-vortex microdiscs for targeted cancer-cell destruction, Nat. Mater., 2010, 9, 165–171 CrossRef CAS PubMed.
- I. Conde-Leborán, D. Baldomir, C. Martinez-Boubeta, O. Chubykalo-Fesenko, M. P. Morales, G. Salas, D. Cabrera, J. Camarero, F. J. Teran and D. Serantes, A Single Picture Explains Diversity of Hyperthermia Response of Magnetic Nanoparticles, J. Phys. Chem. C, 2015, 119, 15698–15706 CrossRef.
- M. Donahue and D. Porter, OOMMF User's Guide, Version 1.2a4. Interagency Report NISTIR 6376, National Institute of Standards and Technology, 1999 Search PubMed.
- C. Munoz-Menendez, I. Conde-Leboran, D. Serantes, R. Chantrell, O. Chubykalo-Fesenko and D. Baldomir, Distinguishing between heating power and hyperthermic cell-treatment efficacy in magnetic fluid hyperthermia, Soft Matter, 2016, 12, 8815–8818 RSC.
- S. Ruta, R. Chantrell and O. Hovorka, Unified model of hyperthermia via hysteresis heating in systems of interacting magnetic nanoparticles, Sci. Rep., 2015, 5, 9090 CrossRef CAS PubMed.
- R. E. Rosensweig, Heating magnetic fluid with alternating magnetic field, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- D. Cabrera, A. Lak, T. Yoshida, M. E. Materia, D. Ortega, F. Ludwig, P. Guardia, A. Sathya, T. Pellegrino and F. J. Teran, Unraveling viscosity effects on the hysteresis losses of magnetic nanocubes, Nanoscale, 2017, 9, 5094 RSC.
- D. B. Reeves and J. B. Weaver, Comparisons of characteristic timescales and approximate models for Brownian magnetic nanoparticle rotations, J. Appl. Phys., 2015, 117, 233905 CrossRef PubMed.
- S. Martel, Magnetic nanoparticles in medical nanorobotics, J. Nanopart. Res., 2015, 17, 75 CrossRef.
| This journal is © the Owner Societies 2018 |