Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An ab initio multiple cloning approach for the simulation of photoinduced dynamics in conjugated molecules
Victor M.
Freixas
 a,
Sebastian
Fernandez-Alberti
a,
Sebastian
Fernandez-Alberti
 *a,
Dmitry V.
Makhov
bc,
Sergei
Tretiak
d and
Dmitrii
Shalashilin
b
*a,
Dmitry V.
Makhov
bc,
Sergei
Tretiak
d and
Dmitrii
Shalashilin
b
aUniversidad Nacional de Quilmes, Roque Saenz Peña 352, B1876BXD Bernal, Argentina. E-mail: sfalberti@gmail.com
bSchool of Chemistry, University of Leeds, Leeds LS2 9JT, UK
cSchool of Mathematics, University of Bristol, Bristol BS8 1TW, UK
dCenter for Nonlinear Studies (CNLS), and Center for Integrated Nanotechnologies (CINT), Los Alamos National Laboratory, Los Alamos, NM 87545, USA
First published on 19th June 2018
Abstract
We present a new implementation of the Ab Initio Multiple Cloning (AIMC) method, which is applied for non-adiabatic excited-state molecular dynamics simulations of photoinduced processes in conjugated molecules. Within our framework, the multidimensional wave-function is decomposed into a superposition of a number of Gaussian coherent states guided by Ehrenfest trajectories that are suited to clone and swap their electronic amplitudes throughout the simulation. New generalized cloning criteria are defined and tested. Because of sharp changes of the electronic states, which are common for conjugated polymers, the electronic parts of the Gaussian coherent states are represented in the Time Dependent Diabatic Basis (TDDB). The input to these simulations in terms of the excited-state energies, gradients and non-adiabatic couplings, is calculated on-the-fly using the Collective Electron Oscillator (CEO) approach. As a test case, we consider the photoinduced unidirectional electronic and vibrational energy transfer between two- and three-ring linear poly(phenylene ethynylene) units linked by meta-substitution. The effects of the cloning procedure on electronic and vibrational coherence, relaxation and unidirectional energy transfer between dendritic branches are discussed.
1 Introduction
Modeling photoinduced dynamics in realistic extended conjugated molecular systems represents one of the major goals in the field of organic photophysics.1 A great variety of new light harvesters are continuously synthesized and are the subject of intensive experimental and theoretical investigations.2,3 The characterization of their optical and electronic properties allows the prediction of their performance in nanophotonic devices such as sensors, solar cells, and a variety of other solar energy conversion applications.4–8Photoexcitation and the subsequent nonradiative electronic and vibrational energy relaxation and redistribution are fundamental processes associated with the efficient conversion of light energy into other usable forms of energy. These processes commonly involve several coupled electronic excited states that introduce transient coherence effects, exciton self-trapping, differential intramolecular energy transfer pathways and optically induced electronic density fluxes.9 An adequate theoretical treatment of such processes can be achieved by using direct or on-the-fly non-adiabatic molecular dynamics methods.10–12 A sub-family of these approaches, based on trajectory surface hopping (SH) algorithms,13–16 have been extensively used to study the photophysics and photochemistry of a wide variety of organic molecules: dendrimers,17–20 nanohoops,21–23 fluorenes,24 fullerenes,25 Ru(II)-based complexes,26 chlorophylls,27–29 retinal,30 nucleotides31–37 and so on. Different SH computational implementations are represented by NEWTON-X,38,39 SHARC (Surface Hopping including ARbitrary Couplings),40 PYXAID (PYthon eXtension for Ab Initio Dynamics)41,42 and NEXMD (Non-adiabatic EXcited-states Molecular Dynamics),12,43 among others.
Despite the success and improvements of direct SH methods, they cannot incorporate nuclear quantum effects in a natural and straightforward manner. Computationally more expensive alternatives are given by methods of Quantum Direct Dynamics (QDD),11 where the effects of nuclear quantum dynamics are included by considering ensembles of coupled trajectory-guided Gaussian basis functions (TBF) that cover the most important parts of the nuclear wave packet, optimizing the number of necessary basis functions.
QDD methods differ by the type of guiding trajectories. The variational multi-configuration Gaussian (vMCG) approach44–46 relies on coupled non-classical variational trajectories. Due to its computational cost and numerical instabilities, current vMCG implementations have only been tested for relatively small organic molecules. As an alternative, the Ab Initio Multiple Spawning (AIMS)47–49 method makes use of a much simpler choice for the evolution of the TBFs. The motion of the centres of Gaussians is determined classically on different electronic excited states. Throughout an AIMS simulation, the basis set is expanded (spawned) in an adaptive way according to transient couplings between states. AIMS was shown to be accurate enough to reproduce spectroscopic measurements for a large variety of conjugated organic molecules.50–52 The Multiconfigurational Ehrenfest (MCE) method,53 which is also based on TBFs moving along independent trajectories, is conceptually in between vMCG and AIMS. MCE employs Ehrenfest mean field trajectories, and the interaction between TBFs determines the evolution of their amplitudes, which is found by solving the time-dependent Schrödinger equation. Since trajectories are propagated independently, different strategies of efficient sampling can be designed. Swarms, pancakes, and trains are among the different sampling techniques that can be applied within the MCE framework.53 These techniques were proven to significantly improve the accuracy of MCE results.
The MCE approach has been successfully applied to simulate photoinduced processes in real molecular systems54,55 including dendritic branches.56 Ehrenfest TBFs represent a good way of guiding the basis when electronic states remain coupled for significant amounts of time throughout the photoinduced nonadiabatic process. However, this way of guiding the basis can become unphysical when two or more electronic states are significantly populated and the appropriate potential energy surfaces have significantly different gradients. In these situations the average is no longer a faithful representation of the whole. In order to overcome this limitation of MCE, the Ab Initio Multiple Cloning (AIMC)57–59 algorithm has been developed. In the AIMC approach, the bifurcations of the wave function after leaving the non-adiabatic coupling region are taken into account through the cloning procedure: each time certain cloning conditions are fulfilled, the basis set is expanded by adding a new TBF that has nonzero Ehrenfest amplitude for only a single state, while the original TBF retains contributions of all other electronic states.
Original versions of MCE and AIMC are formulated in the adiabatic basis representation.55,57 However, photoinduced process in extended polyatomic molecules can involve spatially separated noninteracting electronic states that share the same energy range without significant overlap between their wave functions.60 If such states experience unavoided crossings, the nonadiabatic coupling has sharp peaks strongly localized in the proximity of the exact crossing points while vanishing elsewhere. In these situations, called trivial unavoided crossings, the molecular system must follow the diabatic pathways. Otherwise, unphysical intramolecular energy redistribution could take place in the simulations.61 Within the MCE approach, these sharp crossings make the adiabatic electronic states change instantly within the Gaussian width. In order to deal with these situations, Multiconfigurational Ehrenfest in Time-Dependent Diabatic Basis (MCE-TDDB)56 was developed. In the MCE-TDDB approach, the electronic part of each TBF is represented in a diabatic electronic basis that coincides with an adiabatic basis in the centre of the Gaussian. This diabatic basis changes as the TBF moves, and the amplitude swaps of electronic states at trivial unavoided crossings can be reproduced. Various MCE based methods including MCE-TDDB have recently been reviewed.53
Light harvesting molecular systems, which are composed of a large number of chromophore units, are expected to experience multiple energy relaxation pathways involving events of wave function bifurcation.62 In order to adequately simulate such processes using MCE, cloning algorithms should be included. In a previous work,56 we presented our MCE-TDDB approach that makes use of excited state energies, gradients and non-adiabatic coupling terms calculated on the fly using the Collective Electron Oscillator (CEO) method.63–66 The method was applied to the simulation of the photoinduced dynamics of a model branched dendritic molecule. In this work, we present a further development of MCE-TDDB, the AIMC-TDDB method, that incorporates expanding the TBFs by cloning events. Following our previous MCE-TDDB development, the ultrafast dynamics of electronic and vibrational energy transfer between two- and three-ring linear poly(phenylene ethynylene) (PPE) units linked by meta-substitution is studied. This molecular system represents a building block of more complex light harvesting PPE dendrimers, such as the nanostar.67,68
The paper is organized as follows. In Section 2 we describe the MCE-TDDB method and cloning algorithm. The computational details are described in Section 3. The results of our simulations are presented and discussed in Section 4. Finally, the conclusions are summarized in Section 5.
2 MCE-TDDB method
MCE-TDDB is an efficient implementation of the ab initio MCE approach suitable to simulate photoinduced ultrafast electronic and vibrational energy relaxation and redistribution in large conjugated molecules. While the method has been presented in previous work,56 for the sake of completeness, we briefly reproduce its basic equations below.2.1 Expansion of the wave function
Within the MCE approach, the molecular wave function |Ψ(t)〉 is expanded in a basis of TBFs |ψn(t)〉 as: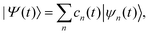 | (1) |
| |ψn(t)〉 = |χn(t)〉|φn(t)〉, | (2) |
The nuclear parts |χn(t)〉 are coherent states (CS)69 running over Ehrenfest trajectories. In the coordinate representation, these CS are given by Gaussian functions centred in the Ehrenfest trajectories with coordinates Rn and momenta Pn:
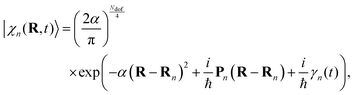 | (3) |
The electronic part, |φn(t)〉, is expanded in terms of eigenfunctions:
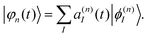 | (4) |
In the original MCE approach, |ϕ(n)I〉 are adiabatic states, |ϕ(n)I〉 = |ϕI(r;R)〉 that parametrically depend on the nuclear degrees of freedom and, thus, are the same for all TBFs. However, in extended polyatomic molecules, |ϕI(r;R)〉 can change significantly with R on the length scale of the nuclear Gaussian TBF widths, in particular, at trivial unavoided crossings.71,72 An adiabatic representation becomes inappropriate in such situations. Instead, we are using time-dependent diabatic electronic states that coincide with adiabatic states in the centre of each Gaussian |ϕ(n)I〉 = |ϕI(r;Rn(t))〉. The TDD basis does not depend explicitly on R and couplings between states originate from their time-dependence through nuclei motion. The TDD basis should not be confused with a diabatic basis, where different states are coupled through the off-diagonal matrix elements of the potential energy operator.
The equations of dynamics in the TDD basis are similar to those in an adiabatic basis, except that the electronic states are now different for different TBFs, and the overlaps between them must be calculated and taken into account. When electronic states change smoothly, these overlaps are close to Kronecker's δIJ for all couples of TBFs with non-zero nuclear part overlap; in this case the TDD approach is equivalent to an adiabatic approach. However, when adiabatic wave-functions change sharply, e.g., at trivial unavoided crossings, the overlap matrixes will be significantly different, and the use of the TDD basis ensures correct evolution of the whole wave-function (1) in the latter case.
2.2 Evolution of TBFs
The motion of the centres of the Gaussians is given by the usual Hamilton equations:| Ṙn = M(−1)Pn, | (5) |
| Ṗn = Fn, | (6) |
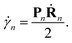 | (7) |
The Ehrenfest force that guides each trajectory n is written as:
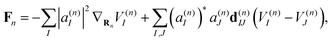 | (8) |
It is important to stress that the force Fn includes two terms.73–75 The first term in eqn (8) is a sum of gradients for all electronic states weighted according to their Ehrenfest populations |a(n)I|2. The second represents the nonadiabatic contribution; the work done by this force reflects the potential energy change due to the electronic exchange between adiabatic states induced by the nonadiabatic coupling vectors d(n)IJ. This second term is consistent with the time evolution of Ehrenfest amplitudes a(n)I dictated by the time-dependent Schrödinger equation:
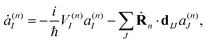 | (9) |
It is easy to see that the first term of eqn (9) introduces fast oscillations of the phases of complex a(n)I amplitudes. In order to avoid numerical inaccuracies associated with these oscillations, we use:
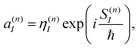 | (10) |
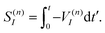 | (11) |
To solve eqn (9) numerically, we separate the time evolution of η(n)I into real η(n)I,r and imaginary η(n)I,i parts, which leads to the coupled equations:
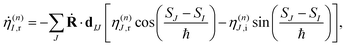 | (12) |
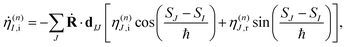 | (13) |
| Ṡ(n)I = −V(n)I. | (14) |
2.3 Evolution of the amplitudes of TBFs
Within the MCE approach, the couplings between TBFs are described by the evolution of amplitudes cn, which is obtained by substituting eqn (1) into the time-dependent Schrödinger equation: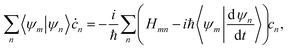 | (15) |
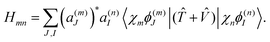 | (16) |
The kinetic energy matrix elements can be obtained analytically as:
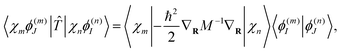 | (17) |
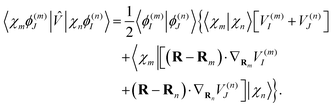 | (18) |
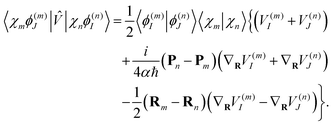 | (19) |
Finally, the term of eqn (15) reflecting the time-dependence of TBFs is evaluated as:
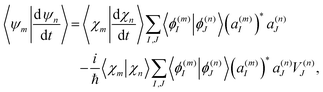 | (20) |
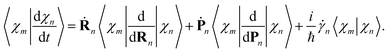 | (21) |
The overlaps 〈ϕ(m)I|ϕ(n)J〉 between the electronic parts of different TBFs can, in principle, be calculated directly. However, we found it more convenient propagating them together with the basis:
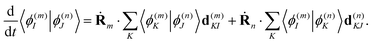 | (22) |
Such an approach may slightly overestimate the electronic overlaps, but the accuracy is compatible with other approximations used in this work. However, the propagation of overlaps, as well as the propagation of Ehrenfest amplitudes aI, cannot reproduce instant swaps of electronic states at trivial unavoided crossings. In order to take these swaps into account, we analyse the overlaps calculated directly at every time step and swap the states when necessary. This includes both the swap of Ehrenfest amplitudes and the appropriate change of overlaps in eqn (22), so that the total wave-function remains the same.
2.4 Calculation of observables
As it was shown in our previous work,56 the expectation value of any operator acting on the electronic subspace can be calculated as: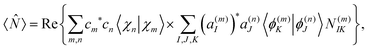 | (23) |
N(m)IK = 〈ϕ(m)I|![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) |ϕ(n)K〉. |ϕ(n)K〉. | (24) |
In this way, electronic state populations can be obtained by replacing ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) in eqn (24) and (23) by the adiabatic population operator
in eqn (24) and (23) by the adiabatic population operator ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) K = |ϕ(n)K〉〈ϕ(n)K| to obtain:
K = |ϕ(n)K〉〈ϕ(n)K| to obtain:
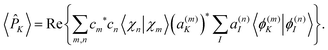 | (25) |
Our current implementation of the MCE approach applies the CEO method63–66 at the configuration interaction singles (CIS) level of theory for on-the-fly calculation of excited state energies, gradients and non-adiabatic coupling terms. Within the CEO approach, the CIS eigenstates, written in the atomic orbital (AO) basis, are frequently denoted as transition density matrices (or electronic normal modes) and can be formally written as:64,76
| (ρ(n)I)i,j = 〈ϕ(n)I|ĉ†iĉj|ϕ(n)g〉, | (26) |
During the dynamics, the intramolecular electronic energy redistribution can be followed using the time-dependent spatial localization of ρ(n)I. Generally, to describe cases of tightly bound Frenkel and charge-transfer delocalized Wannier excitons, the entire transition density matrix needs to be analysed.77,78 However, in the present case of localized Frenkel-type excitons with relatively weak charge transfer character, an analysis of the diagonal part suffices. Consequently, the fraction of ρ(n)I localized on a specific segment or chromophore unit X can be defined as:
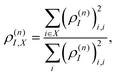 | (27) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) X such that:
X such that:![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) X|ϕ(n)I〉 = ρ(n)I,X|ϕ(n)I〉, X|ϕ(n)I〉 = ρ(n)I,X|ϕ(n)I〉, | (28) |
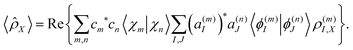 | (29) |
Similarly, the expectation value of the distance between atoms i and j of the molecule Rij = |R(i) − R(j)| can be evaluated as
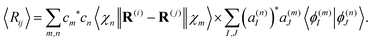 | (30) |
Since oscillations of the distance between atoms are usually much smaller than the distance itself, we can use the following approximation:
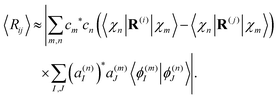 | (31) |
Using the expression for matrix elements 〈χn|R(i)|χm〉,57 and taking into account that the imaginary part of all matrix elements vanishes with the double sum running over scripts m and n; eqn (31) takes the form:
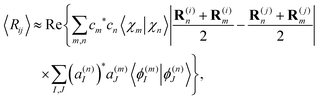 | (32) |
2.5 Cloning algorithm
Ehrenfest TBFs move on average potential energy surfaces (PES) given by contributions of the different electronic excited states that participate in the process. This approach is especially efficient in large conjugated molecules where a wave packet undergoes frequent transition between many coupled electronic states. Nevertheless, the motion on Ehrenfest PESs is not always a faithful representation of the dynamics: splitting of the wave packet should be taken into account when the average force is sufficiently different from the forces for significantly populated individual states. In order to deal with this case, the cloning algorithm57 is applied: the original basis set of TBFs is expanded by “cloning” one TBF into two copies in a way that does not alter the original wave function. This is done by creating one of the clones |ψn1〉 in a pure state and the other clone |ψn2〉 containing all the remaining electronic states: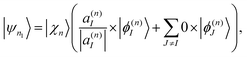 | (33) |
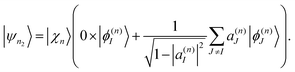 | (34) |
The corresponding amplitudes for these two new TBFs are set to:
| cn1 = cn|a(n)I|, | (35) |
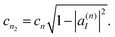 | (36) |
Thus, the contribution of the original TBF to the total wave-function is replaced by the equal contribution of a linear combination of its clones:
| cn|ψn〉 = cn1|ψn1〉 + cn2|ψn2〉. | (37) |
Each TBF can clone several times during the dynamics. Each time it clones, a trajectory is branched into two, increasing the basis set sampling and, therefore, the computational cost. However, due to the rescaling of the amplitudes, the contribution of each new clone to the whole wave function decreases (see eqn (36)). Despite the fact that the integral contribution of these low-amplitude trajectories can be significant, further cloning would be inefficient, as far as an effect per cloning event is concerned. Thus, in the present work, we limited the number of consecutive cloning events to a maximum value of Ncln = 4 per initial TBF.
2.6 Generalized cloning criteria
The cloning procedure should be applied throughout the simulation whenever the Ehrenfest approximation fails to lead to the correct outcome of the process. However, the additional computational cost should be minimized and justified only by a significant contribution to the final accuracy of the results. Therefore, cloning events should be restricted to situations in which certain cloning criteria are fulfilled.Previous cloning criteria57 require imposing absolute threshold values for the breaking force and module of the non-adiabatic coupling vector. However, if we want to use the method for the simulation of the photoinduced dynamics of a large variety of organic molecules with different extended conjugated lengths and mimic different environment and temperature effects, the values of cloning thresholds should be optimized for each particular case. So, it would be useful to develop more general cloning criteria that are defined according to the relative magnitudes and directions of the different components of the Ehrenfest force. Consequently, the thresholds for such cloning criteria do not need to be re-optimized every time, as they are weakly sensitive to the molecular system or the number of excited states involved in the process under study.
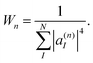 | (38) |
Values of Wn ≈ 1 indicate a complete localization of |φn(t)〉 on a single electronic state, while values of Wn ≈ N correspond to a uniform distribution of |φn(t)〉 among all states. Therefore, by restricting cloning events to situations in which:
| Wn > δclone,1 = 2, | (39) |
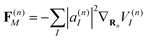 (first term in eqn (8)) and the force F(n)max evaluated on the most populated state, by using a pseudo-angle θ(n) that is defined as:
(first term in eqn (8)) and the force F(n)max evaluated on the most populated state, by using a pseudo-angle θ(n) that is defined as: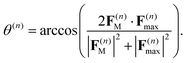 | (40) |
This definition of θ(n) takes into account not only the difference in the directions of F(n)M and F(n)max but also the difference in their magnitudes. In the case when both magnitudes are equivalent, eqn (40), θ(n) is reduced to a standard definition of the angle between two vectors.
It is also important to stress that this criterion accounts only for the contributions of the gradients of each adiabatic state to the Ehrenfest force (first term in eqn (8)) and does not consider the nonadiabatic contributions. Here, it is suitable to identify situations in which the average Ehrenfest force lacks physical meaning, as the different adiabatic forces move nuclei in a bifurcated way.
We clone if:
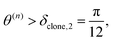 | (41) |
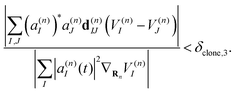 | (42) |
Therefore, criterion #3 addresses situations in which the nonadiabatic contribution to the Ehrenfest force has a significant relative value compared to the contribution of adiabatic forces. Three different values of δclone,3 have been tested. In this work we use δclone,3 = 0.05 unless specifically indicated.
Our three cloning criteria have been chosen in order to be rather independent of the molecular system under study. Nevertheless, they need to be tested on different polyatomic molecules. Outside certain limits, inadequate values of these criteria could lead either to computationally intractable growth in the number of TBFs or to avoiding cloning events altogether.
3 Computational details
The photoinduced unidirectional electronic and vibrational energy transfer between two- and three-ring linear poly(phenylene ethynylene) units linked by meta-substitution (see scheme in Fig. 1) is simulated using the AIMC-TDDB method. This molecular system has been previously studied56 using our implementation of direct MCE-TDDB specifically developed to deal with large conjugated molecular systems. Excited state energies, gradients and non adiabatic couplings are calculated on the fly using CEO77 with the configuration interaction singles (CIS) formalism implemented with the semiempirical Austin Model 1 (AM1) Hamiltonian.79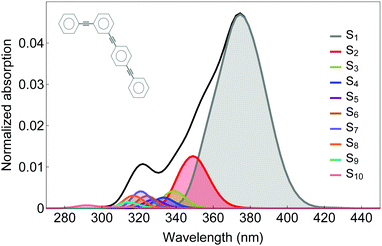 | ||
| Fig. 1 Normalized absorption spectra for our model dendritic molecule (inset) including the contributions of different excited states. | ||
Our simulations have included six singlet electronic states (S1–S6). The initial 100 Ehrenfest TBFs were propagated at constant energy for 150 fs using a time step of 0.02 fs. This basis set was finally expanded to 483 TBFs when cloning events were included. The initial conditions (geometries and nuclei velocities) were obtained by sampling previous 1 ns ground state dynamics equilibrated at 300 K using Frank–Condon excitation with a laser pulse of FWHM = 100 fs centred at 348 nm, which corresponds to the maximum of the absorption spectra shown in Fig. 1.
All Ehrenfest TBFs were calculated independently. The whole molecular wave function (eqn (1)) as well as electronic overlaps (eqn (22)) were propagated in a “post-processing” procedure, providing a framework for extremely efficient parallelization of calculations.
4 Results and discussion
As it was mentioned above, our approach is based on three cloning criteria. On one hand, the first two criteria are designed to ensure meaningful nuclear motion with Ehrenfest TBFs. The purpose of both criteria is optimization of the efficiency of TBFs to explore the dynamically important regions of the conformational space. On the other hand, our third criterion is not strictly necessary and it has been mainly proposed in order to control the rate of basis set growth.57 Therefore, we have first analysed the effectiveness of the third criterion in limiting the number of cloning events by testing different values of δclone,3. Starting with an initial set of 100 TBFs, values of δclone,3 = 0.02, 0.03, and 0.05 expand it to final sets of 177, 311 and 483 TBFs respectively. That is, the total number of cloning events and, therefore, the final number of TBFs increases roughly linearly with the value of δclone,3.A further analysis of the effect of δclone,3 on cloning events is shown in Fig. 2(a), where the % of cloning events per original TBF is displayed. As we can see, values of δclone,3 = 0.02 and 0.03 are too restrictive since they lead to ∼50% and 70% of trajectories without cloning events. In contrast, δclone,3 = 0.05 leads to 70% of original TBFs experiencing cloning events. This can be explained by analyzing Fig. 2(b), which shows the time evolution of the average and standard deviation of the left side of (42) for all of the Ehrenfest trajectories. Values of δclone,3 = 0.02, 0.03, and 0.05 are within 1.3, 1.0 and 0.4 standard deviation units of the distribution. That is, δclone,3 = 0.02 or 0.03 limits cloning events only to relatively infrequent situations throughout the Ehrenfest simulations. Values of δclone,3 larger than 0.05 introduce cloning events in regions of the phase space where the electronic states are strongly coupled, leading to a computationally forbidden increase in the rate of basis set growth.
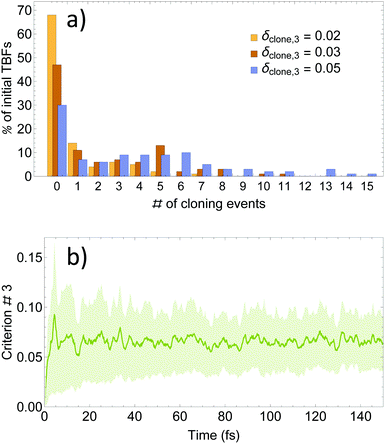 | ||
| Fig. 2 (a) Distribution of cloning events per original TBFs; (b) time evolution of the average and standard deviation values for δclone,3 performed over all the Ehrenfest simulations. | ||
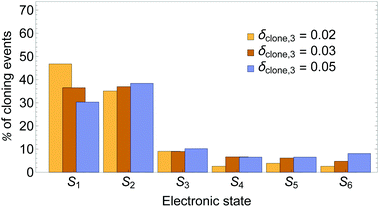
A comparison of distributions of cloning events according to the state that was cloned (i.e., was taken as a specific state in one of the clones) is presented in Fig. 3. It shows that larger values of δclone,3 decrease the % of events when state S1 is cloned, while that for state S2 remains essentially the same. That is, the S2/S1 cloning ratio increases.
While cloning S1 or S2 has an essentially equivalent effect on the dynamics when other states have low populations, these events are associated with different regions of the configuration space with different relative values of nonadiabatic coupling. Previous work80 has shown that while the nuclear motion on S2 pulls the system close to regions of strong coupling between the states, the motion on the S1 state moves it away. Therefore, as it is expected, larger values of δclone,3 introduce more cloning events in the regions of relatively large coupling, that is, situations in which S2 is the most populated state.
Moreover, this behaviour has been shown to guarantee successful S2 → S1 unidirectional energy transfer associated with the efficient energy funnelling in light-harvesting dendrimers through the so-called Shishiodoshi mechanism.81 Therefore, a larger number of events when state S2 is cloned compared to state S1 reinforces these features by emphasizing the role of the nuclear differential motion on S2.
Fig. 4 compares the time evolution of the average populations for the lowest six electronic excited states evaluated using the uncoupled Ehrenfest TBFs (EHR) and AIMC approaches. Our previous work56 shows that the EHR and MCE-TDDB methods produce almost equivalent results due to nuclear decoherence provided by the large number of degrees of freedom at room temperature. The MCE-TDDB calculations have been previously performed in the basis of a swarm of interacting coherent state trains. Each swarm consists of one central trajectory and 9 satellites. So, herein we restrict our comparison of AIMC-TDDB results with those obtained using the EHR dynamics. As it has been previously reported,56 an initially large oscillatory population exchange takes place between S1 and S2 states during the first 20 fs of dynamics after photoexcitation. Since our simulations start from specific states selected according to contributions to the absorption spectra at the laser wavelength (see Section 3 and ref. 56), no cloning events are expected at short times. This is due to criterion #1, the restriction that requires a significant population of at least two electronic states. Therefore, cloning effects are evidenced at longer times. One can see that the EHR results show faster damping of S2–S1 oscillations at longer times compared to the AIMC-TDDB results. Thus, the use of TBF cloning enhances the oscillatory interchange of energy between these states. This is in agreement with Fig. 5 showing the time dependence of NACT1,2 averaged over all EHR and AIMC-TDDB trajectories. Larger values of NACT1,2 for the latter indicate that branching of trajectories at cloning points makes the S1 and S2 states remain coupled at longer times.
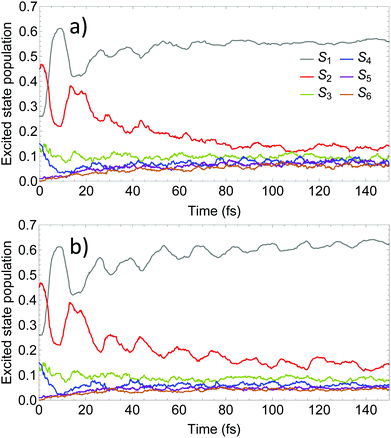 | ||
| Fig. 4 Time evolution of the excited state populations calculated using (a) the Ehrenfest method and (b) the AIMC-TDDB method. | ||
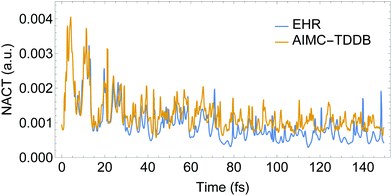 | ||
| Fig. 5 Time evolution of the absolute values of NACT between excited states S1 and S2 obtained from AIMC-TDDB and Ehrenfest simulations. | ||
According to the previous studies of PPE dendritic molecules,80,82 the nuclear motion on S2 pulls the TBF close to regions of the configuration space with strong nonadiabatic coupling. Therefore, this is an expected effect of cloning since, as surface hopping, it highlights nuclear state-specific motions. Nevertheless, surface hopping methods feature classically forbidden hops that hinder S1 → S2 energy transfer. Because of that, while the surface hopping technique does not lead to oscillations between S1 and S2 populations,56 the AIMC-TDDB method does. Besides, we notice that the incorporation of cloning leads to a faster relaxation rate to the S1 state. Namely, the AIMC-TDDB results lie in between the EHR and surface hopping results obtained using the NEXMD approach. Therefore, the effect of state-specific motions on S1 prevails at long times. Nuclear motions on the S2 state lead to regions of the conformational space with a smaller energy gap between the S1 and S2 states, keeping both surfaces close to each other and inducing more efficient coupling between them.
Finally, we should mention that the use of cloning reduces the residual populations of higher-energy states (Sn≥3). These states contribute with weak quasi-random fluctuations of the Ehrenfest force, which may provide a natural decoherence.56 A detailed analysis of the effect of TBF cloning on the coherence, however, is outside the scope of this work.
Our model dendritic molecule can be interpreted as a combination of two independent linear chromophore units with weak coupling between them, that is, a two-ring linear PPE unit linked by meta-substitution to a three-ring linear PPE unit.56,80 While the S2 state is mainly localized on the two-ring linear PPE unit, the lowest S1 state is mainly localized on the three-ring unit. The efficient energy funnelling in light-harvesting dendrimers is conditioned by successful two-ring → three-ring unidirectional energy transfer. Fig. 6 displays the time evolution of the fraction of electronic transition density 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) X〉 (eqn (29)) localized on the two- and three-ring linear PPE units obtained from the EHR and MCE-TDDB simulations. After an initial photoexcitation with the exciton equally distributed between both chromophore units, an effective exciton spatial localization on the three-ring unit is observed during the 150 fs of our simulations. The initial large oscillation in the spatial localization is consistent with the oscillatory population exchange that takes place between the S2 and S1 states (shown in Fig. 4). As we have previously mentioned, cloning events do not take place during the first 20 fs of the dynamics after photoexcitation. Therefore, no differences between simulations with and without cloning are expected. Furthermore, despite a relatively larger oscillatory behaviour for AIMC-TDDB simulations in the range of ∼20–40 fs after photoexcitation, no significant differences can be observed between both methods.
X〉 (eqn (29)) localized on the two- and three-ring linear PPE units obtained from the EHR and MCE-TDDB simulations. After an initial photoexcitation with the exciton equally distributed between both chromophore units, an effective exciton spatial localization on the three-ring unit is observed during the 150 fs of our simulations. The initial large oscillation in the spatial localization is consistent with the oscillatory population exchange that takes place between the S2 and S1 states (shown in Fig. 4). As we have previously mentioned, cloning events do not take place during the first 20 fs of the dynamics after photoexcitation. Therefore, no differences between simulations with and without cloning are expected. Furthermore, despite a relatively larger oscillatory behaviour for AIMC-TDDB simulations in the range of ∼20–40 fs after photoexcitation, no significant differences can be observed between both methods.
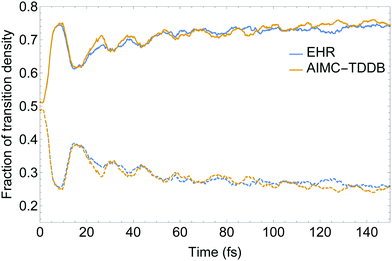 | ||
| Fig. 6 Time evolution of the transition density fractions localized on the two- (dashed) and three-ring (solid) linear PPE units obtained from AIMC-TDDB and Ehrenfest simulations. | ||
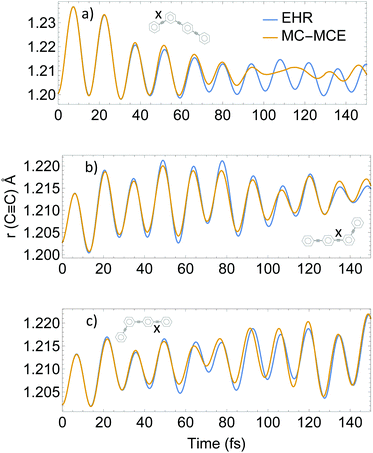
Intramolecular vibrational energy redistribution has shown to be concomitant with intramolecular electronic energy transfer, with the nuclear motions of the ethynylene bonds playing a critical role in the process.56,80Fig. 7 shows the lengths 〈χn‖Ri − Rj‖χm〉 for the three ethynylene bonds of the molecule as a function of time during MC-MCE and EHR simulations. Both methods were able to reproduce an initial excitation and subsequent relaxation of the ethynylene bond localized in the two-ring unit, as well as the gradual excitation at longer times of ethynylene bonds in the three-ring unit.
The use of eqn (32) for calculation of 〈χn‖Ri − Rj‖χm〉 in AIMC-TDDB simulations introduces additional nuclear decoherence effects with respect to decoupled EHR dynamics. This can be seen during relaxation after ∼80 fs of the ethynylene bond in the two-ring unit. Therefore, we confirm that EHR dynamics overestimate nuclear coherence included in the AIMC simulations.
5 Conclusions
Here we numerically improve the previously developed MCE-TDDB approach by introducing a cloning procedure which adapts the basis set to nonadiabatic dynamics and report a new AIMC-TDDB implementation. Multiple cloning can be viewed as an efficient way to perform Multiple Spawning,47–49 which was developed previously to provide a rigorous description of surface hoping. We apply AIMC-TDDB on the system previously studied by MCE-TDDB and observe that cloning affects the results and therefore improves the accuracy of the calculation. We report that the use of cloning in the AIMC-TDDB approach enhances the population exchange between electronic states due to reinforced state specific nuclear motions. The AIMC-TDDB results show more efficient final electronic energy relaxation to the lowest S1 state and lie in between Ehrenfest results and previous surface hopping results. However, in the linear phenylene ethynylene molecule considered in this work, the effect of cloning is not as significant as it was in photodynamical systems studied previously.57,58 This validates our results obtained for the same molecule previously without cloning. This confirms that in systems where many electronic states are strongly coupled with each other, the methods based on Ehrenfest trajectories are efficient and accurate.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SF-A and VMF are supported by CONICET, UNQ, ANPCyT (PICT-2014-2662). DM, DS acknowledge the support from EPSRC through grants EP/P021123/1 and EP/N007549/1 and Leverhulme trust grant RPG-2015-190. This work was performed in part at the Center for Integrated Nanotechnologies, a U.S. Department of Energy, Office of Science user facility at Los Alamos National Laboratory (LANL). LANL is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under contract DEAC52-06NA25396.References
- Computational Photochemistry, ed. M. Olivucci, Theoretical and Computational Chemistry, Elsevier, 2005, vol. 16 Search PubMed.
- Y.-C. Cheng and G. R. Fleming, Annu. Rev. Phys. Chem., 2009, 60, 241–262 CrossRef PubMed.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647 CrossRef PubMed.
- B. C. Satishkumar, L. O. Brown, Y. Gao, C.-C. Wang, H.-L. Wang and S. K. Doorn, Nat. Nanotechnol., 2007, 2, 560–564 CrossRef PubMed.
- M. Granström, K. Petritsch, A. C. Arias, A. Lux, M. R. Andersson and R. H. Friend, Nature, 1998, 395, 257–260 CrossRef.
- Y. Cao, I. D. Parker, G. Yu, C. Zhang and A. J. Heeger, Nature, 1999, 397, 414–417 CrossRef PubMed.
- J.-L. Brédas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1699 CrossRef PubMed.
- H. Sirringhaus, T. Kawase, R. H. Friend, T. Shimoda, M. Inbasekaran, W. Wu and E. P. Woo, Science, 2000, 290, 2123–2126 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, J. Phys., Lett., 2017, 8, 3020–3031 Search PubMed.
- G. A. Worth and M. A. Robb, Applying Direct Molecular Dynamics to Non-Adiabatic Systems, John Wiley & Sons, Inc., 2003, pp. 355–431 Search PubMed.
- G. Worth, M. Robb and B. Lasorne, Mol. Phys., 2008, 106, 2077–2091 CrossRef.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef PubMed.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef.
- J. C. Tully, Faraday Discuss., 1998, 110, 407–419 RSC.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667 CrossRef.
- J. F. Galindo, E. Atas, A. Altan, D. G. Kuroda, S. Fernandez-Alberti, S. Tretiak, A. E. Roitberg and V. D. Kleiman, J. Am. Chem. Soc., 2015, 137, 11637–11644 CrossRef PubMed.
- D. Ondarse-Alvarez, S. Komurlu, A. E. Roitberg, G. Pierdominici-Sottile, S. Tretiak, S. Fernandez-Alberti and V. D. Kleiman, Phys. Chem. Chem. Phys., 2016, 18, 25080–25089 RSC.
- J. Liu and W. Thiel, J. Chem. Phys., 2018, 148, 154103 CrossRef PubMed.
- J. Huang, L. Du, J. Wang and Z. Lan, J. Phys. Chem. C, 2015, 119, 7578–7589 CrossRef.
- L. Adamska, I. Nayyar, H. Chen, A. K. Swan, N. Oldani, S. Fernandez-Alberti, M. R. Golder, R. Jasti, S. K. Doorn and S. Tretiak, Nano Lett., 2014, 14, 6539–6546 CrossRef PubMed.
- N. Oldani, S. K. Doorn, S. Tretiak and S. Fernandez-Alberti, Phys. Chem. Chem. Phys., 2017, 19, 30914–30924 RSC.
- L. Stojanović, S. G. Aziz, R. H. Hilal, F. Plasser, T. A. Niehaus and M. Barbatti, J. Chem. Theory Comput., 2017, 13, 5846–5860 CrossRef PubMed.
- D. Ondarse-Alvarez, N. Oldani, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. A, 2014, 118, 10742–10753 CrossRef PubMed.
- L. Du and Z. Lan, J. Chem. Theory Comput., 2015, 11, 1360–1374 CrossRef PubMed.
- A. J. Atkins and L. González, J. Phys., Lett., 2017, 8, 3840–3845 Search PubMed.
- W. P. Bricker, P. M. Shenai, A. Ghosh, Z. Liu, M. G. M. Enriquez, P. H. Lambrev, H.-S. Tan, C. S. Lo, S. Tretiak, S. Fernandez-Alberti and Y. Zhao, Sci. Rep., 2015, 5, 13625 CrossRef PubMed.
- F. Zheng, S. Fernandez-Alberti, S. Tretiak and Y. Zhao, J. Phys. Chem. B, 2017, 121, 5331–5339 CrossRef PubMed.
- A. Sisto, C. Stross, M. W. van der Kamp, M. O'Connor, S. McIntosh-Smith, G. T. Johnson, E. G. Hohenstein, F. R. Manby, D. R. Glowacki and T. J. Martinez, Phys. Chem. Chem. Phys., 2017, 19, 14924–14936 RSC.
- M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, J. Phys. Chem. A, 2013, 117, 2790–2799 CrossRef PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys., Lett., 2012, 3, 3090–3095 Search PubMed.
- S. Mai, P. Marquetand, M. Richter, J. González-Vázquez and L. González, ChemPhysChem, 2013, 14, 2920–2931 CrossRef PubMed.
- C. E. Crespo-Hernández, L. Martínez-Fernández, C. Rauer, C. Reichardt, S. Mai, M. Pollum, P. Marquetand, L. González and I. Corral, J. Am. Chem. Soc., 2015, 137, 4368–4381 CrossRef PubMed.
- D. Nachtigallová, T. Zelený, M. Ruckenbauer, T. Müller, M. Barbatti, P. Hobza and H. Lischka, J. Am. Chem. Soc., 2010, 132, 8261–8263 CrossRef PubMed.
- T. Zelený, P. Hobza, D. Nachtigallová, M. Ruckenbauer and H. Lischka, Collect. Czech. Chem. Commun., 2011, 76, 631–643 CrossRef.
- T. Zelený, M. Ruckenbauer, A. J. Aquino, T. Müller, F. Lankaš, T. Dršata, W. L. Hase, D. Nachtigallova and H. Lischka, J. Am. Chem. Soc., 2012, 134, 13662–13669 CrossRef PubMed.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef PubMed.
- M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240 CrossRef.
- M. Barbatti, H. Lischka, G. Granucci, M. Persico, M. Ruckenbauer, J. Pittner and F. Plasser, NEWTON-X: A Package for Newtonian Dynamics Close to the Crossing Seam, 2011, http://www.newtonx.org Search PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, V. Chernyak, A. E. Roitberg and S. Tretiak, J. Phys. Chem. B, 2011, 115, 5402–5414 CrossRef PubMed.
- G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508 CrossRef.
- D. Mendive-Tapia, B. Lasorne, G. A. Worth, M. J. Bearpark and M. A. Robb, Phys. Chem. Chem. Phys., 2010, 12, 15725–15733 RSC.
- M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef.
- M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef.
- M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 1998, 108, 7244–7257 CrossRef.
- B. F. E. Curchod, A. Sisto and T. J. Martínez, J. Phys. Chem. A, 2017, 121, 265–276 CrossRef PubMed.
- A. Bera, J. Ghosh and A. Bhattacharya, J. Chem. Phys., 2017, 147, 044308 CrossRef PubMed.
- T. J. A. Wolf, T. S. Kuhlman, O. Schalk, T. J. Martinez, K. B. Moller, A. Stolow and A.-N. Unterreiner, Phys. Chem. Chem. Phys., 2014, 16, 11770–11779 RSC.
- D. V. Makhov, C. Symonds, S. Fernandez-Alberti and D. V. Shalashilin, Chem. Phys., 2017, 493, 200–218 CrossRef.
- D. V. Shalashilin, J. Chem. Phys., 2010, 132, 244111 CrossRef PubMed.
- K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- S. Fernandez-Alberti, D. V. Makhov, S. Tretiak and D. V. Shalashilin, Phys. Chem. Chem. Phys., 2016, 18, 10028–10040 RSC.
- D. V. Makhov, W. J. Glover, T. J. Martinez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- D. V. Makhov, K. Saita, T. J. Martinez and D. V. Shalashilin, Phys. Chem. Chem. Phys., 2015, 17, 3316–3325 RSC.
- D. V. Makhov, T. J. Martinez and D. V. Shalashilin, Faraday Discuss., 2016, 194, 81–94 RSC.
- S. Fernandez-Alberti, A. E. Roitberg, T. Nelson and S. Tretiak, J. Chem. Phys., 2012, 137, 014512 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Chem. Phys. Lett., 2013, 590, 208–213 CrossRef.
- L. Alfonso Hernandez, T. Nelson, M. F. Gelin, J. M. Lupton, S. Tretiak and S. Fernandez-Alberti, J. Phys., Lett., 2016, 7, 4936–4944 Search PubMed.
- S. Mukamel, Nature, 1997, 388, 425–427 CrossRef.
- S. Tretiak, V. Chernyak and S. Mukamel, J. Chem. Phys., 1996, 105, 8914–8928 CrossRef.
- S. Tretiak, W. M. Zhang, V. Chernyak and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13003–13008 CrossRef.
- S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Science, 1997, 277, 781–787 CrossRef.
- S. Swallen, R. Kopelman, J. Moore and C. Devadoss, J. Mol. Struct., 1999, 485, 585–597 CrossRef.
- J. L. Palma, E. Atas, L. Hardison, T. B. Marder, J. C. Collings, A. Beeby, J. S. Melinger, J. L. Krause, V. D. Kleiman and A. E. Roitberg, J. Phys. Chem. C, 2010, 114, 20702–20712 CrossRef.
- D. V. Shalashilin and M. S. Child, Chem. Phys., 2004, 304, 103–120 CrossRef.
- A. L. Thompson, C. Punwong and T. J. Martínez, Chem. Phys., 2010, 370, 70–77 CrossRef.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45–57 CrossRef.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef.
- M. Sebastian, M. Philipp and G. Leticia, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef.
- N. L. Doltsinis, Nonadiabatic Dynamics: Mean-Field and Surface Hopping, in Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, Lecture Notes, ed. J. Grotendorst, D. Marx and A. Muramatsu, NIC Series, John von Neumann Institute for Computing, Jülich, 2002, vol. 10, pp. 377–379 Search PubMed.
- S. L. Fiedler and J. Eloranta, Mol. Phys., 2010, 108, 1471–1479 CrossRef.
- S. Tretiak, V. Chernyak and S. Mukamel, J. Am. Chem. Soc., 1997, 119, 11408–11419 CrossRef.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171–3212 CrossRef PubMed.
- S. A. Mewes, J.-M. Mewes, A. Dreuw and F. Plasser, Phys. Chem. Chem. Phys., 2016, 18, 2548–2563 RSC.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef.
- S. Fernandez-Alberti, V. D. Kleiman, S. Tretiak and A. E. Roitberg, J. Phys. Chem. A, 2009, 113, 7535–7542 CrossRef PubMed.
- S. Fernandez-Alberti, A. E. Roitberg, V. D. Kleiman, T. Nelson and S. Tretiak, J. Chem. Phys., 2012, 137, 22A526 CrossRef PubMed.
- S. Fernandez-Alberti, V. D. Kleiman, S. Tretiak and A. E. Roitberg, J. Phys., Lett., 2010, 1, 2699–2704 Search PubMed.
| This journal is © the Owner Societies 2018 |