Influence of particle viscosity on mass transfer and heterogeneous ozonolysis kinetics in aqueous–sucrose–maleic acid aerosol

Abstract

Mass transfer between the gas and condensed phases in aerosols can be limited by slow bulk diffusion within viscous particles. During the heterogeneous and multiphase reactions of viscous organic aerosol particles, it is necessary to consider the interplay of numerous mass transfer processes and how they are impacted by viscosity, including the partitioning kinetics of semi-volatile organic reactants, water and oxidants. To constrain kinetic models of the heterogeneous chemistry, measurements must provide information on as many observables as possible. Here, the ozonolysis of maleic acid (MA) in ternary aerosol particles containing water and sucrose is used as a model system. By varying the mass ratio of sucrose to MA and by performing reactions over a wide range of relative humidity, direct measurements show that the viscosity of the particle can be varied over 7 orders of magnitude. Measurements of the volatilisation kinetics of MA show that this range in viscosity leads to a suppression in the effective vapour pressure of MA of 3–4 orders of magnitude. The inferred values of the diffusion coefficient of MA in the particle phase closely mirror the expected change in diffusion coefficient from the Stokes–Einstein equation and the change in viscosity. The kinetics of ozonolysis show a similar dependence on particle viscosity that can be further investigated using the kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB). Two scenarios, one constraining the diffusion coefficients for MA to those expected based on the Stokes–Einstein equation and the other including the diffusion coefficients as a fit parameter, yield similarly adequate representations of the ozonolysis kinetics, as inferred from the experimental decay in the signature of the vinylic C–H stretching vibration of MA. However, these two scenarios provide very different parameterisations of the compositional dependence of the diffusion coefficients of ozone within the condensed phase, yielding qualitatively different time-dependent internal concentration profiles. We suggest that this highlights the importance of providing additional experimental observables (e.g. particle size, heterogeneity in composition) if measurements and models are to be universally reconciled.

---

I. Introduction

The presence of aerosol particles in the atmosphere can affect the Earth's climate by directly scattering incoming solar and reflected terrestrial radiation back into the atmosphere.¹ Aerosol particles can also act as cloud condensation nuclei (CCN) and ice nuclei (IN), providing surfaces onto which gas phase species, such as water, can condense and indirectly influence climate.^2–4 Aerosols also impact on air quality, reducing visibility and posing an adverse risk for public health.^5,6 In all of these contexts, a detailed understanding of the chemical and physical processes governing aerosol composition and particle size is critical for quantifying aerosol impacts. Indeed, it has become apparent that the relationships between particle phase state (liquid, crystalline or amorphous),⁷ chemical reactivity, hygroscopicity and component volatilities are poorly constrained.^8–11 This leads to uncertainties in the equilibrium gas-particle partitioning of volatile and semi-volatile components,^12–14 the timescales of responses in particle size and composition to change in environmental conditions,^15,16 and the efficiency of particles as CCN and IN.^7,17–20

Organic compounds constitute a significant proportion of atmospheric aerosol, varying temporally and spatially, and can account for up to 90% of the submicron aerosol mass globally.¹⁰ After their introduction or formation in the atmosphere, organic aerosols undergo further chemical processing by oxidants prevalent in the atmosphere such as ozone and OH radicals.¹¹ Oxidation leads to a highly complex mixture of chemical functionalities and physical properties such as volatility, leading to changes in the partitioning of components between the gas and condensed phases, particle viscosity, and hygroscopicity.^10,21,22 Conventionally, partitioning models have assumed a liquid state for aerosol particles, which attains equilibration with the surrounding gas phase instantaneously, and is homogenous and well mixed in composition, with diffusional mass transfer occurring on a short timescale.^23,24 Nonetheless, evidence from field and laboratory measurements has shown that SOA can exist as an amorphous, ultra-viscous semi-solid and these observations have challenged the theory of instantaneous equilibration, instead suggesting that slow mass transfer could inhibit the approach to equilibrium in the condensed phase.^25–28 Particles that are highly viscous will exhibit decreased diffusion rates and penetration of trace molecules within the particle bulk potentially suggesting that slow diffusion may become the rate-limiting step in heterogeneous reactions.^14,29–31 If the particle bulk is sufficiently viscous, the reaction may even become surface-limited. Slow diffusion can also change the growth of SOA particles from absorptive to adsorptive partitioning, yielding steep concentration gradients throughout the particle and negating a key assumption to partitioning models.^12,32–34

The Stokes–Einstein equation is commonly used to relate the molecular diffusion coefficient, D, of a molecule in the condensed particle phase to the particle viscosity, η:^29,35

where r is the radius of the diffusing molecule, k_B is the Boltzmann constant and T is the temperature. Particles with viscosities approaching that of a glass (η > 10¹² Pa s) have been observed in laboratory studies of atmospheric aerosol surrogates, a departure of 15 orders of magnitude from the viscosities of dilute aqueous solutions (η ∼ 10⁻³ Pa s).^27,35,36 Given relationship (1), a similar span of diffusion coefficients would therefore be expected;^33,37 indeed the S–E equation is often adequate for describing the diffusion properties of molecules percolating a matrix with a similar molecular size.^38,39 However, a divergence from the S–E equation has been observed when using the relationship to assess the diffusion of small molecules, such as water and ozone, through highly complex saccharide matrices of sucrose or secondary organic aerosol, even when the viscosity is measured to be as low as 10 Pa s.^{20,29,35,40–42} These differences can become as large as six orders of magnitude when the viscosity increases to 10⁹ Pa s, highlighting the failings in using the S–E equation for estimating the diffusion properties of atmospheric aerosol. Indeed, the equilibration in the water content in samples of secondary organic aerosol (SOA) has been shown to remain sufficiently fast that kinetic limitations in ambient aerosol can be ignored.^18,19

In a recent study, Marshall et al. reported independent measurements of particle viscosity, water and semi-volatile organic compound (SVOC) mass transport rates, and ozonolysis reactive uptake kinetics in particles composed of a ternary mixture of water–maleic acid–sucrose with the aim of exploring the correlation between diffusivity and viscosity.⁴² Maleic acid (MA) was chosen as the SVOC as it has a pure component vapour pressure of ∼10⁻³ Pa and an olefinic bond that makes it susceptible to ozonolysis, permitting a concurrent investigation of the diffusivity and reactivity over an experimentally convenient timeframe. In addition, the water activity dependence of viscosity for aqueous solutions of sucrose is well documented, it is inert to ozone and has a negligible vapour pressure; thus, the addition of sucrose solely provides an effective means of modifying the particle viscosity. A 5 : 1 mass ratio of sucrose to MA was chosen with particles spanning a viscosity range from <1 to ∼10⁵ Pa s with decrease in relative humidity (RH) from 80 to 15%. Over this viscosity range, water transport kinetics were found to remain fast and proceeded without a bulk kinetic limitation on gas-particle equilibration timescales. Similarly, the kinetics of oxidation were shown to have only a weak dependence on viscosity over this range, showing only a factor of five decrease in ozone uptake coefficient. By contrast, when the volatilisation of the SVOC was assessed, suppressions of the apparent vapour pressure by as much as three orders of magnitude from the pure component vapour pressure were observed across the same viscosity range.

In this publication, we provide a more comprehensive study of the relationships between particle viscosity and the timescales for compositional change (water and SVOC partitioning) and heterogeneous chemistry. By incorporating different mass ratios of sucrose to MA in the initial solution used to form the aerosol and by varying the RH, we show that we can vary the viscosity over a wide range, spanning more than 9 orders of magnitude. We report direct measurements of the particle viscosity, achieved by coalescing pairs of droplets at different water activities. The effective vapour pressure of MA is estimated from the time-dependence in particle size without exposure to ozone. Then, the ozonolysis kinetics are explored with varying particle viscosity. In particular, diffusion coefficients are extracted from the temporal evolution of the Raman intensity profiles using the kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB) developed by Shiraiwa et al. described in Section III.^39,42–44 Our principle objective in this study is to highlight the challenges associated with the rigorous interpretation of detailed experimental data for heterogeneous aerosol chemistry, even when a number of observables (size, composition, viscosity) are available to constrain kinetic fits. We conclude with some general recommendations that should inform the experimental and analysis strategies in future studies.

II. Experimental description

The experimental procedure using aerosol optical tweezers has been described in detail in previous publications and will only be briefly reviewed here.^42,45,46 A plume of aerosol is introduced into the trapping cell with a medical nebuliser. A single droplet is captured at the focal point of the laser (532 nm Opus), formed by passing the beam through a high numerical aperture oil-immersion objective. At the moment of trapping, the sucrose : MA mass ratio is assumed equal to that in the starting nebulised solution, however the volatilisation of MA leads to a gradual change over time. Within the trapping cell, the RH can be controlled by mixing different ratios of dry (<5%) and humidified (>98%) nitrogen flows, with the RH and temperature conditions monitored constantly using a digital capacitance probe (Vaisala HUMI-CAP HMT 330) located prior to the cell. The stability of the droplet is imaged using conventional brightfield microscopy.

The backscattered Raman light from the droplet is focussed onto the entrance slit of a spectrometer and dispersed onto a non-intensified CCD camera. The Raman spectra comprise both spontaneous and stimulated features, as shown in Fig. 1(a). Characteristic spontaneous Raman bands, Stokes shifted from the incident wavelength of 532 nm, are observed for all the chemical functionalities present in the aqueous droplet, including the O–H band (present between 637 and 665 nm), the vinylic C–H band from MA (634–637 nm) and the sp³ hybridised C–H band of sucrose (626–634 nm).⁴⁵ The change in intensity of the vinylic C–H stretch permits the progress of the ozonolysis reaction to be followed, with the temporal evolution for several experiments under similar reaction conditions shown in Fig. 1(b) as examples of the reproducibility of the measurements. Further, a spherical particle acts as a low loss optical cavity with enhancement in the spontaneous Raman signal at wavelengths that are commensurate with whispering gallery modes (WGMs).⁹ By comparing the wavelengths of the experimental WGMs with a library of modes predicted from Mie theory, the radius and refractive index can be inferred for each Raman spectrum.^45,47,48

Fig. 1 (a) Typical Raman spectra of a mixed component aqueous sucrose : MA (3 : 5 mass ratio) droplet prior to and after ozonolysis at an RH of 72%. The initial droplet radius is ∼5.7 μm. (b) Relative change in vinylic C–H band intensity from MA during ozonolysis for 3 experiments at the same initial sucrose : MA mass ratio of 1 : 5, an ozone concentration of 43 ppmv and an RH between 71–77%. (c) An example of the change in droplet radius and refractive index during ozonolysis for a mixed component aqueous sucrose : MA (3 : 5) particle at 72% RH and exposed to 47 ppm ozone.

For oxidation experiments, ozone is introduced into the trapping cell by passing synthetic air through an ozone generator consisting of an UV light source.⁴⁶ Experiments were conducted at a constant ozone concentration, measured using a custom fabricated 10 cm Beer–Lambert cell. The Beer–Lambert cell was initially calibrated by comparing measurements to a commercial ozone analyser (49C ozone analyser, Thermo Environmental Instruments). The reaction between MA and ozone generates products with increased volatilities relative to MA resulting in a change in radius and increased oxidation levels leading to an increase in refractive index (RI). The reaction can be considered complete when the vinylic C–H stretch is no longer apparent in the Raman fingerprint. Notably, there may be a continued change in radius and RI beyond this time, indicative of the slow volatilisation of the products of oxidation and variations in component RI with volatility, as shown in Fig. 1(c).⁴⁶

Viscosity measurements using aerosol optical tweezers are achieved by incorporating a diffractive optic, specifically a spatial light modulator (SLM), into the optical path that allows the trapping of pairs of particles in two optical traps.^35,49,50 The optical landscape is defined by pre-programming a sequence of phase only holograms (kinoforms) into the SLM. At the start of an experiment, the two traps are separated by a few droplet diameters. Then, the distance between the traps is decreased to a point at which the particle touch and coalescence occurs. The coalescence event is followed either by examining the brightfield images (see, for example, the images in Fig. 2(a)) or by recording the elastic backscattered light collected by a silicon photodiode, and using the relaxation time from either technique to infer the particle viscosity.⁵¹ Relaxation timescales between 10⁻⁶ and 10⁻³ s can be followed by the light scattering method; the camera acquisition rate sets the lower limit available to the brightfield imaging technique of 10⁻³ s. At viscosities less than 10 Pa, corresponding to timescales faster than 1 ms, the relaxation timescale, and thus viscosity, is inferred from the decay of the elastic back-scattered light intensity.⁵¹ Above this threshold viscosity, the elastic light scattering signal arises from a convolution of the motion and reorientation of the particle in the trap and the capillarity driven relaxation in shape and so the viscosity must instead be inferred from the relaxation timescale observed in the bright-field images.^35,50 The point at which the two particles have fully merged to form a perfect sphere is determined from the time dependence of the aspect ratio between the polar and equatorial lengths, with the damping time calculated from an exponential fit of the aspect ratio against time.

Fig. 2 (a) Viscosity of ternary MA/sucrose/water aerosol droplets at varying RH measured by aerosol optical tweezers. Sucrose : MA mass ratios of 10 : 1, 5 : 1 and 1 : 5 are indicated by the red, blue and green datasets (points and lines, top to bottom in order), respectively. Multiple measurements are binned into narrow ranges in RH. The viscosity parameterisations for binary aqueous/sucrose and aqueous/MA droplets are shown by the yellow (top) and grey (bottom) lines, respectively, for comparison. The inset images show one example of a coalescence event at an RH of 41% for a sucrose : MA mass ratio of 10 : 1. In this example, the composite particle viscosity is ∼10³ Pa s. (b) Mass fraction of water against viscosity for three different initial mass ratios of sucrose : MA (red 10 : 1, blue 5 : 1, green 1 : 5). The mass fraction of water is calculated from the coalescence relative humidity using the model of Dutcher et al. The ordinate error arises from the error envelope associated with the viscosity parametrisation, while the abscissa errors from the ±2% uncertainty in the RH probe which propagates through to the error in the mass fraction of water in the particle. The mass fraction of water predicted for the RH region where the largest difference in viscosities occurs are shown in the inset.

III. Kinetic modelling

We use the kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB), which provides time and depth-resolved calculation of mass transport and chemical reaction in aerosol particles.⁵² KM-SUB resolves the following processes explicitly: gas-phase diffusion, surface adsorption and desorption, surface-bulk exchange, diffusion of trace gas (O₃) and bulk reactant (MA) in the particle bulk as well as chemical reactions at the surface and in the particle bulk. MA is assumed to react with ozone in a concerted, bimolecular reaction, which yields reaction products that have the same physical properties as the starting compound MA. Secondary reactions involving oxidation products and evaporation of volatile products are neglected for simplicity.

In order to obtain a common kinetic parameter set describing all experimental data sets, we used a global fitting method combining a uniformly-sampled Monte-Carlo (MC) search with a genetic algorithm (GA), the MCGA algorithm.⁵³ In the MC search, kinetic input parameters for KM-SUB were varied randomly within individual bounds. All measurements were fitted simultaneously by the model and the correlation between modelled and experimentally determined decay of maleic acid evaluated in a least-squares fashion. The globally best-fitting parameter sets are fed into the starting population of a genetic algorithm (Matlab Global Optimization Toolbox), in which they are optimised by processes mimicking survival, recombination and mutation in evolutionary biology. To ensure diversity within the pool of parameter sets and to counteract the sampling bias from shallow local minima, the same number of random KM-SUB input parameter sets was added to the starting population. In the GA step, the same parameter boundaries were used as in the preceding MC step. The optimization was stopped when the population was homogeneous and, thus, the increase in correlation with the experimental data had ceased.

The input parameters for KM-SUB derived from experimental data and laboratory conditions are reported in Table 1. Further, substance-specific properties required as input parameters for KM-SUB are taken from the literature and are reported in Table 2. The Henry's law coefficient of ozone (H_cp,O3), the bulk diffusion coefficient of ozone (D_b,O3) and MA (D_b,MA) are RH-dependent parameters. D_b,O3 and D_b,MA were fitted with the constraint that they increase monotonically with an increase of RH. H_cp,O3 can be calculated viaeqn (2) using the solubility in pure water (H_cp,O3,w = 1 × 10⁻⁵ mol cm⁻³ atm⁻¹)⁵⁴ and in the pure organic substance (H_cp,O3,org, used as fit parameter) by using a logarithmic mixing rule:³³

H_cp,O3 = exp((1 − w_org)log(H_cp,O3,w) + w_org log(H_cp,O3,org)) (2)

where w_org is the mass fraction of the organic component. Note that in all fitting scenarios, surface-layer reactions could not be uniquely separated from near-surface bulk reactions with the available experimental data. Both reaction pathways lead to consumption of MA in the outermost particle layer and can typically only be distinguished if oxidant concentrations or particle sizes are varied significantly,⁵⁵ or bulk diffusion coefficients are exceptionally low.^33,56 Hence, the rate of surface-layer reactions, as defined by Pöschl et al.⁵⁷ and originally implemented in KM-SUB, was fixed to zero in all global optimizations in order to reduce model complexity without a reduction of achievable experiment-model correlation. Analogously, the desorption lifetime of ozone at the surface, a parameter determining the rate of surface-layer reactions,⁵⁵ was fixed at a value of 0.1 ms, and showed no sensitivity in any of the model runs (Table 2).

Table 1 KM-SUB input parameters reflecting the environmental conditions during laboratory experiments

Symbol	Unit	10% RH	35% RH	55% RH	75% RH	Meaning
T	K	293				Temperature
[O3]g	cm^−3	9.39× 10^14				Gas phase concentration of ozone
r p	cm	5.36 × 10^−4	5.07 × 10^−4	5.49 × 10^−4	5.50 × 10^−4	Particle radius
[MA]b	cm^−3	1.32 × 10^21	1.18 × 10^21	1.05 × 10^21	8.77 × 10^20	Maleic acid particle bulk concentration

---

Table 2 KM-SUB input parameters reflecting the physicochemical properties of sucrose, maleic acid and ozone

Symbol	Unit	Numerical value	Meaning
α s,0,O3		0.5	Surface accommodation coefficient of ozone on an adsorbate-free surface
D g,O3	cm^2 s^−1	0.14	Ozone gas phase diffusion coefficient
M O3	g mol^−1	48	Molar mass of ozone
M MA	g mol^−1	116.07	Molar mass of maleic acid
M Suc	g mol^−1	342.3	Molar mass of sucrose
ρ MA	g cm^−3	1.59	Density of pure maleic acid
ρ Suc	g cm^−3	1.59	Density of pure sucrose
δ MA	cm	4.95 × 10^−8	Effective molecular diameter of maleic acid
σ O3	cm^2	1.52 × 10^−15	Effective molecular cross section of ozone
H cp,O3,w	mol cm^−3 atm^−1	1.0 × 10^−5	Henry's law coefficient of ozone in pure water
τ d,O3	s	1.0 × 10^−4	Desorption lifetime of ozone

---

IV. Results and discussion

A key aspect of the current work is to explore explicitly the relationship between the rates of evaporation of a SVOC and ozonolysis chemistry with aerosol particle viscosity. Measurements of particle viscosity are first presented from coalescing pairs of particles to provide RH-dependent parameterisations for particles of varying sucrose : MA mass ratio. We then report measurements of volatilisation kinetics without reaction followed by the ozonolysis kinetics of MA in particles of varying viscosity.

IV.a. Compositional dependence of particle viscosity

Measurements of viscosity were performed for three initial sucrose : MA mass ratios of 10 : 1, 5 : 1 and 1 : 5 and the water activity dependencies of viscosity are shown in Fig. 2. All coalescence events for these particle compositions were in the overdamped regime with viscosities higher than 20 mPa s, characterised by coalescence events that proceeded by a slow creeping flow and relaxation to a spherical shape rather than damped oscillations;^35,49 an example is shown in Fig. 2(a). Each data point is the average of several coalescence events performed at similar RHs. Given the uncertainty associated with the viscosity measurement, we report only linear fits for the dependence of the logarithm of the viscosity of RH. For comparison, the linear water activity dependence of aqueous sucrose and aqueous MA droplets are shown in Fig. 2(a).^35,50 The linear fit for binary MA is taken from bulk viscosity data in Gomez et al. which used an automatic capillary viscometer at 25 °C.⁵⁸ Owing to the limited solubility of MA, data are only available up to a mass fraction of MA of 0.402, corresponding to an RH of 90%, estimated using the thermodynamic treatment of Dutcher et al.^59,60 The parameterisation is extrapolated below this RH for comparison with the other data sets.

Discussions within the literature have highlighted the importance of water as a plasticiser, with water molecules increasing the mobility of the organic–aqueous matrix.^35,39 Thus, the viscosity of each mixture decreases with increase in RH. MA is more hygroscopic than sucrose (κ = 0.367 ± 0.021 and 0.115 ± 0.005 respectively);⁶¹ thus, the increase in water content with increase in RH may be expected to be most significant for the more MA rich aerosol particles. To calculate the water content as a mass fraction with varying gas phase RH and sucrose : MA ratio, we have used the thermodynamic model of Dutcher et al.^{42,59,60,62,63} This thermodynamic predictive model uses statistical mechanics and adsorption isotherms to treat aqueous solutions consisting of arbitrary number of solutes.⁶² Coulombic short range electrostatic interactions are used to determine the energy parameters for water sorption onto the hydration shell for each monolayer of the solute molecule in binary systems.⁵⁹ This multilayer adsorption isotherm model is expected to describe particularly well the compositional dependence of water content to zero solvent activity.^60,63 The compositional dependencies on RH and activity coefficients estimated from the isotherm model for the different sucrose : MA mass ratios are shown in Fig. 3, using the model parameters given in Marshall et al.⁴²

Fig. 3 (a) Activity coefficient of MA (mole fraction basis with a pure liquid solute reference state), (b) mass fraction of MA, (c) mole fraction of MA and (d) droplet density as functions of RH from the model of Dutcher et al. Different initial sucrose : MA mass ratios are shown: 1 : 5 (green), 3 : 5 (purple), 2 : 1 (mustard), 3 : 1 (grey), 5 : 1 (blue) and 10 : 1 (red).

When the dependence of aerosol viscosity is reported in terms of mass fraction of water, Fig. 2(b), there is a consistent trend across the compositional range and spanning almost 8 orders of magnitude in viscosity. It must be recognised that the viscosity scale is shown in logarithmic form and the errors in viscosity can be as large as one order of magnitude. A closer examination of the data in Fig. 2(b) may suggest that the aerosol with higher MA fraction is marginally less viscous than the other two; conversely, the aerosol with marginally higher sucrose content may be more viscous, consistent with MA having a minor plasticising effect on the particle viscosity.

IV.b. Volatility of MA from particles of varying viscosity

MA has a pure component vapour pressure of (1.7 ± 0.2) × 10⁻³ Pa, reported from previous optical tweezers measurements,⁴² and can be classified as a SVOC, making it an appropriate proxy compound for secondary organic aerosol to measure the effect of viscosity on volatility and partitioning. The pure component vapour pressure, p⁰_i, can be estimated from the Maxwell equation if the rate of radius (r) change, usually represented as a dependence of r² on t, is measured, as in our previous determination. In the case of a species evaporating from a stationary droplet under isothermal conditions into a gas phase in which the background concentration of the component is zero, the Maxwell equation can be written as:⁴²where M_i is the molar mass of the evaporating species and D_i is the gas-phase diffusion coefficient of species i in the surrounding gas. The mole fraction, mole fraction activity coefficient relative to the pure liquid solute reference state and mass fraction of the semi-volatile in the particle are denoted by x_i, γ_i and F_i, respectively. R is the ideal gas constant, T the temperature and ρ is the density of the aqueous solution droplet. The solution density is calculated assuming a linear mixing rule: mole fractions of each component are calculated from the multilayer adsorption isotherm model at each RH and the mixture density calculated by weighting the pure component density values for water, maleic acid and sucrose, which are 0.997, 1.419 and 1.590 g cm⁻³, respectively.⁶⁴ The gas phase diffusion coefficients of many atmospherically relevant organic compounds have not been measured, but are instead estimated using Chapman–Enskog kinetic theory using Lennard-Jones potential parameters.^42,45 Using this method, the diffusion coefficient of MA is calculated to be 7.2 × 10⁻² cm² s⁻¹. With a constant flow of nitrogen passing through the trapping cell, the partial pressure of the evaporating species at an infinite distance can be assumed equal to zero.

Measurements of the evaporation rate are performed at varying RH, equivalent to varying the mass fraction of solute in the droplet as well as the activity coefficients. During periods of fixed RH, a droplet remains in equilibrium with the surrounding gas phase such that the compositional terms (x_i, γ_i and F_i) and the droplet density would remain constant if the aerosol was a simple binary mixture (MA and water). For the ternary particles considered here, the changing mass of MA in the particle leads to a changing mass fraction of MA relative to total solute over time. However, the very slow volatilisation of MA ensures that we can assume that the relative fractions of MA and sucrose in the particle do not change appreciably during the time period of any measurement presented here. Measurements of volatilisation are made over a period of a few thousand seconds such that the fractional change in radius always remains ≪1%, the same method used in our previous study.⁴² The compositional parameters are derived from the isotherm thermodynamic model as discussed earlier.

The rate of droplet size change at varying RH can be used to explore the dependence of the MA evaporation rate and, thus, the vapour pressure of MA on particle viscosity. Although we use eqn (3) to estimate the value of p⁰_i, it must be recognised that this may not equal the true value of the pure component vapour pressure of MA due to kinetic limitations within the particle bulk that limit the evaporation rate, particularly at low RH and high sucrose mass fraction.⁴² Under these conditions, the apparent vapour pressure inferred from the measurement could be much lower than the previously reported value for MA. Hence, we refer to the value of p⁰_i retrieved from this analysis as the effective vapour pressure; values for particles of widely varying sucrose : MA mass ratio are reported in Fig. 4(a). At high RH, all the measured vapour pressures tend to the pure component vapour pressure of MA. However, as the fraction of sucrose in the particle increases and the RH decreases, the degree of suppression of MA volatility increases, leading to lower values of the effective vapour pressure.

Fig. 4 (a) Dependence of effective vapour pressure on RH for multiple droplets with different initial sucrose : MA mass ratios: 1 : 5 (green), 3 : 5 (purple), 1 : 1 (orange) 2 : 1 (mustard), 3 : 1 (grey), 5 : 1 (blue) and 10 : 1 (red). The grey bar indicates the lower and upper error limits of the pure component vapour pressure for aqueous MA. (b) Variation in the retrieved value of the effective vapour pressure with particle viscosity for particles with different initial sucrose : MA mass ratios of 1 : 5 (green), 5 : 1 (blue) and 10 : 1 (red).

The data presented in Fig. 4(a) were acquired by gradually stepping the RH down in incremental steps in order to measure the RH dependent volatilisation kinetics; thus, some experiments required >12 000 s (>3 hours) to complete. As a further verification of these measurements and to ensure that any trends were not an artefact of varying amounts of MA loss during the measurement period, we performed a number of more rapid measurements where the RH was quickly dropped from >80% to an RH between 20 to 40% in <100 s and the volatilisation kinetics of MA were then measured at this single lower RH. In all cases, these measurements yielded effective vapour pressures that were within the uncertainties of the much longer timescale studies, although uncertainties in all vapour pressure measurements can be as large as one order of magnitude.

Using the viscosity-water activity parameterisations presented in Fig. 2 for a subset of the compositions shown in Fig. 4(a), we are able to explicitly examine the dependence of the effective vapour pressure of MA on the viscosity of the particle from which evaporation is occurring, shown in Fig. 4(b). Unfortunately, the uncertainties in the effective vapour pressure measurements and viscosities are both large and may well originate from the variable particle histories prior to the volatility measurement. As we have identified previously, forming any viscous aerosol particle by drying leads to spatial gradients/heterogeneities in composition and these introduce variability into any subsequent measurement of mass transport kinetics.^65,66 However, the general trends are clear and the volatility suppression is over 3 orders of magnitude with increase in viscosity of over 7 orders of magnitude for the most sucrose rich aerosol (sucrose : MA 10 : 1). A similar trend is observed for the sucrose : MA 5 : 1 ratio. Surprisingly, the aerosol with a sucrose : MA mass ratio of 1 : 5 ratio shows no dependence on viscosity over a viscosity range of ∼3 orders of magnitude. These seemingly different trends in effective vapour pressure with viscosity suggest that the “bulk average” viscosity is not all that is important in determining the apparent volatility. However, it must also be recognised that the effective vapour pressure for the sucrose : MA 1 : 5 mass ratio particles might be expected to fall by at most a factor of 3–4 over the measured viscosity range based on the data for the sucrose : MA 5 : 1 ratio particles; this relatively small change may be concealed by the measurement uncertainties.

The kinetics of the hindered volatilisation of MA from viscous sucrose–MA aerosol particles can be used to estimate the diffusion coefficient of MA in particles of varying composition using the treatment of Abramson et al.⁶⁷ In this model, bulk diffusion is treated as Fickian and it is assumed that the diffusion coefficient of the semi-volatile component is invariant with composition during the evaporation timeframe and the change in radius is small. In our measurements, these conditions are satisfied with the radius change in all measurements ≪1% of the droplet radius over the analysis time period. In addition, we have shown that the interplay of rates of SVOC and water evaporation and their relative timescales must be carefully considered when attempting to identify a true bulk diffusional limitation for the volatilisation of an SVOC from an aerosol particle of ∼5 μm radius.⁶⁸ For illustration of this point, consider the relative rates of SVOC and water evaporation in a scenario where RH is decreased and hence the viscosity of a ternary SVOC/sucrose/water droplet is increased: initially, the rate of water loss slows and becomes more comparable to the rate of loss of the SVOC at intermediate RHs.⁶⁸ Under this regime, the SVOC loss rate is governed by the low component vapour pressure and gas-diffusional transport and only water evaporation is actually limited by slow bulk diffusion. Only upon reducing the RH further does a bulk diffusional limitation imposed on SVOC loss exert an influence and limit the SVOC volatilisation.⁶⁸ With water transport showing much larger divergence from the Stokes–Einstein equation than larger organic molecules,^35,39 it can then be shown that the timescales for SVOC and water evaporation diverge; only under these conditions can the process of SVOC loss, contributing to particle size change, be isolated effectively from the water loss kinetics.⁶⁸ Thus, to infer the bulk diffusion coefficient of MA in aqueous MA/sucrose particles using the model of Abramson et al.,⁶⁷ we limit our analysis to experiments where the RH is sufficiently low that the kinetics of size change can be unambiguously attributed to slow bulk diffusion of MA. Based on our previous calculations for aqueous malonic acid/sucrose particles and consistent with measurements,⁶⁸ the timescale for the malonic acid loss is more than a factor of 20 slower than water loss at an RH of 35% and increases with further decrease in RH. Given the similarity in molecular size, weight and volatility of MA and malonic acid, we consider that this provides an appropriate characterisation for aqueous MA/sucrose particles and we consider only a subset of volatility measurements that have been made at RHs below ∼35%.

Using the model of Abramson et al.,⁶⁷ we have examined the evaporation of particles with sucrose : MA mass ratios of 5 : 1 at 36, 30, 23 and 22% RH. At the higher two RHs, the diffusion coefficients for MA are estimated as (2 ± 1) × 10⁻¹⁶ cm² s⁻¹ and (3 ± 2) × 10⁻¹⁶ cm² s⁻¹, respectively. Below 30% RH, the evaporation leads to a size change of <0.1% (∼5 nm) over a time of >3000 s and, thus, accurate determinations of diffusion coefficients are intractable. Instead, an upper limit can be estimated of 2 × 10⁻¹⁶ cm² s⁻¹. For comparison, these values are within an order of magnitude of an estimate of ∼2 × 10⁻¹⁵ cm² s⁻¹ for a particle of viscosity of 10⁶ Pa s, assuming the Stokes–Einstein relationship of viscosity and diffusion coefficient, eqn (1).⁴² Given the challenging nature of these measurements and the assumptions made in the model treatment, we consider that these are broadly in agreement. These values will be compared with the fitted kinetics for MA ozonolysis in particles of varying viscosity in the following section.

IV.c. Ozonolysis kinetics of MA in particles of varying viscosity

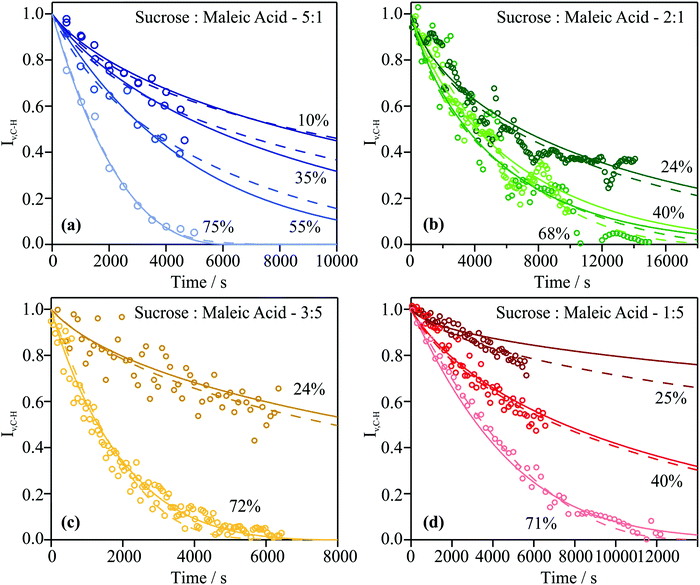
Particles with different sucrose : MA mass ratios were exposed to ozone at concentrations between 36 and 53 ppmv for ∼10 000 seconds at RHs between 10 and 80%. Sucrose is inert to ozone and should not influence the reaction kinetics, other than by modifying the viscosity and composition of the particle in known ways. As the droplet containing MA is exposed to ozone and oxidation of the C=C bond occurs, the intensity of the vinylic band diminishes in the Raman spectrum recorded from the particle. The reaction can be assumed complete when the intensity of the vinylic band reaches zero. The complete ozonolysis of MA occurs on a convenient timescale and leads to the formation of volatile products, such as glyoxylic acid, that are rapidly entrained in the passing gas flow. Measurements for particles of sucrose : MA mass ratios 5 : 1 (at 75, 55, 35 and 10% RH), 2 : 1 (at 68, 40 and 24% RH), 3 : 5 (at 72 and 24% RH) and at 1 : 5 (at 77, 40 and 25% RH) were obtained. As described in Section III, the KM-SUB model was used to obtain a common kinetic parameter set describing all experimental data sets for the ozonolysis experiments. The KM-SUB model fits were obtained using two different scenarios to explore the sensitivity of the fitting when different constraints are imposed on the ozonolysis kinetics.

In the first scenario, the kinetic parameters were optimized using rather few constraints. The MCGA algorithm was used to optimize reaction rate coefficients, the Henry's law coefficient of ozone in pure organics and the bulk diffusion coefficients of ozone and MA. Diffusion coefficients were optimized individually for each particle composition as characterized by sucrose : MA mass ratio and RH. The reaction rate and solubility coefficients on the other hand were assumed to be independent of particle composition (despite the RH dependence of H according to eqn (2)). These properties, which were optimized using the MCGA algorithm, are reported in Table 3 with the constrained search range for each parameter shown. As apparent from the comparisons between the models and measurements shown in Fig. 5, almost all data sets are well-reproduced. There is a tendency for the MA concentration to be slightly underpredicted in the first half of the experiment and over-predicted in the second half of the experiment. It is possible that this stems from the depletion of ozone in the trapping cell at early times through reaction with residual MA throughout the trapping cell, on the cell walls and in the gas phase.

Table 3 KM-SUB kinetic input parameters optimized using the MCGA optimization algorithm

Symbol	Unit	Lower boundary	Upper boundary	Scenario 1	Scenario 2	Meaning
a Value fixed in scenario 2. b Detailed diffusion coefficients provided in Fig. 6 and Tables S1 and S2 (ESI).
k BR	cm^3 s^−1	5 × 10^−19	1 × 10^−17	5.7 × 10^−18	1.7 × 10^−18^a	Bulk reaction rate coefficient
D b,O3	cm^2 s^−1	1 × 10^−10	2 × 10^−4			Bulk diffusion coefficient of ozone
D b,MA	cm^2 s^−1	1 × 10^−15	1 × 10^−8			Bulk diffusion coefficient of maleic acid
H cp,O3,org	mol cm^−3 atm^−1	1 × 10^−5	4 × 10^−4	2.8 × 10^−4	4.6 × 10^−5	Henry's law coefficient of ozone in pure organics

---

Fig. 5 Comparison of KM-SUB model fits (lines) to MA ozonolysis kinetics measurements (points) at different RHs and sucrose : MA mass ratios (as indicated in each panel). The y-axis displays the relative change in vinylic C–H band intensity from MA during ozonolysis. Scenarios 1 and 2 are indicated by the solid and dashed lines, respectively.

In the second scenario, the kinetic parameters were optimized using tighter constraints on the diffusion kinetics. Specifically, the RH-dependent parameterisation of viscosity for the 5 : 1 sucrose : MA mixture was used to obtain D_b,MAvia the Stokes–Einstein equation, which were fixed during the parameter optimization process. For all but the very lowest RH, the viscosities of all particle compositions can be expected to be within one order of magnitude of the value estimated from this treatment (see Fig. 2). Thus, ignoring the potential failure of the Stokes–Einstein equation, any systematic errors in the diffusion coefficient of MA can be expected to be of the same magnitude. Using eqn (1), D_b,MA values were calculated using an effective diameter of maleic acid of 0.495 nm. The bulk reaction rate coefficient k_BR was fixed to a value of 1.7 × 10⁻¹⁸ cm² s⁻¹, as previously reported in the literature (Hoigne and Bader 1983).⁶⁹ Furthermore, the fitting procedure for scenario 2 differed from the procedure in scenario 1. With the MCGA algorithm,⁵³ the Henry's law coefficient of ozone in pure organics, H_cp,org, and the ozone diffusion coefficients, D_b,O3, are obtained using only the data sets at a sucrose : MA mass ratio of 5 : 1 (at four different RHs). These values for k_BR and H_cp,org were kept constant when fitting D_b,O3 for the remaining eight data sets at different mass ratios. As apparent from Fig. 5, the model for this scenario fits the experimental data very well and comparable correlations are obtained with the less constrained fit in scenario 1.

The numerical values of the independently fitted D_b,O3 and D_b,MA are shown in Fig. 6 as a function of RH and for different sucrose : MA mass ratios. To represent the RH dependence of the diffusion coefficients, an equation of Vignes-type, eqn (4) and (5), is used:

α = exp(x_org²(C₁ + 3C₂ − 4C₂x_org)) (5)

where x_org is the molar fraction of organic components (sum of MA and sucrose), D_b,w is the bulk diffusion coefficient in pure water, D_b,org is the bulk diffusion coefficient in pure organics and C₁ and C₂ are fitting coefficients. No clear trends in D_b,O3 was observed between the different MA : sucrose mass ratios and hence a single Vignes-type equation was employed for all compositions. All fitted parameters are also listed in Table S3 (ESI†).

Fig. 6 (a) Diffusion coefficients of ozone (D_b,O3, circular markers) and MA (D_b,MA, open diamond shaped markers) obtained by a free fit to the experimental data according to scenario 1, with sucrose : MA compositions as indicated. The diffusion coefficients for ozone and MA, dashed and solid lines, respectively, have been parameterized using a Vignes-type equation, eqn (4). (b) Diffusion coefficients of ozone (D_b,O3, markers, same colour markers as in (a)) obtained from a fit with a fixed RH dependence for the diffusion coefficients of MA (D_b,MA, black solid line) and fixed bulk reaction rate coefficient according to scenario 2.

Panel (a) shows the results of the fit in scenario 1, whereas panel (b) shows the results according to the more constrained fit in scenario 2. Although the representation of the experimental results is equally good for both model scenarios, Fig. 6 shows very different sets of diffusion coefficients for both optimizations. The values of D_b,O3 estimated in scenario 1 show a strong dependence on RH and are comparable to previously reported values for ozone in the reaction of ozone with shikimic acid particles at varying RH^41,70 and with diffusion coefficients for water in sucrose.¹⁶D_b,O3 and D_b,MA have similar values, with the diffusion of ozone being only slightly faster than diffusion of MA. However, it should be noted that the model's sensitivity to D_b,MA is weak in this scenario, particularly at low RH, leading to large uncertainties as indicated by the overall large error bars in Fig. 6(a).

Fig. 6(b) shows D_b,O3 values for scenario 2. Although D_b,O3 values are broadly consistent with a Vignes-type fit (grey dashed line), the RH dependence is weak in contrast to the fit in scenario 1. Indeed, D_b,O3 values are several orders of magnitude higher than previously inferred in the ozonolysis of shikimic acid and for water in sucrose.^33,41,70 At the intermolecular level, it may be reasonable that D_b,O3 would be larger than the values for water at low moisture content/high viscosity due to hydrogen bonding that can occur between water and sucrose, even though the molecular size of O₃ is larger than water. The difference between diffusion coefficients inferred here and the values for ozone in shikimic acid, however, are surprising. The error bars in Fig. 6(b) are much smaller than the ones in Fig. 6(a), which can be explained by the tighter constraint on kinetic parameters that leaves little flexibility for the value of D_b,O3. It should be noted that the values of D_b,MA determined from the Stokes–Einstein eqn (1) should generally represent a reasonable constraint based on recent inferences of diffusion coefficients for organic molecules in viscous aerosol, which have shown a much tighter adherence to eqn (1) than smaller molecules such as water.^38,39,42 In addition, the diffusion coefficients inferred from eqn (1) and particle viscosity are broadly consistent with the values of diffusion coefficients inferred from the volatilisation measurements in Section IV.b. The Henry's law coefficient for this scenario is calculated according to eqn (2) and the coefficients for pure material given in Tables 1 and 2. The resulting RH-dependence of H_cp,O3 is shown in Fig. S1 (ESI†).

Fig. 7 compares the impact of the differing diffusion coefficients, inferred from scenarios 1 and 2, on the concentration gradient of unreacted MA as a function of radial depth in the particle and time of ozone exposure. Panels (a) and (c) show the concentration profile of MA at a relative humidity of 35% for scenarios 1 and 2, respectively. In both cases, MA is only consumed close to the particle surface, as ozone does not penetrate deep enough into the particle. The diffusion gradient appears less sharp in panel (a) due to faster diffusion of MA in the optimization of scenario 1, which leads to incomplete depletion of MA at the particle surface. Panels (b) and (d) show the concentration profile at a higher humidity of 55%. Panel (d) is very similar to the lower humidity case (c) of scenario 2, albeit a larger penetration depth of ozone due to higher D_b,O3 and the overall lower MA concentration at higher humidity. Panel (b) on the other hand represents the case of a completely mixed particle. The diffusion of MA is fast enough that no radial inhomogeneity persists during oxidation. Similar to what has been observed in the system of shikimic acid (Berkemeier et al. 2016),³³ a strong RH-dependence of bulk diffusion coefficients leads to a switch in diffusive behaviour above a certain RH.

Fig. 7 Concentration profiles of MA for scenario 1 (top) and scenario 2 (bottom) at two different RHs, 35% (left) and 55% (right) for the 5 : 1 sucrose : MA mass atio. For scenario 1, there is a clearly visible switch from a pronounced diffusion gradient at 35% RH to mostly well-mixed MA at 55% RH. In scenario 2, an increase of the penetration depth of ozone with RH leads to an extension of the reactive zone and an overall shallower diffusion gradient.

V. Conclusions

To better understand the transformation processes changing aerosol particle size and composition in complex environments such as the atmosphere, we require experimental tools that are able to probe systems of increasing complexity and models that are able to capture the correct microphysics occurring at the single particle level. In this publication, we provide a comprehensive experimental data set of a benchmark ternary system evolving in composition through volatilisation of a semi-volatile component and undergoing oxidation kinetics. In addition, we provide a comprehensive set of viscosity measurements for particles at steady state compositions, i.e. various mass ratios of sucrose : MA and with varying moisture content, allowing estimations of values for molecular diffusion coefficients. From these data, a clear suppression in the rate of volatilisation is apparent with increasing particle viscosity, i.e. increasing sucrose fraction and decreasing moisture content. The time-dependence of particle size, and fractional change in volume, has been used to provide an estimate of the diffusion coefficient of MA within the viscous particles, yielding values that are broadly consistent (within an order of magnitude) of expected values estimated from the particle viscosity and the Stokes–Einstein equation.

The measured kinetics of the ozonolysis of MA, for particles with varying MA : sucrose mass ratio and at varying RH, are compared to the KM-SUB model, which captures many of the coupled discrete steps required to fully treat the chemical aging. Two contrasting scenarios for constraining the KM-SUB model provide equally good representations of the measured ozonolysis kinetics but with very different values for the diffusion coefficients of ozone (with varying particle composition and RH) and MA. Indeed, in scenario 2, the diffusion coefficient of MA is constrained to the value anticipated from using the measured viscosities and the Stokes–Einstein equation; scenario 1 is unconstrained and yields a limiting diffusion coefficient under the driest conditions which is ∼3 orders of magnitude higher. In addition, the diffusion coefficients of ozone from the two scenarios are different by ∼6 orders of magnitude under the driest conditions and for the most viscous particles. Currently, there is no clear way of identifying which of these two scenarios is physically most appropriate: the decrease in the ozone diffusion coefficient by ∼6 orders of magnitude with increase in viscosity in scenario 1 is consistent with some previous fits to ozonolysis data; scenario 2, however, is consistent with measurements of particle viscosity and with the suppression in volatility of MA.

There are a number of limitations in the current study and many of these also pertain to other studies. Only one experimental observable in the ozonolysis measurements is considered, the change in composition. Additionally, the change in particle size for each particle can be retrieved and could be used to constrain the model fits. Further, from the pattern of WGMs in the Raman spectrum, it should be possible to identify whether or not particles become inhomogeneous during oxidation, as predicted by the model in Fig. 7(a, b and d), or remain homogeneous, as predicted by the model for scenario 1 and the high RH case in Fig. 7(c).⁷¹ More generally, this analysis and interpretation of the experimental data assume that the particle remains homogeneous and that liquid–liquid phase separation does not occur forming MA rich and sucrose rich domains, an assumption that should be verified. The particles can be expected to evolve in viscosity as the ozonolysis chemistry, and any secondary chemistry, proceeds and particle composition changes, potentially leading to a time-dependence in the diffusion coefficients,⁷² something that is completely ignored in the current interpretation. The change in composition may also lead to a change in moisture content due to a change in the hygroscopic nature of the aerosol composition. Clearly, combining the analysis of evolving particle composition with change in particle radius, and providing a fuller coverage of mixture compositions and RHs, should help to more tightly constrain the model although this would require a comprehensive accounting for changes in composition through volatilisation of products, and changes in particle density with composition. This study illustrates the need for more refined measurements of multiple experimental parameters if the kinetic models are to be more fully constrained.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding from the NERC through grants NE/M004600/1 and NE/L006901/1. The modelling effort at the University of Minnesota is supported by the National Science Foundation under Grant No. 1554936. MS acknowledges support from the National Science Foundation (CAREER, AGS-1654104).

References

1. J. Haywood and O. Boucher, Rev. Geophys., 2000, 38, 513–543.
2. D. K. Farmer, C. D. Cappa and S. M. Kreidenweis, Chem. Rev., 2015, 115, 4199–4217.
3. U. Lohmann and J. Feichter, Atmos. Chem. Phys., 2005, 5, 715–737.
4. B. J. Murray, D. O’Sullivan, J. D. Atkinson and M. E. Webb, Chem. Soc. Rev., 2012, 41, 6519–6554.
5. J. Lelieveld, J. S. Evans, M. Fnais, D. Giannadaki and A. Pozzer, Nature, 2015, 525, 367–371.
6. N. Watts, W. N. Adger, P. Agnolucci, J. Blackstock, P. Byass, W. Cai, S. Chaytor, T. Colbourn, M. Collins, A. Cooper, P. M. Cox, J. Depledge, P. Drummond, P. Ekins, V. Galaz, D. Grace, H. Graham, M. Grubb, A. Haines, I. Hamilton, A. Hunter, X. Jiang, M. Li, I. Kelman, L. Liang, M. Lott, R. Lowe, Y. Luo, G. Mace, M. Maslin, M. Nilsson, T. Oreszczyn, S. Pye, T. Quinn, M. Svensdotter, S. Venevsky, K. Warner, B. Xu, J. Yang, Y. Yin, C. Yu, Q. Zhang, P. Gong, H. Montgomery and A. Costello, Lancet, 2015, 386, 1861–1914.
7. M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier, S. N. Pandis, J. Lelieveld, T. Koop and U. Pöschl, Nat. Commun., 2017, 8, 15002.
8. H. Vehkamäki, I. Riipinen and H. Vehkamaki, Chem. Soc. Rev., 2012, 41, 5160–5173.
9. U. K. Krieger, C. Marcolli and J. P. Reid, Chem. Soc. Rev., 2012, 41, 6631–6662.
10. M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. M. Donahue, C. George, A. H. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, T. F. Mentel, A. Monod, A. S. H. Prevot, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, Atmos. Chem. Phys., 2009, 9, 5155–5236.
11. C. E. Kolb and D. R. Worsnop, Annu. Rev. Phys. Chem., 2012, 63, 471–491.
12. S. O’Meara, D. Topping and G. McFiggans, Atmos. Chem. Phys., 2016, 16, 5299–5313.
13. P. F. Liu, Y. J. Li, Y. Wang, M. K. Gilles, R. A. Zaveri, A. K. Bertram and S. T. Martin, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12643–12648.
14. M. Shiraiwa and J. H. Seinfeld, Geophys. Res. Lett., 2012, 39, L24801.
15. D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11613–11618.
16. B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526.
17. D. A. Knopf, P. A. Alpert and B. Wang, ACS Earth Space Chem., 2018, 2, 168–202.
18. D. M. Lienhard, A. J. Huisman, U. K. Krieger, Y. Rudich, C. Marcolli, B. P. Luo, D. L. Bones, J. P. Reid, A. T. Lambe, M. R. Canagaratna, P. Davidovits, T. B. Onasch, D. R. Worsnop, S. S. Steimer, T. Koop and T. Peter, Atmos. Chem. Phys., 2015, 15, 13599–13613.
19. H. C. Price, J. Mattsson, Y. Zhang, A. Bertram, J. F. Davies, J. W. Grayson, S. T. Martin, D. O’Sullivan, J. P. Reid, A. M. Rickards and B. J. Murray, Chem. Sci., 2015, 6, 4876–4883.
20. J. H. Slade, M. Shiraiwa, A. Arangio, H. Su, U. Pöschl, J. Wang and D. A. Knopf, Geophys. Res. Lett., 2017, 44, 1583–1591.
21. J. H. Kroll, N. M. Donahue, J. L. Jimenez, S. H. Kessler, M. R. Canagaratna, K. R. Wilson, K. E. Altieri, L. R. Mazzoleni, A. S. Wozniak, H. Bluhm, E. R. Mysak, J. D. Smith, C. E. Kolb and D. R. Worsnop, Nat. Chem., 2011, 3, 133–139.
22. J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529.
23. J. F. Pankow, Atmos. Environ., 1994, 28, 189–193.
24. J. F. Pankow, Atmos. Environ., 2003, 37, 3323–3333.
25. B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244.
26. E. Mikhailov, S. Vlasenko, S. T. Martin, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2009, 9, 9491–9522.
27. A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirila, J. Leskinen, J. M. Makela, J. K. Holopainen, U. Pöschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, Nature, 2010, 467, 824–827.
28. A. Virtanen, J. Kannosto, H. Kuuluvainen, A. Arffman, J. Joutsensaari, E. Saukko, L. Hao, P. Yli-Pirilä, P. Tiitta, J. K. Holopainen, J. Keskinen, D. R. Worsnop, J. N. Smith and A. Laaksonen, Atmos. Chem. Phys., 2011, 11, 8759–8766.
29. M. Shiraiwa, M. Ammann, T. Koop and U. Pöschl, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11003–11008.
30. V. Perraud, E. A. Bruns, M. J. Ezell, S. N. Johnson, Y. Yu, M. L. Alexander, A. Zelenyuk, D. Imre, W. L. Chang, D. Dabdub, J. F. Pankow and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2836–2841.
31. M. Shiraiwa, A. A. Zuend, A. K. Bertram and J. H. Seinfeld, Phys. Chem. Chem. Phys., 2013, 15, 11441–11453.
32. T. Yli-Juuti, A. Pajunoja, O. P. Tikkanen, A. Buchholz, C. Faiola, O. Väisänen, L. Q. Hao, E. Kari, O. Peräkylä, O. Garmash, M. Shiraiwa, M. Ehn, K. Lehtinen and A. Virtanen, Geophys. Res. Lett., 2017, 44, 2562–2570.
33. T. Berkemeier, S. Steimer, K. U. Krieger, T. Peter, U. Pöschl, M. Ammann and M. Shiraiwa, Phys. Chem. Chem. Phys., 2016, 18, 12662–12674.
34. A. Pajunoja, W. Hu, Y. J. Leong, N. F. Taylor, P. Miettinen, B. B. Palm, S. Mikkonen, D. R. Collins, J. L. Jimenez and A. Virtanen, Atmos. Chem. Phys., 2016, 16, 11163–11176.
35. R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, Chem. Sci., 2013, 4, 2597–2604.
36. M. Song, P. F. Liu, S. J. Hanna, R. A. Zaveri, K. Potter, Y. You, S. T. Martin and A. K. Bertram, Atmos. Chem. Phys. Discuss., 2016, 1–34.
37. T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255.
38. Y. Chenyakin, D. A. Ullmann, E. Evoy, L. Renbaum-Wolff, S. Kamal and A. K. Bertram, Atmos. Chem. Phys., 2017, 17, 2423–2435.
39. H. C. Price, J. Mattsson and B. J. Murray, Phys. Chem. Chem. Phys., 2016, 18, 19207–19216.
40. P. S. J. Lakey, T. Berkemeier, M. Krapf, J. Dommen, S. S. Steimer, L. K. Whalley, T. Ingham, M. T. Baeza-Romero, U. Pöschl, M. Shiraiwa, M. Ammann and D. E. Heard, Atmos. Chem. Phys. Discuss., 2016, 284.
41. S. S. Steimer, T. Berkemeier, A. Gilgen, K. U. Krieger, T. Peter, M. Shiraiwa and M. Ammann, Phys. Chem. Chem. Phys., 2015, 17, 31101–31109.
42. F. H. Marshall, R. E. H. Miles, Y.-C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Chem. Sci., 2016, 7, 1298–1308.
43. C. Pfrang, M. Shiraiwa and U. Pöschl, Atmos. Chem. Phys., 2011, 11, 7343–7354.
44. M. Shiraiwa, C. Pfrang, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2012, 12, 2777–2794.
45. B. J. Dennis-Smither, F. H. Marshall, R. E. H. Miles, T. C. Preston and J. P. Reid, J. Phys. Chem. A, 2014, 118, 5680–5691.
46. B. J. Dennis-Smither, R. E. H. Miles and J. P. Reid, J. Geophys. Res., 2012, 117, D20204.
47. T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210.
48. T. C. Preston and J. P. Reid, J. Opt. Soc. Am. B, 2013, 30, 2113–2122.
49. R. M. Power and J. P. Reid, Rep. Prog. Phys., 2014, 77, 74601.
50. Y. C. Song, A. E. Haddrell, B. R. Bzdek, J. P. Reid, T. Bannan, D. O. Topping, C. J. Percival and C. Cai, J. Phys. Chem. A, 2016, 120, 8123–8137.
51. B. R. Bzdek, L. Collard, J. E. Sprittles, A. J. Hudson and J. P. Reid, J. Chem. Phys., 2016, 145, 54502.
52. M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691.
53. T. Berkemeier, M. Ammann, U. K. Krieger, T. Peter, P. Spichtinger, U. Pöschl, M. Shiraiwa and A. J. Huisman, Atmos. Chem. Phys., 2017, 17, 8021–8029.
54. R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981.
55. T. Berkemeier, A. J. Huisman, M. Ammann, M. Shiraiwa, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2013, 13, 6663–6686.
56. A. M. Arangio, J. H. Slade, T. Berkemeier, U. Pöschl, D. A. Knopf and M. Shiraiwa, J. Phys. Chem. A, 2015, 119, 4533–4544.
57. U. Pöschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023.
58. D. Gomez, A. Soler and R. Font, J. Chem. Eng. Data, 1986, 31, 391–392.
59. P. B. Ohm, C. Asato, A. S. Wexler and C. S. Dutcher, J. Phys. Chem. A, 2015, 119, 3244–3252.
60. C. S. Dutcher, X. Ge, A. S. Wexler and S. L. Clegg, J. Phys. Chem. A, 2013, 117, 3198–3213.
61. A. M. J. Rickards, R. E. H. Miles, J. F. Davies, F. H. Marshall and J. P. Reid, J. Phys. Chem. A, 2013, 117, 14120–14131.
62. C. S. Dutcher, X. Ge, A. S. Wexler and S. L. Clegg, J. Phys. Chem. C, 2012, 116, 1850–1864.
63. C. S. Dutcher, X. Ge, A. S. Wexler and S. L. Clegg, J. Phys. Chem. C, 2011, 115, 16474–16487.
64. C. Cai, R. E. H. Miles, M. I. Cotterell, A. Marsh, G. Rovelli, A. M. J. Rickards, Y.-H. Y. H. Zhang and J. P. Reid, J. Phys. Chem. A, 2016, 120, 6604–6617.
65. A. M. J. A. M. Rickards, Y.-C. Y.-C. Song, R. E. H. R. E. H. Miles, T. C. T. C. Preston and J. P. J. P. Reid, Phys. Chem. Chem. Phys., 2015, 17, 10059–10073.
66. J. W. Lu, A. M. J. Rickards, J. S. Walker, K. J. Knox, R. E. H. Miles, J. P. Reid and R. Signorell, Phys. Chem. Chem. Phys., 2014, 16, 9819–9830.
67. E. Abramson, D. Imre, J. Beránek, J. Wilson and A. Zelenyuk, Phys. Chem. Chem. Phys., 2013, 15, 2983–2991.
68. S. Ingram, C. Cai, Y.-C. Song, D. R. Glowacki, D. O. Topping, S. O’Meara and J. P. Reid, Phys. Chem. Chem. Phys., 2017, 19, 31634–31646.
69. J. Hoigné and H. Bader, Water Res., 1983, 17, 173–183.
70. S. S. Steimer, M. Lampimäki, E. Coz, G. Grzinic and M. Ammann, Atmos. Chem. Phys., 2014, 14, 10761–10772.
71. D. Stewart, C. Cai, J. Nayler, T. C. Preston, J. P. Reid, U. Krieger, C. Marcolli and Y.-H. Zhang, J. Phys. Chem. A, 2015, 119, 4177–4190.
72. N. A. Hosny, C. Fitzgerald, A. Vysniauskas, T. Athanasiadis, T. Berkemeier, N. Uygur, U. Pöschl, M. Shiraiwa, M. Kalberer, F. D. Pope and M. K. Kuimova, Chem. Sci., 2016, 7, 1357–1367.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01666f

‡ The experimental data are provided through the University of Bristol data repository: Reid, J. P. Viscous Aerosol, University of Bristol, 2018, DOI: 10.5523/bris.22m61e0yb1iel2jbn1gfibha5t.

---