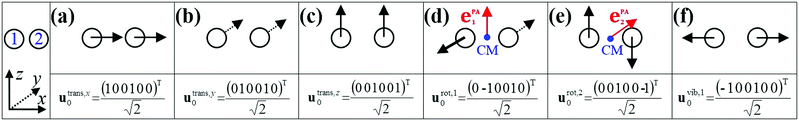Open Access Article
Open Access ArticleA general formulation of the quasiclassical trajectory method for reduced-dimensionality reaction dynamics calculations†
Tibor
Nagy
 *a,
Anna
Vikár
*a,
Anna
Vikár
 a and
György
Lendvay
a and
György
Lendvay
 *ab
*ab
aInstitute of Materials and Environmental Chemistry, Research Centre for Natural Sciences, Hungarian Academy of Sciences, Magyar tudósok körútja 2., H-1117 Budapest, Hungary. E-mail: nagy.tibor@ttk.mta.hu; lendvay.gyorgy@ttk.mta.hu
bDepartment of General and Inorganic Chemistry, University of Pannonia, Egyetem u. 10, H-8800 Veszprém, Hungary
First published on 18th April 2018
Abstract
Dimension reduction by freezing the unimportant coordinates is widely used in intramolecular and reaction dynamics calculations when the solution of the accurate full-dimensional nuclear Schrödinger equation is not feasible. In this paper we report on a novel form of the exact classical internal-coordinate Hamiltonian for full and reduced-dimensional vibrational motion of polyatomic molecules with the purpose of using it in quasiclassical trajectory (QCT) calculations. The derivation is based on the internal to body-fixed frame transformation, as in the t-vector formalism, however it does not require the introduction of rotational variables to allow cancellation of non-physical rotations within the body-fixed frame. The formulas needed for QCT calculations: normal mode analysis and state sampling as well as for following the dynamics and normal-mode quantum number assignment at instantaneous states are presented. The procedure is demonstrated on the CH4, CD4, CH3D and CHD3 isotopologs of methane using three reduced-dimensional models, which were previously used in quantum reactive scattering studies of the CH4 + X → CH3 + HX type reactions. The reduced-dimensional QCT methodology formulated this way combined with full-dimensional QCT calculations makes possible the classical validation of reduced-dimensional models that are used in the quantum mechanical description of the nuclear dynamics in reactive systems [A. Vikár et al., J. Phys. Chem. A, 2016, 120, 5083–5093].
1. Introduction
Dimension reduction is often used in modeling phenomena in chemical physics to reduce the complexity of the model. By selecting the degrees of freedom that are relevant to the investigated properties of the system, one can concentrate the effort on a model whose smaller size allows one to perform a simulation at a higher level of sophistication. In molecular physics, reduced-dimensional (RD) models have been used in the description of nuclear motion both in rovibrational spectroscopy1,2 as well as in molecular3–5 and reaction dynamics simulations.6–17 In both cases, the possibility of simplification is offered by the separation of time scales and the weakness of the coupling between the various modes of nuclear motion.In vibrational spectroscopy, the semi-rigid modes are well described by the normal mode approximation18–20 in which the potential and kinetic energies are considered as quadratic functions of Cartesian or internal coordinates and of the conjugate momenta, resp. The description of large amplitude motion (LAM), in floppy molecules, such as hindered rotor type modes, however, require a more sophisticated treatment, because the quadratic approximation does not work, often within the space swept by the zero-point motion. The frequencies of such modes are generally much smaller than those of stiffer vibrations, and the potential coupling between the fast and slow degrees of freedom is often also limited. A way to achieve a numerically feasible description of vibration of molecules with LAMs is that one reduces the dimensionality of the problem to those of the strongly anharmonic low-frequency modes by freezing the fast vibrations.1,2
In molecular dynamics simulation of, for example, biomolecules in water, when a large number of solvent molecules are present, the high-frequency OH stretching vibrations require the integration time step to be small. However, their instantaneous phase has no effect on the much slower conformational motion, thus one can freeze them,4,5 which allows a significantly faster, yet realistic simulation of the system.
In reaction dynamics, the reactive event often concerns a small number of internal coordinates involving only a few atoms, called active modes, and the rest are considered as “spectators”. Dimension reduction is possible because the potential- and often the kinematic coupling between the active and spectator modes are small. In the corresponding scattering calculation the active degrees of freedom are treated explicitly, while the coordinates of spectator modes are frozen at their values at the saddle point of the potential energy surface (PES) or at the equilibrium geometry of reactant molecules. In quantum and state-to-state quasiclassical dynamical calculations it is necessary to know the quantum states of the reactants and products, for which one needs to properly characterize the vibrational motion involving only the active degrees of freedom of the reactant and product molecules, respectively. This is equivalent to the reduced-dimensional vibrational spectroscopic problem. RD models are mostly used in quantum mechanical simulations of reactions, because of the exponential growth of the computational effort with the number of degrees of freedom,1,2,6–16 but only rarely in quasiclassical trajectory (QCT) simulations, where the growth is linear.
In the QCT method,20,21 the motion of the atoms is described classically and the only nuclear quantum effect considered is that the rovibrational energies of the reactant molecules are discrete. Accordingly, each rovibrational quantum state of the reactant molecules is simulated by an ensemble of semiclassically quantized classical states (i.e. coordinates and momenta). In RD reaction dynamical models the spectator degrees of freedom are frozen during the reaction. This means that the number of vibrational degrees of freedom of the reactant and the product molecules is also reduced. Consequently, the problem of semiclassical quantization also arises when state-to-state reactivity parameters or simply state distributions of product molecules are to be determined. In what follows, the generation of classical states corresponding to a quantum state will be called the direct problem, and the determination of the quantum state corresponding to a given classical state will be referred to as the inverse problem.
Application of dimension reduction in QCT simulations is rather scarce. One of the reasons for this is that there is no general theory for the vibrational analysis, initial state preparation and final state analysis is available. Among the few reduced-dimensional trajectory calculations performed so far, in a set only trivial reductions were applied: some of the Cartesian coordinates were simply disregarded. Lu and Hase22 applied RD models of benzene, obtained by constraining and truncating the molecule to planar C3H3 and C3H moieties to prevent zero-point energy leakage from neighboring high-frequency modes during the simulation of intramolecular vibrational energy redistribution (IVR). Klossika and Schinke23 investigated the photodissociation of HNCO induced by NH vibrational excitation, by constraining the atoms into a plane using a reduced-dimensional analytic potential energy surface calculated only for planar arrangement of atoms.
In another set of dynamical studies the vibrations of molecules or fragments were completely frozen and only their relative motion was simulated. Raff and coworkers24,25 applied rigid-body dynamics to investigate rotational energy transfer between CO2 and He as well as H2. Rotational dynamics in collisions of H2O and H2 with frozen stretch vibrations were studied by Faure et al.26 In some reactive scattering calculations bond lengths and angles were frozen, focusing again on rotational dynamics in the capture step of some bimolecular reactions (Maergoiz et al.,27 Faure et al.,28 Harding et al.29). Harding et al.30 investigated the roaming dynamics of the photochemical decomposition of CH3CHO, where they froze the vibrations of the fragments to avoid zero-point energy leakage and the need for constructing a high-dimensional analytic PES.
More complex constraints were considered by the authors of the present paper in a recent study comparing the results of reduced- and full-dimensional (FD) quasiclassical trajectory calculations. The purpose of that work was to assess the accuracy of the Palma–Clary RD quantum dynamical model of the CH4 + H → CH3 + H2 reaction,31 whose FD counterpart is computationally too expensive to solve. In the present paper the general theory of reduced-dimensional QCT calculations used in that study is described. We demonstrate how the QCT method, including initial condition generation and final state can be consistently applied to RD models involving arbitrary constraints.
In the following, first we describe the three fundamental coordinate systems used in this work (Section 2.1); then in Section 2.2 we derive the vibrational Lagrangian in body-fixed Cartesian coordinates and then the vibrational Lagrangian and Hamiltonian in internal coordinates (Section 2.3). We discuss the connection of our formulation to the t-vector and s-vector formalisms in both full and reduced-dimensionality (Section 2.4). As applications, normal mode analysis (Section 2.5) and normal mode sampling (NMS, Section 2.6) in internal coordinates and the subsequent transformation of states to laboratory frame are described. In Section 2.7, two methods of RD trajectory integration are presented and compared. Section 2.8 is devoted to the inverse problem, where first the classical state given in laboratory frame is transformed to the internal coordinate system, and the normal coordinate displacements and momenta are calculated, from which the normal mode quantum numbers are determined. The equations presented in Section 2 (apart from Section 2.4) hold not only for reduced-dimensional models but are also applicable in full dimensionality and can also serve as a basis in the derivation of RD quantum Hamiltonians. In Section 3, as a proof of principle, the method is applied to a hierarchy of three RD models of the methane molecule CZ3Y, in each of which the CZ3 group is constrained to maintain C3v symmetry. A complete reaction dynamics study based on this theory has been presented in ref. 31.
2. Theory
2.1 Frames and coordinate systems
Derivation of the classical vibrational Hamiltonian in internal coordinates starts from the full Lagrangian expressed in Cartesian coordinates in a space-fixed (a.k.a. laboratory) frame: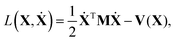 | (1) |
For the description of molecular vibrations, internal coordinates such as valence coordinates (bond lengths, bond and torsion angles etc.) are much more meaningful than Cartesians as the forces acting between atoms are inherently intramolecular, i.e., they do not depend on the position and orientation of the molecule. In addition, the force constants defined in terms of valence coordinates can be rationalized using chemical intuition (for example, they are roughly transferable between molecules).32 Furthermore, the use of internal coordinates is advantageous also when approximations to the Hamiltonian (e.g. quadratic- or quartic-order) are applied as they can describe large amplitude curvilinear motion more effectively than Cartesians.
In general, an internal coordinate is such a function of Cartesian coordinates, whose value is invariant under displacement and rotation of the molecule, thus it is necessarily formulated by using scalar (a·b = aTb), and vector (a × b) products of atomic Cartesian coordinate vector differences Ri − Rj. Consequently, functions of internal coordinates are also internal coordinates. It is worth noting that those internal coordinates that are defined in terms of a cross product (e.g., torsion angles), change sign under mirroring the molecule through a plane (they are pseudoscalars).
For the description of the vibrating molecule one needs to define n independent, otherwise arbitrary internal coordinates y(X) = (y1(X),…,yn(X))T in terms of Cartesian coordinates. n is less than or may be equal to f = 3N − 6, the number of internal degrees of freedom. If n equals f then the set of internal coordinates is complete and the model is called full-dimensional. In reduced-dimensional models the set of irredundant internal coordinates is incomplete (n < f) and the remaining f − n internal degrees of freedom are constrained by fixing f − n functions yn+1(X),…,yf(X) at values yn+1,0,…,yf,0. These constraint functions are generally expressed in terms of the usual valence coordinates. For example, such a function can measure the deviation from some desired symmetry, e.g., it may be the difference of two bond lengths, which is constrained to zero. Variables yn+1(X),…,yf(X) expressing the constraints are formally internal coordinates, because their values should also be independent of the position and the orientation of the molecule. Note that these constrained variables are not included in vector y.
In full-dimensional models of vibrating molecules, the kinetic energy in internal coordinates is given with the help of the Wilson B matrix evaluated at the instantaneous geometry:19
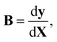 | (2) |
| Gy,vib = BM−1BT | (3) |
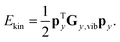 | (4) |
In order to circumvent this problem, we use the inverse transformation, which converts f internal coordinates y to 3N lab Cartesian coordinates X. The inverse function X(y) and its partial derivatives by definition take into account the constraints because they are evaluated under the condition yj(X) = yj,0 for j = n + 1,…,f. However, the internal coordinates do not determine the position and orientation of the molecule in the Cartesian system. To locate and orient the molecule one can utilize an intermediate body-fixed frame and an attached Cartesian coordinate system. In this auxiliary body-fixed frame the Cartesian coordinate 3N-vector and the coordinate 3-vector of atom i will be denoted by x = (x1x, x1y, x1z,…,xNz)T and ri = (xix, xiy, xiz,)T, respectively. The body-fixed coordinates X are connected to the space-fixed frame by an instantaneous translation and rotation, summarized in the function x(X). The definition of the intermediate frame allows us to derive the Lagrangian in internal coordinates via converting the kinetic and potential energy expressions (1) from space-fixed to body-fixed frame and (2) from body-fixed to internal frame using the inverse transformations X(x) and x(y), respectively.
In what follows we proceed on this route in two steps. First we describe the body-fixed frame and its connection to the internal coordinates, x(y) and then its relationship to the space-fixed Cartesian frame, X(x) and show how a classical state given in internal coordinates can be transformed into the space-fixed frame.
There are many possible ways of defining a body-fixed Cartesian frame, and it depends on the system which one is the most favorable. One of the simplest possibilities is that one places the origin either at the center of mass of the molecule or at one of the atoms and selects four non-coplanar atoms within the molecule and orthonormalizes three vectors pointing from one of them to the other three to obtain the basis vectors e (α = x, y, z).
The definition of the body-fixed Cartesian coordinates as a function of internal ones is given by a vector–vector function
| x = x(y), | (5) |
| ẋ = C(y)ẏ. | (6) |
When one knows the x coordinates, the Cartesian coordinates of the atoms in the space-fixed frame can be obtained by considering that the body-fixed and space-fixed Cartesian frames can be brought into overlap by a translation and a rotation, i.e., the ri coordinate vectors need to be rotated by matrix Oframe and shifted by vector Rframe to get the space-fixed coordinates Ri:
| Ri = Rframe + Oframeri. | (7) |
| Ṙi = Ṙframe + Ȯframeri + Oframeṙi, | (8) |
| Ṙi = Ṙframe + (ωframe × Oframe)ri + Oframeṙi. | (9) |
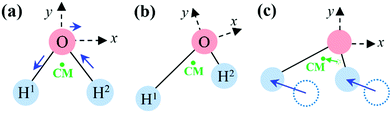
Unless special care is taken, the body-fixed frame does not move together with the molecule: its instantaneous linear (Ṙframe) and angular velocities (ωframe) differ from those of the molecule in the space-fixed frame. For example, when the body-fixed frame for a vibrating water molecule (H2O) is selected to be centered at the O atom with the x-axis parallel to H1H2, then the linear velocity of the origin of the frame is not identical to that of the center of mass, and the antisymmetric OH stretch vibration generates angular motion of the molecule (see Fig. 1).
Obviously, the physically correct description of motion requires both the displacements of the atoms of the molecule in the body-fixed frame and translation + rotation of the body-fixed frame in the lab frame. Consequently, the transformation of internal coordinates and momenta to body-fixed frames according to eqn (5) and (6) usually generates unphysical (often referred to as spurious35) translation and rotation.
When the focus is on the vibrational motion of a molecule, however, the general procedure is that the motion of the body-fixed frame is disregarded and extra steps are made to eliminate the spurious rotation and translation which would falsify the effective masses assigned to internal coordinates. In the t-vector formalism the cancellation of spurious rotation is achieved by the introduction of rotational coordinates when vibrational energy levels are calculated.1,2
In classical mechanics, when a vibrational state is generated by normal mode sampling, the molecule can artificially be cleared of these unwanted velocities.36 In general, it is desirable to avoid the appearance of the unphysical translational and rotational terms, a novel way of which is proposed in the following sections.
2.2 Vibrational Lagrangian in body-fixed Cartesian coordinates
To derive the pure vibrational Lagrangian Lx,vib(x,ẋ) in body-fixed Cartesian coordinates, first the Lagrangian Lx(x,ẋ) for the non-translating and non-rotating body-fixed frame is obtained. To achieve this, one substitutes eqn (7) and (9) into eqn (1) and eliminates the rotational and translational motion of the body-fixed frame by setting Ṙframe = 0 and ωframe = 0. Exploiting that matrix M is diagonal and matrix Oframe is unitary, the kinetic energy function in the new coordinates can be transformed into the same form in body-fixed Cartesian coordinates as it was in the lab Cartesian frame, in accordance with the expectations. The form of the potential energy function will also remain the same because it is a function of internal coordinates only, which are defined with dot and cross products (brief common notation: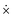 ), that are also left unchanged by Oframe.
), that are also left unchanged by Oframe.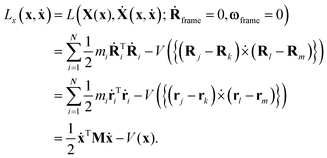 | (10) |
We would like to obtain the pure vibrational Lagrangian. For this we need to decompose the kinetic energy into separate vibrational as well as translational and rotational parts. If one introduces mass-scaled coordinates ![[x with combining tilde]](https://www.rsc.org/images/entities/b_char_0078_0303.gif) = M1/2x, the quadratic form of the kinetic energy expressed in the body-fixed Cartesian frame (Tx) reduces to the square of the mass-scaled velocity vector
= M1/2x, the quadratic form of the kinetic energy expressed in the body-fixed Cartesian frame (Tx) reduces to the square of the mass-scaled velocity vector 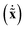 . This form is advantageous, because it allows one to decompose the instantaneous mass-scaled velocity vector into orthogonal translational, rotational and vibrational parts (we show later how). Once these components,
. This form is advantageous, because it allows one to decompose the instantaneous mass-scaled velocity vector into orthogonal translational, rotational and vibrational parts (we show later how). Once these components, 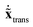 ,
, 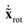 and
and 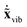 are available, the kinetic energy can also be broken down into the corresponding Ttrans, Trot and Tvib terms:
are available, the kinetic energy can also be broken down into the corresponding Ttrans, Trot and Tvib terms:
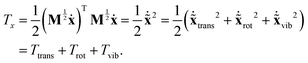 | (11) |
Consequently, the vibrational part can be obtained by eliminating the components of the mass-scaled velocity that correspond to translation and rotation, i.e., projecting the velocities onto the complementary and orthogonal, instantaneous (geometry-dependent) vibrational subspace. If the 3N × 3N matrix that performs the desired projection in the space of mass-scaled velocities is denoted by Pvib(x), the pure vibrational Lagrangian can be formally written as:
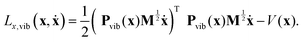 | (12) |
| Pvib(x) = E − Ptrans − Prot(x), | (13) |
The translational subspace of mass-scaled displacements and velocities is spanned by the three 3N-component translational basis vectors utrans,α (α = x, y, z):
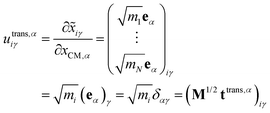 | (14) |
The rotational subspace is spanned by the three 3N-component rotational basis vectors urot,α(x), which describe the relative magnitude of the mass-scaled displacements of atoms due to an infinitesimal rotation of the molecule around the α principal axis (PA) of the instantaneous moment of inertia tensor (α = 1, 2, 3, but not x, y, z). Rotational basis vectors can be calculated from the orthonormal unit vectors of principal axes ePAα (given in the body-fixed frame) and the instantaneous position vectors of atoms ρi := ri − rCM (i = 1,…,N) relative to the center of mass of the molecule, rCM:
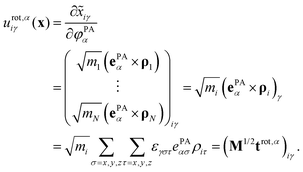 | (15) |
The instantaneous vibrational subspace, which is orthogonal to the translational and rotational subspaces, also depends on the geometry, thus it will span only infinitesimal mass-scaled displacements during the vibration of the molecule. When the shape and the orientation of the molecule do not change during its motion, for example, during the symmetric stretch vibration of CH4 or during the translation of any molecule, the rotational and vibrational subspaces will not change either. A possible orthonormal basis (uvib,i0(xe), i = 1,…,f) of the vibrational subspace at equilibrium geometry (xe) is formed by the vibrational normal mode eigenvectors (see Fig. 2f), which are obtained from harmonic vibrational analysis done in Cartesian frame at xe and are mass-scaled by definition. The orthonormal basis vectors of the translational, rotational and vibrational subspaces of a homonuclear diatomic molecule are summarized in Fig. 2. The orthogonal projection matrices Ptrans and Prot(x) can be defined as dyadic products 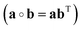 of the relevant basis vectors:
of the relevant basis vectors:
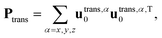 | (16) |
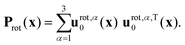 | (17) |
| Mvib(x) = M1/2Pvib(x)M1/2, | (18) |
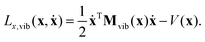 | (19) |
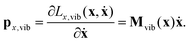 | (20) |
While the velocity vector ẋ may describe translation and rotation in addition to vibration of the molecule in the body-fixed frame, the momentum vector px,vib describes only vibrations, because it is obtained by the singular mass matrix Mvib(x). Thus, the Euler–Lagrange equations of motion cannot describe translation and rotation within the body-fixed frame.
We note that the present derivations are similar to the projection method proposed by Miller et al.37 and Szalay used projections for the approximate decomposition of the kinetic energy in the Eckart frame.38 The difference is that we apply the exact decomposition of the instantaneous kinetic energy.
2.3 Vibrational Hamiltonian in internal coordinates
The vibrational Lagrangian in internal coordinates y and velocities ẏ can be obtained from eqn (19) using the transformations in eqn (5) and (6):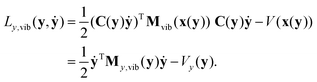 | (21) |
| My,vib(y) = CT(y)M1/2Pvib(x(y))M1/2C(y). | (22) |
At this point, it becomes obvious that by projecting onto the vibrational subspace, we cancel the spurious translation and rotation in the body-fixed frame and the masses corresponding to them will not contaminate the mass matrix assigned to the internal coordinates, which would unphysically increase the matrix elements. Without the projection, for example, harmonic vibrational analysis would give incorrect, reduced frequencies for some of the normal modes.
Eqn (22) applies as it is regardless whether n = f or n < f. Its form implies that in reduced-dimensional models the reduced-dimensional My,vib(y) matrix can also be obtained from the full-dimensional My,vib by simply deleting the rows and columns corresponding to the constrained internal coordinates.
Momenta canonically conjugate to the internal coordinates are obtained as:
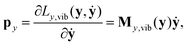 | (23) |
| ẏ = My,vib−1(y)py = Gy,vib(y)py. | (24) |
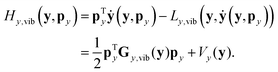 | (25) |
2.4 Connection with the t-vector and the s-vector formalisms
In the previous two sections we derived the vibrational kinetic energy in internal coordinates by introducing the body-fixed frame x and using the inverses of the arbitrarily defined x(X) and y(x) transformations. In this section we show the relationship of our method to those that are generally used for this purpose in the literature, one those based on the X → y transformation1,33,39 (s-vector formalism) as well as on the y → x transformation1,40 (t-vector formalism).The s-vector formalism provides the exact vibrational Hamiltonian for the full-dimensional vibrational problem. To derive the reduced-dimensional kinetic energy and the mass matrices using the X → y transformation, it is necessary to extend the set of variables to a full set of internal variables and first construct the full-dimensional Gy,vib (see eqn (3)). Then one can either calculate the full-dimensional My,vib by inversion, then delete rows and columns and invert again, or directly correct the block of Gy,vib corresponding to the kept variables (ref. 19, Appendix IX) to account for the effect of the constrained ones.
The t-vector formalism requires the definition of a body-fixed frame (e.g., Eckart frame41), which is rarely the absolute co-rotating frame. To compensate for the arising spurious rotation during the change of internal coordinates of the molecule, rotational coordinates need to be introduced and a rovibrational Hamiltonian has to be constructed to make possible the exact description of the vibrational problem. The reduced-dimensional Hamiltonian is directly obtained by using only those vibrational t-vectors which belong to non-constrained internal variables.
The method presented in this work is analogous to the t-vector formalism also in the sense that both are based on the dx/dy derivatives and allow the direct construction of a reduced-dimensional Hamiltonian. However, instead of introducing rotational variables, our method exploits the orthogonality of the mass-scaled translational and (instantaneous) rotational basis vectors (3N-component) to vibrational ones so that rotation and translation are exactly removed. This approach provides a pure vibrational kinetic energy expression equivalent with the one provided with the s-vector formalism.
It can be shown that the inverse mass matrix Gy,vib in the s-vector formalism (eqn (3)) is the inverse of the My,vib mass matrix in eqn (22) and that this does not hold for the reduced-dimensional case as the pure-vibrational infinitesimal mass-scaled Cartesian displacement vectors corresponding to the various internal coordinates are not orthogonal to each other in general. This also implies that the s-vector formalism in full internal dimensionality is in fact a reduced-dimensional approximation, because it considers only vibrations and translational and rotational coordinates are simply omitted. This raises the question how it can be exact for vibrations. The reason for this is the inherent orthogonality of vibrations to rotations and translations in mass-scaled infinitesimal displacement space.
2.5 Normal mode analysis in internal coordinates
During normal mode analysis the vibration of the molecule is approximately decomposed into independent harmonic oscillators using the harmonic approximation to the kinetic and potential energy expressions. The harmonic approximation to the Lagrangian in internal coordinates in the neighborhood of a stationary point y0 can be obtained by replacing the My,vib(y) matrix function with its value at y0, My,vib,0 = My,vib(y0), approximating the potential energy to second order around y0, and setting its zero level to that at geometry y0: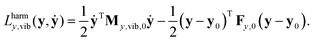 | (26) |
From here on one can follow the standard procedure of normal mode analysis. After introducing mass-scaled vectors of deformation ỹ = My,vib,01/2(y − y0) and velocity 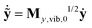 and the
and the ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) y,0 = Gy,vib,01/2Fy,0Gy,vib,01/2 mass-scaled force constant matrix (where Gy,vib,0 = My,vib,0−1) one solves its
y,0 = Gy,vib,01/2Fy,0Gy,vib,01/2 mass-scaled force constant matrix (where Gy,vib,0 = My,vib,0−1) one solves its ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) y,0U = UΛ eigenproblem. Matrix
y,0U = UΛ eigenproblem. Matrix ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) y,0 is symmetric, thus all n eigenvalues λi (in matrix Λ = diag(λ1,…,λn)) are real and the eigenvectors (i.e. columns of U) can be chosen to be orthonormal. If y0 is a potential minimum, all eigenvalues are positive, whereas for a kth-order saddle point k of them are negative. The vector of normal-mode deformation coordinates Q = (Q1,…,Qn)T and the canonically conjugate momentum vector P = (P1,…,Pn)T (in fact, the normal-mode velocity vector
y,0 is symmetric, thus all n eigenvalues λi (in matrix Λ = diag(λ1,…,λn)) are real and the eigenvectors (i.e. columns of U) can be chosen to be orthonormal. If y0 is a potential minimum, all eigenvalues are positive, whereas for a kth-order saddle point k of them are negative. The vector of normal-mode deformation coordinates Q = (Q1,…,Qn)T and the canonically conjugate momentum vector P = (P1,…,Pn)T (in fact, the normal-mode velocity vector ![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) ) are defined as:
) are defined as:
| Q = UTỹ = UTMy,vib,01/2(y − y0), | (27) |
P = ![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) = UTỹ = UTMy,vib,01/2ẏ. = UTỹ = UTMy,vib,01/2ẏ. | (28) |
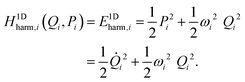 | (29) |
2.6 Normal mode sampling
The purpose of normal mode sampling is the generation of a set of classical states corresponding to a preselected vibrational state of a reactant molecule that will serve as initial conditions for collision or intramolecular trajectories. In QCT calculations, the initial states of molecules are usually generated by assuming that vibration and rotation are separable and the vibrations are well described by the normal mode approximation. The procedure for normal mode sampling is well known for full-dimensional models, but without the proper RD normal mode analysis, it cannot be used in reduced dimensionality. In normal mode sampling it is assumed that the vibrating molecule can be well approximated as a set of independent normal oscillators with n distinct quantum numbers v1,…,vn (n constants of motion). In quasiclassical quantization, normal coordinate and momentum amplitudes (Qi,max, Pi,max =![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) i,max) of each normal mode oscillator are set so that the energy of the oscillator (E1Dharm,i) matches that of the corresponding quantum harmonic oscillator in a given vi quantum state:
i,max) of each normal mode oscillator are set so that the energy of the oscillator (E1Dharm,i) matches that of the corresponding quantum harmonic oscillator in a given vi quantum state: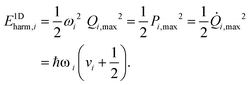 | (30) |
Qi = Qi,max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi,0, φi,0, | (31) |
Pi = ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) i = − i = −![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) i,max i,max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi,0. φi,0. | (32) |
| y = y0 + Gy,vib,01/2UQ, | (33) |
ẏ = Gy,vib,01/2UP = Gy,vib,01/2U![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) . . | (34) |
When the trajectory integration is to be performed in Cartesian coordinates, the state (y,ẏ) needs to be transformed to the body-fixed Cartesian frame and one should ensure that the unphysical translation and rotation generated during transformations in eqn (5) and (6) are removed. To obtain the pure vibrational classical state (x,px,vib), the body-fixed Cartesian coordinates x are calculated from y using eqn (5); the corresponding Cartesian momenta describing vibration only are found by transforming ẏ to ẋ with matrix C(y) and finally to px,vib with matrix Mvib(x) using eqn (6) and (20), respectively:
| px,vib = Mvib(x)ẋ = Mvib(x(y))C(y)ẏ. | (35) |
The ensemble of classical states (x,px,vib) in Cartesian coordinates, which corresponds to the pre-selected vibrational quantum state of the reduced-dimensional model of the reactant molecule is generated by carrying out the sampling procedure many times with different random phases in eqn (31) and (32). It should be noted that the ensemble obtained this way is not monoenergetic. In QCT calculations the nonrotating molecules are randomly oriented before collision. If a rovibrational state is to be generated, then the molecule's angular momentum is also set to that of the desired quantum state. The obtained classical states are in laboratory Cartesian frame and thereby they can be used in the definition of initial conditions of the molecule (X,PX), for QCT calculations.
The standard method to prepare monoenergetic ro-vibrating ensembles by iterative rescaling of deformations and momenta and angular momentum vector adjustment after normal mode sampling has been proposed by Hase and coworkers.42 That method can be generalized to reduced-dimensional models. What remains the same is that the scaling factor is determined in the lab frame. The important difference is that in the full-dimensional model the scaling factor can be applied to scale the lab-frame deformations and momenta. In RD models the rescaling step needs to be performed in internal coordinates, because otherwise it would violate the constraints. It should be noted that the ensembles generated this way are not stationary when allowed to evolve on the real, anharmonic PES.21 Monoenergetic, stationary and accurately quantized ensembles of classical states representing a rovibrational quantum state can be generated by applying the adiabatic principle of classical mechanics. A generalized version of the adiabatic switching method, which accurately includes anharmonicity and coupling of vibrations, has recently been shown to perform well for polyatomic molecules.43 The method has also been extended to generate ensembles corresponding to rovibrational quantum states.
2.7 Dynamics in reduced dimensionality
In reduced-dimensional classical trajectory calculations the equations of motion for the intramolecular motion of molecules have to guarantee the fulfillment of the constraints prescribed by the model. In the following, we discuss two choices: the application of equations of motion in internal coordinates and the integration of the equations of motion in lab Cartesian frame, supplemented by constraint forces. Integration in internal coordinates is more appropriate for the description of a vibrating molecule, whereas the equations presented for integration in 3N Cartesians are equally applicable both to pure bound motion and to scattering problems.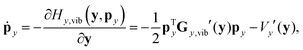 | (36) |
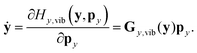 | (37) |
| gi(X) := yn+i(X) − yn+i,0 = 0 i = 1,…,f − n. | (38) |
| ġi(X,Ẋ) = ∇TgiẊ = ∇TgiM−1PX = 0 i = 1,…,f − n, | (39) |
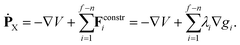 | (40) |
In the alternative method, integration of the equations of motion in Cartesian coordinates under the control of constraints, at least 6 more potential gradient components need to be evaluated; in addition, the constraint forces need to be determined. Yet, the application of Cartesian coordinates together with constraints can be overall cheaper than using internal coordinates, especially when analytic first derivatives of the PES, and first and second analytic derivatives of the constraints are available.
An additional aspect is the accuracy to which the constraints prescribed by the reduced-dimensional model are fulfilled. Integrating in internal coordinates automatically satisfies these constraints. On the other hand, when full-dimensional Cartesian coordinates are used, the constraints are enforced numerically, so that their fulfillment (eqn (38) and (39)) depends on the accuracy of the numerical procedure. Accordingly, in long simulations it is desirable to check regularly how well the constraints are met. If any of them is violated significantly, fulfillment of them can be reestablished by minimizing to zero the sum of the properly scaled squares of the left hand sides of eqn (38) and (39).
2.8 Assignment of normal mode quantum numbers to reduced-dimensional classical states
Solution of the inverse problem, determination of normal mode quantum numbers corresponding to a reduced-dimensional classical state of the molecule is needed when product-state resolved properties are calculated for bimolecular reactions or when the classical evolution of vibrationally excited states of molecules is of interest. Depending on which of the two sets of Hamiltonian equations of motion (Section 2.7) were used for trajectory integration, the classical state of the system is provided either in nonredundant internal coordinates and momenta (y,py) or in space-fixed Cartesian coordinates and momenta (X,PX) fulfilling constraints in eqn (38) and (39).In the former case, since the normal mode analysis of the reduced-dimensional model is done in internal coordinates (see Section 2.5), the state expressed as (y,ẏ = Gy,vib(y)py) can be directly used for quantum number assignment as described below. However, when the state is given in Cartesians, X and PX need to be converted to internal coordinates and velocities. Coordinates y can be computed directly from the X coordinates, which fulfill the f − n constraints given in eqn (38), using the definition of the internal coordinates y(X). Velocities of internal coordinates can be obtained by either numerical derivation along the trajectory or analytical differentiation utilizing the reduced-dimensional variant of Wilson's B matrix (see eqn (2)) and the Cartesian velocities Ẋ = M−1PX:
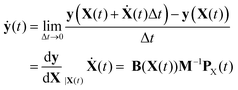 | (41) |
Once the state is given as (y,ẏ), the normal mode coordinates and momenta can be calculated by inverting eqn (33) and (34):
| Q = UTMy,vib,01/2(y − y0), | (42) |
P = ![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) = UTMy,vib,01/2ẏ. = UTMy,vib,01/2ẏ. | (43) |
The E1Dharm,i mode energies can be calculated from the instantaneous normal coordinates and momenta viaeqn (29). The quantum numbers vi are obtained from the energy corresponding to each vibrational mode using the inverse of the harmonic oscillator quantization rule (eqn (30)).
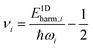 | (44) |
3. Results
3.1 Three reduced-dimensional models of methane
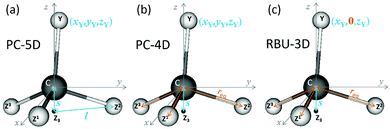
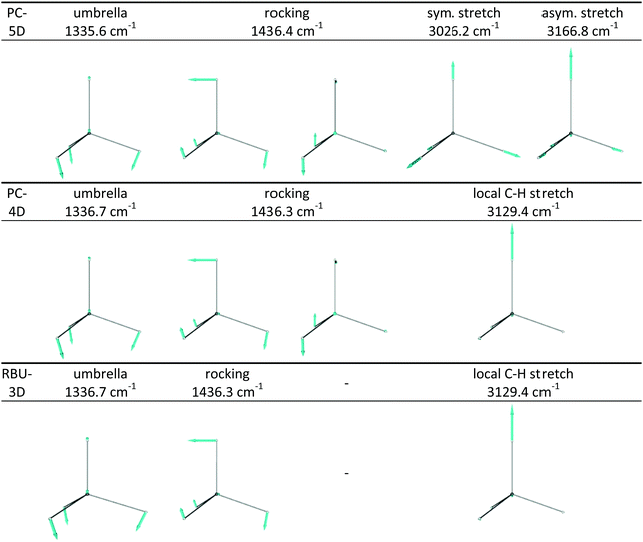
In this section we apply the methods described above to normal mode analysis and sampling in various reduced-dimensional models of methane used in ref. 31 to study RD QCT reaction dynamics calculations of the reaction, which is the most complicated type of reaction for which exact RD quantum mechanical scattering calculations are available.13,46,47 The RD model with the fewest restrictions is the one proposed by Palma and Clary (in the following, PC):9,10 the only constraint is that the CZ3 group keeps C3v symmetry. The model and a series of its versions with additional constraints have been used in numerous quantum scattering simulations. In order to assess the performance of the RD models, Vikár et al.31 compared the results of (quasi)classical trajectory simulations obtained with the Palma–Clary and the full-dimensional models of the CH4 + H → CH3 + H2 reaction with various CH4 isotopologs. We just mention in passing that the PC model was found to give good results in many cases, but its performance proved to depend on the quality of the potential energy surface and the mass combination.31Starting from the PC model, one can design a hierarchy of reduced-dimensional models for methane, in each of which the geometry of the CZ3 moiety is constrained to maintain C3v point group symmetry and by freezing additional types of motion, its internal degrees of freedom are reduced from f = 9 to 5, 4 or 3. Since the three Z atoms are treated as equivalent, such models are suitable for the description of methane isotopologs CHnD4−n with n = 0, 1, 3, 4 but not for CH2D2. In Fig. 3 the models with their reduced sets of internal variables and the attached body-fixed Cartesian frame are shown.
The latter was defined for all models in the same way: the origin was placed at the carbon atom and the axes were determined by the constrained CZ3 moiety: z axis is along the C3v axis, x axis within the YCZ1 plane, forming an acute angle with the CZ1 vector, and the y axis is chosen to ensure that the coordinate system is right-handed.
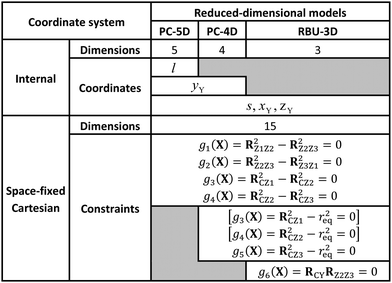
In the “full” Palma–Clary model9 (Fig. 3a) the only constraint is that the CZ3 group is restricted to C3v symmetry, resulting in 5 degrees of freedom for CZ3Y; we abbreviate this model as PC-5D. In the 4D model (called PC-4D, Fig. 3b) considered here, the additional constraint is that the C–Z bond length is frozen at the equilibrium value (req) in CZ3Y as in a frequently applied restricted variant of the Palma–Clary model.9,11,16 In the 3D model (Fig. 3c) we study, the motion of the Y atom is also constrained to one of the symmetry planes (for example in this case to the y plane) of the CZ3 group. This is identical to the three-dimensional methane model in the rotating bond umbrella (RBU) method14,48,49 and will be referred to as RBU-3D. The coordinates as well as the constraint equations used in the internal coordinate and Cartesian representations of the models are shown in Table 1. The common in the applied constraints is that all are defined by sums of dot products, which are very practical because their first and second derivatives have simple analytical forms as shown in the ESI.†
In the following we report on normal mode analysis and the time evolution of ensembles of classical states of methane isotopologs CHnD4−n (n = 0, 1, 3, 4) generated by RD NMS using the three models, performed on the ZBB3 PES.50 At the Td equilibrium geometry the C–H bond length is 2.0579 a0.
3.2 Reduced-dimensional normal mode analysis for methane isotopologs
The frequencies and the nature of normal modes obtained from harmonic vibrational analysis using the procedure described in Section 2.5 are shown in Table 2; the corresponding displacement vectors can be seen in Fig. 4. Vibrations of full-dimensional CH4 and CD4 are characterized by four frequencies, corresponding to one nondegenerate fully symmetric stretch mode (A1 irreducible representation), a pair of doubly degenerate deformation (E) modes, a triply degenerate stretch (T2) and a triply degenerate deformation (T2). Symmetry reduction from Td to C3v by distinguishing one of the ligand atoms in CZ4 from the other three, but not changing its mass and the forces it feels, decomposes each of the T2 modes into a totally symmetric A1 and a doubly degenerate E symmetry mode (according to T2 = A1 ⊕ E) while leaves their frequencies unchanged. The arising A1 stretching mode will be an antisymmetric combination of the C–Y and the symmetric C–Z3 stretching modes, while the new A1 deformation will be the umbrella mode, which is the symmetric deformational mode of the CZ3 moiety. The original totally symmetric A1 stretching mode will preserve its character and frequency.| Isotopolog, sym. group | Irrep![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) degeneracy degeneracy |
Type | Harmonic frequency/cm−1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FD | 5D | 4D | 3D | FD | 5D | 4D | 3D | FD | 5D | 4D | 3D | |
| H3CH | T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | Deg. def. | Umbrella | Umbrella | Umbrella | 1335.6 | 1335.6 | 1336.7 | 1336.7 |
FD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Td Td |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2 | 1 | Deg. def. | Rocking | Rocking | Rocking | 1547.8 | 1436.4 | 1436.3 | 1436.3 |
RD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | Sym. stre. | Sym. stre. | — | — | 3026.1 | 3026.2 | — | — |
T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | Deg. stre. | Antisym.stre. | CH stre. | CH stre. | 3166.7 | 3166.8 | 3129.4 | 3129.4 | |
| D3CH | A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | CD3 sym. def. | Umbrella | Umbrella | Umbrella | 1018.1 | 1018.1 | 1018.1 | 1018.1 |
FD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | — | — | CD3 deg. def. | — | — | — | 1045.7 | — | — | — |
RD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2 | 1 | CD3 rock. | Rocking | Rocking | Rocking | 1305.7 | 1298.4 | 1298.3 | 1298.3 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | CD3 sym. stre. | CD3 stre. | — | — | 2186.5 | 2186.5 | — | — | |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | — | — | CD3 deg. stre. | — | — | — | 2343.2 | — | — | — | |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | CH stre. | CH stre. | CH stre. | CH stre. | 3136.1 | 3136.2 | 3125.9 | 3125.9 | |
| H3CD | E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2 | 1 | CH3 rock. | Rocking | Rocking | Rocking | 1178.3 | 1218.1 | 1218.0 | 1218.0 |
FD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | CH3 sym. def. | Umbrella | Umbrella | Umbrella | 1330.5 | 1330.5 | 1331.8 | 1331.8 |
RD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | — | — | CH3 deg. def. | — | — | — | 1487.9 | — | — | — |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | CD stre. | CD stre. | CD stre. | CD stre. | 2286.7 | 2286.7 | 2290.5 | 2290.5 | |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | CH3 sym. stre. | CH3 stre. | — | — | 3067.6 | 3067.7 | — | — | |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | — | — | CH3 deg. stre. | — | — | — | 3166.4 | — | — | — | |
| D3CD | T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | Deg. def. | Umbrella | Umbrella | Umbrella | 1010.3 | 1010.3 | 1010.4 | 1010.4 |
FD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Td Td |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2 | 1 | Deg. def. | Rocking | Rocking | Rocking | 1094.9 | 1051.8 | 1051.8 | 1051.8 |
RD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3v C3v |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | — | Sym. stre. | Sym. stre. | — | — | 2140.6 | 2140.6 | — | — |
T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1 | Deg. stre. | Antisym.stre. | CD stre. | CD stre. | 2343.1 | 2343.1 | 2286.3 | 2286.3 | |
When symmetry reduction in CZ4 methane isotopologs (i.e. Z = Y, top and bottom rows of Table 2) is caused by constraining the symmetry of the CZ3 group to C3v (leading to the PC-5D model), the fully symmetric stretch mode (involving all four C–Z bonds) remains again intact, whereas the A1 modes resulting from symmetry reduction (the antisymmetric stretch and the umbrella bend) together with their frequencies remain essentially unchanged while the asymmetric CZ3 stretch modes of E symmetry disappear. The original and the resulting doubly-degenerate E-symmetry deformational modes will mix to conform to the constrained C3v symmetry and result in a doubly-degenerate E-symmetry rocking mode with an intermediate frequency. The two combinations violating the C3v symmetry disappear. In CZ3Y methane isotopologs (i.e. Z ≠ Y), whose symmetry is reduced to C3v due to the difference of isotopes Z and Y, the decomposition of the triply-degenerate modes is accompanied by frequency changes and mode mixing. The resulting antisymmetric combination of the local C–Y and symmetric C–Z3 stretching modes of A1 symmetry will mix with the totally symmetric stretching mode (present in CZ4) and gives essentially local A1-symmetry C–Z3 and C–Y stretching modes with significantly different frequencies. Furthermore, a pair of doubly-degenerate rocking modes appears due to mode mixing. When the symmetry of the CZ3 group is constrained to C3v in mixed methane isotopologs according to the PC-5D model, the doubly-degenerate bending and stretching modes which violate the C3v symmetry disappear. The A1-symmetry modes (umbrella and two local stretches) remain essentially intact, while the frequency of the doubly-degenerate rocking mode changes slightly.
Further reduction of dimensionality to four by freezing the C–Z bond lengths of the CZ3 moiety (in the PC-4D model) in CZ4 isotopologs causes the mixing of the symmetric and antisymmetric stretches and results in a local C–Z stretch, whereas in CZ3Y isotopologs removes the C–Z3 stretch, and the frequency of the remaining modes changes slightly. Confining the motion of the Y atom into one of the symmetry planes of CZ3 (in the RBU-3D model) freezes one of the rocking vibrations, without causing any additional frequency change.
3.3 Evolution of reduced dimensional ensembles of classical states of methane isotopologs
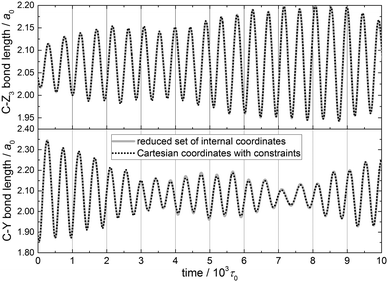
The reduced-dimensional vibrational Hamiltonian in internal coordinates and the equations of motion derived in Section 2.7 allow us to monitor the time evolution of two parameters that proved to be important in the QCT simulations of the abstraction reaction between methane isotopologs (CZ3Y) and H atoms,21,31 namely, the C–Z and C–Y bond lengths.A single classical state corresponding to the ground state of the PC-5D model of the CH4 molecule (Z, Y = H) has been prepared by normal mode sampling (Section 2.6) and propagated in time. Fig. 5 shows the two bond lengths as a function of time up to 104τ0 (1τ0 = atomic time unit ≈0.0242 fs). The equations of motion for the PC-5D model have been integrated in two sets of coordinates, internal (continuous lines) and space-fixed Cartesian (dotted lines, with the constraints being taken into account with the Lagrange multipliers method), yielding identical trajectories (see Fig. 5). One can see that the evolution of the two bond lengths is coupled. At the beginning of this specific trajectory, the amplitude of the bond length oscillation decreases for the C–Y bond and increases for the C–Z bond, indicating energy transfer between them. Later, the coherence of the energy exchange between the two oscillations is reduced, which indicates that other modes are also coupled to these key reaction dynamical parameters.
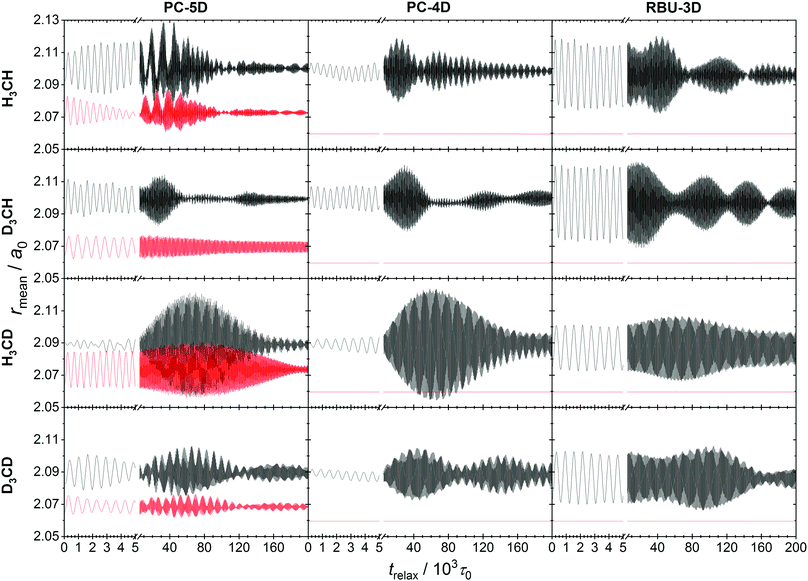
More important is the behavior of an ensemble of classical states that represents a quantum state. Ensembles of 104 classical states corresponding to the ground state of CH4 molecules were prepared by normal mode sampling as described in Section 2.6 for all four methane isotopologs and all three models. No deformation and momentum scaling was applied to make the ensembles monoenergetic. The evolution of the ensemble was simulated using the space-fixed Cartesian frame description with constraints, which were always fulfilled precisely, and the obtained ensemble average C–Y and C–Z bond lengths and normal mode quantum numbers are plotted in Fig. 6 and 7. The oscillations of the average bond length plots indicate the same kind of coherence in the evolution of the members of the ensemble as was reported in ref. 21 for the FD evolution of methane isotopologs. The phenomenon is caused in both cases by the failure of the normal mode approximation. In QCT simulations of the CH4 + H → CH3 + H2 reaction and its isotopologs,21 the temporal oscillation of the average C–Y bond length of the ensemble of methane molecules prepared with normal mode sampling was shown to give rise to “spatial” oscillation of the calculated reaction probabilities and cross sections as a function of initial separation of the reactants. The conversion of the temporal oscillation to spatial can be understood by considering that the ensemble evolves during the initial “free” flight of the reactants as it adapts to the anharmonic PES.
The relaxation dynamics of the methane ensembles generated by normal-mode sampling on the anharmonic PES provides information on the couplings and energy flow between vibrational modes. The coarse-grained pattern of the evolution of the two mean bond lengths in the CZ4 isotopologs indicate initially periodic energy exchange between the two stretching modes of the PC-5D model. The other two models also show beating in their ensemble average bond length oscillation, which suggest significant energy exchange with the bending modes. Eventually, the amplitude of the oscillations decreases as the ensemble adapts to the anharmonic PES and the phases of stretching vibration of the individual trajectories decohere.
The lower the dimensionality of the model, the slower is the decay of coherence in the stretching oscillations, which is consistent with the lower-dimensional, simpler structure of the phase space and suggests that the chaotic character of the vibration is reduced. This is also reflected in the coarse-grained structure of oscillations, which shows regularity and is symmetric with respect to a mean value in the case of all investigated models and isotopologs, except for the evolution of CH4 and CD4 in the PC-5D model.
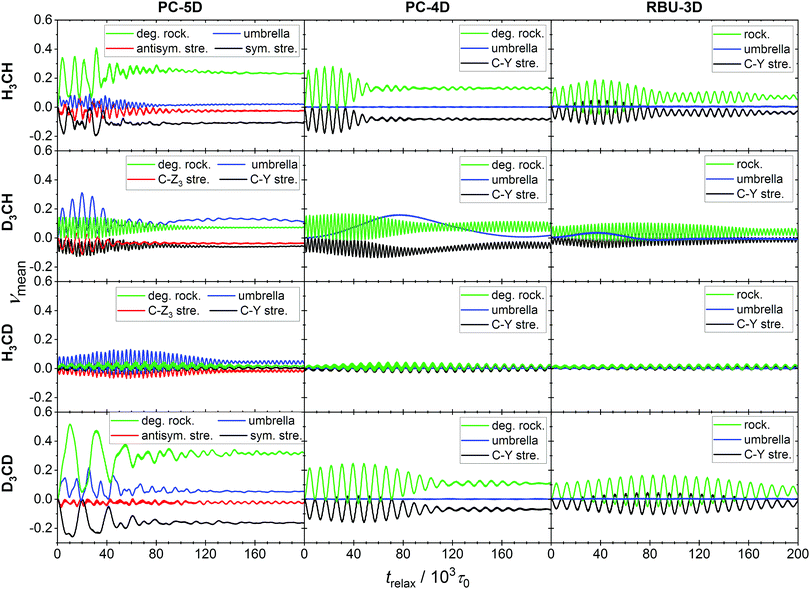
More informative on the intramolecular energy transfer is the evolution of the ensemble average normal mode quantum numbers (see Fig. 7), which also represents a stringent test of the applicability of our method to assigning a vibrational quantum state to the molecule in motion. For the doubly degenerate rocking mode present in the PC-5D and PC-4D models, the sum of the two ensemble averaged quantum numbers was taken, as the degenerate modes are kinematically strongly coupled, thus their individual values are not meaningful. Similarly to the full-dimensional case,21 long-term oscillations can be observed and the patterns hint at significant mode-to-mode energy transfer. The initial value of each quantum number is zero at the NMS preparation, which immediately changes when the atoms are allowed to move.
The pattern of oscillation is in agreement with that of the C–Z and C–Y bond lengths. In the PC-5D model, the CZ4 isotopologs show strong coupling between the symmetric stretch and the rocking modes. In the CZ3Y isotopologs stronger coupling emerges between the “internal” modes of the CZ3 group, i.e. the bond stretching and the umbrella mode. It is obvious, however, that in all cases every mode participates in the energy exchange. In the PC-4D and RBU-3D models where the stretching of C–Z bonds is frozen, intense energy exchange can be observed between the rocking mode(s) and the C–Y stretch modes for CZ4 isotopologs, which is a consequence of Coriolis coupling. Furthermore, these two models in the case of isotopolog CH3D show a very long-period (80–160 × 103) beating-like energy exchange between the C–Y stretch and the umbrella mode. The quantum numbers obtained with our formalism show the expected pattern, confirming the applicability of the formulas.
4. Conclusions
We have presented a formal derivation of the pure vibrational classical Hamiltonian in a nonredundant, but not necessarily full set of internal coordinates, which allowed the extension of the quasiclassical trajectory method to constrained, reduced-dimensional systems. The formalism allows one to carry out harmonic vibrational analysis in any reduced set of coordinates, and generate classical states corresponding to a given quantum state of the molecule using normal mode sampling (the “direct problem”), to simulate dynamics and to find normal mode quantum numbers when a classical state is given, for example, at the end of a QCT simulation (the “inverse problem”). For the implementation of the method, the only system specific formulae need to be provided are the definition of the internal coordinates of the chosen model and their connection to a suitable body-fixed Cartesian frame. Once these are provided, the method works as a black box, because, instead of deriving analytical formulae, the inverse mass matrix and the kinetic energy expression of the vibrational Hamiltonian is constructed numerically. The formalism is universal in the sense that it can be applied to both full- and reduced-dimensional models and that the internal and body-fixed Cartesian coordinate systems can be selected arbitrarily, so it can take into account any geometric constraint. The applicability of the method has been demonstrated in a previous study addressing the comparison of RD and FD models in classical simulations.31Semiclassical methods, such as adiabatic switching43,51,52 (AS) and semiclassical initial value representation53–55 (SC-IVR), based on classically propagated trajectories can also employ the equations derived here, thus the method can be used for the quantization of rovibrational levels of constrained systems with a better computational scaling than quantum mechanical methods.
Finally, we mention that the RD method can enable one to perform QCT calculations when computational complications arise. One such difficulty is that the high computational cost of electronic structure calculations often does not allow the development of a full-dimensional analytic PES, which is required when long and/or a large number of trajectories need to be simulated in a QCT study. Development of a reduced-dimensional analytic PES combined with the theory presented here can provide a means for the dynamical investigation of such systems. Another computational issue is the undesirable leakage of zero-point energy deposited in each vibrational mode to other modes.
Conflicts of interest
There are no conflicts to declare.Appendix
A. Orthogonality of translational and rotational basis vectors
Translational basis vectors utrans,α(x) defined in eqn (14) are orthogonal to each other as their dot products (i.e.utrans,α,Tutrans,β, where α = x, y, z and β = x, y, z) give the corresponding (αβ) elements of the unit matrix times the total mass (M).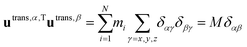 | (A1) |
Rotational basis vectors urot,α(x) (see eqn (15)) are orthogonal to each other as their dot products give the corresponding elements of the moment of inertia tensor (Θαα) defined in the principal axis (PA) frame, which is by definition a diagonal matrix:
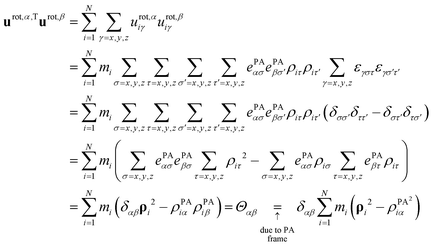 | (A2) |
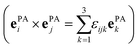 . In the transformations, it was exploited that:
. In the transformations, it was exploited that: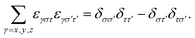 | (A3) |
Rotational basis vectors are orthogonal to translational basis vectors regardless of the definition of vectors ePAα, because their product is a sum of terms that are proportional to the components of the center of mass position vector.
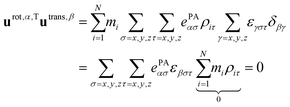 | (A4) |
Acknowledgements
We thank Professors J. M. Bowman for making the potential surface codes available for us. We thank Professor A. G. Császár, Dr V. Szalay and Dr T. Szidarovszky for helpful discussions. This work has been supported by NKFIH, Hungary, (Grant No. K108966 and PD120776 (T. N.)), by the Government of Hungary and the EU via grant VEKOP-2.3.2-16-2017-00013 (G. L.), by COST Action 1401 and by the János Bolyai Research Fellowship (Grant No. BO/00279/16/7 (T.N.)).Notes and references
- E. Mátyus, G. Czakó and A. G. Császár, J. Chem. Phys., 2009, 130, 134112 CrossRef PubMed.
- C. Fábri, E. Mátyus and A. G. Császár, J. Chem. Phys., 2011, 134, 74105 CrossRef PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces. The Jerusalem Symposia on Quantum Chemistry and Biochemistry., ed. B. Pullman, Springer, Dordrecht, 1981, vol. 14, pp. 331–342 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. M. Bowman and A. F. Wagner, in The Theory of Chemical Reaction Dynamics, ed. D. C. Clary, Springer Netherlands, Dordrecht, 1986, pp. 47–76 Search PubMed.
- Q. Sun, D. L. Yang, N. S. Wang, J. M. Bowman and M. C. Lin, J. Chem. Phys., 1990, 93, 4730–4739 CrossRef CAS.
- D. C. Clary, J. Phys. Chem., 1994, 98, 10678–10688 CrossRef CAS.
- J. Palma and D. C. Clary, J. Chem. Phys., 2000, 112, 1859–1867 CrossRef CAS.
- J. Palma and D. C. Clary, J. Chem. Phys., 2001, 115, 2188–2197 CrossRef CAS.
- M. Yang, D. H. Zhang and S. Y. Lee, J. Chem. Phys., 2002, 117, 9539–9542 CrossRef CAS.
- H.-G. Yu and G. Nyman, Chem. Phys. Lett., 1998, 298, 27–35 CrossRef CAS.
- G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 132, 84103 CrossRef PubMed.
- G. Nyman, in Theory of Chemical Reaction Dynamics, NATO Science Series, ed. A. Laganà and G. Lendvay, Kluwer, Dordrecht, 2004, pp. 253–278 Search PubMed.
- D. H. Zhang, M. Yang, M. A. Collins and S. Lee, in Theory of Chemical Reaction Dynamics, NATO Science Series, ed. A. Laganà and G. Lendvay, Kluwer, Dordrecht, 2004, pp. 279–304 Search PubMed.
- W. Zhang, Y. Zhou, G. Wu, Y. Lu, H. Pan, B. Fu, Q. Shuai, L. Liu, S. Liu, L. Zhang, B. Jiang, D. Dai, S. Lee, Z. Z. Xie, B. J. Braams, J. M. Bowman, M. a. Collins, D. H. Zhang and X. Yang, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12782–12785 CrossRef CAS PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2015, 142, 64309 CrossRef PubMed.
- E. B. Wilson, J. Chem. Phys., 1939, 7, 1047–1052 CrossRef CAS.
- E. B. Wilson, J. J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, New York, 1980 Search PubMed.
- L. M. Raff and D. L. Thompson, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, Florida, 1985, vol III, pp. 1–122 Search PubMed.
- T. Nagy, A. Vikár and G. Lendvay, J. Chem. Phys., 2016, 144, 14104 CrossRef PubMed.
- D. Lu and W. L. Hase, J. Chem. Phys., 1988, 89, 6723 CrossRef CAS.
- J.-J. Klossika and R. Schinke, J. Chem. Phys., 1999, 111, 5882–5896 CrossRef CAS.
- C. L. Stroud and L. M. Raff, J. Chem. Phys., 1980, 72, 5479–5488 CrossRef CAS.
- N. Sathyamurthy and L. M. Raff, J. Chem. Phys., 1980, 72, 3163–3178 CrossRef CAS.
- A. Faure, L. Wiesenfeld, M. Wernli and P. Valiron, J. Chem. Phys., 2005, 123, 104309 CrossRef PubMed.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, J. Chem. Phys., 2002, 117, 4201–4213 CrossRef CAS.
- A. Faure, C. Rist and P. Valiron, Astron. Astrophys., 1999, 348, 972–977 CAS.
- L. B. Harding, S. J. Klippenstein and Y. Georgievskii, Proc. Combust. Inst., 2005, 30, 985–993 CrossRef.
- L. B. Harding, Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2010, 114, 765–777 CrossRef CAS PubMed.
- A. Vikár, T. Nagy and G. Lendvay, J. Phys. Chem. A, 2016, 120, 5083–5093 CrossRef PubMed.
- G. Fogarasi, X. Zhou, P. W. Taylor and P. Pulay, J. Am. Chem. Soc., 1992, 114, 8191–8201 CrossRef CAS.
- S. R. Polo, J. Chem. Phys., 1956, 24, 1133 CrossRef CAS.
- J. K. G. Watson, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- C. S. Sloane and W. L. Hase, J. Chem. Phys., 1977, 66, 1523 CrossRef CAS.
- W. L. Hase, Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd,Chichester, UK, 2002 Search PubMed.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- V. Szalay, J. Chem. Phys., 2014, 140, 234107 CrossRef PubMed.
- P. C. Wilson, E. B. Decius, J. C. Cross, E. B. Wilson, J. C. Decius, P. C. Cross and B. R. Sundheim, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, 1955 Search PubMed.
- G. O. Sørensen, Large Amplitude Motion in Molecules II, Springer-Verlag, Berlin/Heidelberg, 1979, pp. 97–175 Search PubMed.
- C. Eckart, Phys. Rev., 1935, 47, 552–558 CrossRef CAS.
- W. L. Hase, Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2002 Search PubMed.
- T. Nagy and G. Lendvay, J. Phys. Chem. Lett., 2017, 8, 4621–4626 CrossRef CAS PubMed.
- L. Bonnet and J. C. Rayez, Chem. Phys. Lett., 2004, 397, 106–109 CrossRef CAS.
- G. Czakó, J. Phys. Chem. A, 2012, 116, 7467–7473 CrossRef PubMed.
- G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 133, 174124 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2012, 137, 244106 CrossRef PubMed.
- H.-G. Yu and G. Nyman, J. Chem. Phys., 1999, 110, 7233 CrossRef CAS.
- H.-G. Yu and G. Nyman, Chem. Phys. Lett., 1999, 312, 585–590 CrossRef CAS.
- Z. Xie, J. M. Bowman and X. Zhang, J. Chem. Phys., 2006, 125, 133120 CrossRef PubMed.
- R. T. Skodje, F. Borondo and W. P. Reinhardt, J. Chem. Phys., 1985, 82, 4611–4632 CrossRef CAS.
- C. Qu and J. M. Bowman, J. Phys. Chem. A, 2016, 120, 4988–4993 CrossRef CAS PubMed.
- A. L. Kaledin and W. H. Miller, J. Chem. Phys., 2003, 118, 7174 CrossRef CAS.
- A. L. Kaledin and W. H. Miller, J. Chem. Phys., 2003, 119, 3078–3084 CrossRef CAS.
- M. Ceotto, S. Atahan, S. Shim, G. F. Tantardini, A. Aspuru-Guzik, G. E. Scuseria and M. J. Frisch, Phys. Chem. Chem. Phys., 2009, 11, 3861 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Method of Lagrange multipliers for holonomic and scleronomic constraints. An efficient form of constraints allowing simple analytic gradients and Hessians. See DOI: 10.1039/c8cp01600c |
| This journal is © the Owner Societies 2018 |