Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding three-body contributions to coarse-grained force fields†
Christoph
Scherer
 * and
Denis
Andrienko
* and
Denis
Andrienko
 *
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: scherer@mpip-mainz.mpg.de; denis.andrienko@mpip-mainz.mpg.de
First published on 10th August 2018
Abstract
Coarse-graining is a systematic reduction of the number of degrees of freedom used to describe a system of interest. Coarse-graining can be thought of as a projection on the coarse-grained degrees of freedom and is therefore dependent on the number and type of basis functions used to represent the coarse-grained force field. We show that many-body extensions of the coarse-grained force field can result in substantial changes of the two-body interactions, making them much more attractive at short distances. This interplay can be alleviated by first parametrizing the two-body potential and then fitting the additional three-body contribution to the residual forces. The approach is illustrated on liquid water where three-body interactions are essential to reproduce the structural properties, and liquid methanol where two-body interactions are sufficient to reproduce the main structural features of the atomistic system. Furthermore, we demonstrate that the structural and thermodynamic accuracy of the coarse-grained models can be controlled by varying the magnitude of the three-body interactions. Our findings motivate basis set extensions which separate the many-body contributions of different order.
I. Introduction
Coarse-graining (CG) is a systematic way to reduce the number of degrees of freedom describing a specific physical system. By combining coherently moving atoms of a molecule into a single interaction site one can increase the simulation times by ten to hundred times compared to the atomistic simulation. The computational cost is reduced in several ways: First, the coarse-grained system has less degrees of freedom. Second, smoother interaction potentials result in a smaller friction and, hence, faster dynamics. Third, one can use a bigger simulation timestep in the integration algorithm.To coarse-grain a specific system, we need to choose coarse-grained degrees of freedom, relate them to the fine-grained description, identify a merit function which quantifies the difference between the fine- and coarse-grained representations, and optimize the coarse-grained potential energy surface (PES). Consistency between the coarse-grained and the fine-grained models can be defined in terms of consistency of the equilibrium probability densities resulting in unique expressions for the CG masses and interaction potential, i.e. the many-body potential of mean force (PMF).1 Evaluating this potential is as computationally demanding as propagating the fine-grained system and, in practice, it is approximated using a limited set of basis functions chosen to represent the interactions at the CG level of resolution.
Several methods have been developed that approximate the many-body PMF, targeting specific properties of the underlying atomistic system. For example, iterative Boltzmann inversion (IBI)2 and inverse Monte Carlo (IMC)3 schemes target structural pair distribution functions. It can be shown that these methods minimize the relative entropy between the CG and atomistic ensembles.4 An alternative route is to match the forces of the CG system to those of the atomistic description, employing force-matching (FM) or multiscale coarse-graining (MS-CG).1,5,6 This approach corresponds to projecting the many-body mean force, i.e., the negative gradient of the many-body PMF, into the space of force fields defined by the CG basis set. It allows to systematically increase the accuracy of the approximation of the many-body PMF by expanding the basis set. FM and structural coarse-graining can be connected via Yvon–Born–Green theory.7,8
The structural accuracy of the force-matched CG model depends on the CG mapping scheme9 and on the ability of the CG basis set to capture the relevant many-body correlations of the mapped ensemble.8 In some cases, force-matched pair potentials reproduce the atomistic pair correlation functions, as for one-cite models of liquid methanol.10,11 However, for liquids with a strong local orientational order, with water being a prominent example, CG pair potentials fail to fully capture the structural correlations of the underlying atomistic system.12–17 Even when the pair potential is able to reproduce the atomistic pair correlation functions, thermodynamic properties are usually not reproduced correctly, for example the cohesive energy can be significantly underestimated.18 This implies that an extension of the basis set is necessary to describe the many-body correlations more accurately.19–23
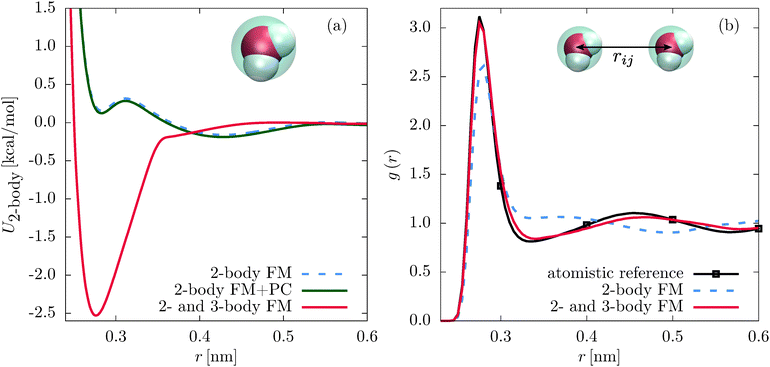
Indeed, coarse-grained models can be improved by including a local density dependent potential24–26 or a short-ranged nonbonded three-body potential,12–14,27–30 such as the Stillinger–Weber31 (SW) potential. These basis set extensions lead to a significant change of the two-body interactions.12,13,24,25 For example, an one-site CG SPC/E water model with the SW potential has a deep attractive well at 2.5 nm, as shown in Fig. 1. In this paper we demonstrate that the change of the pair potential can be tracked back to the non-orthogonality of the three-body and the two-body interactions. In addition, we propose a parametrization scheme which reduces the three-body contribution to the two-body PMF or, in other words, decouples the two- and three-body interaction terms.
II. Methods
A. Atomistic simulations
For atomistic simulations we employ the GROMACS32 package, version 5.1. We use the SPC/E water model33 and the OPLS-AA force field34,35 for methanol. Boxes of 1000 molecules are first equilibrated for 10 ns in the NPT ensemble at T = 300 K and p = 1.0 bar, followed by 10 ns NVT production runs at the average density of the preceding NPT simulations, ρ = 0.998 g cm−3 (water) and ρ = 0.776 g cm−3 (methanol). These values are very close to the experimental densities at normal conditions, ρ = 0.9971 g cm−3 (water)36 and ρ = 0.7872 g cm−3 (methanol).37 To integrate the equations of motion, we use a stochastic dynamics algorithm38 in combination with a Berendsen barostat39 with a time constant of 1 ps, the compressibility parameter of water (4.5 × 10−5 bar−1), and a time step of 1 fs. Electrostatic interactions are treated with a smooth particle mesh Ewald method40 with cubic interpolation, a grid spacing of 0.12 nm and an Ewald accuracy parameter of 10−5. We use a short-range cutoff of 1.2 nm and long-range dispersion corrections for energy and pressure. The OPLS-AA force field is used without constraints.B. Coarse-graining procedure
We replace one water or methanol molecule with a CG bead positioned at its center of mass,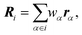 | (1) |
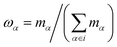 are the weights of each atom of molecule i. The mass of the CG bead is the sum of the atomistic masses: Mi = 18.0154 amu (water) and Mi = 32.0374 amu (methanol).
are the weights of each atom of molecule i. The mass of the CG bead is the sum of the atomistic masses: Mi = 18.0154 amu (water) and Mi = 32.0374 amu (methanol).
To parametrize the FM potentials, the reference force on each CG bead i is calculated as the sum of the atomistic forces,
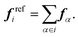 | (2) |
The CG representation of the force is then determined by solving:
fCGil(g1,…,gM) = frefil, i = 1…N,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l = 1…L. l = 1…L. | (3) |
Here, g1,…,gM are the coefficients of the CG force field basis functions, N is the number of CG beads, and L is the number of simulation snapshots per block. We use N = 1000 and L = 20. Given that the CG force field basis functions fCGil depend linearly on the parameters g1,…,gM, eqn (3) is a set of N × L overdetermined linear equations (M < N × L) which we solve with a constrained least-squares solver.
All coarse-graining algorithms are implemented into the VOTCA-CSG package.18
C. Coarse-grained potentials
Nonbonded two-body potentials are represented by cubic splines which depend linearly on the coefficients g1,…,gM. A set of K grid points leads to M = 2K spline coefficients where K of the coefficients are fixed due to constraints guaranteeing the continuity of the first derivatives.The SW three-body potential,
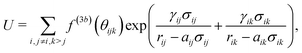 | (4) |
The FM parametrization is implemented in the VOTCA-CSG package18 using a cubic spline representation of f(3b)(θ) with K grid points and a linear dependence on the M = 2K spline coefficients. Treating the two exponential terms, 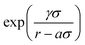 , as prefactors yields a linear set of equations which can be solved by a constrained least-squares solver as in the case of the pair forces. To do so, the remaining parameters aij, aik, σij, σik, γij, and γik, have to be set beforehand. For one CG bead type, as in our case, the number of parameters reduces to aij = aik = a, σij = σik = σ, and γij = γik = γ. Here, a is the three-body short-range cutoff which we choose in a way that the three-body potential is fully switched on in the first coordination shell. Setting σ = 1, the parameter γ controls the steepness of this switching on. In the limit of γ → 0, the SW potential is instantaneously switched on. For water, we refer to the cutoff radius of ref. 13, namely a = 0.37 nm. In the case of liquid methanol, we choose a = 0.45 nm. We systematically vary γ until the structural fit does not improve anymore. The optimal value, in both cases, is γ = 0.08 nm. This means that USW is fully switched on in the first and switched off within the second coordination shell. For more technical details on the FM implementation we refer to the ESI.†
, as prefactors yields a linear set of equations which can be solved by a constrained least-squares solver as in the case of the pair forces. To do so, the remaining parameters aij, aik, σij, σik, γij, and γik, have to be set beforehand. For one CG bead type, as in our case, the number of parameters reduces to aij = aik = a, σij = σik = σ, and γij = γik = γ. Here, a is the three-body short-range cutoff which we choose in a way that the three-body potential is fully switched on in the first coordination shell. Setting σ = 1, the parameter γ controls the steepness of this switching on. In the limit of γ → 0, the SW potential is instantaneously switched on. For water, we refer to the cutoff radius of ref. 13, namely a = 0.37 nm. In the case of liquid methanol, we choose a = 0.45 nm. We systematically vary γ until the structural fit does not improve anymore. The optimal value, in both cases, is γ = 0.08 nm. This means that USW is fully switched on in the first and switched off within the second coordination shell. For more technical details on the FM implementation we refer to the ESI.†
D. CG simulations
Coarse-grained MD simulations are performed at the atomistic density using the LAMMPS package.41 Two-body CG interactions are treated as linear interpolation tables with a short-range cutoff of 1.2 nm. We extend the LAMMPS implementation of the Stillinger–Weber interaction potential to read in tabulated angular dependent potentials. We employ a time step of 1 fs and a chain of three Nose–Hoover thermostats42,43 with a damping parameter of 200 fs when integrating the equations of motion44 for 10 ns in the NVT ensemble. When simulating in the NPT ensemble, we apply an additional chain of three Nose–Hoover barostats with a damping parameter of 1000 fs.E. Calculation of the pair PMF
To separate the two-body and three-body contributions of the CG interaction potential, we evaluate the pair PMF between two coarse-grained sites: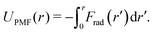 | (5) |
Here, Frad(r) = 〈Fj·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij〉 ≡ 〈−Fi·
ij〉 ≡ 〈−Fi·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij〉 is the projection of the total CG force acting on a CG bead i or j onto the unit distance vector
ij〉 is the projection of the total CG force acting on a CG bead i or j onto the unit distance vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij connecting this pair of beads, averaged over all CG bead pairs with distance r. Note that the total pair UPMF(r) is equivalent to the radial distribution function, since g(r) ∼ exp(−UPMF(r)/kBT). When calculating UPMF(r) for the atomistic simulations, Fi and Fj are evaluated as a weighted sum of all atomistic forces acting on each CG bead i and j, according to eqn (2).
ij connecting this pair of beads, averaged over all CG bead pairs with distance r. Note that the total pair UPMF(r) is equivalent to the radial distribution function, since g(r) ∼ exp(−UPMF(r)/kBT). When calculating UPMF(r) for the atomistic simulations, Fi and Fj are evaluated as a weighted sum of all atomistic forces acting on each CG bead i and j, according to eqn (2).
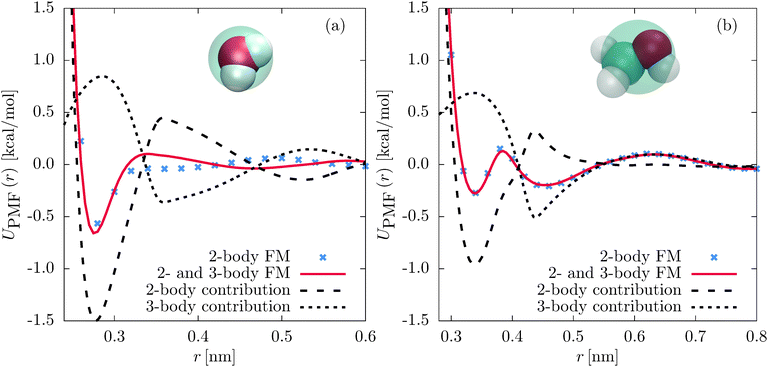
F rad(r) and, thus, UPMF(r) can be evaluated separately for the two-body and three-body interactions by a rerun of the CG trajectory and switching on and off the individual force contributions. That gives the contributions of the two-body and three-body interactions to the total pair PMF, including the effects of correlated forces from the environment. This is comparable to calculating the decomposition of the pair PMF in terms of the MS-CG G-matrix.45
F. Inner product of force field functions
To quantify the degree of correlation between two-body and three-body force field functions, we define an inner product as7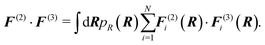 | (6) |
Here, F(ξ)i is the total force on bead i, ξ = 2, 3 corresponds to the two- and three-body contributions, and pR(R) is the CG configuration distribution. We evaluate a normalized inner product of the two-body and three-body contributions to the total force on each CG bead as:
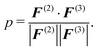 | (7) |
The normalized inner product corresponds to the ensemble average of the inner product of the two-body and three-body contribution on each CG bead and can be converted into an angle:
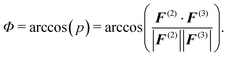 | (8) |
III. Results and discussion
We choose one-site models of liquid water and methanol as test systems where two-body basis functions fail (water) and succeed (methanol) to accurately reproduce the atomistic pair correlation functions. We employ force-matching (FM) to parametrize the tabulated two-body in combination with the three-body Stillinger–Weber (SW) interactions with a flexible angular dependence.A. Structural properties
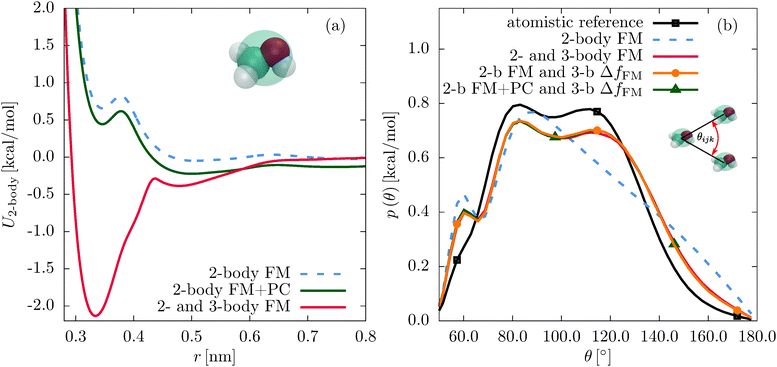
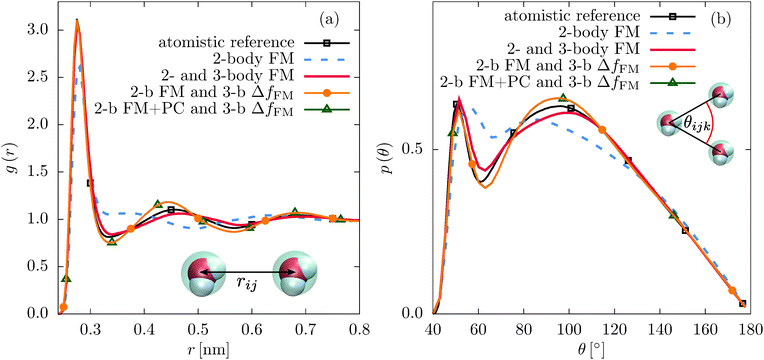
First, we compare the structural correlation functions of the different models. As mentioned above and shown in Fig. 1(b), the CG model of SPC/E water with the three-body SW potential (2- and 3-body FM) reproduces the radial distribution function (RDF) of the atomistic reference better than the model with only pairwise interactions (2-body FM). This also holds for the angular distribution function, as shown in Fig. 5(b). For liquid methanol, the two-body FM model already reproduces the RDF nearly perfectly. Therefore, there is no visible change upon including the three-body SW term, as shown in Fig. S6 of the ESI.† At the same time, the angular distribution function significantly improves, as shown in Fig. 2(b).Next, we focus on the interplay of the two-body and three-body interactions. In Fig. 3, we show the total pair PMF (red solid lines), the two-body (grey dashed lines) and three-body (grey dotted lines) contributions to this potential of mean force for water and methanol. In addition, we show the pair PMF generated by the two-body FM parametrizations as blue crosses. The evaluation of the pair PMF and the decomposition are described in Section IIE. To some extent, the attractive forces of the two-body potential within the first coordination shell are compensated by correlation effects due to two-body interactions with surrounding molecules. This can be seen in the reduced magnitude of the two-body contribution to the pair PMF compared to the direct pair potential (compare Fig. 1(a) and 3(a) for water and Fig. 2(a) and 3(b) for methanol). However, most of the compensation of the two-body attractions comes from short-range repulsive forces of the three-body interactions.
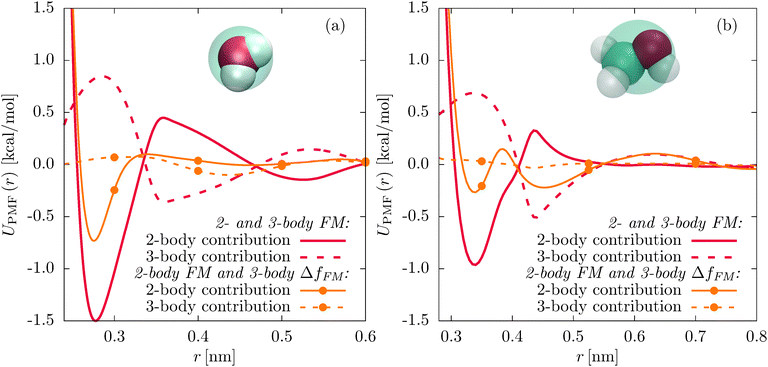
The strong coupling of the two-body and three-body interactions motivates a procedure similar to the subtraction of the Coulomb force from the atomistic reference.46 This can be viewed as a Gram–Schmidt orthogonalization scheme which reduces the coupling between different terms in the CG force field. First, we obtain the CG pair potential by two-body FM. In a second step, we determine the residual force ΔfFM acting on each CG bead by subtracting the two-body force from the total reference force, fref, given by eqn (2):
| ΔfFM = fref − fFM. | (9) |
We now parametrize the three-body SW potential using the residual instead of the reference force. The main effect of the residual force parametrization is a vertical shift of the angular part of the SW potential f(3b)(θ) to smaller values (see Fig. S2(b) and S5(b) of the ESI†). The decompositions of the pair PMFs for the new parametrizations (see Fig. 4, orange solid and dashed lines with dots) clearly show significantly reduced three-body contributions and less attractive two-body contributions to the pair PMFs compared to the unconstrained parametrizations (red solid and dashed lines).
It is essential to check how the residual force parametrizations perform in terms of the liquid structure. In Fig. 5, we compare the RDFs and angular distribution functions of CG beads within the first coordination shell for liquid water. The angular distribution functions of the two different parametrization schemes are very similar. The constrained parametrization (2-b FM and 3-b ΔfFM) also improves the RDF compared to the two-body FM result. For liquid methanol, the same is observed for the angular distribution functions (see Fig. 2(b)). Regarding the RDF, the first peak is slightly suppressed in case of the residual force parametrization (2-body FM and 3-body ΔfFM, Fig. S6 of the ESI†). A similar effect has been observed when adding a many-body local density-dependent potential to a two-body pair potential for liquid methanol.26
As a complementary information to the decomposition of the pair PMF into the two- and three-body interaction terms, we evaluate the inner product p and average angle Φ between the two-body and three-body forces on each CG bead (see eqn (7) and (8)). We find that the constrained parametrization scheme indeed reduces the inner products from p ≈ −0.5 (Φ ≈ 120°) to p ≈ −0.03 (Φ ≈ 92°) (water) and p ≈ −0.6 (Φ ≈ 125°) to p ≈ 0.05 (Φ ≈ 87°) (methanol).
B. Thermodynamics
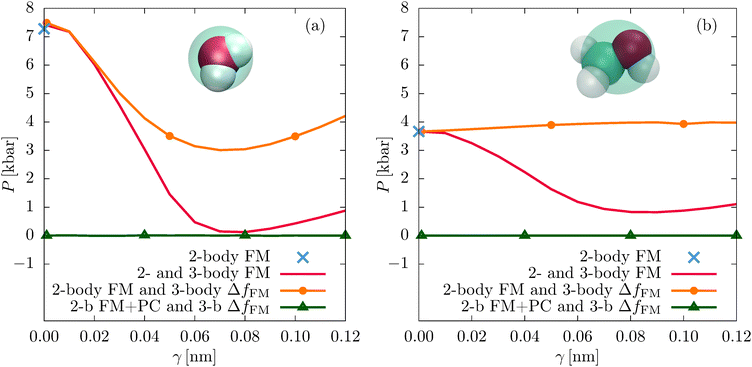
We now assess the performance of the CG models in terms of thermodynamic quantities. In particular, we evaluate the virial pressure P which should be equal to the ambient pressure when simulated at the density of the atomistic model, as well as the enthalpy of vaporization ΔH = Hgas − Hliq. Note that we do not explicitly conduct CG gas phase simulations and assume an ideal CG gas.28,37 In addition, we take into account the actual average pressure of the liquid phase CG simulations. Calculation details can be found in the ESI.†So far, all structural properties referred to a SW interaction parameter of γ = 0.08 nm (see eqn (4)), which is the optimal value regarding the structural accuracy of the models. Fig. 6 shows how P changes with the SW interaction parameter γ for all different parametrization schemes. For the unconstrained models, P decreases with increasing γ until reaching its minimum value at γ = 0.08 nm, namely P = 0.12 kbar for water and P = 0.83 kbar for methanol. This corresponds to system densities of ρ = 0.990 g cm−3 (water) and ρ = 0.613 g cm−3 (methanol) for NPT simulations at 1 atm. These values are close to the atomistic values of ρ = 0.998 g cm−3 (water) and ρ = 0.776 g cm−3 (methanol), and the experimental reference values at normal conditions: ρ = 0.9971 g cm−3 (water36) and ρ = 0.7872 g cm−3 (methanol37), even though these thermodynamic quantities have not been explicitly targeted in our parametrizations as, for example, with an explicit pressure matching scheme.47
The constrained parametrizations (2-body FM and 3-body ΔfFM) yield significantly larger values of P. This is a known issue of the FM method which can be alleviated by adding a small linear perturbation to the two-body FM potential (pressure correction):2,18
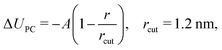 | (10) |
The pressure correction only slightly perturbs the structure of the system. Indeed, the pair and the angular distribution functions of the corrected and uncorrected constrained parametrizations are practically identical (see Fig. 2(b) and 5, and Fig. S6 of the ESI†). The same holds for the decompositions of the two-body PMFs, implying that the pressure correction does not change the inner product of the two- and three-body interactions (see Fig. S3, S4, S7, and S8 of the ESI†).
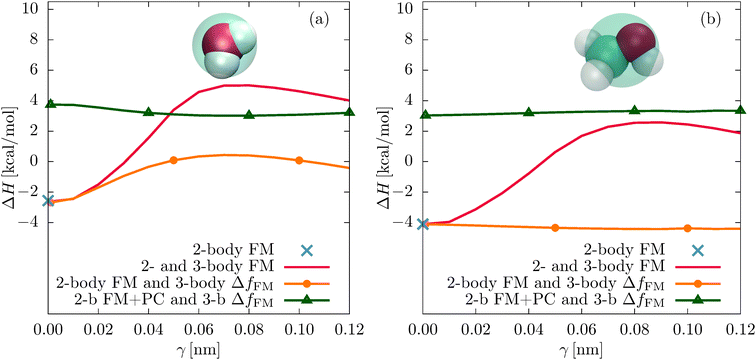
Fig. 7 shows the enthalpies of vaporization ΔH for all different models. Again, the two-body FM value is indicated with a blue cross. The unconstrained parametrizations (2- and 3-body FM) result in a maximum of ΔH at γ = 0.08 nm, where ΔH = 5.01 kcal mol−1 (water) and ΔH = 2.55 kcal mol−1 (methanol). The corresponding atomistic (experimental) values are 11.76 kcal mol−1 (10.52 kcal mol−1) for water28 and 8.94 kcal mol−1 (8.95 kcal mol−1) for methanol.37
The pressure correction significantly improves the vaporization enthalpies of the constrained parametrizations by increasing the cohesive energy. For example, for γ = 0.08 nm, ΔH of water changes from 0.40 kcal mol−1 to 3.01 kcal mol−1 and the vaporization enthalpy of methanol changes from − 4.42 kcal mol−1 to 3.32 kcal mol−1.
IV. Conclusions
We have shown that adding a Stillinger–Weber three-body potential to the coarse-grained force field of liquid water and methanol leads to significantly more attractive pair potentials. This short-range attraction is then compensated by the three-body term. Parametrization of the three-body term using residual forces substantially reduces the three-body contribution to the two-body potential of mean force. At the same time it worsens the thermodynamic properties of the coarse-grained model, quantified by pressure and enthalpy of vaporization. The thermodynamic properties can be corrected by adding a weak long-range attractive potential (pressure correction) without changing the structure of the system and the orthogonality of the three- and two-body contributions. Our findings motivate basis set extensions which separate the many-body contributions of different order.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Joseph Rudzinski, Tristan Bereau, Leanne Paterson, Anton Melnyk, and Kurt Kremer for fruitful discussions as well as Gregory A. Voth for providing reference data of the SW water potential. DFG is acknowledged for financial support through the collaborative research center TRR 146. Open Access funding provided by the Max Planck Society.References
- W. G. Noid, J.-W. Chu, G. S. Ayton, V. Krishna, S. Izvekov, G. A. Voth, A. Das and H. C. Andersen, J. Chem. Phys., 2008, 128, 244114 CrossRef PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624 CrossRef PubMed.
- A. P. Lyubartsev and A. Laaksonen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 3730 CrossRef.
- M. S. Shell, J. Chem. Phys., 2008, 129, 144108 CrossRef PubMed.
- S. Izvekov, M. Parrinello, C. J. Burnham and G. A. Voth, J. Chem. Phys., 2004, 120, 10896 CrossRef PubMed.
- G. Tóth, J. Phys.: Condens. Matter, 2007, 19, 335222 CrossRef PubMed.
- J. W. Mullinax and W. G. Noid, J. Phys. Chem. C, 2010, 114, 5661 CrossRef.
- J. F. Rudzinski and W. G. Noid, Eur. Phys. J.: Spec. Top., 2015, 224, 2193 Search PubMed.
- J. F. Rudzinski and W. G. Noid, J. Phys. Chem. B, 2014, 118, 8295 CrossRef PubMed.
- S. Izvekov and G. A. Voth, J. Chem. Phys., 2005, 123, 134105 CrossRef PubMed.
- J. W. Mullinax and W. G. Noid, J. Chem. Phys., 2009, 131, 104110 CrossRef.
- V. Molinero and E. B. Moore, J. Phys. Chem. B, 2009, 113, 4008 CrossRef PubMed.
- L. Larini, L. Lu and G. A. Voth, J. Chem. Phys., 2010, 132, 164107 CrossRef PubMed.
- A. Das and H. C. Andersen, J. Chem. Phys., 2012, 136, 194114 CrossRef PubMed.
- A. Das and H. C. Andersen, J. Chem. Phys., 2009, 131, 034102 CrossRef PubMed.
- M. Jochum, D. Andrienko, K. Kremer and C. Peter, J. Chem. Phys., 2012, 137, 064102 CrossRef PubMed.
- C. Scherer and D. Andrienko, Eur. Phys. J.: Spec. Top., 2016, 225, 1441 Search PubMed.
- V. Rühle, C. Junghans, A. Lukyanov, K. Kremer and D. Andrienko, J. Chem. Theory Comput., 2009, 5, 3211 CrossRef PubMed.
- A. P. Lyubartsev and A. Laaksonen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 5689 CrossRef.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051 CrossRef.
- A. Tsourtis, V. Harmandaris and D. Tsagkarogiannis, Entropy, 2017, 19, 395 CrossRef.
- M. Dijkstra, J. M. Brader and R. Evans, J. Phys.: Condens. Matter, 1999, 11, 10079 CrossRef.
- P. G. Bolhuis, A. A. Louis and J. P. Hansen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021801 CrossRef PubMed.
- T. Sanyal and M. S. Shell, J. Chem. Phys., 2016, 145, 034109 CrossRef PubMed.
- J. W. Wagner, T. Dannenhoffer-Lafage, J. Jin and G. A. Voth, J. Chem. Phys., 2017, 147, 044113 CrossRef PubMed.
- M. R. DeLyser and W. G. Noid, J. Chem. Phys., 2017, 147, 134111 CrossRef PubMed.
- F. Zipoli, T. Laino, S. Stolz, E. Martin, C. Winkelmann and A. Curioni, J. Chem. Phys., 2013, 139, 094501 CrossRef PubMed.
- J. Lu, Y. Qiu, R. Baron and V. Molinero, J. Chem. Theory Comput., 2014, 10, 4104 CrossRef PubMed.
- G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Chem. Rev., 2016, 116, 7501 CrossRef PubMed.
- A. Das and H. C. Andersen, J. Chem. Phys., 2012, 136, 194113 CrossRef PubMed.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19 CrossRef.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef PubMed.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61 CrossRef PubMed.
- W. F. Van Gunsteren and H. J. C. Berendsen, Mol. Simul., 1988, 1, 173 CrossRef.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef.
- S. Plimton, J. Comput. Phys., 1995, 117, 1 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103 CrossRef.
- J. F. Rudzinski and W. G. Noid, J. Phys. Chem. B, 2012, 116, 8621 CrossRef PubMed.
- W. G. Noid, P. Liu, Y. Wang, J.-W. Chu, G. S. Ayton, S. Izvekov, H. C. Andersen and G. A. Voth, J. Chem. Phys., 2008, 128, 244115 CrossRef PubMed.
- N. J. H. Dunn and W. G. Noid, J. Chem. Phys., 2015, 143, 243148 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Technical details of the CG implementations, the calculation of thermodynamic properties, the tabulated two-body and three-body potentials, and additional figures of CG potentials, distribution functions and PMFs. See DOI: 10.1039/c8cp00746b |
| This journal is © the Owner Societies 2018 |