First-principles method for calculating the rate constants of internal-conversion and intersystem-crossing transitions†
Received
31st December 2017
, Accepted 31st January 2018
First published on 16th February 2018
Abstract
A method for calculating the rate constants for internal-conversion (kIC) and intersystem-crossing (kISC) processes within the adiabatic and Franck–Condon (FC) approximations is proposed. The applicability of the method is demonstrated by calculation of kIC and kISC for a set of organic and organometallic compounds with experimentally known spectroscopic properties. The studied molecules were pyrromethene-567 dye, psoralene, hetero[8]circulenes, free-base porphyrin, naphthalene, and larger polyacenes. We also studied fac-Alq3 and fac-Ir(ppy)3, which are important molecules in organic light emitting diodes (OLEDs). The excitation energies were calculated at the multi-configuration quasi-degenerate second-order perturbation theory (XMC-QDPT2) level, which is found to yield excitation energies in good agreement with experimental data. Spin–orbit coupling matrix elements, non-adiabatic coupling matrix elements, Huang–Rhys factors, and vibrational energies were calculated at the time-dependent density functional theory (TDDFT) and complete active space self-consistent field (CASSCF) levels. The computed fluorescence quantum yields for the pyrromethene-567 dye, psoralene, hetero[8]circulenes, fac-Alq3 and fac-Ir(ppy)3 agree well with experimental data, whereas for the free-base porphyrin, naphthalene, and the polyacenes, the obtained quantum yields significantly differ from the experimental values, because the FC and adiabatic approximations are not accurate for these molecules.
1. Introduction
Molecular photophysics is a rapidly developing research area of molecular and chemical physics.1–3 Interaction of the electromagnetic radiation with molecules, molecular luminescence properties, and transformations of excited electronic energy into vibrational energy are important photophysical processes. Detailed knowledge about these photophysical properties is needed when designing optical molecular devices such as organic light-emitting diodes,4,5 laser applications,6 and other devices that convert light energy or other forms of energy.7 The mechanism of light-induced processes such as the light absorption of photosynthesis can also be understood by studying the photophysical properties of the chlorophylls and other involved molecules.8
Photophysical processes in molecules can be divided into intramolecular and intermolecular ones.9 The intermolecular processes play a key role in luminescence quenching and in deactivating excited electronic states at high molecular concentrations,10 whereas the intramolecular processes depend almost completely on the intrinsic properties of the molecule.11 Photophysical properties like the quantum yields of fluorescence (φfl) and phosphorescence (φphos) are determined by the ratio between the rate constants of radiative (kr) and nonradiative (knr) intramolecular processes.9,10
When a photon is absorbed, molecular systems transfer from the ground state to an excited electronic state, and they can be de-excited via different channels. Radiative deactivation channels comprise emission of a photon with an energy that is smaller than or equal to the excitation energy. Nonradiative channels do not involve any photon emission but the excess energy transfers to vibrational energy leading to an increase of the temperature. Internal conversion (IC) and the intersystem crossing (ISC) are main intramolecular nonradiative processes.9–11 The electronic energy in both processes is converted into molecular vibrations. In the case of IC, the spin multiplicity of the molecule is conserved, whereas ISC involves the initial and final states of different spin multiplicities.1 The IC process occurs due to nonadiabatic coupling interactions. ISC is caused by the spin–orbit coupling interaction. When the concentration of molecules is low, it can be assumed that the total rate constant for the nonradiative process is the sum of the rate constants of the two channels knr = kIC + kISC, where kIC and kISC are the rate constants for IC and ISC, respectively.9,12 The total rate constant for the nonradiative process knr can be estimated experimentally from the quantum yields (φfl, φphos) and from the rate constant of the radiative processes (kr).9,10 However, the experimental determination of kIC and kISC is very difficult.13,14 The rate constants for the radiative transitions can be calculated quantum chemically15–17 employing nonadiabatic molecular dynamics simulations at ab initio levels of theory18–22 or by using specific approximations considering empirical corrections.1,15,23 Molecular dynamics simulations are computationally expensive, which limits their application to smaller molecular systems. The semiempirical approach by Plotnikov, Artyukhov and Maier, which is based on the incomplete neglected differential overlap (INDO) method with a spectroscopic parameterization, can be used for calculating the photophysical properties of large organic molecules.24–31 Maier and Artyukhov employed computational methods based on the theory developed by Robinson, Jortner11 and Plotnikov24 to estimate kIC and kISC at the INDO level of theory.25–28 They calculated the matrix elements of the nonadiabatic coupling and spin–orbit coupling operators for the singlet and triplet electronic states at the INDO level of theory, whereas the vibrational integrals were estimated from the experimental spectroscopic data. The INDO approach renders routine calculations of kIC and kISC for large organic molecules consisting of up to 200 atoms feasible.
However, the semiempirical INDO approach of Artyukhov and Maier can be applied only to molecules consisting of light atoms such as H, C, N, O, F, S, and Cl, whereas it cannot be employed in studies of photophysical properties of organometallic compounds. The semiempirical method has also been found to lead to large errors in the rate constants kIC and kISC for porphyrins and [8]circulenes, because the INDO calculations are not able to provide accurate electronic excitation energies for these molecules. A better accuracy has been obtained for porphyrins and [8]circulenes by combining the INDO method with excitation energies calculated at the time-dependent density functional theory (TDDFT) and correlated ab initio levels of theory.29–33 However, for some [8]circulenes the matrix elements of the nonadiabatic coupling (NACME) and the spin–orbit coupling (SOCME) operators calculated at the INDO level were found to be inaccurate. In this work, the electronic excitation energies, the coupling matrix elements, and the vibrational integrals are calculated at the density functional theory (DFT) and correlated ab initio levels of theory, opening new possibilities of employing the theory of Plotnikov, Robinson, and Jortner without relying on any semiempirical parameters.
In this work we employ the theory of Plotnikov, Robinson, Jortner24 using NACME and SOCME calculated at the DFT and ab initio levels to obtain accurate values for the kIC and kISC rate constants for nonradiative intramolecular transitions. The methods have been used in studies of pyrromethene-567 dye, psoralene, acenes, fac-Alq3, fac-Ir(ppy)3, hetero[8]circulenes, and free-base porphyrin, which are important in the different research areas of photonics. The reference values for the rate constants are also available for these molecules,34–40 since the photophysical properties of these compounds have previously been studied by other groups.29,31,33
2. Theory
2.1. Non-radiative electronic transitions
The general expression for the rate constant of non-radiative electronic transitions derived by Plotnikov, Robinson, Jortner reads11,24| | 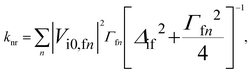 | (1) |
where i is the initial electronic state, f is the final electronic state, n is a vibrational level of f, Γfn is the relaxation width of the vibronic level |fn〉, Δif = |Ei0 − Efn| is the energy difference between the initial and final vibronic states, and Vi0,fn is the matrix element of the perturbation operator. Only the lowest vibronic state is considered for the initial state. The perturbation operator is the spin–orbit coupling interaction for ISC transitions and the non-adiabatic coupling interaction for the IC process. eqn (1) written in atomic units holds at ambient temperatures (T ≤ 300 K) when knr ≪ Γfn. The conditions are generally fulfilled in experimental studies of luminescence properties. Γfn of about 1014 s−1 is generally much larger than the knr of about 107–1012 s−1.24 The Δif value is not larger than 100 cm−1 for polyatomic molecules.24 The expression can be simplified to eqn (2) when assuming that Γfn depends only weakly on the vibrational level n and that Δif ≪ Γfn:24| | 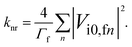 | (2) |
2.2. IC rate constant
In the framework of the adiabatic and Franck–Condon (FC) approximation, Vi0,fn can be written as24,41| | 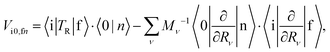 | (3) |
where TR is the kinetic energy operator of the electrons, ν is a nuclear index, Mν is the mass of nucleus ν,  is the nonadiabatic coupling matrix element between the electronic states |i〉 and |f〉, |0〉 is the lowest vibration state of |i〉 and |n〉 is a vibration state of the final electronic state |f〉, Rν is the nuclear coordinates of nucleus ν, and
is the nonadiabatic coupling matrix element between the electronic states |i〉 and |f〉, |0〉 is the lowest vibration state of |i〉 and |n〉 is a vibration state of the final electronic state |f〉, Rν is the nuclear coordinates of nucleus ν, and  is the nonadiabatic coupling matrix element between |0〉 and |n〉. The
is the nonadiabatic coupling matrix element between |0〉 and |n〉. The  and
and  integrals are calculated for the equilibrium geometry (R = R0) of the |f〉 state. Since the first term in eqn (3) is usually much smaller than the second term, eqn (3) can be written as24,42
integrals are calculated for the equilibrium geometry (R = R0) of the |f〉 state. Since the first term in eqn (3) is usually much smaller than the second term, eqn (3) can be written as24,42| | 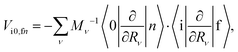 | (4) |
which can be expressed in Cartesian coordinates as| | 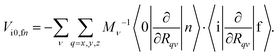 | (5) |
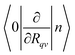 can be written using normal coordinates when the rotational and translational motions have been identified and removed
can be written using normal coordinates when the rotational and translational motions have been identified and removed
| | 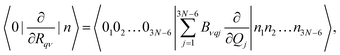 | (6) |
In eqn (6), |0k〉 and |nk〉 are the harmonic oscillator wave functions of the initial and final states, nk is the nth excitation of the kth oscillator, Qj is the normal coordinate of the jth oscillator, Bνqj are matrix elements that describe the connection between the displacements in Cartesian coordinates of νth atom (ΔRqν) in respect to the equilibrium of and normal coordinate (Qj). By inserting eqn (6) into eqn (5) one obtains
| | 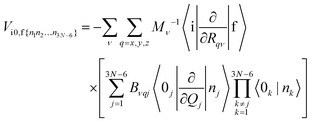 | (7) |
 can be expressed in harmonic approximation as
can be expressed in harmonic approximation as
| | 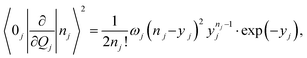 | (8) |
where
yj is the Huang–Rhys factor and
ωj is the vibration frequency of the
jth mode. The Franck–Condon factor 〈0
k|
nk〉 can then be written as
41| |  | (9) |
The final expression is obtained by inserting eqn (8) and (9) into eqn (7):
| |  | (10) |
The IC rate constant can be calculated using
| |  | (11) |
where the expression for
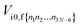
is given in
eqn (10).
Eif is the energy gap between the electronic states |i〉 and |f〉.
2.3. ISC rate constant
The spin–orbit coupling is the perturbation operator of the ISC process. The spin–orbit coupling matrix elements depend only on the space and spin coordinates of the electrons but not on the nuclear ones.1,24 The expression for the ISC rate constant can then be written as| |  | (12) |
The excitations of the normal vibrations with the high frequency at ω = ∼1000–1800 cm−1 and significant Huang–Rhys factor (y > 0.1) are the largest contributions to the summation (Eif = n1ω1 + n2ω2+⋯+ n3N−6ω3N−6) in the expressions for the FC factor in eqn (11) and (12).6,12,24
2.4. Parameters for the calculation of the ISC and IC rate constants
To calculate the ISC and IC rate constants, values for 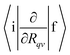 , 〈i|HSO|f〉, yj and ωj, Eif and Γf are needed. In this work,
, 〈i|HSO|f〉, yj and ωj, Eif and Γf are needed. In this work,  is calculated for molecules consisting of more than 50 atoms at the TDDFT level using Turbomole42 and for smaller molecules they are calculated at the CASSCF level of theory in GAMESS-US.43 The Huang–Rhys factors and the vibration frequencies (ωj) are calculated at the DFT and correlated ab initio levels of theory.44 The 〈i|HSO|f〉 matrix elements have been computed at the CASSCF and TDDFT levels.45,46 The line width (Γf) has been estimated using the Lax and Pekar models47–49 in the simulation of molecular vibronic spectra using the displaced oscillator model.
is calculated for molecules consisting of more than 50 atoms at the TDDFT level using Turbomole42 and for smaller molecules they are calculated at the CASSCF level of theory in GAMESS-US.43 The Huang–Rhys factors and the vibration frequencies (ωj) are calculated at the DFT and correlated ab initio levels of theory.44 The 〈i|HSO|f〉 matrix elements have been computed at the CASSCF and TDDFT levels.45,46 The line width (Γf) has been estimated using the Lax and Pekar models47–49 in the simulation of molecular vibronic spectra using the displaced oscillator model.
3. Computational methods and studies
3.1 Studied molecules
The computational methods described above have been employed on a number of molecules with interesting photophysical properties. The studied molecules shown in Fig. 1 comprise the commercial laser dye 1,3,5,7,8-pentamethyl-2,6-diethylpyrromethene-difluoroborate (PM567),34 7H-furo[3,2-g]chromen-7-one (psoralene),35fac-tris(8-hydroxyquinolinato)aluminium (fac-Alq3)38 and fac-tris(2-phenylpyridine)iridium (fac-Ir(ppy)3),39 tetraoxa[8]circulene (4B)36 and its NH substituted and benzoannelated derivatives (AOC) and (1B3N),29 polyacenes (naphthalene, anthracene, tetracene, pentacene, and hexacene),37 and free-base porphyrin (H2P).42
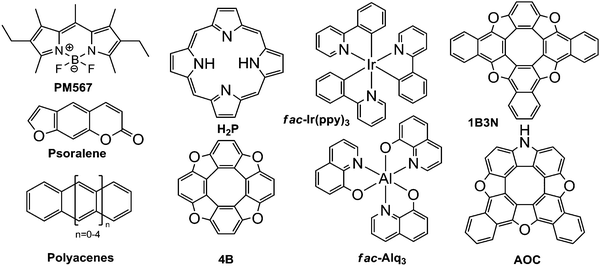 |
| | Fig. 1 The molecular structures of the studied molecules. | |
The molecules were chosen for the following reasons. PM567 has a very large fluorescence quantum yield of φfl = 0.9–1.0 and is therefore often used in laser devices.38 Psoralene has a very small fluorescence quantum yield of φfl ∼ 0.1 and a large kISC37 and is therefore used in photodynamic therapy applications.37 Alq3 and Ir(ppy)3 are used in OLED devices.38,39 The electroluminescence of Alq3 and Ir(ppy)3 is due to fluorescence and phosphorescence, respectively.38,39 The photophysical properties of [8]circulenes have previously been studied by us at the INDO level of theory using the method of Plotnikov, Robinson, Jortner.29
The chosen compounds have very different fluorescence quantum yields φfl. The fluorescence spectrum of the polyacenes has a complicated vibronic fine structure requiring calculations of transition moments between many excited states with different spins.50 The energy gap between the first excited singlet state (S1) and the ground state (S0) systematically reduces from the ultraviolet to infrared spectral region when increasing the number of benzoic rings in the polyacene.50 The calculations on the polyacenes yield a relation between kIC and the optical gap. The present approach is also applied to free-base porphyrin (H2P), because it is well known that the calculation of kIC and kISC for H2P is challenging.1
3.2 Computational methods
The molecular structures of the ground electronic states (S0) of all the molecules except Alq3 and Ir(ppy)3 were optimized at the density functional theory (DFT) level51 using the B3LYP52 exchange–correlation functional and def2-TZVP53 basis sets. For Alq3 and Ir(ppy)3, the ωB97xD functional was employed in the DFT optimization of the molecular structures.54 The def2-TZVP basis sets were used for Alq3. For Ir(ppy)3, we used the LANL2DZ basis set and effective core potentials for Ir and the 6-31G(d,p) basis sets for the rest of the atoms.55 The equilibrium geometry of the first excited electronic state (S1) was obtained at the TDDFT/B3LYP/def2-TZVP level of theory for PM567, psoralene, polyacenes, and free-base porphyrin. The molecular structures of the first excited state (S1) of Alq3 and Ir(ppy)3 were optimized at the TDDFT level using the ωB97xD functional.54 We chose the ωB97xD functional for Alq3 and Ir(ppy)3, because difficulties arise when using the B3LYP functional to properly describe excited states of metal–ligand compounds with significant charge-transfer characteristics, whereas the ωB97xD functional is expected to be able to describe such states better, since it has the correct long-range shape of the potential.39 The molecular structure optimizations were carried out using Gaussian-09 software.56 Only the lowest isomers of fac-Alq3 and fac-Ir(ppy)3 were considered.
Calculations of singlet and triplet excitation energies were carried out using the extended multi-configuration quasi-degenerate perturbation theory at the second order (XMC-QDPT2),57 because this level of theory has been found to yield the correct relative order of the lowest singlet and triplet electronic states for organic and organometallic compounds.58 The XMC-QDPT2 calculations were performed using the optimized molecular structures of the S1 state. In the XMC-QDPT2 calculations, 30 states were included in the effective Hamiltonian. The number of active electrons (e), number of active orbitals (o), and the number of states (s) of the state-average (SA) complete active self-consistent space field (CASSCF) calculations are PM567 (8 e, 6 o, 5 s), psoralene (10 e, 9 o, 5 s), Alq3 (12 e, 9 o, 5 s), Ir(ppy)3 (12 e, 9 o, 5 s), tetraoxa[8]circulene (4B) (10 e, 10 o, 10 s), o-dinaphthalene-containing azatrioxa[8]circulene (AOC) (10 e, 10 o, 10 s), trinaphthalene-containing tetraoxa[8]circulene (1B3N), (10 e, 11 o, 10 s), free-base porphyrin (H2P) (11 e, 14 o, 10 s), naphthalene (12 e, 9 o, 10 s), anthracene (10 e, 10 o, 10 s), tetracene (10 e 11 o, 10 s), pentacene (8 e, 8 o, 10 s), and hexacene (8 e, 8 o, 10 s). The XMC-QDPT2 calculations were carried out using Firefly.59
The discrepancy between the TDDFT and XMC-QDPT2 excitation energies for the S1 → S0 electronic transitions does not exceed 1000–1500 cm−1 for any of the studied compounds. Thus, a combination of the XMC-QDPT2 and TDDFT levels of theory can be used in the calculation of photophysical properties.
3.3 Huang–Rhys factors and vibrational relaxation widths
The yj, ωj, and Γf values were obtained using the Lax and Pekar model,47–49 which is described in detail in ref. 48 and 49. The potential energy surfaces of S0 and S1 are assumed to be harmonic with the same vibrational energies (ωj) for the two states. The energy functions for the two states can then be written as| |  | (13) |
where {Q} is the set of normal coordinates of the harmonic oscillators, 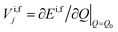 is the gradient of the potential energy surface along the jth mode at a chosen point Q0. From eqn (13) it is easily seen that
is the gradient of the potential energy surface along the jth mode at a chosen point Q0. From eqn (13) it is easily seen that| | 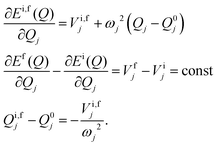 | (14) |
Thus, ΔQj = −(Vfj − Vij)/ωj2 and finally the Huang–Rhys factors (yj) are obtained as
| | 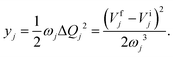 | (15) |
The line width Γf is taken from the generation function for the simulation of the profile of the vibration spectra within the Lax-Pekar model.47–49 The calculated value for Γf is about 1.6 × 1014 s−1 for the S1 state of the studied molecules.
The optimized molecular structures of the S0 and S1 states as well as the gradient and the Hessian calculated for the S0 state were used in the calculation of ωj and Vji,f. In the calculation of the IC rate constants, the Hessian was calculated for the S0 state, whereas the gradient for the S1 state was calculated using the molecular structure of the S0 state. We assume that the vibrational energies (ωj) and the Huang–Rhys factors yi are the same for the IC and ISC processes. Our previous calculations showed that this assumption yields good estimates for the ISC rate constants for several molecules.29,58
3.4 Calculation of matrix elements
The nonadiabatic coupling matrix elements  were calculated with Turbomole at the TDDFT level of theory using the perturbation theory.42,60 The spin–orbit coupling matrix elements 〈S1|HSO|Ti〉 between the S1 state and the energetically lower ith triplet state Ti were calculated at the CASSCF level using Gamess-US.61 The excitation energies calculated at the XMC-QDPT2 level were used as the zeroth-order values. In order to calculate kISC, the one-electron spin–orbit coupling operator of the Pauli-Breit Hamiltonian was used.62 The contributions from the two-electron part of the spin–orbit coupling operator are beyond the Franck–Condon approximation.1 However, previous calculations have shown that the use of the one-electron spin–orbit operator within the FC approximation leads to accurate kISC values for the organic and organometallic compounds.29,58,63
were calculated with Turbomole at the TDDFT level of theory using the perturbation theory.42,60 The spin–orbit coupling matrix elements 〈S1|HSO|Ti〉 between the S1 state and the energetically lower ith triplet state Ti were calculated at the CASSCF level using Gamess-US.61 The excitation energies calculated at the XMC-QDPT2 level were used as the zeroth-order values. In order to calculate kISC, the one-electron spin–orbit coupling operator of the Pauli-Breit Hamiltonian was used.62 The contributions from the two-electron part of the spin–orbit coupling operator are beyond the Franck–Condon approximation.1 However, previous calculations have shown that the use of the one-electron spin–orbit operator within the FC approximation leads to accurate kISC values for the organic and organometallic compounds.29,58,63
3.5 Radiative rate constants and fluorescence quantum yields
When contributions from higher excited states can be neglected, the fluorescence quantum yield from the S1 state can be obtained as9,12| |  | (16) |
where kISTi is a ISC rate constant between S1 and energetically lower triplet states Ti, kr and kIC are the radiative and IC rate constants of the electronic transition from S1 to S0, respectively. The kr can be estimated using the Strickler–Berg equation64| |  | (17) |
where f is the oscillator strength and E(S1 → S0) is the de-excitation energy from S1 to S0.
The table illustrating the employed level of theory is given for clear understanding of the subsequent discussions (Table 1).
Table 1 The employed levels of theory for the compounds under investigation
| Properties |
PM567, psoralene, [8]circuelenes and H2P, polyacenes |
Alq3 |
Ir(ppy)3 |
| Geometries of S0 and S1 states |
DFT/B3LYP/def2-TZVP |
DFT/ωB97xD/def2-TZVP |
DFT/ωB97xD/LANL2DZ and 6-31G(d,p) |
| Energies of S1 → S0 electronic transition and triplet states, oscillator strength (f) |
XMC-QDPT2/def2-TZVP |
XMC-QDPT2/ωB97xD/def2-TZVP |
XMC-QDPT2/ωB97xD/LANL2DZ and 6-31G(d,p) |

|
TD-DFT/B3LYP/def2-TZVP |
TDDFT/B3LYP/def2-TZVP |
TDDFT/B3LYP/def2-TZVP |
| 〈S1|HSO|Ti〉 |
MCSCF/def2-TZVP |
MCSCF/ωB97xD/def2-TZVP |
MCSCF/ωB97xD/LANL2DZ and 6-31G(d,p) |
|
y, ω and Γ |
(TD)-DFT/B3LYP/def2-TZVP |
(TD)-DFT/ωB97xD/def2-TZVP |
(TD)-DFT/ωB97xD/LANL2DZ and 6-31G(d,p) |
4. Results and discussion
4.1. Pm567
The optimized molecular structure of the S1 state is shown in Fig. 2a. The energy levels of the lowest singlet and triplet states and the kIC and kISC rate constants of the transitions are shown in Fig. 2b. Table 2 contains the calculated excitation energy of the S1 state and the excitation energies calculated for the triplet states that are energetically below S1. The calculated excitation energy for S1 agrees well with the experimental value with a deviation of only 0.09 eV. The rate constants in Fig. 2b show that kr is a main deactivation channel of the S1 state. The largest rate constant among the nonradiative transitions is kISC2 due to the small energy gap between S1 and T2. The calculated fluorescence quantum yield (φ) is 0.79, which qualitatively agrees with the experimental one of 0.9.38 Thus, the present approach is able to predict the large (φfl) observed for PM567. The largest values for the Huang–Rhys factors (yj) and corresponding wavenumbers (ωj) are given in Table 3. The vibrational mode at 1255 cm−1 has a large y value of 0.1. Since only one vibrational mode has a large y value in that energy range the nonradiative rate constants kIC and kISC are small as compared with the rate constant of the radiative transition kr.
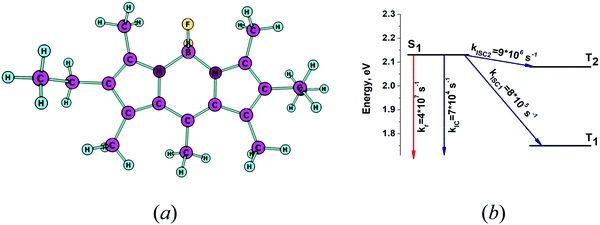 |
| | Fig. 2 (a) The optimized molecular structure of PM567. (b) The energy level diagram for PM567 including the computed values for the radiative and nonradiative rate constants. | |
Table 2 The calculated excitation energies (in eV) of the studied molecules are compared to available experimental data. Calculated oscillator strengths are given in parenthesis
| Compound |
State |
XMC-QDPT2 |
Exp. |
|
Ref. 38.
Ref. 37.
Ref. 29.
Ref. 40.
Ref. 34.
Ref. 35.
|
| PM567 |
S1 |
2.13(0.2) |
2.22a |
| T1 |
1.75 |
— |
| T2 |
2.08 |
— |
|
|
| Psoralene |
S1 |
3.09(0.2) |
3.02b |
| T1 |
2.75 |
2.73b |
| T2 |
3.02 |
— |
|
|
| 4B |
S1 |
2.64 |
2.44c |
| T1 |
1.89 |
|
| T2 (T3) |
2.58 |
|
|
|
| AOC |
S1 |
3.00(0.3) |
3.02c |
| T1 |
1.89 |
|
| T2 |
2.9 |
|
|
|
| 1B3N |
S1 |
2.68(0.5) |
3.08c |
| T1 |
2.1 |
|
| T2 |
2.24 |
|
| T3 |
2.34 |
|
| T4 |
2.64 |
|
|
|
| H2P |
S1 |
1.92 |
2.01d |
| T1 |
1.62 |
1.58d |
| T2 |
1.8 |
|
|
|
| Alq3 |
S1 |
2.33(0.1) |
2.38–2.48e |
| T1 |
1.86 |
— |
|
|
| Ir(ppy)3 |
S1 |
2.74 |
2.69f |
| T1 |
2.37 |
2.44f |
Table 3 Calculated wavenumbers ωj (in cm−1) for a few relevant vibrational modes. The largest Huang–Rhys factors (yj) for the S1 → S0 and S1 → Tj nonradiative transitions are given in parenthesis
| Compound |
ω
j
(yj) |
| PM567 |
210 (0.05); 571 (0.12); 1255 (0.1) |
| Psoralene |
234 (0.29); 396 (0.65); 742 (0.42); 1103 (0.15); 1164 (0.25); 1190 (0.54); 1615 (0.14); 1689 (0.24); 1877 (0.08) |
| 4B |
662 (0.17); 1051 (0.07); 1276 (0.35); 1453 (0.19); 1536 (0.16); 1703 (0.84) |
| AOC |
1308 (0.05); 1473 (0.14); 1675 (0.15); 1678 (0.05) |
| 1B3N |
232 (0.05); 1474 (0.15); 1518 (0.05); 1687 (0.05) |
| H2P |
157 (0.05); 310 (0.14); 1393 (0.03) |
| Alq3 |
141 (0.36); 151 (0.25); 164 (0.08); 185 (0.08); 213 (0.06); 357 (0.54); 422 (0.09); 458 (0.10); 506 (0.12); 554 (0.34); 585 (0.11); 587 (0.13); 661 (0.33); 670 (0.21); 1434 (0.1) 1634 (0.07); 1637 (0.29); 1659 (0.07) |
| Ir(ppy)3 |
121 (0.28); 146 (0.46); 187 (0.08); 258 (0.31); 269 (0.06); 1040 (0.01); 1512 (0.14); 1615 (0.11) |
4.2. Psoralene
The optimized molecular structure of the S1 state of psoralene is shown in Fig. 3a. The energies of the lowest singlet and triplet states and the kIC and kISC rate constants are shown in Fig. 3b. The excitation energies listed in Table 2 agree well with the experimental values. The dominating deactivated channel of the S1 state is via the kISC1 channel, because of the strong spin–orbit coupling interaction between S1 and T1. See Table S1 in the ESI.† The calculated and experimental quantum yields of 0.08 are in perfect agreement.35 The calculated excitation energies were found to agree very well with the experimental ones, even though the solvent effect can be as large as 1% for psoralene.35 The calculated yj and ωj values for psoralene are given in Table 3, where one sees that many vibrational modes with energies larger than 1000 cm−1 have large yj values leading to a high density of FC factors and fast nonradiative transitions. The calculated rate constants explain the low value and the high triplet quantum yield of psoralene.
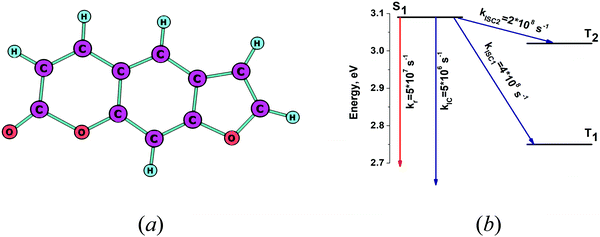 |
| | Fig. 3 (a) The optimized molecular structure of psoralene. (b) The energy level diagram for psoralene including the computed values for the radiative and nonradiative rate constants. | |
4.3. [8]circulenes 4B, AOC and 1B3N
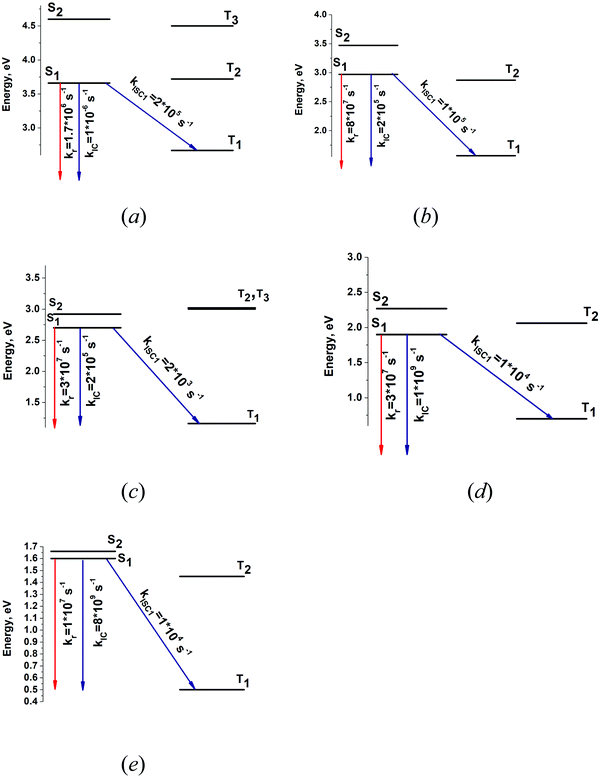
The optimized molecular structures of the S1 state of tetraoxa[8]circulene (4B) and its NH substituted and benzoannelated derivatives (AOC) and (1B3N) are shown in Fig. 3a, c, and e. The energy levels of their lowest singlet and triplet states and the kIC and kISC rate constants are shown in Fig. 3b, d and f, respectively. The lowest excitation energies are given in Table 2. The intensity for the radiative S0–S1 transition for tetraoxa[8]circulene (4B) vanishes in the FC approximation. The transition becomes allowed in the Herzberg–Teller approximation.65 An oscillator strength for 4B of 0.03 is obtained from the experimental extinction coefficient  .66 The spin–orbit coupling matrix elements between S1 and Tj vanish due to symmetry reasons since the molecule belongs to the D4h point group. Thus, IC is the main deactivation channel of the S1 state. The calculated value for φfl is 0.13, which agrees well with the experimental value of 0.09.36 AOC has the largest quantum yield (φfl) of about 1.0, because the rate constant kISC is close to zero and kIC is significantly smaller than kr. The experimental φfl value for AOC is 0.91.29 1B3N has a smaller calculated φfl of 0.56 which is in reasonable agreement with the experimental value of 0.36.29 The reason for the smaller φfl value is the presence of several low-lying triplet states. The main deactivation channel of the S1 state is then the ISC process. The present calculations explain why the studied [8]circulenes have different quantum yields. The largest yj values and the corresponding vibrational energies (ωj) are listed in Table 3. The main vibrational mode for the nonradiative transition is at about 1400 cm−1 for AOC and 1B3N. We have previously calculated kIC and kISC at the INDO level of theory using one vibrational mode with an energy of 1400 cm−1.29 The obtained results were in good agreement with the present ones except for kIC of tetraoxa[8]circulenes (4B), because the NACMEs calculated at the INDO level are inaccurate. The reason for the deviation can be traced back to the large yj factor for the vibrational mode at 1703 cm−1, which consists of vibrational motion inside the macrocycle.65 For the other [8]circulenes (AOC and 1B3N), this mode has a smaller yj value. The present calculations show that the INDO approach does not yield accurate nonradiative rate constants for tetraoxa[8]circulene (4B) (Fig. 4).
.66 The spin–orbit coupling matrix elements between S1 and Tj vanish due to symmetry reasons since the molecule belongs to the D4h point group. Thus, IC is the main deactivation channel of the S1 state. The calculated value for φfl is 0.13, which agrees well with the experimental value of 0.09.36 AOC has the largest quantum yield (φfl) of about 1.0, because the rate constant kISC is close to zero and kIC is significantly smaller than kr. The experimental φfl value for AOC is 0.91.29 1B3N has a smaller calculated φfl of 0.56 which is in reasonable agreement with the experimental value of 0.36.29 The reason for the smaller φfl value is the presence of several low-lying triplet states. The main deactivation channel of the S1 state is then the ISC process. The present calculations explain why the studied [8]circulenes have different quantum yields. The largest yj values and the corresponding vibrational energies (ωj) are listed in Table 3. The main vibrational mode for the nonradiative transition is at about 1400 cm−1 for AOC and 1B3N. We have previously calculated kIC and kISC at the INDO level of theory using one vibrational mode with an energy of 1400 cm−1.29 The obtained results were in good agreement with the present ones except for kIC of tetraoxa[8]circulenes (4B), because the NACMEs calculated at the INDO level are inaccurate. The reason for the deviation can be traced back to the large yj factor for the vibrational mode at 1703 cm−1, which consists of vibrational motion inside the macrocycle.65 For the other [8]circulenes (AOC and 1B3N), this mode has a smaller yj value. The present calculations show that the INDO approach does not yield accurate nonradiative rate constants for tetraoxa[8]circulene (4B) (Fig. 4).
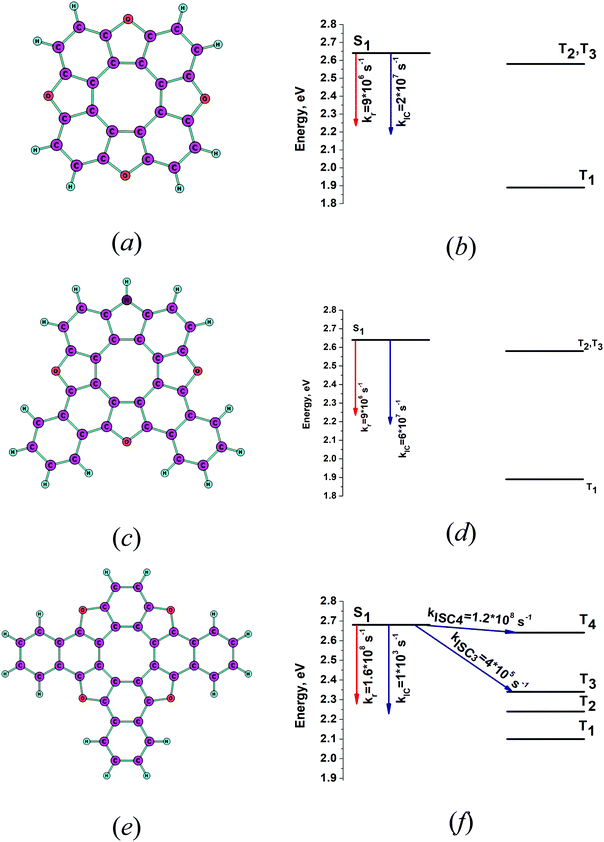 |
| | Fig. 4 The optimized molecular structures of (a) 4B, (c) AOC and (e) 1B3N. The energy levels and rate constants are given for the same molecules in (b), (d), and (f), respectively. | |
4.4. Free-base porphyrin
Calculation of the nonradiative rate constants kIC and kISC for H2P is a challenge.1 Several previous works have shown that the FC approximation is not enough to obtain accurate rate constants.1,15 The intensity of the Q band in the electronic absorption spectrum for H2P can be accurately simulated only when considering vibrational effects at the Herzberg–Teller approximation.67 In this work, we adopted the experimental value 0.03 for the oscillator strength (f) in the calculation of kr using eqn (17). The molecular structure of free-base porphyrin is shown in Fig. 5a and the calculated energy levels and rate constants are presented in Fig. 5b. The calculated rate constants for the nonradiative transitions kIC and kISC are underestimated, because the present calculations yield a quantum yield of 0.96, which is an order of magnitude larger than the experimental value of 0.08.40 A previously calculated value for kISC1 is ∼107 s−1.15 The largest Huang–Rhys factors (yj) and the corresponding vibrational frequencies are listed in Table 3. The calculated yj values are very small leading to an underestimation of the rate constants of the nonradiative transitions. The vibrational modes with energies in the range 1000 cm−1 < ωj < 3000 cm−1 contribute significantly to the FC factor. The yj values of the vibrational modes in this energy range should be about 0.1–0.4. However, the largest yj value is 0.03 for the vibrational mode at 1393 cm−1, which is about one order of magnitude too small. In our previous INDO study considering one vibrational mode at 1400 cm−1, an empirical yj value of 0.3 was used leading to the rather accurate values for kIC and kISC.33 Thus, one has to go beyond the FC approximation in order to obtain accurate values for the nonradiative rate constants of free-base porphyrin.
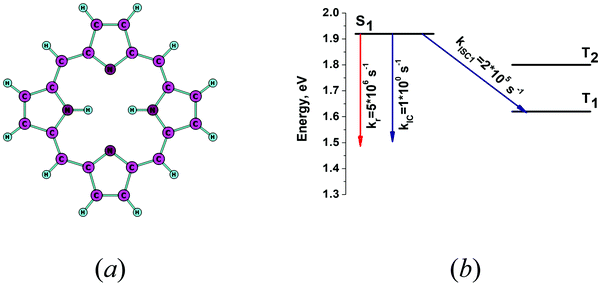 |
| | Fig. 5 (a) The optimized molecular structure of free-base porphyrin (H2P). (b) The energy level diagram for H2P including the computed values for the radiative and nonradiative rate constants. | |
4.5. Alq3 and Ir(ppy)3
The optimized molecular structures of the S1 state of fac-tris(8-hydroxyquinolinato)aluminium (fac-Alq3) and fac-tris(2-phenylpyridine)iridium (fac-Ir(ppy)3) are shown in Fig. 6a and c. The energy levels of the lowest singlet and triplet states and the kIC and kISC rate constants of the transitions are shown in Fig. 6b and d. The calculated excitation energies of the S1 and T1 states are compared with the experimental data in Table 2. The calculated excitation energies agree well with the experimental data. Only the lowest triplet state lies below the S1 state. For Alq3, the radiative and the two nonradiative deactivation channels of the S1 state have almost the same rate constants. The calculated quantum yield (φfl) of 0.25 agrees with the experimental values of 0.04–0.3 that strongly depend on environmental effects.38 For Ir(ppy)3, the ISC process dominates the deactivation of the S1 state due to the strong spin–orbit coupling effects. See Table S1 in the ESI.† The rate constant kISC1 is much larger than kr leading to a very small quantum yield, which agrees with the previously calculated value of about 1012 s−1 for kISC1 and the experimental results.68 The largest yj values and the corresponding vibrational energies (ωj) are reported in Table 3. Alq3 has many more vibrational modes with large yj values than Ir(ppy)3, which explains why Alq3 has a larger kIC rate constant than Ir(ppy)3.
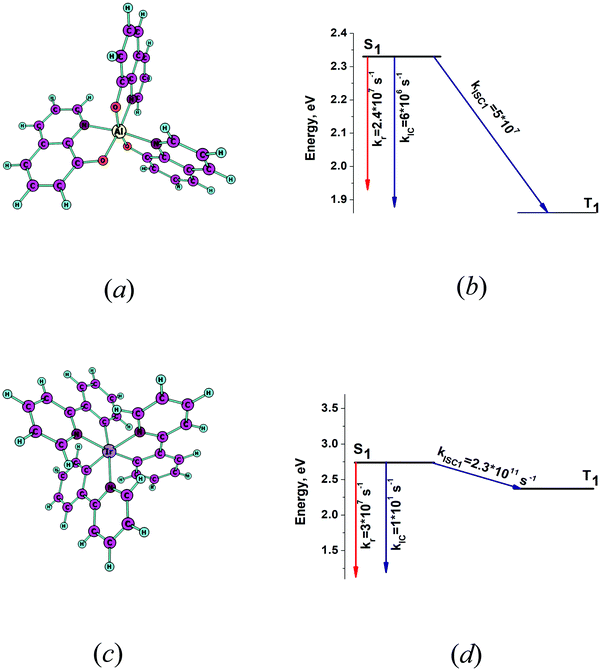 |
| | Fig. 6 (a) The optimized molecular structure of fac-Alq3. (b) The energy-level diagram for fac-Alq3 including the computed values for the radiative and nonradiative rate constants. (c) The optimized molecular structure of fac-Ir(ppy)3. (d) The energy-level diagram for fac-Ir(ppy)3 including the computed values for the radiative and nonradiative rate constants. | |
4.6. Polyacenes
The energy levels of the lowest singlet and triplet states and the kIC and kISC rate constants of the transitions of the polyacenes are shown in Fig. 7. The calculated excitation energies of the S1 and T1 states are compared with the experimental data in Table 4.
 |
| | Fig. 7 The calculated energy levels for (a) naphthalene, (b) anthracene, (c) tetracene, (d) pentacene, (e) hexacene and the computed values of the radiative and nonradiative rate constants. | |
Table 4 The calculated excitation energies (in eV) of the polyacenes are compared with the experimental data
| Compound |
State |
XMC-QDPT2 |
Exp.a |
|
The experimental data are taken from ref. 37.
|
| Naphthalene |
S1 |
3.66(0.003) |
3.86 |
| T1 |
2.67 |
2.63 |
| Anthracene |
S1 |
2.97(0.2) |
3.3 |
| T1 |
1.57 |
1.85 |
| Tetracene |
S1 |
2.7(0.1) |
2.6 |
| T1 |
1.16 |
1.26 |
| Pentacene |
S1 |
1.9(0.1) |
2.1 |
| T1 |
0.7 |
0.95 |
| Hexacene |
S1 |
1.6(0.1) |
1.8 |
| T1 |
0.5 |
0.81 |
The calculated quantum yields (φfl) for naphthalene, anthracene, tetracene, pentacene, hexacene, and heptacene are 0.94, 0.99, 0.99, 0.03, and 0.001 respectively, which can be compared with the experimental values of 0.23, 0.24, 0.21, 0.08, and 0.01.41 The calculated quantum yields differ from the experimental ones, whereas a similar trend is obtained for the polyacenes. The calculated φfl values are not very accurate, because the S1 state is not a pure adiabatic state but consists of a mixture of higher energy states.50 The estimated quantum yields (φfl) agree qualitatively with the experimental ones only when kIC is larger than kISC. For the polyacenes, the calculated kISC contribution to the nonradiative rate constant knr is underestimated. The calculated kIC and kISC rate constants are expected to be rather accurate, whereas they cannot be used for estimating the quantum yield when kIC < kISC. The values of yj and ωj are of the vibrational modes that are most important for the nonradiative transitions are listed in Table 5. The vibrational mode at about 1400 cm−1 has a y value of about 0.3 for all the polyacenes except for tetracene. This mode yields the main contribution to the kISC rate constant. In the calculation of kISC for the polyacenes, it is necessary to consider only this mode, as done by Maier and Artyukhov.25–28
Table 5 Calculated wavenumbers (ωj in cm−1) of the significant vibrational modes for the nonradiative transitions and the corresponding Huang–Rhys factors (yj) for the S1 to S0 nonradiative transition of the polyacenes
| Compound |
ω
j
(yj) |
| Naphthalene |
519 (0.06); 775 (0.23); 1055 (0.1); 1413 (0.36) |
| Anthracene |
398 (0.37); 640 (0.02); 765 (0.02); 1039 (0.01); 1194 (0.08); 1301 (0.16); 1443 (0.44); 1606 (0.40) |
| Tetracene |
318 (0.26); 633 (0.03); 765 (0.04); 1032 (0.01); 1190 (0.04); 1243 (0.17); 1425 (0.15); 1441 (0.19); 1573 (0.02); 1589 (0.25) |
| Pentacene |
263 (0.18); 615 (0.02); 764 (0.05); 1190 (0.03); 1228 (0.17); 1426 (0.24); 1449 (0.08); 1570 (0.15) |
| Hexacene |
225 (0.15); 579 (0.01); 765 (0.1); 1030 (0.01); 1183 (0.05); 1212 (0.11); 1216 (0.01); 1217 (0.06); 1418 (0.25); 1560 (0.06) |
4.7. The analysis of nonadiabatic integrals
Calculations of the nonadiabatic integrals (8) show that the largest integral value of 0.007 a.u. is obtained for the vibrational modes with energies of about 3000 cm−1, because the y value is very small for them. For the other vibrational modes, the integrals (10) are a factor of 2–22 times smaller. The high-frequency modes with ∼3000 cm−1 usually correspond to X–H stretching vibrations, where X = C, N, O or another light atom. The present study shows that in the IC channel, the excitation energy of the S1 state transforms into stretching vibrations of X–H modes, which supports the theory by Plotnikov, Maier and Artyukhov.24–28
5. Summary and conclusions
The proposed computational approach has been used for calculating the rate constants for internal conversion (kIC) and intersystem crossing (kISC) of a number of organic and organometallic compounds. The calculations show that the radiative process dominates for PM567 and AOC. The non-radiative ISC process dominates for psoralene and Ir(ppy)3, whereas the non-radiative IC process dominates for tetraoxa[8]circulene. For Alq3, the rate constants of the radiative and the non-radiative (IC and ISC) processes are of the same size. When the Franck–Condon (FC) and adiabatic approximations are valid, the proposed approach can be used for estimating the fluorescence quantum yield (φfl). For polyacenes and H2P, it is necessary to go beyond the FC and adiabatic approximations. The FC approximation breaks down, when the Huang–Rhys factor (y) is about 0.01–0.04 for modes with energies of about 1000–1800 cm−1 leading to strongly underestimated FC factors. Small values for the FC factor lead to too small calculated values for kIC and kISC. The value of y can be used as a criterion for the applicability of our approach. For H2P, the y value of the vibrational mode at 1393 cm−1 has a small Huang–Rhys factor suggesting that the present approach cannot be applied to free-base porphyrin.
The computations show that in the IC process the excitation energy transfers into the vibrations of the X–H (X = C, N and O) bonds supporting the theory by Plotnikov, Maier and Artyukhov.24–28 However, when estimating the FC factors of the ISC process, all the vibrational modes have to be taken into account, because many vibrational modes with energies in the range of 1000–1800 cm−1 contribute significantly to the FC factor.
The accuracy of the calculated kIC and kISC rate constants depends strongly on the accuracy of the calculated excitation energies of the excited singlet and triplet states. Since the obtained kIC and kISC rate constants depend strongly on the accuracy of the calculated values for the singlet and triplet excitation energies, we calculated the excitation energies at the XMC-QDPT2 level of theory, which is computationally expensive but a feasible level for molecules of this size.69,70
The present approach makes it possible to estimate rate constants for nonradiative transitions (kIC and kISC) for organic and organometallic compounds within the FC and adiabatic approximation by using calculated values for the matrix elements of the spin–orbit coupling interaction and nonadiabatic coupling interaction.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The research was carried out using a grant from the Russian Science Foundation (project No. 17-73-20012). This research has been supported by the Academy of Finland through two projects (275845 and 1309394). DS thanks the Magnus Ehrnrooth Foundation for financial support. CSC – the Finnish IT Center for Science – as well as the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) are acknowledged for computational resources.
References
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CrossRef CAS.
- N. Boens and M. Ameloot, Int. J. Quantum Chem., 2006, 106, 300–315 CrossRef CAS.
- D. Beljonne, Z. Shuai, G. Pourtois and J. L. Bredas, J. Phys. Chem. A, 2001, 105, 3899–3907 CrossRef CAS.
- B. F. Minaev, G. Baryshnikov and H. Ågren, Phys. Chem. Chem. Phys., 2014, 16, 1719–1758 RSC.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS.
- A. J. C. Kuehne and M. C. Gather, Chem. Rev., 2016, 116, 12823–12864 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- V. Ramamurthy and J. Sivaguru, Chem. Rev., 2016, 116, 9914–9993 CrossRef CAS PubMed.
-
S. P. McGlynn, T. Azumi and M. Kinoshita, Molecular Spectroscopy of the Triplet State, Englewood Cliffs, New Jersey, 1969.
-
B. Valeur, Molecular Fluorescence: Principles and Applications, Wiley-VCH GmbH, Weinheim (Federal Republic of Germany), 2002 Search PubMed.
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- V. G. Plotnikov, V. A. Dolgikh and V. M. Komarov, Opt. Spectrosc., 1977, 43, 522–527 Search PubMed.
- N. P. Gritsan, A. D. Gudmundsdóttir, D. Tigelaar, A. Zhu, W. L. Karney, C. M. Hadad and M. S. Platz, J. Am. Chem. Soc., 2001, 123, 1951–1962 CrossRef CAS PubMed.
-
R. A. Caldwell, Laser Flash Photolysis Studies of Intersystem Crossing in Biradicals and Alkene Triplets, in Kinetics and Spectroscopy of Carbenes and Biradicals, ed. M. S. Platz, Springer, Boston, MA, 1990 Search PubMed.
- S. Perun, J. Tatchen and C. M. Marian, ChemPhysChem, 2008, 9, 282–292 CrossRef CAS PubMed.
- J. Tatchen and C. M. Marian, Phys. Chem. Chem. Phys., 2006, 8, 2133–2144 RSC.
- M.-C. Li, M. Hayashi and S.-H. Lin, J. Phys. Chem. A, 2011, 115, 14531–14538 CrossRef CAS PubMed.
- W. Feng, L. Xu, X.-Q. Li, W. Fang and Y. Yan, AIP Adv., 2014, 4, 077131 CrossRef.
- J. Cao and Z.-Z. Xie, Phys. Chem. Chem. Phys., 2016, 18, 6931–6945 RSC.
- J. C. Vincenta and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348 RSC.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- B. F. E. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, J. Chem. Phys., 2016, 144, 101102 CrossRef PubMed.
- J. Li, C.-K. Lin, X. Y. Li, C. Y. Zhu and S. H. Lin, Phys. Chem. Chem. Phys., 2010, 12, 14967–14976 RSC.
- V. G. Plotnikov, Int. J. Quantum Chem., 1979, 16, 527–541 CrossRef CAS.
- G. V. Maier, V. Y. Artyukhov and N. R. Rib, Russ. Phys. J., 1993, 36, 949–954 CrossRef.
- V. Y. Artyukhov, A. I. Galeeva, G. V. Maier and V. V. Ponomarev, Opt. Spektrosk., 1997, 82, 520–523 Search PubMed.
- V. Y. Artyukhov and V. A. Pomogaev, Russ. Phys. J., 2000, 43, 590–600 CrossRef CAS.
- V. A. Pomogaev and V. Y. Artyukhov, J. Appl. Spectrosc., 2001, 68, 251–258 CrossRef CAS.
- G. V. Baryshnikov, R. R. Valiev, N. N. Karaush, V. A. Minaeva, A. N. Sinelnikov, S. K. Pedersen, M. Pittelkow, B. F. Minaev and H. Agren, Phys. Chem. Chem. Phys., 2016, 18, 28040–28051 RSC.
- R. R. Valiev, Yu. N. Kalugina and V. N. Cherepanov, Spectrochim. Acta, Part A, 2012, 99, 122–125 CrossRef CAS PubMed.
- R. R. Valiev, A. N. Sinelnikov, Y. V. Aksenova, R. T. Kuznetsova, M. B. Berezin, A. S. Semeikin and V. N. Cherepanov, Spectrochim. Acta, Part A, 2014, 117, 323–329 CrossRef CAS PubMed.
- G. V. Baryshnikov, R. R. Valiev, B. F. Minaev and H. Agren, New. J. Chem., 2017, 41, 7621–7625 RSC.
- R. R. Valiev, V. N. Cherepanov, V. Y. Artyukhov and D. Sundholm, Phys. Chem. Chem. Phys., 2012, 14, 11508–11517 RSC.
- R. R. Valiev, E. N. Telminov, T. A. Solodova, E. N. Ponyavina, R. M. Gadirov, G. V. Maier and T. N. Kopylova, Chem. Phys. Lett., 2013, 588, 184–187 CrossRef CAS.
- N. G. Bryantseva, I. V. Sokolova, R. M. Gadirov, V. P. Khilya and L. Garazd, J. Appl. Spectrosc., 2009, 76, 813–818 CrossRef CAS.
- B. F. Minaev, G. V. Baryshnikov and V. A. Minaeva, Comput. Theor. Chem., 2011, 972, 68–74 CrossRef CAS.
- N. Nijegorodov, V. Ramachandran and D. P. Winkoun, Spectrochim. Acta, Part A, 1997, 53, 1813–1824 CrossRef.
- V. V. N. Ravi Kishore, K. L. Narasimhan and N. Periasamy, Phys. Chem. Chem. Phys., 2003, 5, 1386–1391 RSC.
- J. Fine, K. Diri, A. I. Krylov, C. Nemirow, Z. Lu and C. Wittig, Mol. Phys., 2012, 110, 1849–1862 CrossRef CAS.
-
D. Dolphin, The Porphyrins, Academic Press, New York, 1978 Search PubMed.
-
P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, 1997 Search PubMed.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed.
-
B. H. Lengsfield and D. R. Yarkony, in State-selected and state-to-state in-molecule reaction dynamics-Part 2, theory, ed. M. Baer and C.-Y. Ng, John Wiley, NY, 1992, ch. 1, pp. 1–71 Search PubMed.
-
V. Barone, J. Bloino and M. Biczysko, Vibrationally-resolved electronic spectra in GAUSSIAN 09, June 24, GAUSSIAN 09 Revision A.02, 2010.
- D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592 CrossRef CAS.
- O. Vahtras and H. Ågren, J. Chem. Phys., 1992, 96, 2118–2126 CrossRef CAS.
- P. V. Yurenev, M. K. Kretov, A. V. Scherbinin and N. F. Stepanov, J. Phys. Chem. A, 2010, 114, 12804–12816 CrossRef CAS PubMed.
- M. K. Kretov, I. M. Iskandarova, B. V. Potapkin, A. V. Scherbinin, A. M. Srivastava and N. F. Stepanov, J. Lumin., 2012, 132, 2143–2150 CrossRef CAS.
- M. K. Kretov, A. V. Scherbinin and N. F. Stepanov, Russ. J. Phys. Chem. A, 2013, 87, 245–251 CrossRef CAS.
- Y. F. Pedash, O. V. Prezhdo, S. I. Kotelevskiy and V. V. Prezhdo, THEOCHEM, 2002, 585, 49–59 CrossRef CAS.
-
M. Casida, Recent Advances in Density Functional Methods Part I, World Scientific, Singapore, 1999, pp. 155–192 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- R. R. Valiev, E. N. Telminov, T. A. Solodova, E. N. Ponyavina, R. M. Gadirov, M. G. Kaplunov and T. N. Kopylova, Spectrochim. Acta, Part A, 2014, 128, 137–140 CrossRef CAS PubMed.
-
A. A. Granovsky, Firefly version 8.0.0, http://classic.chem.msu.su/gran/firefly/index.html.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 2006, 14, 1347–1363 CrossRef.
- G. V. Baryshnikov, R. R. Valiev, B. F. Minaev and H. Agren, New. J. Chem., 2017, 41, 2717–2723 RSC.
-
R. Valiev, I. Benkyi, Y. Konishev, H. Fliegl and D. Sundholm, (to be submitted).
- S. J. Strickler and R. A. Berg, Chem. Phys. Lett., 1964, 37, 814–822 Search PubMed.
- N. N. Karaush, R. R. Valiev, G. V. Baryshnikov, B. F. Minaev and H. Ågren, Chem. Phys., 2015, 459, 65–71 CrossRef CAS.
- R. R. Valiev, V. N. Cherepanov, E. G. Ermolina, R. T. Kuznetsova and D. Sundholm, J. Mol. Model., 2013, 19, 4631–4637 CrossRef CAS PubMed.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- M. Kleinschmidt, C. van Wüllen and C. M. Marian, J. Chem. Phys., 2015, 142, 094301 CrossRef PubMed.
- T. B. Emelina, A. Y. Freidzon, A. A. Bagaturyants and V. E. Karasev, J. Phys. Chem. A, 2016, 120, 7529–7537 CrossRef CAS PubMed.
- A. Y. Freidzon, A. A. Safonov and A. A. Bagaturyants, J. Phys. Chem. C, 2015, 119, 26817–26827 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp08703a |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
V. N.
Cherepanov
a,
G. V.
Baryshnikov
*ab,
V. N.
Cherepanov
a,
G. V.
Baryshnikov
 ac and
D.
Sundholm
ac and
D.
Sundholm
 b
b
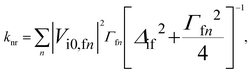
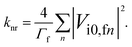
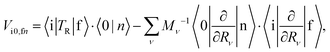
 is the nonadiabatic coupling matrix element between the electronic states |i〉 and |f〉, |0〉 is the lowest vibration state of |i〉 and |n〉 is a vibration state of the final electronic state |f〉, Rν is the nuclear coordinates of nucleus ν, and
is the nonadiabatic coupling matrix element between the electronic states |i〉 and |f〉, |0〉 is the lowest vibration state of |i〉 and |n〉 is a vibration state of the final electronic state |f〉, Rν is the nuclear coordinates of nucleus ν, and  is the nonadiabatic coupling matrix element between |0〉 and |n〉. The
is the nonadiabatic coupling matrix element between |0〉 and |n〉. The  and
and  integrals are calculated for the equilibrium geometry (R = R0) of the |f〉 state. Since the first term in eqn (3) is usually much smaller than the second term, eqn (3) can be written as24,42
integrals are calculated for the equilibrium geometry (R = R0) of the |f〉 state. Since the first term in eqn (3) is usually much smaller than the second term, eqn (3) can be written as24,42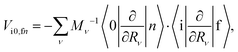
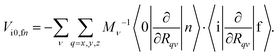
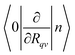 can be written using normal coordinates when the rotational and translational motions have been identified and removed
can be written using normal coordinates when the rotational and translational motions have been identified and removed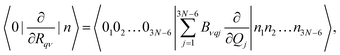
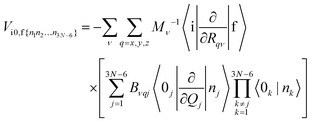
 can be expressed in harmonic approximation as
can be expressed in harmonic approximation as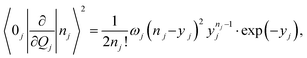



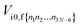 is given in eqn (10). Eif is the energy gap between the electronic states |i〉 and |f〉.
is given in eqn (10). Eif is the energy gap between the electronic states |i〉 and |f〉.

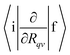 , 〈i|HSO|f〉, yj and ωj, Eif and Γf are needed. In this work,
, 〈i|HSO|f〉, yj and ωj, Eif and Γf are needed. In this work,  is calculated for molecules consisting of more than 50 atoms at the TDDFT level using Turbomole42 and for smaller molecules they are calculated at the CASSCF level of theory in GAMESS-US.43 The Huang–Rhys factors and the vibration frequencies (ωj) are calculated at the DFT and correlated ab initio levels of theory.44 The 〈i|HSO|f〉 matrix elements have been computed at the CASSCF and TDDFT levels.45,46 The line width (Γf) has been estimated using the Lax and Pekar models47–49 in the simulation of molecular vibronic spectra using the displaced oscillator model.
is calculated for molecules consisting of more than 50 atoms at the TDDFT level using Turbomole42 and for smaller molecules they are calculated at the CASSCF level of theory in GAMESS-US.43 The Huang–Rhys factors and the vibration frequencies (ωj) are calculated at the DFT and correlated ab initio levels of theory.44 The 〈i|HSO|f〉 matrix elements have been computed at the CASSCF and TDDFT levels.45,46 The line width (Γf) has been estimated using the Lax and Pekar models47–49 in the simulation of molecular vibronic spectra using the displaced oscillator model.

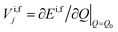 is the gradient of the potential energy surface along the jth mode at a chosen point Q0. From eqn (13) it is easily seen that
is the gradient of the potential energy surface along the jth mode at a chosen point Q0. From eqn (13) it is easily seen that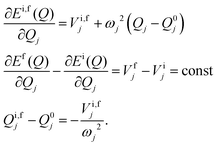
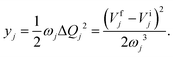
 were calculated with Turbomole at the TDDFT level of theory using the perturbation theory.42,60 The spin–orbit coupling matrix elements 〈S1|HSO|Ti〉 between the S1 state and the energetically lower ith triplet state Ti were calculated at the CASSCF level using Gamess-US.61 The excitation energies calculated at the XMC-QDPT2 level were used as the zeroth-order values. In order to calculate kISC, the one-electron spin–orbit coupling operator of the Pauli-Breit Hamiltonian was used.62 The contributions from the two-electron part of the spin–orbit coupling operator are beyond the Franck–Condon approximation.1 However, previous calculations have shown that the use of the one-electron spin–orbit operator within the FC approximation leads to accurate kISC values for the organic and organometallic compounds.29,58,63
were calculated with Turbomole at the TDDFT level of theory using the perturbation theory.42,60 The spin–orbit coupling matrix elements 〈S1|HSO|Ti〉 between the S1 state and the energetically lower ith triplet state Ti were calculated at the CASSCF level using Gamess-US.61 The excitation energies calculated at the XMC-QDPT2 level were used as the zeroth-order values. In order to calculate kISC, the one-electron spin–orbit coupling operator of the Pauli-Breit Hamiltonian was used.62 The contributions from the two-electron part of the spin–orbit coupling operator are beyond the Franck–Condon approximation.1 However, previous calculations have shown that the use of the one-electron spin–orbit operator within the FC approximation leads to accurate kISC values for the organic and organometallic compounds.29,58,63




 .66 The spin–orbit coupling matrix elements between S1 and Tj vanish due to symmetry reasons since the molecule belongs to the D4h point group. Thus, IC is the main deactivation channel of the S1 state. The calculated value for φfl is 0.13, which agrees well with the experimental value of 0.09.36 AOC has the largest quantum yield (φfl) of about 1.0, because the rate constant kISC is close to zero and kIC is significantly smaller than kr. The experimental φfl value for AOC is 0.91.29 1B3N has a smaller calculated φfl of 0.56 which is in reasonable agreement with the experimental value of 0.36.29 The reason for the smaller φfl value is the presence of several low-lying triplet states. The main deactivation channel of the S1 state is then the ISC process. The present calculations explain why the studied [8]circulenes have different quantum yields. The largest yj values and the corresponding vibrational energies (ωj) are listed in Table 3. The main vibrational mode for the nonradiative transition is at about 1400 cm−1 for AOC and 1B3N. We have previously calculated kIC and kISC at the INDO level of theory using one vibrational mode with an energy of 1400 cm−1.29 The obtained results were in good agreement with the present ones except for kIC of tetraoxa[8]circulenes (4B), because the NACMEs calculated at the INDO level are inaccurate. The reason for the deviation can be traced back to the large yj factor for the vibrational mode at 1703 cm−1, which consists of vibrational motion inside the macrocycle.65 For the other [8]circulenes (AOC and 1B3N), this mode has a smaller yj value. The present calculations show that the INDO approach does not yield accurate nonradiative rate constants for tetraoxa[8]circulene (4B) (Fig. 4).
.66 The spin–orbit coupling matrix elements between S1 and Tj vanish due to symmetry reasons since the molecule belongs to the D4h point group. Thus, IC is the main deactivation channel of the S1 state. The calculated value for φfl is 0.13, which agrees well with the experimental value of 0.09.36 AOC has the largest quantum yield (φfl) of about 1.0, because the rate constant kISC is close to zero and kIC is significantly smaller than kr. The experimental φfl value for AOC is 0.91.29 1B3N has a smaller calculated φfl of 0.56 which is in reasonable agreement with the experimental value of 0.36.29 The reason for the smaller φfl value is the presence of several low-lying triplet states. The main deactivation channel of the S1 state is then the ISC process. The present calculations explain why the studied [8]circulenes have different quantum yields. The largest yj values and the corresponding vibrational energies (ωj) are listed in Table 3. The main vibrational mode for the nonradiative transition is at about 1400 cm−1 for AOC and 1B3N. We have previously calculated kIC and kISC at the INDO level of theory using one vibrational mode with an energy of 1400 cm−1.29 The obtained results were in good agreement with the present ones except for kIC of tetraoxa[8]circulenes (4B), because the NACMEs calculated at the INDO level are inaccurate. The reason for the deviation can be traced back to the large yj factor for the vibrational mode at 1703 cm−1, which consists of vibrational motion inside the macrocycle.65 For the other [8]circulenes (AOC and 1B3N), this mode has a smaller yj value. The present calculations show that the INDO approach does not yield accurate nonradiative rate constants for tetraoxa[8]circulene (4B) (Fig. 4).






