Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The structures of liquid pyridine and naphthalene: the effects of heteroatoms and core size on aromatic interactions†
T. F.
Headen
 *a,
P. L.
Cullen
b,
R.
Patel
b,
A.
Taylor
b and
N. T.
Skipper
*a,
P. L.
Cullen
b,
R.
Patel
b,
A.
Taylor
b and
N. T.
Skipper
 *b
*b
aISIS Neutron Facility, STFC Rutherford Appleton Laboratory, Harwell Campus, Didcot, Oxon OX11 0QX, UK. E-mail: tom.headen@stfc.ac.uk
bUniversity College London, Dept. Physics and Astronomy, Gower Street, London, WC1E 6BT, UK. E-mail: n.skipper@ucl.ac.uk
First published on 10th January 2018
Abstract
Total neutron scattering has been used in conjunction with H/D and *N/15N isotopic substitution to determine the detailed liquid-state structures of pyridine and naphthalene. Analysis of the data via an empirical potential-based structure refinement method has allowed us to interrogate the full six-dimensional spatial and orientational correlation surfaces in these systems, and thereby to deduce the fundamental effects of a heteroatom and aromatic core-size on intermolecular π–π interactions. We find that the presence of a nitrogen heteroatom, and concomitant dipole moment, in pyridine induces surprisingly subtle departures from the structural correlations observed in liquid benzene: in both cases the most probable local motif is based on perpendicular (edge-to-face) intermolecular contacts, while parallel-displaced configurations give rise to a clear shoulder in the correlation surface. However, the effect of the heteroatom is revealed through detailed analysis of the intermolecular orientational correlations. This analysis shows a tendency for neighbouring pyridine molecules to direct one meta- and one para-hydrogen towards the neighbouring aromatic π-orbitals in edge-to-face configurations, while head-to-tail alignment of adjacent nitrogen atoms is favoured in face-to-face configurations. In contrast to this, increasing aromatic core size from one to only two rings has a clear and profound effect on the π–π interactions and liquid structure. Our experiments show that naphthalene–naphthalene contacts are dominated by parallel-displaced configurations, akin to those found in graphite. This marks a fundamental difference with the structure of liquid benzene, in which perpendicular geometries are favoured. Furthermore, it is remarkable to note that in the systems studied, the most favoured spatio-orientational configurations observed in the liquid state are not predicted from ab initio calculations and/or solid state crystallographic studies. This highlights the need for caution when extrapolating the results of crystallographic and computational studies to aromatic interactions in liquids and disordered systems.
Introduction
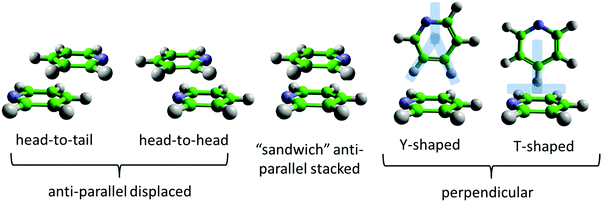
The non-covalent interactions between aromatic rings are of fundamental importance in a large number of biological and chemical processes.1–3 Examples include protein–ligand complexation,4 DNA base stacking,5 supramolecular chemical recognition,6–8 selectivity in chemical reactions,9 aggregation and solvation of carbon nanostructures,10 and petroleum phase behaviour.11,12Unlike other non-covalent interactions, such as hydrogen or halogen bonding, aromatic interactions do not arise from one single dominant interatomic mechanism. Rather, as identified by the model of Hunter and Sanders,13 they arise from a balance between London dispersion, induction, electrostatic, exchange repulsion forces, and (when in solution phase) desolvation effects. London dispersion favours maximum overlap of the molecules and, on its own, would therefore result in face-to-face parallel stacking. However, this geometry is rarely observed in practice. The key additional element of the Hunter and Sanders model is the distribution of charge, with an electrostatically positive σ-framework and negative π-orbitals. The resulting quadrupole moment tips the balance in favour of edge-to-face perpendicular or parallel-displaced geometries (see Fig. 1). Changes in structure and energetics in more complex aromatic interactions are then rationalised through their effect on the electrostatic potential of the ring,14,15 for example with electron withdrawing groups reducing electrostatic repulsion. In recent years, this view has been challenged,9 with the conclusion being that direct interactions between substituents play a significant role rather than being mediated through the π-system.1,16 Indeed strong arguments have been made that, for small aromatics, specific “π–π” interactions are not present at all, or at least that this is a rather misleading term,2,17 and that instead local interactions are the most important consideration.
It is clear, therefore, that interactions between aromatic moieties are far from being fully understood, and remain a fundamental challenge across the molecular sciences. To date, the main tools applied to tackle this problem have been ab initio calculations18–30 and gas phase spectroscopy31,32 of dimers or small clusters, spectroscopy of model systems such as molecular balances,33 solid and liquid state diffraction,34,35 and classical molecular modelling.36–40
As the simplest aromatic molecule and, therefore, benchmark, benzene has received significant attention in this context. Extensive ab initio and experimental studies of the benzene dimer have in general shown a similar energy minimum for parallel-displaced, tilted T-shaped, and perpendicular T-shaped geometries (Fig. 1).18–22 The T-shaped geometry is usually viewed as the global minimum resulting from a C–H⋯π interaction,19–22 which has been referred to as an anti-hydrogen bond, due to the calculated strengthening of the C–H bond.41 Edge-to-face Y-shaped configurations, in which two H atoms are directed towards the acceptor aromatic ring, are slightly higher in energy, but still close to the global energy minimum for the molecular dimer.22 The dominant local motif in liquid benzene is found to be perpendicular Y-shaped, but with a significant shoulder in the correlation density corresponding to a parallel-displaced geometry.42 This structural picture of benzene, as preferring perpendicular interactions that allow significant local C–H⋯π interactions, fits well with the more recent models of aromatic interactions, which prioritise local contacts rather than consideration of interactions purely between π-orbitals.1,17
Key questions regarding aromatic interactions then revolve around our fundamental understanding of the roles of heteroatoms and aromatic core size. Heterocycles and polyaromatic hydrocarbons are less well studied than benzene, but are much more representative of systems relevant to biology, chemical recognition, crystal engineering, nanocarbon solvation, and petroleum phase behaviour. Pyridine and naphthalene therefore arise naturally as model aromatic systems that take us beyond the simple benzene molecule, and allow us to work towards a more complete understanding of aromatic interactions.
Pyridine is one of the simplest heterocyclic aromatics. It has a significant charge redistribution compared to benzene, giving the molecule a gas-phase dipole moment of 2.2 D.43 It might be expected that due to this redistribution of charge, the liquid will have more pronounced orientational structure than benzene. Studies of the pyridine dimer structure by ab initio calculations show a preference for anti-parallel displaced geometries, with the nitrogen near the para-hydrogen on the ring.26–30 T-shaped perpendicular geometries (Fig. 1) have higher energies than parallel-displaced geometries.27,29 To our knowledge, Y-shaped configurations (as shown in Fig. 1) have only been considered by Hohenstein and Sherrill,29 who showed that they are lower in energy than equivalent T-shaped dimers, but still higher in energy than anti-parallel displaced configurations. In the solid state, pyridine has a complex crystal structure, with four crystallographically independent molecules in an approximation to a body-centered cubic arrangement.44,45 Similar to other small aromatics, close parallel stacking is not seen in the crystal structure, with tilted perpendicular nearest neighbour molecules having angles between the aromatic planes in the range 64–68° (as defined in Fig. 2).
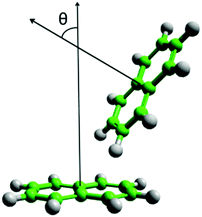 | ||
| Fig. 2 Diagram of definition of theta, angle between normal of aromatic planes, for calculation of angular radial distribution function. | ||
Naphthalene is the simplest polycyclic aromatic hydrocarbon (PAH), consisting of two fused benzene rings. Based on the models outlined above, a sensible preliminary hypothesis is that the increase in aromatic core size will push the balance in intermolecular forces towards dispersion attraction, and therefore parallel motifs. Recent ab initio studies of naphthalene dimers are consistent with this picture, showing a small preference (around 1–2 kcal mol−1) for parallel-displaced arrangements over perpendicular ones.17,23,46 Interestingly, Grimme17 shows that for aromatics larger than benzene, the increased stability of parallel stacking is due to the orbital dependent part of the dispersion energy, rather than the classical r−6 component. This suggests a special role for the π-orbitals in all polyaromatics, in other words a specific π–π interaction. The solid state crystal structure of naphthalene, in contrast, is of a herringbone type,35 with the angle between nearest neighbour aromatic planes being 53°.47 A wider crystallographic study of polyaromatic hydrocarbons shows that there are four distinct types of crystal structure of PAHs, which can be simply predicted based on the molecular structure rules.48 For example condensation of the aromatic core favours parallel structures; the smallest PAH where parallel nearest neighbours are present is pyrene, which has a structure of herringbone molecular diads.
While understanding aromatic interactions in the gas-phase and solid-state is clearly extremely demanding, the liquid-state presents further challenges, due to the complexity and variety of the local molecular environments. The high computational cost of ab initio methods means that calculating intermolecular structure in the bulk liquids is not an option. For this reason, empirically derived classical force-fields must be used. These intermolecular force-fields, such as OPLS-AA,37 are parameterized for a range aromatic molecules, and are able to closely match experimental values for enthalpy of vaporisation, density and heat capacity.36,37 Jorgensen and McDonald37 calculated the N–N radial distribution function for liquid pyridine using OPLS-AA, which showed two broad peaks at ∼4.8 and 6.0 Å. These features were attributed to head-to-head and head-to-tail antiparallel stacked structures (Fig. 1), similar to those seen in ab initio calculation of dimers. However a more detailed analysis by Baker and Grant,36 again using the OPLS-AA force-field, showed that perpendicular arrangements were preferred over parallel ones in the liquid state. This study went further, by proposing a new force-field, OPLS-CS, which more realistically represents the 3-dimensional charge distribution in aromatic molecules, by the use of virtual sites to represent charge in the aromatic ring. Analysis of a simulation of liquid pyridine using this force-field shows a much greater preference for perpendicular nearest neighbour molecules in the liquid state.
Simulation of polyaromatic molecules, such as naphthalene, is less well reported in the literature. Common force-fields, such as OPLS-AA, have the same Lennard-Jones parameters for “fused” aromatic carbon as “CH” aromatic carbon. The reliability of such force-fields when extended to polyaromatic molecules is therefore relatively untested. Explicit parameterization of polyaromatic naphthalene has been performed for the TraPPE forcefield, using phase behaviour data.40 In this study, no structural information is presented for pure liquid naphthalene. However, for concentrated mixtures of naphthalene in methanol there is a clear preference for parallel stacked nearest neighbour molecules.
Neutron scattering is an unparalleled technique in the study of the structure of molecular liquids, and has recently been used to study a number of aromatic liquids.42,49–51 The neutron scattering length is dependent on the isotope. Isotopic substitution, particularly H/D and *N/15N, can therefore be used to provide multiple datasets from the same underlying liquid structure. This, together with simulation based structure refinement, for example Empirical Potential Structure Refinement (EPSR),52 allows spatial and orientational correlations in liquids to be studied in unprecedented detail. Our previous neutron scattering study of liquid benzene,42 later confirmed by Falkowska et al.,50 shows that benzene prefers perpendicular nearest neighbours in a Y-shaped geometry. Parallel displaced geometries are present as a shoulder in the correlation surface, but are not the dominant interaction. Neutron scattering of liquid naphthalene and benzene, both exclusively in their deuterated forms, has been conducted by Misawa and Fukunaga.53 Their total structure factor was fitted to a model consisting of a first term based on a hard sphere structure factor, and a second term describing orientation correlations at short range. For liquid naphthalene, they proposed that the most probable geometry of nearest neighbour molecules is tilted at 52° between the aromatic planes, with two hydrogens pointing towards aromatic core, similar to structures seen in the solid state. Neutron diffraction of pure liquid pyridine has been conducted by McCune et al.49 using H/D isotopic substitution and EPSR, as part of study of pyridine:acetic acid mixtures. The EPSR analysis gave a spatial density function (SDF) that showed nearest neighbour pyridine molecules prefer to lie above and below the aromatic rings, and in five radial lobes, four in-between hydrogen atoms (equivalent to the Y-shaped motif observed in benzene), and one close to the nitrogen heteroatom in the ring. However, in the absence *N/15N isotopic labelling, the underlying role of the nitrogen heteroatom in the orientational structure was missing from this analysis. Key questions therefore remain unanswered regarding the fundamental nature of the spatio-orientational environment in these benchmark aromatic liquids.
In this paper, we have exploited state-of-the-art liquid state neutron diffraction in conjunction with a comprehensive set of H/D and *N/15N isotopic substitutions to obtain unique insight into the structure of liquid benzene and naphthalene. We find that the presence of a nitrogen heteroatom leads to subtle orientational preferences among neighbouring pyridine molecules, while retaining the spatial correlations observed in liquid benzene. In liquid naphthalene, on the other hand, we find that the increase in core size has a dramatic effect on the local structure, leading to a preponderance of parallel-displaced stacking akin to that observed in graphite. Remarkably, the liquid structures are therefore fundamentally different from those observed in the solid (crystalline) state and/or from ab initio calculations. This conclusion has profound implications for our understanding of the role of aromatic interactions in many natural and industrial processes.
Scattering theory
The quantity measured in a neutron scattering experiment is the differential scattering cross-section.54 After appropriate corrections this yields the total structure factor, F(Q). We take advantage of the fact that neutrons scatter from nuclei and therefore the scattering length, bi, is different for different isotopes. Specifically, substitution of hydrogen (bH = −3.74 fm) for deuterium (bD = 6.67 fm), is convenient and relatively easily exchanged for many organic molecules. Moreover, in the current context, we can also exploit the scattering contrast between *N and 15N (b*N = 9.36 fm and b15N = 6.44 fm). By performing the experiment on 3 or more isotopically exchanged samples it is therefore possible for us to determine reliable radial and orientational correlations, as the complimentary data sets place strong constraints on the structure refinement methods.In practice, we measure M data sets, Fi(Q), each of which has a different isotopic composition. The corrected diffraction data is then a weighted sum of the different partial structure factors arising from different pairs of atoms α, β.
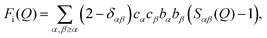 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ (i.e. the magnitude of the momentum change vector of the scattered neutrons), and Sαβ(Q) is the Faber–Ziman partial structure factor involving atoms α and β only. Eqn (1) may be re-written as:
θ)/λ (i.e. the magnitude of the momentum change vector of the scattered neutrons), and Sαβ(Q) is the Faber–Ziman partial structure factor involving atoms α and β only. Eqn (1) may be re-written as: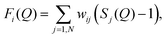 | (2) |
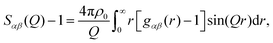 | (3) |
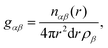 | (4) |
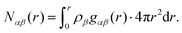 | (5) |
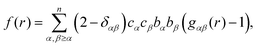 | (6) |
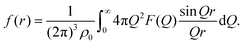 | (7) |
Experimental
Scattering data were collected using the Small Angle Neutron Diffractometer for Liquid and Amorphous Samples (SANDALS) at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, U.K. SANDALS is optimized for the measurement of the structure of liquid and amorphous samples, and in particular for hydrogen/deuterium substitution.55 Neutron scattering of three isotopically distinct samples of liquid naphthalene and four isotopically distinct samples of liquid pyridine were taken at 85 °C and 25 °C respectively. For naphthalene the samples were: (i) fully deuterated naphthalene (>98% deuterated, Sigma Aldrich), (ii) hydrogenated naphthalene (purity > 99.7%, Sigma Aldrich) and (iii) a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 molar mixture of the two. For pyridine the samples were (i) fully deuterated pyridine (99.5% deuterated, Cambridge Isotope Laboratories), (ii) hydrogenated pyridine (anhydrous, 99% purity, Sigma Aldrich), (iii) a 50
50 molar mixture of the two. For pyridine the samples were (i) fully deuterated pyridine (99.5% deuterated, Cambridge Isotope Laboratories), (ii) hydrogenated pyridine (anhydrous, 99% purity, Sigma Aldrich), (iii) a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 molar mixture of the two and (iv) 15N enriched hydrogenated pyridine (>98% 15N, Cambridge Isotope Laboratories). The liquids were used as received and inserted into a flat-plate null coherent scattering titanium/zirconium cell, with 1 mm sample and wall thicknesses. This geometry minimizes multiple neutron scattering and absorption effects. The temperature was maintained via a closed-cycle water bath. Typical counting times were ∼8 hours for each sample. For data correction and calibration, scattering data were also collected from the empty instrument (with and without the empty sample cell), and an incoherent scattering vanadium standard slab of thickness 3 mm. Background, multiple scattering, absorption, and normalization correction procedures were implemented by the GUDRUN suite of programs,56 to give the differential scattering cross-section for each isotopically distinct sample. Particular attention needs to be paid to correction of inelasticity effects, especially for the samples containing hydrogen. The self-scattering background and inelasticity effects were removed from the total differential scattering cross section using an iterative method developed by Soper.57,58
50 molar mixture of the two and (iv) 15N enriched hydrogenated pyridine (>98% 15N, Cambridge Isotope Laboratories). The liquids were used as received and inserted into a flat-plate null coherent scattering titanium/zirconium cell, with 1 mm sample and wall thicknesses. This geometry minimizes multiple neutron scattering and absorption effects. The temperature was maintained via a closed-cycle water bath. Typical counting times were ∼8 hours for each sample. For data correction and calibration, scattering data were also collected from the empty instrument (with and without the empty sample cell), and an incoherent scattering vanadium standard slab of thickness 3 mm. Background, multiple scattering, absorption, and normalization correction procedures were implemented by the GUDRUN suite of programs,56 to give the differential scattering cross-section for each isotopically distinct sample. Particular attention needs to be paid to correction of inelasticity effects, especially for the samples containing hydrogen. The self-scattering background and inelasticity effects were removed from the total differential scattering cross section using an iterative method developed by Soper.57,58
Results and analysis
Empirical potential structure refinement
Empirical Potential Structural Refinement (EPSR) is a means to maximize the information that can be extracted from a set of scattering experiments on a disordered system. The method produces a 3-dimensional ensemble of molecules which is consistent with the measured scattering data, and uses the scattering data as a constraint against which to refine a classical molecular simulation of the system under study. The detailed theory behind the EPSR technique is discussed elsewhere.52,57 In brief, the method starts with an equilibrated Monte Carlo simulation based on initial ‘seed’ potentials. The procedure then iteratively modifies an additional empirical potential, based on the difference between measured and simulated structure factors, until the molecular ensemble becomes consistent with the scattering data. The technique allows known prior information, such as molecular geometry, overlap and electrostatic constraints to be built into the refinement procedure.The EPSR ensemble consists of 1000 molecules for the naphthalene simulations and 500 molecules for pyridine. The ‘seed’ potentials are the atom-centered OPLS-AA force field parameters.37,59 Partial charges and equilibrium molecular geometry for naphthalene were calculated using MOPAC using the PM3 Hamiltonian,60 for pyridine the standard OPLS-AA partial charges and equilibrium molecular geometry were used (C–C bond lengths were slightly shortened, by 0.005 Å from standard OPLS values to give best match to f(r) data). Bonds are represented by a harmonic potential. Intramolecular-angles and dihedrals are maintained by the use of a harmonic potential between the first and third, and first and forth atom respectively. The use of dihedrals is vital to maintain the planarity of the aromatic rings. The coordinates of all atoms were saved every 5 Monte Carlo iterations for a total of over at least 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations. This allows a later analysis of ensemble of molecules consistent with the different scattering datasets. Analysis of EPSR simulation trajectories was conducted using the dlputils61 suite of programmes to obtain the molecule–molecule radial distribution functions, angular radial distribution functions and spatial density functions. The fit of the EPSR simulation to the neutron scattering data is presented below.
000 iterations. This allows a later analysis of ensemble of molecules consistent with the different scattering datasets. Analysis of EPSR simulation trajectories was conducted using the dlputils61 suite of programmes to obtain the molecule–molecule radial distribution functions, angular radial distribution functions and spatial density functions. The fit of the EPSR simulation to the neutron scattering data is presented below.
In addition to the standard EPSR simulation, as outlined above, we conducted a number of other simulations to determine the efficacy of the method and understand how the introduction of the data to the simulation changes the liquid structure observed. Firstly, we conducted an EPSR simulation without refinement to the data, this shows the how well the initial “seed” potential can replicate the experimental data. Secondly we conducted simulations with altered seed potentials, which were run both with and without refinement. We chose to change the seed potentials by multiplying the partial charges by a factor of either 2, 1.5 or 0.5. This has the effect of either exaggerating or diminishing structural features in molecular ensemble when run without refinement. This allowed us to examine whether these structural features are wholly due to the refinement to the data, or due to the simulation methods used.
Liquid pyridine at 25 °C
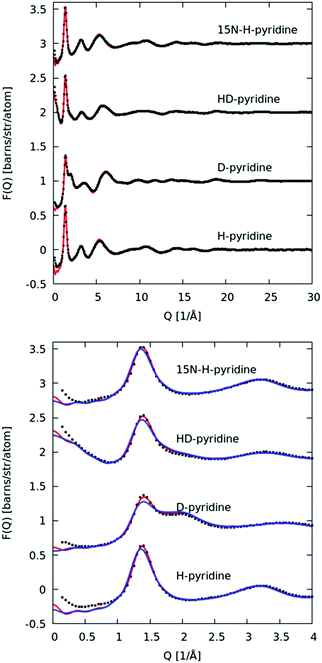
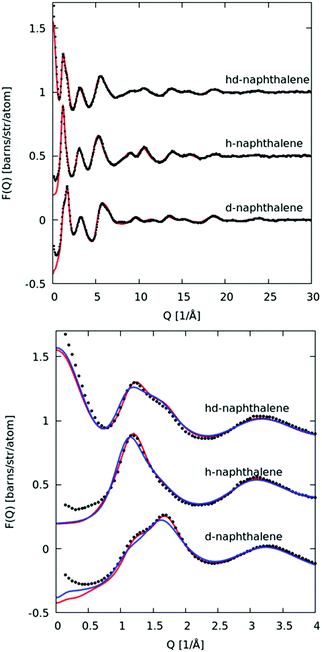
In Fig. 3 we plot the interference differential scattering cross section for the four different isotopically distinct liquid pyridine samples, along with the EPSR fit to the data and the calculated scattering from a Monte Carlo simulation using standard reference potentials, but without refinement to the data. The EPSR fit to the data is very good and there is a clear improvement on the fit when compared to EPSR run without refinement. Fit to the real space Fourier transform of the data is also good (see SI.1, ESI†).Analysis of the full EPSR simulation over many thousands of iterations allows analysis of the local structure around a central pyridine molecule, for example the ring-center to ring-center radial distribution function as shown in Fig. 4. There is a well-defined first solvation shell peak with a maximum at approximately 5.5 Å and first minimum at 7.5 Å. Using this distance to define the first solvation shell, calculation of the N(r) using eqn (5) shows that there are approximately 12.5 molecules in the first solvation shell.
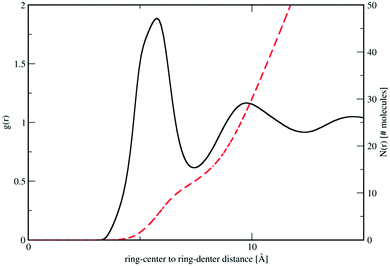 | ||
| Fig. 4 Molecule ring center–center (black) and cumulative coordination number N(r) (red dashed lines) from the refined EPSR simulation for liquid pyridine. | ||
To further interrogate the local orientational structure we calculated the angular radial distribution function, g(r,θ), where θ is the angle between the aromatic cores (see Fig. 2), as calculated using:
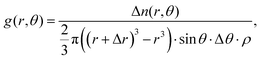 | (8) |
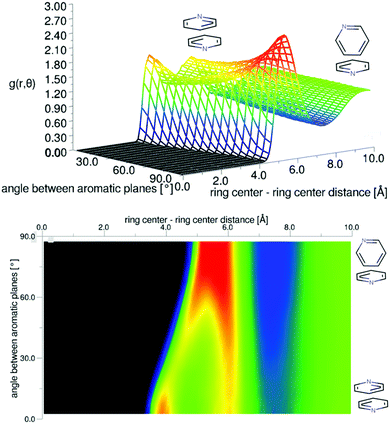 | ||
| Fig. 5 Angular radial distribution function for liquid pyridine as calculated from the refined EPSR simulation, shown in 3D (top) and as a 2D projection (bottom). | ||
The preference for perpendicular nearest neighbour molecules runs counter to ab initio calculations of dimers and small clusters which show an energetic preference for antiparallel stacked nearest neighbours. The result is however similar to calculations from classical simulation studies of bulk phase liquid pyridine.36 For a simulation run using the EPSR Monte Carlo simulation, but without refinement to the data, there is indeed a stronger preference for parallel molecular nearest neighbours (see SI-S2, ESI†). The refinement to the data reduces this parallel peak in the angular radial distribution function. To test this further, two additional EPSR simulations were run with the partial charges changed by a factor of 0.5 and 2 (plots of angular radial distribution functions given in SI-S2, ESI†). Halving the partial charges has the effect of further increasing the parallel peak in the angular radial distribution function when run without refinement to the data. When the refinement to the scattering data is performed, the parallel peak is much reduced and the g(r,θ) is very similar to that produced with standard partial charges. The relatively low preference for parallel molecules, at least compared to theoretical expectations, is then believed to be a strong feature within the data. When run with doubled partial charges and without refinement to the data, the parallel stacking peak in g(r,θ) is completely removed and does not fully return when refined to the data. This suggests it is a small structural feature and is not strongly weighted in the data.
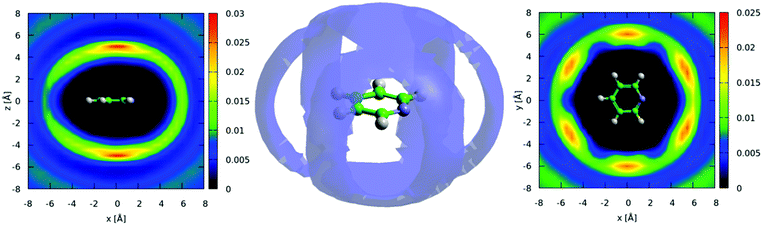
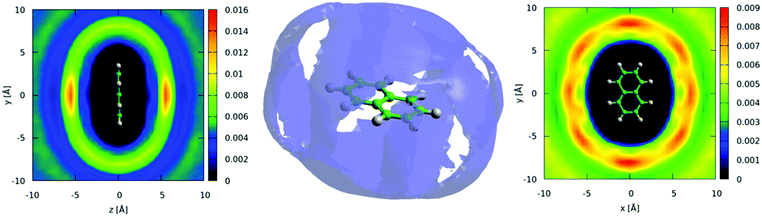
The three-dimensional spatial density function (SDF) for the 25% most likely ring-center to ring-center correlations in the first solvation shell (7.5 Å) are shown in the center of Fig. 6, with 2-dimensional slices revealing further detail of the most likely locations shown to the right and left. This shows a remarkably similar 3-dimensional structure to benzene,42 with significant density above and below the aromatic plane and clearly defined lobes running in-between the hydrogen atoms in the molecule, indicating a “Y-shaped” geometry of nearest neighbour molecules (Fig. 1). Despite the presence of a heteroatom in the aromatic ring, the spatial density function remains surprisingly close to having six-dimensional symmetry. This indicates that the change in electrostatic charge distribution has a rather minimal effect on three-dimensional spatial liquid structure.
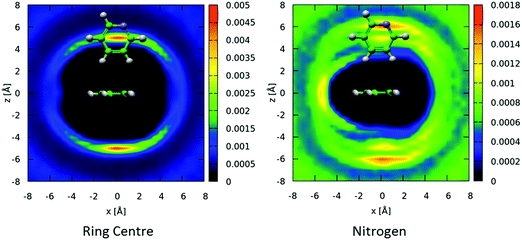
If one looks at the location of the nitrogen atoms in the surrounding molecules there are clear preferential locations. Fig. 7 shows the 3-dimensional spatial density functions for nitrogen (blue) and meta hydrogen atoms (white) around a central pyridine.
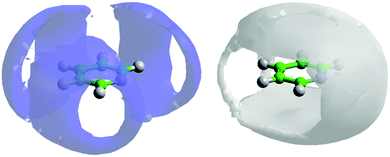 | ||
| Fig. 7 Spatial density function showing the 10% most likely positions of pyridine nitrogen atoms (blue volume – left) and meta-hydrogen atoms (grey volume – right) around a central molecule. | ||
By reference to calculated atomic partial charges62 it can be seen that electrostatic repulsion between the partially negatively charged nitrogen with itself and the meta carbon (C2), plays a strong role in the location of the pyridine nitrogen in the first solvation shell. If we now consider the location of meta hydrogens (H2) around the central molecule, it is clear there is a favourable interaction. It is worth noting the spatial density function of H2 fits almost completely within the free space for the SDF for nitrogen and vice versa. Similar spatial density functions are seen for all other hydrogen atoms on pyridine (see SI-S3, ESI†). The high density of hydrogen about the nitrogen atom, specifically near the nitrogen lone pair, as shown in Fig. 7 may suggest the existence of C–H⋯N hydrogen bonding. However an analysis of the H⋯N partial g(r)'s (see SI-S4, ESI†) do not show any significant H⋯N intermolecular contacts below 2.5 Å, a typical cut-off for hydrogen bonding,63 suggesting only weak hydrogen bonding is present.
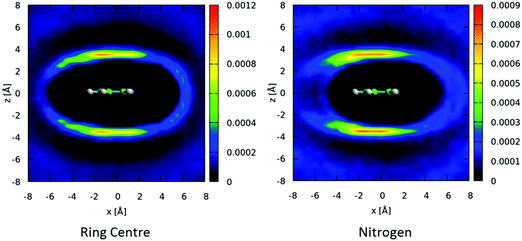
The above spatial density functions are independent of the orientation of the second molecule around the first. From the angular radial distribution functions it is clear that perpendicular arrangement of molecules is preferred. In Fig. 8 we show two-dimensional slices of the spatial density function for the ring center (left) and nitrogen atom (right) of perpendicular nearest neighbour molecules around a central molecule. Perpendicular molecules are (arbitrarily) defined as those where the angle between the aromatic planes is between 80–90°. The ring-centers show a clear preference for being directly above and below the aromatic planes and in-between the hydrogen atoms in equatorial positions. In contrast, the nitrogen atoms on the second molecules show a preference to be in an offset position, with an area of high probability indicating a clear orientational preference – a Y-stacked geometry with the nitrogen of the second molecules pointing away from the first, with the para and meta hydrogens pointing towards the ring of the central molecule as indicated in Fig. 8.
We can similarly study the spatial preferences for parallel nearest neighbour molecules. In Fig. 9 we show 2-dimensional cuts through the spatial density function for molecules where the angle between the aromatic plane is in the range 0–10°. There is a preference for molecules to be above/below the aromatic ring, with a slight preference for a displacement away from the nitrogen of the central molecule. There is also a preference for the nitrogen of the second molecule to be anti-parallel to the first, indicating a head-to-tail antiparallel displaced geometry.
Liquid naphthalene at 85 °C
In Fig. 10 we plot the interference scattering cross section for the three different isotopically distinct liquid naphthalene samples, along with the EPSR fit to the data and the calculated scattering from a Monte Carlo simulation using standard reference potentials, but without refinement to the data. The EPSR fit to the data is very good and there is a clear improvement on the fit when compared to EPSR run without refinement. The fit of the pair correlation function, f(r), i.e. the direct Fourier transform on the F(Q) is shown in the ESI† (SI.1). The real-space fit is also good, confirming the validity of the molecular structure used.In Fig. 11 we show the molecule center–center radial distribution function and the cumulative molecular coordination number (eqn (5)). If we assume the end of the first solvation shell is at 9 Å (the minimum of the g(r)), this gives a coordination number in the first solvation shell of 13.0 molecules.
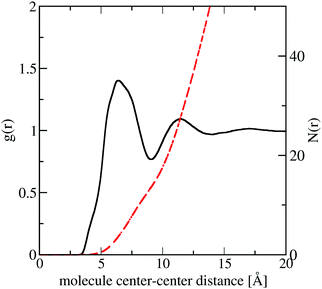 | ||
| Fig. 11 Molecule center–center radial distribution function, g(r) (black) and cumulative coordination number N(r) (red dash) from the refined EPSR simulation for liquid naphthalene. | ||
It is clear that the first solvation shell contains some structure due to the visible shoulders on both sides of the main peak in the g(r). The angular radial distribution function for liquid naphthalene is displayed in Fig. 12.
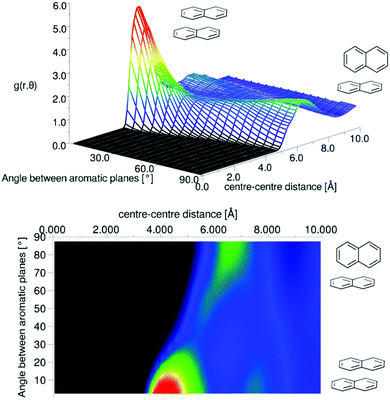 | ||
| Fig. 12 Angular radial distribution function for liquid naphthalene as calculated from the refined EPSR simulation. | ||
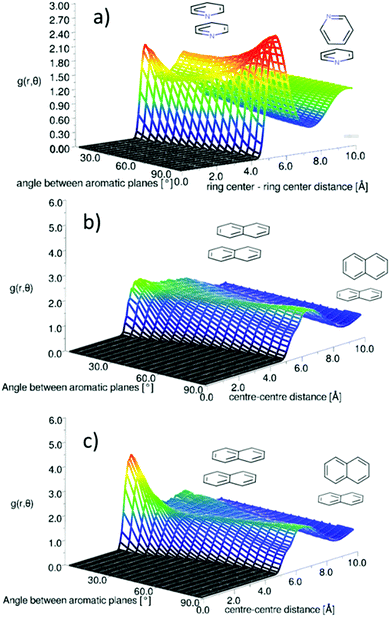
There is a clear peak representing a preference for parallel nearest neighbour molecules. This should be shown in contrast to benzene,42,50 where although a parallel arrangement of the molecules is seen as a shoulder in the angular radial distribution function, it is not a local maximum. It also should be noted that perpendicular nearest neighbours are a local maximum in the data, and of a similar height as seen in liquid benzene. We can calculate the number of molecules in this parallel geometry by defining limits and integrating over θ = 0–30° and r = 0–5.5 Å, giving 0.51 molecules. Although this only represents a relatively small proportion of all molecules in the whole first solvation shell, it does represent 43% of all molecules up to this separation. Also one may consider that, on average, almost half of all molecules are in this closely aligned dimer arrangement. This strong preference for parallel arrangements is a striking feature of the g(r,θ), therefore in order to gain some confidence that this feature was indeed represented in the data we ran test simulations with alternative partial charges in the seed potentials (see SI-S4, ESI†). With only reference potentials used, increasing the partial charges removed the parallel stacking peak, whereas decreasing the partial charges intensified the peak. When we use the EPSR method to refine interatomic potentials to the experimental data, the main features of the angular radial distribution function, are faithfully reproduced (ESI:† Fig. S6). This gives us greater confidence that the preference for parallel nearest neighbour molecules is a strong feature of the experimental data.
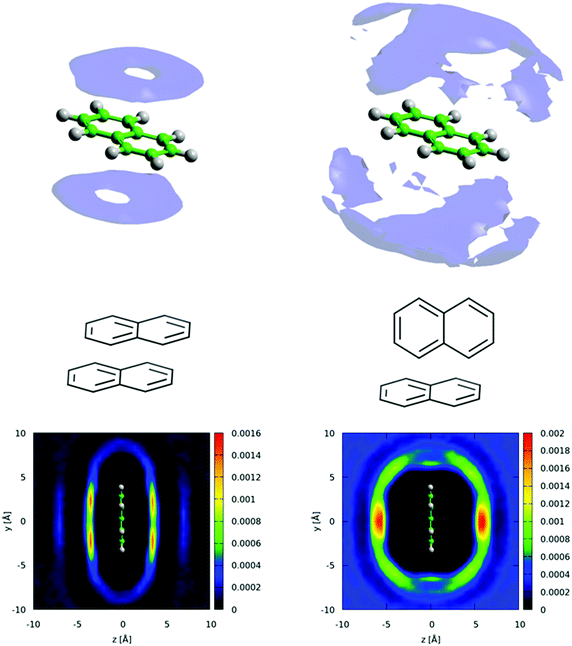
The distribution of molecules in the first solvation shell in three dimensions can be displayed using spatial density functions, showing the volume occupied by the most likely positions of a second molecule around the first up to a certain percentage. In Fig. 13 we show the spatial density functions for naphthalene center–center correlations at the 25% level in the first solvation shell. For increased clarity, Fig. 13 also shows 2 dimensional cuts through the SDF revealing the level of order in the first solvation shell. There is a clear preference for neighbouring molecules to be above and below the aromatic ring (Fig. 13 left). Where there is a preference for molecules to be on the edge of the aromatic plane it is in positions between two hydrogen atoms (Fig. 13 right). This is similar to the “Y-stacking” geometry we noted in similar plots for liquid benzene,42 although the level of order is significantly weaker than seen for benzene (or pyridine).
We can further interrogate the orientational structure of the surrounding naphthalene molecules in the first solvation shell by limiting the calculation of the spatial density function to molecules within a certain orientation range. In Fig. 14 we show the centre–centre spatial density functions for molecules where the angle between the aromatic planes is between 0–10° i.e. parallel, and 80–90° i.e. perpendicular. From Fig. 14 it is clear that parallel molecules are above and below the aromatic plane. A preference for parallel-displaced stacking can be clearly observed in the two dimensional slice through the SDF.
Comparison to simulation
One outstanding and important question is how well standard molecular simulation force fields capture the orientational structure of liquid naphthalene and pyridine. As a starting point to address this we have conducted molecular dynamics simulations of pyridine (Fig. 15a) and naphthalene (Fig. 15b) using the OPLS-AA force-field which has been shown to reproduce the structure of liquid benzene well.64 Further details of the simulations are given in the ESI† (SI-S5). The plots of g(r,θ) show that the OPLS force-field gives a qualitatively similar g(r,θ) for pyridine, albeit with a slightly higher shoulder for parallel neighbours. This relatively simplistic atom centred potential provides a much better description of the orientational structure than the charge separated (OPLS-CS) model that explicitly described the π-electron density, which gives a considerably stronger preference for perpendicular nearest neighbours.36For naphthalene the OPLS-AA force-field clearly does not replicate the experimental g(r,θ), showing no clear preference for parallel nearest neighbours. The OPLS force-field treats the “condensed” carbon as having the same Lennard-Jones parameters as a standard benzene carbon. This is the most obvious over-simplification, which may give rise to this structural discrepancy. The TraPPE forcefield does parameterise different LJ parameters for the condensed carbon atoms.40Fig. 15c shows the angular radial distribution function for naphthalene simulated with the TrappE forcefield, showing a clear similarity to that calculated from the EPSR refined results. These results show the importance of experimental scattering data in benchmarking molecular simulation.
Conclusions
We have conducted neutron scattering investigations of the liquid structures of pyridine and naphthalene, using a comprehensive suite of isotopic substitutions in conjunction with Empirical Potential Structure Refinement (EPSR). This combination of experimental techniques and analysis has allowed us to conduct a full six-dimensional spatial and orientational study of the structure of these archetypal aromatic liquids. By benchmarking these data against the structure of liquid benzene,42 we are then able to address key questions centring around the fundamental roles of a heteroatom and concomitant charge redistribution in the ring (pyridine), and increase in core size (naphthalene). In each case, our results have uncovered major surprises that have a profound impact on our understanding of aromatic interactions. First, in spite of the obvious differences for example in charge distribution, the spatial correlations in liquid pyridine are remarkably similar to those observed in benzene: in both cases the most probable local motif is based on perpendicular (edge-to-face) intermolecular contacts, while parallel-displaced configurations give rise to a clear shoulder in the correlation surface. In fact, it is only through our detailed analysis of the orientational correlations that we are able to identify a tendency for neighbouring pyridine molecules to direct one meta- and one para-hydrogen towards the neighbouring aromatic π-orbitals in edge-to-face configurations, while head-to-tail alignment of adjacent nitrogen atoms is favoured in face-to-face configurations. Second, and in total contrast to the effect of a heteroatom, the impact of increasing core size from one to only two rings is dramatic. In this case, the dominant motif for neighbouring molecules shifts from being perpendicular (edge-to-face) to parallel-displaced (graphite-like). Remarkably, therefore, the most probably motifs in the liquids are not observed in the corresponding crystals, where tilt angles between aromatic planes of 64–68° and 53° are observed for pyridine and naphthalene respectively. It is worth noting, at least qualitatively, the role of entropy in the structures observed in the liquid, as fundamentally it is the level of disorder which differentiates the liquid structure from that seen in the crystal and gas phase dimer/trimer states. It is highly probable that molecular topology plays a significant role in influencing, for example, the balance between entropy and enthalpy changes due to parallel vs. perpendicular stacking. This may help to explain the similarity between in the g(r,θ) for pyridine and benzene, which have a similar molecular topology. Looking forward, the outcome of molecular simulations can be used to guide further calculations of entropic contributions from knowledge of the full orientational correlation function,65,66 which further emphasises the importance of experimental data to provide reliable structural ensembles.Finally our analysis highlights intriguing discrepancies between our experimental findings and the results from ab initio and classical molecular simulation, with wide-ranging consequences for computational studies of condensed sp2 carbon. More generally, we conclude that studies of molecules in the liquid state are essential if we are to understand and predict the role of aromatic interactions in non-crystalline environments, such as those encountered in a wide range of important biological and chemical processes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the UK Science and Technology Facilities Council (STFC) for SANDALS beamtime allocation (experiment RB1210289) and the use of SCARF computational facility for EPSR simulations. The UK Natural and Environmental Research Council (NERC) is acknowledged for support of a PhD studentship for RP.References
- S. E. Wheeler and J. W. G. Bloom, J. Phys. Chem. A, 2014, 118, 6133–6147 CrossRef CAS PubMed.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191 RSC.
- L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef CAS PubMed.
- R. Fasan, R. L. A. Dias, K. Moehle, O. Zerbe, D. Obrecht, P. R. E. Mittl, M. G. Grütter and J. A. Robinson, ChemBioChem, 2006, 7, 515–526 CrossRef CAS PubMed.
- V. L. Malinovskii, F. Samain and R. Häner, Angew. Chem., Int. Ed., 2007, 46, 4464–4467 CrossRef CAS PubMed.
- K. Tahara, T. Fujita, M. Sonoda, M. Shiro and Y. Tobe, J. Am. Chem. Soc., 2008, 130, 14339–14345 CrossRef CAS PubMed.
- J. Yang, M. B. Dewal, D. Sobransingh, M. D. Smith, Y. Xu and L. S. Shimizu, J. Org. Chem., 2009, 74, 102–110 CrossRef CAS PubMed.
- C. M. Fitchett, C. Richardson and P. J. Steel, Org. Biomol. Chem., 2005, 3, 498–502 CAS.
- S. E. Wheeler, A. J. McNeil, P. Müller, T. M. Swager and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 3304–3311 CrossRef CAS PubMed.
- E. M. Pérez and N. Martín, Chem. Soc. Rev., 2015, 44, 6425–6433 RSC.
- O. C. Mullins, H. Sabbah, J. Eyssautier, A. E. Pomerantz, L. Barré, A. B. Andrews, Y. Ruiz-Morales, F. Mostowfi, R. McFarlane, L. Goual, R. Lepkowicz, T. Cooper, J. Orbulescu, R. M. Leblanc, J. Edwards and R. N. Zare, Energy Fuels, 2012, 26, 3986–4003 CrossRef CAS.
- M. R. Gray, R. R. Tykwinski, J. M. Stryker and X. Tan, Energy Fuels, 2011, 25, 3125–3134 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062 CAS.
- F. Cozzi, M. Cinquini, R. Annunziata, T. Dwyer and J. S. Siegel, J. Am. Chem. Soc., 1992, 114, 5729–5733 CrossRef CAS.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed.
- E. Miliordos, E. Aprà and S. S. Xantheas, J. Phys. Chem. A, 2014, 118, 7568–7578 CrossRef CAS PubMed.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS PubMed.
- A. K. Tummanapelli and S. Vasudevan, J. Chem. Phys., 2013, 139, 201102 CrossRef PubMed.
- T. Janowski and P. Pulay, Chem. Phys. Lett., 2007, 447, 27–32 CrossRef CAS.
- O. Bludský, M. Rubeš, P. Soldán and P. Nachtigall, J. Chem. Phys., 2008, 128, 114102 CrossRef PubMed.
- N. O. Dubinets, A. A. Safonov and A. A. Bagaturyants, J. Phys. Chem. A, 2016, 120, 2779–2782 CrossRef CAS PubMed.
- W. Wang, T. Sun, Y. Zhang and Y.-B. Wang, J. Chem. Phys., 2015, 143, 114312 CrossRef PubMed.
- S. Tsuzuki, T. Uchimaru, K. Matsumura, M. Mikami and K. Tanabe, Chem. Phys. Lett., 2000, 319, 547–554 CrossRef CAS.
- D. B. Ninković, G. V. Janjić and S. D. Zarić, Cryst. Growth Des., 2012, 12, 1060–1063 Search PubMed.
- B. K. Mishra and N. Sathyamurthy, J. Phys. Chem. A, 2005, 109, 6–8 CrossRef CAS PubMed.
- B. K. Mishra, J. S. Arey and N. Sathyamurthy, J. Phys. Chem. A, 2010, 114, 9606–9616 CrossRef CAS PubMed.
- E. G. Hohenstein and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 878–886 CrossRef CAS PubMed.
- J. Zhang, Y. Gao, W. Yao, S. Li and F.-M. Tao, Comput. Theor. Chem., 2014, 1049, 82–89 CrossRef CAS.
- W. Kim, M. W. Schaeffer, S. Lee, J. S. Chung and P. M. Felker, J. Chem. Phys., 1999, 110, 11264 CrossRef CAS.
- M. W. Schaeffer, W. Kim, P. M. Maxton, J. Romascan and P. M. Felker, Chem. Phys. Lett., 1995, 242, 632–638 CrossRef CAS.
- P. Li, C. Zhao, M. D. Smith and K. D. Shimizu, J. Org. Chem., 2013, 78, 5303–5313 CrossRef CAS PubMed.
- G. A. Jeffrey, J. R. Ruble, R. K. McMullan and J. A. Pople, Proc. R. Soc. A, 1987, 414, 47–57 CrossRef CAS.
- G. R. Desiraju and A. Gavezzotti, J. Chem. Soc., Chem. Commun., 1989, 621 RSC.
- C. M. Baker and G. H. Grant, J. Chem. Theory Comput., 2007, 3, 530–548 CrossRef CAS PubMed.
- W. L. Jorgensen and N. A. McDonald, THEOCHEM, 1998, 424, 145–155 CrossRef CAS.
- E. Megiel, T. Kasprzycka-Guttman, A. Jagielska and L. Wróblewska, J. Mol. Struct., 2001, 569, 111–119 CrossRef CAS.
- K. Sagarik and E. Spohr, Chem. Phys., 1995, 199, 73–82 CrossRef CAS.
- N. Rai and J. I. Siepmann, J. Phys. Chem. B, 2013, 117, 273–288 CrossRef CAS PubMed.
- P. Hobza, V. Špirko, H. L. Selzle and E. W. Schlag, J. Phys. Chem. A, 1998, 102, 2501–2504 CrossRef CAS.
- T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742 CrossRef CAS PubMed.
- A. D. Buckingham, J. Y. H. Chau, H. C. Freeman, R. J. W. Le Fèvre, D. A. A. S. N. Rao and J. Tardif, J. Chem. Soc., 1956, 0, 1405–1411 RSC.
- D. Mootz and H.-G. Wussow, J. Chem. Phys., 1981, 75, 1517 CrossRef CAS.
- A. T. Anghel, G. M. Day and S. L. Price, CrystEngComm, 2002, 4, 348–355 RSC.
- N. K. Lee, S. Park and S. K. Kim, J. Chem. Phys., 2002, 116, 7910 CrossRef CAS.
- S. C. Capelli, A. Albinati, S. A. Mason and B. T. M. Willis, J. Phys. Chem. A, 2006, 110, 11695–11703 CrossRef CAS PubMed.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 473–482 CrossRef.
- J. A. McCune, A. H. Turner, F. Coleman, C. M. White, S. K. Callear, T. G. A. Youngs, M. Swadźba-Kwaśny and J. D. Holbrey, Phys. Chem. Chem. Phys., 2015, 17, 6767–6777 RSC.
- M. Falkowska, D. T. Bowron, H. G. Manyar, C. Hardacre and T. G. A. Youngs, ChemPhysChem, 2016, 17, 2043–2055 CrossRef CAS PubMed.
- J. Szala-Bilnik, M. Falkowska, D. T. Bowron, C. Hardacre and T. G. A. Youngs, ChemPhysChem, 2017, 18, 2541–2548 CrossRef CAS PubMed.
- A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- M. Misawa and T. Fukunaga, J. Chem. Phys., 1990, 93, 3495 CrossRef CAS.
- H. E. Fischer, A. C. Barnes and P. S. Salmon, Rep. Prog. Phys., 2010, 69, 233–299 CrossRef.
- C. Benmore and A. K. Soper, The SANDALS manual, Rutherford Appleton Laboratory Technical Report, RAL-TR-89-046, 1989.
- A. K. Soper, W. S. Howells and A. C. Hannon, Atlas-Analysis Time-of-flight Diffraction data from Liquid and Amorphous Samples; Rutherford Appleton Laboratory Report RAL-TR-98-006, 1998.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67 CrossRef.
- A. K. Soper, Mol. Phys., 2009, 107, 1667–1684 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS.
- T. G. A. Youngs, DLPUtils, http://https://www.projectaten.com/dlputils.
- W. L. Jorgensen and N. A. McDonald, THEOCHEM, 1998, 424, 145–155 CrossRef CAS.
- I. Y. Torshin, I. T. Weber and R. W. Harrison, Protein Eng., 2002, 15, 359–363 CrossRef CAS PubMed.
- C.-F. Fu and S. X. Tian, J. Chem. Theory Comput., 2011, 7, 2240–2252 CrossRef CAS PubMed.
- A. Henao, A. J. Johnston, E. Guàrdia, S. E. McLain and L. C. Pardo, Phys. Chem. Chem. Phys., 2016, 18, 23006–23016 RSC.
- R. Sharma, M. Agarwal and C. Chakravarty, Mol. Phys., 2008, 106, 1925–1938 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06689a |
| This journal is © the Owner Societies 2018 |