 Open Access Article
Open Access ArticleHigh-speed prediction of computational fluid dynamics simulation in crystal growth
Yosuke
Tsunooka
 *a,
Nobuhiko
Kokubo
a,
Goki
Hatasa
a,
Shunta
Harada
ab,
Miho
Tagawa
ab and
Toru
Ujihara
ab
*a,
Nobuhiko
Kokubo
a,
Goki
Hatasa
a,
Shunta
Harada
ab,
Miho
Tagawa
ab and
Toru
Ujihara
ab
aDepartment of Materials Process Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan. E-mail: tsunooka@unno.material.nagoya-u.ac.jp; shunta.harada@nagoya-u.jp
bCenter for Integrated Research of Future Electronics (CIRFE), Institute of Materials and Systems for Sustainability (IMaSS), Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan
First published on 2nd October 2018
Abstract
Accelerating the optimization of material processing is essential for rapid prototyping of advanced materials to achieve practical applications. High-quality and large-diameter semiconductor crystals improve the performance, reliability and cost efficiency of semiconductor devices. However, much time is required to optimize the growth conditions and obtain a superior semiconductor crystal. Here, we demonstrate a rapid prediction of the results of computational fluid dynamics (CFD) simulations for SiC solution growth using a neural network for optimization of the growth conditions. The prediction speed was 107 times faster than that of a single CFD simulation. The combination of the CFD simulation and machine learning thus makes it possible to determine optimized parameters for high-quality and large-diameter crystals. Such a simulation is therefore expected to become the technology employed for the design and control of crystal growth processes. The method proposed in this study will also be useful for simulations of other processes.
Introduction
High-quality and large-diameter semiconductor crystals improve the performance, reliability, and cost efficiency of semiconductor devices. To obtain superior semiconductor crystals, growth conditions must be optimized for every new improvement in a growth technology, and this process is very time consuming. Thus, the development of novel semiconductor materials can take many decades. Silicon has been one of the most successful materials in the last 50 years. Since the growth of dislocation-free silicon crystal was demonstrated in 1959, the technology employed for the growth of large-diameter and high-quality Si crystals has been improved. The size of wafers has increased up to 100–150 mm (1970s), 150–200 mm (1980s), 150–300 mm (1990s) and 300–450 mm (late 1990s).1 It has thus taken a very long time to develop larger wafers in a “step-by-step” process. Silicon carbide (SiC) and gallium nitride (GaN) wafers, which are next-generation power electronics materials, have recently been developed in the same way. Therefore, we anticipate an innovative process to significantly shorten the time for such wafer development. Accelerating the optimization of material processing is essential for the rapid prototyping of advanced materials for practical applications.Since Baliga suggested the outstanding potential of silicon carbide (SiC),2 SiC power devices have been developed for many applications, including electric vehicles, railway traction inverters, and solar inverters.3 Sublimation is currently employed as a typical SiC growth method. However, further improvement of crystal quality, which cannot be completely achieved by the sublimation method, remains a critical issue. The top-seeded solution growth (TSSG) method for higher-quality SiC crystals is proposed as an alternative to the sublimation method.4
In the TSSG method, the conversion of threading dislocations plays an important role in the improvement of crystal quality.4 Threading dislocations are converted into defects on the basal plane by advancing macrosteps on the growth surface.5–7 These defects then propagate outside the crystal by the advancing macrosteps, which reduces the dislocation density.8 This conversion phenomenon produces high-quality SiC crystals.9 The direction of solution flow is important to control the moderate step height of advancing macrosteps.10 Many researchers reported that the development of macrosteps due to step bunching was suppressed by the solution flow opposing the step-flow direction and moderate step heights were produced.11–13 Moderate supersaturation is also important to produce a smooth surface.14 Under high supersaturation conditions, two-dimensional (2D) nucleation increased, which led to unintentional polytype transformations and a rough growth surface.15,16 Furthermore, high supersaturation at any position other than the seed crystal results in the precipitation of SiC polycrystals, which hamper long-term growth.17 On the other hand, a steep temperature gradient with high supersaturation is effective in increasing the growth rate.18 One of the most important issues in SiC solution growth is increasing the diameter of the grown crystal. Kusunoki et al. fabricated a 3.75 inch crystal using the TSSG method,19 while 6 inch crystals are already commercially available and 8 inch crystals can be fabricated by the sublimation method. To make larger-diameter SiC crystals using the TSSG method, it is necessary to optimize the spatial distribution of supersaturation and the flow velocity in the solution.
To indirectly control the spatial distribution of the composition, temperature, and flow velocity, many growth parameters, such as the heater power, crucible position and rotation, seed crystal position and rotation, growth configuration of the heat insulator, crucible shape, and crucible size must be simultaneously optimized. However, it is practically impossible to optimize all of these parameters experimentally because a single experiment takes too much time. Moreover, it is also impossible to directly observe the spatial distribution of temperature, supersaturation, and flow velocity in solution. Therefore, a number of numerical simulation studies based on computational fluid dynamics (CFD) have been conducted for the optimization of TSSG.19–25 However, even numerical simulations take a very long time to optimize these growth parameters.
Recently, machine learning techniques have been applied to physics, chemistry, and other fields. In the field of materials science, physical properties are predicted using machine learning applied to ab initio calculation data.26–28 In the present study, machine learning was applied to the prediction of CFD numerical results for a solution during SiC solution growth to construct a model that can quickly predict the CFD results for the spatial distribution of supersaturation and flow velocity. The methodology developed here has led to a qualitative change in the role of crystal growth simulation: from understanding phenomena to the design and control of crystal growth processes.
Methods
CFD simulations
The prediction model was constructed using examples of the supersaturation and flow velocity distribution in solution during TSSG processing of SiC. Fig. 1 illustrates the TSSG configuration and the computational domain for the solution in the CFD simulations. In the TSSG process, a pure Si or Si-based solvent is melted in a carbon crucible.15 A SiC seed crystal is then mounted on a graphite rod and immersed in the solution. The seed crystal is typically rotated to stir the solution.The CFD simulation was performed based on a 2D steady axisymmetric model by taking into account the heat transfer, mass transport, and convection in the solution [Fig. 1(b)]. The governing equations that describe the heat and mass transport were numerically solved by the finite volume method using OpenFOAM.29 The solution was assumed to be an incompressible Newtonian liquid. The Boussinesq approximation was adopted; therefore, the thermal buoyancy term was included in the momentum equations. Turbulent flow was considered with the Reynolds-averaged Navier–Stokes (RANS) model because the maximum Reynolds number due to crystal rotation was approximately 3 × 104 in the ranges of the parameters given in Table 2. Solute convection was neglected because the carbon concentration was lower than 1%. Under these assumptions, the governing equations for the solution are given as follows:
Continuity
| ∇·(ρu) = 0, | (1) |
Momentum
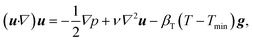 | (2) |
Energy
| u·∇T = α∇2T, | (3) |
Mass transport
| u·∇C = D∇2C, | (4) |
The supersaturation σ was calculated from the following equations:30
| σ = (C − Ceq)/Ceq, | (5) |
| Ceq = Cf(Xeq/(1 − Xeq)), | (6) |
| Xeq = exp(6.249 − 24460/T), | (7) |
| Property | Value |
|---|---|
| Diffusion coefficient, D (m2 s−1) | 1.7 × 10−8 |
| Thermal diffusivity, α (m2 s−1) | 2.55 × 10−4 |
| Thermal expansion coefficient, βT (K−1) | 1.4 × 10−4 |
| Kinetic viscosity, ν (m2 s−2) | 3 × 10−7 |
| Density, ρ (kg m−3) | 2.55 × 103 |
| Molar fraction, Cf (mol m−3) | 9.1 × 104 |
The temperatures at three points on the crucible surface (T1, T2, and T3), the rotation speed of the graphite rod (ω), the diameter of the crucible (DC), the height of the solution (H), the diameter of the seed crystal (DS) and the immersion depth of the seed crystal (d) were set as variable parameters. Table 2 gives the ranges used for these parameters, which were determined based on actual growth experiments. The temperature boundary conditions along the crucible surface were set by linear interpolations between two pairs of points: (1) T1 and T2 and (2) T2 and T3. The temperature of the carbon rod and seed crystal T0, was set to 2143 K. Steady-state was assumed, so that all the scaled residuals of p, u, T and C would level off and reach minima of 10−5.
| Parameter | Lower limit | Upper limit |
|---|---|---|
| T 1 (K) | 2113 | 2173 |
| T 2 (K) | 2113 | 2173 |
| T 3 (K) | 2113 | 2173 |
| ω (rpm) | 0 | 150 |
| D C (mm) | 40 | 100 |
| H (mm) | 10 | 50 |
| D S (mm) | 10 | 50 |
| d (mm) | 0.5 | 4.5 |
Machine learning
Fig. 2 illustrates the procedure used to construct a prediction model with machine learning. Training data were first prepared by running 800 CFD simulations with different values for the variable parameters. The values were randomly selected from the ranges in Table 2. From the training data, a model was constructed that predicts the supersaturation σ, and the fluid velocity at position (r,z). The 400 points shown in Fig. 1(b) were set in the solution discretely to an r- and z-coordinate grid, and the values of supersaturation and solution velocities for r- and z-axial components (ur,uz) were extracted. The eight variable parameters (T1, T2, T3, ω, DC, H, DS, d), the position (r,z) and the parameter (k) to express whether the solvent is present (k = 1 for a position in the solvent and k = 0 for a position without solvent) were then set as descriptors. The parameter k was introduced, so that the neural network could be applied with the different geometrical conditions. Thus, the number of input parameters was 11 and the number of output parameters was 3. Machine learning with a neural network was conducted using Tensorflow.32 The numbers of hidden layers and hidden units in the neural network were 4 and 128, respectively, and a sigmoid activation function was used. Trainable variables in the neural networks were optimized using Adam,33 a method for stochastic optimization, with β1 = 0.9. Another 200 CFD simulations, different from the 800 simulations used for training, were prepared as the test data for validation of the prediction model. To validate the prediction model, the correlation coefficient (R) between the prediction and test data was calculated. For comparison, support vector regression (SVR) was performed using the same training data.Results and discussion
Temperature distributions and flows were predicted from a given set of parameter values using the model constructed by machine learning. The predicted static transport structures of supersaturation and flow velocity vectors are presented in Fig. 3(a). The colour contrast indicates the degree of supersaturation. Two main vortexes are developed. In the bottom vortex (#1), the dominant flow in the crucible is upward from the bottom of the crucible. In the upper vortex (#2), the solution flows from the top of the crucible wall to the seed crystal position. The degree of supersaturation near the seed crystal is relatively high because vortex #1 and vortex #2 transfer carbon from the hotter area near the bottom of the crucible wall and the top of the crucible wall, respectively. A CFD simulation was conducted using the same parameter values, as shown in Fig. 3(b). Note that this CFD simulation was not used for the construction of the prediction model. The distributions of both the flow velocity and supersaturation were similar to those of the prediction. The correlation coefficients for supersaturation and the flow vectors in the r- and z-directions were 0.952, 0.878, and 0.933, respectively.The correlation coefficients of all the 200-test data for supersaturation and the flow vectors in the r- and z-directions were 0.970, 0.957, and 0.961, respectively. It should be emphasized that calculation by machine learning is extremely faster than that by simulation. The average calculation time of 800 simulation data was 3.8 × 103 s. On the other hand, calculation by machine learning under 800 of the same conditions at the same time took only 3.0 × 10−4 s on average per sample. Note that both calculations were performed on a computer equipped with two Intel® Xeon® CPUs E5-2667 v2, whereas simulations were computed in parallel with 16 cores and predictions by machine learning were performed with a single core. Consequently, the entire parameter space can be predicted exhaustively and then optimal conditions can be calculated inductively.
To show the performance of the neural network in comparison with other methods, Fig. 4 shows the correlation coefficients (R) of the neural network and support vector regression (SVR) with different numbers of data sets. When the number of data sets (N) was less than 80, the value of R for the neural network was less than that for SVR. This is because neural network models generally require more training data than SVR models. On the other hand, when N is larger than 80, the value of R for the neural network is larger than that for SVR. The reason for this is that neural network models are more expressive than SVR models.
 | ||
| Fig. 4 Average values of multiple correlation coefficients of flow and supersaturation when using each method. | ||
The optimization of growth parameters was demonstrated by searching from the large number of comprehensively predicted results. Here, we referred to the preferable conditions reported by Daikoku et al.: solution flow from the centre to the periphery gave rise to a smooth surface on the crystal.11 The prediction model enables such a solution flow distribution to be found. Fig. 5 shows the predicted distribution of supersaturation and the flow velocity under a different set of parameter values with a 44 mm diameter crystal. One dominant vortex develops outside of the crucible. The solution flows from the centre to the periphery and a favourable supersaturation distribution, in which the supersaturation near the seed crystal is relatively high and the supersaturation near the crucible bottom and wall is low, is achieved. This indicates that the prediction model enables favourable conditions for crystal growth to be determined. In this study, the conditions among the exhaustive predictions were manually selected; however, the application of the general optimization method to the prediction model enabled more optimum conditions to be found. Again, the proposed model predicted the distribution of both supersaturation and solution flow in the CFD model. The correlation coefficients for supersaturation and the flow vectors in the r- and z-directions were 0.971, 0.994, and 0.990, respectively. In the same way, optimized growth parameters for larger crystals should be quickly found.
The methodology developed here fundamentally alters the value of crystal growth simulations. Simulations have often been used to understand the phenomena that occur in crystal growth. The combination of simulation and machine learning makes it possible to determine optimized parameters for the growth of high quality and large size crystals from a large multidimensional parameter space. Thus, simulation becomes the technology used to design and control crystal growth processes. This methodology could also be applied to other similar processes. This technique is clearly useful for other crystal growth simulations and broadly applicable to any type of process simulation, such as material and device processes. The development of new materials is thus expected to be accelerated significantly using this method.
Conclusions
In summary, a high-speed model was constructed to predict the results of CFD simulations of high-quality SiC crystal growth using the TSSG method. The prediction model was constructed using machine learning with a neural network. At first, 800 CFD simulations were performed to calculate the distribution of supersaturation and the flow velocity for different configurations of temperature and seed crystal rotation. These data were then used to train the prediction model. Finally, it was confirmed that the model reliably predicts the results of CFD simulations. The prediction model was approximately 107 times faster than a CFD simulation. Thus, it is possible to exhaustively predict the distribution of supersaturation and the flow velocity, and accelerate the optimization of high-quality crystal growth. This methodology qualitatively alters the meaning of crystal growth simulation: from the understanding of phenomena to a technology for the design and control of crystal growth processes. This technique is clearly useful for other crystal growth simulations and will be broadly applicable to any type of process simulation, such as material and device processes. The development of new materials is thus expected to be accelerated significantly using this method.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate Dr. Yamamoto, Prof. Takagi, and Prof. Okano of Osaka University for fruitful discussions.Notes and references
- G. Fisher, M. R. Seacrist and R. W. Standley, Proc. IEEE, 2012, 100, 1454–1474 CAS.
- B. J. Baliga, IEEE Electron Device Lett., 1989, 10, 455–457 Search PubMed.
- X. She, A. Q. Huang, O. Lucia and B. Ozpineci, IEEE Trans. Ind. Electron., 2017, 99, 8193–8205 Search PubMed.
- Y. Yamamoto, S. Harada, K. Seki, A. Horio, T. Mitsuhashi and T. Ujihara, Appl. Phys. Express, 2012, 5, 115501 CrossRef.
- S. Harada, Y. Yamamoto, K. Seki, A. Horio, T. Mitsuhashi, M. Tagawa and T. Ujihara, APL Mater., 2013, 1, 022109 CrossRef.
- S. Harada, Y. Yamamoto, K. Seki, A. Horio, M. Tagawa and T. Ujihara, Acta Mater., 2014, 81, 284–290 CrossRef CAS.
- S. Kawanishi, M. Kamiko, T. Yoshikawa, Y. Mitsuda and K. Morita, Cryst. Growth Des., 2016, 16, 4822–4830 CrossRef CAS.
- Y. Yamamoto, S. Harada, K. Seki, A. Horio, T. Mitsuhashi, D. Koike, M. Tagawa and T. Ujihara, Appl. Phys. Express, 2014, 7, 06550 Search PubMed.
- K. Murayama, T. Hori, S. Harada, S. Xiao, M. Tagawa and T. Ujihara, J. Cryst. Growth, 2017, 468, 874–878 CrossRef CAS.
- S. Xiao, S. Harada, K. Murayama, M. Tagawa and T. Ujihara, Cryst. Growth Des., 2016, 16, 6436–6439 CrossRef CAS.
- H. Daikoku, M. Kado, A. Seki, K. Sato, T. Bessho, K. Kusunoki, H. Kaidou, Y. Kishida, K. Moriguchi and K. Kamei, Cryst. Growth Des., 2016, 16, 1256–1260 CrossRef CAS.
- C. Zhu, S. Harada, K. Seki, H. Zhang, H. Niinomi, M. Tagawa and T. Ujihara, Cryst. Growth Des., 2013, 13, 3691–3696 CrossRef CAS.
- T. Umezaki, D. Koike, S. Harada and T. Ujihara, Mater. Sci. Forum, 2015, 821–823, 31–34 Search PubMed.
- N. Komatsu, T. Mitani, T. Takahashi, M. Okamura, T. Kato and H. Okumura, Mater. Sci. Forum, 2012, 740–742, 23–26 Search PubMed.
- S. Harada, K. Seki, Y. Yamamoto, C. Zhu, Y. Yamamoto, S. Arai, J. Yamazaki, N. Tanaka and T. Ujihara, Cryst. Growth Des., 2012, 12, 3209–3214 CrossRef CAS.
- K. Murayama, T. Hori, S. Harada, S. Xiao, M. Tagawa and T. Ujihara, Mater. Sci. Forum, 2017, 897, 24–27 Search PubMed.
- N. Yashiro, K. Kusunoki, K. Kamei and A. Yauchi, Mater. Sci. Forum, 2010, 645–648, 33–36 CAS.
- M. Kado, H. Daikoku, H. Sakamoto, H. Suzuki, T. Bessho, N. Yashiro, K. Kusunoki, N. Okada, K. Moriguchi and K. Kamei, Mater. Sci. Forum, 2012, 740–742, 73–76 Search PubMed.
- K. Kusunoki, N. Okada, K. Kamei, K. Moriguchi, H. Daikoku, M. Kado, H. Sakamoto, T. Bessho and T. Ujihara, J. Cryst. Growth, 2014, 395, 68–73 CrossRef CAS.
- F. Mercier, J. M. Dedulle, D. Chaussende and M. Pons, J. Cryst. Growth, 2012, 312, 155–163 CrossRef.
- J. Lefebure, J. M. Dedulle, T. Ouisse and D. Chaussende, Cryst. Growth Des., 2012, 12, 909–913 CrossRef CAS.
- F. Inui, B. Gao, S. Nakano and K. Kakimoto, J. Cryst. Growth, 2012, 348, 71–74 CrossRef CAS.
- D. Koike, T. Umezaki, K. Murayama, K. Aoyagi, S. Harada, M. Tagawa, T. Sakai and T. Ujihara, Mater. Sci. Forum, 2015, 821–823, 18–21 Search PubMed.
- T. Umezaki, D. Koike, S. Harada and T. Ujihara, Jpn. J. Appl. Phys., 2016, 55, 125601 CrossRef.
- T. Yamamoto, Y. Okano, T. Ujihara and S. Dost, J. Cryst. Growth, 2017, 470, 75–88 CrossRef CAS.
- Informatics for Materials Science and Engineering, ed. K. Rajan, Butterworth-Heinemann, Oxford, 2013 Search PubMed.
- A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Phys. Rev. Lett., 2015, 115, 205901 CrossRef PubMed.
- Y. Hinuma, T. Hatakeyama, Y. Kumagai, L. A. Burton, H. Sato, Y. Muraba, S. Iimura, H. Hiramatsu, I. Tanaka, H. Hosono and F. Oba, Nat. Commun., 2016, 7, 11962 CrossRef CAS PubMed.
- OpenFOAM, http://www.openfoam.com/.
- F. Durand and J. C. Duby, J. Phase Equilib., 1999, 20, 61–63 CrossRef CAS.
- F. Mercier and S. Nishizawa, Jpn. J. Appl. Phys., 2011, 50, 035603 CrossRef.
- Tensorflow, https://www.tensorflow.org/.
- D. P. Kingma and J. Ba, International Conference on Learning Representations (ICLR), 2015 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |




