Open Access Article
Open Access ArticleMeasuring elasticity of wet cellulose fibres with AFM using indentation and a linearized Hertz model
Johannes
Hellwig
 a,
Verónica López
Durán
a and
Torbjörn
Pettersson
a,
Verónica López
Durán
a and
Torbjörn
Pettersson
 *ab
*ab
aFibre and Polymer Technology, KTH Royal Institute of Technology, Teknikringen 56, SE-100 44 Stockholm, Sweden. E-mail: torbj@kth.se
bWallenberg Wood Science Centre, KTH Royal Institute of Technology, Teknikringen 56, SE-100 44 Stockholm, Sweden
First published on 3rd July 2018
Abstract
The mechanical properties of different pulp fibres in liquid were measured using an atomic force microscope. Specifically a custom-made sample holder was used to indent the fibre surface, without causing any motion, and the Young's modulus was calculated from the indentation using a linearized Hertz model.
In recent years, cellulose has become a widely investigated material in many research studies around the world. As a naturally occurring material cellulose provides excellent biodegradability at a very low cost. In many fields cellulose is now being used to replace oil-based materials, which show poor or no natural degradability at all.1 Dry cellulose has inherently good mechanical properties such as strength and toughness, making it ideal for reinforcement applications.2 Naturally occurring cellulose forms a hierarchical structure where cellulose chains are arranged into fibrils that are aligned and embedded in a lignin/hemicellulose matrix forming larger fibres that have excellent mechanical properties.3 For more than a century cellulose fibres have been used for a wide range of applications4 such as paper, packaging,5 hygiene products6 and in composites.7 However, during the last decade, the properties of cellulose on different length scales have been investigated.2,8–11
Cellulose is normally used in end products in dry conditions because the mechanical properties of cellulose change drastically when the fibres are wet. Additionally, moulding and degradation (hydrolysis, enzymatic, etc.) of the cellulose can result in a failure of the dry material unless it is not protected. Nevertheless many new applications are taking advantage of the change in mechanical properties in the wet state and wet cellulose materials have become more in focus.12–14
For all cellulose fibre applications it is important to have a fundamental understanding of the mechanical properties of the fibres and their interaction with water (swelling and enthalpy gain15). Unfortunately, the determination of the mechanical properties of the wet fibres is challenging and literature data relating to the elasticity in the wet state for different fibres is limited.
One instrument used to measure the mechanical properties of a wide range of nano- and microscale materials is the atomic force microscope (AFM). AFM has become widely used to investigate a variety of material properties including the moduli of polymer films and composites16,17 and additionally, the elasticity of benign and cancerous cells.18–20
Various methods have been used to evaluate and measure the mechanical properties of fibres by AFM, for example tensile and three-point bending tests. Fibre tensile properties are evaluated by spanning the fibre between an AFM tip and a hard surface and performing uniaxial stretching along the fibre axis. While individual mineralized collagen fibrils,21 individual collagen fibres22 polyethylene oxide nanofibers23 and poly (L-lactic-co-glycolic acid) fibres24 have been measured, attachment of the fibres to the AFM tip makes tensile measurements technically challenging. In a three-point bending test, fibres are deposited on a substrate with holes or grooves. Fibres lying over such a hole or groove are then bent using an AFM tip in the centre of the fibre bending it in one direction. Such measurements have been made on earlywood and latewood kraft pine fibres25 and Lyocell fibrils.26 Unfortunately, both tensile and three-point bending tests become challenging and time-consuming in a liquid (due to surface adhesion and fibre flexibility), making them not suitable when studying the wet mechanical properties of fibres.
In the present study, the mechanical properties of wet cellulose fibres in liquid have been investigated using a simple indentation measurement in the fibre walls using AFM. Fibres are clamped in the liquid onto a surface by a custom-made sample holder which prevents motion or bending of the fibres. The measured force vs. indentation profile can then be used to fit one of the existing contact mechanics models to extract the Young's modulus for the fibres. The most frequently used model for this type of measurement is the Hertz model.27 More advanced models, based on the Hertz model are: (a) the Derjaguin, Muller and Toporov (DMT) model28 and (b) the Johnson, Kendall and Roberts (JKR) model.29 They include an adhesion force, with specific assumptions for each model, that are not present in the original Hertz model. The JKR model is used for large probes, soft samples and large adhesion while the DMT model is used for small probes, stiffer samples and moderate adhesion. The model used in this work was however the simple Hertz model, since there is no adhesion. The samples were prepared from unbeaten never-dried fully bleached kraft pulps some of which were chemically modified to give different charge densities. Two of the selected pulps were identical with the pulp used in an earlier published article30 and were selected for comparison with earlier flexibility measurements.
Six different never-dried fibres in liquid were tested (see Table 1), two of them with and without the addition of 100 mM sodium chloride. The different fibres were a bleached softwood (60% spruce, 40% pine) kraft pulp with a kappa number κ = 1.2 from Södra Cell in Mörrum (BSW), Sweden, an unbleached thermo mechanical pulp (100% spruce) from the final refiner using about 2000 kW h t−1 from the Stora Enso plant at Hyltebruk, Sweden (TMP), a bleached unbeaten softwood kraft pulp (κ = 48) from SCA Forest Products (Östrand pulp mill, Timrå, Sweden) having a charge density of 60 μeq. g−1. (K48-60), the same pulp were TEMPO oxidized in our laboratory to different degrees giving charge densities of 300, 600, 900 μeq. g−1 (K48-300, K48-600 and K48-900). K48-60 and K48-900 were also tested with 100 mM NaCl.
The BSW, TMP and K48-60 samples were taken from the process lines as liquid suspensions, diluted to 2–8% solids content and kept in cold storage at 7 °C.
The TEMPO-mediated oxidation (4-amino-2,2,6,6-tetramethylpiperidine-1-oxyl (4-AcNHTEMPO)) of K48-60 was performed on never-dried pulp following the procedure describe by Tanaka et al. 2012.31 In brief, the fibres were dispersed in 0.1 M acetate buffer at pH 4.8, after which 4-AcNH-TEMPO and sodium chlorite were added to the dispersion followed by the addition of NaClO. The reaction was allowed to continue at 40 °C for three different times, 48 h, 8 h and 1 h, in order to achieve different charge densities.
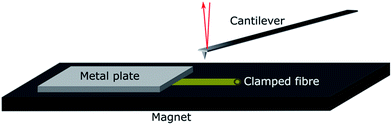
Individual fibres were mounted in the wet state in a specially designed sample holder. The holder was made of a magnetic tape with a thickness of 0.35 mm (G-0100-1, Svenska magnetfabriken) glued to an AFM sample metal plate. The fibres were clamped on the magnet with a thin metal slab with a thickness of 0.02 mm, as shown in Fig. 1.
The individual fibres were placed in the liquid with a pair of tweezers while being viewed under a stereo microscope. During this procedure, the fibres were taken out of the solution, placed on the magnet and immediately covered with solution to prevent any drying of the fibres. The fibres were finally clamped gently with a small metal slab to fix them on the magnet. The holder was completely submerged in the liquid and transferred into the AFM using a liquid cell.
The mechanical properties of individual fibres were measured using an AFM (MultiMode IIIa with PicoForce extension, Veeco Instruments) equipped with a top view microscope. All the measurements were made using a MPP-21100-10 cantilever (spring constant: 1.5 N m−1, rotated tip (symmetric), radius 8 nm, silicon probe, cone angle 17.5°, Bruker, USA) with a length of 215 μm and a tip with the length of 15–20 μm in the liquid cell of the AFM. Indentation measurements in each individual fibre were made as close as possible to the metal plate which clamped the fibre on the magnet to prevent any motion of the fibre due to the indentation into the fibre wall. The measurements were carried out as force maps with 5 × 5 points at different positions on the fibre, but close to the clamp, using a ramping rate of 2 μm s−1 and a maximum force of 3 nN. The Hertz model in linearized form32 were fitted to the force vs. separation curves to extract the Young's modulus of each fibre (see Fig. 2). Linearization of the model means that it is not necessary to know the exact point of contact between the sample surface and probe of the AFM, and thus makes it easier to calculate the Young's modulus.
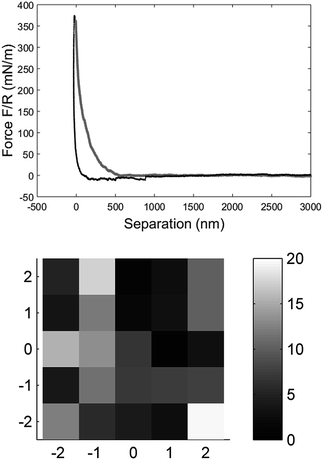 | ||
| Fig. 2 The force vs. separation curve from a single fibre raw data (BSW) converted with the algorithm explained by Senden et al.33 The zero point is arbitrary set at maximum load. The grey line is the approach of the tip to the fibre surface and the black line is the retraction from the surface, force range used for the fitting was 20 to 70 mN m−1 (top). Elasticity map of a measurement with 5 × 5 measurement points over 5 × 5 μm on the fibre surface close to the clamp shown as the Young's modulus calculated for each data point (bottom). | ||
The linearized Hertz model is given by:
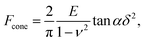 | (1) |
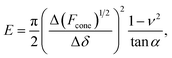 | (2) |
The Young's moduli of the different fibre samples are shown in Table 1. Measurement in bending mode for TMP and BSW samples from a previous paper30 have been included in the table, to make it possible to compare the properties obtained by using two different AFM methods.
The measured and calculated Young's moduli for the TMP fibres are 49 ± 40 kPa and 53 ± 23 kPa for the indentation method and bending method, respectively, and the Young's moduli for the BSW fibres are 7 ± 4 kPa and 5 ± 3 kPa. The values obtained by the two AFM methods show good agreement and are thus not significantly different, confirming that the local indentation of the fibre surface gives the same mechanical properties as the bending of the whole fibre. This agreement indicates that the quicker and simpler local indentation method can be used to determine the Young's modulus in place of whole fibre bending.
The Young's modulus of the TMP fibres is approximately ten times greater than that of the BSW fibres. The BSW fibres have been treated chemically at a high temperature, in contrast to the TMP fibres, and it can be assumed that this makes the BSW fibres softer, more flexible and elastic due to the removal of lignin.34
In all the measurements, the standard deviations are relatively large. These large deviations are expected for natural fibres, as cellulose fibres have structural differences and regions of varying crystallinity along the fibre length.
The Young's modulus of unmodified K48 with a charge density of 60 μeq. g−1 (K48-60) had a significantly higher Young's modulus 14 ± 6 kPa compared to the K48 fibres with higher charge density. After TEMPO oxidation, the Young's modulus decreased with increasing charge of the fibres. At a charge density of 300 μeq. g−1 (K48-300) the Young's modulus was 12 ± 4 kPa, at 600 μeq. g−1 (K48-600) 7 ± 4 kPa and at 900 μeq. g−1 (K48-900) 3 ± 1 kPa.
This decrease in Young's modulus can be explained by two different mechanisms: (1) The introduction of carboxylic groups into the fibre increases the pore size and thus increases the swelling in liquid.35 (2) Any lignin residues in the fibre cell walls are significantly degraded by the TEMPO oxidation, leading to a more flexible fibre.36
The addition of salt significantly lowered the Young's modulus of the fibre samples K48-60 (60 μeq. g−1) and did not change for K48-900 (900 μeq. g−1), and the two fibre samples had the same Young's modulus when immersed in 100 mM sodium chloride solution.
When a system such as a pulp fibre swells, three components to the Gibbs free energy of the swelling system balance the swelling; an ionic contribution, a mixing contribution and a network contribution.37 When the fibres were chemically modified to increase the charge of the fibres, it was observed that at low ionic strength the ionic contribution dominates and controls the elasticity of the fibres. The highest charged fibres are thus the most elastic with the lowest Young's modulus. When 100 mM sodium chloride was added to the dispersion, the increase in ionic strength screens the charges in the fibre and the highest charged and lowest charged fibres then had the same Young's modulus. This is likely due to the screened electrostatic contribution as the fibres should have the same network and mixing contribution. Since they have the same origin from the same pulping process. This is an interesting behaviour and needs a more thorough evaluation in a future study.
Conclusions
The mechanical properties of different cellulose pulp fibres were measured using a simple indentation method with an AFM. The measurements were carried out in a liquid environment using a custom-made sample holder that prevents motion and bending of the individual fibre. The method gives the same results as an earlier study where the fibres were bent over an edge to evaluate the fibre flexibility.30 The new indentation method makes it possible to determine a fibres' elasticity more quickly than three-point bending and tensile measurements using the AFM. The method can be used for all types of fibres, including never-dried fibres provided that the fibre mounting is done under liquid.A bleached softwood kraft pulp and an unbleached TMP pulp were used to validate the method and the calculated mechanical properties were the same as previously reported values for the same fibres. The Young's modulus of the bleached unbeaten softwood kraft pulp decreased with increasing charge density. The presence of salt screens the charged groups in the fibre, and the fibres coming from the same original pulp behaved similarly regardless of charge density.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financial supported by the Jacob Wallenbergs Forskningsstiftelse, the Lars-Erik Thunholms Stiftelse För Vetenskaplig Forskning and VINNOVA, the Swedish Governmental Agency for Innovation Systems, through BiMaC Innovation Excellence Centre.Notes and references
- R. P. Babu, K. O'connor and R. Seeram, Prog. Biomater., 2013, 2, 8 CrossRef PubMed.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- E. Sjöström, Wood Chemistry: Fundamentals and Applications, Academic Press, San Diego, 2nd edn, 1993 Search PubMed.
- J. Hellwig, R. M. P. Karlsson, L. Wagberg and T. Pettersson, Anal. Methods, 2017, 9, 4019–4022 RSC.
- A. Marais, S. Utsel, E. Gustafsson and L. Wågberg, Carbohydr. Polym., 2014, 100, 218–224 CrossRef PubMed.
- J. Henschen, P. A. Larsson, J. Illergård, M. Ek and L. Wågberg, Colloids Surf., B, 2017, 151, 224–231 CrossRef PubMed.
- S. Utsel, A. Carlmark, T. Pettersson, M. Bergström, E. E. Malmström and L. Wågberg, Eur. Polym. J., 2012, 48, 1195–1204 CrossRef.
- E. K. Gamstedt, R. Sandell, F. Berthold, T. Pettersson and N. Nordgren, Mech. Mater., 2011, 43, 693–704 CrossRef.
- A. N. Nakagaito and H. Yano, Appl. Phys. A: Mater. Sci. Process., 2004, 78, 547–552 CrossRef.
- A. N. Nakagaito and H. Yano, Cellulose, 2008, 15, 555–559 CrossRef.
- X. Z. Xu, F. Liu, L. Jiang, J. Y. Zhu, D. Haagenson and D. P. Wiesenborn, ACS Appl. Mater. Interfaces, 2013, 5, 2999–3009 CrossRef PubMed.
- L. Wagberg, G. Decher, M. Norgren, T. Lindstrom, M. Ankerfors and K. Axnas, Langmuir, 2008, 24, 784–795 CrossRef PubMed.
- E. Saarikoski, T. Saarinen, J. Salmela and J. Seppala, Cellulose, 2012, 19, 647–659 CrossRef.
- N. Pahimanolis, A. Salminen, P. A. Penttila, J. T. Korhonen, L. S. Johansson, J. Ruokolainen, R. Serimaa and J. Seppala, Cellulose, 2013, 20, 1459–1468 CrossRef.
- R. G. Hollenbeck, G. E. Peck and D. O. Kildsig, J. Pharm. Sci., 1978, 67, 1599–1606 CrossRef PubMed.
- J. Domke and M. Radmacher, Langmuir, 1998, 14, 3320–3325 CrossRef.
- O. Mermut, J. Lefebvre, D. G. Gray and C. J. Barrett, Macromolecules, 2003, 36, 8819–8824 CrossRef.
- S. E. Cross, Y. S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef PubMed.
- Q. S. Li, G. Y. H. Lee, C. N. Ong and C. T. Lim, Biochem. Biophys. Res. Commun., 2008, 374, 609–613 CrossRef PubMed.
- H. W. Wu, T. Kuhn and V. T. Moy, Scanning, 1998, 20, 389–397 CrossRef PubMed.
- F. Hang and A. H. Barber, J. R. Soc., Interface, 2011, 8, 500–505 CrossRef PubMed.
- J. A. J. van der Rijt, K. O. van der Werf, M. L. Bennink, P. J. Dijkstra and J. Feijen, Macromol. Biosci., 2006, 6, 697–702 CrossRef PubMed.
- E. P. S. Tan, C. N. Goh, C. H. Sow and C. T. Lim, Appl. Phys. Lett., 2005, 86(7), 073115 CrossRef.
- E. P. S. Tan and C. T. Lim, Rev. Sci. Instrum., 2004, 75, 2581–2585 CrossRef.
- N. Navaranjan, R. J. Blaikie, A. N. Parbhu, J. D. Richardson and A. R. Dickson, J. Mater. Sci., 2008, 43, 4323–4329 CrossRef.
- Q. Z. Cheng and S. Q. Wang, Composites, Part A, 2008, 39, 1838–1843 CrossRef.
- H. Hertz, J. Reine Angew. Math., 1882, 92, 110 Search PubMed.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef.
- K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, A, 1971, 324, 301–313 CrossRef.
- T. Pettersson, J. Hellwig, P. J. Gustafsson and S. Stenstrom, Cellulose, 2017, 24, 4139–4149 CrossRef.
- R. Tanaka, T. Saito and A. Isogai, Int. J. Biol. Macromol., 2012, 51, 228–234 CrossRef PubMed.
- P. Carl and H. Schillers, Pflugers Arch. Eur. J. Appl. Physiol., 2008, 457, 551–559 CrossRef PubMed.
- T. J. Senden, Curr. Opin. Colloid Interface Sci., 2001, 6, 95–101 CrossRef.
- S.-Y. Zhang, B.-H. Fei, Y. Yu, H.-T. Cheng and C.-G. Wang, For. Sci. Pract., 2013, 15, 56–60 Search PubMed.
- A. Sbiai, H. Kaddami, H. Sautereau, A. Maazouz and E. Fleury, Carbohydr. Polym., 2011, 86, 1445–1450 CrossRef.
- P. Ma, S. Fu, H. Zhai, K. Law and C. Daneault, Bioresour. Technol., 2012, 118, 607–610 CrossRef PubMed.
- R.-M. P. Karlsson, P. T. Larsson, S. Yu, S. A. Pendergraph, T. Pettersson, J. Hellwig and L. Wågberg, J. Colloid Interface Sci., 2018, 519, 119–129 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |