A DFT study and experimental evidence of the sonication-induced cleavage of molybdenum sulfide Mo₂S₃ in liquids

Abstract

The Mo–S phase diagram exhibits two stable compounds: well-recognized layered molybdenum disulfide MoS₂ and less studied molybdenum sesquisulfide Mo₂S₃. Here, we build a theoretical framework for the exfoliation of Mo₂S₃ based on density functional theory calculations and further experimentally prove its dispersibility under ultrasonic treatment and demonstrate its potential for use in gas detectors. First, we report computational studies of both Mo₂S₃ exfoliation and molecular adsorption on the Mo₂S₃ surface. The calculations reveal the preferential direction for the fragmentation of the Mo₂S₃ crystal along the (1̄01) plane and, likely, chemisorptive interaction of solvent molecules, such as H₂O or DMSO, with the (1̄01) Mo₂S₃ surface. Next, we experimentally study the sonication of bulk Mo₂S₃ samples in organic solvents and show that, indeed, they may be converted to colloidal nanosized sheets. Solid particles in the dispersions retain the initial Mo₂S₃ crystal structure and have the shape of plates with typical thicknesses of 5–30 nm and lateral sizes of 100–400 nm. Finally, we investigate the gas sensing properties of the Mo₂S₃ films deposited from the dispersions towards moisture gas and several representative volatile organic compounds.

---

Introduction

The discovery of the unique graphene properties¹ has triggered significant growth in research on nanosheets, nanoribbons and nanorods of other layered or chain-structured inorganic compounds. In particular, nanosized counterparts of hexagonal boron nitride, transition metal dichalcogenides, trichalcogenides and tetrachalcogenides^2–8 have been the focus of intense research. The structures of all these compounds are characterized by weak van der Waals bonding between covalently assembled layers (or chains), allowing the exfoliation of the compounds to give nanosheets as thin as a single layer. One of the most simple and effective methods to achieve this is through ultrasonic treatment of the layered material in a suitable liquid medium. This strategy is also referred to as liquid phase exfoliation.^2,4,9

Molybdenum disulfide 2H-MoS₂ and its analogues (MoSe₂, WS₂, WSe₂, etc.) are among the compounds whose ability to form colloidal dispersions in polar organic media by ultrasound treatment is most widely studied.⁹ The MoS₂ crystal structure (Fig. 1(a)) is composed of three-atom-thick layers S–Mo–S, oriented across and interacting weakly. As shown in numerous studies focusing on ultrasonic exfoliation, bulk MoS₂ samples can be easily transferred to the nanostate, and the resulting molybdenum disulfide nanosheets show interesting catalytic,¹⁰ electrochemical,^11,12 thermoelectric,^2,13 luminescent^14,15 and gas sensing^16–20 properties.

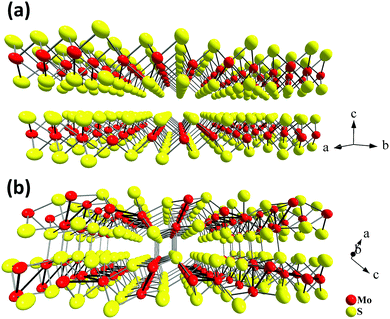Fig. 1 Crystal structures of two stable Mo–S compounds: layered MoS₂ (a) and quasi-layered Mo₂S₃ (b).

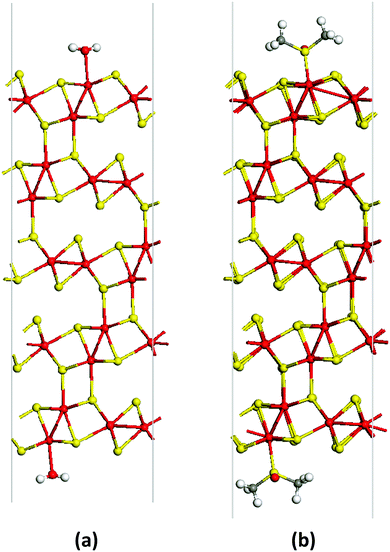
At the same time, there are other interesting and less studied compounds in the transition metal chalcogenide family. One such example is molybdenum sesquisulfide Mo₂S₃.^21–25 Bulk Mo₂S₃ shows unusual electron transport properties at low temperatures due to the metal cluster formation,^26–30 and it has been suggested for use as an element for memory devices.³¹ More recently, Mo₂S₃ was investigated as a cathode material.³² This compound has a complicated quasi-layered crystal structure (Fig. 1(b)) and comprises two crystallographically independent metal chains with short Mo–Mo distances extending in the direction of the b axis (Fig. 1(b)). The comparison of the lattices of Mo₂S₃ and MoS₂ reveals that in the former, two types of bonding between layers are realized, namely, (i) weak van der Waals S⋯S interactions and (ii) covalent bonds between the molybdenum atoms belonging to one layer and the sulfur atoms of the neighboring layer (Fig. 1(b), 2(c) and Fig. S1(c), ESI†). On the other hand, the same structure may be imagined as a stack of molecular 1T-MoS₂ layers intercalated by molecular MoS nanowires (Fig. 1(b), 2(a), (b), Fig. S1(a) and (b), ESI†). Therefore, Mo₂S₃ can be described as a quasi-layered structure, in contrast to the true layered MoS₂, where the neighboring layers are held together only by weak van der Waals interactions. Recently, some molybdenum sesquisulfide nanomaterials were prepared with the morphology of flowers,³³ nanorods,³⁴ and thin layers.^35–37 These Mo₂S₃ nanomaterials were obtained either via high-temperature solid state reactions of MoO₃ with H₂S³⁴ or S,³³ or via thermal decomposition of MoS₂^35,37 or MoS₃.³⁶ However, Mo₂S₃ and, especially its nanostructures, still remain relatively little studied. In particular, there is no information available on the top-down wet chemical preparation of Mo₂S₃ nanostructures, while, as with other nanomaterials, solution processability would be an important step for testing it in potential practical applications. Also, first-principles calculations widely employed to investigate the dynamic stability and electronic structures of 2D materials^38,39 have not been performed for Mo₂S₃ so far.

In the present work, we use density functional theory calculations to prove the possibility of cleaving Mo₂S₃ crystals into sheet-like fragments. The theoretical results are supported by experimental studies of Mo₂S₃ dispersion in various liquids through ultrasonication. Finally, we demonstrate the potential of Mo₂S₃ films prepared from the colloids as sensors for humidity and several volatile organic compounds.

Experimental

Computational details

Apart from the pristine Mo₂S₃ bulk crystal (space group P2₁/m), two-dimensional nanosheets of nanometer thickness are adopted as the basic models for the theoretical study of possible ways to cut a Mo₂S₃ crystal. The nanosheets are designed as 1–5 molecular layers cleaved along either (001) or (1̄01) planes of the Mo₂S₃ crystal, whose unit cells consist of 10 to 50 atoms (Fig. 2, for more details see ESI,† Fig. S1). In addition, their possible surface complexes are considered using the models of Mo₂S₃(1̄01) five-layer nanosheets with adsorbed DMSO or water molecules.

Fig. 2 Three possible methods of cleaving the Mo₂S₃ crystal into nanosheets: (a) along the (001) plane with the removal of unsaturated Mo and S atoms; (b) along the (001) plane and with tetrahedral coordination of surface Mo atoms; (c) along the (1̄01) plane. The unit cells of the model nanosheets are highlighted in blue. Mo and S atoms are painted in red and yellow, respectively. The geometry of all structures is optimized using the DFT method.

All quantum-chemical calculations of the crystallographic and electronic properties of bulk and few-layered Mo₂S₃ were performed within the framework of DFT using the SIESTA 4.0 package.⁴⁰ The exchange–correlation potential within the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof parametrization was used. The core electrons were treated within the frozen core approximation, applying norm-conserving Troullier–Martins pseudopotentials. The valence electrons were taken as 4d⁵5s¹5p⁰ for Mo, 3s²3p⁴3d⁰ for S, 2s²2p⁴ for O, 2s²2p² for C and 1s¹ for H. The pseudopotential core radii were chosen as 2.43 a_B for Mo4d and Mo5s, 2.62 a_B for Mo5p states, and 1.69, 1.45, 1.20 and 0.15 a_B for all S, O, C and H states, respectively. In all calculations, a double-ζ polarized basis set was used. The k-point mesh was generated by the Monkhorst–Pack method. For k-point sampling, a cutoff of 10 Å was used. The real-space grid used for numeric integrations was set to correspond to the energy cutoff of 300 Ry. The calculations of pristine Mo₂S₃ structures were performed using variable-cell and atomic position relaxations, with convergence criteria corresponding to the maximum residual stress of 0.1 GPa for each component of the stress tensor, and the maximum residual force component of 0.05 eV Å⁻¹. In the calculations of two-dimensional adsorption complexes, only the atomic position relaxation was employed, while the lattice parameters were kept as those optimized for clean Mo₂S₃ nanosheets. For all two-dimensional structures, the out-plane lattice parameter was equal to 50 Å to avoid a spurious interaction with the periodic image.

Synthesis of bulk Mo₂S₃

The polycrystalline Mo₂S₃ samples were obtained by a high-temperature (1150 °C) reaction of equivalent MoS₂ and Mo amounts in an evacuated and sealed quartz ampoule.²⁹

Preparation of colloidal dispersions

Fine powder of Mo₂S₃ (50 mg) was mixed with a solvent (30 mL) in a glass vial and ultrasonicated in a “Sapphire” ultrasound bath (ultrasound power 150 W, frequency 35 kHz) during 4 h. Large particles were settled down for 16 h. The upper parts of mixtures were isolated and investigated by a set of methods. Following this procedure, water, ethanol, an ethanol–water mixture (vol. ratio of 1 : 1), isopropanol (i-PrOH), acetonitrile, dimethylformamide (DMF), dimethyl sulfoxide (DMSO), and N-methyl-2-pyrrolidone (NMP) were tested as dispersive media. Solid particles in the form of films were separated from the colloidal dispersions by filtration of the dispersions through the membrane filters with pore size 0.02 μm (Whatman, Anodisc 25). The films were washed with ethanol and dried under mild vacuum at 70 °C for 1 h.

Characterization

X-ray powder diffraction (XRPD) patterns for solid samples (powders and films) were collected using a Philips PW 1830/1710 automated diffractometer (Cu K_α radiation, graphite monochromator, silicon plate as an external standard). Zeta-potentials and dynamic light scattering (DLS) spectra were measured by using ZetaSizer Nano-ZS equipment. The thickness of the particles and surface morphology were evaluated by using a scanning probe microscope (Solver P-47H, NT-MDT, Russia). Images were obtained in atomic force microscopy (AFM) mode using non-contact cantilevers (NSG-11, NT-MDT, Russia). The samples were prepared using several drops of diluted colloidal dispersions in an ethanol–water mixture (vol. ratio of 1 : 1), which were applied to mica pieces, and dried at 70 °C for 2 h. High-resolution transmission electron microscopy (HRTEM) images were obtained by using a JEM-2010 (JEOL Ltd.) microscope with a lattice-fringe resolution of 0.14 nm at an accelerating voltage of 200 kV. Suspensions in the ethanol–water mixture were deposited on carbon film-coated copper grids. The lattice spacing was calculated by fast Fourier transform (FFT) using DigMicrograph (GATAN) software. Energy dispersive X-ray spectroscopy (EDS) was performed on a Hitachi TM3000 TableTop SEM equipped with Bruker QUANTAX 70 EDS equipment. Thermogravimetric analyses (TGA) were carried out on a TG 209 F1 Iris thermobalance (NETZSCH, Germany). The measurements were performed in a helium flow in the temperature range of 30–900 °C using a heating rate of 10 °C min⁻¹, a gas flow rate of 60 mL min⁻¹ and open Al₂O₃ crucibles. The simultaneous TG–DSC/EGA–MS measurement was performed in an apparatus consisting of a STA 449 F1 Jupiter thermal analyzer and a QMS 403D Aëolos quadrupole mass spectrometer (NETZSCH, Germany). The spectrometer was connected online to a thermal analyzer (STA) instrument by a quartz capillary heated to 280 °C. The QMS was operated with an electron impact ionizer with an energy of 70 eV. The ion currents of the selected mass/charge (m/z) numbers were monitored in multiple ion detection (MID) mode with a collection time of 1 s for each channel. The measurements were performed in a helium flow in the temperature range of 30–500 °C using a heating rate of 10 °C min⁻¹, a gas flow rate of 30 mL min⁻¹ and open Al₂O₃ crucibles.

Formation and measurements of a vapor sensing element based on Mo₂S₃ nanosheets

A thin film assembled from Mo₂S₃ colloidal dispersions was used for measurements. The experimental sample was formed by cutting the filtered film. Electrical contacts were made of graphite paste and lead thin copper wires. Electrical resistance of the sample was measured by a standard four-point probe method, with the dc voltage being measured using a Keithley 2000. Vapor-induced changes in the resistance of the experimental sample under room conditions (relative humidity in the laboratory was 12%) were monitored using a glass chamber 8.7 L in volume. A certain volume of H₂O, DMSO, ethanol or acetone was evaporated inside the chamber, with H₂O and DMSO being coated onto filter paper for better evaporation. Once thermodynamic equilibrium was reached, the air-dried Mo₂S₃ sample was placed into the chamber, and the resistance change was registered. After the sample was exposed, it was taken out of the chamber back into room conditions, and resistance relaxation was recorded. The experiment was repeated with varying volumes of water, DMSO, ethanol and acetone.

Results and discussion

DFT calculations of the bulk Mo₂S₃

In order to understand whether free-standing few-layered Mo₂S₃ nanosheets are energetically favorable and/or can be stabilized by adsorbing solvent molecules, DFT calculations have been carried out. As a starting point, the bulk crystal of Mo₂S₃ was studied. The lattice parameters of the bulk Mo₂S₃ after geometry optimization have been found to be a = 6.219 Å, b = 3.232 Å, c = 8.742 Å, and β = 102.67°, which are in fair agreement with experimental data (a = 6.092 Å, b = 3.208 Å, c = 8.633 Å, and β = 102.43°).^31,41 All Mo atoms have a distorted octahedral coordination by S atoms, and the Mo–S bond lengths vary from 2.37 to 2.60 Å. A zigzag-like ordering of Mo atoms along the [010] direction and within the (001) and (1̄01) planes can be distinguished. The average Mo–Mo distances are equal to 2.89 Å and 2.83 Å, which are comparable with the Mo–S bond lengths and suggest the presence of covalent-type Mo–Mo bonding. The latter is confirmed by analysis of the electronic structure.

The calculated band structure and density of electronic states (DOS) for crystalline Mo₂S₃ are depicted in Fig. 3(a) and Fig. S2(A) (ESI†). The compound possesses a metal-like character with the Fermi level hosted at the local DOS minimum. Two main groups of states within the valence band can be outlined, accordingly to the different types of chemical bonding. The first group at −7 to −2 eV is formed by a mixture of S3p- and Mo4d-states, which are responsible for covalent Mo–S bonding. The second group is closer to the Fermi level and is presented mainly by Mo4d-states, providing covalent Mo–Mo bonding and –Mo–Mo– chain formation along the [010] direction.

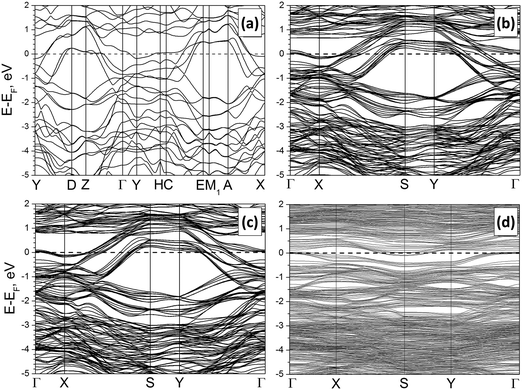Fig. 3 Band structures of the bulk Mo₂S₃ (a), a clean Mo₂S₃(1̄01) five-layer nanosheet (b) and the same nanosheet with H₂O (c) or DMSO molecules (d) anchored to Mo atoms. DFT calculations.

The values of crystal orbital overlap population (COOP) also evidence Mo–Mo bonding. Particularly, COOPs between the nearest neighbor Mo atoms within the (001) and (1̄01) planes are equal to 0.078 e and 0.090 e, respectively, while those between the second neighbor Mo atoms are equal to 0.042 e and 0.040 e. COOPs for the most of the Mo–S bonds within distorted MoS₆ octahedra have values around 0.23–0.26 e. Yet, Mo–S bonds at the boundaries of cross-sections like those drawn in Fig. S1(A) and (C) (ESI†) have lower COOPs of 0.17 and 0.19 e, respectively, and might be the weakest links. Therefore, preferential cleavage or exfoliation of the crystal might be expected along the (001) or (1̄01) planes. This preliminary guess can be proven after the direct calculations of the formation energies for the few-layered sheets.

DFT calculations of few-layered Mo₂S₃ nanosheets

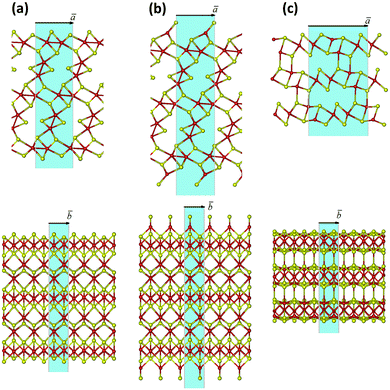
There may exist different directions to cleave a Mo₂S₃ crystal, and the choice may be made intuitively (Fig. 2 and Fig. S1, ESI†). The cleavages of a or b type disclose a stratiform structure of the Mo₂S₃ crystal as a stack of molecular 1T-MoS₂ layers intercalated by molecular MoS nanowires. The nanosheets of a type have an octahedral coordination of all Mo atoms and a sulfur-rich composition approaching Mo₂S₃ with the thickness growth. The strictly stoichiometric nanosheets of b type should have a tetrahedral coordination of surface Mo atoms. In contrast, the cleavage of c type in Fig. 2 and Fig. S1 (ESI†) leads to nanosheets of both unperturbed stoichiometry and Mo coordination.

The initial bond lengths and valence angles within models of all Mo₂S₃ nanosheets corresponded to the ones of the bulk. The vectors along the [100] or [101] directions in the crystal were chosen as the main translation vectors ā for nanosheets of types a or b and c, respectively (Fig. 2 and Fig. S1, ESI†), while the translational vector b̄ for all nanosheets corresponded to b̄ in the crystal. Geometry optimization of 2D nanostructures reveals their slight in-plane contraction depending on the thickness, and a predominant decrease of the lattice parameter a, e.g., stoichiometric nanosheets (Fig. 2(b) (Fig. S1(b), ESI†) and Fig. 2(c) (Fig. S1(c), ESI†)) with thicknesses of 1 and 5 layers undergo contractions of 2% and 0.5%, respectively. The structure of non-stoichiometric nanosheets (Fig. 2(a) and Fig. S1(a), ESI†) with the same thicknesses and compositions of Mo₂S₄ and Mo₂S_3.11 demonstrates contractions of 7% and 1%, respectively. The change in the lattice parameter b is negligible, and its value for thick nanosheets is identical to that for the crystal.

The relative stability of the nanosheets was analyzed as a function of the surface termination and thickness (Fig. 4). The nanosheets with (1̄01) termination (type c, Fig. 2 and Fig. S1, ESI†) appear to be the most stable among all considered types, independent of the nanosheet stoichiometry and thickness. The relative energies of all nanosheets decrease as the nanosheet thickness grows and rapidly converge to the values of the energies of surface formation, namely, 0.15 eV Å⁻² for Mo₂S₃(1̄01) and 0.73 eV Å⁻² for the Mo₂S₃(001) surface. Noteworthy, the first value is only 5 times larger than the typical energy of van der Waals binding within layered dichalcogenides like MoS₂ (∼0.02–0.03 eV Å⁻²).³⁹

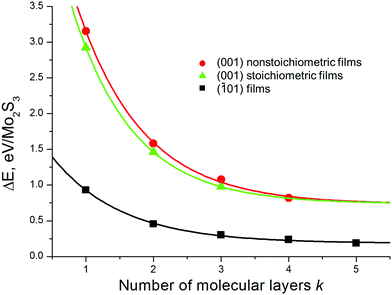Fig. 4 Relative energy of Mo₂S₃ nanosheets as a function of their thickness and the type of cleavage. The bulk Mo₂S₃ crystal is chosen as the reference system. DFT calculations.

The electronic properties of the nanosheets are regulated mostly by their type and weakly depend on the thickness. Main peculiarities in the band structure and DOS of the most stable Mo₂S₃(1̄01) nanosheet consisting of 5 layers are visualized in Fig. 3(b) and Fig. S2(b) (ESI†). Despite the rise of the surface, the metal-like character of Mo₂S₃ is preserved. The DOS profile and distribution of partial DOS, as well as the position of the Fermi level, are very similar to those of the bulk Mo₂S₃. Moreover, certain parts of the band structure of the nanosheet can be correlated with the band structure of the crystal along equivalent points (namely, X–S–Y–Γ and Γ–X in the nanosheet vs. Y–D–Z–Γ and Γ–Y in the crystal). The only difference is a larger dispersion of the bands for the nanosheet due to the simultaneous presence of surface and volume atoms.

Such a great similarity between the electronic properties of Mo₂S₃ within the bulk and within a nanosheet predicates that the intrinsic conductance of the nanosheets should not be too different from that along equivalent directions of the crystal. In addition, the partial DOS analysis of the nanosheet depending on the depth does not reveal an essential difference either in the distribution or in the intensity of Mo4d-states. Therefore, the electric conductivity of the pure surface should not be essentially different from the conductivity of the bulk.

DFT calculations of Mo₂S₃ nanosheets with H₂O or DMSO adsorbates

As our calculations prove the preferential cleavage of the few-layered Mo₂S₃ nanosheets along the (1̄01) plane, in practice it would mean the possibility of their formation and stabilization under the influence of ultrasonication in an organic solvent, much similarly to the truly layered compounds, such as MoS₂ or graphite. In this case, the interactions between the nanosheets and the solvent molecules would play an important role in the stabilization of the colloidal nanosheets. Earlier works employed DFT calculations to study the interactions between MoS₂ nanosheets and amino acids⁴² or protein functional groups.⁴³ Therefore, the study of the stability of adsorption complexes between the Mo₂S₃ surface and solvent molecules was performed using the model of the five-layer Mo₂S₃(1̄01) nanosheet and a single layer of water or DMSO molecules anchored to all Mo surface atoms. H₂O molecules were considered as monodentate O-ligands, while DMSO molecules acted either as bidentate SO-ligands or monodentate O- or S-ligands. In all situations, excluding DMSO anchoring via the S-atom, the adsorption is exothermic and can be characterized as chemisorption. The calculated adsorption energies are equal to −1.32 and −0.71 eV for monodentate H₂O and DMSO O-ligands, respectively, and −1.60 eV for bidentate DMSO. Endothermic adsorption of DMSO molecules as S-ligands with energy +1.14 eV might be explained by a sterical hindrance and a large repulsion between “lying” disc-shaped molecules. There is a small charge transfer around 0.05 e from adsorbed H₂O or DMSO molecules to the Mo₂S₃ part.

The coordination bond lengths within stable adsorption complexes are estimated as 2.36 Å for Mo⋯OH₂, 2.75 Å for Mo⋯O=S(CH₃)₂ and 2.47 Å for Mo⋯S(CH₃)₂=O. No surface reconstruction is revealed after deposition of the water layer, while a slight dispersion in the values of dihedral angles within the Mo₂S₃ part can be detected (Fig. 5).

Fig. 5 Unit cells of the adsorption complex of a Mo₂S₃(1̄01) five-layer nanosheet and monodentate H₂O (a) or bidentate DMSO molecules (b) viewed along the [010] direction. The S=O bonds of DMSO molecules are aligned along the [010] direction. The geometry of both structures is optimized using the DFT method.

A comparison of band structures and DOS distributions between a clean Mo₂S₃ nanosheet and an adsorbate-modified one does not establish an essential difference. Mo₂S₃ preserves the metal-like character even after deposition of molecules at the surface (Fig. S2(d), ESI†). The most pronounced feature is the rise of new impurity levels in DOS. Adsorption of H₂O leads to the rise of the strong localized O2p-states at −12 eV as well as the O2p-states partially overlapping with the bottom of the valence band at −8 and −6 eV. Adsorption of DMSO molecules leads to a similar effect. Then, the DOS profile of the adsorption complex is characterized by O2p- and S3p-states of the S=O group near the bottom of the valence band and the deep states from C and H atoms.

Experimental study of Mo₂S₃ in colloids

Further, theoretically predicted exfoliation of Mo₂S₃ was achieved experimentally. First, the bulk polycrystalline Mo₂S₃ was synthesized by a high-temperature reaction between MoS₂ and Mo; the phase identity was confirmed by the XRPD pattern (Fig. S3, ESI†). The EDS results showed the proportion of molybdenum vs. sulfur atoms to be 40 : 59, which is close to the theoretically calculated value of 2 : 3. Therefore, the samples obtained are the bulk single-phase Mo₂S₃.

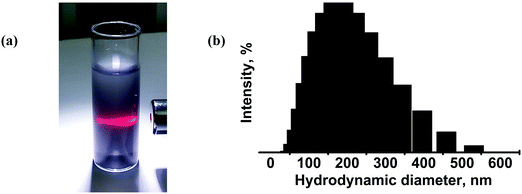
Next, we examined the colloidal dispersions that formed upon sonication of the bulk Mo₂S₃ in organic media. The series of solvents appropriate for liquid phase exfoliation of MoS₂ was tested for Mo₂S₃. The resulting dispersions have a grey color and exhibit the Tyndall effect, showing the presence of colloidal particles in the liquid media (Fig. 6(a)). The average hydrodynamic particle size in dispersions was determined by DLS to be 190 nm with a deviation of 90 nm (Fig. 6(b)). The concentrations (mg L⁻¹) of dispersions in different solvents estimated by the weight method are as follows: water (<20), ethanol (30), ethanol–water mixture (vol. ratio of 1 : 1) (70), i-PrOH (50), acetonitrile (30), DMF (0), and NMP (70). One can see that, similarly to MoS₂, Mo₂S₃ is well dispersed in NMP and an alcohol/water mixture, however, the highest concentration of 130 mg L⁻¹ is found for the Mo₂S₃/DMSO dispersion. The zeta-potentials were measured for colloidal dispersions in the ethanol–water mixture to be about −35 to −40 mV, confirming the good stability of the colloids.

Fig. 6 (a) Photograph of the Mo₂S₃ dispersion in an ethanol–water mixture (vol. ratio of 1 : 1) exhibiting the Tyndall effect. (b) DLS data for the Mo₂S₃ dispersion in the ethanol–water mixture (vol. ratio of 1 : 1). The mean hydrodynamic particle size is 190 nm with a deviation of 90 nm.

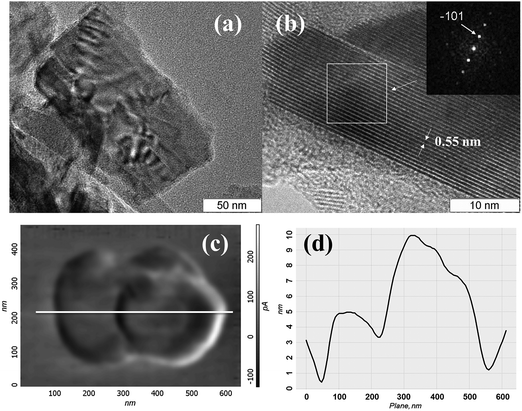
For establishing the morphology of the particles in dispersions, detailed HRTEM and AFM studies have been carried out. HRTEM data (Fig. 7(a), (b) and Fig. S4, ESI†) show that the dispersions contain “crumpled” plate-shaped particles of few hundred nanometers in lateral size. The plate thickness varies from 5 nm to 30 nm. Fig. 7(b) shows the HRTEM image of a ∼15 nm thick plate, with the interplanar spacing being 0.55 nm, that corresponds to the (1̄01) plane. The FFT image in the inset of Fig. 7(b) displays a row of reflections corresponding to the lattice spacing of d₋₁₀₁ = 0.5498 nm. The HRTEM image corresponding to the zone axis [101] was simulated by using Stadelmann's software⁴⁴ and was found in good agreement with the experimental image (see Fig. S5, ESI†). According to the AFM study, particles have the shape of the plates with typical lateral dimensions of 100–400 nm and thicknesses of 8–50 nm. The particle visualized in Fig. 7(c) is the particle that consists of two closely placed particles of about 250 nm in size, and 8–20 nm in thickness (see the profile in Fig. 7(d)). According to the XRPD study (Fig. S6, ESI†), solid particles retain the initial Mo₂S₃ identity independent of the type of solvent.

Fig. 7 HRTEM images of Mo₂S₃ from the ethanol–water dispersion; (a) and (b) close views of a Mo₂S₃ nanosheet as seen from the top and side, respectively; the inset is the FFT pattern from a selected area; (c) AFM image in lateral force mode of particles in the dispersion and (d) their AFM profile.

Therefore, it is clearly shown that the bulk quasi-layered Mo₂S₃ can be successfully dispersed by sonication in various liquid media. The particles in colloids mostly adopt a nanosheet-like morphology that proves the existence of a preferential direction for their exfoliation. This finding is in good agreement with the results of DFT calculations presented in the previous part and with earlier findings on the exfoliation of layered MoS₂. Powerful sonication is known to break both the weak van der Waals bonds and the stronger covalent bonds, thus cutting MoS₂ or graphene into smaller sheets.^45,46 Apparently, in our case of Mo₂S₃, Mo–S bonds between adjacent “layers” (or within them) could be overcome as well. The effectiveness of certain solvents in the stabilization of colloidal nanosheets is often explained in terms of solution thermodynamics. It is argued that successful solvents for many layered materials (MoS₂, h-BN, graphite, etc.) should have surface energies close to those of nanosheets (∼70 mJ m⁻²).² Another aspect to bear in mind is the possibility of chemisorption or chemical interaction between the colloidal nanostructures and solvent molecules.^45,47,48 For our colloidal Mo₂S₃ nanosheets, this version is to some extent corroborated by the observed high negative zeta-potential. A complex of several factors is involved in the dispersion process: (i) breaking of van der Waals bonds, (ii) breaking of covalent Mo–S bonds within the layers and (iii) breaking of interlayer covalent Mo–S bonds. The latter two circumstances would lead to the creation of highly reactive molybdenum centers. Being highly chalcophilic and complex formers as they do, the under-coordinated Mo atoms at the edges and at the surfaces can be stabilized by complexing solvent molecules. In fact, the DFT calculations discussed above predict the stability of such adsorbate complexes. To check this assumption experimentally, we use TGA and mass-spectrum analyses to study Mo₂S₃ deposited from the colloids.

Thermoanalytical and mass-spectrometric analyses

The presence of solvent molecules within the solid phase deposited from the DMSO colloidal dispersion was confirmed by simultaneous TG–DSC/EGA–MS analyses (Fig. 8). When the sample is heated up to 125 °C under an inert atmosphere, the mass loss of about 0.14% is due to the removal of adsorbed water molecules. In the mass-spectrum, a slight increase in the ion current of the particles with m/z = 18 is observed (it is not shown in Fig. 8). Continuous heating up to temperatures in the interval of 125–250 °C leads to a mass loss of 0.4%. This is accompanied by an increase in the ion current of the particles with m/z = 15, 45, 29, 61, 46, 47, and 48. Such a number of fission ions indicates that DMSO molecules are the main gas products evolving at this stage. This temperature interval in the inert atmosphere is in good agreement with the boiling point of pure DMSO (189 °C). We suggest that the absence of currents corresponding to the fission ion with m/z = 63 and the molecular ion with m/z = 78 is due to high temperature (280 °C) in the capillary of the transport line from the STA device to the mass-spectrometer that causes thermal deconstruction of the DMSO molecules. The sum of mass losses when heated up to 850 °C is 1.8%. It may be due to the removal of the products of DMSO decomposition. Therefore, it is probable that the “exposed” molybdenum atoms resulting from the rupture of Mo–S bonds during the ultrasonic treatment of Mo₂S₃ may be stabilized by complexing solvent molecules or their residues, similarly to MoS₂,^45,49 especially, taking into account the formation of many active species through solvent sonolysis.^45,47,48 In previous works, the Mo₂S₃ surface was also shown to have high affinity for some organic molecules, such as anthraquinones.³⁵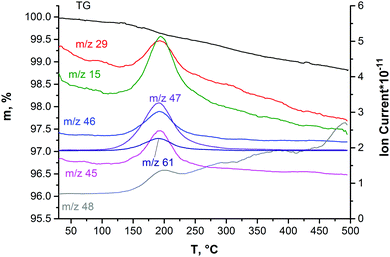

Fig. 8 The data of TG–DSC/EGA–MS obtained on Mo₂S₃ precipitated from the colloidal dispersion in DMSO.

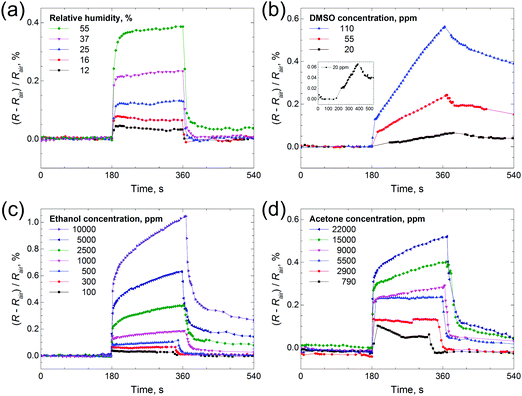
Sensing properties of the Mo₂S₃ thin film toward vapors of H₂O, DMSO, ethanol and acetone

Thin films based on various chalcogenides are researched as sensors towards a range of gases, including ammonia,¹⁶ water^18,50 and volatile organic compounds (toluene, hexane, acetone, etc.).^19,20 We took water, DMSO, ethanol and acetone as sample analytes for testing the sensing properties of the Mo₂S₃ thin film. One can see from Fig. 9 that a positive response is registered for all four gases (resistance is increased), and the response depends on vapor concentration. The electrical resistance response of the Mo₂S₃ sample to the change in humidity is shown in Fig. 9(a). The resistance of the sensing element increases sharply upon contact with water vapor and recovers to its original value once taken out of the chamber. The Mo₂S₃ thin film sensor exhibited a quick response and recovery times of about 30 s for the maximum H₂O concentration (defined as the time required to achieve 90% of the final equilibrium resistance value). This value is well comparable to those of recently reported VS₂-based moisture sensors⁵⁰ and exceeds the characteristics of detectors based on some other nanomaterials.⁵¹ One can see that there are distinct saturations for every H₂O concentration, but there was no saturation for DMSO and for higher concentrations of acetone and ethanol (Fig. 9(b) and (c)). For DMSO the resistance increased linearly within the time range (Fig. 9(b)) and recovered very slowly in comparison with the rest of the analytes studied, with the time for complete recovery after contact with DMSO at a concentration of 110 ppm being about 14 000 s (see Fig. S7, ESI†).

Fig. 9 Time dependence of electrical resistance of the Mo₂S₃ thin film sample in the presence of target gases: (a) H₂O, (b) DMSO, (c) ethanol and (d) acetone. The inset in (b) presents an enlarged view of the response to 20 ppm of DMSO. R_air is the resistance of the sample under room conditions, and the relative humidity in the room was 12%. Each experiment consisted of three 180 s steps: (1) the sample was kept under room conditions, (2) it was placed inside a glass chamber with the vapors and (3) it was taken out of the chamber back into room conditions.

Therefore, the sensing behavior of the Mo₂S₃ film is found to depend strongly on the chemical nature of gas molecules. But generally speaking, the changes in resistance constitute a complex phenomenon in chemiresistor studies and may be related to complicated combined mechanisms of physisorption, chemisorption, charge transfer, etc.,¹⁹ and, moreover, capillary condensation may take place, thereby leading to mechanical separation of the conducting Mo₂S₃ nanoparticles in the film and, as a result causing an increase of electrical resistance.

Conclusions

In summary, a combined computational and experimental study of molybdenum sulfide Mo₂S₃ in its bulk and nanosized states is reported. For the first time, we show that this material with a quasi-layered structure may be exfoliated into sheet-like nanostructures, quite similar to the true layered materials, such as MoS₂, h-BN or graphite. DFT calculations reveal the existence of a preferential exfoliation direction along the (1̄01) plane, implying the breaking of both weak van der Waals bonds and stronger covalent Mo–S bonds between the “layers”. Moreover, the cleaved few-layered structures may be stabilized by chemisorption of organic molecules, such as DMSO, which are often used in practice as solvents. This finding is verified by the experimental observation of sonication-induced colloidal dispersion of Mo₂S₃ in a number of liquids. Stable colloids in DMSO, NMP or an ethanol/water mixture contain rectangular Mo₂S₃ nanosheets, whose stabilization in the dispersed state may be in part due to the surface modification by solvent molecules. The gas sensing properties of a Mo₂S₃ film deposited from the dispersions are investigated for the detection of water, ethanol, acetone, and DMSO. Overall, the presented theoretical study, synthetic method, and demonstration of solution processability of Mo₂S₃ are all important steps for uncovering the potential of this material for various advanced applications, including energy storage, incorporation into composites, etc.

Acknowledgements

The work was supported by the Russian Foundation for Basic Research (17-03-00074). The authors would like to thank Dr I. A. Pyshnaya from the core facility of ICBFM SB RAS for DLS and z-potential measurements.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H. Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571.
3. W. L. Yang, X. D. Zhang and Y. Xie, Nano Today, 2016, 11, 793–816.
4. V. Nicolosi, M. Chhowalla, M. G. Kanatzidis, M. S. Strano and J. N. Coleman, Science, 2013, 340, 1226419.
5. V. E. Fedorov, S. B. Artemkina, E. D. Grayfer, N. G. Naumov, Y. V. Mironov, A. I. Bulavchenko, V. I. Zaikovskii, I. V. Antonova, A. I. Komonov and M. V. Medvedev, J. Mater. Chem. C, 2014, 2, 5479–5486.
6. S. B. Artemkina, T. Y. Podlipskaya, A. I. Bulavchenko, A. I. Komonov, Y. V. Mironov and V. E. Fedorov, Colloids Surf., A, 2014, 461, 30–39.
7. M. N. Kozlova, Y. V. Mironov, E. D. Grayfer, A. I. Smolentsev, V. I. Zaikovskii, N. A. Nebogatikova, T. Y. Podlipskaya and V. E. Fedorov, Chem. – Eur. J., 2015, 21, 4639–4645.
8. P. A. Poltarak, S. B. Artemkina, A. I. Bulavchenko, T. Y. Podlipskaya and V. E. Fedorov, Russ. Chem. Bull., 2015, 64, 1850–1856.
9. E. D. Grayfer, M. N. Kozlova and V. E. Fedorov, Adv. Colloid Interface Sci., 2017, 245, 40–61.
10. D. Voiry, M. Salehi, R. Silva, T. Fujita, M. W. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nano Lett., 2013, 13, 6222–6227.
11. J. Xiao, D. W. Choi, L. Cosimbescu, P. Koech, J. Liu and J. P. Lemmon, Chem. Mater., 2010, 22, 4522–4524.
12. Y. L. Liang, R. J. Feng, S. Q. Yang, H. Ma, J. Liang and J. Chen, Adv. Mater., 2011, 23, 640–643.
13. R. J. Smith, P. J. King, M. Lotya, C. Wirtz, U. Khan, S. De, A. O'Neill, G. S. Duesberg, J. C. Grunlan, G. Moriarty, J. Chen, J. Z. Wang, A. I. Minett, V. Nicolosi and J. N. Coleman, Adv. Mater., 2011, 23, 3944–3948.
14. G. Eda, H. Yamaguchi, D. Voiry, T. Fujita, M. W. Chen and M. Chhowalla, Nano Lett., 2011, 11, 5111–5116.
15. V. Stengl and J. Henych, Nanoscale, 2013, 5, 3387–3394.
16. Y. Yao, Z. Lin, Z. Li, X. Song, K.-S. Moon and C.-P. Wong, J. Mater. Chem., 2012, 22, 13494–13499.
17. Y. Yao, L. Tolentino, Z. Yang, X. Song, W. Zhang, Y. Chen and C.-P. Wong, Adv. Funct. Mater., 2013, 23, 3577–3583.
18. S.-L. Zhang, H.-H. Choi, H.-Y. Yue and W.-C. Yang, Curr. Appl. Phys., 2014, 14, 264–268.
19. J. S. Kim, H. W. Yoo, H. O. Choi and H. T. Jung, Nano Lett., 2014, 14, 5941–5947.
20. X.-Q. Tian, L. Liu, X.-R. Wang, Y.-D. Wei, J. Gu, Y. Du and B. I. Yakobson, J. Mater. Chem. C, 2017, 5, 1463–1470.
21. F. Jellinek, Nature, 1961, 192, 1065–1066.
22. L. Brewer and R. H. Lamoreaux, Bull. Alloy Phase Diagrams, 1980, 1, 93–95.
23. I. G. Vasilyeva and R. E. Nikolaev, J. Alloys Compd., 2008, 452, 89–93.
24. G. T. Huang, W. H. Chao, J. K. Chang, H. D. Liao, D. C. Ling, F. Z. Chien and M. K. Wu, J. Supercond. Novel Magn., 2013, 26, 503–510.
25. S. Leidich, D. Buechele, R. Lauenstein, M. Kluenker and C. Lind, J. Solid State Chem., 2016, 242(part 2), 175–181.
26. R. Deblieck, G. A. Wiegers, K. D. Bronsema, D. Vandyck, G. Vantendeloo, J. Vanlanduyt and S. Amelinckx, Phys. Status Solidi A, 1983, 77, 249–261.
27. R. L. Fagerquist and R. D. Kirby, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3973–3985.
28. A. K. Rastogi, Philos. Mag. B, 1985, 52, 909–919.
29. A. I. Romanenko, F. S. Rakhmenkulov, I. N. Kuropyatnik, V. E. Fedorov and A. V. Mishchenko, Phys. Status Solidi A, 1984, 84, K165–K167.
30. W. J. Schutte, F. Disselborg and J. L. de Boer, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 787–794.
31. V. E. Fedorov, Transition metal chalcogenides. Quasi-onedimensional compounds, Nauka, Novosibirsk, 1988.
32. E. Shembel, R. Apostolova, I. Kirsanova and V. Tysyachny, J. Solid State Electrochem., 2008, 12, 1151–1157.
33. Y. Zhong, Y. Zhang, G. X. Zhang, R. Y. Li and X. L. Sun, Appl. Surf. Sci., 2012, 263, 410–415.
34. R. C. Che, N. Bai and L. M. Peng, Appl. Phys. Lett., 2003, 83, 3561–3563.
35. D. Z. Sun, W. H. Lu, D. Le, Q. Ma, M. Aminpour, M. A. Ortigoza, S. Bobek, J. Mann, J. Wyrick, T. S. Rahman and L. Bartels, Angew. Chem., Int. Ed., 2012, 51, 10284–10288.
36. V. Koroteev, A. Okotrub, Y. V. Shubin and L. Bulusheva, Key Eng. Mater., 2012, 508, 56–60.
37. R. K. Tiwari, J. Yang, M. Saeys and C. Joachim, Surf. Sci., 2008, 602, 2628–2633.
38. L. Debbichi, H. Kim, T. Björkman, O. Eriksson and S. Lebègue, Phys. Rev. B, 2016, 93, 245307.
39. T. Bjorkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
40. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
41. P. Monceau, M. Renard, J. Richard, M. C. Saintlager, H. Salva and Z. Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1646–1648.
42. E. Satheeshkumar, A. Bandyopadhyay, M. B. Sreedhara, S. K. Pati, C. N. R. Rao and M. Yoshimura, ChemNanoMat, 2017, 3, 172–177.
43. G. Guan, S. Zhang, S. Liu, Y. Cai, M. Low, C. P. Teng, I. Y. Phang, Y. Cheng, K. L. Duei, B. M. Srinivasan, Y. Zheng, Y.-W. Zhang and M.-Y. Han, J. Am. Chem. Soc., 2015, 137, 6152–6155.
44. P. Stadelmann, Electro Microscopy Software “JEMS”, version:3.3526U2008. CIME-EPFL, Switzerland, 2008.
45. L. Muscuso, S. Cravanzola, F. Cesano, D. Scarano and A. Zecchina, J. Phys. Chem. C, 2015, 119, 3791–3801.
46. L. Guardia, J. I. Paredes, R. Rozada, S. Villar-Rodil, A. Martinez-Alonso and J. M. D. Tascon, RSC Adv., 2014, 4, 14115–14127.
47. A. Jawaid, D. Nepal, K. Park, M. Jespersen, A. Qualley, P. Mirau, L. F. Drummy and R. A. Vaia, Chem. Mater., 2016, 28, 337–348.
48. J. T. Han, J. I. Jang, H. Kim, J. Y. Hwang, H. K. Yoo, J. S. Woo, S. Choi, H. Y. Kim, H. J. Jeong, S. Y. Jeong, K.-J. Baeg, K. Cho and G.-W. Lee, Sci. Rep., 2014, 4, 5133.
49. R. Bhandavat, L. David and G. Singh, J. Phys. Chem. Lett., 2012, 3, 1523–1530.
50. J. Feng, L. L. Peng, C. Z. Wu, X. Sun, S. L. Hu, C. W. Lin, J. Dai, J. L. Yang and Y. Xie, Adv. Mater., 2012, 24, 1969–1974.
51. Q. Kuang, C. S. Lao, Z. L. Wang, Z. X. Xie and L. S. Zheng, J. Am. Chem. Soc., 2007, 129, 6070–6071.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7tc01320e

---