Ultra-high discharged energy density capacitor using high aspect ratio Na_0.5Bi_0.5TiO₃ nanofibers

Abstract

Ceramic/polymer nanocomposites are attractive for energy storage applications due to their ability to exploit the high permittivity of ceramic fillers and high breakdown strength of the polymer matrix. One challenge for the development of high performance nanocomposites based on ceramic particulates or fibers in a polymer matrix is that they often require a high volume fraction (>50%) to achieve a high permittivity, which is often at the expense of a reduction in dielectric strength and mechanical flexibility. In this paper we demonstrate by both experiment and finite element simulation that high aspect ratio nanofiber fillers offer an effective approach to achieve high energy density and dielectric strength. Lead-free ferroelectric Na_0.5Bi_0.5TiO₃ (BNT) nanofibers with a high aspect ratio (>200) are synthesized by a hydrothermal method and dispersed in a poly(vinylidene difluoride-co-hexafluoropropylene) (P(VDF-HFP)) matrix. The increased fraction of β-phase and the alignment of BNT nanofibers perpendicular to the direction of the applied electric field lead to an enhanced dielectric strength, compared to spherical BNT/P(VDF-FHP) nanoparticles and pure P(VDF-HFP), and experimental measurements are compared with numerical simulations. The results demonstrate that the nanofiber nanocomposites exhibited an ultra-high discharged energy density (12.7 J cm⁻³) and provide an innovative approach to produce high-energy storage density materials.

---

1 Introduction

High power capacitors are widely applied in electronic devices with pulsed power such as radar, electric vehicles, mobile electronics, power electronics, lasers, and rail guns.^1–8 However, these capacitors usually suffer from low energy density, hence they can only be applied in high cost and bulky electronic devices.^9,10 The maximum discharged energy density (U) of linear dielectric materials is defined as:

U = ½ε₀ε_rE_b² (1)

where ε₀ and ε_r are the permittivity of vacuum and the material, respectively, and E_b is the breakdown electric field of the material. It is clear that the energy density is determined by the E_b and ε_r of the dielectric material, and the E_b is a critical factor since U has a quadratic dependence on the E_b.^11–14

In this regard, ceramic/polymer nanocomposites have been investigated since they have the potential to simultaneously optimize the two factors that determine the energy density by exploiting the high permittivity of ceramic fillers and the high breakdown strength of the polymer matrix.^15–17 It has been shown that the microstructural morphology and concentration of the ceramic fillers have a significant influence on the energy storage density of dielectric nanocomposites.^18–21 In our previous work, 0–3 nanocomposites (0-dimensionally spherical nanoparticles dispersed in a 3-dimensionally connected polymer matrix) containing BaTiO₃ and Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ nanoparticles (NPs) dispersed in a poly(vinylidene difluoride-co-hexafluoropropylene), P(VDF-HFP), polymer matrix exhibited a significantly higher permittivity than pure P(VDF-HFP); however, the increased permittivity of the nanocomposite was at the expense of a decreased breakdown strength compared to the pure polymer matrix phase.^9,19 The high volume fraction (>50 vol%) of ceramic nanoparticle fillers that is needed to significantly increase the permittivity can also lead to the formation of defects, such as voids and cracks, in the 0–3 nanocomposite, as well as reduce the mechanical flexibility of the composites.

The complex balance between permittivity and breakdown strength is attributed to the presence of high local electric field concentrations, which are caused by the large contrast in permittivity between the ceramic and polymer matrix phase.²² Recently, it was demonstrated that the use of high aspect ratio one-dimensional nanofiber fillers could be an effective approach to overcome the challenge of increasing the permittivity without leading to a corresponding decrease of breakdown strength and thereby improve the energy density of the nanocomposite.^{9,18,21,23,24} The improvement is thought to be due to the increased permittivity of the high aspect ratio fillers, as demonstrated by theoretical models such as the Maxwell-Garnett model.^18,25 The nature of the distribution of nanofibers in the polymer matrix and their orientation in perpendicular, parallel and random directions relative to the direction of the electric field significantly affects the electric field distribution in the nanocomposite. However, the influence of the morphology of the ceramic nanofibers or nanoparticles in the polymer matrix on the electric field distribution and the effective capacitance of the composites remains unclear. Most ceramic nanofibers/polymer composites in previous reports^11,13 exhibited an increase in discharged energy density with an increase in the fraction of nanofibers; however the manufacture of high aspect ratio nanofibers continues to be a challenge.¹⁸ Thus, it is of interest that dielectric nanocomposites possessing an ultra-high discharged energy density are formed using a relatively small fraction of nanofibers.

Na_0.5Bi_0.5TiO₃ (BNT) is considered to be an excellent lead-free ferroelectric ceramic with a d₃₃ piezoelectric coefficient of approximately 80 pC N⁻¹ and a high relative permittivity of approximately 500 at 1 kHz, which has attracted significant interest because of its potential to replace lead based piezoelectric materials.^26,27 However, research on BNT/polymer composites, especially using the BNT nanofibers to create new nanocomposites for energy storage applications, remains limited.

In this paper, high aspect ratio BNT nanofibers and BNT nanoparticles are synthesized by a simple hydrothermal method by controlling the temperature and NaOH concentration of the reaction. BNT nanofibers and nanoparticles will be examined as a filler introduced into a (P(VDF-HFP)) polymer matrix. To investigate the influence of BNT filler morphology on the permittivity and breakdown strength of the nanocomposites, the localised electric field distribution and capacitance of P(VDF-HFP) nanocomposites with BNT nanofibers and BNT nanoparticles for energy storage applications have also been simulated using a finite element approach (ANSYS).

To enhance the adhesion between the fillers and matrix, the ceramic fillers were initially modified using dopamine, and FT-IR results indicate that the dopamine has led to modification of the BNT by condensation polymerization; the content of dopamine is 2.9 wt%, which is related to the amount of BNT NFs, as shown in Fig. S1 (ESI).†^20,28 The dielectric performance, discharged energy storage density and thermal management of the samples were investigated. This paper will show that the use of high-aspect-ratio BNT nanofibers led to an increased permittivity and high thermal conductivity. Of particular interest is that the discharged energy density of the nanocomposites increased significantly by introducing a low content of BNT nanofibers (2.37 vol%), and the maximum energy density increased to 12.7 J cm⁻³. This work therefore provides a practical route to achieve ultra-high energy storage density with a low level of BNT nanofiber loading.

2 Experimental methods

2.1 Materials

Chemicals were obtained from the following sources and used without further purification: dopamine hydrochloride (Alfa, 99%), P(VDF-HFP) (Aldrich, pellets with less than 15% of HFP), bismuth nitrate pentahydrate (Bi(NO₃)₃·5H₂O), sodium nitrate (NaNO₃), tetrabutyl titanate (Ti(OC₄H₉)₄), acetic acid (CH₃COOH), ethanol (CH₃CH₂OH) and N,N-dimethylformamide (DMF) were all purchased from Sinopharm, China; other reagents were all analytically pure.

2.2 Synthesis of BNT nanofibers and BNT particles

BNT nanofibers and BNT particles were obtained by controlling the hydrothermal reaction temperature and NaOH concentration, as reported in our previous study.²⁹ Specifically, 0.005 mol of Bi(NO₃)₃·5H₂O, 0.01 mol of NaNO₃ and 0.005 mol of Ti(OC₄H₉)₄ were dissolved in 7.5 mL of CH₃COOH, 2.5 mL of distilled water, and 10 mL of CH₃CH₂OH. The Bi(NO₃)₃·5H₂O and NaNO₃ solutions were then mixed with Ti(OC₄H₉)₄ solution, which subsequently formed a suspension with the addition of 10 M of NaOH solution and stirred for 1 h. The BNT nanofibers and particles were synthesized at 150 °C for 48 h with a NaOH concentration of 10 M and 170 °C for 48 h with a NaOH concentration of 10 M, respectively. The products were washed with distilled water several times and dried at 80 °C in an oven.

2.3 Surface functionalization of BNT fillers using dopamine

Dopamine modified BNT was prepared using a method reported previously.²⁰ In a typical reaction, 2 g of BNT powder was dispersed in 20 mL of a mixture of 95 : 5 (v/v) ethanol/H₂O using an ultrasonic processor to increase the hydroxyl groups on the surface of the BNT. The hydroxylated BNT was recovered by centrifugation and dried under vacuum at 60 °C for 12 h, and was dispersed in 0.01 M dopamine hydrochloride aqueous solution, while stirring for 10 h at 60 °C. The functionalized BNT was subsequently separated by centrifugation and rinsed repeatedly with excess deionized water, and finally dried overnight under vacuum at 60 °C.

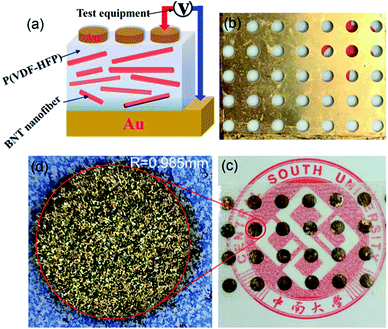
2.4 Preparation of BNT/P(VDF-HFP) nanocomposites

Surface functionalized BNT fillers were dispersed in a 70 : 30 (v/v) acetone/DMF hybrid solvent by sonication and stirring and then mixed with P(VDF-HFP) particles for further stirring and sonication for 48 h. The resulting suspension was then cast onto a clean glass surface, and dried at 80 °C for 12 h under vacuum. The thickness of the final composite film was approximately 10–20 μm. Gold electrodes were sputtered on both sides of the film using a mask with 2 mm diameter eyelets. Fig. 1 shows an illustration of the preparation approach of the flexible BNT nanofiber/P(VDF-HFP). The functionalized BNT NFs were dispersed in the P(VDF-HFP) nanocomposite film and gold electrodes were sputtered on both sides of the film to characterize the electrical properties for storage applications.

Fig. 1 (a) Schematic illustration of BNT NFs/P(VDF-HFP) nanocomposites, (b) metal mask, (c) and (d) optical microscopy images of a P(VDF-HFP) film with 2 mm diameter gold electrodes, the gold regions correspond to a single high magnification electrode.

2.5 Characterization

The crystal structure of the nanocomposites was examined in θ–2θ mode by X-ray diffraction (XRD, Rigaku D-Max/2550VB⁺) utilizing Cu K_α radiation (λ = 1.5418 Å). Transmission electron microscopy (TEM) images were obtained from a JEOL JEM-2100 instrument operating at an accelerating voltage at 200 kV. The samples were prepared by dropping the sample solutions onto carbon coated copper grids and air-drying before measurement. Fourier-transform infrared (FT-IR) spectroscopy was performed with a Nicolet 6700 instrument over the range of 4000–450 cm⁻¹ to determine the functionalization of the samples. Thermogravimetric analysis (TGA, NETZSCH STA 449) was conducted at a heating rate of 10 °C min⁻¹ in a nitrogen flow (20 mL min⁻¹). Characterization of the morphology of the composites was performed by scanning electron microscopy (SEM, JSM-6390). Frequency-dependent permittivity and dielectric loss were measured using an Agilent 4294A LCR meter over a frequency range of 1 kHz to 10 MHz. Leakage current density, endurance testing, electric displacement–electric field (D–E) loops and leakage current were measured using a Precision Premier II ferroelectric polarization tester (Radiant, Inc.) and Delta 9023 furnace. The thermal diffusivity and conductivity of the nanocomposites were measured by a laser flash technique using a thermal constant analyzer (LFA427, Netzsch, Selb, Germany).

3 Results and discussion

3.1 Characterisation of BNT nanofibers and particles

Scanning electron microscopy (SEM) images of the BNT nanofibers and nanoparticles that were hydrothermally prepared are shown in Fig. 2a and b, respectively. The majority of the nanofibers exhibit a high aspect ratio (>200) with an average diameter of approximately 67 nm and average length of 17.78 μm; this was measured from 50 randomly selected nanofibers in an SEM image using ImageJ (Fig. 2d and e). The average diameter of the nanoparticles was measured using a laser particle size analyser and was found to be approximately 800 nm. The XRD pattern of BNT nanofibers and BNT nanoparticles is shown in Fig. 2c, where strong peaks at 2θ of 22, 31, 39, 45, 51, and 56° can be seen in the XRD pattern, which are attributed to the (100), (110), (111), (200), (210) and (211) characteristic peaks respectively of BNT with a pure monoclinic crystalline phase. All of the peaks matched well with the perovskite peaks found in the powder diffraction file database (JCPDS, 46-0001).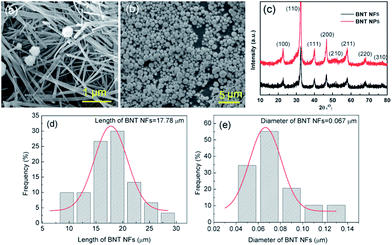

Fig. 2 (a) and (b) SEM images, (c) XRD pattern of BNT nanofibers (NFs) and BNT nanoparticles (NPs), BNT NFs size distribution: (d) length of BNT NFs, (e) diameter of BNT NFs.

Fig. 3a shows a TEM micrograph of a typical single BNT nanofiber synthesized at 170 °C for 48 h with NaOH concentration of 10 M showing a smooth surface with a diameter less than 100 nm. Fig. 3b shows the corresponding high resolution TEM (HRTEM) image. A fast Fourier transform (FFT) pattern of the BNT nanofiber is shown in the inset of Fig. 3b. The clear lattice fringes shown in Fig. 3b of 0.193 nm and 0.224 nm correspond to the (220) and (012) planes and illustrate that the as-synthesized nanofibers were single-crystalline. The parallel lattice spacing was approximately that of monoclinic BNT, which revealed that nanofiber growth was in the [110] direction. The FFT pattern shown in the inset of Fig. 3b further confirmed the monocrystalline nature of the nanofiber and the formation of monoclinic BNT.

Fig. 3 (a) TEM micrograph of a typical single BNT nanofiber and (b) HRTEM image of the BNT nanofiber. The inset image is the selected area electron diffraction (SAED) pattern of the BNT nanofiber.

3.2 Characterisation of the nanocomposites

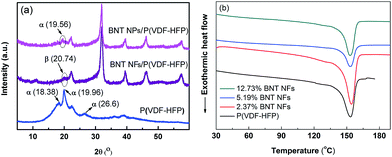
It has been demonstrated that the presence of the polar β-phase in ferroelectric polymers such as P(VDF-HFP) is beneficial for increasing the permittivity and the piezoelectric/ferroelectric properties of the composite due to the large dipolar moment of this particular polar phase.^30–32 The introduction of ceramic fillers into the P(VDF-HFP) matrix led to the formation of a higher fraction of the β-phase by modification of the α-phase.³³Fig. 4a shows the XRD pattern of pure P(VDF-HFP), BNT NPs/P(VDF-HFP) and BNT NFs/P(VDF-HFP) nanocomposites. It can be seen that the pure (unfilled) P(VDF-HFP) exhibited peaks at 2θ = 18.38°, 19.96° and 26.6°, which correspond to the α-phase^30,32 with no β-phase detected. For the BNT nanoparticle/P(VDF-HFP) composite system, the peak of the α-phase at 2θ = 19.56° is weakened, and the α-phase peaks at 2θ = 18.38° and 26.6° both disappear after the introduction of the BNT nanoparticles, which is thought to be due to the addition of the crystalline BNT ceramic changing the crystallinity of the P(VDF-HFP) polymer.

Fig. 4 (a) XRD pattern of pure P(VDF-HFP), BNT nanoparticle/P(VDF-HFP) and BNT nanofiber/P(VDF-HFP) nanocomposite, (b) DSC curves of the BNT NFs/P(VDF-HFP) samples during the second heating at the rate of 10 °C/min under a N₂ atmosphere.

It is notable that the peak at 2θ = 20.74° that corresponds to the β-phase is observed in the XRD pattern of the BNT nanofiber/P(VDF-HFP) nanocomposite in Fig. 4a. Therefore, the introduction of one-dimensional ceramic fillers to P(VDF-HFP) appears to facilitate the formation of the polar β-phase, which can also be observed from the FT-IR results of the P(VDF-HFP) nanocomposites in Fig. S3a.† This is in contrast to zero-dimensional nanoparticle fillers, and indicates that one-dimensional high aspect ratio ceramic fillers may be more effective in increasing the permittivity of nanocomposites due to the formation of the polar β-phase. In addition, one-dimensional ceramic fillers with a high aspect ratio have a larger dipole moment and lower surface energy compared to zero-dimensional particulates, which favours polarization and dispersion.^17,34

To further investigate the influence of the introduction of the ceramic nanofibers on the crystallization of the polymer matrix, differential scanning calorimetry (DSC) curves of the BNT nanofiber/P(VDF-HFP) composites during the second heating circles are shown in Fig. 4b. The melting point (T_m) and crystallinity (χ_c) of the samples were obtained from DSC results, and the corresponding results are summarized in Table 1. It can be seen that the T_m is initially slightly increased then decreased and the χ_c is decreased from 28.7% to 21.6% as the content of BNT NFs increased. The results can be explained by the following reasons. Firstly, the BNT nanofibers act as a new nucleation center, which can decrease the nucleation energy and increase the degree of crystallization of the P(VDF-HFP) matrix on the surface of the BNT nanofibers. Secondly, the introduction of BNT nanofibers decreases the degree of order of the P(VDF-HFP) matrix. Thus, the crystallinity and melting point of the nanocomposites increase with small amounts of BNT nanofibers, however they decrease as the filler loading is increased.

Table 1 The characterization result of P(VDF-HFP) with varied BNT NF contents from DSC curves^a

Sample	T m (K)	ΔHm (J g^−1)	χ c (%)
a The Tm is determined by DSC during the second heating process. The crystallinity (χc) is calculated from the integration of the curves using the formula χc = ΔHm/ΔHm* × 100%, where ΔHm* (approximately 104 J g^−1) is the fusion enthalpy of PVDF with 100% crystallinity.^35
P(VDF-HFP)	426.6	29.8	28.7
2.37% BNT/P(VDF-HFP)	427.7	31.2	30.0
5.19% BNT/P(VDF-HFP)	427.0	29.2	28.1
12.73% BNT/P(VDF-HFP)	426.5	22.5	21.6

---

Fig. 5a–c show SEM images of the surface morphology of the BNT nanofiber/P(VDF-HFP) composite, with increasing loading levels of 2.37 vol%, 5.19 vol% and 12.73 vol% respectively. Fig. 5d shows a cross-section of the nanocomposite with 5.19 vol% of BNT nanoparticles. The high aspect ratio BNT nanofibers are observed in Fig. 5a–c, which are homogeneously dispersed and embedded in the polymer matrix. The formation of agglomerates, voids and cracks is not observed even when the BNT nanofiber loading is increased to 12.73 vol%, as is shown in Fig. 5c. A similar view is shown in Fig. 5d, where the BNT nanoparticles are uniformly dispersed throughout the composite and tightly adhered to the surrounding matrix. Since all the fillers are modified using dopamine (Fig. S1a†) before being incorporated into P(VDF-HFP), the hydroxyl groups in dopamine form strong dipole–dipole interactions with the –F atoms from P(VDF-HFP). In addition, due to the strong electronegative nature of the –F atoms, hydrogen bonding (–F⋯OH–) can be easily formed.³⁰ Therefore, the BNT nanofibers exhibit excellent dispersion and compatibility in the polymer matrix.

Fig. 5 SEM images of top surfaces of BNT nanofiber/P(VDF-HFP) nanocomposite films with various BNT loading levels, (a) 2.37 vol%, (b) 5.19 vol%, (c) 12.73 vol%. (d) SEM cross-section of the nanocomposite with 5.19 vol% BNT nanoparticles.

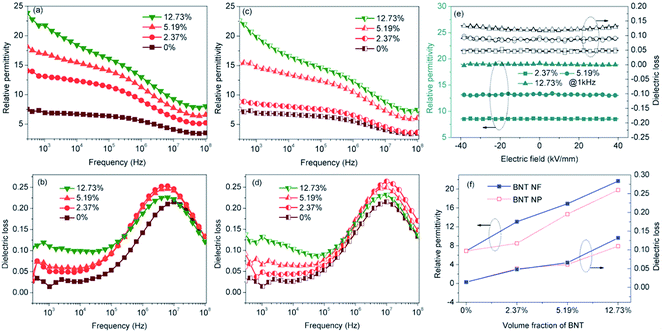
To assess the dielectric properties of the nanocomposites formed using BNT nanofibers and BNT nanoparticles, the frequency dependent permittivity, dielectric loss and electric conductivity of the nanocomposites with various loading levels of BNT nanofibers and BNT nanoparticles are shown over a frequency range of 500 Hz to 10 MHz in Fig. 6. It can be seen that the permittivity of the nanocomposite increased with increasing loading level of either BNT nanofibers or nanoparticles, as shown in Fig. 6a and c, respectively. It is also observed that the permittivity of the nanocomposite with BNT nanofibers is higher than the nanocomposite with BNT nanoparticles at the same volume fraction. This phenomenon is clearly observed in Fig. 6f; for example, at a filler loading level of 5.19 vol% the permittivity of the BNT nanofiber composite is 15% higher than that of the BNT nanoparticle composite. In addition to the increased fraction of the β-phase (Fig. 4a), the increased permittivity of the nanocomposites also arises from the Maxwell–Wagner–Sillars (MWS) interfacial effect, where the phase dependent permittivity (κ(r)) is defined as given below:¹¹

κ(r) = κ^αα(r) + κ^ββ(r) + κ^γγ(r) + κ^ηη(r) (2)

where α, β, γ and η are the BNT nanofiber, BNT nanoparticles, P(VDF-HFP) matrix phases and the interfacial phase. The BNT nanoparticles have an average diameter of 869 nm, as shown in Fig. 2, and are therefore significantly larger than the BNT nanofibers (an average diameter of less than 100 nm), so that the BNT nanofibers have more interface area and interface polarization than the BNT nanoparticles for the same filler volume fraction. In addition, the permittivity of the nanocomposites gradually decreased with increasing frequency, and this trend is more obvious as the filler loading level increases; for example, the permittivity of the nanocomposite with 12.73 vol% BNT nanofibers is 21.7 at 1 kHz and 13.0 at 1 MHz (Fig. 6a). A decrease in permittivity with increasing frequency has been observed to result from the existence of electrical conductivity in the material, which has been simulated using resistor–capacitor networks.³⁶ The properties are relatively independent of the magnitude of the applied electrical field, see Fig. 6e. The nanocomposites also exhibited improved thermal conductivity (Fig. S2†) and increased tensile strength (Fig. S3b†) compared to the pure matrix phase.

Fig. 6 Frequency dependence of the (a) relative permittivity, (b) dielectric loss of the P(VDF-HFP) nanocomposites with BNT nanofibers; (c) relative permittivity and (d) dielectric loss of the nanocomposites with BNT nanoparticles at room temperature. Electric field dependence of the (e) relative permittivity and dielectric loss of the nanocomposites with BNT nanofibers; (f) comparison of the permittivities and dielectric loss at 1 kHz between the nanocomposites with BNT nanofibers and BNT nanoparticles as a function of BNT loading.

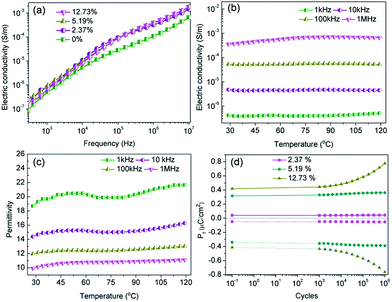
Fig. 7a shows the frequency dependence of electrical conductivity of the BNT NF nanocomposites with various filler loadings. It can be seen that the electrical conductivity increases with increasing frequency and filler loading; this indicates that the nanocomposites behave in a capacitative manner and all exhibit a relatively low electrical conductivity that is less than 6.8 × 10⁻⁷ S m⁻¹. The temperature dependence of the electric conductivity and permittivity of nanocomposites with 12.73 vol% BNT nanofibers at various frequencies is shown in Fig. 7b and c, respectively. The electric conductivity and permittivity of the nanocomposite were stable with a change in temperature, e.g. the electric conductivity was 5.3 × 10⁻⁵ S m⁻¹ at 100 kHz at room temperature and 5.2 × 10⁻⁵ S m⁻¹ when the temperature was increased to 120 °C. The permittivity showed a similar phenomenon, which was 18.7 and 21.8 at room temperature and 120 °C at 1 kHz respectively. These results demonstrate the excellent temperature stability of BNT NFs/P(VDF-HFP) composites in terms of electric conductivity and permittivity.

Fig. 7 (a) Frequency dependence of the electric conductivity; temperature dependence of (b) electric conductivity, (c) relative permittivity of the nanocomposites with 12.73 vol% BNT nanofiber at various frequencies; (d) endurance test of the nanocomposites with various BNT nanofibers with the electric field cycling and pulse field amplitude of 40 kV mm⁻¹.

A high fatigue endurance is necessary for long-term stability during the capacitor charge–discharge cycling process.^37,38 Thus, the residual polarization (P_r) of P(VDF-HFP) nanocomposites with various BNT NF loading levels was investigated as a function of the charge–discharge cycles up to 10⁶ cycles with pulse heights of 40 kV mm⁻¹ and pulse frequency fixed at 1 kHz. It can be seen in Fig. 7d that the P_r of the nanocomposites with 2.37 vol% BNT nanofibers increased by only 6.1% after 10⁶ switching cycles. However, the P_r was increased by 85.7% when the BNT nanofiber content was increased to 12.73 vol% under the same cycling conditions. These results indicate that the P(VDF-HFP) nanocomposites with a low BNT nanofiber content possess superior cycling stability compared with the nanocomposites with a high BNT NF content, which are likely to exhibit a relatively high leakage current density due to the increased oxygen vacancies in ABO₃-type perovskite structures.³⁹

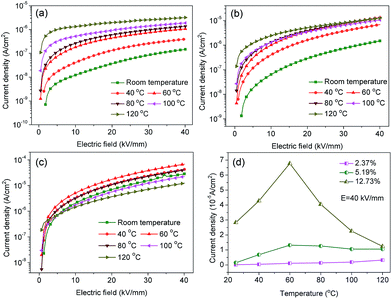
The characteristic leakage current density–electric field curves with various BNT nanofiber contents, temperature and electric field were investigated and are shown in Fig. 8. The nanocomposite with a low BNT nanofiber content (2.37 vol%) was an excellent insulating material for practical applications due to the low leakage current density of 1.47 × 10⁻⁷ A cm⁻² under 40 kV mm⁻¹ at room temperature (Fig. 8a), which increased by more than two orders of magnitude (2.83 × 10⁻⁵ A cm⁻²) when the BNT nanofiber content was increased to 12.73 vol% (Fig. 8c). These results were consistent with the fatigue endurance test shown in Fig. 7d. However, the leakage current showed an obvious temperature diffusion phenomenon, especially when the filler content was low, e.g. the leakage current density of the nanocomposite with 2.37 vol% BNT nanofibers was 1.47 × 10⁻⁷ A cm⁻², which was continuously increased to 3.20 × 10⁻⁶ A cm⁻² as the temperature increased from room temperature to 120 °C under 40 kV mm⁻¹ (Fig. 8a). These results may originate from the relatively low oxygen vacancy concentration and rapid free electron migration with temperature.^37,39,40 The leakage current density of the three samples showed an increase with an increase of the applied electric field (Fig. 8a–c). In the lower field region (<5 kV mm⁻¹), the current density rapidly increased with the applied electric field, whereas the current density showed a lower dependency on the field at higher applied fields. In addition, the nanocomposites exhibited an increased leakage current density as the loading level of the BNT nanofibers increased; for example, the leakage current densities of the nanocomposites with increasing nanofiber contents are 3.94 × 10⁻⁷ A cm⁻² (2.37 vol%), 6.81 × 10⁻⁶ A cm⁻² (5.19 vol%), 4.28 × 10⁻⁵ A cm⁻² (12.73 vol%) at 40 °C under 40 kV mm⁻¹. This is attributed to the high leakage current density of BNT and the defects and space charge introduced by the BNT nanofiber inclusions.⁴¹

Fig. 8 Leakage current density of the nanocomposites with (a) 2.37, (b) 5.19 and (c) 12.73 vol% BNT nanofibers under different temperatures as a function of electric field; (d) current densities of the nanocomposites with various BNT nanofiber loading levels under different temperatures at 40 kV mm⁻¹ electric field.

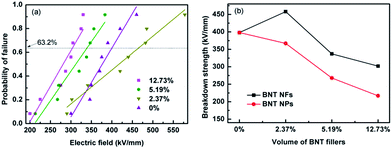
According to eqn (1) the breakdown strength is the key parameter to achieve a high discharge energy density for the composite. The breakdown strength of the BNT nanofiber/P(VDF-HFP) composites with various volume fractions of fillers is shown in Fig. 9, which is analyzed with a two-parameter Weibull distribution function (Fig. 9a), using the equation:

P(E) = 1 − exp[−(E/E₀)^β] (3)

Fig. 9 (a) Weibull distribution of the dielectric breakdown strength of nanocomposites filled with various BNT nanofibers, (b) variation of characteristic breakdown strength from Weibull distribution for samples with various volume fractions of fillers.

The characteristic breakdown strength (E₀) is obtained when the cumulative probability of electric failure (P(E)) equaled 63.2% and β is the shape parameter, as shown in Table S1.†⁴² As shown in Fig. 9a, the characteristic breakdown strength is determined from a fit of eqn (3) to at least eight individual breakdown measurements. As can be seen from Fig. 9a and b, the sample with 2.37 vol% BNT nanofibers exhibited the highest breakdown strength of 458 kV mm⁻¹, which is higher than that of the pure (unfilled) P(VDF-HFP) polymer (398 kV mm⁻¹), a result that has also been reported elsewhere.³³ The breakdown strength decreases to 302 kV mm⁻¹ when the filler loading is increased to 12.73 vol%. As shown by Liu et al.,¹² a low concentration of nanofibers improves the breakdown strength due to a number of reasons. Firstly, the homogeneous dispersion and strong adhesion of the high aspect ratio nanofibers after surface modification in the nanocomposite can reduce charge transfer and prevent the polymer chain from moving freely.¹¹ Secondly, the high aspect ratio nanofibers orientated parallel to the film surface direction during the solution casting process can endure a higher electric field vertical to the film surface direction (see Fig. S4†).^12,43 Finally, the nanofibers also influence the crystallization of the polymer, as seen in Fig. 4. The defects, such as the accumulation and voids in the nanocomposite, inevitably increased when the BNT nanofiber loading increased. The accumulated nanofibers in the nanocomposites can readily form a connected path for the free charge, and the voids will encapsulate the air, therefore, the breakdown strength was decreased. These results indicate that incorporation of a small loading level of BNT NF to the polymer matrix (2.37 vol%) may be an effective method to achieve high energy densities.

The discharged energy density of the samples can be calculated from the electric displacement–electric field (D–E) loops. Fig. 10a shows the D–E loops of the nanocomposites with various loading levels of BNT at an electric field of 300 kV mm⁻¹, and the maximum D–E loops are shown in Fig. S5 (ESI).† As can be seen from Fig. 10a, the electric displacement of the nanocomposites increased with the loading level of BNT nanofibers at the same electric field, while the remnant displacement greatly increased. As a result, the nanocomposites with 12.73 vol% BNT nanofibers showed a low energy density, which is shown in Fig. 10b. The nanocomposite with 2.37 vol% BNT nanofibers have the largest discharged energy densities of 12.7 J cm⁻³, which is more than three times that of the pure (unfilled) P(VDF-HFP). The significant increase in energy density is mainly due to the high breakdown strength and the high effective electric displacement shown in Fig. S6 (ESI).†Table 2 summarizes the previously reported dielectric nanocomposites with different ceramic nanofibers. The discharged energy density achieved in this work using a low content of Na_0.5Bi_0.5TiO₃ nanofibers is superior to the performance of nanocomposites reported elsewhere.

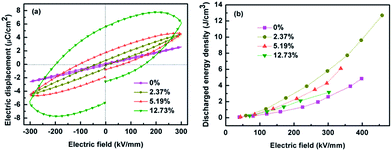Fig. 10 (a) D–E loops of the nanocomposites with various loadings of BNT NFs at the electric field of 300 kV mm⁻¹, (b) discharged energy densities of the nanocomposites with the electric field.

Table 2 Comparison of discharged energy storage density for dielectric composites with different nanofiber fillers

Matrix	Fillers (nanofibers)	Content of fillers (vol%)	Breakdown strength (kV mm^−1)	Discharged energy density (J cm^−3)	Ref.
P(VDF-TrFE)	Bi2O3/Ba0.3Sr0.7TiO3	8.7	155	4.35	5
PVDF	Ba0.6Sr0.4TiO3	7.5	∼300	∼5.5	10
PVDF	SrTiO3	2.5	380	6.8	14
P(VDF-TrFE-CFE)	BaTiO3	17.5	300	10.5	21
PVDF	Ba(Zr0.3Ti0.7)O3	7.5	∼300	∼5	44
PVDF	Ba0.2Sr0.8TiO3	7.5	450	14.9	45
PVDF	TiO2	7.5	300	∼6.5	46
PVDF	BaTiO3@Al2O3	2.5	380	7.1	47
P(VDF-CTFE)	BaTiO3	3	280	8.4	48
P(VDF-HFP)	Na0.5Bi0.5TiO3	2.37	458	12.7	This work

---

3.3 Modelling of composite dielectric materials

Finite element modelling of a single high permittivity inclusion in a low permittivity matrix was used to further understand the energy storage properties of the BNT/P(VDF-HFP) nanocomposites investigated experimentally. Rather than model a complex three-dimensional system, a series of simplified two dimensional models were created to examine the effect of the ceramic filling fraction, aspect ratio and angle of the high permittivity inclusion to the applied electric field direction on both the permittivity and breakdown strength of the nanocomposite. An additional model will be discussed which introduces a polar β-P(VDF-HFP) as an ‘interphase’ between the matrix and the high permittivity inclusion. The modelling software used was ANSYS v15.0 using a two dimensional four-node element type (PLANE13) for electrostatic analysis. In all cases the matrix phase (α-P(VDF-HFP)) was modelled with a relative permittivity, ε_r = 10, and the inclusion was assigned the dielectric properties of BNT (ε_r = 377). It should be noted at this point that units and scales of length are in effect arbitrary in all the analyses so electrical loads applied to the models were selected so that the applied field in each case was unity.

The effective permittivity of the modelled composites was calculated by summing the electrostatic energy of each element and calculating the capacitance, and from this permittivity, using the relationship C = Q/V, where C is the capacitance, Q is the charge and V is the voltage. Electrical breakdown strength was not modelled directly but instead the maximum local electric field (E^max_f) within the composite due to the applied field for each geometry was recorded. The maximum applicable field for a single phase capacitive material, as discussed previously, is the breakdown strength, E_b; above this field the material will no longer store charge as it becomes electrically conductive. When high permittivity phases are introduced into a composite system, the electric field concentrates in the low permittivity phase^16,17,33, which is often the high breakdown strength phase; in the BNT/P(VDF-HFP) composite system explored here the low permittivity polymer phase has a higher breakdown strength.

If it is assumed that there is no change in the breakdown strength of the constituent phases in the creation of the composite, a concentration of electric field within the material is likely to lead to electrical breakdown at applied fields below E_b, such that the maximum field applied to the composite material must be modified by a ‘concentration’ factor of 1/E^max_f so as to ensure the local field does not exceed the breakdown strength at any point within the composite. The effective breakdown strength of the composite can therefore be defined by the relationship:

E^eff_b = E_b/E^max_f. (4)

Our initial model was designed to investigate the effect of filling fraction of the high permittivity BNT phase into the P(VDF-HFP) matrix. A circular BNT inclusion of varying radius (r = 1, 2, 3, 4, 5, 6, 7, 8, 9) was modelled in the center of a square P(VDF-HFP) matrix (20 × 20). A fine triangular finite element mesh was used that satisfactorily mapped the inclusion geometry and electrical loads were applied to the model at boundary lines to simulate electrodes in a parallel plate capacitor, thus generating an electric field across the geometry. An example of such a model can be seen in Fig. 11a which shows that the applied electric field tends to concentrate in the low permittivity matrix phase and is significantly smaller in the high permittivity inclusion. The results from this model for composite permittivity and the inverse of the maximum field (i.e. the factor by which the breakdown strength is modified in eqn (4)) are shown in Fig. 11b. The data have been normalized with respect to the single phase matrix material to demonstrate clearly the effect of the high permittivity inclusions on the effective properties of the composites. It can be seen in Fig. 11b that introducing a high permittivity second phase increases the composite permittivity, however significant increases are not realized until the fill fraction exceeds ∼0.3 (30 vol%) when the modelled permittivity is doubled compared with single phase P(VDF-HFP).³⁶ As the electric field concentrates in the low permittivity phase to such an extent that the field in the high permittivity inclusion is close to zero, it appears that the increase in permittivity is linked to the concentration of the field in the low permittivity polymer phase, meaning that more charge, Q, is stored, as V in the relationship Q = CV is effectively increased for the same overall volume. However, while there is an increase in permittivity, there is also a rapid increase in the maximum electric field at very low volume fraction of the high permittivity second phase, which is likely to lead to a reduction in the effective breakdown strength of the material. The highest fields are observed at the tips of the inclusion parallel to the applied field, as shown in Fig. 11a.

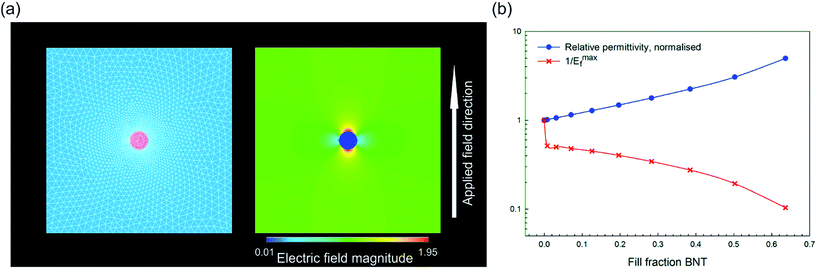Fig. 11 (a) Finite element model for high permittivity inclusion with an aspect ratio of unity and area fraction of 0.00785 with meshed geometry on the left and electric field distribution on the right after application of the electric field; field magnitude is normalized to the distribution in a single phase material (i.e. unity at all locations); (b) effect of area fraction of the high permittivity second phase on the composite permittivity (normalized) and the effective breakdown strength of the material, see eqn (4).

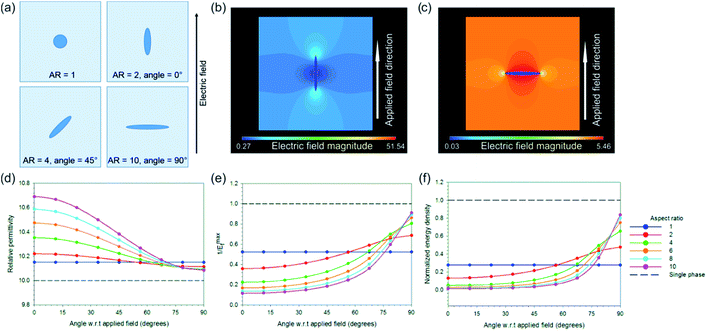
The model above clearly indicates that the inclusion of high permittivity particles can increase the effective permittivity but also increase the maximum electric field and therefore reduce the breakdown strength, which is an important factor from eqn (1). The model is now adapted to investigate how the effective composite permittivity is affected by the aspect ratio of the high permittivity second phase and its orientation/angle relative to the applied electric field. The BNT inclusion was modelled as an ellipse with the aspect ratio defined as the ratio of the radii of the major and minor axes, with an aspect ratio of one being a circular inclusion. Fig. 12a shows example geometries of angle and aspect ratio; aspect ratios ranging from one to 10 have been investigated in this model. The inclusion was modelled in the center of a 20 × 20 P(VDF-HFP) matrix and the angle rotated from 0° (i.e. parallel to the applied field) to 90° (perpendicular to the applied field) in steps of 11.25°. In all cases the fill fraction of the BNT phase was constant at 0.00785. Electric field contour plots of fiber composites (aspect ratio 10) are shown in Fig. 12b and c for angles with respect to a field of 0° and 90°, respectively, and demonstrate that the highest field concentrations occur in the polymer matrix in the vicinity of the high permittivity inclusion, parallel to the field direction. The effect of aspect ratio and angle with respect to the field on the effective permittivity of the composite and the maximum local electric field is shown in Fig. 12d and e. The highest increase in the composite permittivity was found when high aspect ratio inclusions were aligned parallel to the applied field (Fig. 12d), however, this also caused significant increases in the local electric field at the sharp tips of the high permittivity inclusion (Fig. 12e). The normalized energy density for each case was calculated using the relationship u^norm_e = ε_norm/(E^max_f)², where ε_norm is the composite permittivity normalized with respect to the permittivity of the single phase material, and is plotted in Fig. 12f as a function of angle for varying aspect ratios. The composite with high aspect ratio BNT NFs in the direction of perpendicular to the applied field is predicted possessing the highest energy density, however, due to the reduction in 1/E^max_f with the addition of a high permittivity second phase no composite geometry improves on the energy density of the single phase material, shown as a dashed black line in Fig. 12f. Clearly for these composite systems, the introduction of the high permittivity phase increases the local electric field which increases the effective permittivity (Fig. 12d) but also increases the local electric field (Fig. 12e), leading to reduced energy density (Fig. 12e).

Fig. 12 (a) Example geometries investigated via a finite element approach and their corresponding aspect ratios and angles with respect to the applied electric field; (b) and (c) electric field contour plots of fibers modelled parallel and perpendicular to the applied field, respectively, showing that field concentration occurs at sharp tips of the high permittivity phase but in the low permittivity matrix; (d), (e) and (f) effect of aspect ratio and angle on permittivity, field concentration factor (1/E^max_f) and energy density, respectively, normalized to the single phase material shown in all plots with a dashed black line.

In the models discussed to this point the nanoparticle composites (AR = 1) are predicted to have higher permittivity than high aspect ratio nanofiber composites (AR = 10 at 90°) aligned perpendicular to the field direction, which was not the case observed experimentally where the nanofiber composites had superior permittivity to the nanoparticle composites at the same volume fraction of BNT. To understand the reasons behind these results it was necessary to develop a third finite element model whereby a rectangular fiber of varying aspect ratio (aspect ratio = 12.5, 50, 200) and constant filling fraction (0.004) was contained in a rectangular matrix and a polar β-P(VDF-HFP) ‘interphase’ with varying thickness was modelled between the matrix and the high permittivity inclusion. This is included due to the observation that the BNT nanofiber fillers in P(VDF-HFP) facilitate the formation of the polar β-phase, Fig. 4.

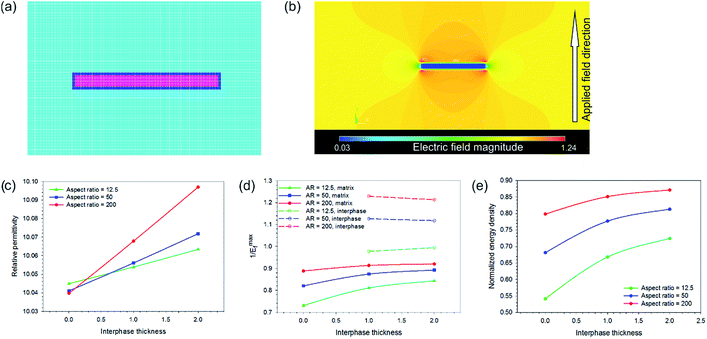
The rectangular model had dimensions of 100 × 500 and was meshed with square elements of equal size; Fig. 13a shows a close up image of the mesh surrounding the fiber. The size of the matrix was selected in this case to ensure that boundary effects did not influence the results as the fiber aspect ratio was increased. Three thicknesses of interphase layer on the surface of the fiber were investigated (element thickness = 0, 1, 2, where t = 0 has no interlayer) for the effect on electric field distribution in the composite and permittivity. The β-P(VDF-HFP) interphase was modelled with a relative permittivity of 15,⁴⁹ compared to a relative permittivity of 10 for the bulk matrix. Electric fields were applied perpendicular to the fiber direction as this was shown to be the best configuration for energy storage, as in Fig. 12c. Reported relative permittivity values for β-P(VDF-HFP) vary between 10 and 60,⁵⁰ which has an effect on the results of this model in terms of the composite permittivity, electric field concentration factor (1/E^max_f) and the normalized energy density, such that increasing the interphase permittivity leads to an increase in the overall permittivity but also increases the maximum local electric field concentration in the matrix, leading to a reduction in the normalized energy density compared to an interphase relative permittivity of 15, see Fig. S7.†

Fig. 13 (a) High permittivity fiber (aspect ratio = 12.5, pink) with the β-P(VDF-HFP) interphase (one element thick, dark blue) in the P(VDF-HFP) matrix (cyan); (b) electric field contour plot of the fiber geometry shown in (a); effect of interphase thickness on (c) permittivity, (d) electric field concentration factor (1/E^max_f) and (e) energy density when the interphase permittivity is 15.

A contour plot of the electric field distribution within a composite with an interphase thickness of one element and a relative permittivity of 15 is shown in Fig. 13b. The presence of the interphase was found to increase the permittivity for all aspect ratios and permittivity was found to increase with increasing interphase thickness. High aspect ratio fillers yield the best improvements in permittivity, see Fig. 13c. This is due to the increase in the surface area of the fiber with aspect ratio and explains why the nanoparticle composites were found experimentally to exhibit a lower permittivity compared to the nanofiber composites at the same BNT volume fraction (see Fig. 6); the use of high aspect nanofibers simply led to a higher volume of the interphase compared to the nanoparticles, which experimentally had a significantly larger diameter than the fibers: 800 nm compared to 67 nm.

The presence of the higher permittivity β-P(VDF-HFP) interphase reduced the field concentration in the P(VDF-HFP) matrix compared to when there was no interphase, which can be seen from the data in Fig. 13d where the solid lines (1/E^max_f in the matrix, colors denote varying aspect ratios) approach unity (i.e. no field concentration) as the interphase thickness is increased. It was also found that increasing the thickness of the β-P(VDF-HFP) layer reduced the field concentration within this phase and higher aspect ratios were also beneficial in this respect, this is indicated by the dashed lines in Fig. 13d. The effect of introducing an interphase on the electric field distribution of the composites may partially explain why experimentally an increase in breakdown strength was observed at low volume fractions of BNT nanofibers, see Fig. 9b, as the field concentrations are reduced due to the more gradual change in permittivity around the high permittivity inclusion. At higher BNT volume fractions the close proximity of neighboring nanofibers is likely to lead to field concentrations that negate the benefits of the nucleation of the interphase, hence the decline in breakdown strength observed experimentally above 2.37 vol% volume fraction of BNT nanofibers. The increase in permittivity and reduction in field concentration with the addition of the interphase leads to higher predicted energy densities than for the composites in all cases, with the best results seen for high aspect ratio fibers with a thick interphase, as shown in Fig. 13e.

4 Conclusions

This paper demonstrates that the use of a small volume fraction of high aspect ratio nanofiber fillers is an effective approach to achieve a nanocomposite architecture capable of achieving a high energy density and high dielectric strength. Lead-free high aspect ratio ferroelectric Na_0.5Bi_0.5TiO₃ (BNT) nanofibers and particles were synthesized by a hydrothermal method. The P(VDF-HFP) nanocomposite films with a variety of BNT nanofibers and nanoparticle loading levels (2.37, 5.19 and 12.73 vol%) were obtained by casting and hot pressing. The relative permittivity of the nanocomposite continuously increased with the level of BNT nanofiber loading, while also maintaining a relatively low dielectric loss (<0.11). A small amount (2.37 vol%) of BNT nanofibers introduced to the polymer matrix increased the fraction of the polar β-phase in the nanocomposite, which led to an increase of the permittivity. Due to the partial perpendicular distribution of BNT nanofibers to the applied electric field direction, the local electric field concentration was reduced, which was investigated in detail by finite element analysis (ANSYS). The presence of high aspect ratio nanofibers with the treatment of surface modification and the alignment of nanofibers perpendicular to the applied electric field led to a high breakdown strength of 458 kV mm⁻¹ for the nanocomposite with 2.37 vol% BNT nanofibers with a corresponding large energy storage density of 12.7 J cm⁻³. The thermal conductivity also increased to 0.67 W m⁻¹ K⁻¹ compared to the pure P(VDF-HFP) polymer (0.2 W m⁻¹ K⁻¹). This research provides a novel nanocomposite approach to produce high energy storage density dielectric materials for advanced electronic and electrical power system applications.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (51672311), Science and Technology Project of Hunan Province, China (no. 2016WK2022), Postdoctoral Research Foundation of Central South University (no. 140050006) and Supported by State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China. Bowen would like to acknowledge funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 320963 on Novel Energy Materials, Engineering Science and Integrated Systems (NEMESIS). Roscow acknowledges EPSRC (UK).

Notes and references

1. B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334–336.
2. M. N. Nadagouda and R. S. Varma, Green Chem., 2007, 9, 632–637.
3. D. R. Wang, T. Zhou, J. W. Zha, J. Zhao, C. Y. Shi and Z. M. Dang, J. Mater. Chem. A, 2013, 1, 6162–6168.
4. Q. Li, K. Han, M. R. Gadinski, G. Zhang and Q. Wang, Adv. Mater., 2014, 26, 6244–6249.
5. P. Hu, Y. Song, H. Liu, Y. Shen, Y. Lin and C.-W. Nan, J. Mater. Chem. A, 2013, 1, 1688–1693.
6. H. Luo, K. C. Zhou, C. R. Bowen, F. Q. Zhang, A. Q. Wei, Z. Wu, C. Chen and D. Zhang, Adv. Mater. Interfaces, 2015, 1600157.
7. Q. Lia, F. H. Liu, T. N. Yang, M. R. Gadinski, G. Z. Zhang, L. Q. Chen and Q. Wang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9995–10000.
8. H. X. Tang, Z. Zhou, C. C. Bowland and H. A. Sodano, Nano Energy, 2015, 17, 302–307.
9. H. Luo, D. Zhang, C. Jiang, X. Yuan, C. Chen and K. Zhou, ACS Appl. Mater. Interfaces, 2015, 7, 8061–8069.
10. C. Jiang, D. Zhang, K. C. Zhou, X. F. Zhou, H. Luo and I. Abrahams, J. Mater. Chem. A, 2016, 4, 18050–18059.
11. X. Hao, J. Zhai and X. Yao, J. Am. Ceram. Soc., 2009, 92, 1133–1135.
12. P. Hu, Y. Song, H. Liu, Y. Shen, Y. Lin and C.-W. Nan, J. Mater. Chem. A, 2013, 1, 1688–1693.
13. L. Xie, X. Huang, K. Yang, S. Li and P. Jiang, J. Mater. Chem. A, 2014, 2, 5244–5251.
14. S. Liu and J. Zhai, J. Mater. Chem. A, 2015, 3, 1511–1517.
15. L. Xie, X. Huang, Y. Huang, K. Yang and P. Jiang, ACS Appl. Mater. Interfaces, 2013, 5, 1747–1756.
16. H. Tang, Z. Zhou and H. A. Sodano, ACS Appl. Mater. Interfaces, 2014, 6, 5450–5455.
17. P. Kim, S. C. Jones, P. J. Hotchkiss, J. N. Haddock, B. Kippelen, S. R. Marder and J. W. Perry, Adv. Mater., 2007, 19, 1001–1005.
18. J. Li, P. Khanchaitit, K. Han and Q. Wang, Chem. Mater., 2010, 22, 5350–5357.
19. H. Luo, C. Chen, K. Zhou, X. Zhou, Z. Wu and D. Zhang, RSC Adv., 2015, 5, 68515–68522.
20. S. K. Patil, M. Koledintseva, R. W. Schwartz and W. Huebner, J. Appl. Phys., 2008, 104, 074108.
21. H. Tang, Y. Lin and H. A. Sodano, Adv. Energy Mater., 2013, 3, 451–456.
22. C. Andrews, Y. Lin and H. A. Sodano, Smart Mater. Struct., 2010, 19, 025018.
23. X. Huang, T. Iizuka, P. Jiang, Y. Ohki and T. Tanaka, J. Phys. Chem. C, 2012, 116, 13629–13639.
24. X. Huang, C. Zhi, P. Jiang, D. Golberg, Y. Bando and T. Tanaka, Adv. Funct. Mater., 2013, 23, 1824–1831.
25. K. Roleder, I. Franke, A. M. Glazer, P. A. Thomas, S. Miga and J. Suchanicz, J. Phys.: Condens. Matter, 2002, 14, 5399–5406.
26. J. Suchanicz, Ferroelectrics, 1998, 209, 561–568.
27. Y. Hou, Y. Deng, Y. Wang and H. Gao, RSC Adv., 2015, 5, 72090–72098.
28. X. Huang, P. Jiang, C. Kim, F. Liu and Y. Yin, Eur. Polym. J., 2009, 45, 377–386.
29. X. F. Zhou, C. Jiang, C. Chen, H. Luo, K. C. Zhou and D. Zhang, CrystEngComm, 2016, 18, 1302–1310.
30. Y. Niu, Y. Bai, K. Yu, Y. Wang, F. Xiang and H. Wang, ACS Appl. Mater. Interfaces, 2015, 7, 24168–24176.
31. L. Xie, X. Huang, C. Wu and P. Jiang, J. Mater. Chem., 2011, 21, 5897–5906.
32. X. Lin, P. H. Hu, Z. Y. Jia and S. M. Gao, J. Mater. Chem. A, 2016, 4, 2314–2320.
33. N. Guo, S. A. DiBenedetto, P. Tewari, M. T. Lanagan, M. A. Ratner and T. J. Marks, Chem. Mater., 2010, 22, 1567–1578.
34. S. Liu, J. Zhai, J. Wang, S. Xue and W. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 1533–1540.
35. J. J. Li, S. B. Tan, S. J. Ding, H. Y. Li, L. J. Yang and Z. C. Zhang, J. Mater. Chem., 2012, 22, 23468–23476.
36. D. P. Almond and C. R. Bowen, Phys. Rev. Lett., 2004, 92, 157601.
37. C. W. Ahn, G. Amarsanaa, S. S. Won, S. A. Chae, D. S. Lee and I. W. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 26381–26386.
38. M. H. Park, H. J. Kim, Y. J. Kim, T. Moon, K. D. Kim, Y. H. Lee, S. D. Hyun and C. S. Hwang, J. Mater. Chem. C, 2015, 3, 6291–6300.
39. X. J. Lou, Appl. Phys. Lett., 2009, 94, 072901.
40. Y. Wang, K. F. Wang, C. Zhu and J. M. Liu, J. Appl. Phys., 2006, 99, 044109.
41. G. Y. Wang, X. Y. Huang and P. K. Jiang, ACS Appl. Mater. Interfaces, 2015, 7, 18017–18027.
42. P. Hu, Y. Shen, Y. Guan, X. Zhang, Y. Lin, Q. Zhang and C.-W. Nan, Adv. Funct. Mater., 2014, 24, 3172–3178.
43. C. A. Grabowski, S. P. Fillery, N. M. Westing, C. Z. Chi, J. S. Meth, M. F. Durstock and R. A. Vaia, ACS Appl. Mater. Interfaces, 2013, 5, 5486–5492.
44. S. H. Liu, S. X. Xue, S. M. Xiu, B. Shen and J. W. Zhai, Sci. Rep., 2016, 6, 26198.
45. H. Tang and H. A. Sodano, Nano Lett., 2013, 13, 1373–1379.
46. H. Tang and H. A. Sodano, Appl. Phys. Lett., 2013, 102, 063901.
47. S. H. Liu, J. Wang, B. Shen, J. W. Zhai, H. S. Hao and L. M. Zhao, J. Alloys Compd., 2017, 696, 136–142.
48. B. Xie, Q. Zhang, H. B. Zhang, G. Z. Zhang, S. Y. Qiu and S. L. Jiang, Ceram. Int., 2016, 42, 19012–19018.
49. P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706.
50. V. Tiwari and G. Srivastava, J. Polym. Res., 2014, 21, 587.

---

Footnote

† Electronic supplementary information (ESI) available: FT-IR spectra of dopamine modified and pristine BNT NFs; thermal conductivity, thermal diffusion and thermal conductivity enhancement of the BNT NF/P(VDF-HFP) nanocomposites; simulation of the distribution of electric field strength of the nanocomposites with BNT nanoparticles or BNT nanofibers; D–E loops of the BNT nanofiber/P(VDF-HFP) nanocomposites with various filler loadings at the largest electric field. Maximum and remnant electric displacement of the BNT nanofiber/P(VDF-HFP) composites with various filler loadings at the largest electric field. See DOI: 10.1039/c7ta00136c

---