Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shape-dependent effective diffusivity in packings of hard cubes and cuboids compared with spheres and ellipsoids
Magnus
Röding
 *
*
RISE Research Institutes of Sweden, Bioscience and Materials, Göteborg, Sweden. E-mail: magnus.roding@ri.se
First published on 25th October 2017
Abstract
We performed computational screening of effective diffusivity in different configurations of cubes and cuboids compared with spheres and ellipsoids. In total, more than 1500 structures are generated and screened for effective diffusivity. We studied simple cubic and face-centered cubic lattices of spheres and cubes, random configurations of cubes and spheres as a function of volume fraction and polydispersity, and finally random configurations of ellipsoids and cuboids as a function of shape. We found some interesting shape-dependent differences in behavior, elucidating the impact of shape on the targeted design of granular materials.
1 Introduction
Granular materials include a broad range of two-phase materials, both natural and synthetic, consisting of discrete solid particles (granules) surrounded by a continuous void phase. Some examples are columns for separation, chromatography, and catalytic reactions, cathode materials for lithium-ion batteries, and pharmaceutical materials for controlled release. Consequently, there is great interest in determining and understanding the effective macroscopic properties of these materials, such as effective diffusivity.1–6 Understanding the impact of microstructural morphology is a key prerequisite for performing the targeted optimization of a material for a specific purpose.7The prototypical examples of granular materials are lattices and random configurations of impermeable spheres. However, contemporary particle synthesis techniques facilitate the production of a broad range of anisotropic nanoparticles, shaped like ellipsoids, rods, disks, cubes, icosahedra, tetrahedra, triangles, prisms, half shells, tripods, and stars, to name a few.8–22 The realization that particles with anisotropic shapes (and also anisotropic interactions) can be used as colloidal building blocks to yield complex structures with novel properties has attracted substantial attention.23–26 A vast body of literature exists on the topic of understanding shape-dependent assemblies of particles including their phase behavior, phase transitions, random close packing, and spontaneous shape-induced crystallization. Just to give a brief account, studies performed include the random close packing of ellipsoids,27 monodisperse and polydisperse hard spheres,28,29 polyhedra including platonic solids,30–33 superballs and superellipsoids,34–36 cubes with round edges,37 and monodisperse and polydisperse cubes and cuboids.38–42 Hard cubes and cuboids and their packing and phase behavior have been studied both as limiting cases of superballs and superellipsoids,35,36 and modeled exactly as cubes and cuboids.39–41 The true nature of their behavior is somewhat elusive; as stated by Jiao and Torquato,31 attempts to create random close packings (or rather maximally random jammed packings) of cubes easily lead to high degrees of order, raising questions concerning the appropriateness of some of the algorithms suggested so far to generate these packings. Nonetheless, random sequential addition39–41 can produce packings with a high degree of randomness, as can the order-constrained stochastic optimization method described in ref. 42.
Effective transport coefficients in random, two-phase materials, and in particular the case of spherical granules is a rather well investigated subject including both effective diffusivity (including other physical processes mathematically analogous to effective diffusivity, such as electrical conductivity, thermal conductivity, and magnetic permeability)43–52 and fluid permeability,53–58 oftentimes incorporating microstructural descriptors such as the n-point correlation (probability) functions for n = 1, 2,… introduced by Brown.59
In light of the increasing capabilities to manufacture anisotropic nanoparticles, the topic of effective macroscopic properties and the impact of shape thereon has become increasingly interesting. Transport properties with anisotropic granules have been investigated in several studies. In ref. 60, random packings of granules shaped as spheres, ellipsoids, cylinders and parallelepipeds were generated using sequential deposition in a gravitational field, and their conductivity, permeability, and diffusivity were studied (but the latter only using ellipsoids for computational reasons). In ref. 61, the impact of shape on the effective permittivity of ellipsoids was studied. In ref. 62, different irregular particle shapes constructed as the union of overlapping spheres were created and the impact on permeability was investigated. Nonetheless, not so much attention has been directed toward aspherical particles and effective diffusivity.
In this work, we performed computational screening of effective diffusivity in packings of (hard and impermeable) cubes and cuboids. Very little work is done in terms of both analytical models and simulations of effective diffusivity for particles with these shapes. As a reference, we compared all the results with packings of spheres and ellipsoids. We studied both periodic (lattice) configurations, i.e. simple cubic crystals and face-centered cubic crystals, and random configurations for different solid volume fractions, polydispersities and shapes. In total, more than 1500 structures are generated and screened for effective diffusivity. The aim of this computational screening paradigm is to explore the effect of varying different geometrical parameters independently, and discover and understand generic design rules for the tailoring of effective transport properties. This effort will aid in guiding future experimental work.
2 Structure generation
We first describe the details of generating the lattice structures in a cubic, periodic simulation domain with side L. A simple cubic (SC) lattice of spheres is generated by placing a single sphere with radius r = 1 in (L/2,L/2,L/2) with L being defined by the solid volume fraction ϕ through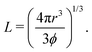 | (1) |
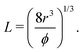 | (2) |
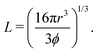 | (3) |
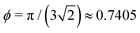 when the spheres tangent each other. An FCC lattice of cubes is generated by placing four cuboids in the same positions as above, with L being
when the spheres tangent each other. An FCC lattice of cubes is generated by placing four cuboids in the same positions as above, with L being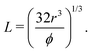 | (4) |
The random microstructures are generated using in-house developed software implemented in Julia (http://www.julialang.org)63 and available in a Github repository (https://github.com/roding/whitefish_generation, version 0.2). Random configurations of non-overlapping particles are generated using a hard particle Markov Chain Monte Carlo (MCMC) algorithm. For spheres, the overlap condition is straightforward. For ellipsoids, the Perram–Wertheim criterion64 for two ellipsoids of arbitrary orientation is used. For cubes and cuboids, a separating axis theorem65 is employed for the detection of overlap for two cuboids. To quantify the degree of overlap, it is further determined how far one of the particles needs to move along the axis defined by their respective center points to remove the overlap. First, particles are assigned uniformly distributed locations and orientations (the latter encoded using a quaternion representation). Second, the configurations are relaxed by sequentially performing random translations of all particles and then random rotations of all particles until no two particles overlap. Proposed translations and rotations are only accepted if they lead to a lower or equal degree of overlap for the considered particle. These ‘local’ stochastic optimization steps eventually lead to a ‘global’ optimization, resulting in no overlap. Third, the configurations are equilibrated by performing a large number of random translations and rotations ensuring a distribution in location and orientation that is as uniform as possible. Now, if the desired solid volume fraction ϕ is less than 0.50, we are done. Otherwise, as a final step, the steps above are performed for ϕ = 0.50 and the configuration is compressed in small steps, Δϕ = 10−5, until the target solid volume fraction ϕtarget is reached. The proposed translations are normal distributed with standard deviation σt in each direction. The proposed rotations are normally distributed with standard deviation σr in a random direction. In every step, σt and σr are chosen in an adaptive fashion to aim for an acceptance probability of 0.25. For very high solid volume fractions, the configuration might get jammed before reaching ϕtarget. In this case, the generation is restarted from scratch with a new random configuration. All configurations have 512 particles (there is a point to having an even cube, i.e. 83, because otherwise the configurations of the cubes actually cannot reach high solid volume fractions in the (artificially) periodic simulation domain). Using a dual Intel Xeon E5-2699 v4 setup, the execution times for the generation are between ∼1 min and ∼2.5 hours (single thread), depending strongly of course on the type of particle and on ϕtarget.
3 Diffusion simulation
Obstructed diffusion in the generated structures is simulated using an in-house developed software also implemented in Julia (http://www.julialang.org)63 in a parallel implementation and also available in a Github repository (https://github.com/roding/whitefish_diffusion, version 0.2). A ‘random walk particle tracking’ technique50 is used, initially placing an ensemble of N = 106 point particles uniformly distributed in the void part of the simulation domain, by rejection sampling. The stochastic particle motion is simulated as a Gaussian random walk with time resolution δt = 2.5 × 10−5 (a.u.) and corresponds to the diffusion coefficient D0 = 1 (a.u.). Hence, random normal distributed displacements are added to the current position in each time step with zero mean and standard deviation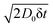 . The positions are recorded at each major time step Δt = 0.01 (a.u.). The simulation proceeds up to tmax = 50 (a.u.) or 100 (a.u.) (for different data sets). Single and multiple rejection boundary conditions are implemented but multiple rejection is used here;66 proposal displacements are generated until one is found that does not mean leaving the void phase. A cell list data structure (with 10 × 10 × 10 cells for large random configurations, but only a single cell for lattice structures) is used to accelerate computations. The computations are run on a variety of architectures comprising around 20 cores yielding execution times between ∼2 hours and ∼30 hours, within the total 5 × 105 core hours used.
. The positions are recorded at each major time step Δt = 0.01 (a.u.). The simulation proceeds up to tmax = 50 (a.u.) or 100 (a.u.) (for different data sets). Single and multiple rejection boundary conditions are implemented but multiple rejection is used here;66 proposal displacements are generated until one is found that does not mean leaving the void phase. A cell list data structure (with 10 × 10 × 10 cells for large random configurations, but only a single cell for lattice structures) is used to accelerate computations. The computations are run on a variety of architectures comprising around 20 cores yielding execution times between ∼2 hours and ∼30 hours, within the total 5 × 105 core hours used.
A time-dependent effective diffusion coefficient (i.e. obstruction factor) is computed as
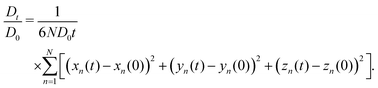 | (5) |
4 Results and discussion
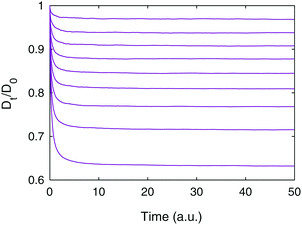
First, we consider the lattice structures, i.e. simple cubic (SC) and face-centered cubic (FCC) configurations of spheres and cubes. Examples of the structures and the results of the diffusion simulations are shown in Fig. 2. For the spheres, the results are in very good agreement with earlier analytical findings67 (see Fig. 2 in this paper, and the solid black lines in the figure herein) and with earlier simulated findings using a very similar simulation technique as herein.50 Obviously, for small ϕ the impact of shape is small, and grows larger for increasing ϕ. The FCC of cubes consistently has the lowest diffusivity of them all. For ϕ smaller than ∼0.4, the SC of cubes has smaller diffusivity than the SC of spheres, whereas for ϕ larger than ∼0.4, the opposite is true. Similarly, for ϕ smaller than ∼0.6, the SC of cubes has a smaller diffusivity than the FCC of spheres, whereas for ϕ larger than ∼0.6, the opposite is true. The 3D checkerboard structure of the FCC of cubes yields very narrow ‘channels’ between large open spaces, even for relatively low solid volume fractions; indeed, for ϕ = 0.5, the void phase is discontinuous and the effective diffusivity is zero. Furthermore, there is some benefit in terms of effective diffusivity in the SC and FCC of spheres as compared to the FCC of cubes as long as the solid volume fraction is not too large, because of a less tortuous path for the diffusing species with smoothed boundaries of the void phase. However, for large solid volume fractions, the SC of cubes can provide highly non-tortuous and straight paths (at least along the axes), simply because packing of cubes is more efficient than that of spheres, leading to rather high diffusivities even for extremely high solid volume fractions. We first believed this to be an artifact of our simulation method, in particular the multiple-rejection boundary conditions, but as can be seen below in Fig. 3, when the ‘straight channels’ are no longer there, the diffusivity indeed drops to zero much more quickly (the curve shown in Fig. 2 would consequently, if we could simulate it, have a very rapid drop to zero as ϕ approaches 1). Hence, the different ordering for different solid volume fractions is the result of a varying trade-off between two competing effects. For lower solid volume fractions, ϕ ≤ 0.4, the smaller diffusivities for cubes is supported through their greater tortuosity as found in ref. 68–70.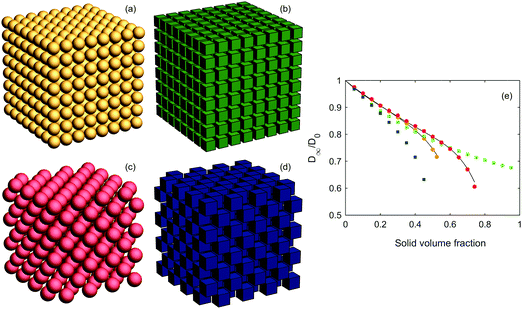 | ||
| Fig. 2 Lattice structures showing (a) a simple cubic lattice of spheres, (b) a simple cubic lattice of cubes, (c) a face-centered cubic lattice of spheres, and (d) a face-centered cubic lattice of cubes. All lattices shown have a solid volume fraction ϕ = 0.4. In (e), effective diffusivities for different volume fractions are shown (yellow circles for the SC of spheres, green squares for the SC of cubes, red circles for the FCC of spheres, and blue squares for the FCC of cubes). Also, the analytical results obtained from ref. 67 are shown for both SC and FCC (black solid lines). | ||
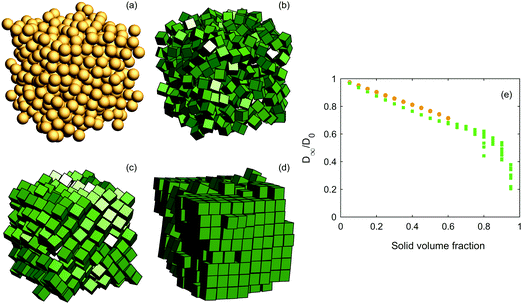
Second, we study random packings for different solid volume fractions. Examples of the structures and results of diffusion simulations are shown in Fig. 3. For low solid volume fractions, spheres yield a higher effective diffusivity than cubes, the same as above. For high solid volume fractions, it appears that the benefit of straight ‘channels’ induced by the cubic shape in lattices is lost for random configurations. This is not surprising; rather, it is intuitively obvious that adjacent cubes randomly displaced from each other can provide a very efficient obstacle. For ϕ larger than ∼0.6, we observe akin to ref. 39–42 that ordering and orientational correlations start manifesting themselves (for ϕ ≥ 0.57, crystallization behaviour has been observed). It can hence be discussed whether these configurations are random and to what extent; herein, it suffices to conclude that our algorithm will create crystals for high solid volume fractions. The substantial spread in effective diffusivity for cubes with solid volume fractions larger than ∼0.6 indicates that it is largely up to chance whether the configuration will provide ‘simple’ paths for the diffusers or not. This may also be highly dependent on the choice of algorithm for generating the configurations. We have a hypothesis that the slightly slowed decrease (the slight ‘bump’) in diffusivity in the range ϕ = 0.6–0.8 depends on the increased ordering among the cubes yielding some ‘channels’ between the cubes, before the effect of a larger solid volume fraction once again starts to dominate. In any case, a more detailed answer on the true effective diffusivity for cubes with very large solid volume fractions would likely require much larger configurations.
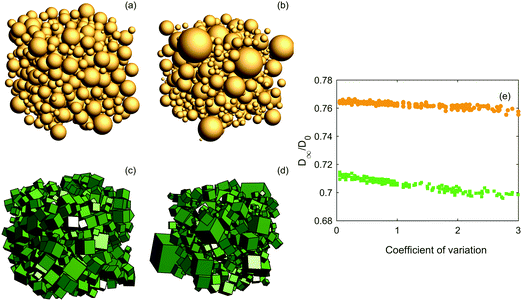
Third, we investigate the effect of polydispersity for ϕ = 0.5 by introducing a lognormal distribution for the particle volumes (due to the family of lognormal distributions being closed under powers, the semi-axes/radii are also lognormally distributed). Examples of the structures and the results of the diffusion simulations are shown in Fig. 4. The coefficient of variation (CV), i.e. the ratio of standard deviation to the mean, is varied from 0 to 3. The effect of polydispersity is not that pronounced, but a slightly decreasing trend for increasing the coefficient of variation is seen. As the calculation of effective diffusivity is a scale-independent problem, increasing the size of all particles would not change anything. However, introducing the occasional large particle through polydispersity will apparently contribute toward blocking the diffusion more efficiently. Although we only investigate for ϕ = 0.5, it is clear that the effect of polydispersity will be positively correlated with solid volume fraction and vanish for ϕ approaching zero.
Fourth, we investigated the effect of shape for ellipsoids and cuboids for ϕ = 0.5. For both particle types, we studied semi-axes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
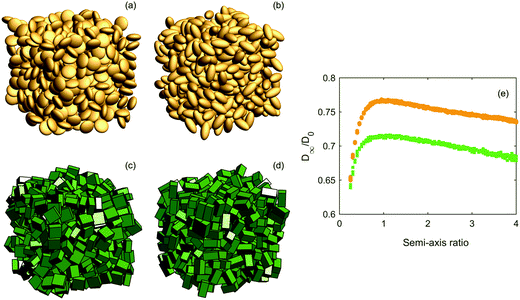
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, where the semi-axis ratio α is varied between 0.25 and 4. Examples of the structures and the results of diffusion simulations are shown in Fig. 5. As can be expected from the results for both mono- and polydisperse packings of spheres and cubes, cuboids do consistently yield lower effective diffusivities than ellipsoids. However, for very oblate particles (to the extent that this is an appropriate word for cuboids), the difference gradually vanishes. The same convergence is not observed for very prolate particles in the investigated α regime, although it seems plausible that for extremely elongated particles, shape (of the cross-section) would once again not matter so much. We investigated this for α = 10 and ϕ = 0.4 (because we cannot reach ϕ = 0.5 for such elongated particles) and somewhat surprisingly found that D/D0 was ∼0.77 for ellipsoids and ∼0.73 for cuboids, i.e. the difference in diffusivity reduces from ∼0.05 to ∼0.04 when jumping from α = 4 to α = 10, suggesting that they ‘converge’ very slowly as α increases. We cannot generate structures with arbitrary large values of α due to numerical issues with the overlap criterion (for ellipsoids) and particles possibly overlapping themselves due to the periodicity of the simulation domain, so we have to settle for this result. Anyhow, the two particle types have the same generic relation between shape and effective diffusivity, suggesting some degree of universality with respect to the aspect ratio impact on diffusivity. The importance of shape and aspect ratio could be due to the shape itself, and also due to the ordering that the shape can impose on the overall structure, or a combination of the two. A deeper analysis of microstructural descriptors would be required to find an answer. Although we only investigated for ϕ = 0.5, it is clear that the effect of shape will be positively correlated with solid volume fraction and vanish for ϕ approaching zero.
α, where the semi-axis ratio α is varied between 0.25 and 4. Examples of the structures and the results of diffusion simulations are shown in Fig. 5. As can be expected from the results for both mono- and polydisperse packings of spheres and cubes, cuboids do consistently yield lower effective diffusivities than ellipsoids. However, for very oblate particles (to the extent that this is an appropriate word for cuboids), the difference gradually vanishes. The same convergence is not observed for very prolate particles in the investigated α regime, although it seems plausible that for extremely elongated particles, shape (of the cross-section) would once again not matter so much. We investigated this for α = 10 and ϕ = 0.4 (because we cannot reach ϕ = 0.5 for such elongated particles) and somewhat surprisingly found that D/D0 was ∼0.77 for ellipsoids and ∼0.73 for cuboids, i.e. the difference in diffusivity reduces from ∼0.05 to ∼0.04 when jumping from α = 4 to α = 10, suggesting that they ‘converge’ very slowly as α increases. We cannot generate structures with arbitrary large values of α due to numerical issues with the overlap criterion (for ellipsoids) and particles possibly overlapping themselves due to the periodicity of the simulation domain, so we have to settle for this result. Anyhow, the two particle types have the same generic relation between shape and effective diffusivity, suggesting some degree of universality with respect to the aspect ratio impact on diffusivity. The importance of shape and aspect ratio could be due to the shape itself, and also due to the ordering that the shape can impose on the overall structure, or a combination of the two. A deeper analysis of microstructural descriptors would be required to find an answer. Although we only investigated for ϕ = 0.5, it is clear that the effect of shape will be positively correlated with solid volume fraction and vanish for ϕ approaching zero.
5 Conclusion
We have performed computational screening of effective diffusivity in lattices and random configurations of cubes and cuboids compared with spheres and ellipsoids. In total, more than 1500 structures were generated and screened for effective diffusivity. Very little is done in terms of both analytical models and simulations of effective diffusivity in the literature for cubic and cuboidal particles. For lattice configurations, the solid volume fraction will determine which shape gives higher and lower effective diffusivity. For random configurations, cubes and cuboids consistently yield lower effective diffusivities. Although the solid volume fraction is the primary determinant of effective diffusivity, shape effects are still substantial and more research is needed to understand them. The shape-dependent differences found in the behavior help in understanding the impact of shape on the targeted design of granular materials, with respect to the relations between porosity, specific surface, pore size distributions, and effective properties. Further work would naturally include an extension to superballs/superellipsoids as well as cubes/cuboids with rounded edges and corners, both of which can ‘interpolate’ between spheres/ellipsoids on the one hand and cubes/cuboids on the other. Furthermore, the use of 2- and 3-point correlation functions as well as other microstructural descriptors will help elucidate the nature of the shape dependence in these systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support of the Swedish Research Council (grant number 2016-03809) and the Swedish Foundation for Strategic Research (the project “Material structures seen through microscopes and statistics”) is acknowledged. The computations were in part performed on resources at Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC). Niklas Lorén is acknowledged for fruitful discussions and reading of the manuscript.References
- M. Kachanov and I. Sevostianov, Effective properties of heterogeneous materials, Springer Science & Business Media, 2013, vol. 193 Search PubMed.
- S. Torquato, Random heterogeneous materials: microstructure and macroscopic properties, Springer Science & Business Media, 2013, vol. 16 Search PubMed.
- J. Giddings, Dynamics of chromatography: principles and theory, CRC Press, 2002 Search PubMed.
- M. Sahimi, Heterogeneous materials I: linear transport and optical properties, Springer, 2003, vol. 22 Search PubMed.
- J. Kärger, D. Ruthven and D. Theodorou, Diffusion in nanoporous materials, Wiley, 2012 Search PubMed.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. Sing, Adsorption by powders and porous solids: principles, methodology and applications, Academic Press, 2013 Search PubMed.
- T. Müllner, K. Unger and U. Tallarek, New J. Chem., 2016, 40, 3993–4015 RSC.
- V. Dugyala, S. Daware and M. Basavaraj, Soft Matter, 2013, 9, 6711–6725 RSC.
- T. Sau and A. Rogach, Adv. Mater., 2010, 22, 1781–1804 CrossRef CAS PubMed.
- Y. Sun and Y. Xia, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- L. Manna, E. Scher and A. Alivisatos, J. Am. Chem. Soc., 2000, 122, 12700–12706 CrossRef CAS.
- R. Jin, Y. Cao, C. Mirkin, K. Kelly, G. Schatz and J. Zheng, Science, 2001, 294, 1901–1903 CrossRef CAS PubMed.
- O. Cayre, V. Paunov and O. Velev, J. Mater. Chem., 2003, 13, 2445–2450 RSC.
- S. Shankar, A. Rai, B. Ankamwar, A. Singh, A. Ahmad and M. Sastry, Nat. Mater., 2004, 3, 482 CrossRef CAS PubMed.
- L. Gou and C. Murphy, Nano Lett., 2003, 3, 231–234 CrossRef CAS.
- T. Ahmadi, Z. Wang, T. Green, A. Henglein and M. El-Sayed, Science, 1996, 272, 1924–1925 CrossRef CAS PubMed.
- N. Malikova, I. Pastoriza-Santos, M. Schierhorn, N. Kotov and L. Liz-Marzán, Langmuir, 2002, 18, 3694–3697 CrossRef CAS.
- E. Greyson, J. Barton and T. Odom, Small, 2006, 2, 368–371 CrossRef CAS PubMed.
- J. Love, B. Gates, D. Wolfe, K. Paul and G. Whitesides, Nano Lett., 2002, 2, 891–894 CrossRef CAS.
- S. Chen, Z. Wang, J. Ballato, S. Foulger and D. Carroll, J. Am. Chem. Soc., 2003, 125, 16186–16187 CrossRef CAS PubMed.
- S.-M. Lee, Y.-W. Jun, S.-N. Cho and J. Cheon, J. Am. Chem. Soc., 2002, 124, 11244–11245 CrossRef CAS PubMed.
- Z. Tang, Y. Wang, S. Shanbhag, M. Giersig and N. Kotov, J. Am. Chem. Soc., 2006, 128, 6730–6736 CrossRef CAS PubMed.
- S. Glotzer and M. Solomon, Nat. Mater., 2007, 6, 557 CrossRef PubMed.
- S. Sacanna and D. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105 CrossRef CAS.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- L. Rossi, S. Sacanna, W. Irvine, P. Chaikin, D. Pine and A. Philipse, Soft Matter, 2011, 7, 4139–4142 RSC.
- A. Donev, I. Cisse, D. Sachs, E. Variano, F. Stillinger, R. Connelly, S. Torquato and P. Chaikin, Science, 2004, 303, 990–993 CrossRef CAS PubMed.
- V. Baranau and U. Tallarek, Soft Matter, 2014, 10, 3826–3841 RSC.
- K. Desmond and E. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022204 CrossRef PubMed.
- J. Baker and A. Kudrolli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061304 CrossRef PubMed.
- Y. Jiao and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041309 CrossRef PubMed.
- U. Agarwal and F. Escobedo, Nat. Mater., 2011, 10, 230–235 CrossRef CAS PubMed.
- P. Damasceno, M. Engel and S. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- R. Batten, F. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061105 CrossRef PubMed.
- G. Delaney and P. Cleary, Europhys. Lett., 2010, 89, 34002 CrossRef.
- R. Ni, A. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Soft Matter, 2012, 8, 8826–8834 RSC.
- M. Marechal, U. Zimmermann and H. Löwen, J. Chem. Phys., 2012, 136, 144506 CrossRef PubMed.
- F. Smallenburg, L. Filion, M. Marechal and M. Dijkstra, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17886–17890 CrossRef CAS PubMed.
- H. Malmir, M. Sahimi and M. Tabar, Sci. Rep., 2016, 6, 35024 CrossRef CAS PubMed.
- H. Malmir, M. Sahimi and M. Tabar, Phys. Rev. E, 2016, 94, 062901 CrossRef PubMed.
- H. Malmir, M. Sahimi and M. Tabar, Phys. Rev. E, 2017, 95, 052902 CrossRef PubMed.
- L. Liu, Z. Li, Y. Jiao and S. Li, Soft Matter, 2017, 13, 748–757 RSC.
- Z. Hashin and S. Shtrikman, J. Appl. Phys., 1962, 33, 3125–3131 CrossRef CAS.
- A. Sen and S. Torquato, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 4504–4515 CrossRef.
- M. Beran, Il Nuovo Cimento, 1965, 38, 771–782 CrossRef.
- G. Milton, Phys. Rev. Lett., 1981, 46, 542 CrossRef.
- S. Torquato, J. Appl. Phys., 1985, 58, 3790–3797 CrossRef.
- Y. Jiao and S. Torquato, Phys. Biol., 2012, 9, 036009 CrossRef PubMed.
- J. Thovert, I. Kim, S. Torquato and A. Acrivos, J. Appl. Phys., 1990, 67, 6088–6098 CrossRef CAS.
- H. Liasneuski, D. Hlushkou, S. Khirevich, A. Höltzel, U. Tallarek and S. Torquato, J. Appl. Phys., 2014, 116, 034904 CrossRef.
- D. Hlushkou, H. Liasneuski, U. Tallarek and S. Torquato, J. Appl. Phys., 2015, 118, 124901 CrossRef.
- M. Palombo, A. Gabrielli, V. Servedio, G. Ruocco and S. Capuani, Sci. Rep., 2013, 3, 2631 CrossRef CAS PubMed.
- S. Prager, Phys. Fluids, 1961, 4, 1477–1482 CrossRef.
- H. Weissberg and S. Prager, Phys. Fluids, 1962, 5, 1390–1392 CrossRef.
- H. Weissberg and S. Prager, Phys. Fluids, 1970, 13, 2958–2965 CrossRef.
- J. Berryman and G. Milton, J. Chem. Phys., 1985, 83, 754–760 CrossRef CAS.
- J. Berryman, J. Chem. Phys., 1985, 82, 1459–1467 CrossRef CAS.
- J. Rubinstein and S. Torquato, J. Fluid Mech., 1989, 206, 25–46 CrossRef CAS.
- W. Brown, J. Chem. Phys., 1955, 23, 1514–1517 CrossRef CAS.
- D. Coelho, J.-F. Thovert and P. Adler, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 1959–1978 CrossRef CAS.
- S. Jones and S. Friedman, Water Resour. Res., 2000, 36, 2821–2833 CrossRef.
- X. Garcia, L. Akanji, M. Blunt, S. Matthai and J. Latham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021304 CrossRef PubMed.
- J. Bezanson, A. Edelman, S. Karpinski and V. B. Shah, SIAM Rev., 2017, 59, 65–98 CrossRef.
- J. Perram and M. Wertheim, J. Comput. Phys., 1985, 58, 409–416 CrossRef CAS.
- C. Ericson, Real-time collision detection, CRC Press, 2004 Search PubMed.
- P. Szymczak and A. Ladd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036704 CrossRef CAS PubMed.
- M. Blees and J. Leyte, J. Colloid Interface Sci., 1994, 166, 118–127 CrossRef CAS.
- J. Comiti and M. Renaud, Chem. Eng. Sci., 1989, 44, 1539–1545 CrossRef CAS.
- Z. Sun, X. Tang and G. Cheng, Microporous Mesoporous Mater., 2013, 173, 37–42 CrossRef CAS.
- E. Garca, P. Boulet, R. Denoyel, J. Anquetil, G. Borda and B. Kuchta, Colloids Surf., A, 2016, 496, 28–38 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |