Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of optical projection in the analysis of membrane fluctuations†
S. Alex
Rautu
a,
Davide
Orsi
 b,
Lorenzo
Di Michele
c,
George
Rowlands
a,
Pietro
Cicuta
b,
Lorenzo
Di Michele
c,
George
Rowlands
a,
Pietro
Cicuta
 *c and
Matthew S.
Turner
*a
*c and
Matthew S.
Turner
*a
aDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK. E-mail: m.s.turner@warwick.ac.uk; Tel: +44 (0)24 7652 2257
bDepartment of Mathematics, Physics and Computer Sciences, University of Parma, Parma, Italy
cCavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE, UK. E-mail: pc245@cam.ac.uk; Tel: +44 (0)1223 337462
First published on 25th April 2017
Abstract
The spectral analysis of thermal fluctuations, or flickering, is a simple and non-invasive method widely used to determine the mechanical properties of artificial and biological lipid membranes. In its most common implementation, the position of the edge of a cell or vesicle is tracked from optical microscopy videos. However, a systematic disagreement with X-ray scattering and micromechanical manipulation data has brought into question the validity of the method. We present an improved analysis protocol that resolves these discrepancies by accounting for the finite vertical resolution of the optics used to image fluctuations.
The spectroscopy of shape fluctuations is a general technique to infer the mechanical properties of soft and biological matter. Specifically, fluid membranes are very soft and analysis of shape conformations allows one to characterise physical properties and aspects of the biochemical activity: the “flickering” of giant unilamellar vesicles (GUVs) and red blood cells (RBC) is a classic example.1 In flicker spectroscopy, the equatorial fluctuations of GUVs are imaged through video microscopy and reconstructed by image analysis, yielding a power spectrum that is then compared to a theoretical model to retrieve the membrane tension σ and the bending rigidity κ. The latter is an intrinsic property of the membrane that affects its dynamics and structure, as well as morphology, motility, and endocytosis in living cells.2 Flickering experiments are widely used to assess the differences in the membrane rigidity of various lipid compositions, since only a basic microscope is needed, the sample preparation procedures are well established and direct manipulation of the membrane can be avoided. However, the absolute value of κ measured via flickering is systematically larger than those obtained by X-ray scattering, direct manipulation of GUVs and active driving,3 as reported in Table 1 for 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC). Here we show that this discrepancy arises from the inadequacy of the theoretical models currently used to fit experimental data. Specifically, these ignore the finite focal depth of the setups used to image the membranes, which ultimately projects some out-of-focus fluctuations onto the imaging plane. We introduce a theoretical model that accurately accounts for these projections, and test it on experimental data collected with a fast scanning confocal microscope, in which the focal depth is precisely set.4 When compared with standard flickering analysis on DOPC vesicles (that gives κ = 28 ± 3kBT), we observe a 30% reduction in the measured values of κ and find an excellent agreement with the alternative experimental methods. Our technique can be applied to any optical microscopy setup, once the focal depth is known; a proof-of-concept analysis of a phase contrast imaging experiment is reported in the ESI.†
| Experimental method | κ/kBT |
|---|---|
| Flicker spectroscopy of GUVs | |
| Literature values10,11 | 28 ± 3 |
| Present work – no optical projection | 27 ± 1 |
| Present work – optical projection | 19 ± 1 |
| Active driving of GUVs10 | 21 ± 3 |
| Pulling membrane tethers12,13 | 20 ± 4 |
| X-ray scattering on bilayer stacks14–17 | 18 ± 2 |
| Micropipette aspiration of GUVs18–20 | 20 ± 2 |
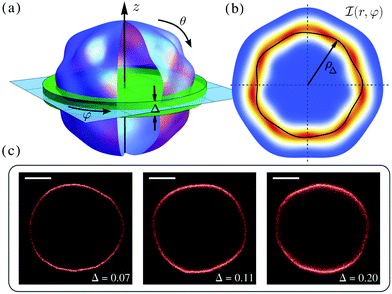
A fluctuating GUV can be described as a quasi-spherical shell S ≡ R[1 + u(θ,φ)]![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) , where (θ,φ) are the spherical angular coordinates, u(θ,φ) is a small deviation about a sphere of radius R, and
, where (θ,φ) are the spherical angular coordinates, u(θ,φ) is a small deviation about a sphere of radius R, and ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) is the radial unit vector (see Fig. 1a). The free-energy of the vesicles is described by the Helfrich Hamiltonian, which depends on κ and σ.5 By expanding this Hamiltonian to second order in u, written in the basis of the spherical harmonics Ymn as
is the radial unit vector (see Fig. 1a). The free-energy of the vesicles is described by the Helfrich Hamiltonian, which depends on κ and σ.5 By expanding this Hamiltonian to second order in u, written in the basis of the spherical harmonics Ymn as 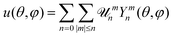 , with
, with ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) mn the mode amplitude, one can express the time-averaged mean square fluctuation amplitudes as follows:6
mn the mode amplitude, one can express the time-averaged mean square fluctuation amplitudes as follows:6
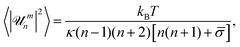 | (1) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = σR2/κ − 2H0R + 2H02R2 is the reduced tension, H0 is the mean spontaneous curvature, kB is the Boltzmann constant, and T is the temperature. The decay time of each mode is given by:6
= σR2/κ − 2H0R + 2H02R2 is the reduced tension, H0 is the mean spontaneous curvature, kB is the Boltzmann constant, and T is the temperature. The decay time of each mode is given by:6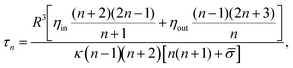 | (2) |
Membrane fluctuations are recorded by microscopy imaging in 2D, normally around the equatorial plane. Thus, experimental data have been typically compared with mode amplitudes obtained by projecting the modes in eqn (1) onto the plane θ = π/2; see ref. 7 and the ESI† for a full derivation. However, due to finite depth of focus, the experiments cannot isolate the signal from the equatorial plane alone. What is actually observed is a projection over the strip of membrane that lies within a focal region near the equator, as shown in Fig. 1(a); this strip can support a spectrum of surface modes that are partially averaged out in projection. This averaging effect is expected to be particularly strong for modes q ≳ 1/Δ, where Δ is a non-dimensional parameter given by the ratio of the focal depth of the microscope to the vesicle radius R.
In the case of fluorescence microscopy, where the membrane is assumed to be uniformly labelled with fluorophores that emit isotropically (see Fig. 1b), we idealise the acquired optical signal as a convolution of the membrane shape with a Gaussian of width equal to the focal depth. Namely, light arriving from height z above (or below) the focal plane has intensity scaled by 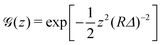 . Thus, the projected intensity field on the equatorial plane is
. Thus, the projected intensity field on the equatorial plane is
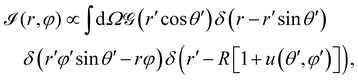 | (3) |
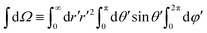 , r and φ are the polar coordinates, and δ is the Dirac delta function. Experiments detect
, r and φ are the polar coordinates, and δ is the Dirac delta function. Experiments detect ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) (r,φ) and locate the apparent membrane contour as the first radial moment
(r,φ) and locate the apparent membrane contour as the first radial moment 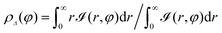 . Deviations of ρΔ(φ) are analyzed in Fourier space, where they are written as μq(t) and are non-dimensionalised by R. By defining
. Deviations of ρΔ(φ) are analyzed in Fourier space, where they are written as μq(t) and are non-dimensionalised by R. By defining 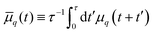 to account for microscope exposure time τ, the mean square amplitude can be exactly computed
to account for microscope exposure time τ, the mean square amplitude can be exactly computed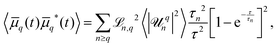 | (4) |
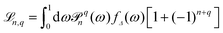 , with
, with ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) qn(cos
qn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) ≡ Yqn(θ,φ = 0), and fΔ(ω) is defined by
θ) ≡ Yqn(θ,φ = 0), and fΔ(ω) is defined by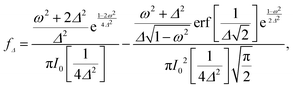 | (5) |
The experiments are performed on GUVs prepared by means of electroformation as in ref. 9, with DOPC and the fluorescent lipid Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (DHPE) in proportions of 99.2% and 0.8%, respectively. Videos of the equatorial fluctuations of GUVs are collected on a Leica TCS SP5 II scanning confocal microscope, using a HCX-PL-APO-CS 40.0× oil immersion objective with numerical aperture NA = 1.30. The focal depth is defined by the pinhole size of the microscope, which allows us to experimentally obtain the value of Δ by fitting the intensity profile along the z-direction to a Gaussian form of standard deviation RΔ. The position of the equatorial contours in every frame is determined with sub-pixel precision by correlating the radial intensity profile with a template. By Fourier transforming the contours and averaging over ∼2000 frames, we extract the mean-squared amplitude of the equatorial modes Fq(Δ), which can be directly compared with the model (eqn (4)); see ESI† for full experimental details. Note that a cutoff condition in the mode spectrum, q ≲ Q, arises due the finite temporal resolution of the microscope, particularly the rate at which the illumination spot is raster-scanned across the field of view. With our setup we typically obtain Q ≈ 20 (see ESI†). The accessible wave number is also limited by the spatial resolution of the setup to q ≲ qw = R/![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) , where
, where ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) is the lateral width of the diffraction-limited illumination spot.
is the lateral width of the diffraction-limited illumination spot.
Using eqn (4), the best-fit values of κ and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) to the experimental spectrum Fq(Δ) are found by means of a maximum posterior estimate,21 assuming a uniform prior and that the measurement errors are independent and Gaussian; namely, we seek to minimise
to the experimental spectrum Fq(Δ) are found by means of a maximum posterior estimate,21 assuming a uniform prior and that the measurement errors are independent and Gaussian; namely, we seek to minimise
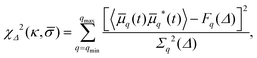 | (6) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n,q2, the sum in eqn (4) is truncated at the mode n = q + 30. On the other hand, the upper bound of the fitting range is selected as one that maximises the posterior probability
n,q2, the sum in eqn (4) is truncated at the mode n = q + 30. On the other hand, the upper bound of the fitting range is selected as one that maximises the posterior probability ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) (qmax|DΔ) based on data DΔ = {Fq(Δ)}q. This can be numerically computed, but further analytical progress can be made by expanding χΔ2(κ,
(qmax|DΔ) based on data DΔ = {Fq(Δ)}q. This can be numerically computed, but further analytical progress can be made by expanding χΔ2(κ,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ) to second order around the best-fit values of κ and
) to second order around the best-fit values of κ and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) , which yields the following expression:
, which yields the following expression: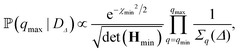 | (7) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) )], and Hmin is the Hessian matrix of eqn (6) evaluated at the best-fit values. We also impose that qmax must be greater than the crossover
)], and Hmin is the Hessian matrix of eqn (6) evaluated at the best-fit values. We also impose that qmax must be greater than the crossover 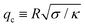 ,‡ and less than the cutoffs qw and Q. In other words, the optimal fit is achieved when χΔ2(κ,
,‡ and less than the cutoffs qw and Q. In other words, the optimal fit is achieved when χΔ2(κ,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ) is minimal and simultaneously its upper bound qmax ∈ (qc, min(qw,Q)] maximises the probability in eqn (7). If qmax lies outside the interval discussed above, then the dataset DΔ is rejected. See ESI† for details, code and example files. The maximum posterior estimate can be applied to datasets
) is minimal and simultaneously its upper bound qmax ∈ (qc, min(qw,Q)] maximises the probability in eqn (7). If qmax lies outside the interval discussed above, then the dataset DΔ is rejected. See ESI† for details, code and example files. The maximum posterior estimate can be applied to datasets ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) containing spectra from N different vesicles imaged with different Δ. In this case, since σ is not a material property of the bilayer, the posterior probability becomes an (N + 1)-dimensional function
containing spectra from N different vesicles imaged with different Δ. In this case, since σ is not a material property of the bilayer, the posterior probability becomes an (N + 1)-dimensional function ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) (κ,
(κ, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 1,…
1,…![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) N|
N|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ), with a different
), with a different ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for each
for each ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -th vesicle. As in eqn (6), we assume a uniform prior and that the measurement errors are independent and Gaussian; thus, maximising this posterior probability function is equivalent to minimizing χ
-th vesicle. As in eqn (6), we assume a uniform prior and that the measurement errors are independent and Gaussian; thus, maximising this posterior probability function is equivalent to minimizing χ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 ≡ ΣΔΣ
2 ≡ ΣΔΣ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) χΔ2(κ,
χΔ2(κ,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), where each individual qmax is given by the maximum of eqn (7).
), where each individual qmax is given by the maximum of eqn (7).
By imaging three GUVs with radii between 6–17 μm at various pinhole sizes, the fluctuation spectrum associated with each Δ yields an individual estimate for κ and σ. A systematic decrease in the inferred value of κ is found when the data is fitted with the model in eqn (4) in comparison with the “standard” model that considers only equatorial fluctuations, i.e. Δ = 0 (see Fig. 2a). Using a maximum posterior estimate based on the data of all the vesicles imaged at different Δ, we find κ = 19 ± 1kBT (Fig. 2b), in perfect agreement with literature values obtained with X-rays and micromanipulation techniques (see Table 1). In contrast, by fitting all spectra with the conventional model (Δ = 0), we find that κ = 27 ± 1kBT, a value compatible with the literature estimates of κ obtained by conventional flickering analysis (see Table 1).
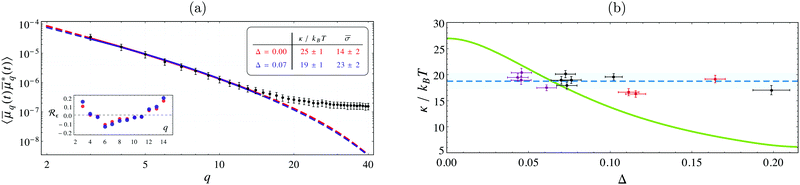 | ||
Fig. 2 (a) Fluctuation spectrum for a GUV (R ≈ 10.2 μm) imaged via confocal fluorescence microscopy, with Δ = 0.07 and τ ≈ 1.2 ms, on a log–log scale. Lines are the best-fit for the “standard” model (i.e. incorrectly assuming Δ = 0, red), and eqn (4) with Δ = 0.07 (blue). Both fits are of similar quality, but their best-fit values are significantly different, see the inset table (same colors). Dashed lines give their extrapolation outside the fitting range. The error-bars are standard errors in the mean, scaled up by a factor 10 to improve visibility. Inset plot shows the residuals Rε(q), normalised to the standard deviation. (b) Values of κ from the analysis of three GUVs of radii 6.4 μm (purple), 10.2 μm (black), and 16.7 μm (red), observed at different values of Δ. The blue dashed line is the estimate of κ from the entire dataset ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , found by maximizing the posterior probability , found by maximizing the posterior probability ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) (κ, (κ,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 1, 1,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 2, 2,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 3| 3|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ), where ), where ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the corresponding reduced surface tension of is the corresponding reduced surface tension of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -th vesicle. This yields κ = 19 ± 1kBT (the blue band is the 95% confidence interval). The green curve shows κ inferred by fitting the data -th vesicle. This yields κ = 19 ± 1kBT (the blue band is the 95% confidence interval). The green curve shows κ inferred by fitting the data ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) at fixed Δ. Large errors arise if Δ is not accounted for correctly; the value κ ≈ 27kBT, found at Δ = 0, corresponds to the use of the “standard” model to fit the experiments. The correction is also important for GUVs of varying radius, even when imaged with same optics. at fixed Δ. Large errors arise if Δ is not accounted for correctly; the value κ ≈ 27kBT, found at Δ = 0, corresponds to the use of the “standard” model to fit the experiments. The correction is also important for GUVs of varying radius, even when imaged with same optics. | ||
Large discrepancies in the inferred surface tension values are also to be expected. To illustrate the dependence of the inferred values of κ with the focal depth, the conventional fitting procedure is repeated at arbitrary non-zero values of Δ for all of the spectra in ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , yielding an interpolated curve depicted by the green line in Fig. 2b. This shows how increasing the focal depth can result in an apparent increase in κ if its effects are not properly analysed.
, yielding an interpolated curve depicted by the green line in Fig. 2b. This shows how increasing the focal depth can result in an apparent increase in κ if its effects are not properly analysed.
In conclusion, a new methodology is developed for the analysis of flickering data that can accurately account for the finite focal depth of the optical imaging setups. Thus, this resolves a systematic inconsistency in the estimated values of bending rigidity, bringing flickering into full quantitative agreement with other methods such as X-ray scattering and micromanipulation techniques. Neglecting this correction leads to a systematic and size-dependent error which is unfortunately present in all (hundreds) published papers. Using our approach, flickering analysis is now competitive in terms of accuracy with the aforementioned methods, allowing the user to exploit its several advantages in terms of easiness of use and simplicity, as it relies on general purpose and easily accessible equipment, it is non-invasive, and can be integrated into microfluidic devices.
Acknowledgements
We acknowledge stimulating discussions with M. Rao, P. Sens, and A. T. Brown, the sample preparation support from L. Parolini, and the help on simulations on the scanning sampling from A. Javer. This research work is funded by EPSRC under grants EP/I005439/1 (Matthew Turner) and EP/J017566/1 (Pietro Cicuta), Project SPINNER 2013, Regione Emilia-Romagna, European Social Fund (Davide Orsi), The Leverhulme Trust and the Isaac Newton Trust through an Early Career Fellowship, the Ernest Oppenheimer Fund, and Emmanuel College Cambridge (Lorenzo Di Michele). A complete dataset in support of this publication is available free of charge at https://doi.org/10.17863/CAM.9209.References
- P. Bassereau, B. Sorre and A. Lévy, Adv. Colloid Interface Sci., 2014, 208, 47–57 CrossRef CAS PubMed.
- R. Lipowsky and E. Sackmann, Structure and Dynamics of Membranes: I. From Cells to Vesicles, Elsevier Science, Amsterdam, 1995 Search PubMed.
- J. F. Nagle, M. S. Jablin, S. Tristram-Nagle and K. Akabori, Chem. Phys. Lipids, 2015, 185, 3–10 CrossRef CAS PubMed.
- J. Mertz, Introduction to Optical Microscopy, Roberts and Company Publishers, Greenwood Village, 2009 Search PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- S. T. Milner and S. A. Safran, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4371–4379 CrossRef CAS.
- J. Pécréaux, H. G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- M. Abramowitz and I. Stegun, Handbook of Mathematical Functions, Dover Publications Inc., New York, 1965 Search PubMed.
- L. Parolini, B. M. Mognetti, J. Kotar, E. Eiser, P. Cicuta and L. Di Michele, Nat. Commun., 2015, 6, 5948 CrossRef CAS PubMed.
- A. T. Brown, J. Kotar and P. Cicuta, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021930 CrossRef PubMed.
- R. S. Gracià, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472 RSC.
- A. Tian, B. R. Capraro, C. Esposito and T. Baumgart, Biophys. J., 2009, 97, 1636–1646 CrossRef CAS PubMed.
- B. Sorre, A. Callan-Jones, J.-B. Manneville, P. Nassoy, J.-F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626 CrossRef CAS PubMed.
- N. Kucerka, Y. Liu, N. Chu, H. I. Petrache, S. Tristram-Nagle and J. F. Nagle, Biophys. J., 2005, 88, 2626–2637 CrossRef CAS PubMed.
- N. Kucerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2006, 208, 193–202 CrossRef PubMed.
- J. Pan, T. T. Mills, S. Tristram-Nagle and J. F. Nagle, Phys. Rev. Lett., 2008, 100, 198103 CrossRef PubMed.
- J. Pan, S. Tristram-Nagle, N. Kucerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- N. Fa, L. Lins, P. J. Courtoy, Y. Dufrêne, P. Van Der Smissen, R. Brasseur, D. Tyteca and M.-P. Mingeot-Leclercq, Biochim. Biophys. Acta, 2007, 1768, 1830–1838 CrossRef CAS PubMed.
- P. Shchelokovskyy, S. Tristram-Nagle and R. Dimova, New J. Phys., 2011, 13, 25004 CrossRef CAS PubMed.
- D. S. Sivia and J. Skilling, Data Analysis – A Bayesian tutorial, Oxford University Press, Oxford, 2nd edn, 2006 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: We provide details on the preparation of GUVs, on the confocal microscopy setup, on the code used to extract the fluctuation spectrum from a video of a GUV, and on the data analysis procedure. We report the complete theoretical derivation of the model at the basis of our Method. We also provide the Matlab routine used to analyse fluctuations of GUVs with example and the Mathematica routine used to fit the fluctuation spectrum and retrieve the mechanical properties of the membrane. See DOI: 10.1039/c7sm00108h |
| ‡ This crossover q-mode separates the regimes in which the membrane is dominated by the surface tension term (q ≲ qc) and the bending rigidity term (q ≳ qc). Thus, we require its value to lie within the fitting range. |
| This journal is © The Royal Society of Chemistry 2017 |