Open Access Article
Open Access ArticleA self-consistent mean-field model for polyelectrolyte gels†
Oleg
Rud
ab,
Tobias
Richter
c,
Oleg
Borisov
ade,
Christian
Holm
c and
Peter
Košovan
 *b
*b
aInstitute of Macromolecular Compounds of Russian Academy of Sciences, 199004, Bolshoy pr. 31, Saint-Petersburg, Russia. E-mail: helvrud@gmail.com
bDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University in Prague, Hlavova 8, 128 00 Praha 2, Czech Republic. E-mail: peter.kosovan@natur.cuni.cz
cInstitute for Computational Physics, University of Stuttgart, Allmandring 3, 70569 Stuttgart, Germany
dInstitut des Sciences Analytiques et de Physico-Chimie pour l'Environnement et les Matériaux, UMR 5254 CNRS UPPA, Pau, France
eSaint-Petersburg National University of Informational Technologies, Mechanics and Optics, 197101, Kronverkskiy pr., 49 A, Saint-Petersburg, Russia
First published on 13th February 2017
Abstract
We present a novel approach to modeling polyelectrolyte gels, exploiting the analogy between star-branched polymers and polymer networks as a computationally inexpensive yet reliable alternative to full-scale simulations. In the numerical mean-field model of a star-like polymer we modify the boundary conditions to represent an infinite network. We validate the predictions of our new model against a coarse-grained simulation model. We also validate it against a phenomenological analytical model which has been previously shown to agree with simulations in a limited range of parameters. The mean-field model explicitly considers local density gradients and agrees with the simulation results in a broad range of parameters, beyond that of the analytical model. Finally, we use the mean-field model for predictions of the swelling behaviour of weak polyelectrolyte gels under different pH conditions. We demonstrate that the local density gradients are important and that the ionization of the weak polyelectrolyte gel is significantly suppressed. Under the studied conditions the effective pKA is about one unit higher than that of the free monomer. This shift in the effective pKA stems from the different pH values inside and outside the gel.
1 Introduction
The swelling capacity of polyelectrolyte gels is much greater than that of neutral polymer gels because of the additional osmotic pressure contributions of small ions confined in the gel and mutual repulsion of polymer-bound charges. While modeling of the swelling behaviour of neutral gels can be considered well understood in terms of the Flory–Rehner theory and the related later developments,1,2 this is not true for polyelectrolyte gels. On the one hand, phenomenological analytical theories exist, which provide relatively simple explanations of the swelling behaviour in terms of different contributions to the free energy.3–6 These theories typically assume a homogeneous gel phase in equilibrium with the bulk solution that can be characterized by a few macroscopic parameters. On the other hand, particle-based coarse-grained models have been used in several simulation studies.7–15 The simulations sample particle configurations and therefore explicitly account for correlations between different species. Their disadvantage is that they are much more computationally expensive when compared to analytical theories. When it comes to modeling pH-sensitive (weak) polyelectrolyte gels, where the dissociation of gel segments is a result of chemical equilibrium determined by solution pH, theoretical and simulation literature is quite scarce. On the side of simulations, an additional limiting factor is the necessity to explicitly account for the dissociation equilibrium. On the theoretical side, it is the lack of suitable analytical models that would account for the different ionizations of polyelectrolytes, as compared to free monomers. Therefore the existing literature employs a number of simplifications, e.g., the use of ideal ionization equilibrium to describe the ionization inside the gel6 in the analytical models or fixed ionization which is assumed to increase linearly with solution pH.16,17 An interesting approach to swelling of nanogels has been proposed by Jha et al.,18,19 which combines explicit particle simulations with a density functional approach used earlier for grafted polyelectrolyte layers.20,21 Using a similar approach, Longo and coworkers14,22 combined coarse-grained simulations with local ionization equilibria to study the swelling of pH-sensitive hydrogel layers. Most of the above simulation works have employed a diamond-like topology for their model networks.7,9–13,15 This is an idealized representation of the most common experimental situation with four chains emanating from each node of the network, e.g. in gels obtained by photocrosslinking. However, model topologies derived from a simple cubic lattice with six chains attached to a node have been used as well.8,14,22 Several other theoretical works on polyelectrolyte microgels explicitly considered density gradients across the gel–solution interface.23,24 However, the above approaches, which require explicit particle simulations, are computationally rather expensive. Apparently, an inexpensive method, which would provide a first approximation to the local density variations inside polyelectrolyte gels and to their ionization response, seems to be lacking.In this work we present a novel approach to model the swelling behaviour of polyelectrolyte hydrogels, based on the numerical self-consistent field model due to Scheutjens and Fleer (SF-SCF),25 which has been used for studies of star-like polyelectrolytes.26–30 We propose that a covalently cross-linked polyelectrolyte hydrogel can be viewed as a collection of spherically symmetric star-like polyelectrolytes, mutually connected together by end segments of the arms, as schematically shown in Fig. 1.
We demonstrate the capabilities of the numerical SF-SCF approach by comparing results to recent simulation data and to an analytical model that has been shown to successfully predict the swelling of polyelectrolyte gels within a limited range of parameters.13
The newly proposed approach has the advantage that it explicitly treats the concentration gradients of all the involved species in the radial direction with respect to the node of the hydrogel network (the centre of the star in the mean-field representation). Once validated against the simulation data on strong polyelectrolyte gels, the SF-SCF approach can be easily extended to predict the swelling of weak polyelectrolyte gels with pH-dependent ionization and to poor solvent conditions, where radial variations of the properties significantly affect the behaviour that result in non-trivial features. The spherical symmetry approximation used in the model provides a correction to the most relevant density gradients in the radial direction, but neglects the angular correlations. At the same time, it allows us to reduce the three-dimensional problem to a one-dimensional one, which saves a tremendous amount of computational cost. In addition, our approach provides a guideline to extrapolate the existing theoretical knowledge about star polyelectrolytes to polyelectrolyte gels.
2 Models
The target system represented by our models is a hydrogel network made up by polyelectrolyte chains. All chains consist of the same number of segments N = 79, and are connected to a diamond-like network with f = 4 chains connected to each node. We consider two situations: (i) a strong polyelectrolyte in which some segments are permanently ionized while others are not; (ii) a weak polyelectrolyte in which all segments are subject to the ionization reactionHA ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) A− + H+ A− + H+ | (1) |
In the strong polyelectrolyte case we fix the degree of ionization α = 1, 1/2, 1/4, and 1/8 with regularly spaced charges, such that one ionized segment on the polymer is followed by (1/α − 1) non-ionized ones. In the weak polyelectrolyte case, the reaction in eqn (1) is characterized by an equilibrium constant, KA. Then pKA and pH are the input parameters of the model, and α is the result of the calculation. We choose pKA = −log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KA = 5 as a typical value for monomers containing weak carboxylic acids, such as acrylic acid.
KA = 5 as a typical value for monomers containing weak carboxylic acids, such as acrylic acid.
In the weak polyelectrolyte case, we use αs to denote the probability that the segment with ranking number s (counted from the network node) is ionized. Then we define the overall degree of ionization of the gel, α as the average over individual segments:
 | (2) |
For the bulk salt concentration we use the values 0.01 M ≤ cbs ≤ 0.2 M in order to cover the range from potable water to seawater, motivated by the potential application of charged hydrogels to water desalination.12,31 The analytical calculations and the numerical mean-field calculations were performed also for a broader range of values of α and cbs than those mentioned above.
We use three different models to study the properties of the gels, each of them employing a different level of approximation.
• The analytical model based on our modification of the theory of Katchalsky and Michaeli,3,13 hereafter referred to as the analytical model.
• The coarse-grained simulation model of the Kremer–Grest type with explicit particles and charges, and implicit solvent, identical to our preceding publication,13 hereafter referred to as the simulation model.
• The mean-field model based on the Scheutjens–Fleer self-consistent field (SF-SCF) model for star-like polyelectrolytes, and on the analogy between gels and stars, hereafter referred to as the mean-field model.
Although the above-mentioned models all represent the same hydrogel, due to the different approximations they differ in some specific details of the representation. In the following paragraphs we briefly outline each of these representations, focusing on the differences. For the analytical model and for the simulation model we only provide a brief description, and refer to the preceding publication for additional details.13
2.1 The analytical model
The analytical model of Katchalsky and Michaeli,3,13,32 that we extended recently to account for finite extensibility of the chains, is based on the analogy between the swelling of a polyelectrolyte gel and stretching of an individual strand between two crosslinks. The end-to-end distance of the strand, Re, and the volume per chain of the gel, V, are coupled assuming affine deformation:| Re3 = AV, | (3) |
 . The affine deformation holds well close to the full extension but deteriorates for less extended chains, which results in systematic errors of up to 30% in the predicted end-to-end distance.13 The mechanical equilibrium is found by balancing different contributions to the pressure (each of them being the derivative of the corresponding free energy contribution):
. The affine deformation holds well close to the full extension but deteriorates for less extended chains, which results in systematic errors of up to 30% in the predicted end-to-end distance.13 The mechanical equilibrium is found by balancing different contributions to the pressure (each of them being the derivative of the corresponding free energy contribution): | (4) |
 | (5) |
 | (6) |
| Posm = kBT(2cgs + αcp − 2cbs), | (7) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1(Re/aN) is the inverse Langevin function to account for finite extensibility. The term Pel in eqn (4) accounts for the intra-chain electrostatic repulsions. Parameter ξ in eqn (5) has been introduced to simplify the notation:
−1(Re/aN) is the inverse Langevin function to account for finite extensibility. The term Pel in eqn (4) accounts for the intra-chain electrostatic repulsions. Parameter ξ in eqn (5) has been introduced to simplify the notation: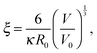 | (8) |
With V0 as the reference state, we define the swelling ratio as
| Q = V/V0. | (9) |
The salt concentration in the gel, cgs, which is needed as an input for the calculation of Posm in eqn (7), and of the Debye screening length in eqn (8), couples the swelling equilibrium and salt partitioning:
 | (10) |
 | (11) |
2.2 The coarse-grained (CG) simulation model
Here, we restrict ourselves to a brief summary, since this model is identical to the one used in our previous publications,12,13 where a full-detailed description can be found. Similar models have been used by other authors to study polyelectrolyte gels.9–11,33–35 In this work, we extended our earlier simulation results beyond the Manning condensation threshold36 to α = 1.0. In brief, the gel network consists of polymer chains interconnected in a diamond topology via the finite-extensible nonlinear elastic potential, with excluded volume modeled by a purely repulsive Weeks–Chandler–Andersen potential. Charged segments, their counterions, as well as salt ions are modeled explicitly as charged particles with excluded volume, while solvent is treated as a dielectric continuum with the relative permittivity εr = 80. Equilibrium with the salt reservoir is ensured by insertion/deletion of salt ions in a semi-grand canonical Monte Carlo manner. The effective particle size and bond length are set to a ≈ 0.35 nm, which ensures that the linear charge density at full ionization is λB/a ≈ 2, where λB ≈ 0.71 nm is the Bjerrum length in water at 300 K. The same ratio of λB/a yields the concentration dependence of the chemical potential of the coarse-grained salt solution which is consistent with experimental data on NaCl up to cbs ≈ 1 M.13We carry out a series of molecular dynamics simulations with the Langevin thermostat for fixed sizes of the simulation box to obtain the pressure–extension relation and interpolate to find the gel volume at a given pressure.
2.3 The numerical mean-field model
Here we exploit the idea originally suggested to us by A. Polotsky, that a gel can be viewed as a collection of interconnected star-like polymers under tension, as illustrated in Fig. 1. As discussed below, this provides some advantages over the traditional depiction as a collection of linear chains.Our mean-field model of a crosslinked gel is derived from the model of a star-like polyelectrolyte,27 based on the Scheutjens–Fleer self-consistent field (SF-SCF) approach described in more detail in Section 2.4. The star is placed in the centre of the spherical coordinate system, and spherical symmetry is assumed, explicitly accounting for the radial gradients in the densities and neglecting all angular correlations.
To map the star to the gel, we use f = 4 arms, each of which has half the length of the strand connecting two nodes of the network, N/2. The key aspect of representing the gel as a star consists of fixing the end segment of each arm at a particular distance,
| Rstar = Re/2, | (12) |
| Rbox = (Aπ/12)−1/3Rstar, | (13) |
Besides the star we introduce salt ions, Na+, Cl−, and water. The bulk concentrations of the salt ions and the H+ ions are fixed in the outermost layer of the box, which defines the boundary condition for the semi-grand canonical calculation. The concentration of OH− ions is determined by explicitly considering the autoprotolysis reaction of water. The salt concentration in the gel is then obtained as the total number of salt ions in the box, divided by the box volume:
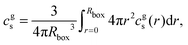 | (14) |
 .
.
In order to get the pressure from the mean field model, we use the partial open Helmholtz free energy, defined as  . This quantity is analogous to the Grand potential for open systems. The main difference is that our system is open to all particles but the macromolecule, which is fixed at the centre, hence the term partial open. We calculate pressure as a numerical derivative using the seven point stencil37
. This quantity is analogous to the Grand potential for open systems. The main difference is that our system is open to all particles but the macromolecule, which is fixed at the centre, hence the term partial open. We calculate pressure as a numerical derivative using the seven point stencil37
 | (15) |
 | (16) |
2.4 The Scheutjens–Fleer self-consistent field implementation
In the Scheutjens–Fleer self-consistent field method, SF-SCF,25,38 the free energy is expressed as a function of the density profiles of all the system components, i.e. polymer segments, free ions, and the solvent. This method has been described many times in the literature. Therefore we only point out the essential parts of it and refer the reader to the existing literature for further details.25,27,29 The one-dimensional spherical approximation employed here reduces the three-dimensional problem to a one-dimensional spherically symmetric problem, which greatly reduces the number of iteration variables and speeds up the search for the optimum solution. Assuming spherical symmetry, the central segment of the star is placed at the centre of a system of M concentric shells (layers) of constant thickness a = 0.35 nm, which also defines the effective size of the monomer and of all other species in the system. The mean-field potential ux(z) experienced by segments of type x in layer z can be expressed as | (17) |
| Gx(z) = exp(−ux(z)) | (18) |
| Gx(z,s|z*,1) = Gx(z)〈Gx(z,s − 1|z*,1)〉 | (19) |
| Gx(z,s|N) = Gx(z)〈Gx(z,s + 1|N)〉 | (20) |
 | (21) |
For weak polyelectrolytes it is necessary to consider different states of the ionizable species (polymer segments and water molecules). Then the above equations are modified such that the fraction of species of type j in state k is given by39
| αj,k(z) = αbj,k(z)Gj,k(z)/Gj(z) | (22) |
 | (23) |
| cH+(z)cOH−(z) = Kw | (24) |
The solution of the set of equations starts from an initial guess of the density profiles, which yield the respective potentials and the statistical weights. Application of the propagator scheme provides a new set of density profiles. The self-consistent solution is reached when the old and the new volume fractions match within a pre-defined accuracy threshold. The final set of density profiles and potentials yield an accurate prediction of the free energy within the mean-field approximation, which consists of replacing explicit inter-particle interactions with a mean-field potential as given in eqn (17). Due to the variational principle, the mean-field free energy is an upper bound to the true free energy with all correlations included. This difference is inherent to the involved approximation and is not related to the above mentioned accuracy threshold.
The SF-SCF formulation is a discrete analogue of the continuous Edwards diffusion equation.41,42 The discrete version implemented on a set of concentric shells (“the lattice”) with lattice spacing a allows for the full enumeration of all the chain configurations starting in the first layer and ending in the layer number given by Rstar, see figure Fig. 1B. This automatically accounts also for finite chain extensibility. The discretised lattice has an important consequence for our depiction of the gel as a collection of stars, sketched in Fig. 1. The SF-SCF approach requires that both Rbox and Rstar are integer multiples of lattice spacing a. If we choose Rstar to be an integer multiple of a, then Rbox obtained from eqn (13) usually is not an integer multiple of a. Therefore we always perform two calculations, with Rbox rounded to the nearest lower and the nearest higher integer multiple of a. These provide us with an upper and lower estimate of the desired result. Therefore, although the SF-SCF calculation can be performed to an arbitrary accuracy, the discretization limits the accuracy of the representation of the gel. All results that we report are arithmetic means of the two calculations, while the error bars represent the upper and lower bound to indicate discretization artifacts.
3 Results and discussion
3.1 Model validation: strong polyelectrolyte gels
Fig. 3 shows the salt partitioning, expressed as the ratio of salt concentration in the gel to that in the bulk, as a function of the total concentration of charged groups bound to the gel, αcp. Following the simple Donnan prediction, the ratio cgs/cbs should be a universal function of αcp, independent of other parameters. The Donnan prediction does not explicitly account for any inter-particle interactions (except for electroneutrality), and in this respect plays the role of the ideal gas approximation. Deviations of the simulation data (empty points in Fig. 3) from the Donnan theory provide a measure of non-ideality, which is well captured by the analytical model at low cbs and low α (see also ESI† Fig. S5 for additional data). This agreement deteriorates with increasing cbs and α. In particular at α = 1 and high cbs the analytical model fails even at the qualitative level, predicting that initially cgs/cbs increases (see also ESI† Fig. 5), which is not observed in the simulation data. This failure is presumably related to the convex shape of the predicted pressure–extension curves in Fig. 2 in the same range of parameters. On the other hand, the mean-field model again retains its qualitative agreement throughout the whole range of parameters. The rather big estimated error in the mean-field model, which increases with α, stems from discretization, as discussed in Section 2.4. Within the accuracy limits set by the discretization, the mean-field model agrees with the simulation results and with the analytical model up to α = 1/2 and higher salt concentrations. At the lowest salt concentrations and α = 1/2, the mean-field model systematically underestimates cgs, and is outperformed by the analytical model. At α = 1, the mean-field model provides poor quantitative predictions, but qualitatively the predicted trend does not contradict the simulation data as it occurred in the case of the analytical model. Last but not least, we should mention that at the highest cbs the uncertainty due to discretization becomes bigger than the difference between simulation results and the Donnan prediction, which makes the mean-field results useless.
 | ||
| Fig. 3 The gel to bulk ratio of salt concentration, cgs/cbs, as a function of the concentration of bound charges in the gel for a system with strand length N = 79, salt concentration cbs = 0.1 M, and three different degrees of ionization: α = 1/4 (green), 1/2 (blue) and 1 (red). The black solid curve displays the Donnan prediction as a reference. The empty symbols show the results of the mean-field calculations, full symbols of matching shape and colour are the corresponding simulation results, and the dashed lines of matching colour represent the corresponding analytical predictions. Error bars of the mean-field results have been omitted for clarity. See the ESI† Fig. S5 for the same plots with error bars. | ||
At the qualitative level, the mean-field model captures all the trends that emerge from the simulation data, in particular the variation of salt content and the pressure–extension relation with the crosslink length, N, the degree of ionization of the polymer, α, and the salt content of the bulk solution, cbs.
At the quantitative level, the mean-field model underestimates the salt content in the gel, and consistent with that it underestimates the pressure inside the gel, and hence overestimates the swelling ratio. This discrepancy produces a systematic deviation which is consistent throughout the whole parameter range. The pressure–extension relation predicted by the SF-SCF approach remains consistent with the simulations (apart from the above-mentioned systematic deviation) even at high cbs or high α, where the analytical model fails. At high α the analytical model predicts a non-monotonic pressure–extension relation, while both the mean-field model and the simulations predict a monotonic dependence.
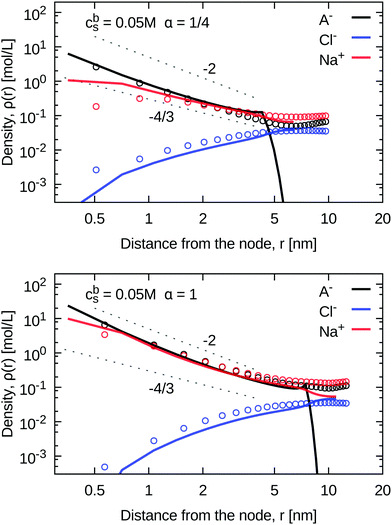 | ||
| Fig. 5 Density profiles from simulations (points) and from the SF-SCF method (lines) at intermediate chain length and salt concentration, at the two extreme ionization degrees: α = 1/4 (top panel), and α = 1 (lower panel). Different particle types (monomers, counterions, coions) are distinguished by colour. The two gray lines with slopes −4/3 and −2 show the scaling prediction for the neutral star and a highly charged star, respectively. See the ESI† Fig. S3 for plots with other combinations of parameters. | ||
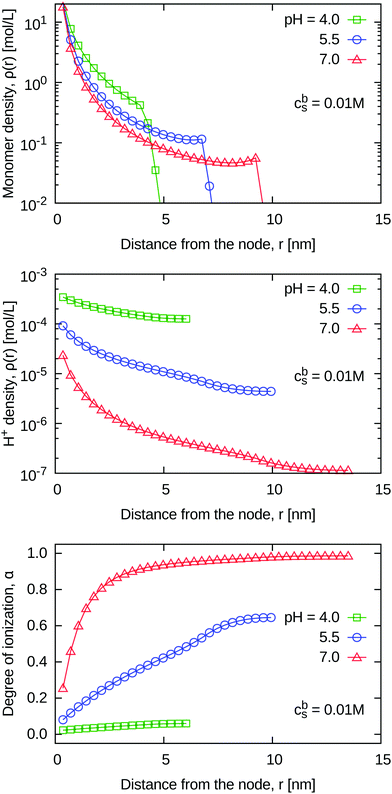
3.2 pH-Sensitive gels
 | ||
| Fig. 6 Degree of ionization of the weak polyelectrolyte gels as a function of chain extension at a fixed salt concentration of cbs = 0.01 M and for different pH values. | ||
This variation of α with chain extension has a pronounced effect on the pressure–extension curves, shown in Fig. 7. With decreasing pH the curves become less steep (the gels are softer) at a given value of Re, and consequently the free swelling equilibrium is attained at a lower chain extension and a lower degree of ionization. Interestingly, if we compare the pressure–extension curves at a given pressure (free swelling equilibrium, P = 0) rather than at a given compression, it turns out that the more ionized gels are softer than the less ionized ones. The trend in the pressure–extension curves with decreasing pH is qualitatively similar to the trend with decreasing ionization in the strong polyelectrolyte gels (Fig. 2). The difference becomes apparent by comparing the data for weak gel at pH 5.5 and a strong gel at α = 0.35. This is the average value of α for the weak polyelectrolyte gel at free swelling equilibrium (zero applied pressure). For the strong polyelectrolyte this was realized by making all segments ionized with a valency of 0.35. In the weak case α decreases with compression, which makes the pressure–extension curve less steep compared to that of the corresponding strong gel.
Predictions of the SF-SCF model for the salinity inside the weak gels exhibit only weak deviations from the Donnan prediction, very similar to the strong case (see the ESI,† Fig. S1). Since the Donnan prediction is a universal function of αcp, the fact that in the weak gel α varies with compression does not significantly change the situation. However, as deduced from the discussion of the strong case, the actual deviations from the Donnan model should be stronger than those predicted by the SF-SCF model.
| 1/α = 1 + 10pKA–pH. | (25) |
 | (26) |
 is the average concentration of H+ inside the gel, defined in analogy with eqn (14). As follows from eqn (23), the ideal titration curve is satisfied locally within each individual layer, if the local pH is used instead of the bulk pH. However, because α and the local pH are coupled by a non-linear relation, if we plot the average α over the whole box as a function of the average pH inside the gel in Fig. 9, this curve does not fully coincide with the ideal titration curve.
is the average concentration of H+ inside the gel, defined in analogy with eqn (14). As follows from eqn (23), the ideal titration curve is satisfied locally within each individual layer, if the local pH is used instead of the bulk pH. However, because α and the local pH are coupled by a non-linear relation, if we plot the average α over the whole box as a function of the average pH inside the gel in Fig. 9, this curve does not fully coincide with the ideal titration curve.
As discussed in detail in our previous publication,29 the shift and deformation of titration curves of star-branched weak polyelectrolytes have two important contributions: (1) inter-arm correlations, which lead to higher cH+(r) and lower α(r) inside the gel as compared to the bulk; (2) intra-arm correlations due to neighbouring groups along the chain. The one-dimensional model of a polyelectrolyte star well accounts for the first but underestimates the second contribution. The latter cannot be explained in terms of the (average) local pH in the gel and becomes important especially at α > 1/2 when the distance between the nearest ionized groups along the chain becomes smaller than the Bjerrum length. Therefore, our mean-field model should reasonably well describe weak polyelectrolyte gels at low α but it underestimates the shift of the titration curve at high α.
4 Conclusions
In this work, we introduced a numerical mean-field model for the swelling of polyelectrolyte gels, based on the analogy between gels and star-like polymers. This model employs the Scheutjens–Fleer self-consistent field approach and assumes spherically symmetric density profiles around the node of the gel network, in analogy with the central segment of star-like polymers. We validated this new model, comparing its predictions with our earlier simulation results and with the analytical model for strong polyelectrolyte gels. Below the Manning condensation threshold, the mean-field model provides quantitatively more accurate predictions of gel swelling than the analytical model. Beyond the condensation threshold the analytical model fails even at the qualitative level, while the mean-field model retains a qualitative agreement with the simulations. For the prediction of salt concentration in the gel, the simulation data exhibit positive deviations from the ideal-gas Donnan approximation. While both models capture the general trend of the deviations, the analytical model tends to overshoot them and the mean-field model tends to underestimate them.Next, we demonstrate a straightforward extension of the new mean-field model to weak polyelectrolyte gels and provide predictions of their swelling as a function of pH. In the weak case, the local coupling between the conformation and ionization is included in the mean-field model and proves to be essential to capture important effects. The degree of ionization of the weak gel changes with compression, and therefore the pressure–extension curves at a given pH are less steep than those for the strong gels at a fixed degree of ionization. The Donnan-like partitioning of the mobile ions between the gel and the bulk also applies to H+ and OH− ions. This results in a lower pH inside the gel than in the bulk, and in the suppressed ionization of the gel as compared to the free monomer. This can be interpreted in terms of effective pKA which is about one unit higher than that of the single monomer. Within the mean-field approximation this suppression of ionization is dominated by the difference between the local and bulk pH, but there is also a clear contribution from the inhomogeneous distribution of charges. The latter is presumably underestimated by the mean-field and should be even more significant in a real system. Some of the above effects were neglected in earlier analytical theories which assumed a homogeneous density inside the gels.
In terms of computational effort, the mean-field calculations are more expensive than solving the analytical model. However, in both cases one calculation of the pressure–extension curve completes within few seconds, so that it can be performed interactively. In contrast, the explicit simulations, which provided our reference data, require several days per each data point on the pressure–extension curve. From this point of view, the new mean-field model provides a promising and cheap alternative for the reliable prediction of the swelling of polyelectrolyte gels in cases where local density gradients are important, simple analytical approaches fail, and explicit simulations are too demanding even at the coarse-grained level.
Acknowledgements
We gratefully acknowledge Dr Lucie Nová for reading the manuscript and providing valuable comments. P. K. and O. R. acknowledge support from the Czech Science Foundation grant (P208/14-23288J) and the Ministry of Education, Youth and Sports (CUCAM CZ.02.1.01/0.0/0.0/15\_003/0000417). P. K., O. R. and O. B. acknowledge support from the Marie Curie International Research Staff Exchange Scheme Fellowship (PIRSES-GA-2013-612562) within the 7th European Community Framework Programme. C. H. and T. R. were supported by the DFG grant HO 1108/26-1 and AR 593/7-1. Computational resources were provided by the CESNET LM2015042 and the CERIT Scientific Cloud LM2015085, provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures”. This work has been partially supported by the Government of Russian Federation, Grant 074-U01, and by the Russian Foundation of Basic Research, Grant 14-03-00372.References
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 512 CrossRef CAS.
- M. Doi, Introduction to Polymer Physics, Clarendon Press, Oxford, 1996 Search PubMed.
- A. Katchalsky and I. Michaeli, J. Polym. Sci., 1955, 15, 69 CrossRef CAS.
- Responsive Gels: Volume Transitions I, ed. K. Dušek, Springer-Verlag, New York, 1993, vol. 109 Search PubMed.
- Y. Huang, I. Szleifer and N. A. Peppas, Macromolecules, 2002, 35, 1373–1380 CrossRef CAS.
- A. A. Polotsky, F. A. Plamper and O. V. Borisov, Macromolecules, 2013, 46, 8702–8709 CrossRef CAS.
- S. Schneider and P. Linse, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 457–460 CAS.
- Z.-Y. Lu and R. Hentschke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061807 CrossRef PubMed.
- S. Edgecombe, S. Schneider and P. Linse, Macromolecules, 2004, 37, 10089–10100 CrossRef CAS.
- B. A. Mann, R. Everaers, C. Holm and K. Kremer, Europhys. Lett., 2004, 67, 786–792 CrossRef CAS.
- B. A. Mann, C. Holm and K. Kremer, J. Chem. Phys., 2005, 122, 154903 CrossRef PubMed.
- J. Höpfner, T. Richter, P. Košovan, C. Holm and M. Wilhelm, Intelligent Hydrogels, Springer International Publishing, 2013, vol. 140, pp. 247–263 Search PubMed.
- P. Košovan, T. Richter and C. Holm, Macromolecules, 2015, 48, 7698–7708 CrossRef.
- G. S. Longo, M. O. de la Cruz and I. Szleifer, Macromolecules, 2011, 44, 147–158 CrossRef CAS.
- I. Adroher-Bentez, S. Ahualli, A. Martn-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Macromolecules, 2015, 48, 4645–4656 CrossRef.
- R. Schroeder, A. a. Rudov, L. A. Lyon, W. Richtering, A. Pich and I. I. Potemkin, Macromolecules, 2015, 48, 5914–5927 CrossRef CAS.
- Z. Posel, Z. Limpouchová, K. Šindelka, M. Lísal and K. Procházka, Macromolecules, 2014, 47, 2503–2514 CrossRef CAS.
- P. K. Jha, J. W. Zwanikken, J. J. de Pablo and M. O. de la Cruz, Curr. Opin. Solid State Mater. Sci., 2011, 15, 271–276 CrossRef CAS.
- P. K. Jha, J. W. Zwanikken, F. A. Detcheverry, J. J. de Pablo and M. Olvera de la Cruz, Soft Matter, 2011, 7, 5965–5975 RSC.
- P. Gong, J. Genzer and I. Szleifer, Phys. Rev. Lett., 2007, 98, 018302 CrossRef PubMed.
- R. Nap, P. Gong and I. Szleifer, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2638–2662 CrossRef CAS.
- G. S. Longo, M. O. de la Cruz and I. Szleifer, J. Chem. Phys., 2014, 141, 124909 CrossRef PubMed.
- T. Colla, C. N. Likos and Y. Levin, J. Chem. Phys., 2014, 141, year CrossRef PubMed.
- A. Moncho-Jorda and J. Dzubiella, Phys. Chem. Chem. Phys., 2016, 18, 5372–5385 RSC.
- G. J. Fleer, M. A. Cohen Stuart, T. Cosgrove and B. Vincent, Polymers at interfaces, Chapman and Hall, London, 1993 Search PubMed.
- J. Klein Wolterink, F. A. M. Leermakers, G. J. Fleer, L. K. Koopal, E. B. Zhulina and O. V. Borisov, Macromolecules, 1999, 32, 2365–2377 CrossRef.
- J. Klein Wolterink, J. van Male, M. A. Cohen Stuart, L. K. Koopal, E. B. Zhulina and O. V. Borisov, Macromolecules, 2002, 35, 9176–9190 CrossRef.
- O. V. Rud, A. A. Mercurieva, F. A. M. Leermakers and T. M. Birshtein, Macromolecules, 2012, 45, 2145–2160 CrossRef CAS.
- F. Uhlík, P. Košovan, Z. Limpouchová, K. Procházka, O. V. Borisov and F. A. M. Leermakers, Macromolecules, 2014, 47, 4004–4016 CrossRef.
- F. Uhlík, P. Košovan, E. B. Zhulina and O. V. Borisov, Soft Matter, 2016, 4846–4852 RSC.
- J. Höpfner, C. Klein and M. Wilhelm, Macromol. Rapid Commun., 2010, 31, 1337 CrossRef PubMed.
- A. Katchalsky, S. Lifson and J. Mazur, J. Polym. Sci., 1953, 11, 409–423 CrossRef CAS.
- B. A. Mann, C. Holm and K. Kremer, Macromol. Symp., 2006, 237, 90–107 CrossRef CAS.
- B. A. Mann, O. Lenz, K. Kremer and C. Holm, Macromol. Theory Simul., 2011, 20, 721–734 CrossRef CAS.
- P. Košovan, T. Richter and C. Holm, Intelligent Hydrogels, Springer International Publishing, 2013, vol. 140, pp. 205–221 Search PubMed.
- G. S. Manning, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS.
- A. Griewank and A. Walther, Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, SIAM, 2nd edn, 2008 Search PubMed.
- J. Scheutjens and G. Fleer, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- R. Israëls, F. A. M. Leermakers and G. J. Fleer, Macromolecules, 1994, 27, 3087–3093 CrossRef.
- R. Israëls, F. A. M. Leermakers, G. J. Fleer and E. B. Zhulina, Macromolecules, 1994, 27, 3249–3261 CrossRef.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford Science Publications, 1986 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, 1979 Search PubMed.
- O. V. Borisov, E. B. Zhulina, F. A. Leermakers, M. Ballauff and A. H. E. Müller, Self Organized Nanostructures of Amphiphilic Block Copolymers I, Springer Berlin Heidelberg, 2011, vol. 241, pp. 1–55 Search PubMed.
- T. M. Birshtein, A. A. Mercurieva, F. A. M. Leermakers and O. V. Rud, Polym. Sci., Ser. A, 2008, 50, 992–1007 CrossRef.
- M. Daoud and J. Cotton, J. Phys., 1982, 43, 531–538 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm02825j |
| This journal is © The Royal Society of Chemistry 2017 |