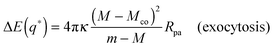DOI:
10.1039/C6SM02796B
(Paper)
Soft Matter, 2017,
13, 2155-2173
Uniform and Janus-like nanoparticles in contact with vesicles: energy landscapes and curvature-induced forces
Received
15th December 2016
, Accepted 9th February 2017
First published on 10th February 2017
Abstract
Biological membranes and lipid vesicles often display complex shapes with non-uniform membrane curvature. When adhesive nanoparticles with chemically uniform surfaces come into contact with such membranes, they exhibit four different engulfment regimes as recently shown by a systematic stability analysis. Depending on the local curvature of the membrane, the particles either remain free, become partially or completely engulfed by the membrane, or display bistability between free and completely engulfed states. Here, we go beyond stability analysis and develop an analytical theory to leading order in the ratio of particle-to-vesicle size. This theory allows us to determine the local and global energy landscapes of uniform nanoparticles that are attracted towards membranes and vesicles. While the local energy landscape depends only on the local curvature of the vesicle membrane and not on the overall membrane shape, the global energy landscape describes the variation of the equilibrium state of the particle as it probes different points along the membrane surface. In particular, we find that the binding energy of a partially engulfed particle depends on the ‘unperturbed’ local curvature of the membrane in the absence of the particle. This curvature dependence leads to local forces that pull the partially engulfed particles towards membrane segments with lower and higher mean curvature if the particles originate from the exterior and interior solution, respectively, corresponding to endo- and exocytosis. Thus, for partial engulfment, endocytic particles undergo biased diffusion towards the membrane segments with the lowest membrane curvature, whereas exocytic particles move towards segments with the highest curvature. The curvature-induced forces are also effective for Janus particles with one adhesive and one non-adhesive surface domain. In fact, Janus particles with a strongly adhesive surface domain are always partially engulfed which implies that they provide convenient probes for experimental studies of the curvature-induced forces that arise for complex-shaped membranes.
1 Introduction
Understanding the interaction between nanoparticles and biomembranes is of key importance in areas such as drug delivery, nanotoxicity, viral infection or biomedical imaging.1–5 The uptake of particles by cells requires the engulfment of the particles by the cell membrane, a process governed by the interplay between particle–membrane adhesion and membrane bending.6,7 Experimentally, the fundamental features of this engulfment process can be studied using model systems such as lipid8–12 vesicles or polymersomes.13
Several computational studies have previously explored the engulfment process of both spherical14–20 and non-spherical particles.21–25 These studies have been impeded by the high dimensionality of the parameter space that describes particle–membrane interactions. Indeed, one may consider (i) different particle properties such as size, adhesiveness, shape and softness; (ii) particles with chemically uniform, Janus-like, or patchy surfaces; (iii) variations in the bending rigidity and spontaneous curvature of the membranes as well as in their phase behavior; or (iv) different geometrical and topological constraints on the membrane, such as closed vesicles with and without volume constraint, which lead to spherical, oblate, prolate, discocyte or stomatocyte-shaped vesicles, as well as planar membranes connected to area reservoirs with a certain membrane tension. Computational studies can typically explore only a small subspace or ‘slice’ of this high-dimensional parameter space, and are therefore limited in their ability to guide future experiments.
Recently, we overcame this limitation for the particular case of rigid spherical particles with a uniform adhesive surface. Such particles can in principle remain free, that is, unbound from the membrane; they can be partially engulfed, when the particles are bound to but not fully covered by the membrane; or they can be completely engulfed, when the entire particle surface is membrane-bound. In ref. 7, we developed a local stability analysis that allowed us to obtain exact analytical conditions for the energetic stability of free and completely engulfed particles. The two stability conditions depend on the particle size and adhesiveness, the material properties of the membrane, and the local curvature of the membrane, which is affected by the geometric constraints acting on the membrane. Combining the two stability conditions with numerical calculations, we found that small particles can exhibit only four distinct behaviors when in contact with a membrane: a particle can either (i) remain free, (ii) become completely engulfed, (iii) be partially engulfed, or (iv) display a bistability between free and completely engulfed states, which are then separated by an energy barrier. The boundaries between these four regimes directly follow from the stability limits associated with the two stability conditions.
Subsequently, in ref. 26, we used the local stability analysis to show that complex-shaped vesicles with non-uniform curvature display different engulfment patterns when exposed to adhesive particles. One example of such a pattern is displayed in Fig. 1(a) for the case of a prolate vesicle.† In this particular example, particles are completely engulfed at the strongly curved poles (green regions) but partially engulfed in the weakly curved equatorial region (blue). However, the approach based on local stability analysis does not give us access to the binding energy and degree of engulfment in the case of partially engulfed particles, or to the height of the energy barrier between free and completely engulfed states in the bistable engulfment regime.
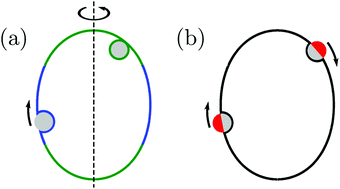 |
| | Fig. 1 (a) A prolate vesicle (green-blue) in contact with uniform adhesive particles (grey) originating from the exterior solution. In this particular example, particles are completely engulfed at the strongly curved poles (green segments) and partially engulfed in the weakly curved equatorial region (blue). Partially engulfed particles experience a curvature-induced force towards regions of lower membrane curvature, whereas completely engulfed particles experience no such force. (b) For the same prolate vesicle, Janus particles with one strongly adhesive (grey) and one non-adhesive (red) surface domain are partially engulfed everywhere on the membrane, and therefore always experience curvature-induced forces towards regions of lower membrane curvature as indicated by the arrows. | |
In the present paper, we develop an analytical expression for the energy of the particle–vesicle system to leading order in the ratio of particle-to-vesicle size. This expression allows us to determine the binding energies and degree of engulfment for partially engulfed particles as well as the barrier heights for particles in the bistable regime. In particular, we find that the binding energy of a partially engulfed particle depends on the local, ‘unperturbed’ curvature of the vesicle in the absence of the particle. As a consequence, partially engulfed particles experience curvature-induced forces towards regions of lower membrane curvature if the particles get in contact with the outer leaflet of the vesicle membrane as in Fig. 1(a), or towards regions of higher membrane curvature if the particles get in contact with the inner leaflet of this membrane. In contrast, completely engulfed particles do not experience such curvature-induced forces.
The membrane curvature-sensing capability of nanoparticles is certainly of theoretical interest, and may be potentially useful in biomedical imaging or drug-delivery applications. However, nanoparticles with a chemically uniform surface are only partially engulfed if their size and adhesiveness are finely tuned with respect to the material properties and local curvature of the membrane.7,26 In order to overcome this limitation, we will also consider Janus particles with one strongly adhesive and one non-adhesive surface domain, see Fig. 1(b), which provides a much more robust method to explore curvature-induced forces. For such Janus particles, the membrane spreads only up to the domain boundaries between the two domains on the particle surface. As a consequence, these particles are always partially engulfed and, thus, subject to curvature-induced forces.
The paper is organized as follows. First, in Section 2 we describe the combined model for the membrane's curvature elasticity and the membrane–particle adhesion used throughout the paper, and briefly summarize the stability limits for free and completely engulfed particles as obtained in ref. 7. These stability limits are then used, in Section 3, to obtain conditions on the energy of the system close to free and completely engulfed states, in the general case of particles of any size. The small particle approximation is finally developed and verified against numerical calculations in Section 4. From this small particle approximation, in Section 5 we obtain the energy landscapes, binding energies, barrier heights, engulfment patterns and curvature-induced forces experienced by uniformly adhesive particles in contact with vesicles. Finally, in Section 6 we describe the curvature-induced forces experienced by Janus-like particles in contact with vesicles of complex shape.
2 Methods
2.1 Interplay of curvature elasticity and adhesion
The fate of a particle that comes into contact with a membrane is determined by the interplay between particle adhesion and membrane bending.6,7 According to the spontaneous curvature model,27,28 the bending energy of a membrane is given by 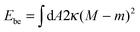 , where the integration runs over the whole surface of the membrane or vesicle. The mean curvature of the membrane is defined as M = (C1 + C2)/2, where C1 and C2 are the principal curvatures, and is taken to be positive or negative if the membrane bulges towards the exterior or interior compartment of the vesicle, respectively. Because we do not consider transformations that change the topology of the membrane, the contribution of the Gaussian curvature to the bending energy is constant and can be omitted. The elastic properties of the membrane are then described by its bending rigidity κ and its spontaneous curvature m. The attractive interaction with the particle is included via the adhesive energy Ead = −|W|Abo, where |W| is the absolute value of the adhesive energy per unit area and Abo the area of the membrane that is bound to the particle.29 The total energy of the system is then given by E = Ebe + Ead.
, where the integration runs over the whole surface of the membrane or vesicle. The mean curvature of the membrane is defined as M = (C1 + C2)/2, where C1 and C2 are the principal curvatures, and is taken to be positive or negative if the membrane bulges towards the exterior or interior compartment of the vesicle, respectively. Because we do not consider transformations that change the topology of the membrane, the contribution of the Gaussian curvature to the bending energy is constant and can be omitted. The elastic properties of the membrane are then described by its bending rigidity κ and its spontaneous curvature m. The attractive interaction with the particle is included via the adhesive energy Ead = −|W|Abo, where |W| is the absolute value of the adhesive energy per unit area and Abo the area of the membrane that is bound to the particle.29 The total energy of the system is then given by E = Ebe + Ead.
We will focus on the engulfment of rigid spherical particles with radius Rpa by a vesicle with fixed total membrane area A and enclosed volume V. Unless otherwise stated, we will consider the case of endocytic engulfment, for which the particles originate from the exterior solution outside the vesicle; the exocytic case of particles originating from the interior of the vesicle is treated in Appendix B. With the exception of Section 6, we will focus on chemically uniform particle surfaces that are characterized by a spatially independent adhesive strength |W|. In Section 6, we will consider Janus particles with two distinct surface domains, only one of which is adhesive.
2.2 Relevant parameters for the vesicle–particle system
The vesicle–particle system has a typical geometry as shown in Fig. 2. In order to minimize the free energy of the system, one can decompose the membrane into a bound and an unbound segment. The bound membrane segment (green) is in contact with the particle and extends up to the contact line, which may in principle have any shape. Irrespective of the latter shape, we can define the bound area fractionwhich is a measure for the degree of engulfment, varying from q = 0 for a free particle to q = 1 for a completely engulfed particle, and can be regarded as the reaction coordinate for the engulfment process. Intermediate q-values with 0 < q < 1 correspond to partially engulfed states. The total membrane area A is equal to the sum of the area Abo of the bound membrane segment and the area Aun of the unbound segment.
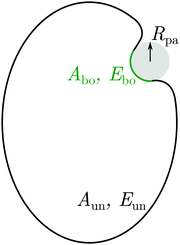 |
| | Fig. 2 Non-axisymmetric geometry of a spherical particle (grey) with radius Rpa adhering to a prolate vesicle. The total energy of the system can be separated into contributions Ebo and Eun from the bound (green) and unbound (black) membrane segments. The total membrane area is A = Abo + Aun. As a reaction coordinate for the engulfment process, we choose the area fraction q = Abo/4πRpa2 of the membrane-covered particle surface. | |
The total membrane area A defines the vesicle size
| | 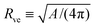 | (2) |
which will be used as the basic length scale. The equilibrium shape of a free vesicle with area
A and enclosed volume
V is then completely determined in terms of the rescaled spontaneous curvature
| | ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve ≡ mRve | (3) |
and the rescaled volume
| | 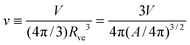 | (4) |
which varies from
v = 1 for a spherical vesicle to
v = 0 for a completely deflated vesicle. For given values of these two parameters, the equilibrium shape of an axisymmetric free vesicle can be directly obtained by the numerical shooting method developed in
ref. 28.
When the membrane is in contact with a chemically uniform nanoparticle of adhesive strength |W|, the deviation of the unbound membrane segment from the nanoparticle is governed by the contact mean curvature
| | 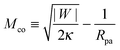 | (5) |
which increases both with increasing particle size
Rpa and increasing adhesive strength |
W|. The quantity
Mco corresponds to the equilibrium mean curvature of the unbound membrane segment along the contact line,
7 both for axisymmetric
29 and non-axisymmetric
30 contact lines. This curvature, which can be positive or negative, represents a material parameter that depends on the adhesive strength |
W| as determined by the membrane–particle interactions and, thus, by the surface chemistry of the particle, on the bending rigidity
κ which varies with the membrane composition, and on the particle size
Rpa. The expression
(5) applies to the endocytic case in which the particles originate from the exterior solution. The contact mean curvature for the exocytic case is given by
eqn (109) in Appendix B.
Note that relation (5) for the contact mean curvature can be rewritten in the form
| | 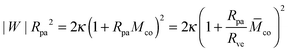 | (6) |
with the rescaled contact mean curvature
| | ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co ≡ McoRve, co ≡ McoRve, | (7) |
which will be useful in order to express the adhesion energy |
W|
Rpa2 in terms of the other parameters.
2.3 Energies of bound and unbound membrane segments
The total energy E of the vesicle–particle system can also be decomposed into the contributions of the bound and unbound membrane segments such that E = Ebo + Eun. The bound membrane segment follows the shape of the particle which implies that the energy Ebo of the bound segment is given by the expression| | | Ebo(q) = [8πκ(1 + mRpa)2 − 4π|W|Rpa2]q | (8) |
which is linear in the bound area fraction q. When we replace the term |W|Rpa2 in (8)via relation (6), the energy of the bound membrane segment becomes| | Ebo(q) = 8πκ[2(![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co) co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa + ( pa + (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 2 − 2 − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co2) co2)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2]q pa2]q | (9) |
with the rescaled particle radius| | ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve. pa ≡ Rpa/Rve. | (10) |
On the other hand, the unbound membrane segment contributes only the bending energy| | 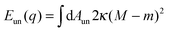 | (11) |
where the integral extends over the area Aun = A − Abo of the unbound segment. In order to obtain the shape of the unbound segment that minimizes Eun for a given value of the bound area fraction q, one typically has to perform a functional minimization of (11), which leads to the well-known Euler–Lagrange or shape equations for a free membrane.27 These have to be solved numerically, with appropriate boundary conditions ensuring a smooth matching with the bound membrane segment, as well as the conservation of the vesicle area and volume, as was done in ref. 7 for the special case of axisymmetric geometries. For the general case of non-axisymmetric geometries, the shape equations cannot be easily solved and one then has to perform time-consuming, direct energy minimization of triangulated membranes.25,31 However, we will see in the following sections that important information about Eun(q) at the boundary values q = 0 and q = 1 can be obtained analytically for the latter case as well.
2.4 Stability of free and completely engulfed particles
In recent work,7 we studied the engulfment of rigid, spherical particles by membranes with non-zero spontaneous curvature. Examination of our numerical results coupled to theoretical considerations led us to discover exact analytical conditions for the stability of free and completely engulfed particle states, corresponding to q = 0 and q = 1, respectively. These conditions involve the particle size, the adhesive strength, the membrane's bending rigidity and spontaneous curvature as well as two local curvatures of the membrane in contact with the particle.
The two stability conditions can be expressed in terms of the derivatives dE/dq of the total energy E(q) at the boundary values q = 0 and q = 1 of the bound area fraction q. The stability limit Lfr of the free particle state is given by
| | 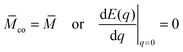 | (12) |
with
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
≡
MRve where
M is the mean curvature of the free membrane segment at the point of initial contact with the particle. The free particle state is stable for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co
co ≤
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
and unstable for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co
co >
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
.
Likewise, the stability limit Lce of the completely engulfed particle state has the form
| | 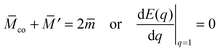 | (13) |
with
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
′ ≡
M′
Rve where
M′ is the mean curvature of the mother vesicle at the position of the narrow neck that connects the mother vesicle to the completely engulfed particle. The completely engulfed state is stable for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co
co +
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
′ ≥ 2
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
and unstable for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co
co +
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
′ < 2
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
.
It is important to note that the curvatures that enter in (12) and (13) have a different character: the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co represents a material parameter, as explained after (5), whereas the mean curvatures
co represents a material parameter, as explained after (5), whereas the mean curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and
and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ represent geometric quantities related to the shape of the vesicle membrane. Because the contact mean curvature
′ represent geometric quantities related to the shape of the vesicle membrane. Because the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co increases both with particle size and adhesive strength, the stability limits (12) and (13) reflect the fact that small or weakly adhesive particles will tend to remain free, whereas larger or more adhesive particles tend to be completely engulfed.
co increases both with particle size and adhesive strength, the stability limits (12) and (13) reflect the fact that small or weakly adhesive particles will tend to remain free, whereas larger or more adhesive particles tend to be completely engulfed.
If the vesicle–particle system is axially symmetric, the contact line is a circle and one may use the wrapping angle ϕ as the reaction coordinate which varies from ϕ = 0 to ϕ = π. The bound area fraction q is then given by 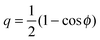 and the stability limits (12) and (13) are then equivalent to d2E/dϕ2|ϕ=0 = 0 and d2E/dϕ2|ϕ=π = 0 as used in ref. 7.
and the stability limits (12) and (13) are then equivalent to d2E/dϕ2|ϕ=0 = 0 and d2E/dϕ2|ϕ=π = 0 as used in ref. 7.
When a membrane segment comes into contact with a spherical particle of radius Rpa, its mean curvature M must satisfy the inequality M > −1/Rpa in order to avoid intersections between the membrane segment and the particle surface. Likewise, when we consider a completely engulfed particle, the mean curvature M′ of the mother vesicle at the neck must fulfill the inequality M′ < 1/Rpa in order to avoid intersections between the membrane of the mother membrane and the particle surface.
3 Energy of the unbound membrane segment
We will now show how the stability limits (12) and (13) lead to expressions for the derivatives of the energy Eun(q) at the boundaries of the energy landscape as defined by the bound area fractions q = 0 and q = 1. Using expression (9) for the energy Ebo of the bound membrane segment, the derivative of the total energy E = Ebo + Eun becomes| | 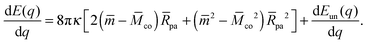 | (14) |
According to stability relations (12) and (13), the first derivative dE(q)/dq vanishes at the boundary values q = 0 and q = 1 which allows us to express the corresponding derivatives dEun(q)/dq in terms of the other parameters. Furthermore, using the alternative form of stability relations (12) and (13), we can express the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co in terms of the other curvatures which leads to
co in terms of the other curvatures which leads to| | 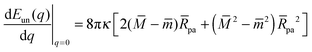 | (15) |
and| | 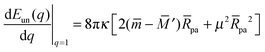 | (16) |
with These two expressions for the first derivatives of Eun(q) at q = 0 and q = 1 are direct consequences of the stability relations and involve no additional approximations. Furthermore, the actual values of the energy of the unbound segment at the boundaries q = 0 and q = 1 can be directly related to the bending energy of free vesicles. Indeed, the case q = 0 trivially corresponds to the free vesicle, and thereforewhere Efr is simply the energy of the free vesicle with total membrane area A, enclosed volume V, and spontaneous curvature m. As mentioned before, in our continuum approach the completely engulfed state represents a limit shape with an ideal neck which costs no energy.28,32,33 The energy of the unbound membrane segment of the mother vesicle after complete engulfment can therefore be calculated aswhere Efr′ is now the energy of an ‘effective’ free vesicle representing the mother vesicle, with total membrane area A − 4πRpa2, enclosed volume V + 4πRpa3/3, and spontaneous curvature m.
4 Particle size small compared to the vesicle size
We will now focus on the case of particles that are much smaller than the vesicle and use the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve as an expansion parameter. In the following sections, we will expand the energies of the membrane–particle system up to first order in
pa ≡ Rpa/Rve as an expansion parameter. In the following sections, we will expand the energies of the membrane–particle system up to first order in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa.
pa.
We will also restrict ourselves to the case of small spontaneous curvatures, which are of the order of the inverse vesicle size, i.e., m ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In the absence of large spontaneous curvatures, the mean curvature at any point of a free vesicle will also be of the order of the inverse vesicle size, and we can therefore always take M ∼
(1). In the absence of large spontaneous curvatures, the mean curvature at any point of a free vesicle will also be of the order of the inverse vesicle size, and we can therefore always take M ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In addition, we will be interested in the behavior of the system in the proximity of the stability limits (12) and (13), which implies that the contact mean curvature is also of the order of the inverse vesicle size, Mco ∼
(1). In addition, we will be interested in the behavior of the system in the proximity of the stability limits (12) and (13), which implies that the contact mean curvature is also of the order of the inverse vesicle size, Mco ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co ∼
co ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In this limit, the energy (9) of the bound membrane segment can be rewritten as
(1). In this limit, the energy (9) of the bound membrane segment can be rewritten as
| | Ebo(q) = 16πκ(![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co) co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paq + paq + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ (κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). pa2). | (20) |
As described in Appendix A, it is not difficult to show that, under the conditions described in the previous paragraph, the difference between the energy Efr of the free vesicle before engulfment and the energy Efr′ of the mother vesicle after complete engulfment is of second order in the particle size, i.e.,
| | Efr′ = Efr + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ (κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). pa2). | (21) |
Likewise, the difference between the mean curvature of the membrane segment in contact with the particle before and after complete engulfment at any given point on the vesicle surface is also of second order in
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa, with
We can now expand
eqn (15)–(19) up to first order in the particle size, which leads to
| | Eun(q = 1) = Efr + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ (κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2) pa2) | (24) |
| | 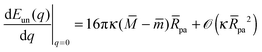 | (25) |
and
| | 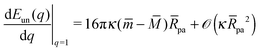 | (26) |
where the asymptotic equality
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
′ ≈
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
has been used in the last equation. Therefore, to first order in the rescaled particle size
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa =
Rpa/
Rve, the properties of the energy function
Eun(
q) at the boundaries depend only on those of the free vesicle before engulfment, namely on the quantities
Efr and
M. In addition,
Eun(
q) attains a particularly symmetric form in the limit of small
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa, with
Eun(0) ≈
Eun(1) and
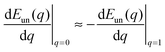
. It is important to note that the derivation of relations
(15)–(19) and (23)–(26) did not involve any assumptions concerning the symmetry of the particle–vesicle geometry. In particular, the use of the bound area fraction
q as a reaction coordinate makes no assumption about the particular shape of the contact line between the particle and the membrane.
The simplest functional form of the energy Eun(q) that satisfies all four asymptotic equalities (23)–(26) is provided by a parabola with an extremum at q = 1/2, as given by
| | Eun(q) = Efr + 16πκ(![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) − − ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ) )![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paq(1 − q) + paq(1 − q) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ (κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). pa2). | (27) |
We have compared this analytical interpolation formula with full numerical calculations for a variety of axisymmetric vesicle shapes that differed in the rescaled volume
v, spontaneous curvature
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
, and local mean curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
at the poles, see
Fig. 3. For each of these shapes, we considered a particle at one of the poles and varied the location of the contact line and, thus, the bound area fraction
q, imposing the condition that the unbound and bound membrane segments join smoothly along the contact line.
33 In all cases studied, the analytical expression
(27) was confirmed by the numerical results to first order in the particle-to-vesicle size,
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa ≡
Rpa/
Rve, see
Fig. 3. In
Fig. 3(a), we show how the full numerical results (colored solid lines) approach the first-order term in
(27) as we reduce the relative particle size and, thus, higher order correction terms ∼
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2
pa2. These higher order corrections depend on the global geometry of the vesicle, as given by its rescaled volume
v and the particular branch of solutions (prolate, oblate,
etc.) to which the vesicle shape belongs, whereas the first order term depends only on the local curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
as demonstrated in
Fig. 3(b).
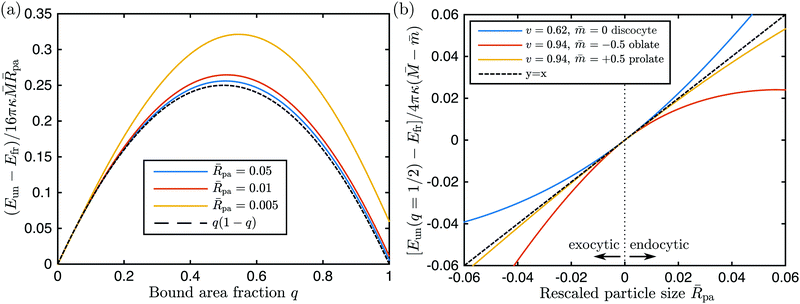 |
| | Fig. 3 (a) Numerically calculated energies of the unbound segment as a function of bound area fraction q, for the endocytic engulfment of a particle at the pole of a discocyte vesicle with rescaled volume v = 0.62 and no spontaneous curvature, for three different values of the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve, see the inset. The rescaling of the energy follows the analytical expression (27) with pa ≡ Rpa/Rve, see the inset. The rescaling of the energy follows the analytical expression (27) with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1.063. As the relative particle size becomes smaller, the numerical curves approach the black dashed line q(1 − q) as described by (27); and (b) numerically calculated energies of the unbound segment at q = 1/2 as a function of the rescaled particle size = −1.063. As the relative particle size becomes smaller, the numerical curves approach the black dashed line q(1 − q) as described by (27); and (b) numerically calculated energies of the unbound segment at q = 1/2 as a function of the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa for the discocyte in (a) and two other vesicle shapes with the rescaled volume v, and spontaneous curvature pa for the discocyte in (a) and two other vesicle shapes with the rescaled volume v, and spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as given in the inset. At their poles, the oblate and the prolate shapes have mean curvatures as given in the inset. At their poles, the oblate and the prolate shapes have mean curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0.263 and 1.530, respectively. Negative values of the rescaled particle size correspond to exocytic engulfment; see Appendix B. At = 0.263 and 1.530, respectively. Negative values of the rescaled particle size correspond to exocytic engulfment; see Appendix B. At ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = 0 all three curves have a common tangent (black dashed line) corresponding to the first-order term in eqn (28). pa = 0 all three curves have a common tangent (black dashed line) corresponding to the first-order term in eqn (28). | |
The evolution of the energy of the unbound segment as a function of the bound area fraction is strongly dependent on the sign of the difference ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) between the mean curvature of the membrane at the contact point and the spontaneous curvature. Indeed, it follows from (27) that the energy of the unbound segment at q = 1/2 has the value
between the mean curvature of the membrane at the contact point and the spontaneous curvature. Indeed, it follows from (27) that the energy of the unbound segment at q = 1/2 has the value
| | 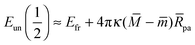 | (28) |
corresponding to an energy maximum for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
>
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
but to an energy minimum for
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
<
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
. Whenever
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
=
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
, the energy of the unbound membrane segment is independent of
q up to first order in the particle size. The particular case
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
=
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
= 0 is consistent with the known results for particles interacting with tensionless planar membranes with no spontaneous curvature,
15 in which case the unbound segment forms a catenoidal shape with
Eun(
q) ≡ 0.
In the small particle limit with M′ ≈ M, the two non-intersection constraints mentioned above can be combined into
| | 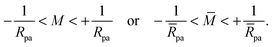 | (29) |
Because the small particle limit considered here implies that
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa ≪ 1, whereas
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
∼
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1), the inequalities in
(29) are automatically fulfilled in this limit and the resulting constraints on
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
do not play any role in the following calculations.
5 Results for uniform particle surfaces
5.1 Local energy landscapes
In the following sections, we will focus on the first order terms proportional to ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, corresponding to small particle-to-vesicle size ratios, and we will ignore higher-order terms
pa, corresponding to small particle-to-vesicle size ratios, and we will ignore higher-order terms ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). Combining expressions (20) and (27) for the energies of the bound and unbound membrane segments, we obtain an analytical expression for the local energy landscape of engulfment as defined bythat has the explicit form
pa2). Combining expressions (20) and (27) for the energies of the bound and unbound membrane segments, we obtain an analytical expression for the local energy landscape of engulfment as defined bythat has the explicit form| | | ΔE(q) = 16πκRpa[(m − Mco)q + (M − m)q(1 − q)] | (31) |
or| | | ΔE(q) = 16πκRpa[(M − Mco)q + (m − M)q2]. | (32) |
The latter expressions are indeed purely local in the sense that they depend only on the mean curvature M of the mother vesicle at the attachment point, and not on the overall shape of the vesicle. In addition to M, the local energy landscape also depends on the contact mean curvature Mco and on the spontaneous curvature m. In the following sections, we will consider particles with a certain radius Rpa exposed to complex-shaped vesicles. Both the contact mean curvature and the spontaneous curvature are then material parameters with fixed values, whereas the mean curvature M varies along the vesicle membrane.
Even though the local energy landscape ΔE(q) as given by eqn (32) is a simple quadratic function of q, this landscape describes a large variety of different cases depending on the relative magnitude of the three curvatures Mco, m, and M. In order to discuss these different cases in a transparent manner, it will be useful to first consider the extrema of ΔE(q) within the physically meaningful interval 0 ≤ q ≤ 1 and to introduce some notation for specific q-values.
The quadratic q-dependence of expression (32) implies that the energy can have at most one extremum in the physically meaningful q-interval with 0 ≤ q ≤ 1. Indeed, the condition 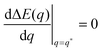 leads to only one solution as given by
leads to only one solution as given by
| | 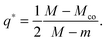 | (33) |
which may or may not lie within the physically meaningful interval 0 ≤
q ≤ 1. The extremum is located at the lower boundary value
| | | q* = qfr ≡ 0 for M = Mco, | (34) |
corresponding to the free particle state, and at the upper boundary value
| | | q* = qce ≡ 1 for M = 2m − Mco, | (35) |
corresponding to the completely engulfed state. Furthermore, the extremum at
q =
q* represents the minimum of a non-inverted parabola for
M <
m and the maximum of an inverted parabola for
m <
M. In order to distinguish these two cases, we will use the notation
and
| | | qmax* ≡ q* for m < M. | (37) |
For the boundary case
m =
M, local energy landscape
(32) becomes linear in
q and does not exhibit any extremum. It is useful to note that the
M-dependence of
q* as given by
(33) stems from the particle-induced energy change of the unbound membrane segment as described by
(27).
The equilibrium state of the particle is provided by the state of minimal energy with bound area fraction q = qeq. Because the physically meaningful q-values must lie within the interval 0 ≤ q ≤ 1, the equilibrium state is provided by a boundary minimum at q = 0 or q = 1 whenever q*<0 or q* > 1. Thus, the equilibrium value of the bound area fraction is given by
corresponding to the free particle state for two different cases: for a non-inverted parabola with
M <
m and
qmin* < 0 as well as for an inverted parabola with
m <
M and
qmax* > 1. Likewise, we have
corresponding to the completely engulfed state for a non-inverted parabola with
M <
m and
qmin* > 1 as well as for an inverted parabola with
m <
M and
qmax* < 0. Furthermore, the equilibrium state corresponds to the bound area fraction
| | | qeq = qmin* with 0 < qmin* < 1, | (40) |
corresponding to a partially engulfed state. Finally, if the local energy landscape exhibits a maximum in the physically meaningful
q-interval, we have two boundary minima at
q =
qfr = 0 and
q =
qce = 1 which are separated by an energy barrier at
| | | qba = qmax* with 0 < qmax* < 1. | (41) |
In the latter case, the two boundary minima have the energies Δ
E(
q = 0) = 0 and
| | | ΔE(q = 1) = 16πκRpa(m − Mco) | (42) |
as follows from
eqn (32) which implies Δ
E(0) < Δ
E(1) for
Mco <
m and Δ
E(1) < Δ
E(0) for
m <
Mco. Therefore, the equilibrium state is provided by the free state with bound area fraction
| | | qeq = qfr = 0 for Mco < m and 0 < qmax* < 1 | (43) |
and by the completely engulfed state with
| | | qeq = qce = 1 for m < Mco and 0 < qmax* < 1. | (44) |
The different cases are illustrated in
Fig. 4 where we plot the rescaled energy landscapes
| | 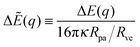 | (45) |
which have the dimensionless form
| | ΔẼ(q) = (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co)q + ( co)q + (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) )q2. )q2. | (46) |
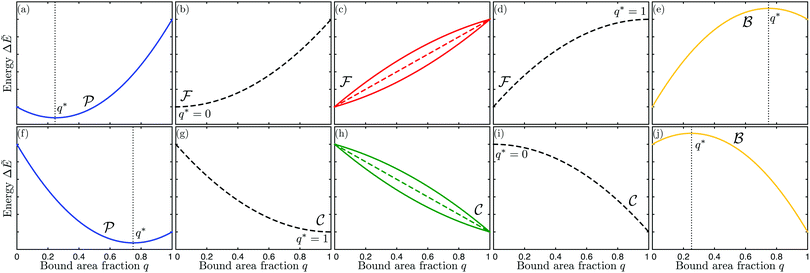 |
| | Fig. 4 Functional dependence of the local energy landscape ΔẼ on the bound area fraction q with 0 ≤ q ≤ 1, as described by eqn (46) for different values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the contact mean curvature , the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co, and the local mean curvature co, and the local mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) of the vesicle membrane. The upper panels (a–e) correspond to of the vesicle membrane. The upper panels (a–e) correspond to ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < co < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the lower panels (f–j) to , the lower panels (f–j) to ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) < < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co. In both rows of panels, the local mean curvature co. In both rows of panels, the local mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) increases from left to right and the dashed energy functions represent marginal or degenerate cases: (a and f) landscapes for partially engulfed particles with a minimum at qeq = qmin* and 0 < qmin* < 1. The landscape in (a) illustrates the case with increases from left to right and the dashed energy functions represent marginal or degenerate cases: (a and f) landscapes for partially engulfed particles with a minimum at qeq = qmin* and 0 < qmin* < 1. The landscape in (a) illustrates the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < 2 co < 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co and the one in (f) the case with co and the one in (f) the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 2 < 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < Mco; (b–d) landscapes for free or non-engulfed particles with a boundary minimum at qeq = 0. These landscapes are obtained for (b) co < Mco; (b–d) landscapes for free or non-engulfed particles with a boundary minimum at qeq = 0. These landscapes are obtained for (b) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co which defines the stability limit of the free state as described by eqn (12); (c) co which defines the stability limit of the free state as described by eqn (12); (c) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < co < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 2 < 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co; and (d) co; and (d) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2 = 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co corresponding to the stability limit of the completely engulfed state as in eqn (13) with co corresponding to the stability limit of the completely engulfed state as in eqn (13) with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ ≈ ′ ≈ ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) . The linear landscape in (c) represents the degenerate case with . The linear landscape in (c) represents the degenerate case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ; (g–i) landscapes for completely engulfed particles with a boundary minimum at qeq = 1. These landscapes are obtained for (g) ; (g–i) landscapes for completely engulfed particles with a boundary minimum at qeq = 1. These landscapes are obtained for (g) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2 = 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co corresponding to the stability limit of the completely engulfed state, (h) 2 co corresponding to the stability limit of the completely engulfed state, (h) 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < co < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co, and (i) co, and (i) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co which defines the stability limit of the free state. The linear landscape in (h) again represents the degenerate case with co which defines the stability limit of the free state. The linear landscape in (h) again represents the degenerate case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ; (e and j) landscapes for bistable engulfment with an energy barrier at qba = qmax* that is located between the two boundary minima at q = 0 and q = 1. The landscape in (e) illustrates the case with ; (e and j) landscapes for bistable engulfment with an energy barrier at qba = qmax* that is located between the two boundary minima at q = 0 and q = 1. The landscape in (e) illustrates the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 2 > 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co > co > ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co and the one in (j) the case with co and the one in (j) the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > > ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co > 2 co > 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co. In all cases, ΔE(q = 0) = 0 by definition. co. In all cases, ΔE(q = 0) = 0 by definition. | |
5.2 Stability and engulfment regimes
Up to first order in the particle-to-vesicle size ratio ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, the stability limits Lfr and Lce of the free and completely engulfed state as given by (12) and (13) can be written as M = Mco and M = 2m − Mco, respectively, because
pa, the stability limits Lfr and Lce of the free and completely engulfed state as given by (12) and (13) can be written as M = Mco and M = 2m − Mco, respectively, because ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ =
′ = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) +
+ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). These stability limits can be directly recovered from expression (33) by imposing q* = qfr = 0 and q* = qce = 1, see relations (34) and (35). In general, expression (31) for the local energy landscape ΔE(q) leads to four qualitatively distinct landscapes corresponding to four distinct stability or engulfment regimes which are separated by the stability limits Lfr and Lce:
pa2). These stability limits can be directly recovered from expression (33) by imposing q* = qfr = 0 and q* = qce = 1, see relations (34) and (35). In general, expression (31) for the local energy landscape ΔE(q) leads to four qualitatively distinct landscapes corresponding to four distinct stability or engulfment regimes which are separated by the stability limits Lfr and Lce:
(i) Free or non-engulfment regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st in which the free state at q = qfr = 0 is stable and the completely engulfed state at q = qce = 1 is unstable. The function ΔE(q) as given by eqn (32) must then increase monotonically with increasing q within the physically meaningful interval 0 < q < 1. This monotonic q-dependence applies both to a parabola with its minimum at q = qmin* ≤ 0, which is obtained for Mco ≤ M < m, and for an inverted parabola with its maximum at q = qmax* ≥ 1 as obtained for m < M ≤ 2m − Mco. These two curvature inequalities can be combined into the condition
st in which the free state at q = qfr = 0 is stable and the completely engulfed state at q = qce = 1 is unstable. The function ΔE(q) as given by eqn (32) must then increase monotonically with increasing q within the physically meaningful interval 0 < q < 1. This monotonic q-dependence applies both to a parabola with its minimum at q = qmin* ≤ 0, which is obtained for Mco ≤ M < m, and for an inverted parabola with its maximum at q = qmax* ≥ 1 as obtained for m < M ≤ 2m − Mco. These two curvature inequalities can be combined into the condition
| | Mco ≤ M ≤ 2m − Mco (![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments) -segments) | (47) |
for the mean curvature
M, including the case
M =
m for which the local energy landscape Δ
E(
q) is linear in
q. It is useful to rearrange the two inequalities for the local mean curvature
M as given by
eqn (47) in order to obtain the upper bounds
| | Mco ≤ min(M,2m − M) (![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments). -segments). | (48) |
for the contact mean curvature
Mco.
Examples of the energy landscapes of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments are displayed in Fig. 4(b)–(d). The inequalities in (47) imply that a free or non-engulfment regime is only present if Mco < m, i.e., if the spontaneous curvature m exceeds the contact mean curvature Mco. For the special case Mco = m, the M-interval in eqn (47) collapses to the single value M = m = Mco, corresponding to the degenerate energy landscape ΔE(q) = 0 for all values of q.
-segments are displayed in Fig. 4(b)–(d). The inequalities in (47) imply that a free or non-engulfment regime is only present if Mco < m, i.e., if the spontaneous curvature m exceeds the contact mean curvature Mco. For the special case Mco = m, the M-interval in eqn (47) collapses to the single value M = m = Mco, corresponding to the degenerate energy landscape ΔE(q) = 0 for all values of q.
(ii) Complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st in which the completely engulfed state at q = qce = 1 is stable, whereas the free state at q = qfr = 0 is unstable. In this case, the function ΔE(q) in (32) must decrease monotonically with increasing q within the whole interval 0 < q < 1. The latter q-dependence applies both to an inverted parabola with its maximum at q = qmax* ≤ 0, which is obtained for m < M ≤ Mco, and to a parabola with its minimum at q = qmin* ≥ 1 as obtained for 2m − Mco ≤ M < m. The two curvature inequalities can be combined into the condition
st in which the completely engulfed state at q = qce = 1 is stable, whereas the free state at q = qfr = 0 is unstable. In this case, the function ΔE(q) in (32) must decrease monotonically with increasing q within the whole interval 0 < q < 1. The latter q-dependence applies both to an inverted parabola with its maximum at q = qmax* ≤ 0, which is obtained for m < M ≤ Mco, and to a parabola with its minimum at q = qmin* ≥ 1 as obtained for 2m − Mco ≤ M < m. The two curvature inequalities can be combined into the condition
| | 2m − Mco ≤ M ≤ Mco (![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments) -segments) | (49) |
for the mean curvature
M, including again the case
M =
m for which the local energy landscape Δ
E(
q) is linear in
q. A rearrangement of the inequalities in
eqn (49) leads to the lower bounds
| | Mco ≥ max(M, 2m − M) (![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments) -segments) | (50) |
for the contact mean curvature
Mco.
Examples of the energy landscapes of ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments are displayed in Fig. 4(g)–(i). The inequalities in (49) imply that a complete engulfment regime is only present for 2m − Mco < Mco, i.e., when the contact mean curvature Mco exceeds the spontaneous curvature m. For the special case m = Mco, the M-interval in eqn (49) collapses to the single value M = Mco = m corresponding again to the degenerate energy landscape ΔE(q) = 0 for all values of q.
-segments are displayed in Fig. 4(g)–(i). The inequalities in (49) imply that a complete engulfment regime is only present for 2m − Mco < Mco, i.e., when the contact mean curvature Mco exceeds the spontaneous curvature m. For the special case m = Mco, the M-interval in eqn (49) collapses to the single value M = Mco = m corresponding again to the degenerate energy landscape ΔE(q) = 0 for all values of q.
(iii) Bistable engulfment regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are locally stable and separated by an intermediate energy barrier at q = qba = qmax*. Now, the function ΔE(q) in eqn (32) represents an inverted parabola with its maximum located within the interval 0 < qmax* < 1. The parabola is inverted for M > m which implies that the inequalities qmax* > 0 and qmax* < 1 are equivalent to M > Mco and Mco > 2m − M, respectively. Therefore, a membrane segment with mean curvature M belongs to the bistable engulfment regime provided
st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are locally stable and separated by an intermediate energy barrier at q = qba = qmax*. Now, the function ΔE(q) in eqn (32) represents an inverted parabola with its maximum located within the interval 0 < qmax* < 1. The parabola is inverted for M > m which implies that the inequalities qmax* > 0 and qmax* < 1 are equivalent to M > Mco and Mco > 2m − M, respectively. Therefore, a membrane segment with mean curvature M belongs to the bistable engulfment regime provided
| | M > max(Mco,2m − Mco) (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments), -segments), | (51) |
which applies to both
Fig. 4(e) and (j). The lower bounds for the local mean curvature
M as provided by
eqn (51) are equivalent to the inequalities
| | 2m − M < Mco < M (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments) -segments) | (52) |
for the contact mean curvature
Mco; and
(iv) Partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are unstable and the parabolic function ΔE(q) in eqn (32) has its minimum located within the interval 0 < qmin* < 1. Because a (non-inverted) parabola corresponds to M < m, the inequalities qmin* > 0 and qmin* < 1 are equivalent to M < Mco and Mco < 2m − M, respectively. As a consequence, the particles are partially engulfed by a membrane segment with mean curvature M provided
st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are unstable and the parabolic function ΔE(q) in eqn (32) has its minimum located within the interval 0 < qmin* < 1. Because a (non-inverted) parabola corresponds to M < m, the inequalities qmin* > 0 and qmin* < 1 are equivalent to M < Mco and Mco < 2m − M, respectively. As a consequence, the particles are partially engulfed by a membrane segment with mean curvature M provided
| | M < min(Mco,2m − Mco) ≤ m (![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments), -segments), | (53) |
which applies to both
Fig. 4(a) and (f) and implies
M <
m because
m is the midpoint between
Mco and 2
m −
Mco. The upper bounds
(53) for the local mean curvature
M are equivalent to the inequalities
| | M < Mco < 2m − M (![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments) -segments) | (54) |
for the contact mean curvature
Mco.
When we specify the above curvature inequalities to the case of vanishing spontaneous curvature, m = 0, we conclude that concave membrane segments with M < −|Mco| belong to the partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st, whereas convex segments with M > +|Mco| represent
st, whereas convex segments with M > +|Mco| represent ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments and exhibit bistable engulfment behavior.
-segments and exhibit bistable engulfment behavior.
The four engulfment regimes just described are visualized in Fig. 5. The upper panel displays these regimes within the (Mco,m)-plane for a fixed value of the local mean curvature M. The lower panel of Fig. 5 depicts the four regimes within the (M,m)-plane for a fixed value of the contact mean curvature Mco. As previously mentioned, the local mean curvature M varies along the surface of a complex-shaped vesicle, whereas the spontaneous curvature m and the contact mean curvature Mco represent material parameters (for fixed particle size Rpa).
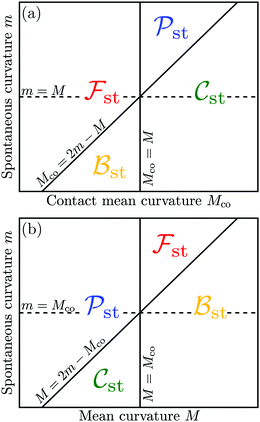 |
| | Fig. 5 (a) Dependence of the free engulfment regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st, complete engulfment regime st, complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st, bistable engulfment regime st, bistable engulfment regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st, and partial engulfment regime st, and partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st on the contact mean curvature Mco and the spontaneous curvature m, for a fixed value of the local mean curvature M; and (b) dependence of the same engulfment regimes on M and m, for a fixed value of Mco. The engulfment diagram in (a) corresponds to inequalities (48), (50), (52) and (54) and the diagram in (b) to relations (47), (49), (51) and (53). st on the contact mean curvature Mco and the spontaneous curvature m, for a fixed value of the local mean curvature M; and (b) dependence of the same engulfment regimes on M and m, for a fixed value of Mco. The engulfment diagram in (a) corresponds to inequalities (48), (50), (52) and (54) and the diagram in (b) to relations (47), (49), (51) and (53). | |
The four stability and engulfment regimes ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st,
st, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st,
st, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st, and
st, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st have been previously derived in ref. 7 and 26, but this derivation was based on the numerical observation that, for particles much smaller than the vesicle, partially engulfed states are only stable if both free and completely engulfed states are unstable. Now, we see that this latter condition is a direct consequence of the energy landscape (32) as obtained to first order in the rescaled particle size
st have been previously derived in ref. 7 and 26, but this derivation was based on the numerical observation that, for particles much smaller than the vesicle, partially engulfed states are only stable if both free and completely engulfed states are unstable. Now, we see that this latter condition is a direct consequence of the energy landscape (32) as obtained to first order in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = Rpa/Rve.
pa = Rpa/Rve.
On the other hand, as we increase the magnitude of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, deviations from the simple parabolic energy landscape become more and more apparent. In particular, numerical results show that new stability regimes appear, in which stable free and completely engulfed states can coexist with stable ‘satellite’ minima, corresponding to partially engulfed states with very low or very high bound area fraction, q ≳ 0 or q ≲ 1. It is now clear that these deviations are a consequence of higher order terms in the rescaled particle size
pa, deviations from the simple parabolic energy landscape become more and more apparent. In particular, numerical results show that new stability regimes appear, in which stable free and completely engulfed states can coexist with stable ‘satellite’ minima, corresponding to partially engulfed states with very low or very high bound area fraction, q ≳ 0 or q ≲ 1. It is now clear that these deviations are a consequence of higher order terms in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, which are expected to depend on the overall shape of the vesicle as well.
pa, which are expected to depend on the overall shape of the vesicle as well.
5.3 Binding energies and barrier heights
For partial engulfment, the energy landscape has a minimum at q* = qmin* with 0 < qmin* < 1 as shown in Fig. 4(a) and (f), corresponding to the curvature inequalities M < Mco < 2m − Mco and M < 2m − Mco < Mco, respectively. The binding energy of the partially engulfed particles is obtained by inserting expression (33) for the location q* = qmin* of the energy minimum back into the energy landscape (31). As a result, we find the binding energy| | 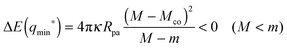 | (55) |
within the partial engulfment regime. For the special case Mco = m, the free and the completely engulfed states have the same energy, ΔE(q = 1) = ΔE(q = 0) = 0 and 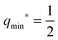 as follows from eqn (32) and (33). In the latter situation, the binding energy attains the particularly simple form
as follows from eqn (32) and (33). In the latter situation, the binding energy attains the particularly simple form| | 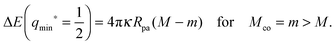 | (56) |
It is useful to note that the M-dependence of the binding energy ΔE(qmin*) in (55) and (56) arises from the M-dependence of the bound area fraction qmin* as given by (33) and, thus, from the particle-induced energy change of the unbound membrane segment as in (27).
For bistable engulfment, the energy landscape has a maximum at q* = qmax* with 0 < qmax* < 1, as shown in Fig. 4(e) and (j), corresponding to the curvature inequalities M > 2m − Mco > Mco and M > Mco > 2m − Mco, respectively. By inserting eqn (33) with q* = qmax* into eqn (31), we obtain the energy barrier height
| | 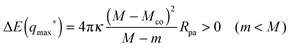 | (57) |
within the bistable engulfment regime. The condition Δ
E(
q = 1) = Δ
E(
q = 0) = 0 which is equivalent to
Mco =
m or
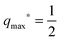
, now defines the transition line at which the free state coexists with the completely engulfed state. Along this transition line, the barrier height has the simple form
| | 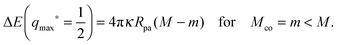 | (58) |
It follows from relationships
(56) and (58) that the magnitude
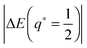
of the typical binding energy or barrier height is proportional to the particle size
Rpa and, thus, decreases with decreasing particle size. This dependence is important because the binding energies and barriers heights obtained here are only relevant as long as their magnitude is large compared to the thermal energy. For lipid bilayers with a negligible spontaneous curvature and a typical bending rigidity
κ = 20
kBT, we have |Δ
E(
q* = 1/2)| >
kBT as long as |
M|
Rpa >
kBT/4π
κ ≃ 1/250 with the segment curvature |
M| of the order of the inverse vesicle size 1/
Rve. As a consequence, if the particle size
Rpa is smaller than about
Rve/250, the binding energies and energy barriers will be ‘blurred out’ by thermal fluctuations.
5.4 Engulfment patterns
In ref. 26, we showed how the dependence of the engulfment behavior on the local curvature of the membrane leads to the formation of engulfment patterns when a complex-shaped vesicle is exposed to many particles. If a vesicle has non-uniform curvature, that is, if the value of M varies along the surface of the vesicle, the vesicle surface may be divided into ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -,
-, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - or
- or ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments according to the local membrane curvature, depending on whether a particle coming into contact with the membrane at that point belongs to the free or non-engulfment regime
-segments according to the local membrane curvature, depending on whether a particle coming into contact with the membrane at that point belongs to the free or non-engulfment regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st, the complete engulfment regime
st, the complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st, the bistable regime
st, the bistable regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st or the partial engulfment regime
st or the partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st.
st.
One example of an engulfment pattern is shown in Fig. 6, corresponding to a discocyte vesicle which is both axially symmetric and up-down symmetric. Inspection of this figure shows that the corresponding engulfment pattern consists of two ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments around the north and south poles, a
-segments around the north and south poles, a ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment or -belt around the equator, and two
-segment or -belt around the equator, and two ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments or -rings which connect the
-segments or -rings which connect the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments with the
-segments with the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -belt.
-belt.
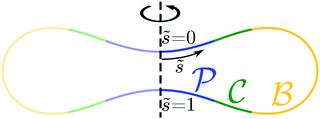 |
| | Fig. 6 Engulfment pattern on a discocyte vesicle with rescaled volume v = 0.62 and zero spontaneous curvature, m = 0, when exposed to small particles with contact mean curvature Mco = 1/(2Rve). The axisymmetric vesicle displays two partially engulfed ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments (blue) around the north and south poles, two completely engulfed -segments (blue) around the north and south poles, two completely engulfed ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments (green), and one bistable -segments (green), and one bistable ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment (yellow) which forms a belt around the equator of the vesicle. -segment (yellow) which forms a belt around the equator of the vesicle. | |
The shape of any axisymmetric vesicle can be parametrized by the arc length s of the shape contour.28 For the discocyte vesicle shape in Fig. 6, the arc length varies from s = 0 at the north pole to s = L = 2.90Rve at the south pole. In order to eliminate one parameter, we now define the rescaled arc length
| | ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ≡ s/L = s/(2.90Rve) ≡ s/L = s/(2.90Rve) | (59) |
and use this variable to describe the position of a particle along the vesicle surface. The
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
-segment around the north pole is now described by 0 ≤
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
<
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1
1 = 0.15, the adjacent
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
-segment by
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1
1 <
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
<
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2
2 = 0.26, the
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
-belt by
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2
2 <
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
<
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3
3 = 0.74, the lower
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
-segment by
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3
3 <
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
<
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4
4 = 0.85, and the
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
-segment around the south pole by
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4
4 <
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
≤ 1. Because of the up-down symmetry of the discocyte shape, the boundary values of the rescaled arc length
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
satisfy the relations
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4
4 = 1 −
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1
1 and
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3
3 = 1 −
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2
2.
The vesicle in Fig. 6 has the rescaled volume v = 0.62 and zero spontaneous curvature, m = 0, and the membrane–particle adhesion is characterized by the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = 1/2. Because
co = 1/2. Because ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co >
co > ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0, the general classification described in Section 5.2 implies that such a vesicle does not exhibit any
= 0, the general classification described in Section 5.2 implies that such a vesicle does not exhibit any ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments and that the rescaled mean curvature
-segments and that the rescaled mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve satisfies
= MRve satisfies
| | ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < − < −![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = −1/2 for the two co = −1/2 for the two ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments, -segments, | (60) |
| | −1/2 < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 1/2 for < 1/2 for ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments, -segments, | (61) |
and
| | 1/2 < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) for for ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments. -segments. | (62) |
Thus, the boundaries between the
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
- and the
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
-segments, which are located at
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1
1 and
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4
4, are characterized by the mean curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
= −1/2. Likewise, the boundaries between the
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
-segments and the
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
-belt have mean curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
= +1/2, see
Fig. 7(a).
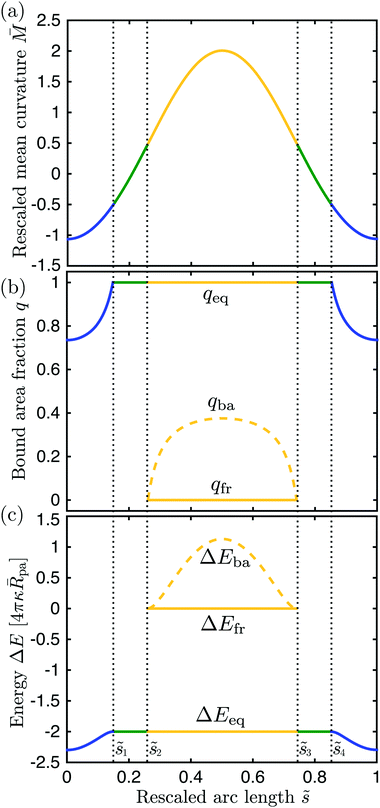 |
| | Fig. 7 Different quantities that determine the engulfment pattern of the discocyte shape in Fig. 6 as a function of the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) : (a) rescaled mean curvature : (a) rescaled mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) of the vesicle membrane, (b) bound area fraction qeq, and (c) global energy landscape ΔEeq = ΔE(qeq). The latter two quantities correspond to the equilibrium state of a particle in contact with the vesicle membrane at of the vesicle membrane, (b) bound area fraction qeq, and (c) global energy landscape ΔEeq = ΔE(qeq). The latter two quantities correspond to the equilibrium state of a particle in contact with the vesicle membrane at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . For the bistable engulfment regime with . For the bistable engulfment regime with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2 = 0.26 < 2 = 0.26 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) < < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3 = 0.74, the free particle states with q = qfr = 0 and ΔEfr ≡ ΔE(qfr) are metastable and separated from the equilibrium states by energy barriers at q = qba with barrier heights ΔEba ≡ ΔE(qba). The color of the lines corresponds to the different membrane segments defined in Fig. 6. 3 = 0.74, the free particle states with q = qfr = 0 and ΔEfr ≡ ΔE(qfr) are metastable and separated from the equilibrium states by energy barriers at q = qba with barrier heights ΔEba ≡ ΔE(qba). The color of the lines corresponds to the different membrane segments defined in Fig. 6. | |
Furthermore, for the discocyte shape in Fig. 6, the local energy landscape as given by (32) has the explicit form
| | 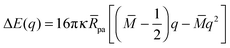 | (63) |
which depends on the mean curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
=
MRve of the membrane segment. As we move along the membrane surface of the vesicle, the mean curvature
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
changes and so does the local energy landscape Δ
E(
q) which attains its maximal or minimal value
| | 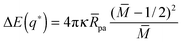 | (64) |
for the bound area fraction
| | 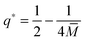 | (65) |
as follows from
(55) and (33).
The functional dependence of the rescaled segment curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) on the rescaled arc length
on the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) is displayed in Fig. 7(a). Both the north and the south pole are characterized by the negative mean curvature
is displayed in Fig. 7(a). Both the north and the south pole are characterized by the negative mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1.063 which implies that the local energy landscape (63) has the form of a non-inverted parabola with its minimum located at the bound area fraction qmin* = 0.735 which is equal to the equilibrium area fractions qeq(
= −1.063 which implies that the local energy landscape (63) has the form of a non-inverted parabola with its minimum located at the bound area fraction qmin* = 0.735 which is equal to the equilibrium area fractions qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 0) and qeq(
= 0) and qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1) of the partially engulfed states at the two poles, see Fig. 7(b). As we move away from the two poles, the mean curvature
= 1) of the partially engulfed states at the two poles, see Fig. 7(b). As we move away from the two poles, the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) increases towards zero and the minimum of the local energy landscape is shifted towards larger values of qmin* = qeq(
increases towards zero and the minimum of the local energy landscape is shifted towards larger values of qmin* = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) until we reach qmin* = qeq(
) until we reach qmin* = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1) = qeq(
1) = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4) = 1 corresponding to the mean curvature
4) = 1 corresponding to the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1/2. The membrane loci with the latter curvature define the boundaries between the
= −1/2. The membrane loci with the latter curvature define the boundaries between the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) - and
- and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments. Moving further towards the equator of the discocyte, the location qmin* of the energy minimum satisfies qmin* > 1 and, thus, moves out of the physically meaningful interval 0 < q < 1. The particle then attains a completely engulfed state corresponding to the boundary minimum at qeq(
-segments. Moving further towards the equator of the discocyte, the location qmin* of the energy minimum satisfies qmin* > 1 and, thus, moves out of the physically meaningful interval 0 < q < 1. The particle then attains a completely engulfed state corresponding to the boundary minimum at qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) = 1.
) = 1.
As we move across one of the two ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments towards the equator, the mean curvature
-segments towards the equator, the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) vanishes at certain arc length values,
vanishes at certain arc length values, ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 + ζ and
1 + ζ and ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4 − ζ with ζ = 0.06. For these membrane loci with
4 − ζ with ζ = 0.06. For these membrane loci with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0, the energy landscape ΔE(q) as given by (63) becomes a linear and monotonically decreasing function of q. Therefore, as we approach
= 0, the energy landscape ΔE(q) as given by (63) becomes a linear and monotonically decreasing function of q. Therefore, as we approach ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0 from negative
= 0 from negative ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) -values, the location qmin* of the energy minimum moves out to infinity. For
-values, the location qmin* of the energy minimum moves out to infinity. For ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 0, on the other hand, the local energy landscape has the form of an inverted parabola, and the location qmax* of its maximum moves out to minus infinity as we approach
> 0, on the other hand, the local energy landscape has the form of an inverted parabola, and the location qmax* of its maximum moves out to minus infinity as we approach ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0 from positive
= 0 from positive ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) -values. With increasing
-values. With increasing ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 0, the maximum of the energy landscape shifts towards less negative values of qmax* until we reach the boundary value qmax* = 0 for membrane curvature M = 1/2. The membrane loci with the latter curvature define the boundaries between the two
> 0, the maximum of the energy landscape shifts towards less negative values of qmax* until we reach the boundary value qmax* = 0 for membrane curvature M = 1/2. The membrane loci with the latter curvature define the boundaries between the two ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments and the
-segments and the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment around the equator. For the latter segment, we have two (meta)stable particle states with area fractions qeq = 0 and qeq = 1 as well as an energy barrier at qba = qmax*, as shown in Fig. 7(b). The location qba of the energy barrier reaches its largest value qba = 0.375 at the equator where the membrane curvature has its largest value
-segment around the equator. For the latter segment, we have two (meta)stable particle states with area fractions qeq = 0 and qeq = 1 as well as an energy barrier at qba = qmax*, as shown in Fig. 7(b). The location qba of the energy barrier reaches its largest value qba = 0.375 at the equator where the membrane curvature has its largest value ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2.006, as follows from (65).
= 2.006, as follows from (65).
5.5 Global energy landscapes
Because the local energy landscape ΔE(q) as given by (32) depends explicitly on the mean curvature M, the variation of M along the membrane surface implies a corresponding variation in the local energy landscape and, thus, in the equilibrium value qeq of the bound area fraction. The latter variation is illustrated in Fig. 7(b) for the case of the discocyte shape in Fig. 6. Because of its axisymmetry, this shape can be parametrized by the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) and the engulfment pattern can then be expressed in terms of the function q = qeq(
and the engulfment pattern can then be expressed in terms of the function q = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) as in Fig. 7(b). We will now use the latter function to define the global energy landscape
) as in Fig. 7(b). We will now use the latter function to define the global energy landscape| | ΔEeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) ≡ ΔE(qeq( ) ≡ ΔE(qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) )) )) | (66) |
with the local energy landscape ΔE(q) as given by eqn (32).
For the discocyte shape, the global energy landscape ΔEeq has the form displayed in Fig. 7(c) which implies that this vesicle–particle system attains its lowest energy state (or ground state) when the nanoparticle is partially engulfed at the north or south pole of the vesicle. Thus, for ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0 and
= 0 and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = 1/2, the energy
co = 1/2, the energy
| | ΔE(qeq = 1) = 16πκ(![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co) co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = −8πκ pa = −8πκ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa pa | (67) |
of the completely engulfed states exceeds the energies of the partially engulfed states which implies that the energy increase of the unbound membrane segments overcompensates the energy decrease of the bound membrane segment as we move from a
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
- to a
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
-segment. Expression
(67) also applies to the completely engulfed states of the
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
-segment around the equator. For the latter segment, the free states with
qeq = 0 are metastable as well but their energy Δ
E(
qeq = 0) = 0 is always larger than the energy Δ
E(
qeq = 1) of the completely engulfed states. The two (meta)stable states are separated by an energy barrier of height Δ
E(
qba) as given by
(64) which attains its largest value Δ
E(
qba) = 14.212
κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa at the equator.
When we defined the global energy landscape by eqn (66), we implicitly assumed that the bound area fraction q of the particle quickly adapts to its local equilibrium value qeq as the particle moves along the surface of the vesicle. For axisymmetric vesicles, we then obtain global energy landscapes that depend only on the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) , as illustrated in Fig. 7(c) for a discocyte shape. These one-dimensional energy landscapes can be generalized in two ways. First, we may consider an arbitrary, non-axisymmetric shape of the free vesicle which can be parametrized by a three-dimensional vector,
, as illustrated in Fig. 7(c) for a discocyte shape. These one-dimensional energy landscapes can be generalized in two ways. First, we may consider an arbitrary, non-axisymmetric shape of the free vesicle which can be parametrized by a three-dimensional vector, ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) =
= ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (s1,s2), that depends on two properly chosen surface coordinates, s1 and s2. The latter coordinates determine both the local mean curvature, M = M(s1,s2), of the vesicle membrane and the position of the particle on this membrane. Second, we may vary the bound area fraction q of the particle independently of its position. As a consequence, the most general energy landscape depends on the three parameters s1, s2, and q and this three-dimensional landscape ΔE = ΔE(s1,s2,q) can be directly obtained from the local landscape as given by eqn (32) when we insert the local mean curvature M = M(s1,s2) into this latter equation.
(s1,s2), that depends on two properly chosen surface coordinates, s1 and s2. The latter coordinates determine both the local mean curvature, M = M(s1,s2), of the vesicle membrane and the position of the particle on this membrane. Second, we may vary the bound area fraction q of the particle independently of its position. As a consequence, the most general energy landscape depends on the three parameters s1, s2, and q and this three-dimensional landscape ΔE = ΔE(s1,s2,q) can be directly obtained from the local landscape as given by eqn (32) when we insert the local mean curvature M = M(s1,s2) into this latter equation.
5.6 Curvature-induced forces
The binding energy of a partially engulfed particle depends on the ‘unperturbed’ curvature M of the adjacent membrane segment, as described by eqn (55) and illustrated by the blue segments of the global energy landscape in Fig. 7(c). Because the binding energy (55) decreases with decreasing curvature M, the particle experiences a curvature-induced force that pulls it towards points of lower mean curvature of the vesicle membrane. For an axisymmetric shape, the curvature-induced force is given by| | 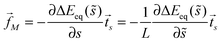 | (68) |
where ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) s is the unit tangent vector of the shape contour at arc length s = L
s is the unit tangent vector of the shape contour at arc length s = L![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . The global energy landscape ΔEeq(
. The global energy landscape ΔEeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) depends on the rescaled arc length
) depends on the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) only via the bound area fraction qeq which varies within a
only via the bound area fraction qeq which varies within a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment but is constant within all other segments, as illustrated in Fig. 7(b). The latter property is true in general because
-segment but is constant within all other segments, as illustrated in Fig. 7(b). The latter property is true in general because ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -, or
-, or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments are characterized by boundary minima with qeq = 0 or qeq = 1 and the corresponding energies ΔE(0) = 0 or ΔE(1) = 16πκRpa(m − Mco) do not depend on
-segments are characterized by boundary minima with qeq = 0 or qeq = 1 and the corresponding energies ΔE(0) = 0 or ΔE(1) = 16πκRpa(m − Mco) do not depend on ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . On the other hand, within a
. On the other hand, within a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, the
-segment, the ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependence of qeq arises only from the
-dependence of qeq arises only from the ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependence of the local mean curvature M = M(
-dependence of the local mean curvature M = M(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) as described by eqn (55). Therefore, the gradient of the global energy landscape has the value
) as described by eqn (55). Therefore, the gradient of the global energy landscape has the value| | 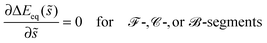 | (69) |
and the ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependent form
-dependent form| | 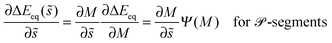 | (70) |
with| | 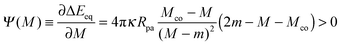 | (71) |
where the latter expression depends on ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) via M = M(
via M = M(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ), see the blue segments in Fig. 7(a). Note that Ψ(M) is always positive because
), see the blue segments in Fig. 7(a). Note that Ψ(M) is always positive because ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments are characterized by the curvature inequalities M < Mco < 2m − M according to eqn (54). A combination of relations (68) and (70) then implies that a partially engulfed particle experiences the curvature-induced force
-segments are characterized by the curvature inequalities M < Mco < 2m − M according to eqn (54). A combination of relations (68) and (70) then implies that a partially engulfed particle experiences the curvature-induced force| | 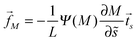 | (72) |
on an axisymmetric vesicle.
For an arbitrarily shaped vesicle, the curvature-induced force has the form
| | 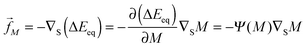 | (73) |
with the surface gradient operator ∇
S. When we parametrize the vesicle shape by the vector-valued function
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif)
(
s1,
s2), we obtain the two tangent vectors
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i
i ≡ ∂
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif)
/∂
si with
i = 1,2 that span the plane tangential to the vesicle surface, the metric tensor
gij =
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i
i·
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) j
j, and the inverse metric tensor (
gij) ≡ (
gij)
−1. The action of the gradient operator ∇
S onto any scalar function
U(
s1,
s2) is then given by
34| | 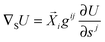 | (74) |
with an implicit summation over repeated indices.
In response to the curvature-induced force ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) M, as given by eqn (72) or (73), partially engulfed particles undergo biased diffusion towards membrane segments with lower curvature, whereas completely engulfed particles do not experience any curvature-induced force and diffuse freely on
M, as given by eqn (72) or (73), partially engulfed particles undergo biased diffusion towards membrane segments with lower curvature, whereas completely engulfed particles do not experience any curvature-induced force and diffuse freely on ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - and
- and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments. However, if a completely engulfed particle diffuses from a
-segments. However, if a completely engulfed particle diffuses from a ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - or
- or ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segment onto an
-segment onto an ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) - or
- or ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, it will unbind or partially unwrap from the membrane. Once on the
-segment, it will unbind or partially unwrap from the membrane. Once on the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, the particle will be pulled towards a membrane segment of minimal mean curvature. At temperature T, the probability to find the particle at a certain position,
-segment, the particle will be pulled towards a membrane segment of minimal mean curvature. At temperature T, the probability to find the particle at a certain position, ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (s1,s2), on the membrane is then proportional to the Boltzmann factor exp[−ΔEeq(
(s1,s2), on the membrane is then proportional to the Boltzmann factor exp[−ΔEeq(![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) )/kBT].
)/kBT].
6 Results for Janus particles
For particles with a chemically uniform surface, partial engulfment is only found if the particle size and adhesiveness, which determine the contact mean curvature Mco, are finely tuned so that M < Mco < 2m − M as in (54). To soften this constraint and to enlarge the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st-regime, we will now consider Janus particles with surfaces that are divided into one adhesive and one non-adhesive domain. The adhesive surface domain is taken to form a spherical cap with area A1 which implies a circular domain boundary of the adhesive surface domain and leads to the adhesive surface area fraction
st-regime, we will now consider Janus particles with surfaces that are divided into one adhesive and one non-adhesive domain. The adhesive surface domain is taken to form a spherical cap with area A1 which implies a circular domain boundary of the adhesive surface domain and leads to the adhesive surface area fraction| | 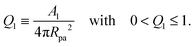 | (75) |
Because the area fraction q of the bound membrane cannot exceed the area fraction of the adhesive surface domain, the accessible q-range is now further restricted to| | | 0 < q ≤ Q1 (Janus particles). | (76) |
The adhesive domain is taken to have the adhesive strength |W1| and the contact mean curvature
| | 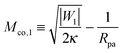 | (77) |
which grows as
for large |
W1|. A membrane segment with local mean curvature
M will start to spread over such an adhesive surface domain provided the free state is unstable which implies dΔ
E/d
q|
q=0 < 0 or
| | | Mco,1 > M (Janus, onset of adhesion) | (78) |
as follows from the local energy landscape Δ
E(
q) in
eqn (32) with
Mco replaced by
Mco,1. Inspection of
Fig. 4 shows that the inequality dΔ
E/d
q|
q=0 < 0 is satisfied within the partial and complete engulfment regimes of the uniform particle with |
W| = |
W1|, as illustrated in
Fig. 4(a) and (f)–(h). The same conclusion follows from
Fig. 5(a).
Because the Janus particle is characterized by the restricted q-range in eqn (76), the equilibrium value q = qJPeq of the membrane's bound area fraction on the Janus particle is given by
| | | qJPeq = Q1 for Q1 ≤ qeq | (79) |
and by
| | | qJPeq = qeq for qeq < Q1 | (80) |
where
qeq denotes the equilibrium value of the bound area fraction of the uniform particle as before. We have tacitly assumed here that the contact line adapts to the domain boundary of the adhesive surface domain and, thus, attains a circular shape as well. In principle, the equilibrium shape of the contact line could be non-circular as for partially engulfed particles with a uniform surface. Therefore, we assume here that the energy cost of forcing the contact line to be circular is of higher order in
Rpa/
Rve. Furthermore, irrespective of the detailed geometry of the contact line, we conclude that a Janus particle with
Q1 < 1 is always partially engulfed by a membrane segment if its mean curvature
M <
Mco,1 as in
eqn (78) and the membrane starts to spread on the adhesive surface domain of the particle.
If the uniform particle with |W| ≡ |W1| is completely engulfed as in Fig. 4(g) and (h), the bound area fraction is qeq = 1, corresponding to a boundary minimum at q = 1. Therefore, in this case, the Janus particle is characterized by the bound area fraction qJPeq = Q1. On the other hand, if the uniform particle with |W| ≡ |W1| is partially engulfed as in Fig. 4(a) and (f), the bound area fraction qeq = qmin* < 1. In the latter case, the membrane will still cover the whole adhesive surface domain provided the area fraction Q1 of this domain satisfies the condition
| | 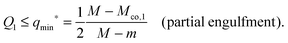 | (81) |
Because
M −
m < 0 in the partial engulfment regime according to
eqn (53) and
M −
Mco,1 < 0 according to
eqn (78), inequality
(81) is equivalent to
| | | Mco,1 ≥ (1 − Q1)M + Q1(2m − M) ≡ ϒ(M,Q1). | (82) |
This inequality becomes particularly simple and reduces to
Mco,1 ≥
m for an adhesive hemisphere with
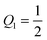
and
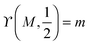
.
Therefore, a membrane segment with local mean curvature M starts to spread onto the adhesive surface domain for Mco,1 > M as in eqn (78) and spreads over the whole domain for Mco,1 ≥ ϒ(M,Q1) as in eqn (82). A combination of these two relationships implies that the adhesive surface domain is fully covered by the bound membrane segment with bound area fraction
| | | qJPeq = Q1 for Mco,1 > max[M,ϒ(M,Q1)], | (83) |
whereas this surface domain is only partially covered with
| | | qJPeq < Q1 for M < Mco,1 < ϒ(M,Q1). | (84) |
The latter case is only possible for
M <
m corresponding to partial engulfment of the uniform particle with |
W| = |
W1|, compare
Fig. 5(a).
We now focus on full coverage of the adhesive surface domain as described by eqn (83) and derive global conditions that ensure such a full coverage by all membrane segments of the vesicle. The function ϒ(M,Q1), defined in eqn (82), monotonically increases and decreases with increasing M for 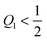 and
and 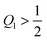 , respectively, and has the value ϒ(M,Q1) = m for
, respectively, and has the value ϒ(M,Q1) = m for 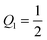 . Therefore, full coverage of the adhesive surface domain is achieved by all membrane segments if
. Therefore, full coverage of the adhesive surface domain is achieved by all membrane segments if
| | 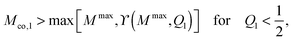 | (85) |
| | 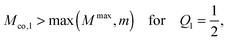 | (86) |
and
| | 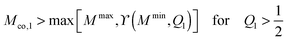 | (87) |
where
Mmax and
Mmin are the maximal and minimal mean curvatures of the complex-shaped vesicle under consideration. In the following sections, we will consider Janus particles with a sufficiently large contact mean curvature
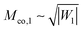
so that one of the conditions
(85)–(87), corresponding to the chosen value of
Q1, is satisfied. The Janus particles are then always partially engulfed with the bound membrane segment covering the whole area
A1 of the adhesive surface domain, and the equilibrium value of the bound area fraction is given by
qJPeq =
Q1 irrespective of the location of the Janus particle on the vesicle membrane.
Using the explicit expression (32) for the local energy landscape ΔE(q), the binding energy
| | | ΔEJPeq ≡ ΔE(q = qJPeq = Q1) < 0 | (88) |
of such a Janus particle is then given by
| | | ΔEJPeq = 16πκRpaQ1[(1 − Q1)M + Q1m − Mco,1]. | (89) |
which becomes
| | | ΔEJPeq = 4πκRpa(M + m − 2Mco,1) for Q1 = 1/2 | (90) |
corresponding to an adhesive hemisphere.
Using the same line of reasoning that led to eqn (72) for uniform particles, the curvature-induced force acting on a partially engulfed Janus particle now has the form
| | 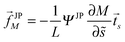 | (91) |
for an axisymmetric vesicle with the
M-independent factor
| | 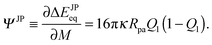 | (92) |
For an arbitrarily shaped vesicle, we now obtain
| | ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) JPM = −16πκRpaQ1(1 − Q1)∇SM JPM = −16πκRpaQ1(1 − Q1)∇SM | (93) |
as follows from
eqn (73) and (92). Thus, the Janus particle is also pulled towards regions of lower membrane curvature. It is interesting to note that, in contrast to the case of uniform particles as described by
eqn (72), the curvature-induced force acting on the Janus particle with
q =
Q1 does not depend on the contact mean curvature
Mco and depends only implicitly on the spontaneous curvature
m via the mean curvature
M.
The curvature-dependent binding energy (89) and the curvature-induced force as given by eqn (91) or (93) have far-reaching consequences. Janus particles in contact with membranes of non-spherical shape will always ‘feel’ the local mean curvature gradient and tend to diffuse towards the points of minimal mean curvature. Biological objects involving complex-shaped membranes include intracellular organelles such as the endoplasmic reticulum,35 dividing cells, red blood cells, and nascent autophagosomes. The shapes of the latter three examples are analogous to prolate, discocyte and stomatocyte vesicles, as shown in Fig. 8(a)–(c). The corresponding energy landscapes experienced by Janus particles are displayed in Fig. 8(d). In the latter figure, we plot the binding energy difference defined by
| | | ΔΔEJPeq(M) ≡ ΔEJPeq(M) − ΔEJPeq(Mmin) | (94) |
between the binding energy for a given point of the vesicle membrane and the binding energy for the point of lowest mean curvature
Mmin as a function of the rescaled arc length
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
for adhesive hemispheres with
Q1 = 1/2. For general values of
Q1, the binding energy difference has the form
| | ΔΔEJPeq(M) = 16πκ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paQ1(1 − Q1)( paQ1(1 − Q1)(![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) − − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) min) min) | (95) |
in terms of rescaled variables and is, thus, directly proportional to the mean curvature difference
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
−
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) min
min. The rescaled arc length
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
is again defined by
eqn (59), where
L denotes the total contour length of the respective vesicle shape. Thus, the parameter
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
varies from
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
= 0 at the north pole to
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
= 1 at the south pole for all vesicle shapes displayed in
Fig. 8(a)–(c).
 |
| | Fig. 8 Axisymmetric equilibrium shapes of (a) prolate, (b) discocyte, and (c) stomatocyte vesicles with zero spontaneous curvature and rescaled volume v = 0.80, 0.62 and 0.40, respectively. The rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) parametrizes the shape contour from the north pole with parametrizes the shape contour from the north pole with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 0 to the south pole with = 0 to the south pole with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1; and (d) energy landscapes ΔΔEJPeq, experienced by a half-adhesive Janus particle as a function of the rescaled arc length = 1; and (d) energy landscapes ΔΔEJPeq, experienced by a half-adhesive Janus particle as a function of the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . These energy landscapes are obtained from the mean curvature M of the vesicle membranes via expression (95) with Q1 = 1/2. The energy landscapes for the prolate and discocyte shapes are symmetric with respect to . These energy landscapes are obtained from the mean curvature M of the vesicle membranes via expression (95) with Q1 = 1/2. The energy landscapes for the prolate and discocyte shapes are symmetric with respect to ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1/2 where they exhibit a minimum and maximum, respectively. The energy landscape for the stomatocyte has a maximum at = 1/2 where they exhibit a minimum and maximum, respectively. The energy landscape for the stomatocyte has a maximum at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = = ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto 0.55, corresponding to the vertical dotted line in (d) and to the black diamond in (c) and (e) positional probabilities ρ of a half-adhesive Janus particle with radius sto 0.55, corresponding to the vertical dotted line in (d) and to the black diamond in (c) and (e) positional probabilities ρ of a half-adhesive Janus particle with radius ![[R with combining overline]](https://www.rsc.org/images/entities/i_char_0052_0305.gif) pa = 0.01 as a function of arc length pa = 0.01 as a function of arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) for the three vesicle shapes in (a)–(c). The probability ρ is proportional to the Boltzmann factor exp[−ΔΔEJPeq( for the three vesicle shapes in (a)–(c). The probability ρ is proportional to the Boltzmann factor exp[−ΔΔEJPeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) )/kBT] and normalized with )/kBT] and normalized with 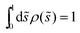 . The three examples shown here correspond to kBT = κ/20. . The three examples shown here correspond to kBT = κ/20. | |
For prolates and discocytes, which are up-down symmetric, particles tend to localize at the equator and at the poles, respectively. For a prolate vesicle, particles can freely diffuse along the equatorial line because all points on this line have the same curvature. For a discocyte vesicle, particles will localize either at the north or at the south pole. In the latter case, the diffusion from one pole to the other is impeded by a large energy barrier located along the equatorial line. These results are consistent with the collective behavior of particles in contact with prolate and discocyte vesicles, as described in ref. 9.
The behavior of Janus particles on stomatocyte-shaped vesicles, which have no up-down symmetry, is more complex. As shown in Fig. 8(c), a stomatocyte shape consists of an outer and an inner membrane segment that are connected by a membrane neck. The inner segment corresponds to a membrane invagination or in-bud. The associated energy landscape ΔΔEJPeq now exhibits two distinct minima: (i) a local, metastable minimum located at the convexly curved north pole; and (ii) a globally stable minimum located at the concavely curved south pole which also represents the pole of the invagination. The energy barrier between these two minima is located at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) =
= ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto ≃ 0.55, right outside of the membrane neck, as indicated by the black diamond in Fig. 8(c). In order to reach the inner membrane segment, a particle attached to the outer segment will have to overcome this energy barrier, whose height is approximately 2κ
sto ≃ 0.55, right outside of the membrane neck, as indicated by the black diamond in Fig. 8(c). In order to reach the inner membrane segment, a particle attached to the outer segment will have to overcome this energy barrier, whose height is approximately 2κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa for a stomatocyte with rescaled volume v = 0.4, as displayed in Fig. 8(c). This implies that particles can spontaneously overcome this barrier via thermal diffusion only if they are sufficiently small. A crossover value
pa for a stomatocyte with rescaled volume v = 0.4, as displayed in Fig. 8(c). This implies that particles can spontaneously overcome this barrier via thermal diffusion only if they are sufficiently small. A crossover value ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa for the particle radius can be estimated from the requirement that 2κ
†pa for the particle radius can be estimated from the requirement that 2κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa ≃ kBT which implies
†pa ≃ kBT which implies ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa ≃ 1/40, assuming a typical bending rigidity for lipid membranes κ = 20kBT. Small particles with radii
†pa ≃ 1/40, assuming a typical bending rigidity for lipid membranes κ = 20kBT. Small particles with radii ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≲
pa ≲ ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa will not encounter any significant barrier, whereas large particles with
†pa will not encounter any significant barrier, whereas large particles with ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≫
pa ≫ ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa will be trapped in the outer membrane segment for a long time. As soon as a Janus particle has overcome the energy barrier close to the membrane neck, it will be strongly pulled through the neck region towards the central part of the invagination as follows from the strong decay of the stomatocyte's energy landscape ΔΔEJPeq for
†pa will be trapped in the outer membrane segment for a long time. As soon as a Janus particle has overcome the energy barrier close to the membrane neck, it will be strongly pulled through the neck region towards the central part of the invagination as follows from the strong decay of the stomatocyte's energy landscape ΔΔEJPeq for ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) >
> ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto, as depicted in Fig. 8(d).
sto, as depicted in Fig. 8(d).
7 Summary and conclusions
In this paper, we derived an analytical theory for the engulfment of rigid spherical nanoparticles by vesicle membranes that allowed us to calculate local energy landscapes for such particles at any point of the vesicle membrane. More precisely, we used the bound area fraction q of the particle surface, see eqn (1), as our basic reaction coordinate and considered the limit in which the particle size Rpa is small compared to the vesicle size Rve. Up to first order in the size ratio Rpa/Rve, we found the explicit form (32) for the local energy landscape ΔE(q) of a uniform particle in contact with a membrane segment of mean curvature M. The most important feature of this energy landscape is that it does not depend on the overall shape of the vesicle.
Another remarkable feature of the local energy landscape ΔE(q) as given by eqn (32) is that it has a simple quadratic dependence on the bound area fraction q, as confirmed by extensive numerical calculations, see Fig. 3. Furthermore, this simple functional form provides a complete classification for the complex engulfment behavior that arises from the interplay of mean curvature M, spontaneous curvature m, and contact mean curvature Mco, as displayed in Fig. 4 and discussed in Section 5.2.
The local energy landscape as given by eqn (32) is intimately related to our previous results, described in ref. 7 and 26. In ref. 7, we made the empirical (numerical) observation that small particles interacting with vesicles exhibit four distinct engulfment regimes: a free regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st in which only the free particle state is stable, a completely engulfed regime
st in which only the free particle state is stable, a completely engulfed regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st in which only the completely engulfed state is stable, a partially engulfed regime
st in which only the completely engulfed state is stable, a partially engulfed regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st in which only the partially engulfed state is stable, and a bistable regime
st in which only the partially engulfed state is stable, and a bistable regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st in which both the free and the completely engulfed states are stable and separated by an energy barrier. We then used this empirical observation to describe the interaction of nanoparticles with complex-shaped vesicles in ref. 26. Because of the local energy landscape derived in the present paper, see eqn (32) and Fig. 4, we now understand that these previous results directly follow from the energetics of the system up to first order in Rpa/Rve. Deviations from this behavior will always be a signature of higher order terms in Rpa/Rve, which are expected to depend on the global shape of the vesicle.
st in which both the free and the completely engulfed states are stable and separated by an energy barrier. We then used this empirical observation to describe the interaction of nanoparticles with complex-shaped vesicles in ref. 26. Because of the local energy landscape derived in the present paper, see eqn (32) and Fig. 4, we now understand that these previous results directly follow from the energetics of the system up to first order in Rpa/Rve. Deviations from this behavior will always be a signature of higher order terms in Rpa/Rve, which are expected to depend on the global shape of the vesicle.
The physically meaningful part of the local energy landscape ΔE(q) is provided by all q-values within the interval 0 ≤ q ≤ 1. When we restrict the energy landscape to this q-range, we always find a state of lowest energy which determines the particle's equilibrium state with bound area fraction q = qeq. For partially engulfed states on ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments, the equilibrium state corresponds to a smooth minimum with qeq = qmin* and 0 < qmin*<1. For all other engulfment regimes, the equilibrium state is provided by a boundary minimum with qeq = qfr = 0 or qeq = qce = 1. As we move along the membrane of a complex-shaped vesicle, the membrane's mean curvature M changes in a continuous manner and so does the local energy landscape as well as the associated equilibrium state qeq. We can then use the energy ΔE(qeq) of the equilibrium particle states to define a global energy landscape ΔEeq for all points on the vesicle membrane. If the vesicle is axisymmetric, its shape can be parametrized by the rescaled arc length
-segments, the equilibrium state corresponds to a smooth minimum with qeq = qmin* and 0 < qmin*<1. For all other engulfment regimes, the equilibrium state is provided by a boundary minimum with qeq = qfr = 0 or qeq = qce = 1. As we move along the membrane of a complex-shaped vesicle, the membrane's mean curvature M changes in a continuous manner and so does the local energy landscape as well as the associated equilibrium state qeq. We can then use the energy ΔE(qeq) of the equilibrium particle states to define a global energy landscape ΔEeq for all points on the vesicle membrane. If the vesicle is axisymmetric, its shape can be parametrized by the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) of the shape contour, see eqn (59), and the global energy landscape is obtained via ΔEeq(
of the shape contour, see eqn (59), and the global energy landscape is obtained via ΔEeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) = ΔE(qeq(
) = ΔE(qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) )) as in eqn (66). One example is provided by the discocyte shape in Fig. 6 with its global energy landscape depicted in Fig. 7(c).
)) as in eqn (66). One example is provided by the discocyte shape in Fig. 6 with its global energy landscape depicted in Fig. 7(c).
For ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) - or
- or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments of the vesicle membrane, the equilibrium states of the particles correspond to the boundary minima of the local energy landscapes with qeq = qfr = 0 or qeq = qfr = 0. The corresponding energies ΔE(0) = 0 and ΔE(1) = 16πκ(m − Mco)Rpa as in eqn (42) do not depend on the local mean curvature M of the segments. As a consequence, the global energy landscape ΔEeq = const for these three types of membrane segments, see Fig. 7(c), and, thus, does not lead to any curvature-induced forces on the particles.
-segments of the vesicle membrane, the equilibrium states of the particles correspond to the boundary minima of the local energy landscapes with qeq = qfr = 0 or qeq = qfr = 0. The corresponding energies ΔE(0) = 0 and ΔE(1) = 16πκ(m − Mco)Rpa as in eqn (42) do not depend on the local mean curvature M of the segments. As a consequence, the global energy landscape ΔEeq = const for these three types of membrane segments, see Fig. 7(c), and, thus, does not lead to any curvature-induced forces on the particles.
For partially engulfed particles on ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments, on the other hand, the equilibrium states are provided by the smooth minima of the local energy landscapes with qeq = qmin* and 0 < qmin* < 1. The latter minima depend on the local mean curvature M as described by eqn (55) and, thus, change as the particle moves along a
-segments, on the other hand, the equilibrium states are provided by the smooth minima of the local energy landscapes with qeq = qmin* and 0 < qmin* < 1. The latter minima depend on the local mean curvature M as described by eqn (55) and, thus, change as the particle moves along a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment with variable mean curvature M. When the particles originate from the exterior solution (endocytosis), the binding energy ΔEeq = ΔE* of the partially engulfed particles is reduced when they move towards membrane segments with lower mean curvature M. In contrast, partially engulfed particles that originate from the interior solution (exocytosis), reduce their binding energy when they move towards membrane segments with higher mean curvature M, see Appendix B. The corresponding curvature-induced forces acting onto particles with a chemically uniform surface have the explicit form as given by eqn (72) for axisymmetric vesicles and by eqn (73) for arbitrarily shaped membranes.
-segment with variable mean curvature M. When the particles originate from the exterior solution (endocytosis), the binding energy ΔEeq = ΔE* of the partially engulfed particles is reduced when they move towards membrane segments with lower mean curvature M. In contrast, partially engulfed particles that originate from the interior solution (exocytosis), reduce their binding energy when they move towards membrane segments with higher mean curvature M, see Appendix B. The corresponding curvature-induced forces acting onto particles with a chemically uniform surface have the explicit form as given by eqn (72) for axisymmetric vesicles and by eqn (73) for arbitrarily shaped membranes.
These curvature-induced forces arise from the M-dependence of the binding energy in eqn (55), which can be traced back to the M-dependence of the particle-induced energy change of the unbound membrane segment, as described by eqn (27). Furthermore, a decomposition of the binding energy (55) into separate contributions from the bound and unbound segments shows that the curvature-induced forces are dominated by the particle-induced energy changes of the unbound segments. Therefore, an endocytic (exocytic) particle moves towards a membrane segment of lower (higher) mean curvature in order to lower the bending energy of the unbound membrane segment in the vicinity of the contact line.
For uniform particles, partial engulfment is only possible if the contact mean curvature Mco, which depends on the particle size and adhesiveness, is finely tuned with the local mean curvature M and the spontaneous curvature m of the membrane, see eqn (54). In contrast, Janus particles with one strongly adhesive and one non-adhesive surface domain are predicted to be always partially engulfed if the contact mean curvature Mco,1 of their strongly adhesive domain satisfies the relevant condition in (85)–(87). The corresponding curvature-induced forces as given by eqn (91) and (93) again pull the Janus particles towards points of minimal membrane curvature in the endocytic case, as illustrated by the energy landscapes in Fig. 8, or towards points of maximal membrane curvature in the exocytic case, as described in Appendix B.
Strictly speaking, the results described here were obtained for a single particle interacting with a vesicle membrane. However, these results should also apply to a finite concentration of such particles provided one can ignore the interactions between the membrane-bound particles. The latter situations is provided by dilute particle concentrations on ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) - or
- or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments of the vesicle membrane. On the other hand, if several partially engulfed particles are present on the vesicle surface, membrane-mediated particle–particle interactions are expected to be important when the particles come close to each other,36,37 and particles may cluster into tubes31 or buds.38 The latter process provides an example of domain-induced budding in which the domains acquire a spontaneous curvature arising from the asymmetry of the membrane-bound particles.39,40
-segments of the vesicle membrane. On the other hand, if several partially engulfed particles are present on the vesicle surface, membrane-mediated particle–particle interactions are expected to be important when the particles come close to each other,36,37 and particles may cluster into tubes31 or buds.38 The latter process provides an example of domain-induced budding in which the domains acquire a spontaneous curvature arising from the asymmetry of the membrane-bound particles.39,40
The curvature-induced forces derived here for partially engulfed particles are conceptually similar to the capillary forces that have been recently described for particles at fluid interfaces41–44 and tense membranes45 of arbitrary shape. The underlying mechanisms are very different, however: in the latter systems, the forces are a consequence of interfacial or membrane tension and of the changes in interfacial or membrane area caused by the presence of the particle. In contrast, for deflated vesicles as considered here, the total membrane area is constant and tension plays no role, which implies that the curvature-induced forces described here are a consequence of pure bending.
Nonspherical vesicles with rescaled volume v < 1 undergo thermally-excited shape fluctuations that lead to deviations from the equilibrium shapes depicted in Fig. 6 and 8. One may then wonder whether these fluctuations can affect the engulfment behavior. The engulfment of a particle takes up excess membrane area or, equivalently, increases the rescaled volume v of the vesicle, as described by eqn (99) in Appendix A. Particle engulfment therefore acts to suppress membrane fluctuations, and this fluctuation effect implies a corresponding entropic contribution to the free energy of the system. However, entropic contributions to the free energy are proportional to the thermal energy kBT, whereas the energy contributions discussed here are proportional to the membrane's bending rigidity κ, which has a typical value of 20kBT. In particular, the entropic contributions to the local energy landscapes should have the form CkBT![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa up to first order in the rescaled particle size
pa up to first order in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, with C being a dimensionless coefficient of order one. In contrast, the local energy landscape as given by eqn (32) is proportional to 16πκ
pa, with C being a dimensionless coefficient of order one. In contrast, the local energy landscape as given by eqn (32) is proportional to 16πκ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≃ 1000kBT
pa ≃ 1000kBT![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa. Therefore, entropic contributions to this local energy landscape can be safely ignored in typical cases.
pa. Therefore, entropic contributions to this local energy landscape can be safely ignored in typical cases.
An important feature of the analytical theory presented here is that it can be used to describe particle engulfment at non-axisymmetric locations of vesicles. Usually, the study of non-axisymmetric membrane geometries requires numerical energy minimization of dynamically triangulated membranes, which is computationally rather costly.25,31 It will certainly be useful to develop similar analytical approaches for other systems of experimental relevance, such as the engulfment of non-spherical or soft particles. Furthermore, the theory developed here is based on local membrane properties, and can therefore be extended to vesicle membranes that undergo phase separation into a liquid-ordered and a liquid-disordered phase. In the latter case, the local bending rigidity and spontaneous curvature experienced by the particle will depend on the particular membrane domain with which it comes into contact. Finally, our analytical expressions for binding energies, energy barriers and curvature-induced forces involve only measurable quantities, and are therefore directly accessible to the experiment.
A Bending energy and mean curvature after complete engulfment
As in the main text, we use the vesicle size 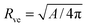 as the basic length scale and the bending rigidity κ as the basic energy scale which leads to the rescaled volume v as in (4) and the rescaled particle size
as the basic length scale and the bending rigidity κ as the basic energy scale which leads to the rescaled volume v as in (4) and the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = Rpa/Rve as well as the rescaled curvatures
pa = Rpa/Rve as well as the rescaled curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve,
= MRve, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ = M′Rve, and
′ = M′Rve, and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. In addition, we will also use the rescaled energies
= mRve. In addition, we will also use the rescaled energies| | | Ēfr ≡ Efr/(8πκ) and Ēfr′ ≡ Efr′/(8πκ) | (96) |
of the free vesicle and the unbound mother vesicle after engulfment.
The equilibrium shape of a free vesicle depends only on the values of the rescaled volume v and the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . For small values of the spontaneous curvature
. For small values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), these shapes are axisymmetric and can be calculated via numerical solution of the so-called shape equations.28 One finds three different branches of stable solutions depending on the values of v and
(1), these shapes are axisymmetric and can be calculated via numerical solution of the so-called shape equations.28 One finds three different branches of stable solutions depending on the values of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , namely the oblate, prolate and stomatocyte branches. Let us assume that we follow the bending energy of the vesicle as a function of v and
, namely the oblate, prolate and stomatocyte branches. Let us assume that we follow the bending energy of the vesicle as a function of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . By solving the shape equations for the free vesicle, one obtains the bending energy of the free vesicle in the form Ēfr = Fj(v,
. By solving the shape equations for the free vesicle, one obtains the bending energy of the free vesicle in the form Ēfr = Fj(v,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ), where the subscript j indicates the branch.
), where the subscript j indicates the branch.
Now, after the free vesicle has engulfed the particle completely, the area A′ and the volume V′ of the mother vesicle are given by
| | 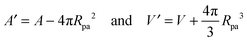 | (97) |
which implies the size
| | 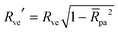 | (98) |
of the mother vesicle which is then characterized by the rescaled volume
| | 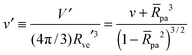 | (99) |
and the rescaled spontaneous curvature
| | ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′ ≡ mRve′ = ′ ≡ mRve′ = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (1 − (1 − ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2)1/2 pa2)1/2 | (100) |
These expressions can be rewritten as
| | 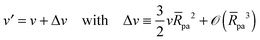 | (101) |
and
| | 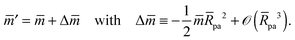 | (102) |
The energy of the mother vesicle is then given by
| | Ēfr′ = Fj(v′,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′) = Fj(v + Δv, ′) = Fj(v + Δv,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) + Δ + Δ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ) ) | (103) |
where we assumed that the shape of the mother vesicle remains, after complete engulfment, on the same branch
j as the shape of the free vesicle. The latter assumption is justified unless the free vesicle is close to a discontinuous shape transition.
26 An expansion of
eqn (103) in powers of
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa now leads to
| | 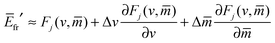 | (104) |
which implies
| | Ēfr′ = Ēfr + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ( (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). pa2). | (105) |
Therefore, up to first order in the rescaled particle size
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa, the bending energy
Ēfr′ of the mother vesicle after engulfment is equal to the bending energy
Ēfr of the free vesicle.
The same construction can be applied to the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) at a given point P of the vesicle. For the free vesicle, we envisage a relation of the form
at a given point P of the vesicle. For the free vesicle, we envisage a relation of the form ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve = fj,P(v,
= MRve = fj,P(v,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ). For the unbound membrane segment of the mother vesicle after engulfment, we then have the analogous relation M′Rve′ = fj,P(v′,
). For the unbound membrane segment of the mother vesicle after engulfment, we then have the analogous relation M′Rve′ = fj,P(v′,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′) or
′) or
| | 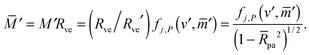 | (106) |
Using again expressions
(101) and (102) for
v′ and
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
′, an expansion in powers of
v′ −
v and
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
′ −
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
leads to
| | 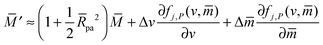 | (107) |
which implies
i.e., the change in the mean curvature at point
P after complete engulfment is again of second order in the rescaled particle size
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa.
B Results for exocytic engulfment
The results for exocytic engulfment can be obtained from those for endocytic engulfment by simply changing the sign of all curvatures, i.e., by replacing M, m, and Mco by −M, −m, and −Mco in the defining eqn (5) for the contact mean curvature Mco, in the local energy landscape ΔE(q) as given by (32), and in the stability relations (47)–(54).
In particular, the contact mean curvature for exocytic engulfment is given by7
| | 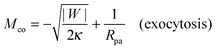 | (109) |
and now decreases both with increasing particle size, and with increasing adhesive strength. Likewise, the local energy landscape Δ
E(
q) has the form
| | | ΔE(q) = 16πκ[(Mco − M)q + (M − m)q2]Rpa | (110) |
for exocytosis which leads to a change of sign for all inequalities that define the stability regimes. As a consequence, the four stability regimes for exocytic engulfment are now given as follows:
(i) Free engulfment regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st for 2m − Mco ≤ M ≤ Mco;
st for 2m − Mco ≤ M ≤ Mco;
(ii) Complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st for Mco ≤ M ≤ 2m − Mco;
st for Mco ≤ M ≤ 2m − Mco;
(iii) Bistable engulfment regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st for M < Mco < 2m − M; and
st for M < Mco < 2m − M; and
(iv) Partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st for 2m − M < Mco < M.
st for 2m − M < Mco < M.
In contrast to the endocytic case, membrane segments with M < m now display bistability, whereas segments with M > m lead to partial engulfment. This can also be inferred from the expression for the binding energies and energy barriers which now has the form in the case of exocytic engulfment
| | 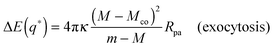 | (111) |
In particular, in the absence of spontaneous curvature, concave membrane segments with
M < 0 now lead to bistable behavior with Δ
E(
q*) > 0, whereas convex membrane segments with
M > 0 lead to partial engulfment with Δ
E(
q*) < 0.
The curvature-induced forces (73) and (93) experienced by uniform and Janus-like particles also change sign in the case of exocytic engulfment. Therefore, the partially engulfed particles will now preferably stay in membrane segments with the largest mean curvature. In particular, the global energy landscapes displayed in Fig. 8(d) change sign or, equivalently, are ‘flipped vertically’ in the case of exocytic engulfment. For prolate vesicles, Janus particles will localize at the north and south poles, whereas they will localize at the equator of discocyte-shaped vesicles. In the case of stomatocyte-shaped vesicles, there will be now a single energy minimum at the position indicated by the black diamond in Fig. 8(c), and therefore particles will tend to localize in a circle just outside of the neck region.
Acknowledgements
This study was supported by the German Research Foundation (DFG) via the IRTG 1524, and the Federal Ministry of Education and Research (BMBF) via the consortium MaxSynBio. Open Access funding provided by the Max Planck Society.
References
- J. Panyam and V. Labhasetwar, Adv. Drug Delivery Rev., 2003, 55, 329–347 CrossRef CAS PubMed.
- P. L. Rodriguez, T. Harada, D. A. Christian, D. A. Pantano, R. K. Tsai and D. E. Discher, Science, 2013, 339, 971–975 CrossRef CAS PubMed.
- N. Lewinski, V. Colvin and R. Drezek, Small, 2008, 4, 26–49 CrossRef CAS PubMed.
- J. Mercer, M. Schelhaas and A. Helenius, Annu. Rev. Biochem., 2010, 79, 803–833 CrossRef CAS PubMed.
- J.-H. Lee, Y.-M. Huh, Y.-w. Jun, J.-w. Seo, J.-t. Jang, H.-T. Song, S. Kim, E.-J. Cho, H.-G. Yoon, J.-S. Suh and J. Cheon, Nat. Med., 2007, 13, 95–99 CrossRef CAS PubMed.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS PubMed.
- A. D. Dinsmore, D. T. Wong, P. Nelson and A. G. Yodh, Phys. Rev. Lett., 1998, 80, 409–412 CrossRef CAS.
- I. Koltover, J. O. Rädler and C. Safinya, Phys. Rev. Lett., 1999, 82, 1991–1994 CrossRef CAS.
- R. Michel, E. Kesselman, T. Plostica, D. Danino and M. Gradzielski, Angew. Chem., Int. Ed., 2014, 53, 12441–12445 CAS.
- A. Meinel, B. Tränkle, W. Römer and A. Rohrbach, Soft Matter, 2014, 10, 3667–3678 RSC.
- F. G. Strobl, F. Seitz, C. Westerhausen, A. Reller, A. A. Torrano, C. Bräuchle, A. Wixforth and M. F. Schneider, Beilstein J. Nanotechnol., 2014, 5, 2468–2478 CrossRef PubMed.
- K. Jaskiewicz, A. Larsen, D. Schaeffel, K. Koynov, I. Lieberwirth, G. Fytas, K. Landfester and A. Kroeger, ACS Nano, 2012, 6, 7254–7262 CrossRef CAS PubMed.
- H. Noguchi and M. Takasu, Biophys. J., 2002, 83, 299–308 CrossRef CAS PubMed.
- M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef PubMed.
- W. T. Góźdź, Langmuir, 2007, 23, 5665–5669 CrossRef PubMed.
- K. A. Smith, D. Jasnow and A. C. Balazs, J. Chem. Phys., 2007, 127, 084703 CrossRef PubMed.
- S. A. Nowak and T. Chou, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021908 CrossRef PubMed.
- S. Cao, G. Wei and J. Z. Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 050901 CrossRef PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Soft Matter, 2016, 12, 581–587 RSC.
- R. Vácha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395 CrossRef PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed.
- C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550 CrossRef CAS PubMed.
- A. H. Bahrami, Soft Matter, 2013, 9, 8642 RSC.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Nano Lett., 2015, 15, 7168–7173 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768–4771 CrossRef CAS.
- M. Deserno, M. M. Müller and J. Guven, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011605 CrossRef PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef PubMed.
- B. Fourcade, L. Miao, M. Rao, M. Wortis and R. Zia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5276–5286 CrossRef CAS.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2016, 12, 8155–8166 RSC.
-
M. do Carmo, Differential geometry of curves and surfaces, Prentice-Hall, Englewood Cliffs, 1976 Search PubMed.
- M. Terasaki, T. Shemesh, N. Kasthuri, R. W. Klemm, R. Schalek, K. J. Hayworth, A. R. Hand, M. Yankova, G. Huber, J. W. Lichtman, T. A. Rapoport and M. M. Kozlov, Cell, 2013, 154, 285–296 CrossRef CAS PubMed.
- T. R. Weikl, M. M. Kozlov and W. Helfrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 10 CrossRef.
- B. J. Reynwar and M. Deserno, Soft Matter, 2011, 7, 8567 RSC.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS PubMed.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- A. Würger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 1–9 CrossRef PubMed.
- P. Galatola and J.-B. Fournier, Soft Matter, 2014, 10, 2197–2212 RSC.
- N. Sharifi-Mood, I. B. Liu and K. J. Stebe, Soft Matter, 2015, 11, 6768–6779 RSC.
- P. Galatola, Soft Matter, 2016, 12, 2802–2804 RSC.
- N. Li, N. Sharifi-Mood, F. Tu, D. Lee, R. Radhakrishnan, T. Baumgart and K. J. Stebe, Langmuir, 2016, 33, 600–610 CrossRef PubMed.
Footnote |
| † The example in Fig. 1(a) corresponds to a prolate vesicle with rescaled volume v = 0.98, see eqn (4), spontaneous curvature m = 3/Rve, and particles with mean contact curvature Mco = 5/Rve, see (5), with the vesicle size Rve as defined in (2). |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Reinhard
Lipowsky
* and
Reinhard
Lipowsky
 *
*
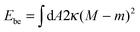 , where the integration runs over the whole surface of the membrane or vesicle. The mean curvature of the membrane is defined as M = (C1 + C2)/2, where C1 and C2 are the principal curvatures, and is taken to be positive or negative if the membrane bulges towards the exterior or interior compartment of the vesicle, respectively. Because we do not consider transformations that change the topology of the membrane, the contribution of the Gaussian curvature to the bending energy is constant and can be omitted. The elastic properties of the membrane are then described by its bending rigidity κ and its spontaneous curvature m. The attractive interaction with the particle is included via the adhesive energy Ead = −|W|Abo, where |W| is the absolute value of the adhesive energy per unit area and Abo the area of the membrane that is bound to the particle.29 The total energy of the system is then given by E = Ebe + Ead.
, where the integration runs over the whole surface of the membrane or vesicle. The mean curvature of the membrane is defined as M = (C1 + C2)/2, where C1 and C2 are the principal curvatures, and is taken to be positive or negative if the membrane bulges towards the exterior or interior compartment of the vesicle, respectively. Because we do not consider transformations that change the topology of the membrane, the contribution of the Gaussian curvature to the bending energy is constant and can be omitted. The elastic properties of the membrane are then described by its bending rigidity κ and its spontaneous curvature m. The attractive interaction with the particle is included via the adhesive energy Ead = −|W|Abo, where |W| is the absolute value of the adhesive energy per unit area and Abo the area of the membrane that is bound to the particle.29 The total energy of the system is then given by E = Ebe + Ead.
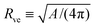
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve
≡ mRve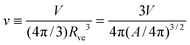
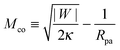
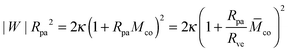
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co ≡ McoRve,
co ≡ McoRve,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co)
co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa + (
pa + (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 2 −
2 − ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co2)
co2)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2]q
pa2]q![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve.
pa ≡ Rpa/Rve.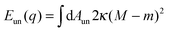
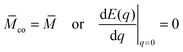
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ≡ MRve where M is the mean curvature of the free membrane segment at the point of initial contact with the particle. The free particle state is stable for
≡ MRve where M is the mean curvature of the free membrane segment at the point of initial contact with the particle. The free particle state is stable for ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co ≤
co ≤ ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and unstable for
and unstable for ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co >
co > ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) .
.
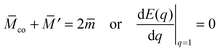
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ ≡ M′Rve where M′ is the mean curvature of the mother vesicle at the position of the narrow neck that connects the mother vesicle to the completely engulfed particle. The completely engulfed state is stable for
′ ≡ M′Rve where M′ is the mean curvature of the mother vesicle at the position of the narrow neck that connects the mother vesicle to the completely engulfed particle. The completely engulfed state is stable for ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co +
co + ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ ≥ 2
′ ≥ 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and unstable for
and unstable for ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co +
co + ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ < 2
′ < 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) .
.
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co represents a material parameter, as explained after (5), whereas the mean curvatures
co represents a material parameter, as explained after (5), whereas the mean curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and
and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ represent geometric quantities related to the shape of the vesicle membrane. Because the contact mean curvature
′ represent geometric quantities related to the shape of the vesicle membrane. Because the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co increases both with particle size and adhesive strength, the stability limits (12) and (13) reflect the fact that small or weakly adhesive particles will tend to remain free, whereas larger or more adhesive particles tend to be completely engulfed.
co increases both with particle size and adhesive strength, the stability limits (12) and (13) reflect the fact that small or weakly adhesive particles will tend to remain free, whereas larger or more adhesive particles tend to be completely engulfed.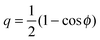 and the stability limits (12) and (13) are then equivalent to d2E/dϕ2|ϕ=0 = 0 and d2E/dϕ2|ϕ=π = 0 as used in ref. 7.
and the stability limits (12) and (13) are then equivalent to d2E/dϕ2|ϕ=0 = 0 and d2E/dϕ2|ϕ=π = 0 as used in ref. 7.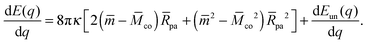
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co in terms of the other curvatures which leads to
co in terms of the other curvatures which leads to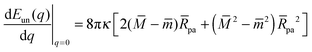
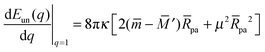
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 2 +
2 + ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′2 − 4
′2 − 4![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′.
′.![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve as an expansion parameter. In the following sections, we will expand the energies of the membrane–particle system up to first order in
pa ≡ Rpa/Rve as an expansion parameter. In the following sections, we will expand the energies of the membrane–particle system up to first order in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa.
pa.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In the absence of large spontaneous curvatures, the mean curvature at any point of a free vesicle will also be of the order of the inverse vesicle size, and we can therefore always take M ∼
(1). In the absence of large spontaneous curvatures, the mean curvature at any point of a free vesicle will also be of the order of the inverse vesicle size, and we can therefore always take M ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In addition, we will be interested in the behavior of the system in the proximity of the stability limits (12) and (13), which implies that the contact mean curvature is also of the order of the inverse vesicle size, Mco ∼
(1). In addition, we will be interested in the behavior of the system in the proximity of the stability limits (12) and (13), which implies that the contact mean curvature is also of the order of the inverse vesicle size, Mco ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/Rve) or
(1/Rve) or ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co ∼
co ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). In this limit, the energy (9) of the bound membrane segment can be rewritten as
(1). In this limit, the energy (9) of the bound membrane segment can be rewritten as![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co)
co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paq +
paq + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ
(κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2).
pa2).![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ
(κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2).
pa2).![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, with
pa, with![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ =
′ = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) +
+ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2).
pa2).![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ
(κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2)
pa2)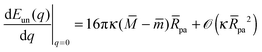
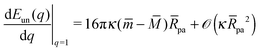
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ ≈
′ ≈ ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) has been used in the last equation. Therefore, to first order in the rescaled particle size
has been used in the last equation. Therefore, to first order in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = Rpa/Rve, the properties of the energy function Eun(q) at the boundaries depend only on those of the free vesicle before engulfment, namely on the quantities Efr and M. In addition, Eun(q) attains a particularly symmetric form in the limit of small
pa = Rpa/Rve, the properties of the energy function Eun(q) at the boundaries depend only on those of the free vesicle before engulfment, namely on the quantities Efr and M. In addition, Eun(q) attains a particularly symmetric form in the limit of small ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, with Eun(0) ≈ Eun(1) and
pa, with Eun(0) ≈ Eun(1) and 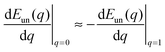 . It is important to note that the derivation of relations (15)–(19) and (23)–(26) did not involve any assumptions concerning the symmetry of the particle–vesicle geometry. In particular, the use of the bound area fraction q as a reaction coordinate makes no assumption about the particular shape of the contact line between the particle and the membrane.
. It is important to note that the derivation of relations (15)–(19) and (23)–(26) did not involve any assumptions concerning the symmetry of the particle–vesicle geometry. In particular, the use of the bound area fraction q as a reaction coordinate makes no assumption about the particular shape of the contact line between the particle and the membrane.
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) )
)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paq(1 − q) +
paq(1 − q) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (κ
(κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2).
pa2).![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , and local mean curvature
, and local mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) at the poles, see Fig. 3. For each of these shapes, we considered a particle at one of the poles and varied the location of the contact line and, thus, the bound area fraction q, imposing the condition that the unbound and bound membrane segments join smoothly along the contact line.33 In all cases studied, the analytical expression (27) was confirmed by the numerical results to first order in the particle-to-vesicle size,
at the poles, see Fig. 3. For each of these shapes, we considered a particle at one of the poles and varied the location of the contact line and, thus, the bound area fraction q, imposing the condition that the unbound and bound membrane segments join smoothly along the contact line.33 In all cases studied, the analytical expression (27) was confirmed by the numerical results to first order in the particle-to-vesicle size, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve, see Fig. 3. In Fig. 3(a), we show how the full numerical results (colored solid lines) approach the first-order term in (27) as we reduce the relative particle size and, thus, higher order correction terms ∼
pa ≡ Rpa/Rve, see Fig. 3. In Fig. 3(a), we show how the full numerical results (colored solid lines) approach the first-order term in (27) as we reduce the relative particle size and, thus, higher order correction terms ∼![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2. These higher order corrections depend on the global geometry of the vesicle, as given by its rescaled volume v and the particular branch of solutions (prolate, oblate, etc.) to which the vesicle shape belongs, whereas the first order term depends only on the local curvature
pa2. These higher order corrections depend on the global geometry of the vesicle, as given by its rescaled volume v and the particular branch of solutions (prolate, oblate, etc.) to which the vesicle shape belongs, whereas the first order term depends only on the local curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) as demonstrated in Fig. 3(b).
as demonstrated in Fig. 3(b).

![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≡ Rpa/Rve, see the inset. The rescaling of the energy follows the analytical expression (27) with
pa ≡ Rpa/Rve, see the inset. The rescaling of the energy follows the analytical expression (27) with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1.063. As the relative particle size becomes smaller, the numerical curves approach the black dashed line q(1 − q) as described by (27); and (b) numerically calculated energies of the unbound segment at q = 1/2 as a function of the rescaled particle size
= −1.063. As the relative particle size becomes smaller, the numerical curves approach the black dashed line q(1 − q) as described by (27); and (b) numerically calculated energies of the unbound segment at q = 1/2 as a function of the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa for the discocyte in (a) and two other vesicle shapes with the rescaled volume v, and spontaneous curvature
pa for the discocyte in (a) and two other vesicle shapes with the rescaled volume v, and spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as given in the inset. At their poles, the oblate and the prolate shapes have mean curvatures
as given in the inset. At their poles, the oblate and the prolate shapes have mean curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0.263 and 1.530, respectively. Negative values of the rescaled particle size correspond to exocytic engulfment; see Appendix B. At
= 0.263 and 1.530, respectively. Negative values of the rescaled particle size correspond to exocytic engulfment; see Appendix B. At ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = 0 all three curves have a common tangent (black dashed line) corresponding to the first-order term in eqn (28).
pa = 0 all three curves have a common tangent (black dashed line) corresponding to the first-order term in eqn (28).![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) between the mean curvature of the membrane at the contact point and the spontaneous curvature. Indeed, it follows from (27) that the energy of the unbound segment at q = 1/2 has the value
between the mean curvature of the membrane at the contact point and the spontaneous curvature. Indeed, it follows from (27) that the energy of the unbound segment at q = 1/2 has the value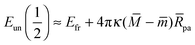
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) >
> ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) but to an energy minimum for
but to an energy minimum for ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) <
< ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . Whenever
. Whenever ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the energy of the unbound membrane segment is independent of q up to first order in the particle size. The particular case
, the energy of the unbound membrane segment is independent of q up to first order in the particle size. The particular case ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0 is consistent with the known results for particles interacting with tensionless planar membranes with no spontaneous curvature,15 in which case the unbound segment forms a catenoidal shape with Eun(q) ≡ 0.
= 0 is consistent with the known results for particles interacting with tensionless planar membranes with no spontaneous curvature,15 in which case the unbound segment forms a catenoidal shape with Eun(q) ≡ 0.
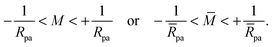
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≪ 1, whereas
pa ≪ 1, whereas ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), the inequalities in (29) are automatically fulfilled in this limit and the resulting constraints on
(1), the inequalities in (29) are automatically fulfilled in this limit and the resulting constraints on ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) do not play any role in the following calculations.
do not play any role in the following calculations.
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, corresponding to small particle-to-vesicle size ratios, and we will ignore higher-order terms
pa, corresponding to small particle-to-vesicle size ratios, and we will ignore higher-order terms ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). Combining expressions (20) and (27) for the energies of the bound and unbound membrane segments, we obtain an analytical expression for the local energy landscape of engulfment as defined by
pa2). Combining expressions (20) and (27) for the energies of the bound and unbound membrane segments, we obtain an analytical expression for the local energy landscape of engulfment as defined by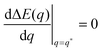 leads to only one solution as given by
leads to only one solution as given by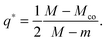
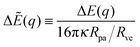
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co)q + (
co)q + (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) )q2.
)q2.
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the contact mean curvature
, the contact mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co, and the local mean curvature
co, and the local mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) of the vesicle membrane. The upper panels (a–e) correspond to
of the vesicle membrane. The upper panels (a–e) correspond to ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co <
co < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the lower panels (f–j) to
, the lower panels (f–j) to ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) <
< ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co. In both rows of panels, the local mean curvature
co. In both rows of panels, the local mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) increases from left to right and the dashed energy functions represent marginal or degenerate cases: (a and f) landscapes for partially engulfed particles with a minimum at qeq = qmin* and 0 < qmin* < 1. The landscape in (a) illustrates the case with
increases from left to right and the dashed energy functions represent marginal or degenerate cases: (a and f) landscapes for partially engulfed particles with a minimum at qeq = qmin* and 0 < qmin* < 1. The landscape in (a) illustrates the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) <
< ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < 2
co < 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co and the one in (f) the case with
co and the one in (f) the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 2
< 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co < Mco; (b–d) landscapes for free or non-engulfed particles with a boundary minimum at qeq = 0. These landscapes are obtained for (b)
co < Mco; (b–d) landscapes for free or non-engulfed particles with a boundary minimum at qeq = 0. These landscapes are obtained for (b) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co which defines the stability limit of the free state as described by eqn (12); (c)
co which defines the stability limit of the free state as described by eqn (12); (c) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co <
co < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 2
< 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co; and (d)
co; and (d) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2
= 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co corresponding to the stability limit of the completely engulfed state as in eqn (13) with
co corresponding to the stability limit of the completely engulfed state as in eqn (13) with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ ≈
′ ≈ ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) . The linear landscape in (c) represents the degenerate case with
. The linear landscape in (c) represents the degenerate case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ; (g–i) landscapes for completely engulfed particles with a boundary minimum at qeq = 1. These landscapes are obtained for (g)
; (g–i) landscapes for completely engulfed particles with a boundary minimum at qeq = 1. These landscapes are obtained for (g) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2
= 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co corresponding to the stability limit of the completely engulfed state, (h) 2
co corresponding to the stability limit of the completely engulfed state, (h) 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co <
co < ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) <
< ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co, and (i)
co, and (i) ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co which defines the stability limit of the free state. The linear landscape in (h) again represents the degenerate case with
co which defines the stability limit of the free state. The linear landscape in (h) again represents the degenerate case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ; (e and j) landscapes for bistable engulfment with an energy barrier at qba = qmax* that is located between the two boundary minima at q = 0 and q = 1. The landscape in (e) illustrates the case with
; (e and j) landscapes for bistable engulfment with an energy barrier at qba = qmax* that is located between the two boundary minima at q = 0 and q = 1. The landscape in (e) illustrates the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 2
> 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co >
co > ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co and the one in (j) the case with
co and the one in (j) the case with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) >
> ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co > 2
co > 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co. In all cases, ΔE(q = 0) = 0 by definition.
co. In all cases, ΔE(q = 0) = 0 by definition.![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, the stability limits Lfr and Lce of the free and completely engulfed state as given by (12) and (13) can be written as M = Mco and M = 2m − Mco, respectively, because
pa, the stability limits Lfr and Lce of the free and completely engulfed state as given by (12) and (13) can be written as M = Mco and M = 2m − Mco, respectively, because ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ =
′ = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) +
+ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2). These stability limits can be directly recovered from expression (33) by imposing q* = qfr = 0 and q* = qce = 1, see relations (34) and (35). In general, expression (31) for the local energy landscape ΔE(q) leads to four qualitatively distinct landscapes corresponding to four distinct stability or engulfment regimes which are separated by the stability limits Lfr and Lce:
pa2). These stability limits can be directly recovered from expression (33) by imposing q* = qfr = 0 and q* = qce = 1, see relations (34) and (35). In general, expression (31) for the local energy landscape ΔE(q) leads to four qualitatively distinct landscapes corresponding to four distinct stability or engulfment regimes which are separated by the stability limits Lfr and Lce:
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st in which the free state at q = qfr = 0 is stable and the completely engulfed state at q = qce = 1 is unstable. The function ΔE(q) as given by eqn (32) must then increase monotonically with increasing q within the physically meaningful interval 0 < q < 1. This monotonic q-dependence applies both to a parabola with its minimum at q = qmin* ≤ 0, which is obtained for Mco ≤ M < m, and for an inverted parabola with its maximum at q = qmax* ≥ 1 as obtained for m < M ≤ 2m − Mco. These two curvature inequalities can be combined into the condition
st in which the free state at q = qfr = 0 is stable and the completely engulfed state at q = qce = 1 is unstable. The function ΔE(q) as given by eqn (32) must then increase monotonically with increasing q within the physically meaningful interval 0 < q < 1. This monotonic q-dependence applies both to a parabola with its minimum at q = qmin* ≤ 0, which is obtained for Mco ≤ M < m, and for an inverted parabola with its maximum at q = qmax* ≥ 1 as obtained for m < M ≤ 2m − Mco. These two curvature inequalities can be combined into the condition![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments)
-segments)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments).
-segments).![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments are displayed in Fig. 4(b)–(d). The inequalities in (47) imply that a free or non-engulfment regime is only present if Mco < m, i.e., if the spontaneous curvature m exceeds the contact mean curvature Mco. For the special case Mco = m, the M-interval in eqn (47) collapses to the single value M = m = Mco, corresponding to the degenerate energy landscape ΔE(q) = 0 for all values of q.
-segments are displayed in Fig. 4(b)–(d). The inequalities in (47) imply that a free or non-engulfment regime is only present if Mco < m, i.e., if the spontaneous curvature m exceeds the contact mean curvature Mco. For the special case Mco = m, the M-interval in eqn (47) collapses to the single value M = m = Mco, corresponding to the degenerate energy landscape ΔE(q) = 0 for all values of q.![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st in which the completely engulfed state at q = qce = 1 is stable, whereas the free state at q = qfr = 0 is unstable. In this case, the function ΔE(q) in (32) must decrease monotonically with increasing q within the whole interval 0 < q < 1. The latter q-dependence applies both to an inverted parabola with its maximum at q = qmax* ≤ 0, which is obtained for m < M ≤ Mco, and to a parabola with its minimum at q = qmin* ≥ 1 as obtained for 2m − Mco ≤ M < m. The two curvature inequalities can be combined into the condition
st in which the completely engulfed state at q = qce = 1 is stable, whereas the free state at q = qfr = 0 is unstable. In this case, the function ΔE(q) in (32) must decrease monotonically with increasing q within the whole interval 0 < q < 1. The latter q-dependence applies both to an inverted parabola with its maximum at q = qmax* ≤ 0, which is obtained for m < M ≤ Mco, and to a parabola with its minimum at q = qmin* ≥ 1 as obtained for 2m − Mco ≤ M < m. The two curvature inequalities can be combined into the condition![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments)
-segments)![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments)
-segments)![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments are displayed in Fig. 4(g)–(i). The inequalities in (49) imply that a complete engulfment regime is only present for 2m − Mco < Mco, i.e., when the contact mean curvature Mco exceeds the spontaneous curvature m. For the special case m = Mco, the M-interval in eqn (49) collapses to the single value M = Mco = m corresponding again to the degenerate energy landscape ΔE(q) = 0 for all values of q.
-segments are displayed in Fig. 4(g)–(i). The inequalities in (49) imply that a complete engulfment regime is only present for 2m − Mco < Mco, i.e., when the contact mean curvature Mco exceeds the spontaneous curvature m. For the special case m = Mco, the M-interval in eqn (49) collapses to the single value M = Mco = m corresponding again to the degenerate energy landscape ΔE(q) = 0 for all values of q.![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are locally stable and separated by an intermediate energy barrier at q = qba = qmax*. Now, the function ΔE(q) in eqn (32) represents an inverted parabola with its maximum located within the interval 0 < qmax* < 1. The parabola is inverted for M > m which implies that the inequalities qmax* > 0 and qmax* < 1 are equivalent to M > Mco and Mco > 2m − M, respectively. Therefore, a membrane segment with mean curvature M belongs to the bistable engulfment regime provided
st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are locally stable and separated by an intermediate energy barrier at q = qba = qmax*. Now, the function ΔE(q) in eqn (32) represents an inverted parabola with its maximum located within the interval 0 < qmax* < 1. The parabola is inverted for M > m which implies that the inequalities qmax* > 0 and qmax* < 1 are equivalent to M > Mco and Mco > 2m − M, respectively. Therefore, a membrane segment with mean curvature M belongs to the bistable engulfment regime provided![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments),
-segments),![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments)
-segments)![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are unstable and the parabolic function ΔE(q) in eqn (32) has its minimum located within the interval 0 < qmin* < 1. Because a (non-inverted) parabola corresponds to M < m, the inequalities qmin* > 0 and qmin* < 1 are equivalent to M < Mco and Mco < 2m − M, respectively. As a consequence, the particles are partially engulfed by a membrane segment with mean curvature M provided
st in which both the free state at q = qfr = 0 and the completely engulfed state at q = qce = 1 are unstable and the parabolic function ΔE(q) in eqn (32) has its minimum located within the interval 0 < qmin* < 1. Because a (non-inverted) parabola corresponds to M < m, the inequalities qmin* > 0 and qmin* < 1 are equivalent to M < Mco and Mco < 2m − M, respectively. As a consequence, the particles are partially engulfed by a membrane segment with mean curvature M provided![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments),
-segments),![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments)
-segments)![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st, whereas convex segments with M > +|Mco| represent
st, whereas convex segments with M > +|Mco| represent ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments and exhibit bistable engulfment behavior.
-segments and exhibit bistable engulfment behavior.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st, complete engulfment regime
st, complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st, bistable engulfment regime
st, bistable engulfment regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st, and partial engulfment regime
st, and partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st on the contact mean curvature Mco and the spontaneous curvature m, for a fixed value of the local mean curvature M; and (b) dependence of the same engulfment regimes on M and m, for a fixed value of Mco. The engulfment diagram in (a) corresponds to inequalities (48), (50), (52) and (54) and the diagram in (b) to relations (47), (49), (51) and (53).
st on the contact mean curvature Mco and the spontaneous curvature m, for a fixed value of the local mean curvature M; and (b) dependence of the same engulfment regimes on M and m, for a fixed value of Mco. The engulfment diagram in (a) corresponds to inequalities (48), (50), (52) and (54) and the diagram in (b) to relations (47), (49), (51) and (53).![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st,
st, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st,
st, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st, and
st, and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st have been previously derived in ref. 7 and 26, but this derivation was based on the numerical observation that, for particles much smaller than the vesicle, partially engulfed states are only stable if both free and completely engulfed states are unstable. Now, we see that this latter condition is a direct consequence of the energy landscape (32) as obtained to first order in the rescaled particle size
st have been previously derived in ref. 7 and 26, but this derivation was based on the numerical observation that, for particles much smaller than the vesicle, partially engulfed states are only stable if both free and completely engulfed states are unstable. Now, we see that this latter condition is a direct consequence of the energy landscape (32) as obtained to first order in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = Rpa/Rve.
pa = Rpa/Rve.![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, deviations from the simple parabolic energy landscape become more and more apparent. In particular, numerical results show that new stability regimes appear, in which stable free and completely engulfed states can coexist with stable ‘satellite’ minima, corresponding to partially engulfed states with very low or very high bound area fraction, q ≳ 0 or q ≲ 1. It is now clear that these deviations are a consequence of higher order terms in the rescaled particle size
pa, deviations from the simple parabolic energy landscape become more and more apparent. In particular, numerical results show that new stability regimes appear, in which stable free and completely engulfed states can coexist with stable ‘satellite’ minima, corresponding to partially engulfed states with very low or very high bound area fraction, q ≳ 0 or q ≲ 1. It is now clear that these deviations are a consequence of higher order terms in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, which are expected to depend on the overall shape of the vesicle as well.
pa, which are expected to depend on the overall shape of the vesicle as well.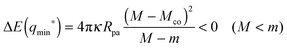
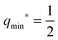 as follows from eqn (32) and (33). In the latter situation, the binding energy attains the particularly simple form
as follows from eqn (32) and (33). In the latter situation, the binding energy attains the particularly simple form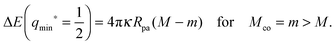
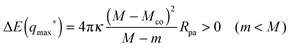
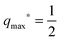 , now defines the transition line at which the free state coexists with the completely engulfed state. Along this transition line, the barrier height has the simple form
, now defines the transition line at which the free state coexists with the completely engulfed state. Along this transition line, the barrier height has the simple form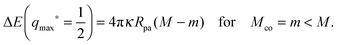
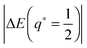 of the typical binding energy or barrier height is proportional to the particle size Rpa and, thus, decreases with decreasing particle size. This dependence is important because the binding energies and barriers heights obtained here are only relevant as long as their magnitude is large compared to the thermal energy. For lipid bilayers with a negligible spontaneous curvature and a typical bending rigidity κ = 20kBT, we have |ΔE(q* = 1/2)| > kBT as long as |M|Rpa > kBT/4πκ ≃ 1/250 with the segment curvature |M| of the order of the inverse vesicle size 1/Rve. As a consequence, if the particle size Rpa is smaller than about Rve/250, the binding energies and energy barriers will be ‘blurred out’ by thermal fluctuations.
of the typical binding energy or barrier height is proportional to the particle size Rpa and, thus, decreases with decreasing particle size. This dependence is important because the binding energies and barriers heights obtained here are only relevant as long as their magnitude is large compared to the thermal energy. For lipid bilayers with a negligible spontaneous curvature and a typical bending rigidity κ = 20kBT, we have |ΔE(q* = 1/2)| > kBT as long as |M|Rpa > kBT/4πκ ≃ 1/250 with the segment curvature |M| of the order of the inverse vesicle size 1/Rve. As a consequence, if the particle size Rpa is smaller than about Rve/250, the binding energies and energy barriers will be ‘blurred out’ by thermal fluctuations.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -,
-, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - or
- or ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments according to the local membrane curvature, depending on whether a particle coming into contact with the membrane at that point belongs to the free or non-engulfment regime
-segments according to the local membrane curvature, depending on whether a particle coming into contact with the membrane at that point belongs to the free or non-engulfment regime ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st, the complete engulfment regime
st, the complete engulfment regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st, the bistable regime
st, the bistable regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st or the partial engulfment regime
st or the partial engulfment regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st.
st.
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments around the north and south poles, a
-segments around the north and south poles, a ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment or -belt around the equator, and two
-segment or -belt around the equator, and two ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments or -rings which connect the
-segments or -rings which connect the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments with the
-segments with the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -belt.
-belt.![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ≡ s/L = s/(2.90Rve)
≡ s/L = s/(2.90Rve)![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment around the north pole is now described by 0 ≤
-segment around the north pole is now described by 0 ≤ ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) <
< ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 = 0.15, the adjacent
1 = 0.15, the adjacent ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segment by
-segment by ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 <
1 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) <
< ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2 = 0.26, the
2 = 0.26, the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -belt by
-belt by ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2 <
2 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) <
< ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3 = 0.74, the lower
3 = 0.74, the lower ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segment by
-segment by ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3 <
3 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) <
< ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4 = 0.85, and the
4 = 0.85, and the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment around the south pole by
-segment around the south pole by ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4 <
4 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ≤ 1. Because of the up-down symmetry of the discocyte shape, the boundary values of the rescaled arc length
≤ 1. Because of the up-down symmetry of the discocyte shape, the boundary values of the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) satisfy the relations
satisfy the relations ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4 = 1 −
4 = 1 − ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 and
1 and ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3 = 1 −
3 = 1 − ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2.
2.
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = 1/2. Because
co = 1/2. Because ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co >
co > ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0, the general classification described in Section 5.2 implies that such a vesicle does not exhibit any
= 0, the general classification described in Section 5.2 implies that such a vesicle does not exhibit any ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -segments and that the rescaled mean curvature
-segments and that the rescaled mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve satisfies
= MRve satisfies![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < −
< −![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = −1/2 for the two
co = −1/2 for the two ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments,
-segments,![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) < 1/2 for
< 1/2 for ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments,
-segments,![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) for
for ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments.
-segments.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) - and the
- and the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments, which are located at
-segments, which are located at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 and
1 and ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4, are characterized by the mean curvature
4, are characterized by the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1/2. Likewise, the boundaries between the
= −1/2. Likewise, the boundaries between the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments and the
-segments and the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -belt have mean curvature
-belt have mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = +1/2, see Fig. 7(a).
= +1/2, see Fig. 7(a).

![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) : (a) rescaled mean curvature
: (a) rescaled mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) of the vesicle membrane, (b) bound area fraction qeq, and (c) global energy landscape ΔEeq = ΔE(qeq). The latter two quantities correspond to the equilibrium state of a particle in contact with the vesicle membrane at
of the vesicle membrane, (b) bound area fraction qeq, and (c) global energy landscape ΔEeq = ΔE(qeq). The latter two quantities correspond to the equilibrium state of a particle in contact with the vesicle membrane at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . For the bistable engulfment regime with
. For the bistable engulfment regime with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 2 = 0.26 <
2 = 0.26 < ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) <
< ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 3 = 0.74, the free particle states with q = qfr = 0 and ΔEfr ≡ ΔE(qfr) are metastable and separated from the equilibrium states by energy barriers at q = qba with barrier heights ΔEba ≡ ΔE(qba). The color of the lines corresponds to the different membrane segments defined in Fig. 6.
3 = 0.74, the free particle states with q = qfr = 0 and ΔEfr ≡ ΔE(qfr) are metastable and separated from the equilibrium states by energy barriers at q = qba with barrier heights ΔEba ≡ ΔE(qba). The color of the lines corresponds to the different membrane segments defined in Fig. 6.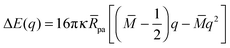
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve of the membrane segment. As we move along the membrane surface of the vesicle, the mean curvature
= MRve of the membrane segment. As we move along the membrane surface of the vesicle, the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) changes and so does the local energy landscape ΔE(q) which attains its maximal or minimal value
changes and so does the local energy landscape ΔE(q) which attains its maximal or minimal value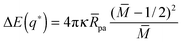
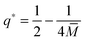
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) on the rescaled arc length
on the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) is displayed in Fig. 7(a). Both the north and the south pole are characterized by the negative mean curvature
is displayed in Fig. 7(a). Both the north and the south pole are characterized by the negative mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1.063 which implies that the local energy landscape (63) has the form of a non-inverted parabola with its minimum located at the bound area fraction qmin* = 0.735 which is equal to the equilibrium area fractions qeq(
= −1.063 which implies that the local energy landscape (63) has the form of a non-inverted parabola with its minimum located at the bound area fraction qmin* = 0.735 which is equal to the equilibrium area fractions qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 0) and qeq(
= 0) and qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1) of the partially engulfed states at the two poles, see Fig. 7(b). As we move away from the two poles, the mean curvature
= 1) of the partially engulfed states at the two poles, see Fig. 7(b). As we move away from the two poles, the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) increases towards zero and the minimum of the local energy landscape is shifted towards larger values of qmin* = qeq(
increases towards zero and the minimum of the local energy landscape is shifted towards larger values of qmin* = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) until we reach qmin* = qeq(
) until we reach qmin* = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1) = qeq(
1) = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4) = 1 corresponding to the mean curvature
4) = 1 corresponding to the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = −1/2. The membrane loci with the latter curvature define the boundaries between the
= −1/2. The membrane loci with the latter curvature define the boundaries between the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) - and
- and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments. Moving further towards the equator of the discocyte, the location qmin* of the energy minimum satisfies qmin* > 1 and, thus, moves out of the physically meaningful interval 0 < q < 1. The particle then attains a completely engulfed state corresponding to the boundary minimum at qeq(
-segments. Moving further towards the equator of the discocyte, the location qmin* of the energy minimum satisfies qmin* > 1 and, thus, moves out of the physically meaningful interval 0 < q < 1. The particle then attains a completely engulfed state corresponding to the boundary minimum at qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) = 1.
) = 1.![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments towards the equator, the mean curvature
-segments towards the equator, the mean curvature ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) vanishes at certain arc length values,
vanishes at certain arc length values, ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 1 + ζ and
1 + ζ and ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) 4 − ζ with ζ = 0.06. For these membrane loci with
4 − ζ with ζ = 0.06. For these membrane loci with ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0, the energy landscape ΔE(q) as given by (63) becomes a linear and monotonically decreasing function of q. Therefore, as we approach
= 0, the energy landscape ΔE(q) as given by (63) becomes a linear and monotonically decreasing function of q. Therefore, as we approach ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0 from negative
= 0 from negative ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) -values, the location qmin* of the energy minimum moves out to infinity. For
-values, the location qmin* of the energy minimum moves out to infinity. For ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 0, on the other hand, the local energy landscape has the form of an inverted parabola, and the location qmax* of its maximum moves out to minus infinity as we approach
> 0, on the other hand, the local energy landscape has the form of an inverted parabola, and the location qmax* of its maximum moves out to minus infinity as we approach ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 0 from positive
= 0 from positive ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) -values. With increasing
-values. With increasing ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) > 0, the maximum of the energy landscape shifts towards less negative values of qmax* until we reach the boundary value qmax* = 0 for membrane curvature M = 1/2. The membrane loci with the latter curvature define the boundaries between the two
> 0, the maximum of the energy landscape shifts towards less negative values of qmax* until we reach the boundary value qmax* = 0 for membrane curvature M = 1/2. The membrane loci with the latter curvature define the boundaries between the two ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments and the
-segments and the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment around the equator. For the latter segment, we have two (meta)stable particle states with area fractions qeq = 0 and qeq = 1 as well as an energy barrier at qba = qmax*, as shown in Fig. 7(b). The location qba of the energy barrier reaches its largest value qba = 0.375 at the equator where the membrane curvature has its largest value
-segment around the equator. For the latter segment, we have two (meta)stable particle states with area fractions qeq = 0 and qeq = 1 as well as an energy barrier at qba = qmax*, as shown in Fig. 7(b). The location qba of the energy barrier reaches its largest value qba = 0.375 at the equator where the membrane curvature has its largest value ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = 2.006, as follows from (65).
= 2.006, as follows from (65).![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) and the engulfment pattern can then be expressed in terms of the function q = qeq(
and the engulfment pattern can then be expressed in terms of the function q = qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) as in Fig. 7(b). We will now use the latter function to define the global energy landscape
) as in Fig. 7(b). We will now use the latter function to define the global energy landscape![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) ≡ ΔE(qeq(
) ≡ ΔE(qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ))
))![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0 and
= 0 and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co = 1/2, the energy
co = 1/2, the energy![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) co)
co)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = −8πκ
pa = −8πκ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa
pa![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) - to a
- to a ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segment. Expression (67) also applies to the completely engulfed states of the
-segment. Expression (67) also applies to the completely engulfed states of the ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segment around the equator. For the latter segment, the free states with qeq = 0 are metastable as well but their energy ΔE(qeq = 0) = 0 is always larger than the energy ΔE(qeq = 1) of the completely engulfed states. The two (meta)stable states are separated by an energy barrier of height ΔE(qba) as given by (64) which attains its largest value ΔE(qba) = 14.212κ
-segment around the equator. For the latter segment, the free states with qeq = 0 are metastable as well but their energy ΔE(qeq = 0) = 0 is always larger than the energy ΔE(qeq = 1) of the completely engulfed states. The two (meta)stable states are separated by an energy barrier of height ΔE(qba) as given by (64) which attains its largest value ΔE(qba) = 14.212κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa at the equator.
pa at the equator.
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) , as illustrated in Fig. 7(c) for a discocyte shape. These one-dimensional energy landscapes can be generalized in two ways. First, we may consider an arbitrary, non-axisymmetric shape of the free vesicle which can be parametrized by a three-dimensional vector,
, as illustrated in Fig. 7(c) for a discocyte shape. These one-dimensional energy landscapes can be generalized in two ways. First, we may consider an arbitrary, non-axisymmetric shape of the free vesicle which can be parametrized by a three-dimensional vector, ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) =
= ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (s1,s2), that depends on two properly chosen surface coordinates, s1 and s2. The latter coordinates determine both the local mean curvature, M = M(s1,s2), of the vesicle membrane and the position of the particle on this membrane. Second, we may vary the bound area fraction q of the particle independently of its position. As a consequence, the most general energy landscape depends on the three parameters s1, s2, and q and this three-dimensional landscape ΔE = ΔE(s1,s2,q) can be directly obtained from the local landscape as given by eqn (32) when we insert the local mean curvature M = M(s1,s2) into this latter equation.
(s1,s2), that depends on two properly chosen surface coordinates, s1 and s2. The latter coordinates determine both the local mean curvature, M = M(s1,s2), of the vesicle membrane and the position of the particle on this membrane. Second, we may vary the bound area fraction q of the particle independently of its position. As a consequence, the most general energy landscape depends on the three parameters s1, s2, and q and this three-dimensional landscape ΔE = ΔE(s1,s2,q) can be directly obtained from the local landscape as given by eqn (32) when we insert the local mean curvature M = M(s1,s2) into this latter equation.
![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) s is the unit tangent vector of the shape contour at arc length s = L
s is the unit tangent vector of the shape contour at arc length s = L![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . The global energy landscape ΔEeq(
. The global energy landscape ΔEeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) depends on the rescaled arc length
) depends on the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) only via the bound area fraction qeq which varies within a
only via the bound area fraction qeq which varies within a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment but is constant within all other segments, as illustrated in Fig. 7(b). The latter property is true in general because
-segment but is constant within all other segments, as illustrated in Fig. 7(b). The latter property is true in general because ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -, or
-, or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments are characterized by boundary minima with qeq = 0 or qeq = 1 and the corresponding energies ΔE(0) = 0 or ΔE(1) = 16πκRpa(m − Mco) do not depend on
-segments are characterized by boundary minima with qeq = 0 or qeq = 1 and the corresponding energies ΔE(0) = 0 or ΔE(1) = 16πκRpa(m − Mco) do not depend on ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . On the other hand, within a
. On the other hand, within a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, the
-segment, the ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependence of qeq arises only from the
-dependence of qeq arises only from the ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependence of the local mean curvature M = M(
-dependence of the local mean curvature M = M(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) as described by eqn (55). Therefore, the gradient of the global energy landscape has the value
) as described by eqn (55). Therefore, the gradient of the global energy landscape has the value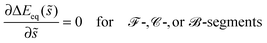
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) -dependent form
-dependent form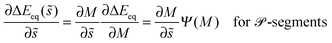
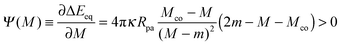
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) via M = M(
via M = M(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ), see the blue segments in Fig. 7(a). Note that Ψ(M) is always positive because
), see the blue segments in Fig. 7(a). Note that Ψ(M) is always positive because ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments are characterized by the curvature inequalities M < Mco < 2m − M according to eqn (54). A combination of relations (68) and (70) then implies that a partially engulfed particle experiences the curvature-induced force
-segments are characterized by the curvature inequalities M < Mco < 2m − M according to eqn (54). A combination of relations (68) and (70) then implies that a partially engulfed particle experiences the curvature-induced force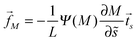
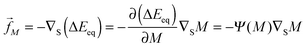
![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (s1,s2), we obtain the two tangent vectors
(s1,s2), we obtain the two tangent vectors ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i ≡ ∂
i ≡ ∂![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) /∂si with i = 1,2 that span the plane tangential to the vesicle surface, the metric tensor gij =
/∂si with i = 1,2 that span the plane tangential to the vesicle surface, the metric tensor gij = ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) i·
i·![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) j, and the inverse metric tensor (gij) ≡ (gij)−1. The action of the gradient operator ∇S onto any scalar function U(s1,s2) is then given by34
j, and the inverse metric tensor (gij) ≡ (gij)−1. The action of the gradient operator ∇S onto any scalar function U(s1,s2) is then given by34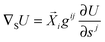
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) M, as given by eqn (72) or (73), partially engulfed particles undergo biased diffusion towards membrane segments with lower curvature, whereas completely engulfed particles do not experience any curvature-induced force and diffuse freely on
M, as given by eqn (72) or (73), partially engulfed particles undergo biased diffusion towards membrane segments with lower curvature, whereas completely engulfed particles do not experience any curvature-induced force and diffuse freely on ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - and
- and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segments. However, if a completely engulfed particle diffuses from a
-segments. However, if a completely engulfed particle diffuses from a ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) - or
- or ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) -segment onto an
-segment onto an ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) - or
- or ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, it will unbind or partially unwrap from the membrane. Once on the
-segment, it will unbind or partially unwrap from the membrane. Once on the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment, the particle will be pulled towards a membrane segment of minimal mean curvature. At temperature T, the probability to find the particle at a certain position,
-segment, the particle will be pulled towards a membrane segment of minimal mean curvature. At temperature T, the probability to find the particle at a certain position, ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (s1,s2), on the membrane is then proportional to the Boltzmann factor exp[−ΔEeq(
(s1,s2), on the membrane is then proportional to the Boltzmann factor exp[−ΔEeq(![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) )/kBT].
)/kBT].![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st-regime, we will now consider Janus particles with surfaces that are divided into one adhesive and one non-adhesive domain. The adhesive surface domain is taken to form a spherical cap with area A1 which implies a circular domain boundary of the adhesive surface domain and leads to the adhesive surface area fraction
st-regime, we will now consider Janus particles with surfaces that are divided into one adhesive and one non-adhesive domain. The adhesive surface domain is taken to form a spherical cap with area A1 which implies a circular domain boundary of the adhesive surface domain and leads to the adhesive surface area fraction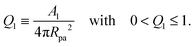
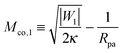
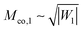 for large |W1|. A membrane segment with local mean curvature M will start to spread over such an adhesive surface domain provided the free state is unstable which implies dΔE/dq|q=0 < 0 or
for large |W1|. A membrane segment with local mean curvature M will start to spread over such an adhesive surface domain provided the free state is unstable which implies dΔE/dq|q=0 < 0 or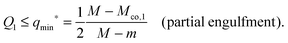
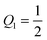 and
and 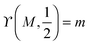 .
.
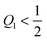 and
and 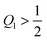 , respectively, and has the value ϒ(M,Q1) = m for
, respectively, and has the value ϒ(M,Q1) = m for 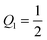 . Therefore, full coverage of the adhesive surface domain is achieved by all membrane segments if
. Therefore, full coverage of the adhesive surface domain is achieved by all membrane segments if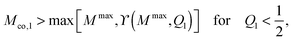
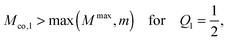
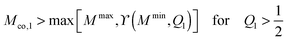
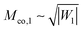 so that one of the conditions (85)–(87), corresponding to the chosen value of Q1, is satisfied. The Janus particles are then always partially engulfed with the bound membrane segment covering the whole area A1 of the adhesive surface domain, and the equilibrium value of the bound area fraction is given by qJPeq = Q1 irrespective of the location of the Janus particle on the vesicle membrane.
so that one of the conditions (85)–(87), corresponding to the chosen value of Q1, is satisfied. The Janus particles are then always partially engulfed with the bound membrane segment covering the whole area A1 of the adhesive surface domain, and the equilibrium value of the bound area fraction is given by qJPeq = Q1 irrespective of the location of the Janus particle on the vesicle membrane.
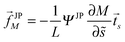
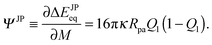
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) JPM = −16πκRpaQ1(1 − Q1)∇SM
JPM = −16πκRpaQ1(1 − Q1)∇SM![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) for adhesive hemispheres with Q1 = 1/2. For general values of Q1, the binding energy difference has the form
for adhesive hemispheres with Q1 = 1/2. For general values of Q1, the binding energy difference has the form![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) paQ1(1 − Q1)(
paQ1(1 − Q1)(![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) min)
min)![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) −
− ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) min. The rescaled arc length
min. The rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) is again defined by eqn (59), where L denotes the total contour length of the respective vesicle shape. Thus, the parameter
is again defined by eqn (59), where L denotes the total contour length of the respective vesicle shape. Thus, the parameter ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) varies from
varies from ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 0 at the north pole to
= 0 at the north pole to ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1 at the south pole for all vesicle shapes displayed in Fig. 8(a)–(c).
= 1 at the south pole for all vesicle shapes displayed in Fig. 8(a)–(c).

![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) parametrizes the shape contour from the north pole with
parametrizes the shape contour from the north pole with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 0 to the south pole with
= 0 to the south pole with ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1; and (d) energy landscapes ΔΔEJPeq, experienced by a half-adhesive Janus particle as a function of the rescaled arc length
= 1; and (d) energy landscapes ΔΔEJPeq, experienced by a half-adhesive Janus particle as a function of the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) . These energy landscapes are obtained from the mean curvature M of the vesicle membranes via expression (95) with Q1 = 1/2. The energy landscapes for the prolate and discocyte shapes are symmetric with respect to
. These energy landscapes are obtained from the mean curvature M of the vesicle membranes via expression (95) with Q1 = 1/2. The energy landscapes for the prolate and discocyte shapes are symmetric with respect to ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1/2 where they exhibit a minimum and maximum, respectively. The energy landscape for the stomatocyte has a maximum at
= 1/2 where they exhibit a minimum and maximum, respectively. The energy landscape for the stomatocyte has a maximum at ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) =
= ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto 0.55, corresponding to the vertical dotted line in (d) and to the black diamond in (c) and (e) positional probabilities ρ of a half-adhesive Janus particle with radius
sto 0.55, corresponding to the vertical dotted line in (d) and to the black diamond in (c) and (e) positional probabilities ρ of a half-adhesive Janus particle with radius ![[R with combining overline]](https://www.rsc.org/images/entities/i_char_0052_0305.gif) pa = 0.01 as a function of arc length
pa = 0.01 as a function of arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) for the three vesicle shapes in (a)–(c). The probability ρ is proportional to the Boltzmann factor exp[−ΔΔEJPeq(
for the three vesicle shapes in (a)–(c). The probability ρ is proportional to the Boltzmann factor exp[−ΔΔEJPeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) )/kBT] and normalized with
)/kBT] and normalized with 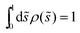 . The three examples shown here correspond to kBT = κ/20.
. The three examples shown here correspond to kBT = κ/20.![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) =
= ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto ≃ 0.55, right outside of the membrane neck, as indicated by the black diamond in Fig. 8(c). In order to reach the inner membrane segment, a particle attached to the outer segment will have to overcome this energy barrier, whose height is approximately 2κ
sto ≃ 0.55, right outside of the membrane neck, as indicated by the black diamond in Fig. 8(c). In order to reach the inner membrane segment, a particle attached to the outer segment will have to overcome this energy barrier, whose height is approximately 2κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa for a stomatocyte with rescaled volume v = 0.4, as displayed in Fig. 8(c). This implies that particles can spontaneously overcome this barrier via thermal diffusion only if they are sufficiently small. A crossover value
pa for a stomatocyte with rescaled volume v = 0.4, as displayed in Fig. 8(c). This implies that particles can spontaneously overcome this barrier via thermal diffusion only if they are sufficiently small. A crossover value ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa for the particle radius can be estimated from the requirement that 2κ
†pa for the particle radius can be estimated from the requirement that 2κ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa ≃ kBT which implies
†pa ≃ kBT which implies ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa ≃ 1/40, assuming a typical bending rigidity for lipid membranes κ = 20kBT. Small particles with radii
†pa ≃ 1/40, assuming a typical bending rigidity for lipid membranes κ = 20kBT. Small particles with radii ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≲
pa ≲ ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa will not encounter any significant barrier, whereas large particles with
†pa will not encounter any significant barrier, whereas large particles with ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≫
pa ≫ ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) †pa will be trapped in the outer membrane segment for a long time. As soon as a Janus particle has overcome the energy barrier close to the membrane neck, it will be strongly pulled through the neck region towards the central part of the invagination as follows from the strong decay of the stomatocyte's energy landscape ΔΔEJPeq for
†pa will be trapped in the outer membrane segment for a long time. As soon as a Janus particle has overcome the energy barrier close to the membrane neck, it will be strongly pulled through the neck region towards the central part of the invagination as follows from the strong decay of the stomatocyte's energy landscape ΔΔEJPeq for ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) >
> ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) sto, as depicted in Fig. 8(d).
sto, as depicted in Fig. 8(d).![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st in which only the free particle state is stable, a completely engulfed regime
st in which only the free particle state is stable, a completely engulfed regime ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st in which only the completely engulfed state is stable, a partially engulfed regime
st in which only the completely engulfed state is stable, a partially engulfed regime ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st in which only the partially engulfed state is stable, and a bistable regime
st in which only the partially engulfed state is stable, and a bistable regime ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st in which both the free and the completely engulfed states are stable and separated by an energy barrier. We then used this empirical observation to describe the interaction of nanoparticles with complex-shaped vesicles in ref. 26. Because of the local energy landscape derived in the present paper, see eqn (32) and Fig. 4, we now understand that these previous results directly follow from the energetics of the system up to first order in Rpa/Rve. Deviations from this behavior will always be a signature of higher order terms in Rpa/Rve, which are expected to depend on the global shape of the vesicle.
st in which both the free and the completely engulfed states are stable and separated by an energy barrier. We then used this empirical observation to describe the interaction of nanoparticles with complex-shaped vesicles in ref. 26. Because of the local energy landscape derived in the present paper, see eqn (32) and Fig. 4, we now understand that these previous results directly follow from the energetics of the system up to first order in Rpa/Rve. Deviations from this behavior will always be a signature of higher order terms in Rpa/Rve, which are expected to depend on the global shape of the vesicle.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments, the equilibrium state corresponds to a smooth minimum with qeq = qmin* and 0 < qmin*<1. For all other engulfment regimes, the equilibrium state is provided by a boundary minimum with qeq = qfr = 0 or qeq = qce = 1. As we move along the membrane of a complex-shaped vesicle, the membrane's mean curvature M changes in a continuous manner and so does the local energy landscape as well as the associated equilibrium state qeq. We can then use the energy ΔE(qeq) of the equilibrium particle states to define a global energy landscape ΔEeq for all points on the vesicle membrane. If the vesicle is axisymmetric, its shape can be parametrized by the rescaled arc length
-segments, the equilibrium state corresponds to a smooth minimum with qeq = qmin* and 0 < qmin*<1. For all other engulfment regimes, the equilibrium state is provided by a boundary minimum with qeq = qfr = 0 or qeq = qce = 1. As we move along the membrane of a complex-shaped vesicle, the membrane's mean curvature M changes in a continuous manner and so does the local energy landscape as well as the associated equilibrium state qeq. We can then use the energy ΔE(qeq) of the equilibrium particle states to define a global energy landscape ΔEeq for all points on the vesicle membrane. If the vesicle is axisymmetric, its shape can be parametrized by the rescaled arc length ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) of the shape contour, see eqn (59), and the global energy landscape is obtained via ΔEeq(
of the shape contour, see eqn (59), and the global energy landscape is obtained via ΔEeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) ) = ΔE(qeq(
) = ΔE(qeq(![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) )) as in eqn (66). One example is provided by the discocyte shape in Fig. 6 with its global energy landscape depicted in Fig. 7(c).
)) as in eqn (66). One example is provided by the discocyte shape in Fig. 6 with its global energy landscape depicted in Fig. 7(c).![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) - or
- or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments of the vesicle membrane, the equilibrium states of the particles correspond to the boundary minima of the local energy landscapes with qeq = qfr = 0 or qeq = qfr = 0. The corresponding energies ΔE(0) = 0 and ΔE(1) = 16πκ(m − Mco)Rpa as in eqn (42) do not depend on the local mean curvature M of the segments. As a consequence, the global energy landscape ΔEeq = const for these three types of membrane segments, see Fig. 7(c), and, thus, does not lead to any curvature-induced forces on the particles.
-segments of the vesicle membrane, the equilibrium states of the particles correspond to the boundary minima of the local energy landscapes with qeq = qfr = 0 or qeq = qfr = 0. The corresponding energies ΔE(0) = 0 and ΔE(1) = 16πκ(m − Mco)Rpa as in eqn (42) do not depend on the local mean curvature M of the segments. As a consequence, the global energy landscape ΔEeq = const for these three types of membrane segments, see Fig. 7(c), and, thus, does not lead to any curvature-induced forces on the particles.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segments, on the other hand, the equilibrium states are provided by the smooth minima of the local energy landscapes with qeq = qmin* and 0 < qmin* < 1. The latter minima depend on the local mean curvature M as described by eqn (55) and, thus, change as the particle moves along a
-segments, on the other hand, the equilibrium states are provided by the smooth minima of the local energy landscapes with qeq = qmin* and 0 < qmin* < 1. The latter minima depend on the local mean curvature M as described by eqn (55) and, thus, change as the particle moves along a ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) -segment with variable mean curvature M. When the particles originate from the exterior solution (endocytosis), the binding energy ΔEeq = ΔE* of the partially engulfed particles is reduced when they move towards membrane segments with lower mean curvature M. In contrast, partially engulfed particles that originate from the interior solution (exocytosis), reduce their binding energy when they move towards membrane segments with higher mean curvature M, see Appendix B. The corresponding curvature-induced forces acting onto particles with a chemically uniform surface have the explicit form as given by eqn (72) for axisymmetric vesicles and by eqn (73) for arbitrarily shaped membranes.
-segment with variable mean curvature M. When the particles originate from the exterior solution (endocytosis), the binding energy ΔEeq = ΔE* of the partially engulfed particles is reduced when they move towards membrane segments with lower mean curvature M. In contrast, partially engulfed particles that originate from the interior solution (exocytosis), reduce their binding energy when they move towards membrane segments with higher mean curvature M, see Appendix B. The corresponding curvature-induced forces acting onto particles with a chemically uniform surface have the explicit form as given by eqn (72) for axisymmetric vesicles and by eqn (73) for arbitrarily shaped membranes.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) -,
-, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) - or
- or ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) -segments of the vesicle membrane. On the other hand, if several partially engulfed particles are present on the vesicle surface, membrane-mediated particle–particle interactions are expected to be important when the particles come close to each other,36,37 and particles may cluster into tubes31 or buds.38 The latter process provides an example of domain-induced budding in which the domains acquire a spontaneous curvature arising from the asymmetry of the membrane-bound particles.39,40
-segments of the vesicle membrane. On the other hand, if several partially engulfed particles are present on the vesicle surface, membrane-mediated particle–particle interactions are expected to be important when the particles come close to each other,36,37 and particles may cluster into tubes31 or buds.38 The latter process provides an example of domain-induced budding in which the domains acquire a spontaneous curvature arising from the asymmetry of the membrane-bound particles.39,40![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa up to first order in the rescaled particle size
pa up to first order in the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, with C being a dimensionless coefficient of order one. In contrast, the local energy landscape as given by eqn (32) is proportional to 16πκ
pa, with C being a dimensionless coefficient of order one. In contrast, the local energy landscape as given by eqn (32) is proportional to 16πκ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa ≃ 1000kBT
pa ≃ 1000kBT![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa. Therefore, entropic contributions to this local energy landscape can be safely ignored in typical cases.
pa. Therefore, entropic contributions to this local energy landscape can be safely ignored in typical cases.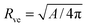 as the basic length scale and the bending rigidity κ as the basic energy scale which leads to the rescaled volume v as in (4) and the rescaled particle size
as the basic length scale and the bending rigidity κ as the basic energy scale which leads to the rescaled volume v as in (4) and the rescaled particle size ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa = Rpa/Rve as well as the rescaled curvatures
pa = Rpa/Rve as well as the rescaled curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve,
= MRve, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ = M′Rve, and
′ = M′Rve, and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. In addition, we will also use the rescaled energies
= mRve. In addition, we will also use the rescaled energies![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . For small values of the spontaneous curvature
. For small values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ∼
∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), these shapes are axisymmetric and can be calculated via numerical solution of the so-called shape equations.28 One finds three different branches of stable solutions depending on the values of v and
(1), these shapes are axisymmetric and can be calculated via numerical solution of the so-called shape equations.28 One finds three different branches of stable solutions depending on the values of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , namely the oblate, prolate and stomatocyte branches. Let us assume that we follow the bending energy of the vesicle as a function of v and
, namely the oblate, prolate and stomatocyte branches. Let us assume that we follow the bending energy of the vesicle as a function of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . By solving the shape equations for the free vesicle, one obtains the bending energy of the free vesicle in the form Ēfr = Fj(v,
. By solving the shape equations for the free vesicle, one obtains the bending energy of the free vesicle in the form Ēfr = Fj(v,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ), where the subscript j indicates the branch.
), where the subscript j indicates the branch.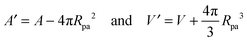
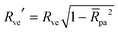
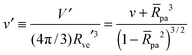
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′ ≡ mRve′ =
′ ≡ mRve′ = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (1 −
(1 − ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2)1/2
pa2)1/2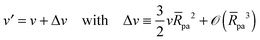
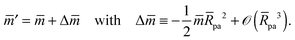
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′) = Fj(v + Δv,
′) = Fj(v + Δv,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) + Δ
+ Δ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) )
)![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa now leads to
pa now leads to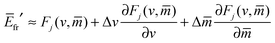
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2).
pa2).![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa, the bending energy Ēfr′ of the mother vesicle after engulfment is equal to the bending energy Ēfr of the free vesicle.
pa, the bending energy Ēfr′ of the mother vesicle after engulfment is equal to the bending energy Ēfr of the free vesicle.
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) at a given point P of the vesicle. For the free vesicle, we envisage a relation of the form
at a given point P of the vesicle. For the free vesicle, we envisage a relation of the form ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = MRve = fj,P(v,
= MRve = fj,P(v,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ). For the unbound membrane segment of the mother vesicle after engulfment, we then have the analogous relation M′Rve′ = fj,P(v′,
). For the unbound membrane segment of the mother vesicle after engulfment, we then have the analogous relation M′Rve′ = fj,P(v′,![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′) or
′) or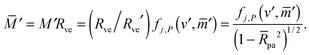
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′, an expansion in powers of v′ − v and
′, an expansion in powers of v′ − v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ′ −
′ − ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) leads to
leads to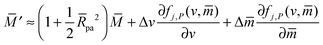
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ′ =
′ = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) +
+ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa2),
pa2),![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) pa.
pa.
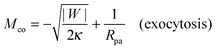
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) st for 2m − Mco ≤ M ≤ Mco;
st for 2m − Mco ≤ M ≤ Mco;![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) st for Mco ≤ M ≤ 2m − Mco;
st for Mco ≤ M ≤ 2m − Mco;![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) st for M < Mco < 2m − M; and
st for M < Mco < 2m − M; and![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) st for 2m − M < Mco < M.
st for 2m − M < Mco < M.