DOI:
10.1039/C6SM02643E
(Paper)
Soft Matter, 2017,
13, 1267-1275
Analytical form of the autocorrelation function for the fluorescence correlation spectroscopy†
Received
23rd November 2016
, Accepted 10th January 2017
First published on 13th January 2017
Abstract
Fluorescence correlation spectroscopy (FCS) can provide information about diffusion coefficients and rate constants of chemical reactions in small systems of interacting molecules. However, the interpretation of FCS experiments depends crucially on the model of the autocorrelation function for the fluorescence intensity fluctuations. In this theoretical work, we consider a system of fluorescent molecules that diffuse and interact with massive particles, e.g. surfactant micelles. Using the general formalism of FCS, we derive a new analytical approximation of the autocorrelation function for systems in which both diffusion and a binary reaction occur. This approximation provides a smooth interpolation between the limit of fast reaction (much faster than diffusion), and the opposite limit of slow reaction. Our studies of noncovalent interactions of micelles with dyes by FCS provided an experimental case to which the approximate autocorrelation function was successfully applied [X. Zhang, A. Poniewierski, A. Jelińska, A. Zagożdżon, A. Wisniewska, S. Hou and R. Hołyst, Soft Matter, 2016, 12, 8186–8194].
1 Introduction
Fluorescence correlation spectroscopy is an experimental technique to study dynamics of various complex systems at a molecular level. It takes advantage of thermal noise present in any macroscopic system due to the atomic structure of matter. FCS is based on the measurement of fluctuations in the fluorescence intensity in a small observation volume of the solution defined by an incident beam of light. In turn, the intensity fluctuations are caused by the fluctuations in the concentration of fluorescent molecules or particles in the illuminated volume. Since such fluctuations are relatively large at low concentration of fluorescent species, FCS is a suitable tool for applications in analytical chemistry, biophysics and cell biology. There are also other possible sources of fluctuations in the fluorescence intensity, such as rotational diffusion, triplet-state excitation or conformational motions. Modern implementations of FCS and examples of its application can be found in a review article by Krichevsky and Bonnet1 but the principles of this method were presented a long time ago in a series of papers by Magde et al.2–4 The advantage of FCS is that it does not require any external perturbation of the system studied, which can be either in an equilibrium state or in a nonequilibrium steady state.5 For example, FCS was used to monitor fast biochemical kinetic processes, such as formation of supramolecular complexes with dye molecules,6,7 to measure interaction of labeled molecules with immobile binding sites within live cells,8 or to explore protein dynamics in the microsecond time region.9
Diffusion of fluorescently labeled molecules can also be studied by a related technique called fluorescence recovery after photobleaching (FRAP).10–13 Both FCS and FRAP are used to estimate diffusion coefficients. For example, the movement of messenger molecules, which are responsible for regulation of various processes in cells, usually occurs in the presence of traps. The combination of diffusion and reactions with traps can be described in terms of an effective concentration-dependent diffusion coefficient which is smaller than the diffusion coefficient in a medium without traps. Since FCS and FRAP use different ways of averaging over ensembles of particles, a question arises what effective diffusion coefficients are actually measured by these techniques.11,13–15 We should also mention other approaches to extract rate constants of second-order chemical reactions which frequently appear in chemistry and biology. One of them is the observation of reaction-diffusion processes in a microchannel.16 Another method called equilibrium capillary electrophoresis of equilibrium mixtures was used by Mironov et al.17 to determine the equilibrium and rate constants for weak noncovalent interactions. They studied a fast binary reaction in which a ligand binds reversibly to a target forming a complex.
The object of interest of FCS experiments is the autocorrelation function of intensity fluctuations defined as:1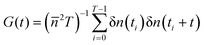 , where n(t) is the number of collected photons in the time interval Δt, δn(t) = n(t) −
, where n(t) is the number of collected photons in the time interval Δt, δn(t) = n(t) − ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is its deviation from the mean value
is its deviation from the mean value ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , and T is the total number of accumulated sampling intervals Δt. If the system is ergodic, which is usually assumed, the time average can be replaced by an ensemble average (denoted 〈
, and T is the total number of accumulated sampling intervals Δt. If the system is ergodic, which is usually assumed, the time average can be replaced by an ensemble average (denoted 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉), i.e., G(t) = 〈δn(0)δn(t)〉/
〉), i.e., G(t) = 〈δn(0)δn(t)〉/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) 2. Then δn(t) is connected to the concentration fluctuations of the fluorescent components and the formalism of statistical mechanics is used to express G(t) in terms of the kinetic processes present in the system. If these fluctuations are due to diffusion and chemical reactions the measurement of G(t) can provide information about the diffusion coefficients of fluorescent molecules as well as rate constants of the chemical reactions. It was first demonstrated by Magde et al.2 for the reversible binding of ethidium bromide (EtBr) to DNA: EtBr + DNA ⇄ EtBr·DNA, where EtBr is a small interacting dye and the complex EtBr·DNA is strongly fluorescent. Finally, we note that to study biochemical systems also high-order fluorescence correlation analysis can be used, besides G(t).18
2. Then δn(t) is connected to the concentration fluctuations of the fluorescent components and the formalism of statistical mechanics is used to express G(t) in terms of the kinetic processes present in the system. If these fluctuations are due to diffusion and chemical reactions the measurement of G(t) can provide information about the diffusion coefficients of fluorescent molecules as well as rate constants of the chemical reactions. It was first demonstrated by Magde et al.2 for the reversible binding of ethidium bromide (EtBr) to DNA: EtBr + DNA ⇄ EtBr·DNA, where EtBr is a small interacting dye and the complex EtBr·DNA is strongly fluorescent. Finally, we note that to study biochemical systems also high-order fluorescence correlation analysis can be used, besides G(t).18
In this theoretical work and the accompanying experimental paper,19 we apply FCS to study the kinetics of binary reactions A + B ⇄ C. The theoretical model of the autocorrelation function introduced by Elson and Magde,3 modified later by Krichevsky and Bonnet,1 is based on linearized reaction-diffusion equations. We use this model to derive an approximate formula for G(t), which is then applied to fit the experimental data.19 In our case, A is a surfactant micelle and B is a fluorescent dye that reacts with A to form complex C through noncovalent interactions. It is known that physical aggregation of the dye to the micelle can be used to study formation of micelles by FCS, in particular, the aggregate size and critical micelle concentration.20,21 However, in contrast to the reaction of EtBr with DNA, the fluorescence of the dye does not change after binding to the micelle. This makes determination of the reaction rates more difficult because the general analytical form of G(t) is not known and simple expressions for it are obtained only in two cases: (1) free diffusion and (2) the limit of fast reaction. In case (2), G(t) has a similar form as for free diffusion of two components but with an effective concentration-dependent diffusion coefficient, plus a term characteristic of chemical reaction. This additional term decays exponentially with time and vanishes when the optical properties of the dye and complex are the same.
Our paper is organized as follows. In the next section, we recall briefly the theoretical model of the autocorrelation function. In Section 3, we present our approximate analytical form of the autocorrelation function, Ga(t), and compare it with G(t) computed directly from the theoretical model. We also discuss applications of Ga(t) to selected problems. Finally, Section 4 is devoted to conclusions. The derivation of Ga(t) and other mathematical details can be found in ESI.†
2 Theoretical model
2.1 Concentration fluctuations
The reactionis characterized by the equilibrium constant| | 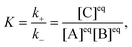 | (2) |
where k+ and k− are the rate constants for the forward and backward reaction, respectively, and [j]eq, j = A, B, C, denote the equilibrium concentrations. The local concentration Cj depends on the space point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and time t, and it fluctuates around the equilibrium value due to diffusion and the chemical reaction. Its fluctuations are defined by δCj(
and time t, and it fluctuates around the equilibrium value due to diffusion and the chemical reaction. Its fluctuations are defined by δCj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = Cj(
,t) = Cj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) − [j]eq and the linearized kinetic equations for the fluctuations of all components in an ideal solution assume the following form1,3
,t) − [j]eq and the linearized kinetic equations for the fluctuations of all components in an ideal solution assume the following form1,3| | 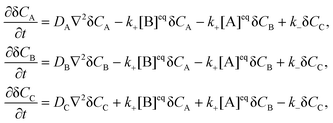 | (3) |
where DA, DB and DC denote the corresponding diffusion coefficients. These coupled partial differential equations are transformed to a set of ordinary differential equations by means of Fourier transform:| | 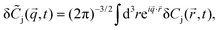 | (4) |
and then solved by the standard method of normal modes (ESI†). In what follows we assume that the binding of a dye to a much bigger micelle does not affect the diffusion coefficient of the complex, hence DA = DC = D ≪ DB.
2.2 FCS autocorrelation function
It is assumed that the illumination intensity profile, I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), is Gaussian:1
), is Gaussian:1| | 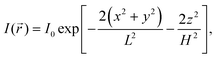 | (5) |
where H and L are the sizes of the beam waist in the direction of the propagation of light and in the perpendicular direction, respectively, and the aspect ratio ω = H/L is usually greater than 1. The value of ω measured in our experimental studies was close to 5.19 In principle, it is possible to change ω by changing the diameter of the beam waist L. It can be achieved by means of stimulated emission depletion (STED) far-field fluorescence nanoscopy, which allows to spatially resolve heterogeneous dynamics in complex systems.22,23 We return to this point in Section 3.
The autocorrelation function of our interest is given by
| | 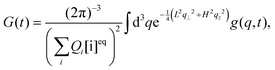 | (6) |
where
| | 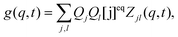 | (7) |
and
Qk is the product of the absorption cross section by the fluorescence quantum yield and the efficiency of fluorescence for the component
k. The matrix
Zjl(
q,
t) is related to the correlations of concentration fluctuations as follows
| | 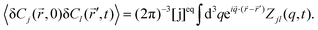 | (8) |
Moreover, it is assumed that at
t = 0 the concentration fluctuations of different components, or of the same component at different space points, are not correlated,
i.e.,
| | 〈δCj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,0)δCk( ,0)δCk(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′,0)〉 = [j]eqδjkδ( ′,0)〉 = [j]eqδjkδ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) − − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′), ′), | (9) |
where δ(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
−
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
′) is the Dirac
δ-function in three dimensions. In our case, component A is not fluorescent (
QA = 0), thus
| | | g(q,t) = QB2[B]eqZBB(q,t) + 2QBQC[B]eqZBC(q,t) + QC2[C]eqZCC(q,t), | (10) |
where we have used the relation [C]
eqZCB = [B]
eqZBC. The explicit expressions for
ZBB,
ZBC and
ZCC in terms of the eigenvalues and eigenvectors are presented in ESI.
† The form of
G(
t) depends on the relation between the chemical relaxation rate for
reaction (1):
R =
k+([A]
eq + [B]
eq) +
k−, and the diffusion times of the fluorescent components B and C through the focal volume, defined by
τB =
L2/(4
DB) and
τC =
τA =
L2/(4
D), respectively.
2.3 Limiting cases
It is instructive to consider the two limits: fast reaction and fast diffusion. The first limit corresponds to reactions that are much faster than the diffusion time of the dye (R−1 ≪ τB). The second limit corresponds to reactions whose relaxation time is much longer than the diffusion time of the slower component, i.e., R−1 ≫ τA ≫ τB. These two cases are particularly simple as G(t) becomes a combination of the normalized autocorrelation functions for one-component diffusion in three dimensions: h(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = (1 +
) = (1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) )−1(1 +
)−1(1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) /ω2)−1/2, where
/ω2)−1/2, where ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) is the lag time expressed in the units of the appropriate diffusion time. In this work, all autocorrelation functions at t = 0 are normalized to unity.
is the lag time expressed in the units of the appropriate diffusion time. In this work, all autocorrelation functions at t = 0 are normalized to unity.
2.3.1 Fast reaction.
In the limit of fast reaction (R → ∞), the following formula for the autocorrelation function holds:| | G∞(t) = {yβQC2h(t/τA) + (1 − y)[QB(1 − β) + QCβ]2h(t/τ+) + (1 − y)β(1 − β)(QB − QC)2e−Rth(t/τ−)}/![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) 2, 2, | (11) |
where ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) 2 = QB2(1 − y)(1 − β) + QC2β, τ± = L2/(4D±), and D+ = Dβ + DB(1 − β), D− = D(1 − β) + DBβ are effective concentration-dependent diffusion coefficients. The parameters β = k+[A]eq/R and y = K[B]eq/(1 + K[B]eq) are dimensionless and can vary from 0 to 1. G∞(t) can be treated as the first term of the asymptotic expansion of G(t) in the powers of R−1. In eqn (11), only the last term depends on the kinetics of the chemical reaction but it vanishes when the optical properties of the complex and dye are the same (QB = QC). Then it is necessary to include the terms of order R−1 or higher to determine the relaxation rate.
2 = QB2(1 − y)(1 − β) + QC2β, τ± = L2/(4D±), and D+ = Dβ + DB(1 − β), D− = D(1 − β) + DBβ are effective concentration-dependent diffusion coefficients. The parameters β = k+[A]eq/R and y = K[B]eq/(1 + K[B]eq) are dimensionless and can vary from 0 to 1. G∞(t) can be treated as the first term of the asymptotic expansion of G(t) in the powers of R−1. In eqn (11), only the last term depends on the kinetics of the chemical reaction but it vanishes when the optical properties of the complex and dye are the same (QB = QC). Then it is necessary to include the terms of order R−1 or higher to determine the relaxation rate.
2.3.2 Fast diffusion.
In the limit of fast diffusion (R → 0), ZBC(q,t) does not contribute to g(q,t) and the autocorrelation function is given by| | 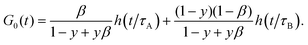 | (12) |
To express the amplitudes in (11) and (12) we have used the identity: β[B]eq = (1 − y)(1 − β)[C]eq (see ESI†).
3 Results and discussion
To the best of our knowledge the general explicit formula for the autocorrelation function defined by eqn (6) is not known. Although the integral over the wave vectors can be performed numerically, it is desirable to have a simple ansatz for G(t), especially if both fast and slow reactions are to be studied. However, the power expansion in R−1 becomes problematic in the case of slow reactions. Here we propose such an ansatz. It is based on the observation that the integrand in eqn (6) simplifies both for small and large wave vectors. Therefore, we split the integration over q into two intervals: 0 < q < qc and q > qc, where 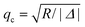 and Δ = D − DB < 0. In what follows we assume that QB = QC = Q19 but the general situation of different fluorescence of the free dye and complex is considered in ESI† (see also Section 3.1.2).
and Δ = D − DB < 0. In what follows we assume that QB = QC = Q19 but the general situation of different fluorescence of the free dye and complex is considered in ESI† (see also Section 3.1.2).
3.1 Approximate FCS autocorrelation function
The approximate autocorrelation function is given by the following formula (ESI†):| | 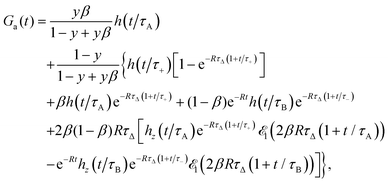 | (13) |
where hz(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = (1 +
) = (1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) /ω2)−1/2 and τΔ = L2/(4|Δ|). For convenience, we have introduced the function
/ω2)−1/2 and τΔ = L2/(4|Δ|). For convenience, we have introduced the function 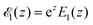 , where
, where 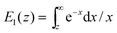 is the exponential integral.24 Expression (13) provides an approximate interpolation of G(t) between the limits of fast reaction and fast diffusion, given by eqn (11) and (12), respectively, and the transition from G∞(t) to G0(t) is governed by the exponential factor e−RτΔ.
is the exponential integral.24 Expression (13) provides an approximate interpolation of G(t) between the limits of fast reaction and fast diffusion, given by eqn (11) and (12), respectively, and the transition from G∞(t) to G0(t) is governed by the exponential factor e−RτΔ.
To demonstrate the utility of approximation (13), we compare Ga(t) with G(t) defined by eqn (6) and obtained by numerical integration. First, we transform the integral over the wave vectors in eqn (6) into a one-dimensional integral:
| | 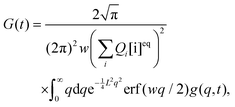 | (14) |
where
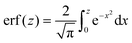
is the error function
24 and
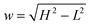
. The integral in
eqn (14) is performed numerically and the autocorrelation function obtained in this way, denoted
Gn(
t), is normalized to unity at
t = 0. To simplify the comparison of
Ga(
t) with
Gn(
t), we assume
y = 0. This is justified because the first term in
eqn (13) is exact and the remaining terms do not depend on
y except for the amplitude. In fact,
y was always very small (≲10
−3) in our experimental studies.
19 The relation between the diffusion coefficients is expressed by a dimensionless parameter
d =
D/(
D +
DB).
In Fig. 1, we compare Gn(t) with Ga(t) for four values of R in the decreasing order. The autocorrelation functions for the limits of fast reaction, G∞(t), and fast diffusion, G0(t), are also shown. We observe that both Gn(t) and Ga(t) are limited by G∞(t) from below and by G0(t) from above. For the largest value R = 10 (Fig. 1a), which is close to the fast reaction limit, Ga(t) is practically indistinguishable from Gn(t) and both are very close to G∞(t). Larger discrepancies between Gn(t) and Ga(t) occur for R = 1 (Fig. 1b) but they decrease again for smaller values of R (Fig. 1c and d). In the case R = 0.1 (Fig. 1c), both Gn(t) and Ga(t) cannot be distinguished from G0(t) for times t ≲ 1. The effect of the chemical reaction on the autocorrelation function becomes visible only for longer times (t ≳ 1). A similar situation occurs for the smallest relaxation rate R = 0.01 (Fig. 1d) but visible deviations of the autocorrelation function from G0(t) appear at longer times than for the faster reaction. We have also checked that Gn(t) and Ga(t) are practically indistinguishable from G0(t) when R ≲ 0.001.
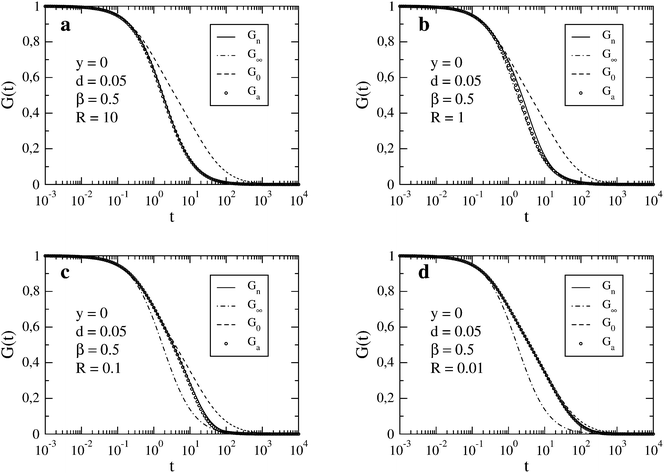 |
| | Fig. 1 FCS autocorrelation function for the set of parameters y, d, β and R specified in the individual figures. The time t and inverse of the relaxation rate, R−1, are expressed in the units of τΔ. In the legend, Gn results from the numerical integration (see eqn (14)), G∞ and G0 correspond to the limits of fast reaction and fast diffusion, respectively (see eqn (11) and (12)), and Ga is the approximation given by eqn (13). | |
In Fig. 2, we show the case of a slow reaction (R = 0.01) for a large difference between the diffusion coefficients of the micelle and dye (d = 0.005). We observe a qualitative change of G0(t) upon decreasing d. For sufficiently small d, three roughly linear regions can be distinguished in the plot of G0vs. ln(t/τΔ). This is due to a large difference between the diffusion times τA and τB (cf.eqn (12)). As in the case d = 0.05, Gn(t) and Ga(t) follow G0(t) up to a certain value of t. Then they separate gradually from G0(t). The slower the reaction is, the later that separation occurs. For long times, Gn(t) and Ga(t) approach G∞(t), and eventually become indistinguishable from it. Here we have restricted our presentation only to β = 0.5, which corresponds to [B]eq ≈ [C]eq ≪ [A]eq, but for the comparison we have also studied β = 0.2 and β = 0.8 (ESI†).
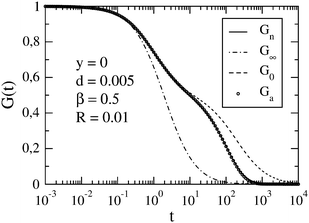 |
| | Fig. 2 FCS autocorrelation function for the set of parameters y, d, β and R specified in the figure. The meaning of symbols is the same as in Fig. 1. | |
A better agreement between Gn(t) and Ga(t) can be achieved if we allow a different value of the relaxation rate in Ga(t) from that used in Gn(t). To find the best fit, we minimize the function 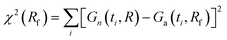 at fixed R; other parameters are the same for both functions. In the case shown in Fig. 1c (R = 0.1), the best fit to Gn(t,R) by Ga(t,Rf) is obtained for Rf = 0.0805. In this way, we can estimate the error of using the approximate autocorrelation function to fit experimental data instead of the true one. In Fig. 3, we show the best fit in the case of largest discrepancies between Gn(t) and Ga(t) (cf.Fig. 1b). Here the best fit value of the relaxation rate, Rf = 0.474, equals approximately half of the actual value R = 1 used in Gn(t).
at fixed R; other parameters are the same for both functions. In the case shown in Fig. 1c (R = 0.1), the best fit to Gn(t,R) by Ga(t,Rf) is obtained for Rf = 0.0805. In this way, we can estimate the error of using the approximate autocorrelation function to fit experimental data instead of the true one. In Fig. 3, we show the best fit in the case of largest discrepancies between Gn(t) and Ga(t) (cf.Fig. 1b). Here the best fit value of the relaxation rate, Rf = 0.474, equals approximately half of the actual value R = 1 used in Gn(t).
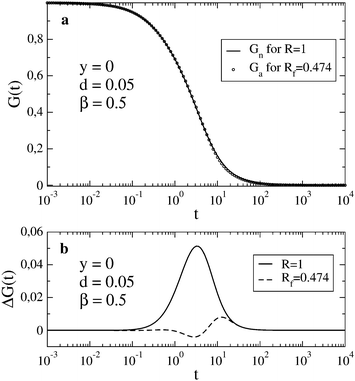 |
| | Fig. 3 In (a), Gn(t) for R = 1 is shown together with the best fit by Ga(t) obtained for Rf = 0.474. In (b), the deviation ΔG(t) = Gn(t) − Ga(t) is shown for the case presented in Fig. 1b (solid line) and for the best fit shown in (a) (dashed line). | |
In this work, we have assumed a fixed value of ω = H/L (ω = 5) but in STED experiment, it is possible to change the diameter of the focal spot L. By decreasing L, the characteristic times of diffusion are decreased by the factor L2, which shifts the dimensionless relaxation time RτΔ to a lower value. For instance, if L is reduced by the factor of 10 the autocorrelation function in Fig. 1b changes roughly to that shown in Fig. 1d. The comparison is not exact, however, because it does not take into account the increase of ω, which affects the asymptotic behavior of G(t) for long times. The decay of G(t) follows from the form of the autocorrelation function for one-component diffusion in three dimensions: h(t/τ) = (1 + t/τ)−1(1 + t/ω2τ)−1/2, but a large value of ω practically reduces the effect of diffusion to two dimensions.
3.1.1 Asymptotic behavior of the autocorrelation function.
To visualize the asymptotic behavior of G(t) for both short and long times, we plot f(t) = [G(t) − G∞(t)]/[G0(t) − G∞(t)]. As shown in Fig. 4, f(t) → 0 when t → ∞. Since for long times G0(t) and G∞(t) decay as t−3/2 with different amplitudes (see eqn (11) for QB = QC and eqn (12)), we conclude that also [G(t) − G∞(t)]/G∞(t) → 0, which means that G(t) tends asymptotically to G∞(t) for t → ∞. The limit t → 0 can be studied by direct calculation (not presented here). For QB = QC, the function g(q,t) given by eqn (10) (see also eqn (S6) in ESI†) and its first and second derivatives at t = 0 do not depend on R, and the third derivative is proportional to R. Therefore G(t) − G0(t) ∝ Rt3 for small t, whereas G0(t) − 1 ∝ t, hence [G(t) − G0(t)]/[G0(t) − 1] ∝ Rt2. It means that G(t) tends asymptotically to G0(t) in the limit t → 0. In Fig. 4, this asymptotic behavior of G(t) is visualized by the function f(t) but because G0(t) − G∞(t) ∝ t2 for t → 0, we have| | 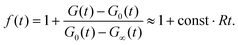 | (15) |
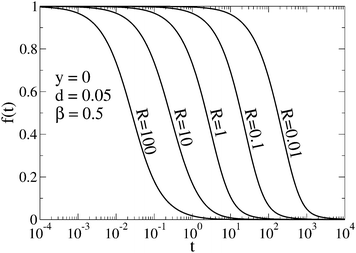 |
| | Fig. 4 Function f(t) = [G(t) − G∞(t)]/[G0(t) − G∞(t)] shows that G(t) tends asymptotically to G0(t) for t → 0 and to G∞(t) for t → ∞. The curves correspond to selected values of the relaxation rate and G(t) is represented by Gn(t). | |
3.1.2 Application of the approximate formula to first order reactions.
So far, we have considered only second order reactions but the formalism presented above can be easily adapted to first order reactions, e.g., the unimolecular isomerization.1 This is not surprising because eqn (3) are of first order due to linearization around the equilibrium state. For the reaction:the reaction-diffusion equations assume the following form| | 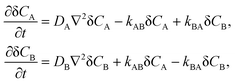 | (17) |
where kAB and kBA are the rate constants. In the case of unimolecular isomerization, it is usually assumed that the diffusion coefficients are equal (DA = DB = D) and only the state A is fluorescent (QA = Q, QB = 0). Then the solution of eqn (17) is very simple and the normalized autocorrelation function is given by1| | | G(t) = (1 + t/τD)−1(1 + t/τD)−1/2(1 + Ke−t/τ)(1 + K)−1, | (18) |
where K = kAB/kBA = [B]eq/[A]eq is the equilibrium constant, τD = L2/(4D) and τ = 1/(kAB + kBA) is the relaxation time of the chemical reaction.
If both states exhibit the same fluorescence (QA = QB = Q) but DA ≠ DB then the approximate autocorrelation function given by eqn (13) can be applied to reaction (16) after some modifications. In the case DA > DB, we obtain
| | 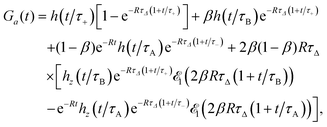 | (19) |
where now
R =
kAB +
kBA,
β =
kAB/
R =
K/(1 +
K),
τA =
L2/(4
DA),
τB =
L2/(4
DB),
τΔ =
L2/(4|
Δ|),
Δ =
DA −
DB,
τ± =
L2/(4
D±),
D+ =
DA(1 −
β) +
DBβ and
D− =
DAβ +
DB(1 −
β). To obtain
Ga(
t) for
DB >
DA, the state A should be interchanged with B in
eqn (19). Thus,
K and
β should be replaced with
K−1 and 1 −
β, respectively, whereas
τ± and
τΔ do not change.
Finally, if DA ≠ DB and QA ≠ QB we can adapt formula (S32) in ESI† to reaction (16). For QA = Q, QB = 0 and DA > DB, we obtain
| | 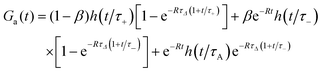 | (20) |
Then the case
DA =
DB =
D corresponds to the limit
τΔ → ∞ and
τ+ =
τ− =
τA in
eqn (20), hence
| | | Ga(t) = h(t/τA)(1 − β + βe−Rt), | (21) |
which is equivalent to
eqn (18).
3.2 Discussion
We have derived an approximate analytical expression for the FCS autocorrelation function to study the kinetics of the reaction of micelles with fluorescent dyes. A micelle and dye form a complex whose diffusion coefficient is approximately the same as for a free micelle. We have also assumed that the optical properties of the complex and free dye are the same, which is justified in the context of our experimental studies.19
We note that a related problem of a molecule diffusing and binding to an immobile substrate with some association and dissociation rates was studied by Ribeiro at al.8 The FCS autocorrelation function derived from their model was used to estimate the model parameters from the experimental data. The authors defined four simplified regimes in terms of relations between the rate constants and diffusion coefficient of the molecule, which they called: the pure-diffusion, effective-diffusion, hybrid-model and reaction-dominant regimes. Except the hybrid-model regime, the autocorrelation function has a simple analytical form in the remaining regimes. If none of the simplified regimes is suitable for fitting the data then the full model of the autocorrelation function is used to determine the diffusion coefficient as well as the association and dissociation rates. To adapt Ga(t) given by eqn (13) to immobile binding sites, we take the limit D → 0, which in our case corresponds to immobile micelles. A similar approach was used by Wirth et al. in the studies of fluorophors interacting with heterogeneous chemical interfaces.25 To describe lateral diffusion and strong reversible adsorption, they used the model of Elson and Magde3 with two nondiffusing species (only the flourophor diffuses) and derived an analytic solution to the FCS autocorrelation function under the condition of rare strong adsorption.
In a more recent work, Ipiña and Dawson15 considered the same theoretical model of diffusion and reaction as we do in this work. They tried various approximate forms of G(t) to explore the transition between the limits of fast reaction and fast diffusion for which the autocorrelation function is known. In these approximations, the autocorrelation functions for free diffusion of two or three components were combined with exponentially decaying factors. Such an approach introduces additional fitting parameters, however.
To go beyond the limits of fast reaction and fast diffusion, we have taken a different route from that presented by Ipiña and Dawson15 since the approximation of the autocorrelation function derived by us follows directly from the theoretical model of Krichevsky and Bonnet.1 In this way the number of fitting parameters remains the same as in the original G(t). Our approximation reproduces G(t) for chemical reactions that are either much faster or much slower than the diffusion times of fluorescent molecules through the focal volume. Moreover, in contrast to other approximations which impose some restrictions on the model parameters, Ga(t) is well defined in the whole parameter space. We observe that for short times the shape of G(t) computed from the theoretical model approaches the fast diffusion limit, whereas for long times it approaches the fast reaction limit. This shows that any approximate autocorrelation function should reproduce both limits correctly. Despite some numerical discrepancies between G(t) and Ga(t) the latter exhibits qualitatively correct time evolution.
Below we discuss a few specific issues in more detail.26
3.2.1 Time-dependent diffusion coefficient.
The time evolution of the autocorrelation function studied in this work suggests that diffusion of a fluorescent particle which changes its state due to a chemical reaction could be explained by a time-dependent diffusion coefficient. To check this possibility, we consider the mean-square displacement, 〈r2〉, of a particle that can exist in two states characterized by different diffusion coefficients.27 In our case, the free state (f) and bound state (b) correspond to the free dye and micelle-dye complex, respectively. With some simplifications it is possible to express the reaction-diffusion equations in terms of the probability densities of these states: Pf(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and Pb(
,t) and Pb(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) (details will be presented elsewhere). Then 〈r2〉 is calculated as a function of time and the result depends on the initial conditions. We consider two initial conditions: a free dye at the origin and a complex at the origin, hence
,t) (details will be presented elsewhere). Then 〈r2〉 is calculated as a function of time and the result depends on the initial conditions. We consider two initial conditions: a free dye at the origin and a complex at the origin, hence| | 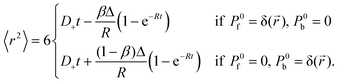 | (22) |
For times t ≪ R−1, 〈r2〉 is proportional to t (normal diffusion) with the diffusion coefficient of the free dye in the first case and of the complex in the second case. For times t ≫ R−1, 〈r2〉 is also proportional to t but the diffusion coefficient tends to D+ in both cases. If the initial conditions Pf(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = (1 − β)δ(
,t) = (1 − β)δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and Pb(
) and Pb(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = βδ(
,t) = βδ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) are assumed, where 1 − β and β are the equilibrium probabilities of the states f and b, respectively, then 〈r2〉 = D+t for all times. According to eqn (22) the time-dependent diffusion coefficient, defined as
) are assumed, where 1 − β and β are the equilibrium probabilities of the states f and b, respectively, then 〈r2〉 = D+t for all times. According to eqn (22) the time-dependent diffusion coefficient, defined as 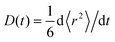 , changes from the value for the free dye or complex, in the limit t → 0, to D+, in the limit t → ∞. In experiment, such a crossover may resemble transient anomalous diffusion, defined by 〈r2〉 ∝ tα if t ≪ tCR and 〈r2〉 ∝ t if t ≫ tCR, where α is the exponent of anomalous diffusion and tCR is the crossover time. It is argued that transient anomalous subdiffusion (α < 1) occurs in some systems with a hierarchy of binding sites.28–30
, changes from the value for the free dye or complex, in the limit t → 0, to D+, in the limit t → ∞. In experiment, such a crossover may resemble transient anomalous diffusion, defined by 〈r2〉 ∝ tα if t ≪ tCR and 〈r2〉 ∝ t if t ≫ tCR, where α is the exponent of anomalous diffusion and tCR is the crossover time. It is argued that transient anomalous subdiffusion (α < 1) occurs in some systems with a hierarchy of binding sites.28–30
3.2.2 Tracer diffusion in polymer solutions.
Our approximate form of the autocorrelation function might be applied to the problem of tracer diffusion in polymer solutions, which was studied by means of FCS and coarse-grained molecular dynamics simulations.31 In a dilute polymer solution, a dynamic exchange between the polymer-bound and free state of the tracer occurs. Consequently, the form of the autocorrelation function G(t) depends on the relation between the characteristic length scales of the tracer diffusion in the two states and the size of the focal volume L. This is because a given process can be resolved by FCS if its characteristic length scale is grater than L.32 Thus, if the displacements in the bound, Lb, and free, Lf, states satisfy the inequality Lf > Lb > L then G(t) is bimodal (two-component diffusion), whereas in the opposite case, G(t) is unimodal (one-component effective diffusion). To apply a similar reasoning to our dye-micelle solution, we assume the time tb = 1/k− ≈ 1/[R(1 − β)] for the bound state, provided [C]eq ≪ [A]eq, and tf = 1/(k+[A]eq) = 1/(Rβ), for the free state, hence Lb2 ≈ D/[R(1 − β)] and Lf2 ≈ DB/(Rβ). Then the condition Lb > L leads to the inequality:| | 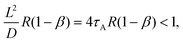 | (23) |
where τA = L2/4D = (d−1 − 2)τΔ and d = D/(D + DB). In Fig. 1, we have β = 0.5, d = 0.05, hence 4τAR(1 − β) = 36RτΔ, which means that condition (23) is satisfied only for RτΔ = 0.01 (Fig. 1d). Indeed, G(t) in Fig. 1d is rather well approximated by the two-component model but some deviations appear at long times. For D ≪ DB, we have RτΔ/τ+ ≈ tb−1 and RτΔ/τ− ≈ tf−1. Assuming for simplicity that RτΔ ≈ RτB ≪ 1, we rewrite eqn (13) as follows| | 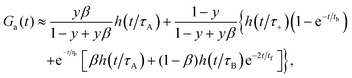 | (24) |
where we have included only the zeroth order terms in RτΔ and used the relation R = tb−1 + tf−1. Eqn (24) shows that deviations of G(t) from the two-component model are not observed in FCS only if tb, tf ≫ τA (in Fig. 1d, τA/tb = 0.09). If Lb < L and Lf > L, which corresponds to 4τAR(1 − β) > 1 and 4τBRβ < 1, we can still use approximation (24), provided the condition RτΔ ≪ 1 holds. For instance in Fig. 1c, we have 4τAR(1 − β) = 3.6 > 1, 4τBRβ ≈ 0.2 and tb = tf = 20τΔ. Then G(t) contains a bimodal piece, for t ≪ tb, and a unimodal piece (effective diffusion), for t ≫ tb. Finally, the case Lb < L, Lf < L is shown in Fig. 1a, where 4τAR(1 − β) = 360, 4τBRβ ≈ 20, tb = tf = 0.2τΔ; here G(t) is definitely unimodal.
3.2.3 Stick-and-diffuse model.
The stick-and-diffuse model was used by Yeung et al.33 to explain the dynamics of vesicles in hippocampal synapses, studied previously by FCS (vesicles were fluorescently labeled). The model assumes that the vesicles bind and release from the cellular cytomatrix and diffuse freely when they are not bound. We show below a qualitative agreement between Ga(t) and the autocorrelation function derived by Yeung et al. However, we have not attempted a detailed comparison. To make contact with the stick-and-diffuse model, we mimic vesicles in the bound state (component C) by taking the limit of immobile micelles in eqn (13), whereas component B corresponds to freely diffusing vesicles. Thus, we assume D → 0, hence τA → ∞, τΔ = τB, τ+ = τB/(1 − β) and τ− = τB/β. Then omitting the first term in eqn (13) which is now a constant, we obtain the following expression for the normalized autocorrelation function| | Ga(t) = h(t/τ+)(1 − e−RτB−t/tb) + {β + (1 − β)h(t/τB)e−2t/tf + 2β(1 − β)RτB[![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(2τB/tf) − hz(t/τB) 1(2τB/tf) − hz(t/τB)![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(2(τB + t)/tf) × e−2t/tf]}e−RτB−t/tb, 1(2(τB + t)/tf) × e−2t/tf]}e−RτB−t/tb, | (25) |
where tb and tf have the same meaning as in Section 3.2.2. R and β can be expressed in terms of tb and tf: R = tf−1 + tb−1 and β = tb/(tf + tb). We consider three limiting cases. In the limit tb ≪ τB ≪ tf, we have RτB ≫ 1, β ≪ 1 and τ+ ≈ τB. Then Ga(t) ≈ h(t/τB) corresponds to free diffusion of vesicles. In the limit tf, tb ≪ τB, we have RτB ≫ 1 and Ga(t) ≈ h(t/τ+) corresponds to the effective diffusion with the diffusion coefficient D+ = DB(1 − β). Finally, if τB ≪ tb, tf the terms proportional to RτB can be neglected and e−RτB ≈ 1 in eqn (25). In addition, if tb and tf are of the same order then also τ+ ≪ tb, tf. Thus, for times t ≫ τB, the decay of the autocorrelation function depends only on tb. These results are consistent with the stick-and-diffuse model. The last one follows from the fact that the fluorescence intensity is essentially uncorrelated between bound states when τB ≪ tf.33 In our case, the long time behavior of the autocorrelation function can be approximated by (see eqn (25))The same exponential decay was also found by Ribeiro et al.8 in the reaction-dominant regime.
4 Conclusions
The application of FCS to the determination of the relaxation rate is limited to a certain range of R because the autocorrelation function for very fast and very slow reactions cannot be distinguished from G∞(t) and G0(t), respectively. This range increases when the ratio D/DB decreases and reduces to zero at D = DB. Our approximate autocorrelation function can be applied to both fast and slow reactions, in contrast to the power expansion in R−1 which is suitable for fast reactions. However, the discrepancies between Ga(t) and Gn(t) grow when R approaches τΔ−1. The dependence of Ga(t) on R provides a smooth interpolation between the limits of fast reaction and fast diffusion. At constant R, Ga(t) exhibits a crossover between the diffusion of independent fluorescent components, described by G0(t) at short times, and the effective diffusion, described by G∞(t) at long times, as it is shown in Fig. 1c. In the case of slow reactions, however, the region of long times may not be accessible experimentally (see Fig. 1d and 2). This crossover can be explained as follows. At short times, fluctuations in the number of particles in the focal volume due to diffusion contribute to G(t) at all length scales while the reaction plays a minor role. Therefore, we observe diffusion of independent fluorescent particles: free dyes and complexes. At long times, only the fluctuations of large length scales (small wave vectors), comparable to the size of the focal volume, give significant contributions to G(t), which means that the signal from particles of different kinds cannot be distinguished. Since the concentration of the dye is usually very small (y ≈ 0) the separate contribution to the autocorrelation function from the complexes can be neglected (see the first term in eqn (13)). Then G(t) corresponds to the diffusion of a hypothetical single component with the effective diffusion coefficient D+ = Dβ + DB(1 − β).
To conclude, the kinetics of chemical reaction (1) manifests itself during the transition of the autocorrelation function from the short-time behavior characterized by G0(t) to the long-time behavior characterized by G∞(t). Whether both types of behavior can really be observed in the FCS experiment depends on the system studied. This transition is reproduced qualitatively by the approximate autocorrelation function, Ga(t), derived in the present work (eqn (13)). The accuracy of Ga(t) depends on the parameters of the model, mainly on the relaxation rate R, but it should be sufficient to fit the FCS experimental data. In fact, for small values of RτΔ, the contribution from the last two terms in eqn (13) can be neglected, which leads to a simplified form of Ga(t) (without the exponential integral) (ESI†). We have tested the latter approximation recently,19 using two different experimental techniques: FCS and the Taylor dispersion analysis.34,35
Acknowledgements
We would like to thank Dr Jędrzej Szymański for discussion. This work was supported by the NCN under the Maestro grant UMO-2011/02/A/ST3/00143.
References
- O. Krichevsky and G. Bonnet, Rep. Prog. Phys., 2002, 65, 251–297 CrossRef CAS.
- D. Magde, E. L. Elson and W. W. Webb, Phys. Rev. Lett., 1972, 29, 705–708 CrossRef CAS.
- E. L. Elson and D. Magde, Biopolymers, 1974, 13, 1–27 CrossRef CAS.
- D. Magde, E. L. Elson and W. W. Webb, Biopolymers, 1974, 13, 29–61 CrossRef CAS PubMed.
- E. L. Elson, Traffic, 2001, 2, 789–796 CrossRef CAS PubMed.
- W. Al-Soufi, B. Reija, M. Novo, S. Felekyan, R. Kühnemuth and C. A. M. Seidel, J. Am. Chem. Soc., 2005, 127, 8775–8784 CrossRef CAS PubMed.
- J. Widengren, J. Dapprich and R. Rigler, Chem. Phys., 1997, 216, 417–426 CrossRef CAS.
- A. Michelman-Ribeiro, D. Mazza, T. Rosales, T. J. Stasevich, H. Boukari, V. Rishi, C. Vinson, J. R. Knutson and J. G. McNally, Biophys. J., 2009, 97, 337–346 CrossRef CAS PubMed.
- E. Bismuto, E. Gratton and D. C. Lamb, Biophys. J., 2001, 81, 3510–3521 CrossRef CAS PubMed.
- D. Axelrod, D. E. Koppel, J. Schlessinger, E. Elson and W. W. Webb, Biophys. J., 1976, 16, 1055–1069 CrossRef CAS PubMed.
- B. L. Sprague and J. G. McNally, Trends Cell Biol., 2005, 15, 84–91 CrossRef CAS PubMed.
- B. L. Sprague, R. L. Pego, D. A. Stavreva and J. G. McNally, Biophys. J., 2004, 86, 3473–3495 CrossRef CAS PubMed.
- B. Pando, S. P. Dawson, D. D. Mak and J. E. Pearson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 5338–5342 CrossRef CAS PubMed.
- L. Sigaut, M. L. Ponce, A. Colman-Lerner and S. Ponce Dawson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051912 CrossRef PubMed.
- E. P. Ipiña and S. P. Dawson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022706 CrossRef PubMed.
- J.-B. Salmon, C. Dubrocq, P. Tabeling, S. Charier, D. Alcor, L. Jullien and F. Ferrage, Anal. Chem., 2005, 77, 3417–3424 CrossRef CAS PubMed.
- G. G. Mironov, V. Okhonin, S. I. Gorelsky and M. V. Berezovski, Anal. Chem., 2011, 83, 2364–2370 CrossRef CAS PubMed.
- A. V. Melnykov and K. B. Hall, J. Phys. Chem. B, 2009, 113, 15629–15638 CrossRef CAS PubMed.
- X. Zhang, A. Poniewierski, A. Jelińska, A. Zagożdżon, A. Wisniewska, S. Hou and R. Hołyst, Soft Matter, 2016, 12, 8186–8194 RSC.
- H. Zettl, Y. Portnoy, M. Gottlieb and G. Krausch, J. Phys. Chem. B, 2005, 109, 13397–13401 CrossRef CAS PubMed.
- H. Schuch, J. Klingler, P. Rossmanith, T. Frechen, M. Gerst, J. Feldthusen and A. H. E. Muller, Macromolecules, 2000, 33, 1734–1740 CrossRef CAS.
- C. Eggeling, C. Ringemann, R. Medda, G. Schwarzmann, K. Sandhoff, S. Polyakova, V. N. Belov, B. Hein, C. von Middendorff, A. Schönle and S. W. Hell, Nature, 2009, 457, 1159–1163 CrossRef CAS PubMed.
- J. T. King, C. Yu, W. L. Wilson and S. Granick, ACS Nano, 2014, 8, 8802–8809 CrossRef CAS PubMed.
-
G. B. Arfken, H. J. Weber and F. E. Harris, Mathematical Methods for Physicists, Academic Press, 7th edn, 2012 Search PubMed.
- M. J. Wirth, M. D. Ludes and D. J. Swinton, Appl. Spectrosc., 2001, 55, 663–669 CrossRef CAS.
- These issues were suggested by a referee.
-
N. G. van Kampen, Stochastic processes in physics and chemistry, Elsevier, 3rd edn, 2007, ch. 7 Search PubMed.
- M. J. Saxton, Biophys. J., 2007, 92, 1178–1191 CrossRef CAS PubMed.
- N. Destainville, A. Saulière, L. Salomé and M. J. Saxton, Biophys. J., 2008, 95, 3117–3119 CrossRef CAS PubMed.
- M. J. Saxton, Biophys. J., 2012, 103, 2411–2422 CrossRef CAS PubMed.
- A. Vagias, R. Raccis, K. Koynov, U. Jonas, H.-J. Butt, G. Fytas, P. Košovan, O. Lenz and C. Holm, Phys. Rev. Lett., 2013, 111, 088301 CrossRef PubMed.
- J. Enderlein, Phys. Rev. Lett., 2012, 108, 108101 CrossRef PubMed.
- C. Yeung, M. Shtrahman and X.-I. Wu, Biophys. J., 2007, 92, 2271–2280 CrossRef CAS PubMed.
- A. Bielejewska, A. Bylina, K. Duszczyk, M. Fiałkowski and R. Hołyst, Anal. Chem., 2010, 82, 5463–5469 CrossRef CAS PubMed.
- A. Majcher, A. Lewandrowska, F. Herold, J. Stefanowicz, T. Słowiński, A. P. Mazurek, S. A. Wieczorek and R. Hołyst, Anal. Chim. Acta, 2015, 855, 51–59 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm02643e |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Andrzej
Poniewierski
and
Xuzhu
Zhang
*,
Andrzej
Poniewierski
and
Xuzhu
Zhang
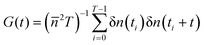 , where n(t) is the number of collected photons in the time interval Δt, δn(t) = n(t) −
, where n(t) is the number of collected photons in the time interval Δt, δn(t) = n(t) − ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is its deviation from the mean value
is its deviation from the mean value ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , and T is the total number of accumulated sampling intervals Δt. If the system is ergodic, which is usually assumed, the time average can be replaced by an ensemble average (denoted 〈
, and T is the total number of accumulated sampling intervals Δt. If the system is ergodic, which is usually assumed, the time average can be replaced by an ensemble average (denoted 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉), i.e., G(t) = 〈δn(0)δn(t)〉/
〉), i.e., G(t) = 〈δn(0)δn(t)〉/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) 2. Then δn(t) is connected to the concentration fluctuations of the fluorescent components and the formalism of statistical mechanics is used to express G(t) in terms of the kinetic processes present in the system. If these fluctuations are due to diffusion and chemical reactions the measurement of G(t) can provide information about the diffusion coefficients of fluorescent molecules as well as rate constants of the chemical reactions. It was first demonstrated by Magde et al.2 for the reversible binding of ethidium bromide (EtBr) to DNA: EtBr + DNA ⇄ EtBr·DNA, where EtBr is a small interacting dye and the complex EtBr·DNA is strongly fluorescent. Finally, we note that to study biochemical systems also high-order fluorescence correlation analysis can be used, besides G(t).18
2. Then δn(t) is connected to the concentration fluctuations of the fluorescent components and the formalism of statistical mechanics is used to express G(t) in terms of the kinetic processes present in the system. If these fluctuations are due to diffusion and chemical reactions the measurement of G(t) can provide information about the diffusion coefficients of fluorescent molecules as well as rate constants of the chemical reactions. It was first demonstrated by Magde et al.2 for the reversible binding of ethidium bromide (EtBr) to DNA: EtBr + DNA ⇄ EtBr·DNA, where EtBr is a small interacting dye and the complex EtBr·DNA is strongly fluorescent. Finally, we note that to study biochemical systems also high-order fluorescence correlation analysis can be used, besides G(t).18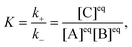
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and time t, and it fluctuates around the equilibrium value due to diffusion and the chemical reaction. Its fluctuations are defined by δCj(
and time t, and it fluctuates around the equilibrium value due to diffusion and the chemical reaction. Its fluctuations are defined by δCj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = Cj(
,t) = Cj(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) − [j]eq and the linearized kinetic equations for the fluctuations of all components in an ideal solution assume the following form1,3
,t) − [j]eq and the linearized kinetic equations for the fluctuations of all components in an ideal solution assume the following form1,3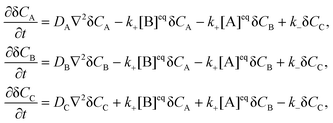
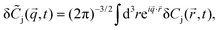
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), is Gaussian:1
), is Gaussian:1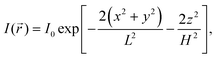
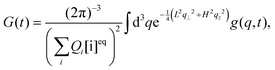
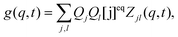
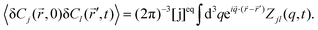
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,0)δCk(
,0)δCk(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′,0)〉 = [j]eqδjkδ(
′,0)〉 = [j]eqδjkδ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′),
′),![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) is the Dirac δ-function in three dimensions. In our case, component A is not fluorescent (QA = 0), thus
′) is the Dirac δ-function in three dimensions. In our case, component A is not fluorescent (QA = 0), thus![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = (1 +
) = (1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) )−1(1 +
)−1(1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) /ω2)−1/2, where
/ω2)−1/2, where ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) is the lag time expressed in the units of the appropriate diffusion time. In this work, all autocorrelation functions at t = 0 are normalized to unity.
is the lag time expressed in the units of the appropriate diffusion time. In this work, all autocorrelation functions at t = 0 are normalized to unity.
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) 2,
2,![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) 2 = QB2(1 − y)(1 − β) + QC2β, τ± = L2/(4D±), and D+ = Dβ + DB(1 − β), D− = D(1 − β) + DBβ are effective concentration-dependent diffusion coefficients. The parameters β = k+[A]eq/R and y = K[B]eq/(1 + K[B]eq) are dimensionless and can vary from 0 to 1. G∞(t) can be treated as the first term of the asymptotic expansion of G(t) in the powers of R−1. In eqn (11), only the last term depends on the kinetics of the chemical reaction but it vanishes when the optical properties of the complex and dye are the same (QB = QC). Then it is necessary to include the terms of order R−1 or higher to determine the relaxation rate.
2 = QB2(1 − y)(1 − β) + QC2β, τ± = L2/(4D±), and D+ = Dβ + DB(1 − β), D− = D(1 − β) + DBβ are effective concentration-dependent diffusion coefficients. The parameters β = k+[A]eq/R and y = K[B]eq/(1 + K[B]eq) are dimensionless and can vary from 0 to 1. G∞(t) can be treated as the first term of the asymptotic expansion of G(t) in the powers of R−1. In eqn (11), only the last term depends on the kinetics of the chemical reaction but it vanishes when the optical properties of the complex and dye are the same (QB = QC). Then it is necessary to include the terms of order R−1 or higher to determine the relaxation rate.
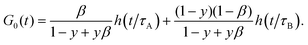
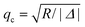 and Δ = D − DB < 0. In what follows we assume that QB = QC = Q19 but the general situation of different fluorescence of the free dye and complex is considered in ESI† (see also Section 3.1.2).
and Δ = D − DB < 0. In what follows we assume that QB = QC = Q19 but the general situation of different fluorescence of the free dye and complex is considered in ESI† (see also Section 3.1.2).
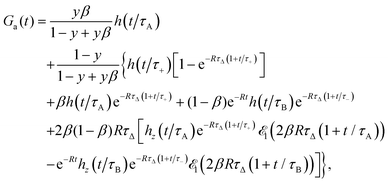
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = (1 +
) = (1 + ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) /ω2)−1/2 and τΔ = L2/(4|Δ|). For convenience, we have introduced the function
/ω2)−1/2 and τΔ = L2/(4|Δ|). For convenience, we have introduced the function 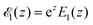 , where
, where 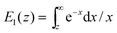 is the exponential integral.24 Expression (13) provides an approximate interpolation of G(t) between the limits of fast reaction and fast diffusion, given by eqn (11) and (12), respectively, and the transition from G∞(t) to G0(t) is governed by the exponential factor e−RτΔ.
is the exponential integral.24 Expression (13) provides an approximate interpolation of G(t) between the limits of fast reaction and fast diffusion, given by eqn (11) and (12), respectively, and the transition from G∞(t) to G0(t) is governed by the exponential factor e−RτΔ.
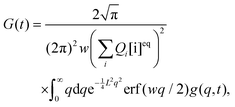
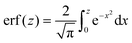 is the error function24 and
is the error function24 and 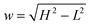 . The integral in eqn (14) is performed numerically and the autocorrelation function obtained in this way, denoted Gn(t), is normalized to unity at t = 0. To simplify the comparison of Ga(t) with Gn(t), we assume y = 0. This is justified because the first term in eqn (13) is exact and the remaining terms do not depend on y except for the amplitude. In fact, y was always very small (≲10−3) in our experimental studies.19 The relation between the diffusion coefficients is expressed by a dimensionless parameter d = D/(D + DB).
. The integral in eqn (14) is performed numerically and the autocorrelation function obtained in this way, denoted Gn(t), is normalized to unity at t = 0. To simplify the comparison of Ga(t) with Gn(t), we assume y = 0. This is justified because the first term in eqn (13) is exact and the remaining terms do not depend on y except for the amplitude. In fact, y was always very small (≲10−3) in our experimental studies.19 The relation between the diffusion coefficients is expressed by a dimensionless parameter d = D/(D + DB).


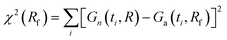 at fixed R; other parameters are the same for both functions. In the case shown in Fig. 1c (R = 0.1), the best fit to Gn(t,R) by Ga(t,Rf) is obtained for Rf = 0.0805. In this way, we can estimate the error of using the approximate autocorrelation function to fit experimental data instead of the true one. In Fig. 3, we show the best fit in the case of largest discrepancies between Gn(t) and Ga(t) (cf.Fig. 1b). Here the best fit value of the relaxation rate, Rf = 0.474, equals approximately half of the actual value R = 1 used in Gn(t).
at fixed R; other parameters are the same for both functions. In the case shown in Fig. 1c (R = 0.1), the best fit to Gn(t,R) by Ga(t,Rf) is obtained for Rf = 0.0805. In this way, we can estimate the error of using the approximate autocorrelation function to fit experimental data instead of the true one. In Fig. 3, we show the best fit in the case of largest discrepancies between Gn(t) and Ga(t) (cf.Fig. 1b). Here the best fit value of the relaxation rate, Rf = 0.474, equals approximately half of the actual value R = 1 used in Gn(t).
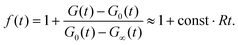
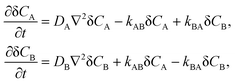
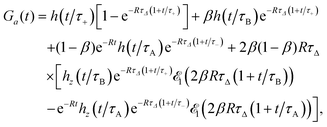
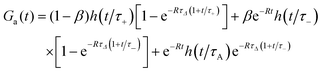
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and Pb(
,t) and Pb(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) (details will be presented elsewhere). Then 〈r2〉 is calculated as a function of time and the result depends on the initial conditions. We consider two initial conditions: a free dye at the origin and a complex at the origin, hence
,t) (details will be presented elsewhere). Then 〈r2〉 is calculated as a function of time and the result depends on the initial conditions. We consider two initial conditions: a free dye at the origin and a complex at the origin, hence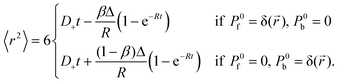
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = (1 − β)δ(
,t) = (1 − β)δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and Pb(
) and Pb(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = βδ(
,t) = βδ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) are assumed, where 1 − β and β are the equilibrium probabilities of the states f and b, respectively, then 〈r2〉 = D+t for all times. According to eqn (22) the time-dependent diffusion coefficient, defined as
) are assumed, where 1 − β and β are the equilibrium probabilities of the states f and b, respectively, then 〈r2〉 = D+t for all times. According to eqn (22) the time-dependent diffusion coefficient, defined as 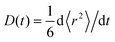 , changes from the value for the free dye or complex, in the limit t → 0, to D+, in the limit t → ∞. In experiment, such a crossover may resemble transient anomalous diffusion, defined by 〈r2〉 ∝ tα if t ≪ tCR and 〈r2〉 ∝ t if t ≫ tCR, where α is the exponent of anomalous diffusion and tCR is the crossover time. It is argued that transient anomalous subdiffusion (α < 1) occurs in some systems with a hierarchy of binding sites.28–30
, changes from the value for the free dye or complex, in the limit t → 0, to D+, in the limit t → ∞. In experiment, such a crossover may resemble transient anomalous diffusion, defined by 〈r2〉 ∝ tα if t ≪ tCR and 〈r2〉 ∝ t if t ≫ tCR, where α is the exponent of anomalous diffusion and tCR is the crossover time. It is argued that transient anomalous subdiffusion (α < 1) occurs in some systems with a hierarchy of binding sites.28–30
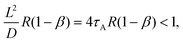
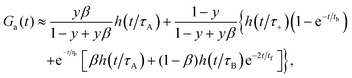
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(2τB/tf) − hz(t/τB)
1(2τB/tf) − hz(t/τB)![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(2(τB + t)/tf) × e−2t/tf]}e−RτB−t/tb,
1(2(τB + t)/tf) × e−2t/tf]}e−RτB−t/tb,
