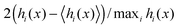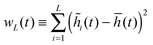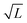DOI:
10.1039/C6SM01978A
(Paper)
Soft Matter, 2017,
13, 376-385
Interface stability, interface fluctuations, and the Gibbs–Thomson relationship in motility-induced phase separations
Received
26th August 2016
, Accepted 28th November 2016
First published on 29th November 2016
Abstract
Minimal models of self-propelled particles with short-range volume exclusion interactions have been shown to exhibit the signatures of phase separation. Here I show that the observed interfacial stability and fluctuations in motility-induced phase separations (MIPS) can be explained by modeling the microscopic dynamics of the active particles in the interfacial region. In addition, I demonstrate the validity of the Gibbs–Thomson relationship in MIPS, which provides a functional relationship between the size of a condensed drop and its surrounding vapor concentration. As a result, the late-stage coarsening dynamics of MIPS at vanishing supersaturation follows the classic Lifshitz–Slyozov scaling law.
1 Introduction
Phase separation is a ubiquitous phenomenon in nature and is manifested by the partitioning of a system into compartments with distinct properties, such as the different particle densities in the two co-existing phases in the case of liquid–vapour phase separation. Phase separation under equilibrium dynamics is a well-investigated physical phenomenon.1,2 Recently, signatures of phase separation have been reported in non-equilibrium systems consisting of active particles.3–19 It is therefore a natural question to ask to what degree we can extend our knowledge of equilibrium phase separation to the phase separation phenomenon observed in active systems. In the case of minimal models of active particles with simple volume exclusion interactions, the phenomenon of motility-induced phase separations (MIPS) has received considerable interest.3,5,8–18 In particular, the idea of an effective surface tension in motility-induced phase separations (MIPS) has been advocated.15,18 At the gas–liquid interface in thermal equilibrium, surface tension results from the pulling of molecules at the interface due to their attractive interactions.20 In a system of active particles with purely repulsive interactions, it is unclear how such “pulling” can occur as the particles can only push. To probe what happens at the interface, I have studied the microscopic dynamics of the active particles in the interfacial region using a combination of simulation and analytical methods. Specifically, using mean-field type arguments, I will demonstrate how pressure balance is achieved between the condensed phase and the dilute (vapor) phase, and how the Gibbs–Thomson relationship arises in a system where a circular condensed drop co-exists with the vapour phase. Furthermore, by incorporating the stochastic nature of particle dynamics, I will explain the scaling between the interfacial width and the system size recently observed in MIPS.18
1.1 Motility-induced phase separation
I will first focus on a minimal model system that exhibits MIPS in two dimensions (2D)—a collection of self-propelled particles with excluded area interactions that undergo rotational fluctuations. Specifically, the dynamical equations are| | 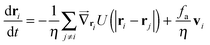 | (1) |
| | 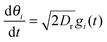 | (2) |
where i is an integral index enumerating the particles in the system, vi ≡ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + sin
+ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θiŷ with the angle θi (with respect to the x-axis) being the orientation of the i-particle, gi(t) is a noise term with Gaussian probability distribution with zero mean and unit variance, Dr sets the magnitude of the rotational fluctuations, U(·) corresponds to the potential function for short-ranged area exclusion interactions, η is the drag coefficient and fa is the constant active force that drives the particles in the system. In particular, u ≡ fa/η is the constant speed of a particle when it is not within the area exclusion zone of another particle. Previous numerical work has indicated that phase separation in this minimal system occurs as u increases, but the actual form of U is unimportant.8,11,14 For instance, U could be in the form of a Weeks–Chandler–Andersen potential:21
θiŷ with the angle θi (with respect to the x-axis) being the orientation of the i-particle, gi(t) is a noise term with Gaussian probability distribution with zero mean and unit variance, Dr sets the magnitude of the rotational fluctuations, U(·) corresponds to the potential function for short-ranged area exclusion interactions, η is the drag coefficient and fa is the constant active force that drives the particles in the system. In particular, u ≡ fa/η is the constant speed of a particle when it is not within the area exclusion zone of another particle. Previous numerical work has indicated that phase separation in this minimal system occurs as u increases, but the actual form of U is unimportant.8,11,14 For instance, U could be in the form of a Weeks–Chandler–Andersen potential:21| | 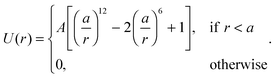 | (3) |
This will be the particular form of the potential function utilized in this work. Also, the time and length units will be set as having a = 1 and Dr = 3. Note that I will focus exclusively on the non-equilibrium dynamics of the system and therefore translational Brownian motion is ignored.
2 Flat interface
2.1 Point particles
To understand the microscopic dynamics at the interface, it is instructive to first look at a system of point particles, i.e., the interaction potential U is zero. Even this simple system distinguishes itself from the equilibrium system in that aggregation will spontaneously occur in the proximity of a force-absorbing but frictionless wall (left column of Fig. 1). In other words, the particles are free to slide and rotate at the wall, but they cannot penetrate the wall. Further complex patterns are revealed when one looks at the particles' orientation distribution as well as the position distribution (Fig. 1(e)). At the wall, most of the particles are left-going, as indicated by the high concentration of orientation at around θ ≃ π. This results from the fact that only left-going particles remain at the wall. Just outside the wall, the distribution is highly peaked at θ just below π/2 and just above 3π/2, which reflects the particles' orientation after they move away from the wall. The orientation anisotropy decays as a particle moves away from the wall.
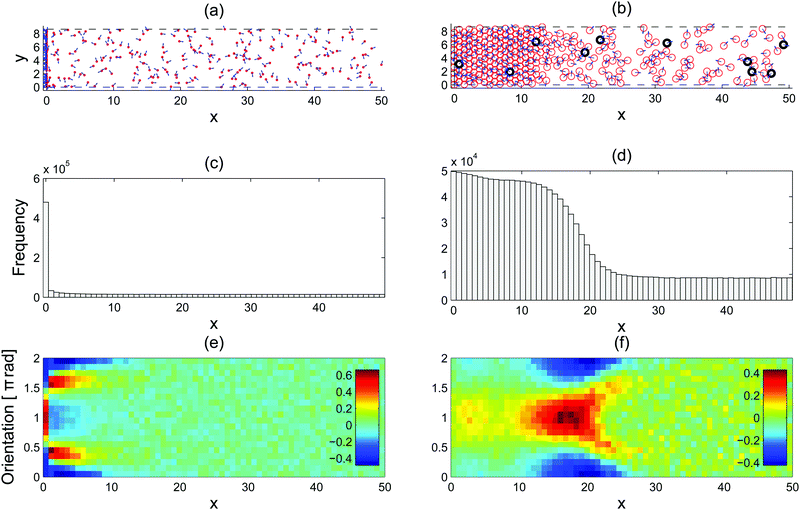 |
| | Fig. 1 Steady-state configurations of active particles confined by a force absorbing wall on the left: point particles (left column) and repulsive particles (right column). (a and b) A snapshot of the system at the end of the simulations with the orientations depicted by the blue arrows. The red circles depicted in (b) are of diameter a = 1. The wall at x = 0 is perfectly force absorbing (see A.1 for simulation details). (c and d) The histograms show the horizontal distributions of the particles. (e and f) The colourmaps show the deviation from the mean in the particles' orientations at different horizontal positions. The colour scale corresponds to the measure: 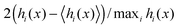 where i is the row index and hi(x) is the frequency. The simulation parameters are: fa = 100, η = 1, a = 1, Dr = 3, and A = 25/6. where i is the row index and hi(x) is the frequency. The simulation parameters are: fa = 100, η = 1, a = 1, Dr = 3, and A = 25/6. | |
In this system, the pressure acting on the wall can be expressed as
| | 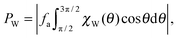 | (4) |
where the orientation distribution function of the particles at the wall per unit length is denoted by
χW(
θ). Note that since we are dealing with a 2D system, the unit of pressure is [force]/[length].
To further analyse χW(θ), one can perform dimensional analysis to conclude that
| | 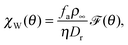 | (5) |
where
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
θ) is a function dependent only on
θ, and
ρ∞ is the particle concentration far from the wall. To obtain the exact functional form of
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
θ), one needs to solve a set of two coupled differential equations under mixed boundary conditions,
22 whose solution consists of a series of Mathieu functions. Unfortunately, the expansion coefficients in the series are not analytically tractable and so an analytical expression is lacking. However,
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
θ) can be readily estimated numerically (left column of
Fig. 1), which allows one to obtain the following equation:
| | 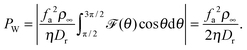 | (6) |
The second expression is equivalent to the swim pressure
23–26 of a system of active particles in 2D, which I have obtained here numerically.
2.2 Repulsive particles
Remarkably, much of what we have seen in the point particle case remains true when we add mutually repulsive interactions to the particles. When a force absorbing but frictionless wall constitutes the left boundary of a semi-infinite system, phase separation occurs where the condensed phase is located close to the wall (Fig. 1(b)). Inside the condensed phase, the orientation is isotropic (Fig. 1(f)). The reason behind the isotropy is that the impeded motility of the particles make them stay for a duration much longer than the orientation decoherence time ≃1/Dr. However, note that the particles' locations are not frozen in time as shown by the black particles in Fig. 1(b), which were the first column of particles next to the wall at the beginning of the simulation. As a particle moves further to the right, it first encounters a layer of left-going particles (shown by the bright red patch centred at x ≃ 17 in Fig. 1(f)). This represents the accumulation of particles with an orientation highly centred at around θ ≃ π, analogous to the accumulation of active point particles at the wall, except that the particles are now spread over a range of x positions due to volume exclusion interactions. Further rightwards, we encounter a pattern of two escape trajectories away from the interfacial region indicated by the two red-yellow branches emerging from the red patch. As a particle moves further away to the right, the orientation becomes isotropic again. From this discussion, it is clear that in the bulk of the condensed and vapour phases, the corresponding orientation distributions are both isotropic, while in the interfacial region separating them there is a high level of orientation anisotropy.
Let us now calculate the force exerted on the wall by the active force of these particles. Since in the condensed phase, the orientation is isotropic, the pressure felt by the wall due to these active forces is
| | 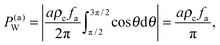 | (7) |
where
ρc is the concentration in the bulk condensed phase. Due to the orientation isotropy, the expression here scales like
fa instead of
fa2 in the point particle system (
eqn (6)). Besides the active force contribution, the wall will also feel additional forces arising from the repulsive interactions, which, we will see, constitute an important contribution in achieving a pressure balance in the interfacial region in MIPS (Section 2.4).
2.3 Locating the interface
The concentration variation across the two phases shown in Fig. 2(a) is similar to a typical equilibrium phase separation. What distinguishes MIPS is the high orientational anisotropy between the phases (Fig. 2(b) and (c)). As for equilibrium fluids, the location of a sharp interface between the two phases can be defined somewhat arbitrarily.27 In the case discussed here, since the pronounced minimum of 〈vx〉 ≡ 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is easy to locate (indicated by the red broken line) and its location also marks the onset of the increase in Qyy ≡ −〈cos(2θ)/2〉 (the yy component of the nematic order parameter Q),28 which signifies the escape of particles from the condensed phase, it is a convenient choice for the interface location. In other words, this convention implies that right outside the interface of the condensed phase, there is a layer of particles travelling preferentially along the interface, as indicated by the peak in Qyy (Fig. 2(c)). The active forces of these escaped particles are potentially the cause of the emergence of a negative surface tension according to its mechanical definition.18 The definition of the interface location has of course no physical significance, but this does provide a working definition useful for the sharp interface model discussed below.
θ〉 is easy to locate (indicated by the red broken line) and its location also marks the onset of the increase in Qyy ≡ −〈cos(2θ)/2〉 (the yy component of the nematic order parameter Q),28 which signifies the escape of particles from the condensed phase, it is a convenient choice for the interface location. In other words, this convention implies that right outside the interface of the condensed phase, there is a layer of particles travelling preferentially along the interface, as indicated by the peak in Qyy (Fig. 2(c)). The active forces of these escaped particles are potentially the cause of the emergence of a negative surface tension according to its mechanical definition.18 The definition of the interface location has of course no physical significance, but this does provide a working definition useful for the sharp interface model discussed below.
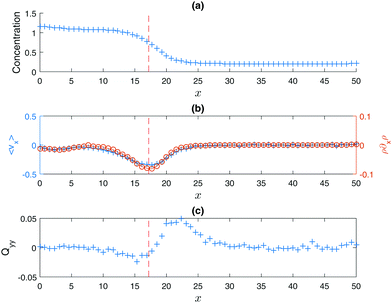 |
| | Fig. 2 (a) Particle concentration as a function of x. The same figure as in Fig. 1(d). (b) The mean horizontal component of the particles' orientations 〈vx〉 vs. x (+ symbols, left y-axis), and ρ∂xρ vs. x (○ symbols, right axis). (c) The yy component of the nematic order parameter Q vs. x, where Qyy ≡ −〈cos(2θ)/2〉 so that a high Qyy signifies that the orientations of the particles are preferentially pointing up or down. Similar to equilibrium fluids, defining the location of a sharp interface is somewhat arbitrary.27 The working definition proposed here is that the interface is set to be at the pronounced minimum of |〈vx〉|. | |
2.4 Interface stability
2.4.1 Pressure balance at a sharp interface.
In this section we will see how pressure balance can be achieved in MIPS. Note that the discussion in this section amounts to a simplified exposition of that in ref. 23 and 29. Its presentation here is for the self-containedness of this paper and will help in understanding the approximations used in the later sections.
I will start by discussing a sharp interface model. In this drastically simplified model, let us imagine that the phase separated system is partitioned by a sharp interface where in the vapour phase, the concentration is low enough for the system to behave like a system of active point particles, and in the condensed phase, the orientation distribution is isotropic. One can imagine such a system by first rotating Fig. 1(e) by 180° and then collating it to Fig. 1(f) on the left. As calculated before, the pressure exerted by the vapour phase on the sharp interface is fa2ρv/(2ηDr) (eqn (6)); this pressure is balanced by the pressure exerted by the condensed phase: aρcfa/π + Pr, where the first term comes from the active force (eqn (7)) and the second denotes the pressure arising from the repulsive force due to the area exclusion interactions. In other words, pressure balance is achieved if
| | 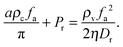 | (8) |
For the simulation parameters used in
Fig. 1 (with the units set by
a = 1 and
Dr = 3),
aρcfa/π ≃ 30,
Pr ≃ 230 and
ρvfa2/(2
ηDr) ≃ 330. We thus see that in the simulated system, the L. H. S. and the R. H. S. of
eqn (8) are of the same order of magnitude, indicating that the pressure balance conditions are qualitatively satisfied. In addition, we see that much of the active force coming from the vapour phase is used to compress the condensed phase
via the pressure
Pr. Note that although
eqn (8) provides a pressure balance condition for the system, it does not mean that any system satisfying this condition is stable as it may still be unstable against fluctuations. This is not dissimilar to equilibrium fluids where pressure balance together with chemical potential balance is needed to achieve phase stability.
The pressure balance condition in eqn (8) already allows for crude estimation of the minimal active force required for MIPS. I assume for simplicity that at the onset, (i) the condensed phase is not very compressed and so we can ignore Pr,30 and (ii) the concentration ratio between the condensed phase and the dilute phase (ρc/ρv) is of order 1, which leads us to the minimal force requirement below for MIPS:
| | 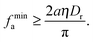 | (9) |
The above condition comes from the pressure balance condition at the interface alone. Interestingly,
eqn (9) reproduces the same scaling as obtained by Redner
et al. via a different approximation.
11 The result also supports the notion that the Péclet number (Pe), usually defined as Pe ∝
fa/(
aηDr) in this context, is a key control parameter in MIPS.
11,31
From this sharp interface model, we can now see why the condensed phase with a high density of active and repulsive particles can remain stable against a backdrop of dilute concentration of active particles – the active particles in the vapour phase impact an active pressure that scales as fa2 directed towards the normal of the interface, while the countering active pressure from the condensed phase scales as fa. The quadratic dependence on the active force is due to the fact that only particles pushing against the interface remain at the interface, while particles oriented away from the interface leave. The escaping particles thus open up space for other particles that serve to push against the interface. From this perspective, the low concentration in the vapour phase is paramount for the stability of MIPS, otherwise the particles oriented away from the interface may be unable to leave effectively.
2.4.2 Force balance in an interface of finite width.
Let us now go beyond the previous sharp interface picture and see what happens within the interfacial region from the view point of particle dynamics. Ignoring fluctuations, the stability of the interface means that if a particle happens to be lying at the interface it will, on average, remain put. In our minimal model, a particle can only move due to two reasons: (i) its own active force driving it to move in the direction dictated by its orientation, and (ii) a repulsive force that pushes it away from its neighbours if it is less than a unit distance away from them. While the second force is common in both active and passive (equilibrium) systems, the active force is unique to non-equilibrium systems. Consider now a particle located at x0 inside the interfacial region, i.e., where 〈vx(x0)〉 is varying (Fig. 2). Since 〈vx(x0)〉 < 0, the active force will on average drive this particle to the left. Moreover, there are repulsive forces coming from the neighbouring particles on the right hand side fr(x0 + Δx). For the particle to remain still, the sum of these forces must be countered by the repulsive forces coming from the left. Therefore,| | | fr(x0 − a/2) = fa〈vx(x0)〉 + fr(x0 + a/2). | (10) |
Since the repulsive forces come from the repulsive potential function U, let us replace the repulsive force by the pressure Pp(x) (subscript p for passive) resulting from the corresponding system with the same particle configuration and interaction potentials, but with the active force omitted. Since fr(x) ≃ aPp(x), eqn (10) leads to| | | fa〈vx(x0)〉 ≃ a[Pp(x0 + a/2) − Pp(x0 − a/2)] | (11) |
| | 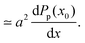 | (12) |
In principle, Pp(x) depends on the exact configuration of particles in the system, but if one adopts the simplifying assumption that the passive pressure depends solely on the particle concentration, one can then increase Pp(x) with respect to concentration ρ(x):| | Pp(x) = c0 + c1ρ(x) + c2ρ(x)2 + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ρ3). (ρ3). | (13) |
For equilibrium fluids, this is of course the virial expansion, where c0 = 0 and c1 = kBT.27 Since our system is fundamentally not in equilibrium (no translational Brownian motion, i.e., kBT = 0), there is no guarantee that the same would apply here. But let us assume that such an expansion is possible in our system, and that Pp develops purely due to the repulsive interactions between particles. We thus expect that c0 = 0 = c1 because as the concentration goes to zero, there would not be any pairwise interactions. Therefore, the first non-trivial term in the expansion is c2ρ2. Note that c2 > 0 since Pp arises purely due to the repulsive interactions. One could also incorporate active pressure into the analysis as, for example, done by Winkler et al.32
Here, to order ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ρ2), eqn (12) then leads to
(ρ2), eqn (12) then leads to
| | 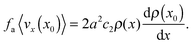 | (14) |
Remarkably, the simulation result shown in
Fig. 2(b) indeed seems to vindicate
eqn (14).
3 Circular interface
We have seen in the previous section how pressure balance is achieved at a flat interface. However, previous 2D simulation studies have shown that similar to equilibrium phase separation, if the condensed phase in MIPS does not span the system size, the condensed phase is circular. Here, we will see how the curvature of the interface affects the particle dynamics at the interface, and its consequence in terms of the coarsening dynamics. We will first study the emergence of the Gibbs–Thomson relationship using dimensional analysis.
3.1 Gibbs–Thomson relationship: dimensional analysis
In equilibrium phase separation, the Gibbs–Thomson (GT) relationship dictates that the concentration ϕR right outside a droplet (of the condensed phase) of radius R is| | 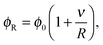 | (15) |
where ϕ0 is the supersaturation concentration, i.e., the threshold concentration beyond which phase separation occurs, and 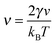 is the capillary length with γ being the surface tension and v being the volume of the molecule. Since the concentration in the vapour phase outside a big drop is lower than that outside a small drop, a diffusive flux is set up which transfers the material from the small droplet to the big droplet. This is the Ostwald ripening mechanism that dominates the phase separation kinetics at the late stage for systems with a small supersaturation.33
is the capillary length with γ being the surface tension and v being the volume of the molecule. Since the concentration in the vapour phase outside a big drop is lower than that outside a small drop, a diffusive flux is set up which transfers the material from the small droplet to the big droplet. This is the Ostwald ripening mechanism that dominates the phase separation kinetics at the late stage for systems with a small supersaturation.33
I will now discuss why the GT relationship would arise naturally in our active system. In the minimal MIPS system considered, the only parameters in the dynamical equations are the free roaming speed u = f/η, the rotational diffusion coefficient Dr, and the length scale of the short range area exclusion interaction a. Denoting now the vapour density far from a drop of radius R by ρR*, and the density inside the drop (the condensed phase) by ρc, then by dimensional analysis we have
| | 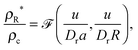 | (16) |
where
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
is some unknown scaling function dependent on its two dimensionless arguments. If we now assume that
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
is regular with respect to the second argument in the sense that a Taylor series expansion exists (around
u/
DrR = 0), then the ratio above can be re-expressed as
| | 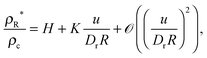 | (17) |
where
H and
K are now just dimensionless functions of the first argument (
u/
Dra),
i.e.,
R-independent. In terms of
ρ∞*,
eqn (17) can be re-written as
| | 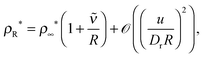 | (18) |
where
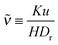
, which may be termed as the effective capillary length. In the large
R limit,
eqn (18) becomes exactly the GT relationship in
eqn (15). This analysis provides an intuitive reason why one would naturally expect the GT relationship to emerge as the drop radius increases in MIPS.
3.2 Gibbs–Thomson relationship: numerics
I will now test eqn (18) by simulating a coarse-grained model of MIPS. Let us first consider what happens to an active particle in the condensed phase at a curved periphery (Fig. 3(a)). For such a particle, I assume that it occupies a zone of radius ã (shown in red) sandwiched by two zones occupied by two neighbouring particles (light blue). Note that since the concentration at the interface may not reach the level of optimal packing concentration (≃0.91), ã should be greater than the particle's diameter a. Indeed, Fig. 2(a) suggests that the concentration is around 0.72 at the interface, which indicates that ã ≃ 1.2. To incorporate the effects of the neighbouring particles on the pink particle, I assume that as a result of the caging effect, the particle can only move out of the droplet if its orientation is within the 2σ range depicted. Based on the diagram shown in Fig. 3, a simple trigonometric exercise leads to| | 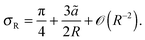 | (19) |
As expected, a lower curvature leads to a smaller escape range (smaller σR).
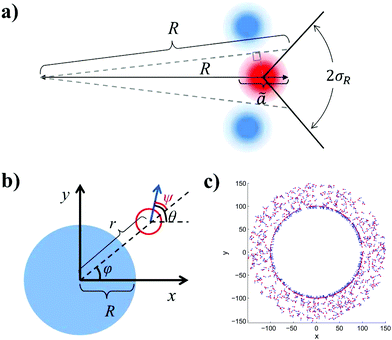 |
| | Fig. 3 (a) A schematic of the interfacial condition at a curved interface of curvature R−1. The particle is assumed to occupy a zone of diameter ã and the particle can leave the droplet if its orientation is within the escape range of 2σR indicated. (b) A schematic showing a droplet (blue) in the condensed phase of the radius R located at the origin co-existing with the dilute medium (vapour phase). An active particle (red circle) with orientation θ (blue arrow) is located at the position (r, φ). The angle ψ is equal to the difference between the orientation θ and the azimuthal coordinate φ. (c) A snapshot of a simulated system with 1000 active point particles (red dots with orientations indicated by blue arrows) in an annular system with inner radius R = 100 and outer radius R + Lr = 150. | |
To analyse how the variation in the escape orientation range affects the phase separated system at the steady-state, I have considered here a system with one condensed drop of radius R co-existing with the vapour phase (Fig. 3(b)). I have denoted the particle distribution function in the vapour phase by pR(r, φ, θ), where the first two arguments correspond to the particles' locations and the last argument corresponds to the particles' orientations. Due to rotational symmetry, one can eliminate one angular argument by introducing the variable ψ ≡ θ − φ,34 and study instead the reduced distribution function 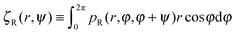 . On the drop's periphery, the corresponding reduced distribution function is denoted by χR(ψ). Since the periphery is assumed to be infinitely thin, χR is only a function of ψ and is therefore dimensionless. In addition, I have assumed that drops of all sizes have the same interior concentration ρc, χR(ψ) and are thus related to the ρc as follows:
. On the drop's periphery, the corresponding reduced distribution function is denoted by χR(ψ). Since the periphery is assumed to be infinitely thin, χR is only a function of ψ and is therefore dimensionless. In addition, I have assumed that drops of all sizes have the same interior concentration ρc, χR(ψ) and are thus related to the ρc as follows: 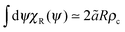 .
.
To study the distribution functions, I assume again that the vapour concentration is low enough that pairwise repulsive interactions can be ignored, and simulate the dynamics of active point particles, i.e., non-interacting active particles, in an annular geometry of inner radius R and outer radius R + Lr (Fig. 3(b)). As in the linear case, the particles' orientations are randomised if they reach the outer circular boundary, while if the i-th particle reaches the inner boundary, its positions will remain fixed until its orientation is within the escape range, i.e., until ψi is between σR and σR. The simulation results are shown in (Fig. 4). Away from the interface, it is observed that the concentration rapidly reaches a stationary value 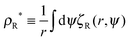 for, say, r > R + 20 (Fig. 4(a)). As expected from previous discussion, the vapor concentration ρR* decreases with R since a flatter interface leads to a narrower escape range, which leads to a smaller outflux of particles from the condensed phase. Fig. 4(b) shows that ρR* decays to ρ∞* (the vapour concentration as R → ∞) like R−1, which, as we have seen, is consistent with the Gibbs–Thomson relationship in equilibrium systems.
for, say, r > R + 20 (Fig. 4(a)). As expected from previous discussion, the vapor concentration ρR* decreases with R since a flatter interface leads to a narrower escape range, which leads to a smaller outflux of particles from the condensed phase. Fig. 4(b) shows that ρR* decays to ρ∞* (the vapour concentration as R → ∞) like R−1, which, as we have seen, is consistent with the Gibbs–Thomson relationship in equilibrium systems.
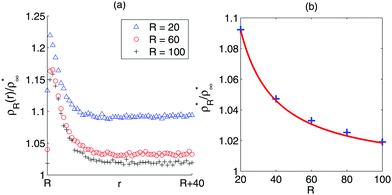 |
| | Fig. 4 (a) The variation in the vapour concentration 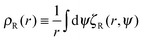 away from the interface of droplets with sizes R = 20, 60, 100. The concentration decays rapidly from the interface and reaches a stationary value ρR* a short distance away from the interface. (b) ρR*/ρ∞* vs. R. The curve decays to 1 like R−1, which is consistent with the Gibbs–Thomson relationship (eqn (18)). Blue crosses represent the simulation results and the red curve depicts the function 1 + 1.84R−1. Note that the constant ρ∞* is estimated numerically from the Gibbs–Thomson relationship. See A.2 for simulation details. away from the interface of droplets with sizes R = 20, 60, 100. The concentration decays rapidly from the interface and reaches a stationary value ρR* a short distance away from the interface. (b) ρR*/ρ∞* vs. R. The curve decays to 1 like R−1, which is consistent with the Gibbs–Thomson relationship (eqn (18)). Blue crosses represent the simulation results and the red curve depicts the function 1 + 1.84R−1. Note that the constant ρ∞* is estimated numerically from the Gibbs–Thomson relationship. See A.2 for simulation details. | |
4 Fluctuating interface
I have so far ignored fluctuations in the interfacial profile. In reality, the interface of course fluctuates, which is already discernible from the spatially constrained system shown in Fig. 1(b). In particular, previous simulation results point to the scaling law:18where wL is the steady state interfacial width:| | 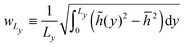 | (21) |
with ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) being the average position of the interface. Here, the symbol
being the average position of the interface. Here, the symbol ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) (y) denotes the location of the interface, i.e., the location of the peak of 〈vx〉 (Fig. 2). To understand the scaling observed, let us consider the effects of the interface curvature on the particle exchange dynamics. Although the previous section focuses only on a circular interface, i.e., the curvature is positive, one can easily extend eqn (19) to allow for a concave interface as well (Fig. 5). The physical motivation behind the formula is the same, a particle at a highly convex portion of the interface will have a wider escape orientation range (red particle in Fig. 5) than a particle at a highly concave interface (green particle).
(y) denotes the location of the interface, i.e., the location of the peak of 〈vx〉 (Fig. 2). To understand the scaling observed, let us consider the effects of the interface curvature on the particle exchange dynamics. Although the previous section focuses only on a circular interface, i.e., the curvature is positive, one can easily extend eqn (19) to allow for a concave interface as well (Fig. 5). The physical motivation behind the formula is the same, a particle at a highly convex portion of the interface will have a wider escape orientation range (red particle in Fig. 5) than a particle at a highly concave interface (green particle).
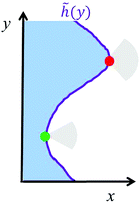 |
| | Fig. 5 Schematic depicting a wavy interface where the condensed phase is depicted in blue. The location of the interface (purple) is given by the function ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) (y). Due to the caging effect from neighbouring particles, the red particle at the interface will have a higher chance of escaping compared to the green particle because the escape orientation range (grey area) is bigger. (y). Due to the caging effect from neighbouring particles, the red particle at the interface will have a higher chance of escaping compared to the green particle because the escape orientation range (grey area) is bigger. | |
Since the fluctuations ultimately come from the fluctuating dynamics of particle exchange at the interface, we need to model the steady-state dynamics of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) stochastically. The simplest equation of motion (EOM) for the interface that incorporates both the effects of stochasticity and curvature-modified outflux is
stochastically. The simplest equation of motion (EOM) for the interface that incorporates both the effects of stochasticity and curvature-modified outflux is
| | 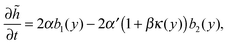 | (22) |
where
α denotes the rate of particles coming at the interface, and thus contributing to the growth of
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif)
, while
α′(1 +
β′
κ(
y)) denotes the rate of the particles escaping, with the effect of the local interface curvature (
κ(
y) = ∂
2![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif)
/∂
y2) taken into account. The noise terms are
bi(
x) which are Markovian, spatially independent and are either 0 or 1 with equal probability. Since the interface does not move in the steady state by assumption,
α has to be identical to
α′. From now on, I will focus exclusively on the hydrodynamic limits (large temporal and spatial scales). So let us coarse grain
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif)
by defining a new coarse-grained height function
h(
y):
| | 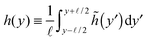 | (23) |
where
a ≪
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
≪
Ly and
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
is large enough that
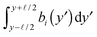
become Gaussian as a result of the central limit theorem. The EOM of
h(
y) is then
| | 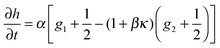 | (24) |
| | 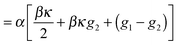 | (25) |
where
gi are now Gaussian noises such that
| | 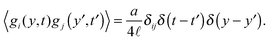 | (27) |
In the long-wavelength limit, the fluctuating term
αβκg2 ∼ ∂
2h/∂
y2 → 0 and so the only relevant fluctuations come from the Gaussian fluctuations
α(
g1 −
g2). Therefore, in the hydrodynamic limits,
eqn (25) is exactly the Edwards–Wilkinson model,
35 with the effective surface tension given by
αβ/2. Note that the effective surface tension here is always positive, which is a requirement for having a stable interface. As such this effective surface tension is distinct from the mechanical definition of surface tension, which has been shown to be negative in MIPS.
18 As mentioned in Section 2.2, the negative tension around the interface is likely to be caused by the particles escaping from the condensed phase that are now travelling close to being parallel to the interface. Consistent with our definition of the location of the interface (
Fig. 2), these escaped particles are not considered to be part of the condensed phase and are thus ignored in our discussion of the interfacial fluctuations. In other words, the effective surface tension derived here is distinct from the mechanical definition of the surface tension discussed by Bialké
et al.18
Given that our stochastic model is equivalent to the Edwards–Wilkinson model, the temporal and steady-state dynamics of interfacial width are known to follow the scaling form:
| | 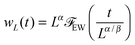 | (28) |
for some scaling functions
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EW
EW(·) (
Fig. 6). In a 2D system where the interface is a line,
α = 1/2 and
β = 1/4.
35,36 As shown in
Fig. 6, these expectations are confirmed with direct simulation of a discretised version of the original EOM in
eqn (22). This model thus provides an analytical argument supporting the steady state scaling
wL(
t → ∞) ∼
L1/2 recently observed numerically.
18
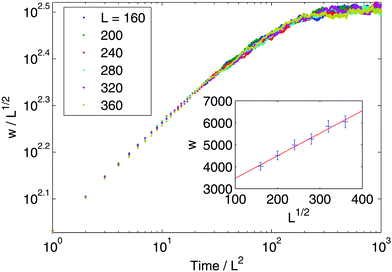 |
| | Fig. 6 Interface fluctuations as measured by the interface width 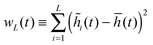 . The curve collapse of systems with difference linear dimension L upon rescaling is predicted using the EW model. Inset plot: The interface width at the final time wL(tf) shows a linear dependence with . The curve collapse of systems with difference linear dimension L upon rescaling is predicted using the EW model. Inset plot: The interface width at the final time wL(tf) shows a linear dependence with 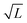 , where L is the system size. Blue crosses represent the simulation results and the red line is a guide for the eyes. See Appendix A.3 for simulation details. , where L is the system size. Blue crosses represent the simulation results and the red line is a guide for the eyes. See Appendix A.3 for simulation details. | |
To summarise this section, I have incorporated the caging effect as discussed in Section 3 into the modelling of the stochastic dynamics of particle exchanges at the interface. The model equation is then shown to be equivalent to the Edward–Wilkinson model in the hydrodynamic limits. In particular, the emergence of the effective surface tension term (αβκ/2) from the particle dynamics at the interface also explains why the interface is flat when both phases span the system, and circular when one phase does not span the system.
5 MIPS in 3D
I have so far analysed the interfacial properties in MIPS in 2D using a combination of analytical and numerical methods. Here I will extrapolate the obtained results to MIPS in 3D.
5.1 Flat interface
Utilizing the sharp interface model for MIPS in 3D, the pressure balance equation in eqn (8) becomes| | 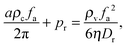 | (29) |
where on the R. H. S. the active force contribution corresponds to the swim pressure of active particles in 3D in the vapour phase,23 and on the L. H. S., the first term comes from the active contribution to the force assuming again that the orientation is isotropic in the condensed phase. With regards to the minimal active force required for MIPS, using the approximations that fr is negligible and that ρc/ρv ≃ 1, we arrive at| | 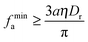 | (30) |
which is very similar to the expression in 2D (eqn (9)).
5.2 Spherical interface
The dimensional analysis presented in Section 3.1 also includes spherical drops in 3D. Therefore, if the assumption that the escape range decreases with the curvature of the drop, then the Gibbs–Thomson relationship should emerge in the large drop limit (eqn (18)). In particular, we again expect the MIPS coarsening kinetics to be equivalent to the equilibrium scheme at low supersaturation.15,33,37
5.3 Interface fluctuations
For MIPS in 3D, the interface is two dimensional and so there are two principal curvatures. If we adopt the natural assumption that the escape range now depends on the mean curvature, then the theoretical analysis presented in Section 4 applies in 3D in a straightforward manner. As a result, keeping only the linear terms will again lead to the Edwards–Wilkinson model in the hydrodynamic limits.
6 Discussion and outlook
In this paper I have investigated the microscopic dynamics of active particles in the interfacial regions in MIPS using a combination of simulations and analytical arguments, and demonstrated (i) how interface stability is achieved, (ii) why the GT relationship emerges in MIPS, and (iii) how interface fluctuations scale with the system size. Therefore, I have shown that all the observed “surface tension” related phenomena found in MIPS result from the microscopic dynamics of the active particles. More specifically, I have demonstrated that pressure balance in MIPS is achieved because of the orientation anisotropy in the region, which leads to a high active force directed towards the condensed phase. By incorporating the caging effects of neighbouring particles in the peripheral of a condensed drop, I have shown how the Gibbs–Thomson relationship emerges naturally in MIPS, which dictates that the larger the condensed drop, the smaller the vapour concentration outside the drop. If the supersaturation level is small, the GT relationship leads to diffusive transfer of active particles from small drops to larger drops. As a result, the late-stage coarsening kinetics in an active phase-separating system should follow the temporal scaling as in equilibrium phase separation: i.e., the average droplet size in the system 〈R(t)〉 scales as15,33,37t1/3. In addition, the droplet size distribution should approach asymptotically the universal size distribution obtained by Lifshitz and Slyozov.33 Lastly, motivated by the same caging effects, I have proposed a stochastic model that describes the interfacial fluctuations in MIPS. In this model, the probability of particles leaving the interface is assumed to be dependent on the interface curvature. An analytical argument was then provided to show that the proposed model belongs to the same universality class as the Edwards–Wilkinson model.
There are a number of future research directions that are of interest. For instance, phase separation may play a role in cytoplasmic re-organisation during asymmetric cell division.38,39 How the activity in the cytoplasm due to the many motor proteins contributes to such re-organisation via phase separation awaits more attention. Moreover, the fact that active phase separation occurs naturally raises the question of the existence of the critical point as in the equilibrium case. The critical transition in incompressible active fluids has recently been shown to give rise to a novel universality class.40 Furthermore, if a critical transition exists in MIPS, will the critical exponents be identical to those in the equilibrium case which belong to the Ising universality class? This question awaits further investigation.
Appendix A Simulation details
A.1 Particle dynamics simulation
For the simulation results reported in Section 2 (Fig. 1 and 2), I numerically integrate the Langevin equations for each particle in the bulk of the system of size Lx × Ly by using the following updated equations:| | 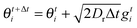 | (31) |
| | 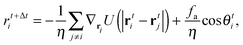 | (32) |
where gti are Gaussian distributed random variables with zero mean and unit variance, and U is given by the Weeks–Chandler–Andersen potential shown in eqn (3). The periodic boundary condition is enforced in the y, direction; while in the x direction, if xt+Δti < 0, then it is reset to zero, and if xt+Δti > Lx, then xt+Δti = Lx and θt+Δti is an angle chosen at random.
The parameters of the simulations are: Δt = 10−5, a = 1, η = 1, fa = 100, Dr = 3, and A = 25/6 for repulsive particles and A = 0 for point particles. The system has width Lx = 50 and height Ly = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(π/3), with 300 particles initialized in the configuration of a hexagonal lattice (with spacing 1) next to the left boundary, and random orientations. Two hundred million time steps are evolved to equilibrate the system and then data are collected in the subsequent two hundred million time steps.
sin(π/3), with 300 particles initialized in the configuration of a hexagonal lattice (with spacing 1) next to the left boundary, and random orientations. Two hundred million time steps are evolved to equilibrate the system and then data are collected in the subsequent two hundred million time steps.
A.2 Point particles in an annular geometry
For the simulation results reported in Section 3 (Fig. 3), the system is now annular with inner radius R and outer radius R + Lr. The same updates as in eqn (31) and (32) are included for the point particles in the bulk of the system. Concerning the boundary conditions, if rt ≤ R then the particle becomes part of the condensed drop periphery, and the orientation follows the update:| | 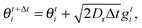 | (33) |
while the position remains the same until ψt ≡ |θt − φt| < σR (Fig. 3(b)), in which case the particle leaves the condensed phase. If rt+Δti > R + Lr, then rt+Δti = R + Lr and θt+Δti is an angle chosen at random.
For distinct annulus geometry, the density ρR(r) is normalised by ρc, which is the density of particles at the inner circular wall. This is based on the assumption that ρc is the same irrespective of drop sizes.
The parameters of the simulations are: Δt = 10−3, η = 1, fa = 100, Dr = 3, and A = 0. The system has 1000 particles initialized with random orientations and positions. Twenty million time steps are evolved to equilibrate the system and then data are collected in the subsequent twenty million time steps. Simulations are performed for R = 20, 40, 60, 80 and 100, while Lr is always 50.
A.3 Fluctuating interfaces
To simulate interface fluctuations according to eqn (22), I discretise the interface (a line) into L sites with height values hi where i = 1,…,L. Periodic boundary conditions are enforced. The updates are performed as follows:| | ht+Δti = hti + [1 + β(hti−1 + hti+1 − 2hti)]![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti − [1 − β(hti−1 + hti+1 − 2hti)] ti − [1 − β(hti−1 + hti+1 − 2hti)]![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti, ti, | (34) |
where ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti are either 0 or 1 chosen with equal probability, and β = 0.1. The system sizes simulated are L = 160, 200, 240, 280, 320 and 360. The total number of time steps simulated for each system size is 5L2/2.
ti are either 0 or 1 chosen with equal probability, and β = 0.1. The system sizes simulated are L = 160, 200, 240, 280, 320 and 360. The total number of time steps simulated for each system size is 5L2/2.
Acknowledgements
I thank Christoph Weber (Max Planck Institute for the Physics of Complex Systems), Fernando Peruani (Université Nice Sophia Antipolis) and Richard Sear (University of Surrey) for stimulating discussions and for their comments on the manuscript.
References
-
C. Domb, J. L. Lebowitz and M. S. Green, Phase Transitions and Critical Phenomena, Academic Press, 1983 Search PubMed.
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720 CrossRef CAS PubMed.
- F. Peruani, T. Klauss, A. Deutsch and A. Voss-Boehme, Phys. Rev. Lett., 2011, 106, 128101 CrossRef PubMed.
- J. P. D. Clewett, K. Roeller, R. M. Bowley, S. Herminghaus and M. R. Swift, Phys. Rev. Lett., 2012, 109, 228002 CrossRef PubMed.
- F. D. C. Farrell, M. C. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101 CrossRef CAS PubMed.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. E. Cates, D. Marenduzzo, A. N. Morozov and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, EPL, 2013, 101, 20010 CrossRef CAS.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 55701 CrossRef PubMed.
- J. Bialké, H. Löwen and T. Speck, EPL, 2013, 103, 30008 CrossRef.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 4351 CAS.
- A. Y. Grosberg and J. F. Joanny, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 32118 CrossRef CAS PubMed.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 18301 CrossRef PubMed.
- J. Bialké, J. T. Siebert, H. Löwen and T. Speck, Phys. Rev. Lett., 2015, 115, 98301 CrossRef PubMed.
-
R. P. Sear, 2015, arXiv:1503.06963.
- A. Marchand, J. H. Weijs, J. H. Snoeijer and B. Andreotti, Am. J. Phys., 2011, 79, 999–1008 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- See eqn (15), (17) and (18) in C. F. Lee, New J. Phys., 2013, 15, 055007 CrossRef.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 28103 CrossRef CAS PubMed.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477–6484 RSC.
- S. A. Mallory, A. Šarić, C. Valeriani and A. Cacciuto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 52303 CrossRef CAS PubMed.
- A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar and J. Tailleur, Nat. Phys., 2015, 11, 673–678 CrossRef CAS.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 2006 Search PubMed.
-
P. G. de Gennes and J. Prost, The Physics of Liquid Crystals International Series of Monographs on Physics, Oxford University Press, USA, 1995 Search PubMed.
- A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates and J. Tailleur, Phys. Rev. Lett., 2015, 114, 198301 CrossRef PubMed.
- An anonymous referee has indicated that numerical simulation shows that Pr is about a third of the other terms at the onset of MIPS. However, eqn (9) remains valid as Pr does not depend on the Péclet number at the onset, as shown in the preceding paper.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- R. G. Winkler, A. Wysocki and G. Gompper, Soft Matter, 2015, 11, 6680–6691 RSC.
- I. Lifshitz and V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- A. Pototsky and H. Stark, EPL, 2012, 98, 50004 CrossRef.
- S. F. Edwards and D. R. Wilkinson, Proc. R. Soc. London, Ser. A, 1982, 381, 17–31 CrossRef.
-
A. L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth, Cambridge University Press, 1995 Search PubMed.
- J. Yao, K. R. Elder, H. Guo and M. Grant, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 8173–8176 CrossRef.
- C. Brangwynne, C. Eckmann, D. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. Hyman, Science, 2009, 324, 1729–1732 CrossRef CAS PubMed.
- C. F. Lee, C. P. Brangwynne, J. Gharakhani, A. A. Hyman and F. Julicher, Phys. Rev. Lett., 2013, 111, 088101 CrossRef PubMed.
- L. Chen, J. Toner and C. F. Lee, New J. Phys., 2015, 17, 042002 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
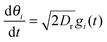
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + sin
+ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θiŷ with the angle θi (with respect to the x-axis) being the orientation of the i-particle, gi(t) is a noise term with Gaussian probability distribution with zero mean and unit variance, Dr sets the magnitude of the rotational fluctuations, U(·) corresponds to the potential function for short-ranged area exclusion interactions, η is the drag coefficient and fa is the constant active force that drives the particles in the system. In particular, u ≡ fa/η is the constant speed of a particle when it is not within the area exclusion zone of another particle. Previous numerical work has indicated that phase separation in this minimal system occurs as u increases, but the actual form of U is unimportant.8,11,14 For instance, U could be in the form of a Weeks–Chandler–Andersen potential:21
θiŷ with the angle θi (with respect to the x-axis) being the orientation of the i-particle, gi(t) is a noise term with Gaussian probability distribution with zero mean and unit variance, Dr sets the magnitude of the rotational fluctuations, U(·) corresponds to the potential function for short-ranged area exclusion interactions, η is the drag coefficient and fa is the constant active force that drives the particles in the system. In particular, u ≡ fa/η is the constant speed of a particle when it is not within the area exclusion zone of another particle. Previous numerical work has indicated that phase separation in this minimal system occurs as u increases, but the actual form of U is unimportant.8,11,14 For instance, U could be in the form of a Weeks–Chandler–Andersen potential:21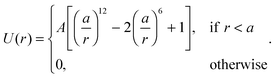
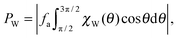
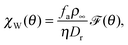
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (θ) is a function dependent only on θ, and ρ∞ is the particle concentration far from the wall. To obtain the exact functional form of
(θ) is a function dependent only on θ, and ρ∞ is the particle concentration far from the wall. To obtain the exact functional form of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (θ), one needs to solve a set of two coupled differential equations under mixed boundary conditions,22 whose solution consists of a series of Mathieu functions. Unfortunately, the expansion coefficients in the series are not analytically tractable and so an analytical expression is lacking. However,
(θ), one needs to solve a set of two coupled differential equations under mixed boundary conditions,22 whose solution consists of a series of Mathieu functions. Unfortunately, the expansion coefficients in the series are not analytically tractable and so an analytical expression is lacking. However, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (θ) can be readily estimated numerically (left column of Fig. 1), which allows one to obtain the following equation:
(θ) can be readily estimated numerically (left column of Fig. 1), which allows one to obtain the following equation: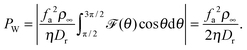
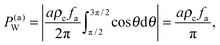
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is easy to locate (indicated by the red broken line) and its location also marks the onset of the increase in Qyy ≡ −〈cos(2θ)/2〉 (the yy component of the nematic order parameter Q),28 which signifies the escape of particles from the condensed phase, it is a convenient choice for the interface location. In other words, this convention implies that right outside the interface of the condensed phase, there is a layer of particles travelling preferentially along the interface, as indicated by the peak in Qyy (Fig. 2(c)). The active forces of these escaped particles are potentially the cause of the emergence of a negative surface tension according to its mechanical definition.18 The definition of the interface location has of course no physical significance, but this does provide a working definition useful for the sharp interface model discussed below.
θ〉 is easy to locate (indicated by the red broken line) and its location also marks the onset of the increase in Qyy ≡ −〈cos(2θ)/2〉 (the yy component of the nematic order parameter Q),28 which signifies the escape of particles from the condensed phase, it is a convenient choice for the interface location. In other words, this convention implies that right outside the interface of the condensed phase, there is a layer of particles travelling preferentially along the interface, as indicated by the peak in Qyy (Fig. 2(c)). The active forces of these escaped particles are potentially the cause of the emergence of a negative surface tension according to its mechanical definition.18 The definition of the interface location has of course no physical significance, but this does provide a working definition useful for the sharp interface model discussed below.

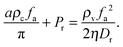
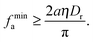
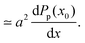
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ρ3).
(ρ3).![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ρ2), eqn (12) then leads to
(ρ2), eqn (12) then leads to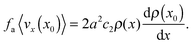
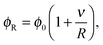
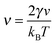 is the capillary length with γ being the surface tension and v being the volume of the molecule. Since the concentration in the vapour phase outside a big drop is lower than that outside a small drop, a diffusive flux is set up which transfers the material from the small droplet to the big droplet. This is the Ostwald ripening mechanism that dominates the phase separation kinetics at the late stage for systems with a small supersaturation.33
is the capillary length with γ being the surface tension and v being the volume of the molecule. Since the concentration in the vapour phase outside a big drop is lower than that outside a small drop, a diffusive flux is set up which transfers the material from the small droplet to the big droplet. This is the Ostwald ripening mechanism that dominates the phase separation kinetics at the late stage for systems with a small supersaturation.33
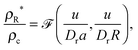
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is some unknown scaling function dependent on its two dimensionless arguments. If we now assume that
is some unknown scaling function dependent on its two dimensionless arguments. If we now assume that ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is regular with respect to the second argument in the sense that a Taylor series expansion exists (around u/DrR = 0), then the ratio above can be re-expressed as
is regular with respect to the second argument in the sense that a Taylor series expansion exists (around u/DrR = 0), then the ratio above can be re-expressed as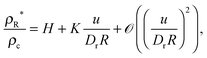
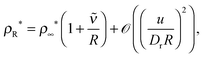
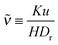 , which may be termed as the effective capillary length. In the large R limit, eqn (18) becomes exactly the GT relationship in eqn (15). This analysis provides an intuitive reason why one would naturally expect the GT relationship to emerge as the drop radius increases in MIPS.
, which may be termed as the effective capillary length. In the large R limit, eqn (18) becomes exactly the GT relationship in eqn (15). This analysis provides an intuitive reason why one would naturally expect the GT relationship to emerge as the drop radius increases in MIPS.
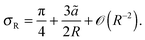
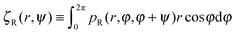 . On the drop's periphery, the corresponding reduced distribution function is denoted by χR(ψ). Since the periphery is assumed to be infinitely thin, χR is only a function of ψ and is therefore dimensionless. In addition, I have assumed that drops of all sizes have the same interior concentration ρc, χR(ψ) and are thus related to the ρc as follows:
. On the drop's periphery, the corresponding reduced distribution function is denoted by χR(ψ). Since the periphery is assumed to be infinitely thin, χR is only a function of ψ and is therefore dimensionless. In addition, I have assumed that drops of all sizes have the same interior concentration ρc, χR(ψ) and are thus related to the ρc as follows: 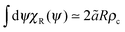 .
.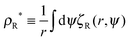 for, say, r > R + 20 (Fig. 4(a)). As expected from previous discussion, the vapor concentration ρR* decreases with R since a flatter interface leads to a narrower escape range, which leads to a smaller outflux of particles from the condensed phase. Fig. 4(b) shows that ρR* decays to ρ∞* (the vapour concentration as R → ∞) like R−1, which, as we have seen, is consistent with the Gibbs–Thomson relationship in equilibrium systems.
for, say, r > R + 20 (Fig. 4(a)). As expected from previous discussion, the vapor concentration ρR* decreases with R since a flatter interface leads to a narrower escape range, which leads to a smaller outflux of particles from the condensed phase. Fig. 4(b) shows that ρR* decays to ρ∞* (the vapour concentration as R → ∞) like R−1, which, as we have seen, is consistent with the Gibbs–Thomson relationship in equilibrium systems.
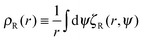 away from the interface of droplets with sizes R = 20, 60, 100. The concentration decays rapidly from the interface and reaches a stationary value ρR* a short distance away from the interface. (b) ρR*/ρ∞* vs. R. The curve decays to 1 like R−1, which is consistent with the Gibbs–Thomson relationship (eqn (18)). Blue crosses represent the simulation results and the red curve depicts the function 1 + 1.84R−1. Note that the constant ρ∞* is estimated numerically from the Gibbs–Thomson relationship. See A.2 for simulation details.
away from the interface of droplets with sizes R = 20, 60, 100. The concentration decays rapidly from the interface and reaches a stationary value ρR* a short distance away from the interface. (b) ρR*/ρ∞* vs. R. The curve decays to 1 like R−1, which is consistent with the Gibbs–Thomson relationship (eqn (18)). Blue crosses represent the simulation results and the red curve depicts the function 1 + 1.84R−1. Note that the constant ρ∞* is estimated numerically from the Gibbs–Thomson relationship. See A.2 for simulation details.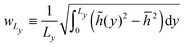
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) being the average position of the interface. Here, the symbol
being the average position of the interface. Here, the symbol ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) (y) denotes the location of the interface, i.e., the location of the peak of 〈vx〉 (Fig. 2). To understand the scaling observed, let us consider the effects of the interface curvature on the particle exchange dynamics. Although the previous section focuses only on a circular interface, i.e., the curvature is positive, one can easily extend eqn (19) to allow for a concave interface as well (Fig. 5). The physical motivation behind the formula is the same, a particle at a highly convex portion of the interface will have a wider escape orientation range (red particle in Fig. 5) than a particle at a highly concave interface (green particle).
(y) denotes the location of the interface, i.e., the location of the peak of 〈vx〉 (Fig. 2). To understand the scaling observed, let us consider the effects of the interface curvature on the particle exchange dynamics. Although the previous section focuses only on a circular interface, i.e., the curvature is positive, one can easily extend eqn (19) to allow for a concave interface as well (Fig. 5). The physical motivation behind the formula is the same, a particle at a highly convex portion of the interface will have a wider escape orientation range (red particle in Fig. 5) than a particle at a highly concave interface (green particle).
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) stochastically. The simplest equation of motion (EOM) for the interface that incorporates both the effects of stochasticity and curvature-modified outflux is
stochastically. The simplest equation of motion (EOM) for the interface that incorporates both the effects of stochasticity and curvature-modified outflux is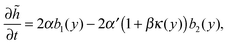
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) , while α′(1 + β′κ(y)) denotes the rate of the particles escaping, with the effect of the local interface curvature (κ(y) = ∂2
, while α′(1 + β′κ(y)) denotes the rate of the particles escaping, with the effect of the local interface curvature (κ(y) = ∂2![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) /∂y2) taken into account. The noise terms are bi(x) which are Markovian, spatially independent and are either 0 or 1 with equal probability. Since the interface does not move in the steady state by assumption, α has to be identical to α′. From now on, I will focus exclusively on the hydrodynamic limits (large temporal and spatial scales). So let us coarse grain
/∂y2) taken into account. The noise terms are bi(x) which are Markovian, spatially independent and are either 0 or 1 with equal probability. Since the interface does not move in the steady state by assumption, α has to be identical to α′. From now on, I will focus exclusively on the hydrodynamic limits (large temporal and spatial scales). So let us coarse grain ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) by defining a new coarse-grained height function h(y):
by defining a new coarse-grained height function h(y):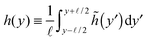
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≪ Ly and
≪ Ly and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is large enough that
is large enough that 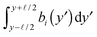 become Gaussian as a result of the central limit theorem. The EOM of h(y) is then
become Gaussian as a result of the central limit theorem. The EOM of h(y) is then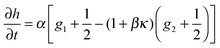
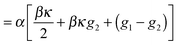
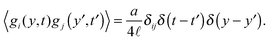
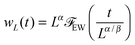
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) EW(·) (Fig. 6). In a 2D system where the interface is a line, α = 1/2 and β = 1/4.35,36 As shown in Fig. 6, these expectations are confirmed with direct simulation of a discretised version of the original EOM in eqn (22). This model thus provides an analytical argument supporting the steady state scaling wL(t → ∞) ∼ L1/2 recently observed numerically.18
EW(·) (Fig. 6). In a 2D system where the interface is a line, α = 1/2 and β = 1/4.35,36 As shown in Fig. 6, these expectations are confirmed with direct simulation of a discretised version of the original EOM in eqn (22). This model thus provides an analytical argument supporting the steady state scaling wL(t → ∞) ∼ L1/2 recently observed numerically.18
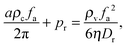
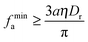
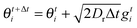
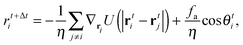
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(π/3), with 300 particles initialized in the configuration of a hexagonal lattice (with spacing 1) next to the left boundary, and random orientations. Two hundred million time steps are evolved to equilibrate the system and then data are collected in the subsequent two hundred million time steps.
sin(π/3), with 300 particles initialized in the configuration of a hexagonal lattice (with spacing 1) next to the left boundary, and random orientations. Two hundred million time steps are evolved to equilibrate the system and then data are collected in the subsequent two hundred million time steps.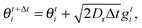
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti − [1 − β(hti−1 + hti+1 − 2hti)]
ti − [1 − β(hti−1 + hti+1 − 2hti)]![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti,
ti,![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ti are either 0 or 1 chosen with equal probability, and β = 0.1. The system sizes simulated are L = 160, 200, 240, 280, 320 and 360. The total number of time steps simulated for each system size is 5L2/2.
ti are either 0 or 1 chosen with equal probability, and β = 0.1. The system sizes simulated are L = 160, 200, 240, 280, 320 and 360. The total number of time steps simulated for each system size is 5L2/2.