A study on the nature of the thermal decomposition of methylammonium lead iodide perovskite, CH3NH3PbI3: an attempt to rationalise contradictory experimental results
Alessandro
Latini
,
Guido
Gigli
and
Andrea
Ciccioli
 *
*
Dipartimento di Chimica, Università di Roma La Sapienza, p.le Aldo Moro 5, Roma, I-00185, Italy. E-mail: andrea.ciccioli@uniroma1.it
First published on 8th May 2017
Abstract
The nature of the gas phase product released during the thermal decomposition of CH3NH3PbI3 (methylammonium lead iodide) to PbI2 (lead diiodide) under vacuum is discussed on the basis of thermodynamic predictions, recently published experimental results, and new experiments presented here. From the limited data currently available, the nature of the main decomposition path is not clear because, both, the process releasing HI(g) + CH3NH2(g) (1) and that leading to NH3(g) + CH3I(g) (2) were observed under different conditions. Our thermodynamic analysis showed that process (2) is largely favoured for all the CH3NH3PbX3 (X = Cl, Br, I) compounds. However, Knudsen effusion mass spectrometry experiments (temperature range 140–240 °C) showed that HI(g) and CH3NH2(g) were the predominant species in the vapor, with process (2) occurring to a much smaller extent than suggested by the thermodynamic driving force, thus being of minor importance under effusion conditions. We also found that this process was comparatively enhanced by high temperatures and low effusion rates (high impedance orifice). Our experimental evidence suggested that the thermodynamically favoured process (2) was affected by a significant kinetic hindrance. Overall, the prevailing decomposition path is likely to markedly depend on the actual operative conditions.
Introduction
The most investigated among light harvester materials based on organic–inorganic hybrid perovskites, is most likely methylammonium lead iodide, CH3NH3PbI3, with a maximum conversion efficiency exceeding 20%.1–3 However, a problem with large-scale applications is the low stability of this and similar compounds.4–6 Great effort has been made in the last few years to investigate in detail the degradation of this material under several external factors usually involved in the operation of photovoltaic devices, such as humidity, irradiation, and electrical current.3–8 With regards to the interactions with water, various degradation paths were suggested depending on the specific conditions applied, involving the formation of PbI2, I2, H2, methylamine, and hydrated forms of CH3NH3PbI3.8–10 Theoretical approaches were also used to investigate the degradation mechanism at the atomic scale.11,12 Various protection strategies were proposed based on the encapsulation and interface engineering techniques8,13 as well as a number of chemical modifications including partial substitution of iodine with other halide species,14 longer alkylammonium chains,15 replacement of lead by other elements such as bismuth,16 and/or partial substitution of alkylammonium ions with different cations, such as Cs+ and formamidinium.17Apparently, less attention was paid to the study of the intrinsic thermal instability of CH3NH3PbI3, (i.e., the degradation behaviour under heating in vacuum or inert atmosphere). A few recent reports addressed this issue, both by experiments18,19 and by theoretical calculations.20 While the formation of PbI2 as the condensed phase degradation product is well established, far less information is available about the gaseous products released upon degradation. This information is of interest to optimize the synthetic conditions and annealing of this material.18,21,22
The thermal degradation of CH3NH3PbX3 (X = Cl, Br, I) proceeds by the release of volatile products, as reported in several studies based on thermogravimetry (TGA).23,24 This is the reason why, despite the order of enthalpies of formation, which follows an increasing trend going from Cl to Br to I,25 the actual stability under real conditions is reversed, with CH3NH3PbI3 being more stable than CH3NH3PbCl3.24 On the basis of mass loss data, Dualeh et al.24 proposed a pathway based on the consecutive loss of HI(g) and CH3NH2(g). However, classic thermogravimetric experiments provided the total mass loss rate, with no direct information on the gaseous species released during decomposition.
To the best of our knowledge, the direct detection of the nature of the vapor phase produced from CH3NH3PbX3 thermal degradation was only reported by Williams et al.23 in a work based on TGA coupled with FTIR (Fourier transform infrared) spectroscopy. The conclusion of this study was that at 265 °C, the simple methylammonium halides CH3NH3Cl and CH3NH3I decomposed to give HCl(g) and CH3NH2(g) and CH3I(g) and NH3(g), respectively. With regards to the lead halide perovskites, IR spectra in ref. 23 were complicated by the superposition of solvent (DMF) peaks. However, at 230 °C, IR peaks of HCl(g) and CH3NH2(g) began to appear for CH3NH3PbI3−xClx, whereas only a weak signal for ammonia was recognizable for CH3NH3PbI3.23
In 2016, two reports appeared in the literature specifically addressing the problem by the direct mass spectrometric observation of the evolving gases. The first contribution was provided by our group26 based on evaporation experiments carried out for all three CH3NH3PbX3 compounds under Knudsen effusion conditions (KEMS, Knudsen effusion mass spectrometry), with a mass spectrometric analysis of the effusing vapours in the overall temperature range of 50–166 °C (53–134 °C for CH3NH3PbI3), encompassing the conditions used for the operation of the photovoltaic devices. On this basis, the following decomposition process was proposed to take place under the above mentioned experimental conditions:
| CH3NH3PbI3(s) = PbI2(s) + CH3NH2(g) + HI(g) | (1) |
Similar results were found for chloride and bromide perovskites.
Shortly after, Juarez-Perez et al.27 used thermogravimetry coupled with mass spectrometry to investigate the mass loss process of CH3NH3PbI3 (and CH3NH3I) in open-crucible conditions under a helium flow at 300–420 °C. They concluded that the degradation process instead took place in the following manner:
| CH3NH3PbI3(s) = PbI2(s) + CH3I(g) + NH3(g) | (2) |
It is worth noting that the decomposition path (2) had been already observed in quaternary alkylammonium halides R4NX,28,29 where no hydrogen atom was present in the cation, whereas process (1) was proposed for primary, secondary and tertiary alkylammonium counterparts, including the compounds RNH3X of interest here.28–31
In summary, the decomposition path of the CH3NH3PbX3 perovskite material appears to still be controversial. Herein, we present further KEMS experiments to shed some light on the somehow contradictory results of the few experimental studies available to date. A brief thermodynamic analysis of the competition between processes (1) and (2) under equilibrium conditions is first presented.
Thermodynamic analysis
From a purely thermodynamic point of view (physicochemical equilibrium), the competition between processes (1) and (2) for the generic perovskite halide CH3NH3PbX3 is governed by the Kp ratio. To evaluate the prevailing process, this quantity is calculated as follows: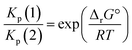 | (3) |
| CH3NH2(g) + HX(g) = CH3X(g) + NH3(g) | (4) |
In terms of partial pressures of the two gaseous species, p(HX) = p(CH3NH2) = p(1) and p(NH3) = p(CH3X) = p(2), eqn (3) becomes
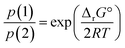 | (5) |
The ΔrG° of reaction (4) was calculated from the thermodynamic properties of the four species involved using the database IVTANTHERMO32 for all species except CH3NH2(g) (not included in ref. 32), for which the database by Frenkel et al.33 was used. The derived ΔrG° values can be approximated by the following linear relationships in the 298.15–700 K temperature range:
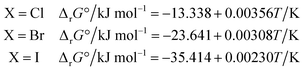 | (6) |
As expected, the entropic term has a very small influence on the ΔrG° value in the temperature range of interest, but it governs the increasing trend of ΔrG° with temperature.
In the temperature range of interest according to eqn (6), ΔrG° is strongly negative. Therefore, on a thermodynamic basis, we conclude that all three lead halide perovskites CH3NH3PbX3 (X = Cl, Br, I) should decompose to give ammonia and methyl halide as the predominant gaseous species under equilibrium conditions. From eqn (5) and (6), the plot reported in Fig. 1 was obtained for p(1)/p(2), showing process (2) as the major process in all cases, and particularly favoured for iodine. The contribution of process (2) decreases with increasing temperature, with a trend more pronounced for iodine.
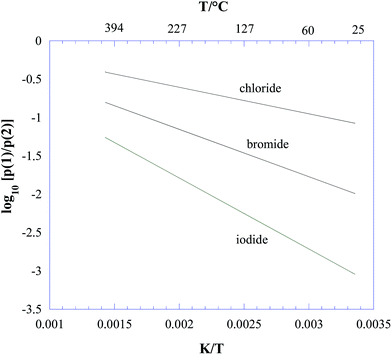 | ||
| Fig. 1 Thermodynamic competition between the decomposition processes (1) CH3NH3PbX3(s) = PbX2(s) + CH3NH2(g) + HX(g) and (2) CH3NH3PbX3(s) = PbX2(s) + CH3X(g) + NH3(g), with X = Cl, Br, I, expressed by the ratio between the corresponding equilibrium partial pressures (see eqn (3)–(5) in the text). | ||
More insight into this thermodynamic prediction can be obtained from the data in Table 1, where the standard formation enthalpies ΔfH° (kJ mol−1) at 298 K are reported for all the species involved. Basically, the thermodynamic competition between (1) and (2) was driven by the different stabilities of CH3NH2(g) and NH3(g) (the latter being more stable by 23.4 kJ mol−1) and of HX(g) and CH3X(g). As evident from Table 1, both hydrogen halides and methyl halides became more unstable going from Cl to I, but the trend for HX was more pronounced, making the formation of HI particularly unfavoured compared to that of CH3I. As a consequence, in the case of iodine, process (2) was particularly favoured.
As far as thermodynamic equilibrium is concerned, the above analysis and conclusions apply as such to the decomposition equilibria of the simple methylammonium halides as well. As mentioned in the introduction, these compounds are reported28 to decompose releasing methylamine and hydrogen halide in the gas phase, which is in contrast with thermodynamic predictions. However, more recently, Williams et al.23 reported spectroscopic evidence supporting process (1) for CH3NH3Cl and process (2) for CH3NH3I.
It is also interesting to note that according to eqn (6), the tendency towards decomposition would significantly increase from chloride to iodide, whereas the opposite trend was reported on the basis of TGA24 and Knudsen effusion26 measurements. Thus, this confirmed that the actual degradation process does not take place under thermodynamic control.
Based on eqn (3)–(5), the above reported thermodynamic estimate has the advantage of being independent from the thermodynamic properties of CH3NH3PbI3, which are not well established. From heat capacity measurements,34 an absolute entropy of 374.1 J K−1 mol−1 at 298 K was reported. With regards to the enthalpy of formation, our tensimetric value26 (−375.7 ± 9.7 kJ mol−1 at 298 K) is not in good agreement with the only available calorimetric result (−341.7 ± 1 kJ mol−1),25 whereas is in satisfactory agreement with values from first-principle calculations.20 Even by assuming a more negative value of −375.7 ± 9.7 kJ mol−1 for the enthalpy of formation, partial pressures of NH3 and CH3I of about 4 × 10−3 bar at 500 K were estimated – a huge volatilization was never experimentally observed.
The comparison between the thermodynamic analysis and the experimental findings on CH3NH3PbI3 summarized in the introduction led us to conclude that the decomposition of this compound took place under kinetic control, regardless of the prevalence of process (1) or (2). It is interesting to note that in the previous literature28,29 on alkylammonium halide degradation, the decomposition of quaternary salts was reported to begin at much higher temperatures than primary, secondary and ternary ones. Since quaternary salts are the only species where process (1) cannot occur due to the lack of N–H bonds, it is clear that the breaking of C–N bonds required in process (2) is kinetically slow.
In conclusion, several important questions were raised from the above analysis. In particular, the detection of the decomposition channel (1) rather than the thermodynamically favoured path (2) in the KEMS experiment26 and the opposite findings resulting from the TGA-MS results27 call for further experimental investigations, which were undertaken in the present study and are reported below.
Experimental details
Samples of CH3NH3PbI3 were synthesized and characterized as reported elsewhere.26All the experiments were carried out by a mass spectrometry technique described in our previous study.26 In a typical experiment, vapours effusing from a heated Knudsen-type source are ionized by an electron beam with an energy that could be varied from the appearance potential of a given ion up to 80 eV. The cations that are produced enter a magnetic sector zone where they were deflected according to their mass/charge ratio. The ion current of a given ion is finally measured by an electron multiplier detector.
In addition to the experiments performed under Knudsen effusion conditions with effusion orifices of different impedances (see next section), we carried out a free surface evaporation experiment (Langmuir conditions). Unlikely KEMS experiments, where the sample is placed inside a graphite Knudsen cell and the effusing flow is analysed by the mass spectrometer, in the Langmuir-type experiment, the sample was contained in an open crucible, also made of graphite, directly facing the ion source.
In all the experiments, the instrumental conditions were similar to those of ref. 26. As a rule an electron energy of 25 eV was used. The intensity of each peak was background-subtracted by shifting a movable shutter placed just above the orifice in order to measure only the portion of the signal due to the vapour species coming from evaporation.
Both the initial samples and the vaporized residues were analysed by X-ray diffraction (XRD) analysis. As expected, XRD spectra collected after vaporization experiments showed the presence of PbI2 alone (complete decomposition) or together with residual CH3NH3PbI3 (partial decomposition) in all cases. In the experiments where complete decomposition was allowed to occur, a gradual drop of all the ion intensities was observed rather than a sharp fall, similar to observations reported in TGA studies for primary, secondary and tertiary alkylammonium bromides and iodides.30,31
Results and discussion
We previously reported CH3NH3PbI3 to decompose following process (1), CH3NH3PbI3(s) = PbI2(s) + CH3NH2(g) + HI(g), on the basis of KEMS measurements performed at 53–134 °C, low enough to encompass the real temperatures of photovoltaic devices.26 The most intense signals recorded in the mass spectra of the vapours produced by heating CH3NH3PbI3 in a Knudsen source were those at m/z = 31 and 128, assigned as molecular ions of the neutral precursors CH3NH2(g) and HI(g). Other clear signals were detected at m/z = 30 and 127, assigned to fragment ions of the same parent species. Similar results were found for the chloride and bromide perovskites. Total pressures in the 10−9 bar to 10−5 bar range were measured within this temperature interval.Shortly afterwards, Juarez-Perez et al.27 investigated the mass loss of CH3NH3PbI3 (and CH3NH3I) in open-crucible conditions under a helium flow using thermogravimetry coupled to mass spectrometry. On the basis of mass spectra collected at 300–420 °C, in which a significant mass loss occurred, the authors concluded that the degradation process taking place was instead CH3NH3PbI3(s) = PbI2(s) + CH3I(g) + NH3(g) (2). Because of detection limits, the temperature range covered in the their TGA-MS experiments27 was significantly higher than ours, as well as than the temperatures of interest for practical applications of perovskite-based devices. However, the presence of the CH3I(g) species at much lower temperatures (down to 80 °C) was also reported in the ESI of the same study, pushing the limits of the technique by a clever variation of the heating method that involved oscillating heating/cooling cycles.
The results reported in ref. 27 are in part consistent with the previous TGA-FTIR study by Williams et al.23 In the latter, lead halide perovskites CH3NH3PbI3−xClx and CH3NH3PbI3 were subjected to evaporation in the form of dimethylformamide solutions, and the vapours were transferred from the TGA apparatus to the FTIR assembly by means of a heated (300 °C) line. Although the interpretation of IR spectra was made difficult by the superposition of solvent bands, peaks of HCl(g) and CH3NH2(g) were reported to appear for CH3NH3PbI3−xClx at 230 °C, whereas only a weak signal of ammonia was recognized for CH3NH3PbI3.23 Further measurements carried out on silica-desiccated materials gave no significant mass loss signal up to 250 °C.
Possible reasons for these discrepancies are factors such as different temperature ranges, kinetic effects, heating rates, static vs. dynamic regimes, effusion vs. free-surface conditions, vacuum vs. carrier gas atmosphere, and the presence/absence of a vapor transfer line. The new KEMS experiments presented here were planned in particular to investigate the effect of temperature, kinetic hindrance and evaporation conditions on the decomposition behaviour of CH3NH3PbI3. The following experiments were performed:
(1) An experiment was performed under the same conditions used in our previous study26 (i.e., typical effusion cells with an orifice of 1 mm diameter and negligible thickness). In the following, these experiments will be indicated as “low impedance KEMS”, where, as usual in gas-flow terminology, the term “impedance” borrowed from electricity was used in the sense of “resistance to flow”. Measurements were done at T = 473 K and T = 514 K. These experiments were aimed at further confirming the findings of our previous paper,26 paying special attention to the possible presence of the gaseous products of process (2) (m/z = 142 for CH3I and/or 17 for NH3) in addition to those of process (1). Indeed, our mass spectrometry measurements were done in single ion monitoring mode, and in that study,26 the strong signals corresponding to HI(g) (m/z = 128) and CH3NH2(g) (31) were extensively monitored as a function of temperature, whereas only few scans were done in the lower and higher mass ranges.
(2) A control experiment under Langmuir conditions (see Experimental section), designed to test the hypothesis that the different evaporation modes used in our KEMS measurements26 (effusion) and in Juarez-Perez's experiments (open crucible)27 could strongly affect the decomposition behaviour. These measurements were performed at T = 493 K (i.e. the average temperature of the KEMS experiments).
(3) An additional Knudsen-type experiment was carried out with a cell having a smaller effusion orifice (0.5 mm diameter) and a thicker cap (0.65 mm) to create a high impedance path to the effusing vapor (“high impedance KEMS”). Since reaching thermodynamic equilibrium inside the cell was favoured in this configuration due to the lower effusion rate, this experiment aimed at giving information on the kinetic/thermodynamic competition between the two decomposition channels. Moreover, in order to investigate the effect of temperature, these experiments were performed in a larger temperature range, from 416 K to 503 K.
In all the experiments, the most intense signals observed were those at m/z = 128, 31, and 30, assigned to the neutral precursors HI(g) and CH3NH2(g). These results clearly confirmed the conclusion of our previous study, where the main decomposition channel was process (1). However, clear, though lower background-subtracted signals were also observed at m/z = 142, assigned to the species CH3I(g) produced in process (2). We also observed a measurable signal at m/z = 17 and 18. The former could be assigned to NH3+ as well as to OH+, the latter coming from fragmentation of H2O(g) (m/z = 18). Less intense signals were measured at m/z = 127 and 254, corresponding to I and I2: the former coming probably from the fragmentation, the latter from the thermal decomposition of HI(g).32 Interestingly, a small peak (less than 1% of the most intense signals) was finally observed at m/z = 159 due to the undissociated species CH3NH3I(g).
Overall, very significant differences were found in the intensity ratios of the relevant species in the three series of experiments above. To investigate the competition between the two decomposition channels, we followed the intensity ratios of HI/CH3I (128/142) and CH3NH2/CH3I (31/142) rather than the corresponding ratios involving NH3 instead of CH3I, due to the overlapping of the former with OH.
It should be noted that in KEMS experiments, the ion intensity ratios are proportional, not equal, to the corresponding ratios of the partial pressures inside the cell because multiplier gains and ionization cross sections are not included (see below and ref. 26).
In Table 2, the intensity ratios of 128/142 and 31/142 measured in the three experiments above are reported. The same ratios are also plotted in Fig. 2. It is worth noting that, due to the higher sensitivity of KEMS compared to TGA, our measurements were done at lower temperatures than in ref. 23 and 27, much closer to the actual operative conditions of photovoltaic devices.
| T/K | HI/CH3I | CH3NH2/CH3I | ||||
|---|---|---|---|---|---|---|
| Low impedance KEMS | High impedance KEMS | Langmuir | Low impedance KEMS | High impedance KEMS | Langmuir | |
| 416.0 | 683.3 | 200.0 | ||||
| 417.8 | 509.1 | 139.4 | ||||
| 460.9 | 109.3 | 25.6 | ||||
| 464.5 | 81.4 | 20.0 | ||||
| 472.5 | 1165.4 | 319.2 | ||||
| 474.0 | 63.3 | 13.6 | ||||
| 493.0 | 294.9 | 90.4 | ||||
| 498.0 | 24.6 | 6.1 | ||||
| 502.6 | 25.7 | 5.3 | ||||
| 503.0 | 27.1 | 5.6 | ||||
| 514.1 | 294.1 | 75.9 | ||||
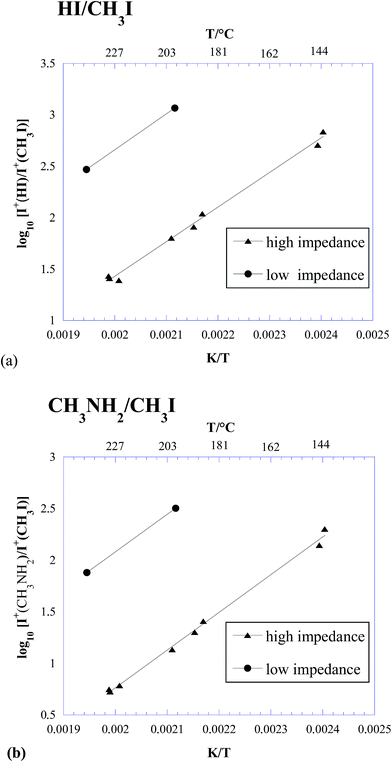 | ||
| Fig. 2 Logarithmic plot of the HI/CH3I (a) and CH3NH2/CH3I (b) ion intensity ratios measured under different effusive conditions. | ||
Some important conclusions can be drawn from Table 2 and Fig. 2:
(i) Under all the explored conditions, process (1) prevailed over process (2). Since the ion intensity ratios are a good approximation to the corresponding partial pressure ratios, results in Fig. 2 are in clear contrast with the thermodynamic predictions reported in Fig. 1.
(ii) Under typical conditions for Knudsen effusion experiments, such as those used in ref. 26 and in the above described experiment 1 (“low impedance KEMS”), process (1) was overwhelmingly dominant, with a contribution from process (2) below 1%. This finding confirmed our previous results.26
(iii) Under free-surface conditions, process (2) seemed slightly enhanced (see Table 2), but not to such a large extent to explain the different behaviour observed in ref. 27.
(iv) A significant increase in the contribution of process (2) was observed under conditions where the effusion rate was lower (high impedance orifice, i.e., closer to equilibrium conditions).
(v) The contribution of process (2) considerably increased with increasing temperature, again in contrast with thermodynamic predictions reported in the previous section (see Fig. 1).
Points (iv) and (v) in particular led us to conclude that the thermodynamically favoured process (2) suffered from severe kinetic limitations, which could be partly overcome at high temperatures and/or low effusion rates. This could be explained by taking into account the fact that breaking the hydrogen bond in the methylammonium cation leading to the release of methylamine and hydrogen iodide requires a much lower energy than the rupture of the N–C bond necessary to produce methyl iodide and ammonia.30,31 Note that not only process (2) is kinetically limited, but also the gas phase equilibration according to eqn (4) was far from being attained. The theoretical analysis reported in ref. 27, based on gas phase DFT calculations, partially confirmed this view, although no transition state was found leading to the formation of HI and CH3NH2 as final products.
The evidence that increasing temperature enhances process (2) over process (1) was consistent with the fact that the former was observed from 300 °C to 420 °C in ref. 27. In addition, we made an attempt to convert the ion intensity ratio in Fig. 1a (high impedance data) into the corresponding partial pressure ratio, in order to estimate the temperature where p(HI) and p(CH3I) became equal. As discussed elsewhere,26 this conversion required a knowledge or estimation of the ionization cross sections (σ) of the species involved. By adopting the values σ(HI) = 6.47 Å2 (ref. 12) and σ(CH3I) = 10.3 Å2 (ref. 35), and by neglecting the very small contribution of the detector gain, an extrapolated temperature of about 385 °C was determined, well within the above mentioned temperature range.
Conclusions
On the basis of the above discussion, we conclude that in the temperature range (140–240 °C) and under the various experimental conditions explored, the thermal decomposition of CH3NH3PbI3 mainly takes place by the release of HI(g) and CH3NH2(g) as gaseous products. The process leading to NH3(g) and CH3I(g) was thermodynamically favoured, but kinetically hindered, most probably because of the more complex rearrangements and bond breaking necessary to form NH3 and CH3I in the gaseous phase from the crystal. As a consequence, the latter process remained as a minor decomposition channel despite its higher thermodynamic driving force. However, kinetic hindrance was shown to significantly diminish at higher temperatures and under low effusion rate conditions (high impedance orifice), which allowed for the thermodynamic control to be favoured. On the other hand, when carried out under free-surface (Langmuir) conditions, the decomposition behaviour did not show important changes compared to effusion conditions. Overall, our analysis showed that the decomposition path of CH3NH3PbI3 and related light harvesters markedly depends on a number of experimental conditions that can favour the thermodynamic or kinetic control, with temperature, heating rate, static/dynamic regime, and vacuum vs. carrier gas atmosphere playing key roles.Further investigations are needed for an in-depth understanding of the microscopic/mechanistic aspects of the evaporative decomposition of these compounds, to clarify the degradation pathway followed by CH3NH3PbI3-based photovoltaic devices under actual operating conditions and to assess more effective protection strategies.
Acknowledgements
The idea for this study originated from a private communication between the present authors and Dr Emilio J. Juarez-Perez, first author of ref. 27. The fruitful discussion with Dr Juarez-Perez is gratefully acknowledged.References
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356 CAS.
- L. K. Ono and Y. Qi, J. Phys. Chem. Lett., 2016, 7, 4764–4794 CrossRef CAS PubMed.
- H. Yuan, E. Debroye, K. Janssen, H. Naiki, C. Steuwe, G. Lu, M. Moris, E. Orgiu, H. Uji-i, F. De Schryver, P. Samrì, J. Hofkens and M. Roeffaers, J. Phys. Chem. Lett., 2016, 7, 561–566 CrossRef CAS PubMed.
- P. Docampo and T. Bein, Acc. Chem. Res., 2016, 49, 339–346 CrossRef CAS PubMed.
- J. S. Manser, M. I. Saidaminov, J. A. Christians, O. M. Bakr and P. V. Kamat, Acc. Chem. Res., 2016, 49, 330–338 CrossRef CAS PubMed.
- R. Gottesman and A. Zaban, Acc. Chem. Res., 2016, 49, 320–329 CrossRef CAS PubMed.
- F. Matsumoto, S. M. Vorpahl, J. Q. Banks, E. Sengupta and D. S. Ginger, J. Phys. Chem. C, 2015, 119, 20810–20816 CAS.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- N. Guangda, G. Xudong and W. Liduo, J. Mater. Chem. A, 2015, 3, 8970–8980 Search PubMed.
- A. M. A. Leguy, Y. Hu, M. Campoy-Quiles, M. I. Alonso, O. J. Weber, P. Azarhoosh, M. van Schilfgaarde, M. T. Weller, T. Bein and J. Nelson, Chem. Mater., 2015, 27, 3397–3407 CrossRef CAS.
- E. Mosconi, I. M. Azpiroz and F. De Angelis, Chem. Mater., 2015, 27, 4885–4892 CrossRef CAS.
- L. Zhang and P. H.-L. Sit, J. Phys. Chem. C, 2015, 119, 22370–22378 CAS.
- D. Koushik, W. J. H. Verhees, Y. Kuang, S. Veenstra, D. Zhang, M. A. Verheijen, M. Creatore and R. E. I. Schropp, Energy Environ. Sci., 2017, 10, 91–100 CAS.
- R. Ruess, F. Benfer, F. Böcher, M. Stumpp and D. Schlettwein, ChemPhysChem, 2016, 17, 1505–1511 CrossRef CAS PubMed.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235 CrossRef CAS PubMed.
- R. L. Z. Hoye, R. E. Brandt, A. Osherov, V. Stevanović, S. D. Stranks, M. W. B. Wilson, H. Kim, A. J. Akey, J. D. Perkins, R. C. Kurchin, J. R. Poindexter, E. N. Wang, M. G. Bawendi, V. Bulović and T. Buonassisi, Chem.–Eur. J., 2016, 22, 2605–2610 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. Khaja Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997 CAS.
- B. Conings, J. Drijkoningen, N. Gauquelin, A. Babayigit, J. D'Haen, L. D'Olieslaeger, A. Ethirajan, J. Verbeeck, J. Manca, E. Mosconi, F. De Angelis and H.-G. Boyen, Adv. Energy Mater., 2015, 5, 1500477 CrossRef.
- A. F. Akbulatov, S. Y. Luchkin, L. A. Frolova, N. N. Dremova, K. L. Gerasimov, I. S. Zhidkov, D. V. Anokhin, A. Z. Kurmaev, K. J. Stevenson and P. A. Troshin, J. Phys. Chem. Lett., 2017, 8, 1211–1218 CrossRef CAS PubMed.
- E. Tenuta, C. Zheng and O. Rubel, Sci. Rep., 2016, 6, 37654 CrossRef CAS PubMed.
- Z. Song, S. C. Watthage, A. B. Phillips, B. L. Tompkins, R. J. Ellingson and M. J. Heben, Chem. Mater., 2015, 27, 4612–4619 CrossRef CAS.
- D. P. Nenon, J. A. Christians, L. M. Wheeler, J. L. Blackburn, E. M. Sanehira, B. Dou, M. L. Olsen, K. Zhu, J. J. Berry and J. M. Luther, Energy Environ. Sci., 2016, 9, 2072–2082 CAS.
- A. E. Williams, P. J. Holliman, M. J. Carnie, M. L. Davies, D. A. Worsley and T. M. Watson, J. Mater. Chem. A, 2014, 2, 19338–19346 CAS.
- A. Dualeh, P. Gao, S. I. Seok, M. K. Nazeeruddin and M. Grätzel, Chem. Mater., 2014, 26, 6160–6164 CrossRef CAS.
- G. P. Nagabhushana, R. Shivaramaiah and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7717–7721 CrossRef CAS PubMed.
- B. Brunetti, C. Cavallo, A. Ciccioli, G. Gigli and A. Latini, Sci. Rep., 2016, 6, 31896 CrossRef CAS PubMed . Corrigendum: Sci. Rep., in press Search PubMed.
- E. J. Juarez-Perez, Z. Hawash, S. R. Raga, L. K. Ono and Y. Qi, Energy Environ. Sci., 2016, 9, 3406–3410 CAS.
- M. Sawicka, P. Storoniak, P. Skurski, J. Błażejowski and J. Rak, Chem. Phys., 2006, 324, 425–437 CrossRef CAS.
- M. Sawicka, P. Storoniak, J. Błażejowski and J. Rak, J. Phys. Chem. A, 2006, 110, 5066–5074 CrossRef CAS PubMed.
- P. Dokurno, J. Lubkowski and J. Błażejowski, Thermochim. Acta, 1990, 165, 31–48 CrossRef CAS.
- J. Lubkowski and J. Błażejowski, Thermochim. Acta, 1990, 157, 259–277 CrossRef CAS.
- V. S. Iorish, IVTANTHERMO database-Version 3.0, Glushko Thermocenter of Russian Academy of Sciences, 2005 Search PubMed.
- M. Frenkel, G. J. Kabo, K. N. Marsh, G. N. Roganov and R. C. Wilhoit, Thermodynamics of Organic Compounds in the Gas State, CRC Press, 1994 Search PubMed.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- J. N. Bull, P. W. Harland and C. Vallance, J. Phys. Chem. A, 2012, 116, 767–777 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |
