Proton transfer in microbial electrolysis cells†
Abhijeet P.
Borole
 *abc and
Alex J.
Lewis
c
*abc and
Alex J.
Lewis
c
aBiosciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831-6226, USA. E-mail: borolea@ornl.gov; Fax: +1 865 574 6442
bDepartment of Chemical and Biomolecular Engineering, The University of Tennessee, Knoxville, TN 37996, USA
cBredesen Center for Interdisciplinary Research and Education, The University of Tennessee, Knoxville 37996, USA
First published on 15th February 2017
Abstract
Proton transfer and electron transfer are of prime importance in the development of microbial electrochemical cells. While electron transfer is primarily controlled by biology, proton transfer is controlled by process engineering and cell design. To develop commercially feasible technologies around the concept of a bioelectrochemical cell, real feedstocks have to be explored and associated limitations have to be identified. In this study, the proton transfer rate was quantified for a microbial electrolysis cell (MEC) and its dependence on process parameters was investigated using a proton balance model. The reaction system consisted of a biomass-derived pyrolytic aqueous stream as a substrate producing hydrogen in a flow-through MEC. The proton transfer rate increased with anode flow rate and organic loading rate up to a maximum of 0.36 ± 0.01 moles per m2 per h, equivalent to a hydrogen production rate of 9.08 L per L per day. Higher rates of hydrogen production, reaching 11.7 ± 0.2 L per L per day were achieved, when additional protons were provided via the cathode buffer. Electrochemical impedance spectroscopy shows that proton transfer was the dominant resistance in the production of hydrogen. The quantification of proton transfer rates for MECs with potential for biorefinery application and the demonstration of high hydrogen production rates approaching those required for commercial consideration indicate the strong potential of this technology for renewable hydrogen production. Understanding the transport phenomenon in bioelectrochemical cells is of great significance since these systems have potential for wide-ranging applications including energy production, bioremediation, chemical and nanomaterial synthesis, electro-fermentation, energy storage, desalination, and produced water treatment. Electron transfer in anode biofilms has been investigated extensively, but proton transfer studies are also important, since many cathodic half reactions require protons as the reactant. Determination of transport rates via proton balance was investigated in microbial electrolysis cells, which can be applied to other forms of microbial electrochemical systems. These systems have a unique niche in the development of future biorefineries as a means of recovering energy from waste streams with potential for water recycle, making them an integral part of the water–energy nexus focus area.
1. Introduction
Reaction engineering and mass transfer are two important areas for further study of microbial electrochemical cells. Further diversification of these systems into broader applications via multiple reaction chemistries and using a range of feedstocks is taking place.1 Biomass and waste streams can be converted into fuels, chemicals and high-value intermediates via integration of varied conversion platforms such as bioconversion, thermoconversion and electrosynthesis. Proton transfer and electron transfer are at the heart of these microbial electrochemical systems as they carry the charge and energy from the anode to the cathode.2 Electron transfer studies have been the core of bioelectrochemical systems' development over the past decade.3–5 As we gain a better understanding of the extracellular electron transfer process, other characteristics and rate limitations are becoming evident. Proton transfer is one such limitation which can be as important as the electron transfer. Transport of protons or cations is necessary to maintain high performance of microbial electrochemical cells.6–8 For electrolysis cells producing hydrogen, availability of protons at the cathode surface is key to productivity. Formation of thick electroactive biofilms greater than 50 microns has been reported for the anode.9–11 The high cell density in the anode can result in a high level of metabolic conversion rates. Depending on the exoelectrogen population density, electron and proton generation itself may not be a limitation.7 Proton diffusion out of the biofilm has been reported to be a potential limitation in the bioanode.8 Use of higher buffer strength has been shown to partially alleviate this problem, however, diffusion of the buffer ions from the biofilm to the cathode can still be a limitation. The use of engineered bioanodes with flow-through porous electrodes to minimize the proton transfer issues has been reported previously, transferring the protons from the biofilm into the bulk anode liquid.12,13 However, quantification of the proton transfer rates, particularly in microbial electrolysis cells (MECs) has not been reported to date.Hydrogen has numerous applications ranging from direct use as a fuel in fuel cells to production of liquid fuels via hydrogenation or as a reagent in the chemical industry. Development of transportation fuels from biomass is a critical need to enable continued use of existing infrastructure. We have recently demonstrated use of MECs for producing hydrogen from a pyrolysis-derived biomass aqueous stream.14 The development of electroactive biofilms for conversion of such biorefinery streams has been investigated,14,15 resulting in current densities up to 4 A m−2. While the current densities have been quantified, the proton transfer rates related to hydrogen production in MECs have not been investigated. It is important to quantify these rates and compare them with electron transfer rates, metabolic rates of exoelectrogen reactions and other processes occurring in the MEC to enable further development of the microbial electrochemical technology.
Impedance analysis has been used to delineate the various steps involved in electron transfer from the anode to the cathode.16–18 Direct electron transfer via cell–electrode contact or nanowire connection between cells and electrodes has been shown to result in low impedances;17,19–21 however, quantification of the impedances related to diffusive or convective charge transport has not been reported. Understanding the impedance related to long distance charge transfer associated with cations, protons or other products and intermediates can provide new insights into the transport phenomena in MECs.
This study investigates the proton transfer rate between the anode and cathode via a proton balance in MECs. The changes in pH within the anode and cathode are modelled incorporating the Henderson–Hasselbalch equation. The rate of proton transfer is calculated using detailed pH and current measurements. Model equations describing the effect of anode flow rate, organic loading rate, cell voltage and other parameters on the dynamics of proton transfer are described. Impedance spectroscopy is used to quantify the resistances associated with anodic and cathodic processes. The total cell resistance is calculated and compared with that reported for other high performing MECs. The analysis is done for a reaction system involving a biomass-derived pyrolytic aqueous stream generating hydrogen in a flow-through MEC. A bioanode developed previously via optimization of electroactive biofilm growth11,14,22 was employed which resulted in high rates of exoelectrogenesis/electron transfer quantified by current densities exceeding 10 A m−2. Quantification of the proton transfer rates enables identification of limitations that need to be overcome for commercial application of this technology.
2. Experimental
2.1 MEC construction and operation
The rate of proton transfer was determined in a two chamber MEC separated by Nafion 115, which contained a porous, flow-through anode consisting of carbon felt as the electrode material. The cathode was a platinum-deposited carbon cloth with a surface area of 12.56 cm2. The cathode and anode chambers were 16 mL each. The membrane and cathode were purchased as a membrane electrode assembly (FuelCellEtc., Inc., TX). Further details of the MEC design can be found elsewhere.14 The cathode buffer was a 100 mM potassium phosphate buffer. A buffered nutrient medium was circulated through the porous anode and recycled using an external reservoir (Fig. 1) containing 100 mL of liquid as described previously.15 The nutrient medium contained 53 mM potassium phosphate buffering salts, adjusted to a pH of 7.2. The anode was poised at −0.2 V vs. Ag/AgCl reference electrode (BASi, Inc.) placed in the effluent line at the exit of the anode. A switchgrass-derived pyrolysis aqueous phase was used as the substrate, which was fed into the liquid stream entering the anode. Performance of this MEC and the typical efficiency parameters have been reported recently.15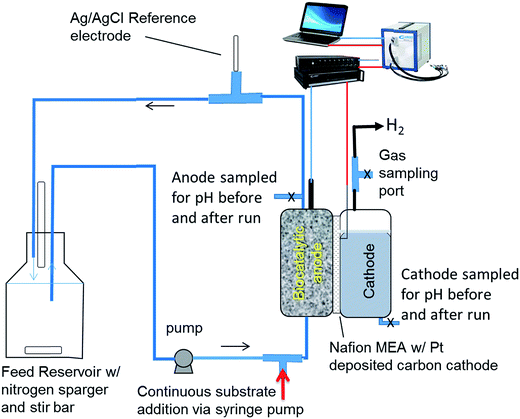 | ||
| Fig. 1 Schematic of the MEC system producing hydrogen used for investigating proton transfer between the anode and cathode and EIS analysis. | ||
In this study, the rate of proton transfer was calculated at various flow rates ranging from 0.3 to 3.6 mL min−1 and organic loading rates ranging from 0.85 to 100 g per L per day. In experiments studying the effect of flow rate, the rate of addition of the substrate into the anode line was kept constant. In order to calculate the proton transfer rate between the anode and cathode, pH measurements were made for the anode and cathode liquid before and after the experiments, which lasted from 6 to 48 hours. On an average, the run time for the experiments was 23 hours. Only at the highest loading of 100 g per L per day, the run time was short (6 hours) due to significant changes occurring in the pH of the anode. For all experiments with loading rate from 0.53 to 20 g per L per day, the run time was about 22–24 hours. Two replicate MECs were used in the pH measurements and the average of the two data points is reported. The standard deviation for the two MECs is reported with error bars shown on the plots. Additional experiments were conducted by varying the substrate concentration from 0.026 g L−1 to 0.052 g L−1 at a constant flow rate (3.6 mL min−1), which increased the OLR from 10 to 20 g per L per day. Additional details are given in Table S1.†
The effect of adding a salt on the proton transfer rate was evaluated by preparing a nutrient medium with 5 g L−1 and 10 g L−1 of NaCl. The salt was used in addition to the nutrient salts present in the medium used for the MEC experiments. The experiment was conducted at an organic loading rate of 10 g per L per day and a flow rate of 3.6 mL min−1. Current and hydrogen production was measured over a period of 22 hours. The buffer concentration in the cathode was 200 mM. The conductivities of the anode and cathode solutions were measured to assess the transfer of salt ions from the anode to the cathode.
2.2 Proton balance calculations
In order to determine the rate of proton transfer, proton balance calculations were carried out on the cathode and the anode. The moles (m) of protons required at the cathode for hydrogen production can be given as:| m[H+],cat = 1/2 × mH2 | (1) |
The moles of protons consumed at the cathode can be determined as follows:
| m[H+],cat = [m[H+],cat]t0 − [m[H+],cat]tend + m[H+],an–cat | (2) |
| m[H+],an–cat = 1/2 × mH2 − [m[H+],cat]t0 + [m[H+],cat]tend | (3) |
Since a buffer solution was used in the cathode, the last two terms have to be determined using the Henderson–Hasselbalch equation as described in the ESI.†
The moles of protons transferred from the anode to the cathode have to be generated at the anode or provided via the buffering capacity of the anode solution, which can be described as follows:
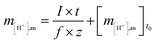 | (4) |
| m[H+],an > m[H+],an–cat | (5) |
Once the above equation is verified, the rate of proton transfer from the anode to the cathode can be calculated as follows:
| R[H+],ano→cat = [m[H+],an→cat]/t | (6) |
| RA[H+],ano→cat = [m[H+],an→cat]/[Am × t] | (7) |
The proton balance also provides a way to calculate the charge transfer from the anode to the cathode besides that which occurs via protons, i.e., the charge balance caused by other cations, which can be given as follows:
| m[cations],an–cat = m[H+],cat − m[H+],an–cat | (8) |
The following assumptions were made in the development of the model:
(i) Charge balance occurs in the MEC by transfer of cations as well as protons from the anode to the cathode. Transfer of cations other than protons to the cathode results in utilization of protons for hydrogen production, resulting in an increase in the pH of the cathode solution. It is assumed that the Henderson–Hasselbalch equation represents the equilibrium in the cathode buffer, allowing calculation of the protons used in the cathode due to change in pH.
(ii) The equilibrium constant for water dissociation is equal to 10−14 at all concentrations of the cathode buffer/salts, including the solutions resulting from transfer of cations into the cathode.
(iii) The transfer of water molecules from the anode to the cathode is negligible.
2.3 Process model and empirical correlations
The proton transfer between the anode and cathode is driven by the difference in proton concentration between the two electrode chambers and the potential difference. The pH polarization between the anode and the cathode and the hydrodynamics within the anode and cathode define the proton gradient determining the proton concentration at the membrane interface. The rate of proton transfer between the electrodes can therefore be described as a function of the proton concentration at the interface [Hint+] and the potential difference (ΔV) between the two electrodes:| [RA[H+],ano→cat] = f([Hint+],ΔV) | (9) |
The interface proton concentration, [Hint+] depends on the mass transfer and fluid flow on either side of the membrane. In this study, the cathode liquid was stagnant, however, various flow rates of the anode fluid were examined. The effect of the anode flow rate (Qan) on the interface proton concentration and consequently the proton transfer rate can therefore be described as:
| [Hint+] = f(Qan) | (10) |
In addition, the proton concentration at the interface is a function of the organic loading rate (OLR), since the rate of production of protons, i.e., the anodic reaction, depends on the rate of substrate addition:
| [Hint+] = f(OLR) | (11) |
In the MEC experiments conducted in this study, the anode potential was fixed, therefore, the cathode potential and the ΔV between the anode and cathode are likely to vary. The rate of anode reaction, which also generates the electrons, is therefore likely to influence the ΔV. The rate of anode reaction, in turn, is a function of the organic loading rate, therefore the ΔV can be described as:
| ΔV = f(OLR) | (12) |
Thus, the rate of proton transfer can be described as follows:
| RA[H+],ano→cat = f(Qan,OLR) | (13) |
A plot of RA[H+],ano→catvs. Qan and OLR can identify potential correlations between these parameters.
Finally, the rate of hydrogen production is a function of the proton concentration in the cathode and the electron concentration. The proton concentration in the cathode depends on the buffer concentration in the cathode (Bcat) and the rate of proton transfer from the anode to the cathode. The electron concentration on the other hand is a function of the cathode potential. Thus, the rate of hydrogen production can be written as:
| RH2 = f(Bcat,RA[H+],ano→cat,Vcat) | (14) |
If the dependence of the rate of hydrogen production on buffer strength and cathode volume is negligible, it can be calculated directly from the rate of proton transfer as follows:
| RH2 = RA[H+],ano→cat × Am/VAn × VM/n | (15) |
| 2H+ + 2e− → H2 | (16) |
2.4 Electrochemical impedance spectroscopy
Electrochemical impedance spectroscopy (EIS) measurements were performed using a Gamry Instrument series Reference 3000 potentiostat. The measurements were done under potentiostatic EIS conditions for the whole cell using a two-electrode configuration. The anode served as the working electrode and the cathode as the counter and reference. The EIS experiments were conducted at varying flow rates similar to those described previously for quantifying proton transfer, in which the anode was poised at a potential of −0.2 V vs. the Ag/AgCl reference electrode. In the EIS experiments, however, since the anode was poised vs. the cathode, which served as the reference electrode, it was poised at the cell voltage measured during the proton transfer measurements conducted under chronoamperometric conditions. The result was essentially the anode being poised at a potential of −0.2 V vs. the Ag/AgCl electrode. The cell voltage reached at the end of each experiment ranged between 0.77 and 1.2 V and is given in Table S2.† The goal was to determine the impedance of the cell during the operation of the MEC under the same operating conditions used for hydrogen production measurements. The other operating conditions of these experiments are given in ESI Table S1.† The measurements were conducted at a flow rate of 0.3, 2 and 3.6 mL min−1, at a constant substrate concentration of 0.026 g L−1. Additionally, experiments were also performed at two additional concentrations: 0.052 g L−1 and 0.98 g L−1, at a flow rate of 3.6 mL min−1 and 0.19 mL min−1, respectively.2.5 Equivalent circuit modeling
Analysis of the electrochemical impedance spectra was conducted via equivalent circuit modeling (ECM). Data fitting was carried out using the Simplex method for multi-parameter fitting provided with the EChem analyst program (Gamry Instruments). The results were checked with the Levenberg–Marquardt method as well to confirm the model parameters. Various models with varying degrees of complexity were developed and tested to fit the data over multiple iterations of the starting values for each of the electrochemical parameters (Fig. S1†). The model that made physical sense and included representative elements for processes expected to occur in the MEC was used. The choice of the model was also based on the fit of the data with the least number of parameters to keep it from becoming overly complicated. This model is shown in Fig. S1-A.† Typical MEC models consist of a capacitor and a resistor in parallel, one for each, anode and cathode with a resistor in between the anode and cathode, representing the membrane and solution impedance.17,23 In addition to these components, other impedance elements such as Warburg impedance have been used when mass transfer has been an issue.20 The model used here includes Warburg impedance in the cathode as well as anode chamber to account for the proton transfer resistance. The physical significance of each of the circuit components is also identified in Fig. S1-A† and discussed further in the Results section. The anode was described using a resistance due to charge transfer reaction representing the conversion of the substrate to electrons and protons and a Warburg impedance. These two components are included in series since the production of protons and their transfer to cathode occur in series. Each of these components is connected with a constant phase element (CPE) in parallel since a double layer forms on the electrode surface as well as on the biofilm since both the surfaces are charged and are distinct from each other.3. Results and discussion
3.1 Effect of organic loading rate on proton transfer rate
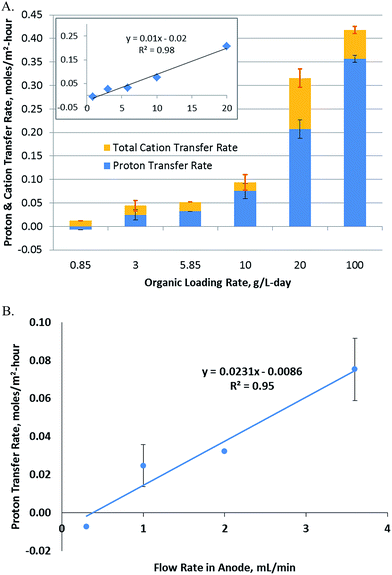
The rate of hydrogen production is typically a function of OLR, concentration, retention time and other process parameters. In order to determine the importance of mass and charge transfer, particularly proton transfer, the rate of proton transfer was calculated as per eqn (3). Further, the area-specific proton transfer rate was calculated by normalizing with respect to the membrane surface area using eqn (7). This was plotted vs. the OLR, which was varied over a 100-fold range (Fig. 2A). The results show a linear relationship between RA[H+],ano→cat (referred to as RA, henceforth) and OLR up to an OLR of 20 g per L per day with a regression constant of 0.95 (inset, Fig. 2A). Lack of data fitting over the whole range of OLRs studied indicates that other factors may be controlling the rate of proton transfer at higher OLRs.The proton transfer rate was found to be negative at the lowest OLR studied. This means that the protons were transferred from the cathode to anode instead of the reverse direction at this OLR. This was most likely due to the low pH in the cathode (6.9) vs. anode (7.2) at the start of the experiment. The RA was also a function of the duration of the experiment. The rate was calculated as an average over the whole duration of the experiment, so while a negative rate is expected at time 0 for all OLRs, the net proton transfer is expected to become positive for higher OLRs as observed from the experimental results. RA is an important parameter considering the long term operation of MECs, since the use of buffer in the cathode to provide protons for hydrogen evolution is not a sustainable option. Production of hydrogen has to be sustained by the proton transfer from the anode to the cathode, since supplying protons to the cathode externally may not be economically feasible. The maximum RA was determined to be 0.36 ± 0.01 moles per m2 per h, which was observed at an OLR of 100 g per L per day.
3.2 Effect of flow rate on proton transfer
Changes in RA were also studied with respect to the flow rate of the fluid flowing through the porous anode. As described in eqn (10), the proton concentration at the membrane interface is likely to be a function of the flow rate and hydrodynamics in the anode (Fig. 2B). A linear relationship was observed over a 10-fold range with a regression constant of 0.95. Unlike OLR, the relationship of RAvs. flow rate was linear over the whole range of flow rates studied. A negative RA was observed at the lowest flow rate, which indicates that at this flow rate, the protons flow from the cathode to anode. As explained previously, this was potentially due to the lower starting pH in the cathode compared to the anode. Proton generation was taking place in the anode at a rate of 42 ± 5 μmoles per h, based on the current observed, however, transfer of these protons to the cathode did not occur and a reverse flow of protons was observed at the rate of 9 μmoles per h. Thus, at the low flow rate of 0.3 mL min−1, the rate of proton transfer from the anode biofilm to the membrane was probably too low to allow transfer of protons to the cathode. The results show that a threshold flow rate of 0.4 mL min−1 was needed to obtain a positive RA for the experimental system used in this study.3.3 Dependence of hydrogen production on proton transfer
Investigations into the relationship between hydrogen productivity and the rate of proton transfer showed that a direct relationship existed between the two parameters. The rate of proton transfer obtained at varying flow rates and OLRs was plotted vs. hydrogen productivity (Fig. 3). Hydrogen can be produced using protons available in the cathode or those transferred from the anode to the cathode. Fig. 3 uses the latter as the x-axis, showing that the hydrogen produced is directly related to protons transferred from the anode to the cathode. In order to assess the contribution of the protons available in the cathode buffer to hydrogen production, Fig. 2A can be utilized. The orange portion of the bars in Fig. 2A (above the blue bars) represents the cations transferred from the anode to the cathode. This is equivalent to the protons available in the cathode, which are used for hydrogen production. This requires an equivalent charge balance via transfer of cations from the anode to the cathode, which is represented by the visible orange portion of the bars. Comparing the contributions of the cations and protons transferred to the cathode, it is observed that majority of the hydrogen produced came from the protons transferred from the anode to the cathode. Thus, hydrogen production was significantly dependent on the proton transfer rate.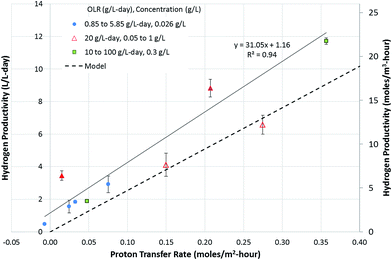 | ||
| Fig. 3 Relationship between proton transfer rate and hydrogen productivity. The solid line represents a linear regression fit through the experimental data. The hydrogen production rate was also calculated using eqn (15) and is plotted as a dashed line. The experimental data indicate a hydrogen productivity of 1.2 L per L per day in the absence of proton transfer from the anode to the cathode, which is attributed to the buffering capacity of the cathode solution, supported by charge balancing via cation transfer from the anode to the cathode. The secondary y-axis denotes the hydrogen productivity in moles per m3 per hour. | ||
The plot in Fig. 3 shows a positive y-intercept of 1.16, which is the hydrogen production rate at zero proton transfer rate. This represents the amount of hydrogen production coming from the protons available in the cathode buffer. This is maintained relatively constant at all OLRs, as observed by the difference between the experimental data and the dotted line in Fig. 3. The latter represents hydrogen produced from the protons transferred from the anode to the cathode (eqn (15)). The rate of hydrogen production was modeled in the absence of the cathode buffer and assuming a negligible effect of cathode voltage. The total hydrogen produced is a function of two parameters: the cathode buffer concentration and the cathode voltage (eqn (14)). The dependence of the hydrogen productivity on these two parameters has been reported in the literature.24,25 The rate of hydrogen production obtained experimentally is always higher than that predicted by eqn (15). For example, a productivity of 11.7 ± 0.2 L per L per day was obtained at an OLR of 100 g per L per day, which is higher than that obtained by eqn (15), which is 9.08 L per L per day. This higher productivity is due to the additional protons available at the cathode added at the start of the experiment via the buffer. In the absence of the protons present in the cathode buffer, the expected hydrogen productivity is lower as represented by the dashed line. The maximum hydrogen production rate is obtained at a proton transfer rate of 0.36 moles per m2 per day. Cation transfer other than that by protons has been reported in the literature,26,27 which is likely to be occurring in the MECs studied here as well, which provides the charge balancing, enabling higher hydrogen productivity than that expected by proton transfer alone.
The results point out another aspect of the MEC related to bioanode performance, i.e., the anode is capable of delivering a higher current capable of sustaining a hydrogen productivity of 11.7 L per L per day. However, the proton transfer limits the hydrogen productivity once the protons in the cathode (provided at the start of the experiment) are depleted. To examine the effect of protons available in the cathode, the experiment conducted at the OLR of 20 g per L per day was carried out in two phases. In the first phase (4 hours), the experiment was initiated with a cathode buffer pH of 6.9. In the second phase, the experiment was continued for another 21 hours, without adjusting the pH of the cathode, which reached 12.2 at the end of 4 hours. Two data points were obtained for these experiments as shown by hollow triangles. The results of the phase 2 experiments reached a proton transfer rate approached by the modelled rate (Fig. 3). This is due to operation of the MEC under proton-limiting conditions in the cathode. Thus, to achieve a higher hydrogen productivity equivalent to the electron production rate realized by the microbial conversion rate at the anode, the proton transfer rate needs to be improved. The proton transfer rate required to reach the productivity of 11.7 L per L per day without relying on the protons in the cathode solution is about 0.46 moles per m2 per hour.
3.4 Effect of salt concentration on the proton transfer rate
In addition to the effect of flow rate and loading rate, the effect of different salt concentrations present in the anode solution was examined. An increase in the conductivity of anode solution has been reported to result in higher current densities. In the MEC experiments conducted here, the current densities increased slightly at a salt concentration of 5 g L−1, but did not change significantly for the experiment with 10 g L−1 NaCl. The hydrogen productivity, however, clearly declined with increasing salt concentration. This may appear to be unusual, however, analysis of the proton availability and measurement of the conductivity and pH of the anode and cathode solutions provide clues as to why this is happening. A change in pH from 6.9 to 12.2 corresponds to the utilization of 1.09 mmoles of protons in the cathode. The final pH of the cathode in these experiments was close to 12.2. Thus, at a minimum, 1.09 mmoles of cations need to be transported from the anode to the cathode. Conductivity measurements made on the cathode solutions at the end of the experiments showed that the amount of cations transported to the cathode increased as the salt concentration in the anode increased (Table 1). This is expected, since the amount of cations transferred to the cathode depends on their concentration in the anode, however, it also affects the number of protons transferred to the cathode. Protons are essential for hydrogen production, therefore, as a consequence of lower proton availability in the cathode, the hydrogen productivity drops. The proton transfer rate is correspondingly lower at higher salt concentrations (Table 1). The reduction in proton transfer rate and the hydrogen productivity with an increase in the salt concentration is statistically significant as shown by the p-value for the data for the two parameters, both of which were lower than 0.05 (0.0395 and 0.0456, respectively).| NaCl added in anode medium | |||
|---|---|---|---|
| 0 g L−1 | 5 g L−1 | 10 g L−1 | |
| Current density, A m−2 | 4.5 ± 0.16 | 4.68 ± 0.15 | 4.4 ± 0.36 |
| Cathode conductivity at the end of the run, mS cm−1 | 24.31 ± 3.7 | 24.8 ± 3.0 | 27.27 ± 0.9 |
| % charge transferred by cations contributing to hydrogen production | 32.1% ± 0.001 | 34.2% ± 0.016 | 39.1 ± 0.043 |
| Proton transfer rate, moles per m2 per h | 0.082 ± 0.001 | 0.075 ± 0.005 | 0.063 ± 0.011 |
| Hydrogen productivity, L per L per day | 3.39 ± 0.01 | 3.21 ± 0.15 | 2.87 ± 0.32 |
3.5 Impedance analysis
The anode impedance is typically made up of several components, which describe the multiple processes occurring in the anode. These processes include the substrate mass transfer from the bulk fluid to the cells, biochemical reaction converting the substrate into electrons, protons, intermediates and carbon dioxide, electron transfer from the cell surface to the electrode, proton/cation transfer from the cell surface to the membrane, then to the cathode catalytic surface, and finally, the hydrogen evolution reaction. The bioelectrochemical reaction at the anode and the cathodic proton reduction reaction can be modeled as a charge transfer resistance, which was investigated in this study using resistors. The biochemical reaction at the anode has been described via a Nernst–Monod model28 or a Butler–Volmer–Monod model.29 The mass transfer is typically represented by Warburg impedance. In order to further understand the effect of process conditions on hydrogen production and their relationship with proton transfer, the diffusion of protons in the anode and cathode was quantified via impedance analysis. Two diffusion terms were included in the ECM, one for each chamber. The Warburg impedance for a finite boundary layer is given as: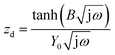 | (17) |
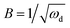 | (18) |
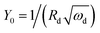 | (19) |
Furthermore, the diffusion frequency and the diffusion resistance related to proton transfer are defined as:
| ωd = D/δ2 | (20) |
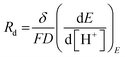 | (21) |
D is the diffusion coefficient of the species of concern, in this case, the proton and (dE/d[H+])E is the slope of the coulometric titration curve. The diffusion frequency and diffusion resistance can be calculated from the impedance data and further used to calculate the boundary layer thickness, δ and diffusion resistance.
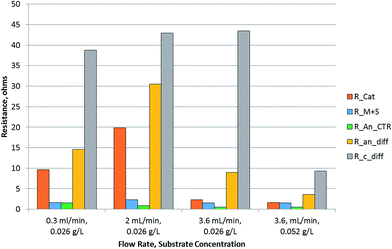
The fitting of the data to the ECM is shown in Fig. 4. It shows a Nyquist plot under various conditions with the model fitting overlaid on the experimental data points. The parameters δ and Rd were calculated from the fitted parameters (Table 2). The results indicate that the boundary layer thickness in the anode did not change significantly and stayed in the range of 123–170 microns. This is a layer within which a proton gradient exists. It is known that the anode biofilm thickness varies from a few microns to over 150 microns,9,10,30 so the boundary layer thickness obtained is likely to be composed of the biofilm with a small layer of liquid beyond which the proton concentration becomes equal to the bulk concentration. The diffusion resistance on the other hand, which is primarily a derivative of the potential with respect to proton concentration (eqn (21)), showed larger change over the conditions studied, indicating that the potential and the proton gradients within the biofilm are responsible for the diffusion resistance. The change in the diffusion resistance was not a linear function of the flow rate indicating that the relationship is rather complex, since it is a function of the proton as well as potential gradient in the biofilm. Furthermore, the potential complex nature of the system, which included a 3-dimensional electrode and a multi-substrate/multi-organism reaction system may lead to further non-linear characteristics, not captured by the simplified Warburg diffusion model. The boundary layer thickness determined for the cathode was much smaller, potentially due to the absence of a biofilm in the cathode and the small thickness of the cathode electrode compared to the anode. The diffusion resistance of the cathode, however, was larger than the anode. This may be due to the fact that the proton concentration gradient is likely to be much steeper in the cathode due to rapid consumption of protons for hydrogen evolution. The diffusion resistance is also a function of the boundary layer thickness (eqn (21)), therefore, a lower δ would further increase the diffusion resistance, as was observed experimentally. Increasing the concentration of the substrate from 0.026 to 0.052 g L−1 resulted in a decrease in the anode as well as cathode diffusion resistance, likely due to the higher proton production rate in the anode and transfer to the cathode. This shows that the substrate concentration was also a limiting factor in the performance of the MEC.
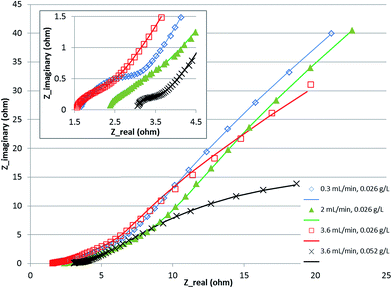 | ||
| Fig. 4 Nyquist plot for MEC at various flow rates and concentration. Symbols show experimental data and the line shows equivalent circuit model fitting. | ||
| Warburg impedance parameters | 0.3 mL min−1, 0.026 g L−1 | 2 mL min−1, 0.026 g L−1 | 3.6 mL min−1, 0.026 g L−1 | 3.6 mL min−1, 0.052 g L−1 | |
|---|---|---|---|---|---|
| Anode | δ, mm | 144 | 123 | 148 | 170 |
| R d, ohm | 14.6 | 30.5 | 9.0 | 3.6 | |
| Cathode | δ, mm | 3 | 16 | 20 | 5 |
| R d, ohm | 38.8 | 42.9 | 43.4 | 9.3 | |
A bar chart of the resistances resulting from diffusion as well as kinetic limitations is plotted in Fig. 5. It is observed that the diffusion resistance was dominant among all the resistances in the MEC. The anode diffusion resistance was an order of magnitude higher than the anode charge transfer resistance. Comparing the two half-cell reactions, the cathode reaction was found to exhibit larger resistance. This could be due to either the proton or electron transfer rates to the cathodic catalytic site. To assess whether the electron transfer was limiting, the half-cell potentials were measured at the cathode. The cathode potential was below −1.0 V for all experiments. It reached −1.18 V for the condition at which the maximum current density was obtained. The cathode potential can drop to such negative levels only when sufficient rate of electron production and transfer to the cathode exists. This suggests that electron transport to the cathode may not be a limiting factor in the MEC. The pH of the cathode was found to increase above 13 units, indicating that the proton concentration at the cathode was very low. This evidence points towards proton transfer being the limiting factor in hydrogen production.
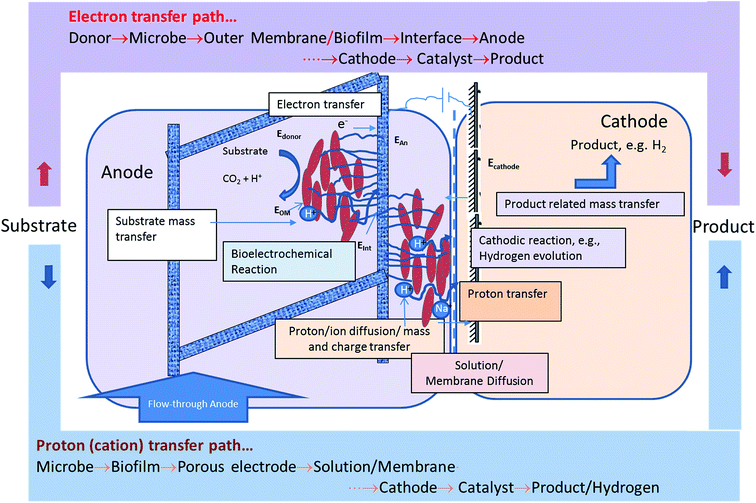
Fig. 6 shows the mass transfer, charge transfer and electron transfer processes occurring in the MEC. It also shows the path protons and electrons have to traverse between the anode and the cathode to produce hydrogen. The protons are produced and released from the cell surface and go through a tortuous path via the exopolysaccharide layer, the biofilm, the interstitial space between the fibers of the carbon felt, reaching the bulk anode liquid, followed by transport through the membrane to the cathode, then to the catalyst surface to produce a hydrogen molecule. The electrons, on the other hand, have a more direct path if a biofilm containing a conductive exopolysaccharide layer or nanowires is present. The bioanode used in this study was demonstrated to contain Geobacter sulfurreducens.14 Support for the formation of highly conductive biofilms containing G. sulfurreducens exists in the literature.19 Furthermore, the method used for bioanode development in this study was based on an optimization method developed for minimizing the reliance on mediator-based electron transfer and maximization of direct electron transfer.22,31 The observed results indicate that the electron transport resistance of the anode biofilm is not a dominant resistance.
3.6 Total cell resistance and further optimization
In the results obtained in this study, the proton transport was found to be a limiting factor in MEC performance under most conditions. There are several ways the proton transfer limitation can be reduced. One potential solution is the use of an anion exchange membrane (AEM). Sleutels et al. quantified the effect of the type of membrane on cell resistance.32 Use of an AEM was reported to result in a cell resistance of 900 ohm cm2, while a cation exchange membrane (CEM) resulted in a cell resistance of 1380 ohm cm2. The membrane component itself was about 20% of the overall cell resistance. The membrane resistance calculated for the CEM used in our study via EIS was relatively lower and constituted about 9.3% of the combined cell resistances and also included the solution resistance. The type of membrane can be an important contributing factor to the overall cell resistance, since it affects polarization as well as direct charge/mass transport between the two electrodes. The model reported by Sleutels et al. lumped some of these impedances into a reaction-related resistance parameter identified as the ‘equilibrium’ resistance,32 while the ECM analysis binned these impedances differently, which may explain the inconsistencies in the calculated membrane resistances.The total cell resistance can be determined using the cell voltage and the current. Ki et al.33 have reported an apparent resistance (Rapp) for the cell which is calculated as follows:
| Rapp = Vcell/I | (22) |
| Electrode spacing/membrane | OLR, g per L per day; substrate | Cell voltage, V | Current density, A m−2 | Apparent impedance, ohm cm2 | Rate of ion transfer, moles per m2 per hour | H2 productivity, L per L per day | Reference |
|---|---|---|---|---|---|---|---|
| a Rate of proton transfer determined using current production in the absence of hydrogen production rate. | |||||||
| ES = 2.25 cm | Fed-batch, 1 g L−1; acetate | 0.9 | 8 | 1125 | 0.08 | 2.1 | 36 |
| ES = 2.25 cm | Fed-batch, 1 g L−1; acetate | 1.2 | 12 | 1000 | 0.12 | 3.3 | 36 |
| ES = 0.07 cm | 8; acetate | 1.2 | 6.04 | 1987 | 0.18 | 4.6 | 37 |
| ES = 0.07 cm | 8; sWW | 1.02 | 6.64 | 1536 | 0.21 | 5.3 | 37 |
| AEM | 6.3; acetate | 1.2 | 11 | 1091 | 0.07 | 1.6 | 38 |
| CEM | 35; acetate | 1 | 7.2 | 1389 | 0.27 | NA | 32 |
| AEM | 35; acetate | 1 | 10.2 | 980 | 0.38 | NA | 32 |
| AEM | 3.4; acetate | 0.82 | 10 | 820 | 0.37 | NA | 33 |
| AEM | 3.4; acetate | 0.85 | 10 | 850 | 0.37 | NA | 33 |
| AEM | 3.4; acetate | 1.15 | 14 | 821 | 0.52 | NA | 33 |
| CEM | 10; pyrolysis BOAP | 0.8 | 3.3 | 2398 | 0.08 | 2.9 | This work |
| CEM | 20; pyrolysis BOAP | 1.07 | 10.7 | 1000 | 0.27 | 6.6 | This work |
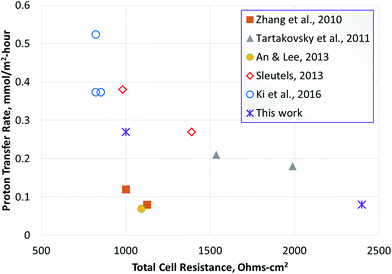
In order to compare the proton transfer rate, an estimated rate of proton/ion transfer was also calculated for the studies reported in Table 3 (using eqn (15)). This was based on the hydrogen productivity reported in the studies. Some of the studies did not report hydrogen production, therefore the rate of proton transfer could not be calculated, however; a pseudo-ion transfer rate was calculated using the current densities reported. The results show that among the studies reporting the hydrogen production rate, the proton transfer rate achieved in this study was the highest. Considering the studies where hydrogen production rate was not reported, the maximum pseudo-ion transfer rate computed was 0.52 moles per m2 per hour. This was based on studies reported by Ki et al., using a cathode sparged with carbon dioxide.33 While this method can reduce cell resistance and improve the current density, it poses a challenge for hydrogen recovery from the gas mixture.
Tartakousky et al. developed a real-time voltage optimization method to minimize power requirement for hydrogen production.37 The data included in Table 3 are for optimal values obtained by this method. The apparent resistance obtained from these studies can be considered optimal for the conditions used in those experiments. Furthermore, this study used a membrane-less MEC. Despite these design and process optimization measures, the predicted ion transfer rate was 0.21 moles per m2 per hour. The rates obtained in this study were comparable to the optimal rates reported by Tartakousky et al. for their system.37
3.7 Implications for production of hydrogen in biorefinery and other applications
A plot of ion transfer rate vs. apparent resistance shows an inverse relationship between the two parameters (Fig. 7). This indicates that ion transfer between the anode and cathode may represent a key parameter in determining the performance of microbial electrolysis cells. There is certainly room for further optimization of the MEC process reported here for conversion of biomass-derived liquid stream, either using alternate membranes or changes in process conditions to reduce pumping costs, etc. Thus, the use of AEM or nanoporous membranes and use of higher substrate concentration, while maintaining the hydrodynamic conditions to achieve effective proton transfer from the biofilm to the bulk anode solution can lead to optimal conditions for proton transfer in the anode.The analysis of proton transfer reported in this study was conducted using a real feedstock for hydrogen production vs. use of acetate or simulated wastewaters. This is significant because it gives direct insight into the potential alterations needed for implementing the technology for renewable hydrogen production. The results show that the MEC performance is approaching the threshold current density of 20 A m−2 required for economic feasibility of the MEC technology.39 While the commercial feasibility of hydrogen production in the biorefinery using MEC technology depends on a number of other factors such as feedstock cost, processing costs, co-benefits such as wastewater clean-up, contaminant removal to enable water recycle, etc., the ability to generate hydrogen at rates >10 L per L per day, while identifying the limitations for further improvement, improves the feasibility of implementing this technology in the biorefinery. The improvement in proton transfer rate via optimization of flow rate, design of electrodes, membrane, etc., at higher organic loading rates are the next steps in achieving rates of hydrogen production above 15 L per L per day. Production of renewable hydrogen from wastes generated in the biorefinery40–42 has potential to increase the efficiency of the overall process and improve resource utilization for production of fuels and chemicals. Thus, MECs can be an important contributor to the development of bioeconomy in the 21st century.
4. Conclusion
Quantification of the proton transfer rates in microbial electrolysis cells (MECs) was conducted using a proton mass balance. A maximum proton transfer rate of 0.36 ± 0.01 moles per m2 per hour was obtained, which was a function of the organic loading rate and the anode flow rate. The availability of protons in the cathode buffer resulted in a 28% higher hydrogen productivity of 11.7 ± 0.2 L per L per day, compared to 9.08 L per L per day, achievable based on protons transferred from the anode chamber alone. This suggests that proton transfer limits overall hydrogen productivity and that the anode is capable of metabolizing the substrate and transferring electrons to the cathode at higher rates compared to the proton transfer rate. Electrochemical impedance spectroscopy supported this conclusion as evidenced by the proton transfer rate being the dominant resistance among all resistances in the MEC. It was further determined that the diffusion resistance which depends on the term dE/d[H+] controlled the proton transfer resistance. Alleviation of the proton transfer limitation in MECs processing the biomass-derived pyrolysis aqueous phase can enable application of the MEC technology for generation of renewable hydrogen in the biorefinery.Acknowledgements
Funding from the U.S. Department of Energy, BioEnergy Technologies Office under the Carbon, Hydrogen and Separations Efficiency for Bio-oil Pathways (CHASE) program and ORNL Seed Money Program is acknowledged. AJL was partially supported by the Bredesen Center for Interdisciplinary Research and Education. The manuscript has been co-authored by UT-Battelle, LLC, under Contract No. DEAC05-00OR22725 with the U.S. Department of Energy.References
- Y. Zhang and I. Angelidaki, Water Res., 2014, 56, 11–25 CrossRef CAS PubMed.
- S. C. Popat and C. I. Torres, Bioresour. Technol., 2016, 215, 265–273 CrossRef CAS PubMed.
- D. R. Lovley, Energy Environ. Sci., 2011, 4, 4896–4906 CAS.
- K. Rabaey, L. T. Angenent, U. Schroder and J. Keller, Bioelectrochemical Systems: from Extracellular Electron Transfer to Biotechnological Application, IWA Publishing, London, UK, 2010 Search PubMed.
- Y. Yang, M. Xu, J. Guo and G. Sun, Process Biochem., 2012, 47, 1707–1714 CrossRef CAS.
- D. S. Aaron, C. Tsouris, C. Y. Hamilton and A. P. Borole, Energies, 2010, 3, 592 CrossRef CAS.
- J. T. Babauta, H. D. Nguyen, T. D. Harrington, R. Renslow and H. Beyenal, Biotechnol. Bioeng., 2012, 109, 2651–2662 CrossRef CAS PubMed.
- C. I. Torres, A. K. Marcus and B. E. Rittmann, Biotechnol. Bioeng., 2008, 100, 872–881 CrossRef CAS PubMed.
- H. Beyenal and J. T. Babauta, Biochem. Soc. Trans., 2012, 40, 1315–1318 CrossRef CAS PubMed.
- D. R. Bond, S. M. Strycharz-Glaven, L. M. Tender and C. I. Torres, ChemSusChem, 2012, 5, 1099–1105 CrossRef CAS PubMed.
- A. P. Borole, G. Reguera, B. Ringeisen, Z.-W. Wang, Y. Feng and B. H. Kim, Energy Environ. Sci., 2011, 4, 4813–4834 CAS.
- A. P. Borole, C. Y. Hamilton, T. A. Vishnivetskaya, D. Leak, C. Andras, J. Morrell-Falvey, B. H. Davison and M. Keller, J. Power Sources, 2009, 191, 520–527 CrossRef CAS.
- T. Sleutels, R. Lodder, H. V. M. Hamelers and C. J. N. Buisman, Int. J. Hydrogen Energy, 2009, 34, 9655–9661 CrossRef CAS.
- A. J. Lewis, S. Ren, X. Ye, P. Kim, N. Labbe and A. P. Borole, Bioresour. Technol., 2015, 195, 231–241 CrossRef CAS PubMed.
- A. J. Lewis and A. P. Borole, Biochem. Eng. J., 2016, 116, 95–104 CrossRef CAS.
- Z. He and F. Mansfeld, Energy Environ. Sci., 2009, 2, 215–219 CAS.
- A. P. Borole, D. S. Aaron, C. Tsouris and C. Y. Hamilton, Environ. Sci. Technol., 2010, 44, 2740–2745 CrossRef CAS PubMed.
- X. Dominguez-Benetton, S. Sevda, K. Vanbroekhoven and D. Pant, Chem. Soc. Rev., 2012, 41, 7228–7246 RSC.
- N. S. Malvankar, M. T. Tuominen and D. R. Lovley, Energy Environ. Sci., 2012, 5, 5790–5797 CAS.
- R. P. Ramasamy, Z. Y. Ren, M. M. Mench and J. M. Regan, Biotechnol. Bioeng., 2008, 101, 101–108 CrossRef CAS PubMed.
- C. I. Torres, A. K. Marcus, H. S. Lee, P. Parameswaran, R. Krajmalnik-Brown and B. E. Rittmann, FEMS Microbiol. Rev., 2010, 34, 3–17 CrossRef CAS PubMed.
- O. Ichihashi, T. Vishnivetskaya and A. P. Borole, ChemElectroChem, 2014, 1, 1940–1947 CrossRef CAS.
- R. P. Ramasamy, V. Gadhamshetty, L. Nadeau and G. R. Johnson, Biotechnol. Bioeng., 2009, 104(5), 882–891 CrossRef CAS PubMed.
- A. W. Jeremiasse, H. V. Hamelers, J. M. Kleijn and C. J. Buisman, Environ. Sci. Technol., 2009, 43, 6882–6887 CrossRef CAS PubMed.
- B. E. Logan, D. Call, S. Cheng, H. V. M. Hamelers, T. Sleutels, A. W. Jeremiasse and R. A. Rozendal, Environ. Sci. Technol., 2008, 42, 8630–8640 CrossRef CAS PubMed.
- R. A. Rozendal, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2006, 40, 5206–5211 CrossRef CAS PubMed.
- Z. Lu, D. Chang, J. Ma, G. Huang, L. Cai and L. Zhang, J. Power Sources, 2015, 275, 243–260 CrossRef CAS.
- D. I. Torres, A. K. Marcus, P. Parameswaran and B. E. Rittmann, Environ. Sci. Technol., 2008, 42, 6593–6597 CrossRef PubMed.
- H. V. M. Hamelers, A. ter Heijne, N. Stein, R. A. Rozendal and C. J. N. Buisman, Bioresour. Technol., 2011, 102, 381–387 CrossRef CAS PubMed.
- J. T. Babauta and H. Beyenal, J. Electrochem. Soc., 2014, 161, H3070–H3075 CrossRef.
- A. P. Borole, Microbial fuel cell with improved anode, US Pat. 7695834, UT-Battelle, LLC, USA, 2010.
- T. H. Sleutels, A. Ter Heijne, C. J. Buisman and H. V. Hamelers, Int. J. Hydrogen Energy, 2013, 38, 7201–7208 CrossRef CAS.
- D. Ki, S. C. Popat and C. I. Torres, Chem. Eng. J., 2016, 287, 181–188 CrossRef CAS.
- K. Zuo, L. Yuan, J. Wei, P. Liang and X. Huang, Bioresour. Technol., 2013, 146, 637–642 CrossRef CAS PubMed.
- Y. Zhang and I. Angelidaki, Water Res., 2015, 81, 188–195 CrossRef CAS PubMed.
- Y. M. Zhang, M. D. Merrill and B. E. Logan, Int. J. Hydrogen Energy, 2010, 35, 12020–12028 CrossRef CAS.
- B. Tartakousky, P. Mehta, G. Santoyo and S. R. Guiot, Int. J. Hydrogen Energy, 2011, 36, 10557–10564 CrossRef.
- J. An and H.-S. Lee, RSC Adv., 2013, 3, 14021–14028 RSC.
- T. Sleutels, A. Ter Heijne, C. J. N. Buisman and H. V. M. Hamelers, ChemSusChem, 2012, 5, 1012–1019 CrossRef CAS PubMed.
- A. P. Borole, Biofuels, Bioprod. Biorefin., 2011, 5, 28–36 CrossRef CAS.
- A. P. Borole and J. Mielenz, Int. J. Hydrogen Energy, 2011, 36, 14787–14795 CrossRef CAS.
- T. C. Pannell, R. K. Goud, D. J. Schell and A. P. Borole, Biochem. Eng. J., 2016, 116, 85–94 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7se00034k |
| This journal is © The Royal Society of Chemistry 2017 |