Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the self-assembled structures and pKa of hydrogels using electrochemical methods†
Emily R.
Cross
 and
Dave J.
Adams
and
Dave J.
Adams
 *
*
School of Chemistry, University of Glasgow, Glasgow, G12 8QQ, UK. E-mail: dave.adams@glasgow.ac.uk
First published on 14th January 2019
Abstract
The surface chemistry of the aggregated structures that form the scaffold in self-assembled hydrogels – their charge, hydrophobicity and ion-binding dynamics – plays an important role in determining the gel properties and the gel's suitability for specific applications. However, there are limited methods available for the study of this surface chemistry. Here, we show that electrochemical techniques can be used to measure the surface chemical properties of the self-assembled aggregate structures and also to determine the pKa of the gelators. We also provide a method to quickly determine whether a functionalised-dipeptide will form a gel or not. This method has scope for use in high-throughput screening and further complex pH-triggered self-assembled gelation systems.
Introduction
Low molecular weight gelators are molecules that self-assemble into one-dimensional aggregated structures, most commonly fibres.1–4 Gels are formed when these fibres entangle and immobilise solvent. Unlike polymer-based hydrogels, which are held together by covalent bonds, low molecular weight hydrogels are held together only by intermolecular forces such as hydrogen bonding and π–π stacking.2,3,5 This allows for reversibility and potentially greater control over the assembly process.2,3,5 The gelators self-assemble into the fibres that lead to a hydrogel due to a triggered decrease in the solubility of the gelator in solution as depicted in Fig. 1a. There are many possible methods to reduce the solubility and many gelators are modified to suit a self-assembly regime to achieve useful gels.1–3,5–7 Their versatility means low molecular weight hydrogels have uses in applications such as sensors, cell growth, photocatalytic hydrogen production and organic photovoltaic devices.2,3,5,8–12In this work, we use a range of LMWGs that have an aromatic group attached to a dipeptide (Fig. 2).13 The dipeptides contain a carboxylic acid group which is deprotonated at high pH, which allows the LMWG to be dispersed in water. To lower the solubility of the gelator, the pH is decreased. Lowering the pH past the apparent pKa of the carboxylic acid of the gelator results in protonation of the carboxylic acid, and the gelator becomes insoluble. Gelators such as these are widely used.9,14,15 Generally, these gelators are used as single component systems, with one molecule forming the network. There is increasing interest in multicomponent systems, where two (or more) gelators self-assemble, either interacting to provide a co-assembled network, or independently to form self-sorted networks.6,16–18 Multicomponent systems provide opportunity for materials which were not possible with only one component.16,17,19–25 For example, self-sorted systems can be prepared using a pH-triggered approach using two gelators which have different pKas. As the pH is lowered below the pKa of the first gelator, its self-assembly is triggered.26 Only after the pKa of the second gelator is reached, does self-assembly of the second gelator occur (Fig. 1b).
For both single and multicomponent gelator systems, the apparent pKa is therefore clearly important, with the pH at which the gels are formed being related to the apparent pKa.27,28 The gel properties are determined by the fibre network, and this is affected by the degree of charge on the fibres. However, there are limited methods available to readily determine the apparent pKa and to probe the assembly process. Methods to characterise the fibre interactions during self-assembly are also limited.29 The charge, hydrophobicity and ion-binding dynamics of the gelators and fibres play an important role in self-assembly which ultimately determines the suitability of the gels for specific applications.29
The pKa is formally defined as the pH when 50% of the molecules in aqueous solution exist in a protonated form and the other half are deprotonated.30 If gelators are aggregated, in a multicomponent system, or have two or more apparent pKa values, then the definition is not as simple. For example, there are no methods to determine accurately whether 50% of the gelator is protonated or not without knowing the degree of aggregation. If aggregation occurs, this can result in stabilisation of charge and a pKa that is higher than expected.27,28 Therefore, developing a method that can determine the pKa/isoelectric point of a gelator would significantly benefit the field.
Here, we describe an electrochemical technique that can be used to analyse the interactions between the ions and the aggregated structure of the gelator (ion–fibre) during real-time gelation. The method allows us to determine the apparent pKa values and follow the evolution of the ion–fibre interactions as gelation occurs. This method can be applied to single as well as multicomponent systems.
Experimental
Gelator solutions were prepared at high pH at a concentration of gelator of 10 mg mL−1 for use in a multicomponent system and 5 mg mL−1 for single component systems, as described in the ESI.† To these gelator solutions, we added [Ru(NH3)6]Cl3 (TM). This TM used as the cation is electrochemically reversible in aqueous solution.31 Based on previous work,32–34 where the cross-linking of gelator fibres with cations produced hydrogels at high pH, we rationalised that cross-linking or interactions with the TM should also lead to a degree of immobilisation of the TM at high pH. As pH is decreased to below the pKa of the gelator, the carboxylic acid will be protonated and the TM will then be free to diffuse through the solution. The electrochemical techniques rely upon this change in binding, shown schematically in Fig. 3.Given the diffusion coefficient of the TM is dependent upon its radius of hydration and the viscosity it experiences through solution via the Stokes–Einstein equation (eqn (1)), we should observe an increase in diffusion coefficient when the transition metal becomes free in solution.
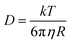 | (1) |
Using the Randles–Sevcik equation (eqn (2)), we can determine the change in diffusion coefficient by measuring the change in peak oxidation current of the TM as a function of pH or time.35 When the TM is bound to the gelator at high pH, we expect the conductivity will be low due to the increase in the radius of diffusing species around the TM, whereas below the pKa we expect the conductivity of the TM to be higher due to the lower radius of hydration. We assume the free TM will be able to travel freely through the pores of the gel implying that the viscosity will be similar to water. A large increase in conductivity will therefore signify the pKa value.
 | (2) |
Results and discussion
Cyclic voltammetry
We begin by discussing the pH titration method. A common method of triggering gelation for dipeptide gelators such as those used here is to use pH. Initially, a solution at high pH is prepared, and then gels are formed by lowering the pH using hydrochloric acid.36–38 When adding aliquots of hydrochloric acid and measuring pH, a plateau around the pKa value is observed.28,39 This method is commonly used to determine the apparent pKa of such gelators.27,28 However, with this method the volume of gelator solution increases with the addition of acid which can be problematic if the pKa is dependent upon concentration.28Nonetheless, lowering the pH by additions of aliquots of HCl, we were able to record the TM–gelator interactions using cyclic voltammetry. The TM was added to the gelator solution at pH 10. After each addition of HCl (0.1 M), the pH was measured and a CV was recorded to observe the peak current for the TM. For this family of gelator, at high pH typically worm-like micelles or diffuse aggregates are formed stabilised by the deprotonated carboxylic acid (the type of aggregate can be determined by NMR for example).32,40 Either kind of structure should be able to bind to the positively-charged TM. When the peak current is low, this suggests that the TM is bound to the gelators, due to the increase in apparent radius of the TM. When the current peak is high, we suggest the concentration of free TM in solution is high due to the apparent decrease in radius of the TM, resulting in a high diffusion coefficient. This implies that more gelator molecules are protonated and not binding to the TM.
The diffusion coefficient was calculated at different pH values (Fig. 4), exemplified for molecules 1–4 (see Fig. 2). For the molecules that form gels by this method, after initial additions of HCl, we observe small changes in the diffusion coefficient, as would be expected with a system above the pKa. For 1 and 4, there is a slight initial increase in diffusion coefficient as pH decreases, whereas for 2 & 3 there is a slight decrease in diffusion coefficient. This suggests differences in the self-assembly regime but could also be due to subtle changes in the viscosity as the pH is lowered. With subsequent additions of HCl, we observed a rapid linear increase in the diffusion coefficient. This is where we identify the pKa to be. A similar trend was observed in all gelators measured where the change in gradient of diffusion coefficient and pH was used to determine the pKa value. We note that the values determined agree well with the values previously measured by a pH titration.28,41 A summary of the recorded pKa values with literature values is provided in Table S1 (ESI†).
Not all molecules in this family form gels.14 When aliquots of HCl were added to a solution of a molecule that does not form a gel (e.g.5 and 10), there was again an initial small change in the diffusion coefficient (Fig. 4e and f). However, at a critical pH, there was a sharp decrease in diffusion coefficient. This sharp decrease in diffusion coefficient was a result of the gelator molecules forming a visible precipitate which sedimented to the bottom of the vial stopping the TM from diffusing to the electrode surface. We again associate this with the apparent pKa.
By measuring the difference between the peak current at pH 9.5 and at pH 4.5, we can therefore use this method to screen whether or not a molecule has the potential to be an effective pH-triggered gelator or not (Fig. 5). A positive Δ current value represents a molecule capable of forming a gel whereas a negative value suggests precipitation. Whilst for some systems, this is no more effective than simply testing gelation by adding acid and inverting the vial, we highlight that pH-triggered gelation is highly dependent on the method of acid addition.42,43 Hence, this method can be used to show whether a gel could form or not, whilst a simple addition of acid to quickly lower the pH can sometimes result in samples where it is difficult to unambiguously demonstrate that a gel has formed.14 Our method also has the potential to be used on small volumes, where again unambiguously assigning gelation is difficult. We envisage that this method could be installed as part of a high throughput screening process for pH triggered self-assembled hydrogels.
Continuous cyclic voltammetry
Adding mineral acids can often result in systems that are strongly affected by kinetics, leading to issues with mixing.42,43 To get around this, we have developed methods to allow homogeneous gels to be formed. One such method is to lower the pH by the addition of glucono-δ-lactone (GdL).43,44 GdL slowly hydrolyses to gluconic acid, which lowers the pH of the system without the need for stirring.43 GdL produces gels which tend to have homogenous properties.43 Due to this slow hydrolysis, and so the slow self-assembly process, to determine the pKa we need a method that records data over the period of time and that does not distort the network.After adding GdL to a solution of a gelator, continuous cyclic voltammograms (CVs) were run over 16 hours with a scan rate of 0.04 V s−1vs. an Ag/AgCl (3 M) reference electrode allowing the diffusion coefficient as a function of time to be determined. By measuring the evolution of pH at the same time as the CVs, we expected to determine the pH when the increase in diffusion coefficient was observed. The results for gelator 1 and 4 are shown in Fig. 6a and b. A very slight increase of diffusion coefficient was observed around pH 6.0 for 1 and pH 5.8 for 4. Although these values correspond to the pKa values obtained in the pH titration data above, the method itself did not provide data that was easy to interpret. The change in linearity of the diffusion coefficient is more gradual over a larger pH range compared to the sharp change with HCl titration. Therefore, this makes it more difficult to determine the pKa value and the method not optimal.
Multiple pulse amperometry
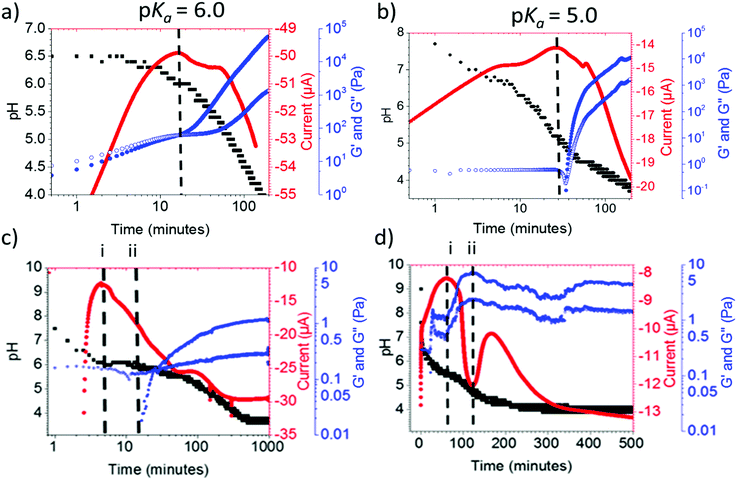
Because of the difficultly in determining the pKa from the data using continuous CVs, we moved to using multiple pulse amperometry (MPA). In MPA, the potential is switched between the reduction and oxidation potential in a binary fashion. The method differs from cyclic voltammetry where the potential is instead swept linearly between two potentials. MPA increased the number of data points that could be collected in unit time twenty-fold. MPA is also easy to set up experimentally and is more time and labour efficient compared to titration methods.MPA was applied to a gelation system with GdL and the pH was measured over time. Fig. 7a and b show the MPA and pH evolution for gelators 1 and 2 respectively. The maximum current peak occurs at the pH where we expect pKa to occur from data in Fig. 4. Measuring the rheology concurrently with the pH and current during gelation allows us to correlate between when the pKa is observed and the onset of gelation. The onset of gelation can be identified as the large increase in storage modulus (G′), this increase in G′ can be observed for 1 and 2 in (Fig. 7a and b) at the same time point as the current peak. We would expect this from our previous work.28
The situation for 1 and 2 is straightforward. The MPA method can however be used to understand less straightforward cases. For example, for 6 (Fig. 7c), we observe the maximum current peak shown with the dashed line labelled (i) at pH 6.0. As the pH buffers around this value there is an increase in G′ at the same pH shortly afterwards, shown with the dashed line labelled (ii). This suggests that once the pKa is reached at (i), there is a time delay in the formation of a network that immobilises water being formed. However, it is important to point out that both the current peak and G′ onset (i) and (ii), occur at the same pH value.
When using this method for a system that does not form a gel, 5, two peaks in the current were found (Fig. 7d, labelled (i) and (ii)). At points (i) (pH 5.7) and (ii) (pH 5.0), there appears to be a shift in charge. After peak at point (i), the current value becomes more negative suggesting more TM is free in solution. After point (ii), the current value becomes less negative suggesting there is less TM free in solution. Coupling the MPA data with rheological time sweeps, there is an increase in G′ at point (i). This suggests the formation of a network that immobilises water. Next, we can see the G′ peaks at point (ii), it is at this point the gel is most stiff. Then after point (ii), as the current tends to zero, the G′ value decreases. Finally, after second peak the current becomes more negative again, the change in G′ continues to decrease which corresponds to the formation of the precipitate.
Multicomponent systems
In multicomponent systems composed of two gelators, we would expect the TM to bind to both gelators at high pH. From our previous work, addition of GdL leads to sequential assembly as long as the pKa of each gelator is different (Fig. 1b).26 As pH is lowered below the pKa of the first gelator, we would expect displacement of the TM from this gelator by protons. This would increase the concentration of free TM in solution resulting in an increase in current. Then, as the pH reaches the pKa of the second gelator, further displacement of TM and a final increase in current would be expected (shown schematically in Fig. 3b).We applied the MPA method to a multicomponent system consisting of gelators 2 and 8. These dipeptides were chosen on the basis of the large difference in single component pKa values.28,45 However, any combination could be used. The evolution of current, pH, storage and loss moduli are shown in Fig. 8. Highlighted are the two pKa values for 2 and 8. Within two minutes after the addition of GdL, the pH decreased to the pKa of gelator 8. At this point, an increase in G′ is observed and we also just pass the first peak in current. This suggests 8 is forming a network in the absence of 2. Once the pKa of 2 has been reached, we observe a second increase in G′ and the beginning of a second current peak. This would suggest 8 is beginning to assemble.26 Finally, at pH 3.8 the pKa of GdL is observed, shown by another current peak.
Conclusions
We have demonstrated how electrochemical techniques can be used to probe the surface chemistry of self-assembled hydrogel fibres including their charge and ion-binding dynamics. This included developing a new pKa determination method for this class of amino acids or dipeptides. We were able to determine whether a functionalised-dipeptide would self-assemble to form a hydrogel or precipitate, and at what pH this occurs. Furthermore, we developed a method to probe the real-time self-assembly kinetics of a functionalised-dipeptide using multiple pulse amperometry, rheology and pH evolution. Finally, we expanded this method to complex multicomponent systems and were able to observe the surface chemistry of the individual fibres forming as pH was lowered. The future scope of this work includes use in high-throughput screening for pH-triggered systems and further complex gelation systems. Finally, whilst conceptually zeta potential measurements could be used in a similar fashion,46 zeta potential measurements are recorded for all charged species in solution. This means that it difficult to identify between gelator fibres and other charged species present. This also means for multicomponent systems, the differentiation between charged species would be near impossible.Conflicts of interest
There are no conflicts to declare.Acknowledgements
ERC thanks the University of Glasgow for a studentship. DA thanks the EPSRC for a Fellowship (EP/L021978/1) ERC and DA would like the thank Bart Dietrich and Emily Draper (University of Glasgow) for synthesising some of the gelators used here and helpful discussions.Notes and references
- R. G. Weiss, J. Am. Chem. Soc., 2014, 136, 7519–7530 CrossRef CAS PubMed.
- P. Terech and R. G. Weiss, Chem. Rev., 1997, 97, 3133–3160 CrossRef CAS PubMed.
- M. d. Loos, B. L. Feringa and J. H. v. Esch, Eur. J. Org. Chem., 2005, 3615–3631 CrossRef.
- E. R. Draper and D. J. Adams, Chem, 2017, 3, 390–410 CAS.
- N. M. Sangeetha and U. Maitra, Chem. Soc. Rev., 2005, 34, 821–836 RSC.
- E. R. Draper and D. J. Adams, Chem. Soc. Rev., 2018, 47, 3395–3405 RSC.
- A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002–8018 CrossRef CAS PubMed.
- A. S. Weingarten, R. V. Kazantsev, L. C. Palmer, M. McClendon, A. R. Koltonow, P. S. SamuelAmanda, D. J. Kiebala, M. R. Wasielewski and S. I. Stupp, Nat. Chem., 2014, 6, 964–970 CrossRef CAS PubMed.
- S. Ghosh, V. K. Praveen and A. Ajayaghosh, Annu. Rev. Mater. Res., 2016, 46, 235–262 CrossRef CAS.
- A. R. Hirst, D. K. Smith, M. C. Feiters and H. P. M. Geurts, Langmuir, 2004, 20, 7070–7077 CrossRef CAS PubMed.
- E. M. Ahmed, J. Adv. Res., 2015, 6, 105–121 CrossRef CAS PubMed.
- J. P. Wojciechowski, A. D. Martin and P. Thordarson, J. Am. Chem. Soc., 2018, 140, 2869–2874 CrossRef CAS PubMed.
- S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177 RSC.
- J. K. Gupta, D. J. Adams and N. G. Berry, Chem. Sci., 2016, 7, 4713–4719 RSC.
- X. Du, J. Zhou, J. Shi and B. Xu, Chem. Rev., 2015, 115, 13165–13307 CrossRef CAS PubMed.
- L. E. Buerkle and S. J. Rowan, Chem. Soc. Rev., 2012, 41, 6089–6102 RSC.
- B. O. Okesola and A. Mata, Chem. Soc. Rev., 2018, 47, 3721–3736 RSC.
- P. Makam and E. Gazit, Chem. Soc. Rev., 2018, 47, 3406–3420 RSC.
- R. Kubota, S. Liu, H. Shigemitsu, K. Nakamura, W. Tanaka, M. Ikeda and I. Hamachi, Bioconjugate Chem., 2018, 29, 2058–2067 CrossRef CAS PubMed.
- E. R. Cross, S. Sproules, R. Schweins, E. R. Draper and D. J. Adams, J. Am. Chem. Soc., 2018, 140, 8667–8670 CrossRef CAS PubMed.
- H. Shigemitsu, T. Fujisaku, W. Tanaka, R. Kubota, S. Minami, K. Urayama and I. Hamachi, Nat. Nanotechnol., 2018, 13, 165–172 CrossRef CAS PubMed.
- E. V. Alakpa, V. Jayawarna, A. Lampel, K. V. Burgess, C. C. West, S. C. J. Bakker, S. Roy, N. Javid, S. Fleming, D. A. Lamprou, J. Yang, A. Miller, A. J. Urquhart, P. W. J. M. Frederix, N. T. Hunt, B. Péault, R. V. Ulijn and M. J. Dalby, Chem, 2016, 1, 298–319 CAS.
- N. Singh, K. Zhang, C. A. Angulo-Pachón, E. Mendes, J. H. van Esch and B. Escuder, Chem. Sci., 2016, 7, 5568–5572 RSC.
- S. Mytnyk, A. G. L. Olive, F. Versluis, J. M. Poolman, E. Mendes, R. Eelkema and J. H. van Esch, Angew. Chem., 2017, 129, 15119–15123 CrossRef.
- D. J. Cornwell, O. J. Daubney and D. K. Smith, J. Am. Chem. Soc., 2015, 137, 15486–15492 CrossRef CAS PubMed.
- K. L. Morris, L. Chen, J. Raeburn, O. R. Sellick, P. Cotanda, A. Paul, P. C. Griffiths, S. M. King, R. K. O’Reilly, L. C. Serpell and D. J. Adams, Nat. Commun., 2013, 4, 1480 CrossRef PubMed.
- C. Tang, A. M. Smith, R. F. Collins, R. V. Ulijn and A. Saiani, Langmuir, 2009, 25, 9447–9453 CrossRef CAS PubMed.
- L. Chen, S. Revel, K. Morris, L. C. Serpell and D. J. Adams, Langmuir, 2010, 26, 13466–13471 CrossRef CAS PubMed.
- M. Wallace, J. A. Iggo and D. J. Adams, Soft Matter, 2017, 13, 1716–1727 RSC.
- J. Reijenga, A. van Hoof, A. van Loon and B. Teunissen, Anal. Chem. Insights, 2013, 8, 53–71 CAS.
- N. A. Morris, M. F. Cardosi, B. J. Birch and A. P. F. Turner, Electroanalysis, 1992, 4, 1–9 CrossRef CAS.
- L. Chen, T. O. McDonald and D. J. Adams, RSC Adv., 2013, 3, 8714–8720 RSC.
- H. McEwen, E. Y. Du, J. P. Mata, P. Thordarson and A. D. Martin, J. Mater. Chem. B, 2017, 5, 9412–9417 RSC.
- S. Roy, N. Javid, P. W. J. M. Frederix, D. A. Lamprou, A. J. Urquhart, N. T. Hunt, P. J. Halling and R. V. Ulijn, Chem. – Eur. J., 2012, 18, 11723–11731 CrossRef CAS PubMed.
- Y. Wang, J. G. Limon-Petersen and R. G. Compton, J. Electroanal. Chem., 2011, 652, 13–17 CrossRef CAS.
- V. Jayawarna, M. Ali, T. A. Jowitt, A. F. Miller, A. Saiani, J. E. Gough and R. V. Ulijn, Adv. Mater., 2006, 18, 611–614 CrossRef CAS.
- Y. Zhang, H. Gu, Z. Yang and B. Xu, J. Am. Chem. Soc., 2003, 125, 13680–13681 CrossRef CAS PubMed.
- Z. Yang, G. Liang, M. Ma, Y. Gao and B. Xu, J. Mater. Chem., 2007, 17, 850–854 RSC.
- C. Tang, R. V. Ulijn and A. Saiani, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 111 CrossRef PubMed.
- A. D. Martin, J. P. Wojciechowski, A. B. Robinson, C. Heu, C. J. Garvey, J. Ratcliffe, L. J. Waddington, J. Gardiner and P. Thordarson, Sci. Rep., 2017, 7, 43947 CrossRef PubMed.
- K. A. Houton, K. L. Morris, L. Chen, M. Schmidtmann, J. T. A. Jones, L. C. Serpell, G. O. Lloyd and D. J. Adams, Langmuir, 2012, 28, 9797–9806 CrossRef CAS PubMed.
- W. Helen, P. de Leonardis, R. V. Ulijn, J. Gough and N. Tirelli, Soft Matter, 2011, 7, 1732–1740 RSC.
- D. J. Adams, M. F. Butler, W. J. Frith, M. Kirkland, L. Mullen and P. Sanderson, Soft Matter, 2009, 5, 1856–1862 RSC.
- Y. Pocker and E. Green, J. Am. Chem. Soc., 1973, 95, 113–119 CrossRef CAS PubMed.
- E. R. Draper, E. G. B. Eden, T. O. McDonald and D. J. Adams, Nat. Chem., 2015, 7, 848 CrossRef CAS PubMed.
- A. D. Martin, J. P. Wojciechowski, H. Warren, M. in het Panhuis and P. Thordarson, Soft Matter, 2016, 12, 2700–2707 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02430h |
| This journal is © The Royal Society of Chemistry 2019 |