Capturing students’ abstraction while solving organic reaction mechanism problems across a semester
M. L.
Weinrich
and
H.
Sevian
*
Department of Chemistry, University of Massachusetts Boston, Boston, MA 02125, USA. E-mail: hannah.sevian@umb.edu
First published on 10th November 2016
Abstract
Students often struggle with solving mechanism problems in organic chemistry courses. They frequently focus on surface features, have difficulty attributing meaning to symbols, and do not recognize tasks that are different from the exact tasks practiced. To be more successful, students need to be able to extract salient features, map similarities to problems seen previously, and extrapolate while solving problems. In short, students must be able to recognize and generate abstractions. To help students in learning to solve problems, we need a better understanding of the nature of students’ capacity for abstraction. Building upon an exploratory study (Sevian H., Bernholt S., Szteinberg G. A., Auguste S. and Pérez L. C., (2015), Use of representation mapping to capture abstraction in problem solving in different courses in chemistry, Chem. Educ. Res. Pract., 16(3), 429–446), we applied the representation mapping model of Hahn and Chater (1998a) to characterize the abstraction employed by students while solving mechanistic problems in organic chemistry, and to measure students’ growth in abstraction capacity across a semester. This model operationalizes abstraction by considering (a) the ways in which students match existing knowledge to new instances (abstracting) and (b) the level of abstractness of students’ representations. We describe characteristic indicators of abstracting and abstractness. Trends were observable in the abstraction present in the reasoning of successful and unsuccessful problem solvers. Students who proposed plausible solutions used both strict or partial matching, but students who proposed implausible solutions tended to use strict matching. Students who proposed plausible solutions utilized higher levels of abstractness. This indicates that flexibility in abstraction processes may be important to successfully solve problems. The findings have implications for developing instructors’ assessment practices in ways that build students’ abstraction capacity.
Introduction
A frequent refrain of students heard in chemistry courses is, “I didn’t know how to do that exam problem. We’ve never done a problem like this before.” Students often struggle with problem solving that requires them to be able to extract salient features, map similarities to problems seen previously, extrapolate, and make inferences. However, problem solving ability is a crucial component in science, technology, engineering and mathematics (STEM) curricula and a necessary skill in the workforce (Jonassen, 2011a, 2011b). Researchers have explored many different aspects of problem solving ranging from the process of problem solving (e.g.Bodner and Herron, 2002) to characterizing features of problems that affect students’ success in solving problems (e.g.Johnstone, 1993). Domin and Bodner (2012) note that problem solving is often characterized by a dichotomy of algorithmic or conceptual approaches (Stamovlasis et al., 2005), but that additional features are necessary to robustly understand problem solving, such as abstraction in students’ representations.Students’ capacity for abstraction is a vital aspect of problem solving. Although concrete external representations may be useful when solving simple problems, abstractions are essential when the problem at hand is sufficiently complex (Koedinger et al., 2008). Problem solving can be facilitated through abstraction processes, and the ability to use and generate abstractions can be developed through comparisons, generalization, and case-based learning (Gentner and Medina 1998; Gentner et al., 2003; Son et al., 2008). Processes of making comparisons can guide students from concrete to abstract ways of thinking because making comparisons provides a mechanism to promote learning by facilitating abstraction of knowledge that can be applied to new problems (Gentner and Medina, 1998). Rule-based processes (e.g. symbolic statements with logical connectives) have also been argued to play an important role in developing abstraction capacity (Hahn and Chater, 1998a, 1998b).
To understand and enhance students’ capacity for abstraction during problem solving, and to compare abstraction within and across disciplines, a domain-independent method of measuring abstraction is needed, which can be tested and compared across many disciplines. The representation mapping framework of Hahn and Chater (1998a) offers a lens to operationalize abstraction and distinguish among different reasoning approaches by considering (a) the ways in which students match existing knowledge to new instances and (b) the level of abstractness of students’ representations. We have shown that this framework holds promise in measuring abstraction while solving a variety of chemistry problems in different chemistry courses across the undergraduate curriculum (Sevian et al., 2015), and we are currently also investigating the application of this framework in electrical engineering. The present contribution focuses on applying this model to characterizing the abstraction employed by students while solving mechanistic problems in organic chemistry, and measuring students’ growth in abstraction capacity across a semester of organic chemistry.
Research questions
The primary research question investigated in this study is: What are the ways that students approach problem solving in reaction mechanism problems in organic chemistry? Three sub-questions were explored:• How do students use abstraction while solving reaction mechanism problems in organic chemistry?
• Does the use of abstraction change for students across the semester?
• What types of abstraction are used more commonly by successful and unsuccessful problem solvers?
Problem solving in organic chemistry
The approaches students take to problem solving and the reasoning they use during problem solving have been explored for different types of problems in organic chemistry, such as spectroscopy problems (Cartrette and Bodner, 2010), predicting products of chemical reactions, and proposing mechanisms (Kraft et al., 2010). Cartrette and Bodner (2010) found that graduate students who were more successful in solving spectroscopy problems: (1) were more consistent in their approaches to problems, no matter how easy or hard, (2) utilized more of the information that was provided to them, (3) wrote out partial solutions as they solved the problems, and (4) checked their final answers. In contrast, the less successful problem solvers: (1) were less consistent in their approach to problems, (2) tended to focus on just one aspect of a problem in order to devise a solution, (3) did not write out partial solutions as they solved problems, and (4) did not check their final answers. This suggests that the strategies used to problem solve are considerably different for successful and unsuccessful problem solvers. Kraft et al. (2010) found three main reasoning types that students used to solve mechanistic tasks: rule-based, case-based (most frequent), and model-based. Students who used rule-based reasoning tended to be unsuccessful on these problems because, although they used productive rules such as ‘nucleophiles attack electrophiles’, they tended to solve these complex problems by using only a single variable instead of taking a multi-variable problem-solving approach. Students who used case-based reasoning – for example, remembering a specific reaction and attempting to apply it to a problem – tended to be successful because “it allowed the students to reproduce a sequence of events without necessarily understanding any of the intermediate steps or stages” (p. 288). Additionally, the authors found that the small number of students who used model-based reasoning – for example, applying mechanistic models such as SN1 or SN2 – were successful because they were able to break problems down into manageable chunks. Christian and Talanquer (2012) found similar results and used comparable names to describe categories of reasoning.Abstraction in organic chemistry problem solving
In order to solve problems in organic chemistry, experts utilize abstract concepts. Visualizations are used to make abstract concepts concrete by transforming the unobservable into visual symbols (Hinze et al., 2013). When solving problems about reaction mechanisms, experts represent abstract concepts using symbols and formalisms, such as the electron-pushing formalism (Bhattacharyya, 2013). Other researchers have also observed this: “In order for students to be able to draw a correct arrow-pushing mechanism, they must simultaneously keep in the mind an array of chemical principles, many complex and abstract theories, and numerous facts” (Ferguson and Bodner, 2008). However, students often struggle drawing reaction mechanisms because they do not always attribute meaning to the symbols used to represent changes in chemical structure during a reaction. Instead, students take a connect-the-dots or decorating-with-arrows approach to proposing mechanisms (Bhattacharyya and Bodner, 2005; Ferguson and Bodner, 2008; Grove et al., 2012b). They may associate a word or symbol (e.g., NaBH4) with a particular situation (i.e. reduction) and can correctly utilize the word or symbol even when they do not have a robust understanding of the meaning behind it (Ferguson and Bodner, 2008). These verbalisms (“parrot-like repetition of words”) can occur when a concept is detached from students’ concrete experiences and is viewed as excessively abstract (Vygotsky, 1986). When a representation is exceedingly abstract, instead of reasoning with the underlying concept, students begin to “reason with the representation itself” (Strickland et al., 2010). Students’ difficulties with understanding abstract representations in organic chemistry may lead them to make surface-level analogies, which can result in instructors thinking that they approach “similar” problems in inconsistent ways (Bhattacharyya, 2008). Graulich et al. (2012) have shown that high-achieving students (in solving mechanistic problems) are able to make abstractions about six-electron rearrangements by uncovering structural similarities about this type of reaction. Importantly, these students were able to explain the abstractions they used.Students’ struggles and successes may depend on their ability to understand and utilize abstractions. Students often struggle with solving mechanism problems in organic chemistry courses. They frequently focus on surface features, have difficulty attributing meaning to the symbols used, and do not recognize tasks that are different from the exact tasks they practiced. To be more successful, students need to be able to extract salient features, map similarities to problems seen previously, extrapolate, and make inferences while solving problems. In short, students must be able to recognize and generate abstractions. In order to help students in learning to solve problems, we need a better understanding of the nature of students’ use of and capacity for abstraction. To robustly characterize students’ abstraction during problem solving, we employed the representation mapping framework of Hahn and Chater (1998a) to measure abstraction (Sevian et al., 2015).
Representation mapping model
A variety of researchers interested in studying student problem solving have identified diverse approaches that examine how people use their prior understanding when confronting new problems. Many researchers have considered transfer, according to various definitions (Hammer et al., 2005; Schwartz et al., 2005). Other researchers have taken an ethnographic approach to studying what it means to know and practice a discipline (Hall and Stevens, 1995).Hahn and Chater (1998a, 1998b) developed the representation mapping framework to consolidate multiple lines of research on students’ problem solving processes in a comprehensive way. As a result, different frameworks presented in the literature may converge under this model. For example, they explain that analogical reasoning (Seifert, 1989) is arguably similar to two types of reasoning that are explained by the representation mapping model, similarity-based and prototype reasoning. Additionally, representation mapping builds upon the dichotomy of abstract versus concrete representations by considering how representations are matched, and incorporates rules and similarity processes which are not distinguished in typical analyses in transfer experiments (Hahn and Chater, 1998a). While other frameworks, such as mental models (Gentner and Stevens, 1983), may also be used to characterize students’ problem solving in terms of how prior knowledge is used when confronting a new problem, the representation mapping model avoids the assumption of an expert-novice paradigm which views a discipline as a stable body of knowledge (Stevens et al., 2008). Consequently, this framework was selected for its comprehensive nature to capture a diversity of students’ abstraction and cognitive processes and its ability to characterize students’ abstraction in chemistry (Sevian et al., 2015).
The representation mapping model characterizes abstraction by comparing how a student's representations are used in these processes. The model examines reasoning based on the internal representations students use as mental resources (stored knowledge representation) and create (new instance representation) while solving problems. While interacting with a problem, the problem solver starts to view the problem and builds a new instance representation of the problem. Interacting with the problem cues prior knowledge, and from this a stored knowledge representation is formed. The stored knowledge representation and new instance representation interact to arrive at a solution. The two representations are defined as:
• New instance representation: how the student views and approaches the problem at hand.
• Stored knowledge: what resources the student applies to solve the problem.
Representation mapping characterizes the stored knowledge and new instance representations, and then compares the abstraction in using these representations in two ways: (1) the level of abstractness (noun) of each representation, and (2) the action of abstracting (verb) between representations.
Abstractness (noun)
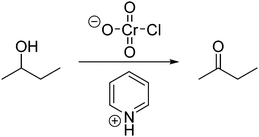
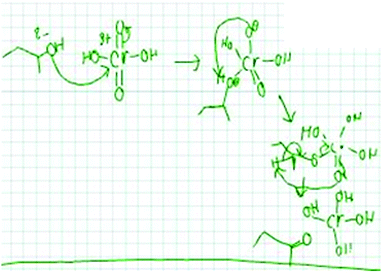
Abstractness (noun) is the degree of abstraction (non-concrete references, additional symbol systems, or underlying relations) present in the way a person imagines a problem (i.e. a representation or mental resource). According to Schwartz (1995), when creating visualizations in biology from textual information, a student's representations were considered abstract if: (1) the visualization was removed from or did not directly portray the surface features of the original text, (2) linkages were made in a general way that connected underlying relations, and (3) the visualization did not specifically refer to the original entity in a concrete way. When predicting the motion of a sequence of gears, representations that involved numerical symbols were considered to have greater abstractness than hand gestures. With the numerical symbols students separated out attributes that were not represented by the concrete hand gestures. Similarly, Domin and Bodner (2012) defined abstractness, while graduate students solved problems about two-dimensional nuclear magnetic resonance spectroscopy, as “a measure of the degree to which the constructed representation incorporates additional symbol systems that were not part of the original presented instructional episode. The presumption is that these elements are prior knowledge contributions from the student's cognitive schema” (p. 838). The representation mapping model compares the relative abstractness of the stored and new instance representations. For example, when asked to propose a mechanism for the problem in Fig. 1, a hypothetical student could say “I need to form a line here and here on this structure and get rid of this OH to get to the product.” This student is talking about very explicit features of the problem, whereas, another student could say “oxygen is electronegative and it's pulling electron density away from this carbon. Maybe I will start by thinking about how the carbon attached to the oxygen could be an electrophile in this reaction.” This second hypothetical student included additional concepts that were not explicitly mentioned in the given problem and instead linked the problem to underlying relations. Thus, the latter hypothetical student utilized representations that were relatively higher in abstractness. | ||
| Fig. 1 Propose a mechanism. | ||
Abstracting (verb)
Abstracting (verb) is the act of abstraction (e.g. simplifying, generalizing, and extracting pertinent information) as an ability. Giunchiglia and Walsh (1992) defined the act of abstraction as ‘‘the process of mapping a representation of a problem onto a new representation’’ (p. 323). This characterizes what is matched between the stored and new instance representations. How the two representations are matched can be strict or partial, according to the representation mapping model (Hahn and Chater, 1998a). To illustrate this with an example (Sevian et al., 2015), an individual could have a new instance representation of new straight-chain carbon compound with a C–C double bond (p. 432) and could match this to stored knowledge in different ways. If the stored knowledge was if the compound has a chain of carbons AND there is a C–C double bond, then it is always an alkene (p. 432), the individual could strictly match the existing knowledge, which was stored as a rule, to the new instance representation. In this case, if the antecedent of the stored rule (chain of carbons and C–C double bond) is satisfied by the new instance representation, then the consequent (it is an alkene) applies to the new instance. Alternatively, if the stored knowledge was a set of past instances with category labels (ethane is called an ‘alkane’ and cyclohexene is called an ‘alkene’), then the new instance representation could be classified as an alkene if the most similar past instance was classified as an alkene. Not all aspects of the stored knowledge instances are the same as those in the new instance, but the aspects considered to be important are most similar. In this case, the individual would be using partial matching.The representation mapping framework provides a possibility space of reasoning types (Table 1) by considering both abstractness and abstracting. In terms of abstracting, when the representations are strictly matched the student could be using either rule-based or memory bank reasoning. When the representations are partially matched, the student could be using prototype or similarity-based reasoning. In terms of abstractness, when a student's representations are both of approximately equal abstractness (either both relatively low or both relatively high) the student could be using similarity-based reasoning (if the representations are partially matched) or memory bank reasoning (if the representations are strictly matched). When one of a student's representations is of greater relative abstractness than the other (stored > new, or new > stored), the student could be using prototype reasoning (if the representations are partially matched) or rule-based reasoning (if the representations are strictly matched).
|
Method
Context and participants
This research was conducted at a medium-sized non-traditional university in the Northeastern United States, where the ethnic diversity of the student body was 38% Caucasian (non-Hispanic), 15% African American, 12% Hispanic, 12% Asian, and 23% from other ethnicities. The professor teaching Organic Chemistry II was recruited via email and volunteered. Student participants in this study were recruited from this Organic Chemistry II course via announcements during lecture and laboratory, and were volunteers. With the professor's consent, students were offered extra credit for participating in the study. Data from a random sample of 20 of the 43 participants (Table 2) were analysed for this contribution. Each student was assigned a random number using a random number generator and the first twenty numbers were selected for analysis, after checking that the selection was representative of the participants in terms of course grade. There was not a significant difference in the final grades for the random sample (M = 81.3, SD = 10.9) and the participants (M = 80.1, SD = 9.9); t(27) = 0.445, p < 0.05. However, there was a significant difference in the final grades of the random sample (M = 81.3, SD = 10.9) and the class (M = 68.5, SD = 24.4); t(67) = 3.57, p < 0.05. The random sample was representative of the students who chose to participate, but was not representative of the class. There appeared to be a smaller proportion of “A” students who participated and none of the students who failed the class participated in this study. The professor was male and had two years of experience teaching. This study was approved by the institution's IRB.| n | Average | St. dev. | Skew | Kurtosis | |
|---|---|---|---|---|---|
| Course | 87 | 68.5 | 24.4 | −1.6 | 1.5 |
| All participants | 43 | 80.1 | 9.90 | −0.6 | 0.1 |
| Random selection | 20 | 81.3 | 11.0 | −0.8 | 0.2 |
Data collection
Semi-structured interviews were conducted to elicit participants’ problem solving while working on problems from their Organic Chemistry II course. The professor was interviewed before two exams (the first and third, of three, exams) and the students were interviewed within the week after each of these exams. A LiveScribe pen was used to associate what the participants drew with what they were saying while they drew. During the interview, the professor was asked to describe the main material he expected students to master in that part of the course. Then he was asked to pick two problems from the exam that he believed could best assess whether a student “got it” as far as the main material was concerned. This was clarified to mean, if he was short of time and had to grade only part of the exam, which problems would best assess the students’ mastery of the material covered? He was asked to show how he expected a proficient student to solve the problem, as well as whether he thought about the problem differently than this. For each of these problems, he was asked to provide another problem that would assess similar content but would not be the same problem or one that students in the course had seen before. Then, he was asked to show how he expected a proficient student to solve each similar problem. Finally, he was asked to provide an alternative problem that was not on the exam, but could have been on the exam, and would assess material that was core to this section of the course. Again, he was asked to show how a proficient student would solve the problem, and to identify any differences in how he thought about the problem. We chose one of the exam problems on which to interview students, based on which problem students had enough time to finish. For this contribution, we analysed students’ approaches only to the mechanism problems proposed by the professor, as we hypothesize that students may have different approaches to different types of questions (e.g. predict the product, mechanism, synthesis, etc.). We are currently preparing an analysis of students’ approaches to multiple different types of problems. Table 3 shows the mechanism problems proposed by the professor for each exam.| Exam 1 | Exam 3 |
|---|---|
|
1A: Exam Problem
Please provide the complete mechanism for the following transformation. |
3A: Exam Problem
Please provide the complete mechanism for the following transformation. |
|
|
|
1B: Similar Problem
Please provide the complete mechanism for the following transformation. |
3B: Similar Problem
Please provide the complete mechanism for the following transformation. |
|
|
During the interviews, students were asked to walk us through how they solved or would solve each of these problems (Table 3). After they described their solution process, they were asked additional questions such as: How did you know to do this step (or idea expressed by student)? How does this compare to other problems you have seen? In what ways is this similar to/different from other problems you have seen? What was the easiest/most difficult part of the problem? We were not necessarily interested in the student's feeling about the problems; rather, this question helped us identify what aspects of solving the problem were the most important to the student. To ensure confidentiality, each student's solution to a problem was assigned a label from 01 to 20 along with an indication of the exam (1 or 3) and problem (A = exam problem, B = similar problem). For example, 05-3B was the fifth student on the third exam for the similar problem. All students were interviewed on their thought process for the exam problem (A) before the similar problem (B) (Sevian et al., 2015).
Data analysis
Audio recordings were transcribed and interviews were coded while the researchers simultaneously viewed the LiveScribe video of the student's drawing and listened to the student's audio. We used the software Dedoose to code and qualitatively analyse the data. The unit of analysis was the solved problems (20 students solved four problems each totalling 80 solved problems). For each student's solution to each problem, we wrote a summary describing the student's solution process. We then applied the representation mapping framework (Hahn and Chater, 1998a; Sevian et al., 2015) to analyse the data. This involved identifying a student's new instance and stored knowledge representations, how these representations were matched (abstracting) and the level of abstractness in each representation. The new instance representation was identified by noticing the cues the student paid attention to in the problem. How the student described the problem was used to characterize the student's new instance representation. The stored knowledge representation was identified by observing the type of information the student drew upon. This representation was characterized based on the student's statements or justifications of facts, relations, or concepts and references made to knowledge learned in the course. We were focused on analysing how the students solve the problems, how they view the problems, and the types of generalizations they make. This was done by determining whether the students were partially or strictly matching their stored knowledge and new instance representations. There were instances where students used both aspects of partial and strict matching. In these cases, when matching was not clear, we disaggregated components of the student's solution process in order to identify the most prominent way of matching representations utilized by the student. The level of abstractness of each of these representations was characterized by paying attention to how far removed the student's representation was from the explicit information in the problems. Additionally, the plausibility of a student's mechanism was characterized based upon the student's written work. This measure was developed to correspond to prospective exam grading, and reflected how likely a student's mechanism might be, how well the drawing followed organic mechanism conventions, and how similar it was to generally accepted proposed mechanisms students learned in their course. Indicators of abstractness, abstracting, and plausibility are described in the Results section. We noticed that a propensity of A problems happened to be better examples to illustrate our findings. All problems had a distribution of reasoning. Thus, this selection is not indicative of differences between problems. One researcher analysed all of the data. For interrater reliability, the other author independently analysed interviews by characterizing a student's new instance and stored knowledge representation and the abstractness and abstracting used by the student to solve a problem. The two researchers discussed their analyses until they were in agreement. This process continued until the researchers agreed on all points of the analysis for a student's solution before discussing them. This was done for 15% of the data.Results
Characterization of students’ abstraction during problem solving hinges on elucidating what their new instance and stored knowledge representations were. The types of cues to which students paid attention and the ways they described the problems allowed us to identify different types of new instance representations. For example, some students noticed specific atoms and connections of atoms in the problems. Others identified specific compounds or categorized part of a molecule based on a functional group name. Some students imagined the structures in these problems and made explicit the charges, electrons, or relative electron density. As students paid attention to cues in the problems, they also drew upon different types of stored knowledge. Some students referred to a familiar compound, a type of reaction they learned in class, or a specific case they saw previously. Some students justified their mechanisms by stating facts, relations, or concepts. Many students described sequences of events, whereas others additionally incorporated information about properties or functions of chemical entities. Once we identified the new instance and stored knowledge representations, we characterized how students matched these representations (abstracting) and the abstractness of their representations.Abstractness
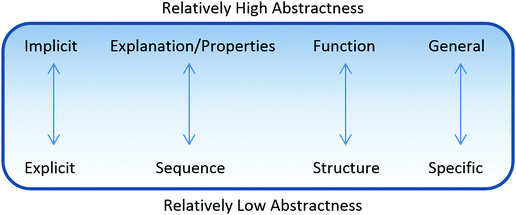
In characterizing the abstractness of students’ representations, we found that students utilized representations with a range of abstractness. Four main types of indicators of abstractness were observed in the data (Fig. 2). One indicator of different levels of abstractness was how removed a student's representation was from the surface features of the problem. Some students focused on very explicit features of the problems while other students incorporated more implicit features as they discussed how they approached a problem. Students’ representations with lower levels of abstractness tended to focus on more explicit features whereas representations with higher levels of abstractness tended to focus on more implicit features. This appeared as a continuum in many cases, rather than as a dichotomy, i.e. some representations contained indicators with both high and low abstractness. Additionally, we found that representations involved a description of the sequence of events (relatively low abstractness) in the mechanism, whereas other representations were based on explanations for why each step could happen (relatively high abstractness). Most representations involved the structure of the molecules within the description of a mechanism (relatively low abstractness), whereas a few representations incorporated the functions of the entities involved (relatively high abstractness). The fourth indicator was whether specific terminology (relatively low abstractness) or more generalized terminology (relatively high abstractness) was utilized. A holistic analysis of all indicators was used to determine whether each of a student's representations was relatively high or relatively low, prioritizing the indicators associated with the main lines of reasoning taken by the student over extra information that the student also noted that was not as relevant to the student's process of solving the problem. It is important to note that the scientific accuracy of the representations was less important than the types of indicators in the assignment of level of abstractness. However, scientific accuracy played some role, for links had to be discerned between features of the problem and abstractness that students included in their representations. | ||
| Fig. 2 Indicators of relatively high and low levels of abstractness identified in the data. | ||
13_1B: I'm just, well I assume this is going to connect to the double somehow and then it's gonna probably get this hydrogen is probably going to get deprotonated by the pyridine,
Interviewer: Write here
13_1B: Oh yeah I know, so I assume something like you know, let's see probably something to the effect of, well I mean I don't, this might hit this and pop off and then maybe, so that'll go back and, which is back? This might go back and so would probably be something like that, this would knock off the Cl and not the OH. [drawing in Fig. 3]
 | ||
| Fig. 3 Student 13's written response to exam 1 problem B. | ||
The new instance representation in this example was intertwined with the student's stored knowledge representation. He noticed in this problem the presence of a double bond, that connections could be made, and that pyridine was present along with a Cl and OH. In his new instance, he focused on features that were explicitly written in the problem (double bond, Cl, OH, etc.). The stored knowledge representation included what pyridine was and that the Cl gets knocked off instead of OH. Again, the way he indicated his stored knowledge relied on the explicit features of the problem. This solution was coded as having relatively equal levels of abstractness in the student's new instance and stored knowledge representations, which both had relatively low levels of abstractness.
In contrast, a different student started by making implicit features of an exam problem explicit:
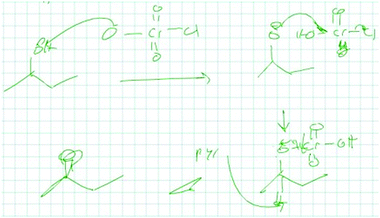
07_1A: Okay I'll do it out. So here I have this starting material that I drew in with the electron pairs. So I had these electron pairs come and attack this Cr because that's gonna have the delta positive because of all the oxygens around it pulling the electron density away. [drawing in Fig. 4]
 | ||
| Fig. 4 Student 7's written response to exam 1 problem A. | ||
Student 7's first step was to draw out the structure while incorporating implicit aspects of the structure not shown in the problem. Her new instance representation involved redrawing the starting material while noticing, and making explicit, aspects that were implicitly represented in the problem, such as electron pairs, a delta-positive charge, and that there was an entity present pulling electron density away. This demonstrated a relatively high level of abstractness. Her stored knowledge representation contained relatively equal abstractness as her new instance representation. While solving this problem, Student 7's stored knowledge was intertwined with her new instance representation and involved drawing electron pairs to make explicit the charge density features, and the idea that oxygen pulls electron density away from Cr leaving a partial positive charge at Cr. Throughout the data, we observed representations to occur on a continuum of focusing on more explicit aspects of the problem (like 13_1B) to more implicit aspects (like 7_1A).
14_3A: I know with, what is it? a ketone, when you add a peroxy acid you basically just insert the O in the alpha like in the place of the alpha carbon, the oxygen and then I just looked at the substitution that carbon is what? secondary this one's tertiary one two three yea so I knew it would go on the tertiary side just like that so that made sense …. then you know for the mechanism …. I mean this is mostly just memorization in the chapter most of the stuff attacks that carbon double bond to the oxygen so the first step is pretty easy …. yea and then the rest, after that, it just made sense to me after I looked at the mechanism a few times because this is positive so I knew this changed … you know there's a hydride shift I think that's how [prof name] did it, the book did little bit differently … but yea … I mean I knew basically the positive charge had to switch from here to here cause this was going to leave so, yea this mechanism wasn't that tough for me, especially compare to more complicated mechanisms in the chapter, but yea, I just knew basically that there was the … the carbon shift over to the O to get it inserted to get the oxygen inserted there … so yea… [drawing in Fig. 5]
 | ||
| Fig. 5 Student 14's written response to exam 3 problem A. | ||
Student 14 paid attention to the substitution, bonding patterns, and charge. Although there are other aspects of this student's representations that were of relatively higher abstractness, in his new instance representation he focused on structural aspects with relatively low abstractness. He described changes in the structures of the compounds, such as where the O would be inserted, and not how entities functioned in the reaction. In contrast, the following excerpt illustrates an approach to a problem on the first exam:
03_1A: I just observed that this is an oxygen, so clearly it has a partial negative charge, you know it's nice and electronegative and this chromium which probably isn't very electronegative to begin with at all has four oxygens on it so it is very very very like positive you know so I just figured that like if anything going to happen, this would you know donate some electron density there [drawing in Fig. 6]
 | ||
| Fig. 6 Student 3's written response to exam 1 problem A. | ||
Student 3 discussed the structure of the entities involved, but he did so in order to think about the function of donating electron density. Discussing the mechanism in a functional way was considered as an indicator of relatively high abstractness.
These were the most prevalent indicators of abstractness identified in this sample of students’ solved problems. In general, while some representations had indicators of relatively low and high levels of abstractness, we coded each representation as either high or low abstractness in order to represent the student's overall solution process on the problem. To do this, we paid particular attention to the aspects of the solution process that the student emphasized while solving the problem.
First, information about a student's stored knowledge representation was nearly always more plentiful in the interviews than information about the new instance representation. Thus, there was a continuum of how much information was there in order to make an assessment of the degree of abstractness of each representation. For example, when Student 18 solved problem 3B (Fig. 7), he redrew the starting material, noted a rule (the most substituted carbon is more likely to move, and it has to do with energy), described a mechanism guided by electrons and their “wants”, and then explained that he could use a rule about which groups move in practice problems he had done with different R structures (he mentioned a ketone, a methyl, and a phenyl). In this description, only the first aspect of the narrative (redrawing the starting material) and the functional groups identified in the last point (ketone, methyl, and phenyl) belong to the new instance representation. These are both categorized as relatively high abstractness because the student focuses on implicit features and generalized terminology. All the other pieces of what the student said belong to the stored knowledge representation, in which he demonstrated relatively high abstractness in terms of how he considered mechanisms (electrons and their “wants”), and generalized rather than specific ideas (generalized mechanism applied to a ketone and guided by electron density).
 | ||
| Fig. 7 Student 18's written response to exam 3 problem B. | ||
Second, in some cases (28 of the 80 solved problems, or 35% of the time), the solutions presented by students contained stored knowledge or new instance representations with greater abstractness in some indicators and less abstractness in other indicators. The frequency with which this occurred across the four types of reasoning (Table 1) did not differ from the frequency with which it did not occur. A chi-squared test of independence was performed to examine the relationship between type of reasoning and whether there appeared a continuum in degrees of abstractness in either representation. The relation was not significant, χ2(2, N = 80) = 5.08, p = 0.166.
In all cases in which this type of continuum occurred, the indicator that had different abstractness than the overall assessment of abstractness of the representation was more extraneous to the student's main line of reasoning in the problem. For example, consider how Student 17 solved problem 3B:
17_3B: yea, it's just easy to see what goes where, I mean that's the way he taught it to us, I mean it kind of makes it a little bit easier, if we didn't need to do the mechanism part, I mean just leave it like that we would know… the lone pairs attack that ketone which that pops out and goes up makes this O minus, and then you get the same thing you get the hydride shift because that H, that O doesn't want to be positive, so then this bond goes to here, that oxygen, that bond between the two oxygens breaks off.
Interviewer: so how do you know that that one, how do you know which ones?
17_3B: because it's more, it's a better attacking group I believe, that's what they use it for, it's more substituted, it's benzylic, its benzene ring, let me draw this… so you still have that minus charge here, all these electrons, one of these pair of electrons go down… yea ok so once this negative charge, the electrons go down forms a double bond O and then you get your final product right there.
This student's stored knowledge representation included high abstractness in how he thought about the mechanism (arrows show both where the electrons move, but also where the atoms go) and in considering that this problem fit a general mechanism. However, he also paid attention to symbols and structure more than function (less abstractness in this indicator). Since the crux of his reasoning was identifying the best attacking group in a Baeyer Villiger mechanism, his stored knowledge representation was assessed as high abstractness due to the abstractness in the explanation/properties vs. sequence indicator.
Abstracting
Following the results on abstractness of students’ representations, we now consider how students matched their representations, or their abstracting. Abstracting, in the representation mapping model, is the actions taken when matching the new instance representation to the stored knowledge representation. This matching can be ether partial or strict. The different ways in which the representations were partially or strictly matched by students in our sample are summarized in Table 4. We discuss the typical abstraction demonstrated, in terms of abstractness of representations and actions of abstracting (strict or partial matching) in each of the quadrants of the representation mapping model (Table 1).| Partial matching | Strict matching |
|---|---|
| Partial matching of stored and new instance representations involved arguing on a general level and removing particulars from a problem to compare to previous experiences in a partial way. Students often started problems by identifying the type of problem present and recognizing that problem as fitting a particular template. Alternatively, students built new knowledge or relations in the absence of recalled information by extracting relevant features. Student also based their reasoning on similar cases by identifying underlying patterns. | Strict matching of stored and new instance representations involved comparing the problem to previous problems strictly by making one-to-one matches of representations. Students often modified problems to make the problem visually match the way they were accustomed to seeing it. Students tended to focus on remembering steps they needed to perform. Students also seemed to scan through a mental list for a procedure or solution that directly applied to the problem at hand and adjusted the mechanism toobey a rule. |
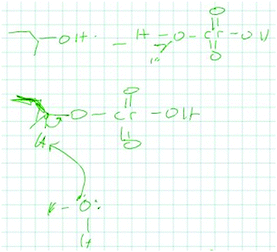
13_1A: the Jones reagent right, mechanisms I, for the mechanism there's a picture in the book, and really the way I did it was just I remembered the picture basically, well obviously, but I couldn't quite remember how the hydrogens hold on let me just draw this out, so I just remember the hydrogens this OH gets knocked off I think here and which, yeah. I just remember that was the first image I remember and like I said I forget how this the OH comes off, probably protonated and then comes off and maybe this attacks, I don't quite remember. [drawing in Fig. 8]
 | ||
| Fig. 8 Student 13's written response to exam 1 problem A. | ||
Student 13 remembered a picture from the book from his stored knowledge and strictly applied it to the problem at hand to describe a sequence of events. He attempted to pair one-to-one his solution to this problem and what he remembered seeing but he questioned whether or not he recalled the picture correctly. He focused on the movement of atoms (OH gets knocked off, this attacks) and on describing the steps he needed to perform. He was directly applying a memorized sequence of events and was not storing or searching for a more generalized representation of the problem. He got stuck because he could not quite remember the sequence of events from his picture in the book. Based on strictly matching his stored and new instance representations, this student could be using either memory-bank or rule-based reasoning. However, both his new instance and stored knowledge were relatively low in abstractness since he focused on explicit features of the problem such as the types of atoms involved based explicit features he remembered from his picture of the book. Thus, this student utilized memory bank reasoning.
Memory bank reasoning occurs when both of the representations are either relatively low, or both are relatively high in abstractness. Among the problems in which memory bank reasoning was used in this sample, low–low abstractness representations were used in 68% of the cases, and high–high were used in 32%. In most cases, students using representations that both had low levels of abstractness primarily concentrated on describing the sequence of a mechanism and cueing on structural features of molecules. For example, solutions of problem 1A involved describing sequences of steps (06_1A: So from here I had the oxygen attack the chromine and then the oxygen double bond goes up). In contrast, in cases where both representations had high levels of abstractness, students’ memory bank reasoning tended to emphasize generalized ideas over specific terminology. For example, cases of high–high abstractness in memory bank reasoning included seeing problem 1A as belonging to a generalized mechanism for a Jones reaction (20_1A: And it's different enough where we're used to seeing the chromium or the Jones as a little bit different where he throws the chlorine in there), or noticing that problem 3A was a general mechanism of a nucleophile attacking a partial positive charge (12_3A: so I drawed the structure of the reagent and then what I did was make a nucleophile attack at the most partial positive portion of the compound).
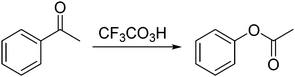
04_3A: I actually got caught on this problem in the first place because when I was looking at the reagents they were using, CF3CO3H so I was blanking on which one it was; I was thinking it looks like the Wittiger reaction, because the way I was thinking… not the Wittiger the Witting reaction, that's how you say his name and I kind of remember it being from yea I do little tricks and the name itself has like three letter t's so I think of the three oxygens that are in there [drawing in Fig. 9]
 | ||
| Fig. 9 Student 4's written response to exam 3 problem A. | ||
This student searched for a procedure or solution to apply to the problem at hand. Her prior knowledge was stored as a rule (if three oxygens are present in the reagent then it is a Wittig reaction). She recognized that a category (Wittig) applied to the problem because the antecedent of a rule was satisfied (three oxygens were present in CF3CO3H). This strict matching of representation was considered rule-based reasoning (as opposed to memory bank reasoning) because the stored knowledge representation (the rule) was relatively higher in abstractness than the new instance representation (noticing three oxygens were present).
Rule-based reasoning can occur when the new instance has higher abstractness than the stored knowledge representation, or vice versa. Of the 19 cases of rule-based reasoning in the sample, only in 4 of these did the former situation (new > stored) occur, and all of these occurred on problems 1A and 1B. In addition, in all four cases, there was some aspect of continuum to the student's explanation, and none of the problems were solved in fully plausible ways (this is discussed later). These four cases all involved a student generating greater abstractness in order to solve the problem. For example, in solving problem 1B, Student 19 used her knowledge of charges to reason through the mechanism (19_1B: I started by the negative charge on oxygen to get the hydrogen, and then bringing that to the other oxygen) and later (19_1B: what I want to do is move the electron down, but I don’t know if that's right). She attempted several strategies and she eventually categorized this as an elimination mechanism (19_1B: I want to make this chlorine go away… and I’d have this chlorine attack this hydrogen to do an elimination and make this leave…).
In the following case of similarity-based reasoning, the student struggled with problem 1A during the exam and did not feel that he knew where to go. In the absence of knowing exactly how to draw the mechanism he did the following:
03_1A: I just observed that this is an oxygen, so clearly it has a partial negative charge, you know it's nice and electronegative and this chromium which probably isn't very electronegative to begin with at all has four oxygens on it so it is very very very like positive you know so I just figured that like if anything going to happen, this would you know donate some electron density there […] I did not really know where to go, so I was just trying to find the most quickest way to get to the carbonyl […] I just need to find some way to do like the elimination to get the double bond there [drawing in Fig. 6]
Student 3 tried to remember a mechanism but could not recall it. Instead, he tried to reason through the problem based on stored knowledge about relative electron density and interactions between molecules in general. This student was extracting and focusing on key features of the problem and partially matching his stored knowledge to this problem. By partially matching representations he could be using similarity-based or prototype reasoning. In this case, both the stored knowledge and new instance representations were relatively high in abstractness. Thus, this student utilized similarity-based reasoning.
17_1A: I was doing the PCC mechanism and it's similar to this, instead of the… one of the hydrogens on the, actually… I think there were two hydrogens on the alcohol group at one point and one of the hydrogens snaps down to form the double bond and then that bond between the oxygen and the chromium goes to the chromium [drawing in Fig. 10]
 | ||
| Fig. 10 Student 17's written response to exam 1 problem A. | ||
Student 17 used the PCC (pyridinium chlorochromate) mechanism as a category from his stored knowledge that he could select particular features from as a specific example to apply to the problem at hand. He identified a pattern and utilized a similar case as an example to approach this problem. Based on his partial matching of representations this student used either similarity-based or prototype reasoning. Since this student's stored knowledge was relatively higher in abstractness than his new instance, he was using prototype reasoning. He used his stored knowledge about the PCC mechanism as a prototype for the reaction at hand.
Patterns
The reasoning processes used by the 20 students in all four problems are shown in Table 5. To solve these problems, students used memory-bank, rule-based, and similarity-based reasoning relatively equally, but prototype reasoning occurred infrequently. Students used strict matching (59%) more often than partial matching (41%). In terms of the abstractness of students’ representations, there were 22 instances (28%) in which both of the student's representations (stored knowledge and new instance) were relatively low in abstractness, 28 instances (35%) in which one representation was of higher abstractness than the other, and 30 instances (37%) in which both representations were relatively high.| Abstractness | Abstracting | |
|---|---|---|
| Partial | Strict | |
| Diff | Prototype 9 (11%) | Rule-based 19 (24%) |
| Same | Similarity-based 24 (30%) | Memory bank 28 (35%) |
Overall, across the semester these students used strict and partial matching relatively equally between the first exam and the third exam (Fig. 11). However, there appeared to be an increase in the level of abstractness of students’ representations from the first to the third exam (Fig. 12 and Table 6). As shown in Table 6, and discussed earlier in the section on Abstractness, cases of new > stored abstractness in representations was only observed on problems 1A and 1B. There appeared to be greater reliance on memory bank reasoning in problem 1B than in the other problems, but other than this, types of reasoning were fairly evenly used across all the problems. Other researchers have demonstrated that the type of problem may influence how students reason (Grove et al., 2012a), thus it is reasonable to speculate that this may be relevant here as well. Since there were only four different problems in this study, we refrain from analysing ways that the type of problem may have played a role in influencing students’ reasoning; however, this will be explored considerably in our next paper where we analyse many more problems. Thus, we now move from considering the unit of analysis as the solved problem (n = 80) to considering students (N = 20) as the unit of analysis.
 | ||
| Fig. 11 Frequency of types of abstracting (strict and partial matching of representations) in the exam 1 and exam 3 interviews. | ||
 | ||
| Fig. 12 Frequency of levels of abstractness (stored and new instance representations relatively low in abstractness, L/L; stored knowledge representation greater or less abstractness than the new instance representation, S><N; stored and new instance representations relatively high in abstractness, H/H) in the exam 1 and exam 3 interviews. | ||
| Problem | Strict matching | Partial matching | Plausibility (same order as the four reasoning types) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Memory bank | Rule-based | Similarity-based | Prototype | ||||||||
| Low-low | High-high | S > N | N > S | Low-low | High-high | S > N | N > S | Plausible | Partially plausible | Implausible | |
| 1A | 5 | 3 | 2 | 2 | 1 | 5 | 1 | 1 | 5|1|6|0 | 1|0|0|0 | 2|3|0|2 |
| 1B | 10 | 1 | 1 | 2 | 2 | 3 | 1 | 0 | 0|0|2|0 | 1|3|1|1 | 10|0|2|0 |
| 3A | 2 | 3 | 6 | 0 | 0 | 6 | 3 | 0 | 2|3|5|3 | 1|3|1|0 | 2|3|0|0 |
| 3B | 2 | 2 | 6 | 0 | 0 | 7 | 3 | 0 | 2|2|5|3 | 1|1|0|0 | 1|3|2|0 |
Individual students across the semester
Individual students changed the way they matched their representations (partially or strictly) across the semester. Most students changed the type of matching they used (13) and some stayed the same (7). Overall, individual students relatively equally moved toward using more partial matching or more strict matching. Across the semester, about half (11) of the students continued to use or switched to using more partial matching, and the others (9) continued to use or switched to using more strict matching. For example, a student who strictly matched her stored knowledge and new instance representations on problem 1A, but partially matched her stored and new instance representations for problems 1B, 3A, and 3B was tallied as moving toward partial matching.For the abstractness of individual students’ representations, many students (14) increased the level of abstractness of their representations between the first and third exams. Three students stayed at the same level of abstractness. Only a few students (3) decreased in abstractness across the two exams.
Plausibility
Students used different types of abstracting between representations (Fig. 13) and had different abstractness of their representations (Fig. 14) when they proposed plausible, partially plausible, or implausible mechanisms. Students who proposed plausible mechanisms tended to use strict or partial matching equally well, but students who proposed implausible mechanisms tended to use strict matching. Students who proposed plausible mechanisms tended to utilize higher levels of abstractness in their representations than students who proposed implausible mechanisms. | ||
| Fig. 13 Percentage of types of abstracting (strict and partial matching of representations) for instances of implausible, partially plausible, and plausible drawn mechanisms. | ||
 | ||
| Fig. 14 Percentage of levels of abstractness (stored and new instance representations relatively low in abstractness, L/L; stored knowledge representation greater or less abstractness than the new instance representation, S><N; stored and new instance representations relatively high in abstractness, H/H) for instances of implausible, partially plausible, and plausible drawn mechanisms. | ||
Abstraction trends
Two major themes emerged from the data in terms of levels of abstractness across the semester and trends of reasoning associated with plausibility of students’ mechanism.13_1A: Okay so for this, the Jones reagent right, mechanisms I, for the mechanism there's a picture in the book, and really the way I did it was just I remembered the picture basically, well obviously, but I couldn't quite remember how the hydrogens hold on let me just draw this out, so I just remember the hydrogens this OH gets knocked off I think here and which, yeah. I just remember that was the first image I remember and like I said I forget how this the OH comes off, probably protonated and then comes off and maybe this attacks, I don't quite remember. But then I do remember this there's the H here, so then I had this, what was it, was that how I did it? I think so yeah, and it would attack the proton in this, is that how it works? I think that's possibly how I did it and then this forms the ketone and kicks the Cr the Cr off, like I said I just from basic, it was just basic mechanism and mostly remembering the picture, which kind of a cheat way to do it, but you know I guess yeah. [continued by saying he panicked and messed up the test] [drawing in Fig. 8]
In Student 13's new instance representation, he identified that the Jones reagent was present. He focused on the explicit symbols of the atoms in this problem and described a sequence of events. His stored knowledge representation was a picture he recalled seeing in a book. Again, he tended to focus on explicit features of the problem (OH, H, Cr) while describing the sequence of events he recalled seeing in the book's picture. Although he used some general terminology (ketone), overall he utilized a relatively low level of abstractness for both his stored and new instance representations. In terms of abstracting, he strictly matched his stored knowledge representation to his new instance representation for this problem. However, on the third exam he began to incorporate higher levels of abstractness. The following quotation is his explanation of his process for solving the exam 3 problem:
13_3A: okay, so it just … you see the peroxy acid so it is Baeyer Villiger … so the Baeyer Villiger what I remember is it is just a shift … a shift of whatever is the best migratory group … so it is going to be the methyl here … so then it just a matter of … you know … remembering what the mechanism is you know these mechanisms are just you know you just have to memorize them that's it there is not a lot of thought for them so … fortunately, I remembered the mechanism and so anyway … just do all the problems … so, I think for this mechanism it is important to just draw the peroxy acid like you know adjacent to it in the appropriate manner makes it easier to do the mechanism so … the OH on the end there attacks the carbonyl, pops it up so … I actually did the same thing that I did on the test … sorry … it is actually a minus … so now they are connected … I think you should draw the H on top cause it is going to shift in a second and … so it's even more confusing if you turn it the other way but anyway … I think this is the shift here … this mechanism is almost screwed up here anyway, so it hydrogen shifts to the other carbonyl that is going to make way for the … carboxylic acid to pop up … but anyway I did actually the same thing here if you see I because you've got to use the methyl shift over here so like it's harder to do it if it's on the opposite side so I just kind of reversed it over there … so I knew it was there but I just did not remembered to appropriately place it until I actually went through it.
Interviewer: and then can you describe to me that appropriate placement so why does it need to be redrawn?
13_3A: so I think the right order is hydrogen, tertiary, secondary, and phenyl and then primary and then methyl so I think this is could be secondary so like it just this left side is going to shift and so you need to kind of flipped to make it little more clear I think so then you just do the negative charge comes back and forces the shift, forces the break at the cleavage between the two oxygens and this kicks everything back up and so… that's a messed up ring but whatever…
Interviewer: cool, so can you describe to me why you did this step, the first step?
13_3A: the first step, it's just the OH nucleophilic attacks the ring kind of like you know part of this chapter in the beginning is the acetyl formation it is kind … it is not …. this would be positive […] [drawing in Fig. 15]
 | ||
| Fig. 15 Student 13's written response to exam 3 problem A. | ||
In his new instance representation, he began the problem by seeing a more general category (that a peroxy acid was present) and identified that this problem was a Baeyer Villiger reaction. He stated that his process was just a matter of remembering the mechanism by memorizing it and that there was not a lot of thought involved, but luckily he remembered this mechanism. He described some parts of the sequence of the mechanism, including both explicit features and general categories (OH on the end attacks the carbonyl). It was important for him to draw the structure in the orientation he had seen it before (strict matching). He remembered in his stored knowledge the “right” order of which groups shift (hydrogen, tertiary, secondary, phenyl, primary, then methyl), and in his new instance representation he identified that there was a secondary group that would shift. When describing the group shifting, he thought about more implicit features (negative charge). When asked to describe his reasoning for the first step, he then continued by extracting and focusing on key features and argued on general level (nucleophilic attack, acetyl formation). In both his stored and new instance representations, he utilized more general terminology and implicit features (peroxy acid, carbonyl, carboxylic acid, charge, nucleophile, acetyl formation). Although he mainly focused on describing a sequence of events, he was also able to incorporate some explanation utilizing the properties of the entities involved (first step happened because OH is nucleophilic). Holistically, we coded this student as utilizing a high level of abstractness for both his new instance and stored knowledge representations.
In terms of abstracting, his reasoning included some instances of partial matching, but also instances of strict matching. Strictly drawing the structure in the way he had seen it before seemed more important in his solution process than identifying the general category of acetyl formation. Although this was borderline, we coded this student as utilizing strict matching for this problem because the strict matching occurred in the dominant part of his reasoning.
02_3A: okay… so…the most impressing stuff for me is about this reagent… and I remember the professor said the second one and this one break to here …
Interviewer: so, does drawing the reagent out help you for anything?
02_3A: yea…it help a lot because it shows how it breaks and how arrangement and which oxygen will attack to the original one… that's how I got for the attack… I remember […]
Interviewer: how do you know that these were the right steps to take to solve this problem?
02_3A: I just memorized it…like…
Interviewer: so, what do you memorize?
02_3A: because I watched this video, the lecture again before the exam, like about two, three hours ago… and because I know with this stuff the one I really do not get it … so just memorized it…
Interviewer: okay so, you didn’t understand it but you memorized it or?
02_3A: I mean, I understand how it works but I do not know why like this one will attach here and I do not know why this will break and attach here… [drawing in Fig. 16]
 | ||
| Fig. 16 Student 2's written response to exam 3 problem A. | ||
Several aspects of Student 2's drawing indicated an implausible mechanism. The student's interpretation of the chemical formula for CF3CO3H was an unlikely arrangement of atoms that the professor did not intend the student to draw. Additionally, the student drew curved arrows showing where atoms would end up. These did not represent a likely flow of electrons, as he drew an arrow pointing to the bond that the oxygen ends up in between instead of an area with less electron density. When talking through his thinking, the student demonstrated low abstractness for both his stored and new instance representations and utilized strict matching. He started by drawing what he remembered about the reagent. He knew which steps to take in drawing the mechanism because he had memorized them. He focused on discussing explicit features of the mechanism. He also explicitly stated that in his approach he did not know why the steps happen in the mechanism.
In contrast, students who drew plausible mechanisms tended to utilize partial matching (58%) and high levels of abstractness (55% high/high, 39% S><N, 6% low/low) more often than students who drew implausible mechanisms (Fig. 12 and 13). For example, the following student drew a plausible mechanism and demonstrated partial matching and high levels of abstractness in both of his representations:
01_3A: the first thing I looked at was the presence of a ketone and then I looked at the reagent. I recognized immediately that the reagent was a peroxyacid and those are used either to make an epoxide or to also perform a Baeyer Villiger reaction so given that you can't epoxidize this moiety I decided to go with the Baeyer Villiger since that's what we've also been tested on as well, or what we were going to be tested on… and then the mechanism is honestly through practice and through rehearsal is how I did this actually, I know the, this OH actually comes in and attacks the ketone affording you this and then once the lone pairs from the ketone kick back down it actually migrates the more stably formed, I guess you could say, carbocation and then migrates that onto the oxygen and then everything else is a cascade and everything just shifts, follows through with all these arrows
Interviewer: so all this migration going on
01_3A: yea just the migration of electrons and then from there I just got that and then also your by product, and that's how I solved that [drawing in Fig. 17]
 | ||
| Fig. 17 Student 1's written response to exam 3 problem A. | ||
Student 1 drew a plausible mechanism which contained structures and curved arrows in a way that followed the convention of representing where electron density could move during the reaction. While discussing his reasoning in solving the problem, he demonstrated partial matching by fitting this scenario to a pre-existing template while letting the other features of the problem fall away. Both his stored knowledge and new instance representations were of high abstractness, as he utilized generalized terminology (peroxyacid, epoxide, ketone), focused on implicit features (lone pairs, migration of electrons), and incorporated an explanation (more stable).
While Student 1 demonstrated similarity-based reasoning, other types of reasoning were also associated with drawing plausible mechanisms. Another student who drew a plausible mechanism instead utilized strict matching:
09_3A: I had studied this question like this mechanism before I came so I actually knew what was going to happen …so and I remembered before the class started when he was teaching this mechanism he said that for like when you have a molecule like this one that the end result will always be that the oxygen will be in between the side with the more substituted carbon… yea …so I knew that the oxygen had to be between this the second … no is it the tertiary carbon and the secondary carbon towards the ketone […] he had given us the product already …just like I thought it would be so the oxygen in between where I expected it to be …. so I remember that the alcohol at the end of the reagent is going to attack the ketone …and so it did … so when the oxygen on the alcohol attacked the ketone of course this breaks the carbon octet rule and then it will push up the electrons towards the oxygen on the ketone to cause a negative charge… and so it will have a negative charge… and the oxygen will also get a positive charge because it has more than it wants to have … and so it will be connected like that … and then I know that there will be a hydrogen shift … towards the ketone from the nucleophile… electrophile I confuse the two … but the reagent and then so once the proton shift happens there'll be a rearrangement and the oxygen oxygen bond will break and towards the oxygen and this will pull up the electrons because it does it has more than it wants to and it wants to have just two, two bonds …and then there will be rearrangement to bring in the oxygen to where it is supposed to end up … and then everything will be back to normal … will be stable again … so that's how I thought of this question [drawing in Fig. 18]
 | ||
| Fig. 18 Student 9's written response to exam 3 problem A. | ||
Student 9 saw this question and recognized that she had studied it. She then directly applied steps for this mechanism in the way they “always” happen. She strictly matched her stored knowledge to this problem but was able to draw a plausible mechanism. Thus, although students who drew implausible mechanisms tended to use strict matching, use of strict matching does not seem to hinder the ability to draw a plausible mechanism. It may be the case that proficient students (students who can draw a plausible mechanism) have learned when different types of reasoning may be appropriate. It may be faster to strictly match a new problem to one's stored knowledge in some instances, while for other problems a more general way of thinking (similarity-based) may be needed. However, plausibility was only determined based on what the student drew. The way this student talked through her solution process uncovered limitations in the proficiency of this student (alcohol instead of hydroxyl or peroxy acid attacked the ketone, confusion about electrophiles and nucleophiles, electrons move because of the wants of molecules). Thus, it may also be the case that students using strict matching may be able to draw a plausible mechanism but have underlying limitations with their conceptual understanding. However, there were not enough examples of this in our data to be able to draw generalizations.
Discussion and conclusions
In our exploratory study (Sevian et al., 2015) which applied the representation mapping framework of Hahn and Chater (1998a) to characterize students’ reasoning processes and the types of abstraction that students use, we presented a big-picture goal of separating the supply of abstraction presented by students from the demand for abstraction presented by problems, in order to better understand how students’ abstraction capacity builds across an entire undergraduate STEM curriculum. This paper addresses the supply problem. Applying the representation mapping model, we uncovered students’ stored knowledge and new instance representations, characterized the degree of abstractness in students’ representations, and examined how students matched their representations (abstracting) while solving reaction mechanism problems in organic chemistry. Based on our analysis, we make three main claims about abstraction in problem solving and compare these to other studies with which there is overlap. Next, we describe a limitation of the representation mapping model, and finally we consider implications of our findings.Claim 1
There are four major dimensions in which abstractness of both stored knowledge and new instance representations can be characterized (see Fig. 2 ). These were explicit vs. implicit features of the problem in the representation, sequence of events vs. explanation of properties, structure vs. function, and specific vs. generalized terminology. Similar to the results of Anzovino and Bretz (2015), most students in our study focused on the structure of the chemical entities involved and not on describing the function of these entities while reasoning through the mechanisms. Students tended to focus on describing the sequence of the mechanism and seemed to conceptualize a mechanism as a movement of symbols (Bodner and Domin, 2000; Bhattacharyya and Bodner, 2005; Ferguson and Bodner, 2008; Grove et al., 2012b). Similar to the study by Graulich et al. (2012), we found that students who drew plausible mechanisms (high achieving students) were able to explain the meaning behind the abstractions they used. Within some types of reasoning, we also found characteristic reliance on specific dimensions. In particular, when students utilized rule-based reasoning, they tended to have stored knowledge representations with higher abstractness mainly considered as explanation of properties (e.g., how a mechanism occurs) matched to new instance representations with lower abstractness mainly considering structural features of molecules (e.g., noticing atoms and combinations rather than functional groups that tend to have consistent properties).Claim 2
The abstractness of students’ representations tends to increase across a semester in particular ways. While students’ capacity for abstraction should increase as learning happens, our analysis uncovered particular trends in the ways it increases. The type of abstracting (strict or partial) changed slightly from use of partial matching 35% of the time in problems 1A and 1B, to use of partial matching 48% of the time in problems 3A and 3B (see Fig. 11). Although the four reasoning types described by the representation mapping model do not fit one-to-one with the reasoning patterns described by Kraft et al. (2010) and Christian and Talanquer (2012), this model allows for a characterization of students’ abstraction processes. The major change that occurred across the semester was from memory bank reasoning (with mainly low levels of abstractness in both representations) to the other three types of reasoning (see Table 6). Secondarily, there were changes in similarity-based reasoning from low–low to high–high abstractness in the representations. Both of these trends could be explained, in part, by students building clearer differentiation between categories of reaction mechanisms. Another change that occurred across the semester was in the direction of difference in representation abstractness in rule-based and prototype reasoning. As we noted previously (Sevian et al., 2015), the rule-based reasoning described in earlier studies (Kraft et al., 2010; Christian and Talanquer, 2012) corresponds to stored > new abstractness in representations in the representation mapping model. Also, the model-based reasoning in Kraft et al. (2010) seems to correspond to new > stored, while model-based reasoning in Christian and Talanquer (2012) seems to be stored > new. We speculated that both of these correspond to prototype reasoning in the representation mapping model. On exam 1 problems, half of the cases of rule-based and prototype reasoning had new > stored, while on exam 3 problems none of them did (they were all stored > new). Considering our cases of prototype reasoning, students either (a) compared specific cases in order to generalize across cases and derived a functional or conceptual relation [new > stored] or (b) selected and applied particular features of a general category as a specific example to the problem at hand [stored > new]. In the former situation (new > stored), it may be the case that such a process of generating abstractness in a representation occurs during learning. However, exams usually are not designed as learning opportunities (though if they are, they may tend to occur earlier in the course when students have more to figure out about how to study for exams) so perhaps this is why prototype reasoning was observed less often, and why new > stored disappeared on exam 3 problems.Claim 3
The ability to use partial matching seems to accompany having more plausible solutions. Trends were observable in the types of reasoning processes and abstraction used by successful and unsuccessful problem solvers in this study. Students who proposed plausible solutions used both strict and partial matching, but students who proposed implausible solutions were more likely to use strict matching (see Fig. 13). Students who proposed plausible solutions utilized higher levels of abstractness in their representations than students who proposed implausible solutions (see Fig. 14). Perhaps a proficient student (i.e. one who draws plausible mechanisms) has learned when different types of reasoning may be appropriate and is able to flexibly utilize different types of abstraction depending on the demands of a problem. These trends suggest that the representation mapping model is able to be used to track changes in abstraction capacity of students over time. Our next steps include tracking a cohort of students across several courses in the undergraduate curriculum.Limitations
The representation mapping model is not comprehensive. The originators of this model predicted that there would be cases of reasoning that would rest outside the possibility space of their model (Hahn and Chater, 1998a, p. 203):Outside the space entirely are processes which do not involve matching the novel instance to stored representations of any kind and, hence, are alternatives to both rule- and similarity-based accounts. For example, generalization might be based on simple failure to discriminate different perceptual stimuli, rather than on stored knowledge. More interestingly, an input–output mapping might be performed without consulting any stored representations.
In applying the representation mapping model, we found the model to generally be useful, but strict vs. partial and the comparison of abstractness dimensions of the possibility space are not always cleanly differentiable. In some cases, this may be because of “failure to discriminate” in generalization or “input–output mapping”, e.g., when generalizing from something that the student has not indicated as stored knowledge. More often, students tended to use multiple lines of reasoning in an explanation, and some of them had differences in the abstracting, as well as in the abstractness dimensions, than others. As described in the section on Continuums, we found this to occur more often with assessing abstractness than with abstracting. With several of these, we broke down the interview into subsections of reasoning and examined differences in abstractness along the path of reasoning taken, and observed that the patterns were mainly consistent in how a student reasoned throughout a problem. Thus, when we assigned the abstractness comparison for a case of problem solving as low–low, high–high, stored > new, or new > stored, we aimed to build a first characterization based on dichotomous assignments of high or low abstractness. Nevertheless, the dichotomy is a limitation of the model.
Implications
This study also has important implications for instructors. According to Jonassen (2011a, 2011b), assessment guides learning. Students focus on and are adept at learning what is going to be tested. “Their strategic knowledge is based on the assumption that what is “on the test” is what is important to teachers, professors, and trainers. Unfortunately, that is not a good assumption. What is important to teachers, professors, and trainers often has little to do with the kinds of assessments they use” (Jonassen, 2011a, p. 353). Based on the results of our study, a goal for instructors should be to develop students’ ability to use multiple different reasoning processes and different types of abstraction while solving different problems. Assessments could be tailored to this goal. To develop greater flexibility in abstraction, problems could be given that are more easily solved by rule- or similarity-based reasoning in order to give students practice with different processes. In creating feedback or answer keys to classroom assessments, instructors could show students several ways of answering problems with different reasoning processes. Additionally, instructors could develop problems that push students’ abstractness up by scaffolding the types of abstractness required by problems. In order to do this, we need a better understanding of the characteristics of problems that lead students to use different types of abstraction processes.Returning to the larger scope of this research pursuit, we hypothesize that an abstraction threshold exists in each undergraduate STEM curriculum, where a typical student's capacity for abstraction and flexibility in utilizing different types of abstractions (the supply of abstraction) does not meet the abstraction demanded by the problems the student encounters, and this threshold affects student performance and retention (Sevian et al., 2015). In this contribution we have focused on characterizing the abstraction that students supply to solve organic mechanism problems. In order to uncover and characterize an abstraction threshold across an undergraduate curriculum, we need a method to characterize the abstraction demanded by the problems with which students are presented. We are currently investigating different methods to characterize the demand of a problem in ways that do not depend on how a student solves the problem.
Appendix
Table 7 presents a summary of all of the coding. Examples used in the main body of the paper are greyed so that readers may judge the representativeness of the examples, including two further examples provided after the table. As noted in the paper, we found that a propensity of examples came from problems 1A and 3A, rather than 1B and 3B. During the interviews, A problems always preceded B problems, and students often referred while solving B problems to things they said while solving A problems. Therefore, the A problems tended to be better examples to illustrate our findings.
|
Further examples from the data are shown here, to illustrate our method of coding the interviews. The full process is described in the data analysis section of the Method above. Here we present the meta-level data for two problems. For each problem, we first summarized in narrative form the student's problem-solving process, considering both the interview and the student's written explanation using the LiveScribe pen. Next, we identified which portions of this referred to stored knowledge and new instance representations, and highlighted the aspects of these in order to assess the degree of abstractness in the four indicators (see Fig. 2). Then, we focused on the actions taken by the student in matching the two representations. As noted in the section about continuums in describing abstractness, in cases where there was mixed (i.e., both low and high) abstractness in one or both representations, the determination of abstractness of a representation was assessed by the indicators that mattered most in how the student matched the two representations, since this formed the crux of the student's reasoning.
Example 1: 17_1B
17_1B: It might come up on the test and I wanted to make sure that I knew it so I looked it up on Google and this is how they show you to do this mechanism […] if you don't know it you're not going to figure it out [drawing in Fig. 19] | ||
| Fig. 19 Student 17's written response to exam 1 problem B. | ||
It is important to note that whether students were coded as partially or strictly matching their representations depended on what the students said about the problem and their previous experiences. In this example, the characterization of strict or partial matching did not depend on the researchers’ opinions of whether this student's mechanism was “how they show you” on Google, but instead how the student viewed his solution (Ellis, 2007).
Example 2: 5_1A
05_1A: When I practice it at home it was a primary alcohol which would have give me a carboxylic acid, but this is a secondary […] so Jones mechanism […] the whole concept, like the idea of taking the hydrogen and eliminating it was the same instead of the methyl group. It would have been OH off the methyl group, so that was an additional step we would have to do but over here we didn’t have to. [drawing in Fig. 20]. | ||
| Fig. 20 Student 5's written response to exam 1 problem A. | ||
Acknowledgements
The authors are grateful to Sascha Bernholt and Gabriela Szteinberg for data collection efforts, and to the Reviewers for their critical feedback which contributed to improvements. The authors wish to acknowledge the funding source, US National Science Foundation award 1348722, that supported our work. Any opinions, conclusions, or recommendations expressed in this paper are those of the authors, and do not necessarily reflect the views of the funding sources.Notes and references
- Anzovino M. E. and Lowery Bretz S., (2015), Organic chemistry students' ideas about nucleophiles and electrophiles: the role of charges and mechanisms, Chem. Educ. Res. Pract., 16, 797–810.
- Bhattacharyya G., (2008), Who am I? What am I doing here? Professional identity and the epistemic development of organic chemists, Chem. Educ. Res. Pract., 9, 84–92.
- Bhattacharyya G., (2013), From source to sink: mechanistic reasoning using the electron-pushing formalism, J. Chem. Educ., 90(10), 1282–1289.
- Bhattacharyya G. and Bodner G. M., (2005), “It gets me to the product”: how students propose organic mechanisms, J. Chem. Educ., 82(9), 1402–1407.
- Bodner G. M. and Domin D. S., (2000), Mental models: the role of representations in problem solving in chemistry, Univ. Chem. Educ., 4(1), 24–30.
- Bodner G. M. and Herron J. D., (2002), Problem-solving in chemistry, in Gilbert J. K., et al. (ed.), Chemical education: towards research-based practice, Netherlands: Kluwer Academic Publishers, pp. 235–266.
- Cartrette D. P. and Bodner G. M., (2010), Non-mathematical problem solving in organic chemistry, J. Res. Sci. Teach., 47(6), 643–660.
- Christian K. and Talanquer V., (2012), Modes of reasoning in self-initiated study groups in chemistry, Chem. Educ. Res. Pract., 13, 286–295.
- Domin D. and Bodner G., (2012), Using students’ representations constructed during problem solving to infer conceptual understanding, J. Chem. Educ., 89(7), 837–843.
- Ellis A. B., (2007), A taxonomy for categorizing generalizations: generalizing actions and reflection generalizations, J. Learn. Sci., 16(2), 221–262.
- Ferguson R. and Bodner G. M., (2008), Making sense of the arrow-pushing formalism among chemistry majors enrolled in organic chemistry, Chem. Educ. Res. Pract., 9(2), 102–113.
- Gentner D. and Medina J., (1998), Similarity and the development of rules, Cognition, 65, 263–297.
- Gentner D. and Stevens A. L., (1983), Mental models, Hillsdale, NJ: Erlbaum.
- Gentner D., Loewenstein J. and Thompson L., (2003), Learning and transfer: a general role for analogical encoding, J. Educ. Psychol., 95, 393–408.
- Giunchiglia F. and Walsh T., (1992), A theory of abstraction, Artif. Intell., 57, 323–389.
- Graulich N., Tiemann R. and Schreiner P. R., (2012), Heuristic chemistry–a qualitative study on teaching domain-specific strategies for the six-electron case, Chem. Educ. Res. Pract., 13, 337–347.
- Grove N. P., Cooper M. M. and Cox E. L., (2012a), Does mechanistic thinking improve student success in organic chemistry? J. Chem. Educ., 89(7), 850–853.
- Grove N. P., Cooper M. M. and Rush K. M., (2012b), Decorating with arrows: toward the development of representational competence in organic chemistry, J. Chem. Educ., 89(7), 844–849.
- Hahn U. and Chater N., (1998a), Similarity and rules: distinct? Exhaustive? Empirically distinguishable? Cognition, 65, 197–203.
- Hahn U. and Chater N., (1998b), Understanding similarity: a joint project for psychology, case-based reasoning and law, Artif. Intell. Rev., 12, 393–427.
- Hall R. and Stevens R., (1995), Making space: A comparison of mathematical work in school and professional design practices, in Star S. L. (ed.), Cultures of computing, Oxford, UK: Blackwell, pp. 118–145.
- Hammer D., Elby A., Scherr R. E. and Redish, E. F., (2005), Resources, framing, and transfer, in Mestre, J. P. (ed.), Transfer of learning from a modern multidisciplinary perspective, Greenwich, CT: Information Age, pp. 89–120.
- Hinze S. R., Rapp D. N., Williamson V. M., Shultz M. J., Deslongchamps G. and Williamson K. C., (2013), Beyond ball-and-stick: students' processing of novel STEM visualizations, Learn. Instr., 26, 12–21.
- Johnstone A. H., (1993), Introduction, in Wood C. and Sleet R. (ed.), Creative problem solving in chemistry, London: The Royal Society of Chemistry, pp. 4–6.
- Jonassen D., (2011a), Designing for problem solving, in Reiser R. and Dempsey J. (ed.), Trends and issues in instructional design and technology, Boston, MA: Pearson Education, pp. 64–74.
- Jonassen D., (2011b), Learning to solve problems: a handbook for designing problem-solving learning environments, New York, NY: Routledge.
- Koedinger K. R., Alibali M. W. and Nathan M. J., (2008), Tradeoffs between grounded and abstract representations: evidence from algebra problem solving, Cognitive Sci., 2(2), 366–397.
- Kraft A., Strickland A. M. and Bhattacharyya G., (2010), Reasonable reasoning: multi-variate problem-solving in organic chemistry, Chem. Educ. Res. Pract., 11, 281–292.
- Schwartz D. L., (1995), The emergence of abstract representations in problem solving, J. Learn. Sci., 4(3), 321–354.
- Schwartz D. L., Bransford J. D. and Sears D., (2005), Efficiency and innovation in transfer, in Mestre J. P. (ed.), Transfer of learning from a modern multidisciplinary perspective, Greenwich, CT: Information Age, pp. 1–51.
- Seifert C., (1989), Analogy and case-based reasoning, in Bareiss R. (ed.), Proceedings: Case-Based Reasoning Workshop, San Mateo, CA: Morgan Kaufmann.
- Sevian H., Bernholt S., Szteinberg G. A., Auguste S. and Pérez L. C., (2015), Use of representation mapping to capture abstraction in problem solving in different courses in chemistry, Chem. Educ. Res. Pract., 16(3), 429–446.
- Son J. Y., Smith L. B. and Goldstone R. L., (2008), Simplicity and generalization: short-cutting abstraction in children's object categorizations, Cognition, 108, 626–638.
- Stamovlasis D., Tsaparlis G., Kamilatos C., Papaoikonomou D. and Zaratiadou E., (2005), Conceptual understanding vs. algorithmic problem solving: further evidence from a national chemistry examination, Chem. Educ. Res. Pract., 6, 104–118.
- Stevens R., O'Connor K., Garrison L., Jocuns A. and Amos D. M., (2008), Becoming an engineer: toward a three dimensional view of engineering learning, J. Eng. Educ., 97(3), 355–368.
- Strickland A. M., Kraft A. and Bhattacharyya G., (2010), What happens when representations fail to represent?: graduate students’ mental models of organic chemistry diagrams, Chem. Educ. Res. Pract., 11(4), 293–301.
- Vygotsky L., (1986), Thought and language, Cambridge, MA: The MIT Press.
| This journal is © The Royal Society of Chemistry 2017 |