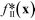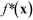Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning reaction products by constrained optimisation†
Barnaby E.
Walker
 a,
James H.
Bannock
a,
James H.
Bannock
 ab,
Adrian M.
Nightingale
ab,
Adrian M.
Nightingale
 c and
John C.
deMello
c and
John C.
deMello
 *ab
*ab
aCentre for Plastic Electronics, Department of Chemistry, Imperial College London, Exhibition Road, South Kensington, London SW7 2AY, UK. E-mail: j.demello@imperial.ac.uk
bCentre for Organic Electronic Materials, Department of Chemistry, NTNU, N-7491 Trondheim, Norway
cFaculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
First published on 20th September 2017
Abstract
We describe an effective means of defining optimisation criteria for self-optimising reactors, applicable to situations where a compromise is sought between several competing objectives. The problem is framed as a constrained optimisation, in which a lead property is optimised subject to constraints on the values that other properties may assume. Compared to conventional methods (using weighted-sum- and weighted-product-based merit functions), the approach described here is more intuitive, easier to implement, and yields an optimised solution that more faithfully reflects user preferences. The method is applied here to the synthesis of o-xylenyl adducts of Buckminsterfullerene, using a cascadic reaction of the form X0 → X1 → X2 → … XN. Specifically, we selectively target the formation of the (technologically useful) first- and second-order adducts X1 and X2, while at the same time suppressing the formation of unwanted higher-order products. More generally, the approach is applicable to any chemical optimisation involving a trade-off between competing criteria. To assist with implementation we provide a self-contained software package for carrying out constrained optimisation, together with detailed tutorial-style instructions.
The goal of finding an efficient route to a target molecule, while at the same time minimising the formation of unwanted side products, lies at the heart of synthetic chemistry. In the ideal case, where the target molecule corresponds to the sole end-point of a reaction, a near-quantitative product yield may be readily achieved by allowing the reaction to progress to completion. More often than not, however, the target is just one of several possible end products, or else it is an intermediate that can only be obtained by quenching the reaction before it has reached completion. In such circumstances, a mixture of reaction products is inevitably obtained, with the yield of the target molecule depending on the (typically unknown) kinetics of the reaction and the specific reaction conditions employed. Manually searching for reaction conditions that deliver an acceptable yield of the target molecule is a laborious undertaking, requiring extensive experimentation and chemical intuition. Even then, there is no guarantee the chosen conditions will correspond to the best attainable solution.
In this paper we set out an easily-implemented and fully automated approach for preferentially synthesising one or more target molecules amongst a larger group of possible products, using a technique that (given sufficient time) will yield a globally optimised solution. Our approach builds on previous work in the area of ‘intelligent’ or ‘self-optimising’ reactors,1–5 using an automated reactor with on-line analysis and algorithmic control to repeatedly update the reaction conditions until a desired goal has been achieved. For each set of reaction conditions tested, the system is allowed to stabilise, a measurement is made using the on-line analysis system, and a scalar merit value that quantifies the acceptability of the product is then extracted from the data. In this way the overall physical process may be treated as a mathematical objective function in which the inputs are the selected reaction conditions and the output is the merit value. Assuming lower merit values signify superior products, optimisation of the chemical process is formally equivalent to minimisation of the associated objective function, and may accordingly be achieved using numerical techniques.
In two of the earliest reports in the field, self-optimisation was used by Krishnadasan et al.1 in 2007 to tailor the spectral characteristics of metal chalcogenide quantum dots and by McMullen et al.6 in 2010 to optimise the Knoevenagel condensation reaction of p-anisaldehyde and malononitrile. Further important contributions in the area have been made by the groups of Bourne,7,8 Jensen,9–11 and Poliakoff.12–14 Using a variety of in-line/on-line analysis techniques – including infrared absorption spectroscopy,9 visible fluorescence spectroscopy,1 chromatographic separations,6,8,10–15 nuclear magnetic resonance,16 and mass spectrometry7,17 – self-optimisation has been successfully used to optimise the yield and/or production rate of a variety of target molecules6–17 and to control the physical properties of materials.1,18 The above optimisations were carried out using a mixture of local6,9–18 and global1,6–8 search methods. For unknown chemical systems that may potentially exhibit multiple optima, global routines that fit measured data to approximating surfaces are typically preferred since they do not get trapped in sub-optimal local minima, can cope with measurement noise, and – by avoiding the need for derivative calculations – require relatively few function evaluations to locate optima. In situations where the chemical parameter space is monotonic with a single minimum (or multiple minima exist but the approximate location of the global minimum is known) local search methods may sometimes offer faster convergence.
In many cases a trade-off or compromise must be reached between several competing criteria. Mathematically, this may be achieved through the use of a compound merit function, typically formed from a weighted sum19,20 or weighted product20,21 of individual merit functions that separately take into account each property being optimised. Weighted-product-based merit functions were used by Krishnadasan et al. to maximize the intensity of quantum dot emission at a target wavelength1 and by Jumbam et al. to achieve an optimised trade-off between the production rate and yield of methylated ethers;15 while weighted-sum-based merit functions were used by Moore et al. to achieve an optimised trade-off between the production rate and the conversion efficiency of a Paal–Knorr reaction.9
The above studies showed that merit-based multi-objective optimization can be a powerful method for chemical optimization. However, its success hinges on the ability of the merit function to reduce multiple property values to a single, meaningful number that can be used to objectively rank the adequacy of different outcomes. Unfortunately, devising a suitable merit function can be a fraught endeavor,17,19 especially when there are more than two parameters to balance: extensive physical experimentation and mathematical manipulation is often required to find an appropriate form of merit function that sensibly balances the different optimisation criteria and, even then, there is no guarantee that the merit-based ranking will fully accord with user perception.
The lack of a straightforward method for codifying product requirements in the form of chemical merit functions is a major obstacle to the widespread deployment of self-optimising reactors. What is needed is an easily implemented procedure that allows a user to set out all requirements in a simple, intuitive form that can then be directly translated into a usable merit function without significant experimentation or mathematical effort. Here we demonstrate how this may be readily achieved by configuring the problem as a constrained optimisation, in which a lead property is optimised, subject to lower and upper limits being placed on the values that other properties of interest may assume. By way of example, in a typical polymerization reaction, the lead property might be the conversion rate (which we wish to maximize), while typical constrained properties could include the weight-averaged molecular weight (which should fall between certain application-dependent bounds) and the polydispersity index (which should not exceed a maximum level).
The constraints are handled here using an analytical procedure due to Huyer and Neumaier.22,23 In the discussion below we focus primarily on implementational aspects of the method; a description of its mathematical basis may be found in the ESI.† We assume that our goal is to minimise the lead property subject to specific constraints on other properties (if the goal were to maximize the lead property, we would minimize its negative). For each constrained property the user specifies a range of values [FLower, FUpper] within which that property should preferably lie plus a parameter ΔF corresponding to the maximum permitted deviation from the preferred range (see Fig. S1a†). Property values that lie within the preferred range [FLower, FUpper] completely satisfy user specifications and hence are said to be “fully feasible”. Values that lie outside the preferred range but within the expanded range [FLower − ΔF, FUpper + ΔF] partially satisfy user requirements and are said to be “semi feasible” (since they lie within a permitted margin of the preferred range). Values outside the expanded range do not meet user requirements and are said to be “infeasible”. It is the goal of the optimisation procedure to identify the set of reaction conditions that minimises the value of the lead property, while at the same time ensuring the values of all constrained properties are feasible or at worst semi-feasible (i.e. they lie within or as close as possible to their preferred windows).
The procedure begins with an initial search of the chemical parameter space to identify at least one data point that completely satisfies all constraints (see Methods). This is typically a straightforward task since any fully feasible point will suffice, irrespective of its lead property value. Two experimental parameters are extracted from these initial measurements: f0 the value of the lead property at the best feasible point (i.e. the feasible point with the lowest lead property value); and Δ, the median value of |f(x) − f0| where f(x) is the value of the property at the data point x.
Using the experimentally determined parameters f0 and Δ, together with the user defined-parameters FLower, FUpper and ΔF for each constrained property, one may then construct a merit function fsoft(x) that takes into account both the value of the lead property and the specified constraints:
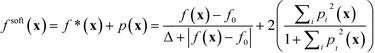 | (1) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) of the global minimum of fsoft(x).
of the global minimum of fsoft(x).
We note here some pertinent properties of eqn (1). The first term f*(x) is simply a rescaled variant of the original unconstrained merit function f(x): f*(x) varies monotonically with f(x), so the optima of f*(x) occur at the same locations as the optima of f(x). The second term p(x) is a penalty term that has the effect of increasing the value of fsoft(x) whenever a property value lies outside its preferred window (otherwise if all constraints are satisfied its value is zero). From the construction of eqn (1), the merit values are bounded to lie between −1 and 3. Fully feasible points have merit values less than one (with x0 having a merit value of zero), infeasible points have merit values greater than zero, while semi-feasible points can span the range from −1 to 2. It follows from these properties that the optimisation procedure will never prefer an infeasible point over a feasible point (since the infeasible point will always have a higher merit value than x0). Moreover, it will only prefer a semi-feasible point over the best identified feasible point if the value of the lead property at the semi-feasible point is substantially lower than that at the best identified feasible point (resulting in a lower overall merit value). The complete step-by-step procedure for carrying out the constrained optimisation is summarised in the flow diagram of Fig. S1b† for a problem involving two constrained variables. The diagram makes clear the simplicity of the procedure, which in practice is scarcely more difficult to implement than a standard unconstrained optimisation. Importantly, the optimisation routine requires little prior knowledge of the system being optimised and, by using only easily supplied values for the constraints, avoids the usual need for laborious tuning of penalty parameters (see ESI† and ref. 24).
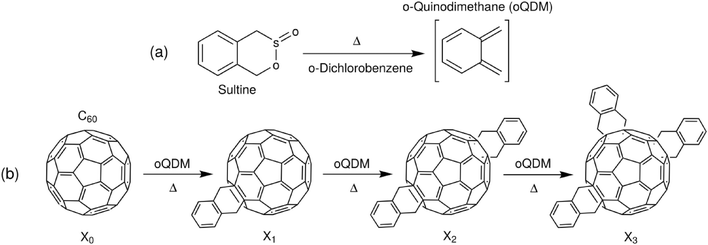
To exemplify the application of the procedure to chemical optimisation, we show how it may be used to tune the products of a cascadic reaction of the type X0 → X1 → X2 → … XN. It is a characteristic feature of such reactions that a mixture of products is present at all intermediate times, with the instantaneous distribution of products depending (in an often complicated way) on the underlying kinetics of the reaction. For the purposes of exposition, we specifically focus on the synthesis of o-xylenyl adducts of Buckminsterfullerene by the reaction of C60 with cyclic esters of a hydroxy sulfinic acid (sultines),25 see Scheme 1. While these molecules have important applications as light-harvesting agents and electron conductors,25–27 the details of their use need not concern us here. Suffice to say, it is frequently the first- and second-order adducts that are used in practice, with the presence of significant quantities of higher-order adducts having a detrimental impact on optoelectronic behaviour.28 Hence, there is a need to identify reaction conditions that maximise the yields of singly- and doubly-functionalised molecules, while minimising the fractions of higher-order adducts.
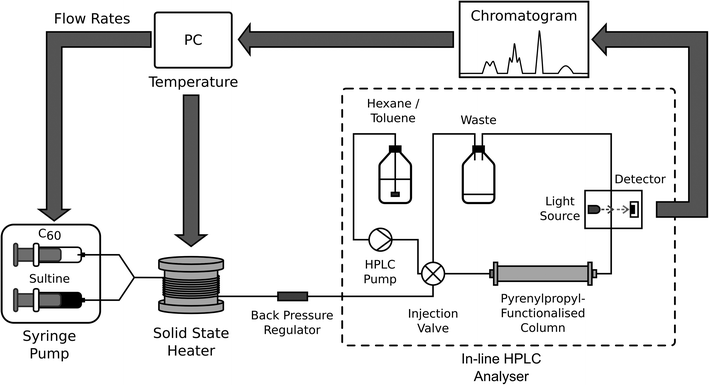
The high stabilities of the reagents used in the synthesis of o-xylenyl-functionalised C60 make it a viable candidate for self-optimisation, with the one-pot nature of the reaction lending itself to straightforward automation. Here we used a simple single-phase, capillary-based flow reactor,‡ incorporating: two syringe pumps, separately loaded with C60 and sultine solutions; a passive y-shaped mixer for bringing the two solutions into contact; and a cylindrical solid-state heater for thermally activating the reaction (see Fig. 1 and Methods). Control over the time, temperature and chemical composition of the reaction was achieved by making independent adjustments to the infusion rates of the two reagent streams and the temperature of the heater.
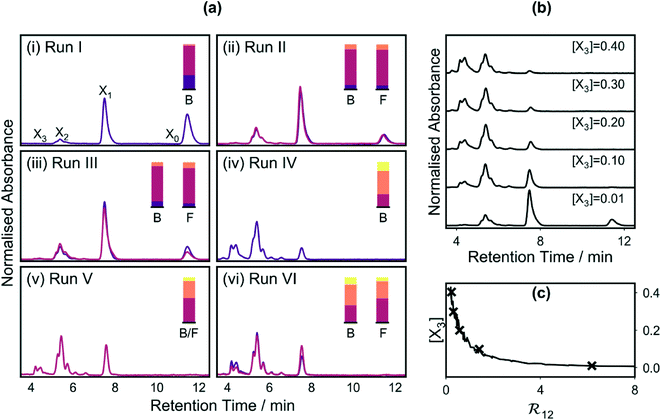
High performance liquid chromatography (HPLC) was selected for on-line analysis, being a moderately fast, flow-compatible method for analysing multicomponent solutions. HPLC has been successfully applied to self-optimising reactors by the groups of Jensen6,10,11 and Bourne.8 For the current work, discrimination of the o-xylenyl adducts was achieved using pyrenylpropyl-functionalised silica as the stationary phase and a mixture of toluene and hexane as the mobile phase27 (the affinity of the C60 adducts to the mobile phase rises substantially with increasing order number, resulting in progressively shorter and well separated elution times). Following each change of reaction conditions, the system was allowed to stabilize for a time period equal to twice the current calculated residence time. A sample of the product mixture was then taken by diverting the out-flow of the reactor to a sample coil, from where it was injected into an HPLC column using a high-pressure switching valve. Detection was carried out optically by absorption spectroscopy. For ease of comparison all chromatograms reported here have been normalised to the total area under the measured peaks. The relative concentrations of the adducts were determined from the areas under the chromatographic peaks, using a calibration curve.
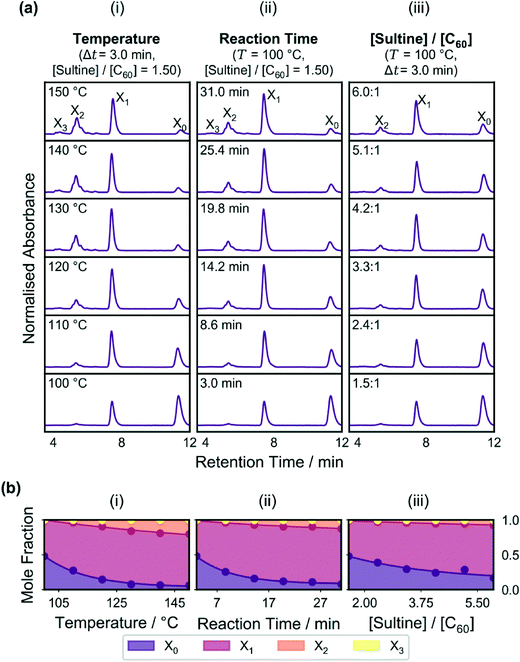
Initial testing of the reactor was carried out by varying in turn the reaction temperature, reaction time and molar ratio of sultine to C60, while holding the other two parameters constant. The effects of varying these parameters on the measured chromatograms are shown in Fig. 2a(i–iii), while the effects on the mole fractions of the adducts are shown in the stacked area plots of Fig. 2b(i–iii). Up to four distinct and well separated chromatographic peaks were observed in each case at elution times of approximately 4.4, 5.4, 7.5, and 11.4 min, corresponding to triply-(X3), doubly-(X2), singly-(X1) and un-(X0) functionalised C60, respectively (see Methods). Similar trends are evident in each plot, with there being a reduction in the C60 peak accompanied by an increase in the other peaks as the variable parameter was increased. Hence, for the conditions tested, increases in the temperature, reaction time and sultine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C60 ratio all resulted in increased conversion of C60 into higher-order adducts in broad accordance with expectation.
C60 ratio all resulted in increased conversion of C60 into higher-order adducts in broad accordance with expectation.
The plots in Fig. 2 show smooth trends in the concentrations of the adducts as the reaction parameters were varied, indicating a well controlled reaction environment and low noise in the measurement system – necessary characteristics for developing a reliable self-optimising reactor. However, collectively, the plots represent a very limited data set since only one reaction parameter was varied in each case, with the other two being held fixed. There is no guarantee similar trends would be obtained for different values of the fixed parameters (indeed, given the cascadic nature of the reaction, the mole fractions of all species must eventually decrease as the reaction proceeds and they are converted into higher-order adducts in contrast to the behaviour seen in Fig. 2).
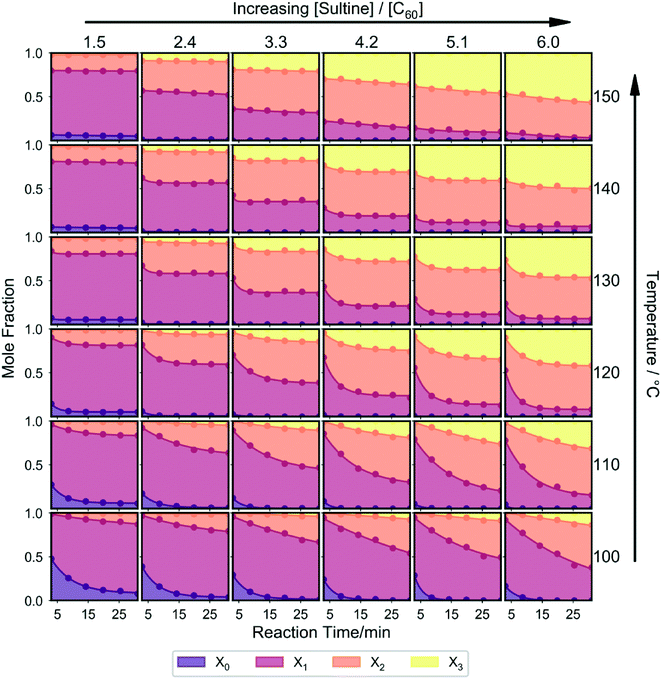
For a more complete understanding of how the distribution of reaction products depends on the reaction conditions, the three-dimensional parameter space should be mapped out by varying all reaction parameters in parallel. The result of doing this at a coarse level – using a 6 × 6 × 6 set of evenly spaced grid points for the temperature, time and sultine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C60 ratio – is shown in Fig. 3. The measurements were carried out in a randomized order, with several sets of reaction parameters being repeated multiple times. Chromatograms for the replicate measurements showed only slight differences (see Fig. S2†), indicating negligible system drift over the timescale of the measurement run, with only small sample-to-sample variations due to minor reactor instability and/or measurement errors.
C60 ratio – is shown in Fig. 3. The measurements were carried out in a randomized order, with several sets of reaction parameters being repeated multiple times. Chromatograms for the replicate measurements showed only slight differences (see Fig. S2†), indicating negligible system drift over the timescale of the measurement run, with only small sample-to-sample variations due to minor reactor instability and/or measurement errors.
A number of general observations may be made about the data in Fig. 3: as before, in all cases a mixture of reaction products was obtained; increasing the reaction time, temperature and/or sultine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C60 ratio resulted in a progressive reduction in the mole fraction of unreacted C60 and a progressive increase in the mole fraction of the (typically unwanted) third-order adduct; at lower temperatures the (typically preferred) first- and second-order adducts were the dominant products, while at higher temperatures and sultine
C60 ratio resulted in a progressive reduction in the mole fraction of unreacted C60 and a progressive increase in the mole fraction of the (typically unwanted) third-order adduct; at lower temperatures the (typically preferred) first- and second-order adducts were the dominant products, while at higher temperatures and sultine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C60 ratios the second- and third-order adducts dominated; an increase in higher-order adducts was evident at higher temperatures and sultine concentrations, under which conditions C60 was fully depleted during the reaction, consistent with the cascadic reaction mechanism.
C60 ratios the second- and third-order adducts dominated; an increase in higher-order adducts was evident at higher temperatures and sultine concentrations, under which conditions C60 was fully depleted during the reaction, consistent with the cascadic reaction mechanism.
The systematic, reproducible nature of the data in Fig. 3 and S2† suggest the complete system – i.e. the reagents, reactor and measurement system taken as a whole – is a good candidate for self-optimisation (reproducibility being a pre-requisite for successful optimisation). As noted above, first- and second-order adducts of C60 are typically preferred for electronic applications, with the presence of higher-order adducts often having a detrimental impact on optoelectronic behaviour. Hence, as an initial test, a simple unconstrained optimisation was carried out, in which we sought to minimise the formation of the third-order adduct by setting the merit function – i.e. the quantity to be minimised – equal to the mole fraction of the third-order adduct, [X3] (see Table S1†).
For all optimisation runs reported here we used the global optimisation code Stable Noisy Optimisation by Branch and Fit (SNOBFit)22 – a noise-tolerant routine that first divides the search space into separate boxes that each contain one sampled data point, and then forms quadratic models around each point; local searching is handled by selecting the model minima as new evaluation points, and global searching is handled by making measurements in large boxes (which correspond to large regions of unexplored territory). In each iteration, a batch of new points is selected for testing, some for local optimisation and others for global searching. In all cases: the temperature was varied between 100 and 150 °C; the reaction time was varied between 3 and 31 min; the flow-rate ratio was varied between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2;§ the routine was started ‘cold’, i.e. with no pre-supplied measurement data; and approximately one hundred trial measurements were carried out during each search, of which 30% were selected for global searching and 70% for local refinement (see Methods).
2;§ the routine was started ‘cold’, i.e. with no pre-supplied measurement data; and approximately one hundred trial measurements were carried out during each search, of which 30% were selected for global searching and 70% for local refinement (see Methods).
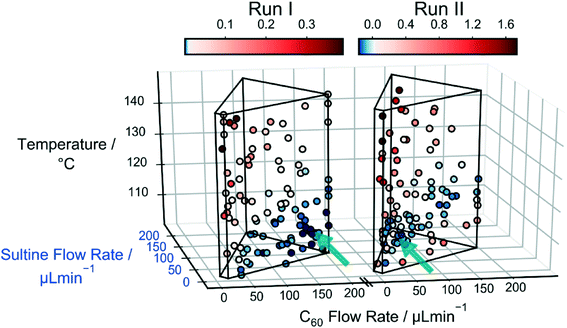
The left side of Fig. 4 shows a scatter plot of the sampled data from run I, in which the marker locations indicate the reaction conditions and the colours denote the merit values: lower merit values are denoted by darker colours; and, for ease of distinction, merit values higher than the median value of 0.011 are coloured red, while those lower than the median value are coloured blue (pale, near-white markers denote points with merit values equal or close to the median value). The wire-frame ‘cage’ denotes the bounds defined by the flow rate and temperature constraints. The algorithm has evidently sampled certain regions of the parameter space preferentially – in particular the region next to the lower half of the right face of the cage, corresponding to lower temperatures and lower sultine concentrations. The data markers in this region are all coloured blue, signifying low merit values, i.e. low mole fractions of the third-order adduct.
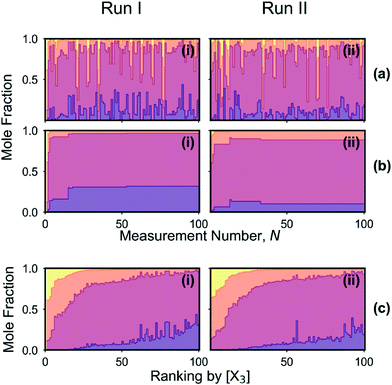
The mole fractions [X0], [X1], [X2] and [X3] of the four adducts are plotted against measurement number in Fig. 5a(i). The mole fraction distribution can be seen to fluctuate substantially between successive measurements due to local searching at the beginning of each batch of points, and global searching at the end of each batch: in the local phase, the parameter space is sampled preferentially in regions where the existing merit values are low, yielding new merit values that are typically low also; in the global phase, unexplored regions of the parameter space are sampled where the merit values tend to be large (but where superior, as yet undiscovered, minima might potentially exist). Insight into the behaviour of the algorithm can be drawn from Fig. 6a(i) and (ii) which show successive merit values and a histogram of the merit values, respectively. The plots indicate that the algorithm preferentially explored regions of the parameter space that yielded low merit values, with more than 80% of sampled data points having merit values of 0.050 or less (compared to a maximum measured value of 0.389). The best point with the lowest merit value of 0.001 had mole fractions of 0.318, 0.649, 0.033 and 0.001 for the zero-, first-, second- and third-order adducts, respectively, confirming effective suppression of the third-order adduct.
Fig. 5b(i) shows mole fractions for the best result obtained so far versus measurement number, N. Changes in the best result occur whenever the most recently tested reaction conditions give rise to a product distribution with a lower merit value than the previous best result, i.e. a lower mole fraction for the third-order adduct. Improvements occurred at N = 5, 15, 18 and 53, with the mole fraction of the third-order adduct falling from an initial value of 0.384 at N = 1 to a value of 0.001 at N = 53. At the same time, the concentration of unreacted C60 increased from an initial value of 0.000 at N = 1 to a value of 0.318 at N = 53. Hence, it is evident that the reduction in [X3] was primarily achieved at the expense of an undesirable drop in C60 conversion.
To improve the conversion rate, a second optimisation (run II) was carried out in which the mole fraction of the third-order adduct was again minimized, but constraints were applied to the combined mole fraction of the (desired) first- and second-order adducts: soft and hard lower limits of 90 and 60%, respectively, were imposed on the combined mole fraction [X1,2] = [X1] + [X2], using a constraint window for [X1,2] of [0.9, 1.0] and a ΔF value of 0.3. The right side of Fig. 4 shows a scatter plot of the measurements made during run II, where merit values above the median value (0.020) are again coloured red and those below the median value are coloured blue. As before, the algorithm preferentially sampled the low temperature, low sultine region close to the right face of the cage. However, this time the majority of sub-median data points occurred close to the foremost ‘spine’ of the cage, corresponding to lower flow rates, i.e. longer reaction times. Hence, in common with the unconstrained case of run I, the algorithm ensured a low mole fraction of the third-order adduct by selecting low temperatures and low sultine concentrations, but this time it selected longer reaction times that resulted in higher C60 conversion. The best point with the lowest merit value of −0.166 had mole fractions of 0.101, 0.784, 0.110 and 0.004 for [X0], [X1], [X2] and [X3].
The mole fraction distribution is plotted against measurement number in Fig. 5a(ii). While the observed behaviour is similar to that seen in Fig. 5a(i) for run I – with the mole fractions again fluctuating substantially between successive measurements as the optimisation routine switched between local and global searching – the average height of the dark purple bars that denote unreacted C60 is significantly lower. Hence, compared to the first optimisation run, the algorithm preferentially selected reaction conditions that resulted in substantial conversion of C60. Fig. 5b(ii) shows mole fractions for the best result to date versus N, where the best result corresponds to the outcome with the lowest (soft) merit value. Improvements occurred at N = 3, 13, 14 and 33, with [X3] assuming respective values of 0.013, 0.006, 0.005 and 0.004 and [X0] assuming respective values of 0.067, 0.155, 0.134 and 0.101. Hence, although the initial reduction in [X3] was again achieved at the cost of an increase in [X0], the C60 concentration subsequently dropped without the concentration of the third-order adduct increasing. The algorithm therefore succeeded in its aim of minimizing the amount of the third-order adduct, while also achieving a close to 90% yield of first- and second-order adducts.
The contrasting behaviour of the constrained and unconstrained optimisation runs can be seen more easily by ranking the data from Fig. 5a(i) and (ii) in order of decreasing third-order adduct. While the two ranked plots in Fig. 5c(i) and (ii) are qualitatively similar in appearance – with the concentrations of the second- and third-order adducts decreasing and the concentrations of the zero- and first-order adducts broadly increasing from left to right – clear differences are evident: the average mole fraction of the third-order adduct is slightly higher in the case of the constrained optimisation (run II), while the average mole fraction of unreacted C60 is markedly lower. Hence it is evident that, during run II, the algorithm preferentially probed regions of the parameter space that resulted in high C60 conversion.
The behaviour of (the constrained optimisation) run II can be understood by examining the plots in Fig. 6b, which show successive values and the corresponding histograms for the total objective function fsoft(x), the transformed merit function f*(x) and the constraint function p(x). It can be seen that the algorithm preferentially explored regions of the chemical parameter space that yielded low merit values, with these low values being achieved through a combination of low f*(x) values and low p(x) values. The f*(x) values, while running from −0.227 to 0.887, were strongly biased towards negative values, indicating that the algorithm identified many points that yielded a lower third-order adduct concentration than the first identified feasible point x0 (identified at N = 1). In addition, the p(x) values were preferentially skewed towards zero, signifying a strong bias towards points that satisfied or nearly satisfied the constraint: of the 100 measurements, 46 resulted in a p(x) value of zero, corresponding to fully feasible points that completely satisfied the applied constraint (i.e. yielded a combined mole fraction for X1 and X2 of >90%).
Fig. 7a(i) shows the chromatogram corresponding to the lowest merit value (0.001) obtained during run I, while Fig. 7a(ii) shows chromatograms for the lowest merit value (−0.166) and the lowest fully feasible merit value (−0.123) obtained during run II. Comparing these chromatograms, it can be seen that [X1,2] was substantially higher for run II (∼0.9) than run I (0.68), consistent with the successful application of the constraint in the former case. The fully feasible and semi-feasible chromatograms of Fig. 7a(ii) are very similar to one another, implying similar amounts of the four adducts in both cases. The best feasible point had a third-order adduct mole fraction of 0.007 and a combined mole fraction [X1,2] of 0.905 for the first- and second-order adducts, compared to values of 0.004 and 0.894 for the best semi-feasible point. Hence, comparing the best point and the best feasible point, it is clear that – in accordance with the discussion above – an improvement (reduction) in the primary parameter [X3] was achieved through a slight violation of the constraint on [X1,2]. The violation in this particular case was rather small since the best feasible point had an [X3] value that was already close to the lowest possible value of zero, so straying far outside the feasible zone would have caused a substantial increase in p(x) without significantly reducing f*(x).
In run II, a constraint was applied to [X1,2], the combined mole fraction of the first- and second-order adducts, but the relative amounts of the two mole fractions were allowed to vary freely. While the best point and best feasible points corresponded to product mixtures that contained substantially more of the first-order adduct than the second-order adduct, this was not specifically encoded within the merit function. To ensure such an outcome, it is necessary to impose a constraint on the ratio ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 = [X1]/[X2], alongside the existing constraint on [X1,2]. To demonstrate the feasibility of doing this, in the next optimisation run (run III), we additionally sought to enforce a lower limit of 4
12 = [X1]/[X2], alongside the existing constraint on [X1,2]. To demonstrate the feasibility of doing this, in the next optimisation run (run III), we additionally sought to enforce a lower limit of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 on the ratio
1 on the ratio ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 = [X1]/[X2], using a constraint window of [4, ∞] and a ΔF value of 0.3¶ (while maintaining the existing constraint on [X12]).
12 = [X1]/[X2], using a constraint window of [4, ∞] and a ΔF value of 0.3¶ (while maintaining the existing constraint on [X12]).
Scatter plots for run III, plots of mole fractions and merit values versus measurement number, and histograms of fsoft(x), f*(x) and p(x) are provided in Fig. S3.† The chromatograms for the best point and the best feasible point, obtained at measurement numbers 26 and 99 respectively, are shown in Fig. 7a(iii). The best feasible point had mole fractions of 0.085, 0.778, 0.128 and 0.009, implying an ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 value of ∼6.1
12 value of ∼6.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and an [X12] value of 0.906 – both values being consistent with the specified limits. The best point by contrast had mole fractions of 0.129, 0.776, 0.091 and 0.004, implying an
1 and an [X12] value of 0.906 – both values being consistent with the specified limits. The best point by contrast had mole fractions of 0.129, 0.776, 0.091 and 0.004, implying an ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 value of ∼8.5
12 value of ∼8.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and an [X12] value of 0.867 – the slight violation of the [X12] constraint having led to a beneficial reduction in [X3] from 0.009 to 0.004.
1 and an [X12] value of 0.867 – the slight violation of the [X12] constraint having led to a beneficial reduction in [X3] from 0.009 to 0.004.
Obtaining a product mixture that is rich in the first-order adduct is not especially difficult, and indeed occurred by chance in run II, even without imposing a constraint on ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12. For the fourth optimisation run (run IV), we sought to obtain a product mixture that contained more of the second-order adduct than the first-order adduct. Owing to the cascadic nature of the reaction, this is a substantially harder challenge since the second-order product lies adjacent in the reaction sequence to the unwanted third-order adduct, meaning conditions that favour the formation of the second-order product are liable to promote (to a lesser extent) the unwanted formation of the third-order product.
12. For the fourth optimisation run (run IV), we sought to obtain a product mixture that contained more of the second-order adduct than the first-order adduct. Owing to the cascadic nature of the reaction, this is a substantially harder challenge since the second-order product lies adjacent in the reaction sequence to the unwanted third-order adduct, meaning conditions that favour the formation of the second-order product are liable to promote (to a lesser extent) the unwanted formation of the third-order product.
To assess the feasibility of attaining an end-product rich in the second-order adduct, we placed what we hoped would be a physically achievable upper limit of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 on the ratio
2 on the ratio ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 = [X1]/[X2], using a constraint window of [0, 0.5] and a ΔF value of 0.3, while again maintaining the constraint on [X12]. The resultant scatter plots, plots of mole fraction and merit value versus measurement number, and histograms of fsoft(x), f*(x) and p(x), are provided in Fig. S4.† In contrast to the previous results, no feasible point was identified during the course of the run, with the histogram for p(x) spanning the range 0.280 to 1.999 due to partial (0 < p(x) ≤ 1) or complete (p(x) > 1) violation of at least one of the constraints in all cases. There were 50 cases of partial violations, of which 36 were due to partial violation of the yield constraint only, and 14 were due to partial violation of both constraints. There were 50 cases of full violations, of which 2 were due to full violation of the yield constraint, 26 were due to full violation of the ratio constraint, and 22 were due to full violation of both constraints. The constraint violations are consistent with the difficulty noted above of suppressing the formation of the third-order adduct, while at the same time trying to achieve a high mole fraction of the second-order adduct.
12 = [X1]/[X2], using a constraint window of [0, 0.5] and a ΔF value of 0.3, while again maintaining the constraint on [X12]. The resultant scatter plots, plots of mole fraction and merit value versus measurement number, and histograms of fsoft(x), f*(x) and p(x), are provided in Fig. S4.† In contrast to the previous results, no feasible point was identified during the course of the run, with the histogram for p(x) spanning the range 0.280 to 1.999 due to partial (0 < p(x) ≤ 1) or complete (p(x) > 1) violation of at least one of the constraints in all cases. There were 50 cases of partial violations, of which 36 were due to partial violation of the yield constraint only, and 14 were due to partial violation of both constraints. There were 50 cases of full violations, of which 2 were due to full violation of the yield constraint, 26 were due to full violation of the ratio constraint, and 22 were due to full violation of both constraints. The constraint violations are consistent with the difficulty noted above of suppressing the formation of the third-order adduct, while at the same time trying to achieve a high mole fraction of the second-order adduct.
The chromatogram for the best point in run IV, i.e. the point with the lowest soft merit value (−0.212), is shown in Fig. 7a(iv). From the areas under the chromatographic peaks, [X0], [X1], [X2] and [X3] were determined to be 0.001, 0.288, 0.510 and 0.201, respectively. Hence, even at the best point, a substantial amount of the third-order adduct was present and both constraints were partially violated, with [X12] having a value of 0.798 (i.e. less than 0.9) and ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 having a value of 0.564 (i.e. greater than 0.5). As expected from the above discussion, in an effort to find conditions that came close to satisfying the constraint on
12 having a value of 0.564 (i.e. greater than 0.5). As expected from the above discussion, in an effort to find conditions that came close to satisfying the constraint on ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12, the algorithm identified conditions that resulted in a high concentration of the third-order adduct and virtually no C60.
12, the algorithm identified conditions that resulted in a high concentration of the third-order adduct and virtually no C60.
The difficulty of simultaneously achieving a high ratio of the second- to first-order adducts, while at the same time suppressing formation of the third-order adduct is evident from Fig. 7b, which shows chromatograms (acquired during run IV) at several illustrative values of [X3]. From the chromatograms, it is evident that the ratio of the first-order adduct to the second-order adduct decreases steadily as [X3] increases. In Fig. 7c, the ratio ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 is plotted against the mole fraction [X3] for each measurement in run IV. The data points lie on a trade-off curve, with desired reductions in
12 is plotted against the mole fraction [X3] for each measurement in run IV. The data points lie on a trade-off curve, with desired reductions in ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 leading to an unwanted increase in [X3]. From the trade-off curve, it is evident that [X3] can only be kept below the 10% level (which we consider to be an acceptably low value) if
12 leading to an unwanted increase in [X3]. From the trade-off curve, it is evident that [X3] can only be kept below the 10% level (which we consider to be an acceptably low value) if ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 is greater than approximately 1.5. Armed with this information, a fifth optimisation run (run V) was carried out using an expanded constraint window for
12 is greater than approximately 1.5. Armed with this information, a fifth optimisation run (run V) was carried out using an expanded constraint window for ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 of [0, 1.5] and the same ΔF value of 0.3. Scatter plots for run V, plots of the mole fraction distributions and merit values versus measurement number, and histograms of fsoft(x), f*(x) and p(x) are provided in Fig. S5.†
12 of [0, 1.5] and the same ΔF value of 0.3. Scatter plots for run V, plots of the mole fraction distributions and merit values versus measurement number, and histograms of fsoft(x), f*(x) and p(x) are provided in Fig. S5.†
Using the expanded constraint window for ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12, an initial feasible point x0 was found at N = 21. The same point turned out to be both the best feasible point and the point with the lowest overall merit value (see Fig. 7a(v) for chromatogram). The mole fractions for [X0], [X1], [X2] and [X3] were 0.007, 0.535, 0.373 and 0.085, respectively, corresponding to values of 0.909 and 1.43 for [X12] and
12, an initial feasible point x0 was found at N = 21. The same point turned out to be both the best feasible point and the point with the lowest overall merit value (see Fig. 7a(v) for chromatogram). The mole fractions for [X0], [X1], [X2] and [X3] were 0.007, 0.535, 0.373 and 0.085, respectively, corresponding to values of 0.909 and 1.43 for [X12] and ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 in close agreement with the trade-off curve of Fig. 7c. Hence, given the successful discovery of a fully feasible solution in run V, it is evident that data generated in an initial optimisation run based on unsatisfiable constraints (i.e. run IV) may nonetheless still be used to identify more appropriate constraints for future runs. In this way, it is easy to learn from experience and progressively modify constraints over a number of repeat runs until the constraints are appropriately matched to the underlying chemical system.
12 in close agreement with the trade-off curve of Fig. 7c. Hence, given the successful discovery of a fully feasible solution in run V, it is evident that data generated in an initial optimisation run based on unsatisfiable constraints (i.e. run IV) may nonetheless still be used to identify more appropriate constraints for future runs. In this way, it is easy to learn from experience and progressively modify constraints over a number of repeat runs until the constraints are appropriately matched to the underlying chemical system.
While the merit functions proposed above are sensible choices for achieving the intended outcomes, they are not the only options. The same (or at least a similar) result should be obtained for any sensibly constructed merit function that has been designed to achieve a particular goal. Based on the trade-off curve of Fig. 7c, as an alternative to the merit function used for optimisation run V, the ratio ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 could be used as the principal property to be minimised, subject to [X12] lying in the constraint window [0.9, 1.0] (using here the same ΔF value of 0.3). The results of framing the merit function in this way were investigated in run VI. The chromatograms for the best feasible point and the best point are shown in Fig. 7a(vi) and can be seen to closely match those of the previous run, confirming the approximate equivalence of the optimisation criteria. The best feasible point had mole fractions of 0.007, 0.527, 0.378 and 0.087 for [X0], [X1], [X2] and [X3], corresponding to values of 0.906 and 1.393 for [X12] and
12 could be used as the principal property to be minimised, subject to [X12] lying in the constraint window [0.9, 1.0] (using here the same ΔF value of 0.3). The results of framing the merit function in this way were investigated in run VI. The chromatograms for the best feasible point and the best point are shown in Fig. 7a(vi) and can be seen to closely match those of the previous run, confirming the approximate equivalence of the optimisation criteria. The best feasible point had mole fractions of 0.007, 0.527, 0.378 and 0.087 for [X0], [X1], [X2] and [X3], corresponding to values of 0.906 and 1.393 for [X12] and ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 in reasonably close agreement with the best feasible point of run V. The best point by contrast had mole fractions of 0.004, 0.382, 0.458 and 0.157, corresponding to a favourable reduction in
12 in reasonably close agreement with the best feasible point of run V. The best point by contrast had mole fractions of 0.004, 0.382, 0.458 and 0.157, corresponding to a favourable reduction in ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 (to 0.833) at the expense of an unfavourable reduction in [X12] (to 0.840).
12 (to 0.833) at the expense of an unfavourable reduction in [X12] (to 0.840).
Discussion and conclusion
The results presented above illustrate the use of self-optimisation in two distinct forms: the first form, blind discovery, relates to the optimisation of an unknown system, for which little information is available at the outset; while the second, rediscovery, relates to a repeat optimisation of a (partially) known system. In the case of blind discovery, it is not known in advance what can be achieved by the system. Physically plausible constraints must therefore be proposed on the basis of physicochemical intuition in the hope that an acceptable solution will be attained. The acceptability or otherwise of the solution is determined by the appropriateness of the constraints chosen. In cases where the solution is not acceptable to the user, blind optimisation may be straightforwardly followed by one or more refinement stages, in which the constraint windows are iteratively modified to achieve a superior outcome.Rediscovery relates to repeat optimisations of a well understood system for which a near optimal outcome is known in advance, but the detailed reaction conditions needed to achieve that outcome remain to be discovered. This might be the case, for instance, when resuming a previously optimised reaction after changing reagent batches or otherwise servicing/modifying the reactor, or on transferring the reaction to a similar, but untested, reactor. In such cases, it is reasonable to expect broadly equivalent behavior across the reaction runs and between reactors, but the detailed mapping of reaction conditions onto the final product may differ due to slight differences in reagent compositions or the mechanical configuration of the reactor(s).
Most of the optimisation runs reported above were carried out in the manner of blind runs, where we postulated appropriate constraints without using information gained in previous runs to guide our choice. Rather loose constraints were applied that had a significant chance of being satisfied immediately, recognising they could if necessary be tightened in subsequent runs to achieve a superior outcome. Run V is an example of rediscovery in the sense that we used the trade-off information acquired during run IV to identify an achievable solution with an acceptable mole fraction distribution. We then modified the upper limit on ![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) 12 accordingly to deliver that solution in run V (run VI may be considered an example of re-optimisation for similar reasons).
12 accordingly to deliver that solution in run V (run VI may be considered an example of re-optimisation for similar reasons).
We stress again that the merit functions used here are constructed entirely on the basis of easily acquired physical information and consequently, once the appropriate constraints are established, they may be written down directly with no further work or mathematical manipulation being required on the part of the user. For the benefit of readers wishing to implement the procedure described in this paper, we have provided an easy-to-use self-contained software package (see https://github.com/jdmgroup/SNOBFit_for_chemical_optimisations) that takes care of the construction and subsequent optimisation of the merit function, together with detailed tutorial-style instructions. We hope the provision of this software will substantially simplify the implementation of self-optimising reactors, and so encourage their wider adoption by the general chemistry community.
Beyond the tuning of product distributions, the procedure used here is also applicable to reactions where product yield must be balanced against practical factors such as production rates and/or materials and energy costs. The approach has further applications in materials optimisation, where a compromise must frequently be reached between several physicochemical properties. For instance, using a conventional weighted product based multi-objective merit function, Krishnadasan et al.1 reported a self-optimising reactor that optimised the emission intensity of quantum dots at a chosen emission wavelength. Owing to the difficulty of identifying weights that accurately encapsulated the intended outcome, small (nm-level) deviations from the target wavelength were heavily penalized even when they resulted in a substantial improvement in emission intensity. Framing the same problem as a constrained optimisation – in which the intensity is maximized subject to the emission wavelength lying in a prescribed range – would allow the trade-off to be precisely encoded within the merit function in a way that more closely reflects typical user preferences.
In summary, we have described a simple procedure for constructing multi-objective merit functions for self-optimising reactors. Framing the problem as a constrained optimisation, in which a principal property is optimised subject to soft and hard constraints on the other parameters, allows the optimisation criteria to be set out in a manner that is intuitive even for the non-specialist. The specific method for constructing chemical utility functions used here offers substantial advantages over conventional approaches based on weighted sums and products, both in terms of their ease of construction and their mathematical behaviour. In particular, the merit function may be written down directly from the specified constraints without the need to tune weighing coefficients or penalty parameters, and given sufficient time (if satisfiable constraints are selected) the solution is guaranteed to minimise the lead property, while ensuring all other properties lie within the prescribed boundaries. The generic approach is not tied to any specific optimisation algorithm and consequently can be expected to simplify the implementation of self-optimising reactors in many situations, while at the same time yielding improved reaction products that more closely match user requirements.
Methods
Preparation of precursors for o-xylenyl C60 adducts
C60 was obtained from Solenne BV, while all other chemicals were obtained from Sigma-Aldrich. Sultine (1,4-dihydro-2,3-benzoxothiin 3-oxide) was synthesised using the protocol described in Kim et al.25 A stock solution of sultine was prepared by dissolving under argon the unpurified product in o-dichlorobenzene (o-DCB) at a concentration of 1.4 mg mL−1. A stock solution of C60 was prepared by dissolving under argon the as-received C60 in o-DCB at a concentration of 2 mg mL−1. The stock solutions were stored under argon for up to a week before use.Reactor setup
The reagent solutions were transferred to separate 500 mL flasks, where they were stored under argon and delivered to the reactor by a dual-channel continuous-flow syringe pump (Syrris Asia), using PTFE tubing (1 mm I.D., 2 mm O.D., Polyflon Technology Ltd.). The two solutions were merged using a static y-shaped mixer (PEEK, P-512, Upchurch Scientific). Using the same diameter PTFE tubing, the mixed reagents were passed helically around a heater formed from a solid 88 mm-diameter cylindrical block of aluminium containing three symmetrically disposed inset cartridge heaters (3/8′′ × 2′′, 150 W, RS Components Ltd.). The temperature of the heater surface was monitored using a K-type flag-style thermocouple (25 × 13 mm, FL-K-2M, Labfacility) connected to a microcontroller (Arduino Uno) via a thermocouple amplifier (MAX6675, Adafruit). The total length of tubing in contact with the heater was 119 cm, equating to a heated reactor volume of 0.931 mL. The heater was enclosed in a plastic box, containing two fans inset into the walls for air cooling. The heater and fans were controlled by the microcontroller, using the Arduino PID library. A back-pressure regulator (20 psi, PEEK, Upchurch Scientific) was placed at the outflow of the reactor. The destination of the product stream was controlled by an injection valve as described below. The total length of tubing in the reactor was 202 cm, equating to a total reactor volume V of 1.587 mL.On-line HPLC analysis
Eluent solvent (hexane/toluene, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) was passed through a pyrenylpropyl-functionalised silica column (BuckyPrep, Cosmosil) using an HPLC pump (Model 12-6, SSI). Sample loading and injection were controlled by an injection valve (MXP-7900, Rheodyne) connected to the outflow of the reactor via a sample coil (stainless steel, Upchurch Scientific, Vcoil = 5 μL). The sample transmittance after the column was monitored using a 390 nm light-emitting diode and an amplified silicon photodiode (OPT101, Texas Instruments), which were placed either side of transparent perfluoroalkoxy tubing (I.D. 0.50 mm, O.D 1/16 in, Upchurch Scientific). A second amplified silicon photodiode arranged at 90° to the LED allowed the signal from the first photodiode to be corrected for fluctuations in LED light intensity. The signals from the photodiodes were acquired using a data acquisition card (NI-6211, National Instruments) controlled by a MATLAB script.
3) was passed through a pyrenylpropyl-functionalised silica column (BuckyPrep, Cosmosil) using an HPLC pump (Model 12-6, SSI). Sample loading and injection were controlled by an injection valve (MXP-7900, Rheodyne) connected to the outflow of the reactor via a sample coil (stainless steel, Upchurch Scientific, Vcoil = 5 μL). The sample transmittance after the column was monitored using a 390 nm light-emitting diode and an amplified silicon photodiode (OPT101, Texas Instruments), which were placed either side of transparent perfluoroalkoxy tubing (I.D. 0.50 mm, O.D 1/16 in, Upchurch Scientific). A second amplified silicon photodiode arranged at 90° to the LED allowed the signal from the first photodiode to be corrected for fluctuations in LED light intensity. The signals from the photodiodes were acquired using a data acquisition card (NI-6211, National Instruments) controlled by a MATLAB script.
Manual operation
The heater, injection valve and syringe pump were controlled by a PC across the universal serial bus (USB). A custom-written MATLAB script was used to step through a pre-determined sequence of reaction conditions. The set-point temperature of the heater was updated at the start of each step. Following a delay of at least one minute as described below, the two syringe pumps containing the C60 and sultine solutions were set to the specified volumetric flow-rates (FC60and FSultine), with the injection valve oriented in the inject position (i.e. with the sample loop between the eluent stream and the column), so that the product flowed directly to the collection flask. The flow was allowed to stabilize for a duration Δt equal to twice the mean residence time (Δt = 2V/[FC60 + FSultine]). The injection valve was then switched to the load position (i.e. the sample loop was inserted between the product stream and the collection flask) and held there for a duration sufficient for 50 μL (= 10Vcoil) of fluid to pass through. With the product loaded in the sample coil, the injection valve was switched back to the inject position, causing the product to be carried by the eluent stream into the column. Chromatograms were obtained by recording the signals from the two photodiodes for thirteen minutes. The next step was started while the chromatogram from the previous step was still being recorded by first updating the target temperature and waiting for it to stabilize and then, at a time Δt before the end of the current HPLC measurement, setting the syringe pumps to infuse at the new flow rates.Automated operation
For ease of use a class-based MATLAB wrapper was written for the SNOBFit functions provided by Huyer and Neumaier.|| At the start of each optimisation run, using a Latin Hypercube design, SNOBFit selected a batch of npoint randomised data points inside the region bounded by the parameter constraints. In subsequent iterations, SNOBFit selected new data points for measurement in batches of size nreq. New batches were generated until the total number n of function evaluations exceeded a pre-set limit ncall (the final batch was carried out to completion). To initialise the soft optimisations, a feasible point x0 satisfying the condition p(x0) = 0 was first identified by running an unconstrained optimisation, using the penalty function p(x) as the objective function to be minimised. Once a feasible point had been found, soft merit values for all data points so far measured were calculated using eqn (1). The optimisation run was then restarted using the soft merit function f*(x) as the objective function. In cases where no feasible point had been found after fifty function evaluations, the soft optimisation was instead started using 2fmax − fmin as a proxy for a feasible point (see main text).The following SNOBFit parameters (see ref. 2) were used:
| Parameter | Value | Description |
|---|---|---|
| N | 3 | Number of reaction parameters |
| Δf | 0.02 | Uncertainty in f, used for fitting |
| n point | N + 4 = 7 | Number of points in initial batch |
| n req | N + 4 = 7 | Number of points in subsequent batches |
| n call | 100 | Maximum number of function calls |
| p | 0.3 | Probability of generating a point away from a minimum: used to control the balance of local and global searching. |
Data statement
The datasets generated during the current study are available in the Imperial College Box repository at:https://imperialcollegelondon.box.com/v/tuning-reaction-products
The optimisations were carried out using an easy-to-use, custom-written, class-based wrapper for SNOBFit which, together with detailed tutorial-style instructions, may be obtained from:
https://github.com/jdmgroup/SNOBFit_for_chemical_optimisations
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
B. W. is funded under an EPSRC Doctoral Training Centre in Plastic Electronics (grant number EP/G037515/1). J. B. acknowledges financial support from an EPSRC Doctoral Prize Fellowship (Imperial College). The authors are grateful to Mr. Simon Turner and Mr. Lee Tooley (Department of Chemistry, Imperial College London) for assisting in the construction of prototype instrumentation.References
- S. Krishnadasan, R. J. C. Brown, A. J. deMello and J. C. deMello, Lab Chip, 2007, 7, 1434–1441 RSC.
- D. C. Fabry, E. Sugiono and M. Rueping, React. Chem. Eng., 2016, 1, 129–133 CAS.
- B. J. Reizman and K. F. Jensen, Acc. Chem. Res., 2016, 49, 1786–1796 CrossRef CAS PubMed.
- K. M. Tibbetts, X.-J. Feng and H. Rabitz, Phys. Chem. Chem. Phys., 2017, 19, 4266–4287 RSC.
- N. Holmes and R. A. Bourne, in Chemical Processes for a Sustainable Future, ed. T. Letcher, J. Scott and D. Patterson, The Royal Society of Chemistry, 2015, pp. 28–43 Search PubMed.
- J. P. McMullen and K. F. Jensen, Org. Process Res. Dev., 2010, 14, 1169–1176 CrossRef CAS.
- N. Holmes, G. R. Akien, R. J. D. Savage, C. Stanetty, I. R. Baxendale, A. J. Blacker, B. A. Taylor, R. L. Woodward, R. E. Meadows and R. A. Bourne, React. Chem. Eng., 2016, 1, 96–100 CAS.
- N. Holmes, G. R. Akien, A. J. Blacker, R. L. Woodward, R. E. Meadows and R. A. Bourne, React. Chem. Eng., 2016, 1, 366–371 CAS.
- J. S. Moore and K. F. Jensen, Org. Process Res. Dev., 2012, 16, 1409–1415 CrossRef CAS.
- B. J. Reizman and K. F. Jensen, Chem. Commun., 2015, 51, 2–5 RSC.
- J. P. McMullen, M. T. Stone, S. L. Buchwald and K. F. Jensen, Angew. Chem., Int. Ed., 2010, 49, 7076–7080 CrossRef CAS PubMed.
- R. A. Bourne, R. A. Skilton, A. J. Parrott, D. J. Irvine and M. Poliakoff, Org. Process Res. Dev., 2011, 15, 932–938 CrossRef CAS.
- Z. Amara, E. S. Streng, R. A. Skilton, J. Jin, M. W. George and M. Poliakoff, Eur. J. Org. Chem., 2015, 2015, 6141–6145 CrossRef CAS.
- A. J. Parrott, R. A. Bourne, G. R. Akien, D. J. Irvine and M. Poliakoff, Angew. Chem., Int. Ed., 2011, 50, 3788–3792 CrossRef CAS PubMed.
- D. N. Jumbam, R. A. Skilton, A. J. Parrott, R. A. Bourne and M. Poliakoff, J. Flow Chem., 2012, 2, 24–27 CrossRef CAS.
- V. Sans, L. Porwol, V. Dragone and L. A. Cronin, Chem. Sci., 2015, 6, 1258–1264 RSC.
- D. E. Fitzpatrick, C. Battilocchio and S. V. Ley, Org. Process Res. Dev., 2016, 20, 386–394 CrossRef CAS.
- S. Krishnadasan, A. Yashina, A. J. DeMello and J. C. DeMello, in Advances in Chemical Engineering, ed. J. C. Schouten, Elsevier, Amsterdam, 2010, vol. 38, pp. 195–231 Search PubMed.
- R. T. Marler and J. S. Arora, Struct. Multidiscip. Optim., 2010, 41, 853–862 CrossRef.
- E. Triantaphyllou and B. Shu, Encycl. Electr. Electron. Eng., 1998, vol. 15, pp. 175–186 Search PubMed.
- J. R. S. C. Mateo, in Multi Criteria Analysis in the Renewable Energy Industry, Springer, London, 2012, pp. 19–22 Search PubMed.
- W. Huyer and A. Neumaier, ACM Trans. Math. Softw., 2008, 35, 1–25 CrossRef.
- S. Dallwig, A. Neumaier and H. Schichl, in Developments in Global Optimization, ed. I. M. Bomze, T. Csendes, R. Horst and P. M. Pardalos, Springer US, 1997, pp. 19–36 Search PubMed.
- Ö. Yeniay, Math. Comput. Appl., 2005, 10(1), 45–56 Search PubMed.
- K. Kim, H. Kang, S. Y. Nam, J. Jung, P. S. Kim, C.-H. Cho, C. Lee, S. C. Yoon and B. J. Kim, Chem. Mater., 2011, 23, 5090–5095 CrossRef CAS.
- D. J. Kang, H. Kang, C. Cho, K. Kim, S. Jeong, J.-Y. Lee and B. J. Kim, Nanoscale, 2013, 5, 1858–1863 RSC.
- X. Meng, W. Zhang, Z. Tan, C. Du, C. Li, Z. Bo, Y. Li, X. Yang, M. Zhen, F. Jiang, J. Zheng, T. Wang, L. Jiang, C. Shu and C. Wang, Chem. Commun., 2012, 48, 425–427 RSC.
- H. Kang, K. Kim, T. E. Kang, C.-H. Cho, S. Park, S. C. Yoon and B. J. Kim, ACS Appl. Mater. Interfaces, 2013, 5, 4401–4408 CAS.
- H. Seyler, W. W. H. Wong, D. J. Jones and A. B. Holmes, J. Org. Chem., 2011, 76, 3551–3556 CrossRef CAS PubMed.
- T. Martin and T.-S. Tan, in Proceedings of the Fifteenth Eurographics Conference on Rendering Techniques, Eurographics Association, 2004, pp. 153–160 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7re00123a |
| ‡ A flow synthesis for indene C60 adducts has previously been reported by Seyler et al.29 |
| § When the sultine flow rate (FS), the C60 flow rate (FC60) and the temperature (T) are plotted along the x, y and z axes, respectively, the constraints define a right prism shaped parameter space with vertical walls and a trapezoidal base (see Fig. 4) – the non-parallel sides of the base being due to the constraints imposed on the flow-rate ratio. SNOBFit by contrast accepts only box-bounded constraints, corresponding to a rectangular prism shaped parameter space. The trapezoidal flow constraints were handled by a two-stage transformation of the external variables FS and FC60 to box-bounded internal variables. The first stage involved a rotation of each coordinate [FS, FC60] by 45°, the angle between the axis of symmetry of the trapezium and the y-axis; while the second stage involved a mapping of each rotated coordinate to the internal rectangular space used by SNOBFit, using the shadow-map algorithm of Martin and Tan.30 |
| ¶ In this work, we were primarily interested in achieving fully feasible solutions, for which the exact ΔF value chosen is of secondary importance. Hence a common value of 0.3 was used for all constraints. |
| || http://www.mat.univie.ac.at/~neum/software/snobfit/. |
| This journal is © The Royal Society of Chemistry 2017 |