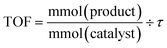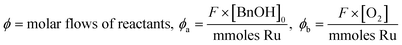Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Catalysis in flow: O2 effect on the catalytic activity of Ru(OH)x/γ-Al2O3 during the aerobic oxidation of an alcohol†
John B.
Brazier
a,
Klaus
Hellgardt
*b and
King Kuok (Mimi)
Hii
 *a
*a
aDepartment of Chemistry, Imperial College London, Exhibition Road, South Kensington, London SW7 2AZ, UK. E-mail: mimi.hii@imperial.ac.uk
bDepartment of Chemical Engineering, Imperial College London, Exhibition Road, South Kensington, London SW7 2AZ, UK. E-mail: k.hellgardt@imperial.ac.uk
First published on 4th January 2017
Abstract
Changes in the turnover frequency (TOF) of Ru(OH)x/γ-Al2O3 during aerobic oxidation of benzyl alcohol in a plug flow differential reactor were monitored online using an inline FTIR instrument over extended periods of time (up to 72 h). A new equation for catalyst deactivation is derived, to account for the different lengths of time the catalyst is exposed to the reactants (benzyl alcohol and O2). Catalyst activity and stability are dependent on the amount of O2 in the system; catalyst deactivation can be attributed to two simultaneous processes: a fast and reversible inhibition by the benzoic acid side product and a slower and irreversible loss of catalytic sites due to reduction of Ru. At steady state, the reaction rate is zero-order in benzyl alcohol and partial positive order in O2. Finally, the suitability of a packed-bed (integral) reactor for the reaction is discussed.
Introduction
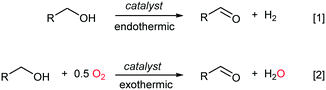
In recent years, catalytic aerobic oxidation reactions in the liquid phase have become an important topic in catalysis research, driven by the need for reaction technologies that can be employed for biomass conversion,1 and for more sustainable processes for the fine chemicals and pharmaceutical industries.2,3 In terms of process safety and control, it is widely acknowledged that aerobic oxidation reactions are best implemented in continuous flow using heterogeneous catalysts.4 Conversion of alcohols to their corresponding carbonyl compounds (aldehydes or ketones) is an important functional group transformation in organic chemistry. This can be achieved most atom-efficiently by the catalytic dehydrogenation of an alcohol to generate an equivalent of H2 (Scheme 1, eqn (1)), which is an endothermic process. Alternatively, O2 can be added to provide the thermodynamic driving force for the reaction to proceed exothermally without compromising its ‘green’ credentials, as only water is generated as a by-product (Scheme 1, eqn (2)). Currently, the oxidative dehydrogenation of alcohols is used industrially for the production of formaldehyde and acetaldehyde, as well as fragrance aldehydes from C5–C14 aliphatic alcohols; all these were performed in the gas phase over heterogeneous catalysts.5Pt, Pd, Au and Ru are frequently reported to have very good catalytic activity and selectivity for the aerobic oxidation of alcohols to aldehydes and ketones in an organic solvent,6 although none of these have yet been implemented on an industrial scale. In a flow regime, the longevity of a catalyst is a major determinant of its economic viability, therefore it is important to understand how catalyst activity (TOF) is affected by reaction parameters, including temperature and pressure, as well as how it may be affected by the length of time the catalyst is exposed to the reactants. Interestingly, O2 has been simultaneously reported to have both positive and negative effects on the catalyst activity; while the catalytic activity of Pd catalysts has been directly correlated to the number of oxidized PdO sites,7,8 Pt- and Au-based catalysts are known to deactivate as a result of over-oxidation of the metal.9–11
In contrast, the role of O2 in Ru-catalysed aerobic reactions is largely unknown and a subject of some considerable debate. Ru(OH)x/γ-Al2O3 was first reported by Yamaguchi and Mizuno12,13 to be an active catalyst for the selective oxidation of a wide range of alcohols to aldehydes and ketones. In these reports, reactions were performed in a batch reactor, with azeotropic removal of water and under an O2 flow. Under these conditions, the reaction rate was found to be insensitive to O2 pressure (between 0.5–3.5 bar). Subsequently, we have shown that Ru(OH)x/γ-Al2O3 can be employed in a packed bed.14 In this system, a solution of the alcohol was pre-saturated with O2 prior to introduction to the catalyst bed, and the differential reactor was operated in a continuous recycle mode (semi-batch). Under these conditions, the reaction is accelerated by an increase in the O2 pressure/concentration, contradicting the result in the earlier report.
On the other hand, the stability of the catalyst was first investigated on a continuous flow platform by Bavykin et al., using a multichannel microreactor with staged injection of O2.15 In this work, the oxidation of benzyl alcohol was used as a model reaction to investigate the deactivation of Ru(OH)x/γ-Al2O3. Operating under a kinetic regime, the reaction was reported to be zero-order in O2, and catalyst deactivation was reported to follow a single exponential decay:
| TOFt = TOF0 × e−kt | (1) |
Note that the simple expression does not take into account the concentrations of the reactants.16 More recently, the stability of a Ru(OH)x/γ-Al2O3 catalyst was reassessed by Mannel et al. using a packed bed reactor over an extended period of time (72 h).17 In this system, the oxidation of benzyl alcohol was performed under a slug flow regime using 8% O2 in N2 (below the limiting O2 concentration of the solvent). Under these (oxygen-lean) conditions, catalyst deactivation was neither linear nor first order. The authors reported ‘a rapid decrease in activity during the first 50 turnovers, but the activity stabilizes substantially beyond this point’, and the reaction rate (keff) was correlated with the quantity of benzyl alcohol that was exposed to the catalyst (ρ), which was fitted empirically to an extended exponential equation:
| keff = k0e−(βρ)n | (2) |
| TOFt = TOF0e−(βρ)n | (3) |
In these forms, catalyst deactivation (β) can be correlated to the contact time between the catalyst and benzyl alcohol (ρ). However, there is uncertainty to the meaning of the power value (n = 0.156), which cannot be correlated to any reaction parameter. Moreover, the effect of O2 is not accounted for using this model.
It is entirely possible that O2 can have important effects on both the intrinsic kinetics of the catalytic reaction (reaction order) and the deactivation pathway(s). In order to understand the different roles of O2, we initiated a study to correlate the catalyst activity and stability of Ru(OH)x/γ-Al2O3 to the molar flow of both of the reactants (benzyl alcohol and O2) under different temperatures and pressures. The result of the study revealed that O2 does have a rather complex role: while an increased O2 pressure accelerates the reaction rate and prevents the loss of active sites (via Ru reduction), it also simultaneously generates benzoic acid that pacifies the active catalyst sites.
Experimental
Materials
5 wt% Ru(OH)x/γ-Al2O3 (4.84 wt% in Ru) was purchased from Alfa Aesar and sieved (150–250 μm) prior to use. Where required, catalysts were diluted with SiC (Alfa Aesar) which was sieved (250–425 μm), washed with water and ethanol, and dried prior to use. Benzyl alcohol (Sigma-Aldrich) was distilled from sodium borohydride prior to use. All solutions were prepared under nitrogen using dry tert-amyl alcohol (Sigma-Aldrich) and stored in the reagent reservoir under a drying tube (CaSO4).Methods
Cartridges were packed with catalyst under suction to promote efficient packing. A typical cartridge contains 300 mg of Ru(OH)x/γ-Al2O3 or 1.4 g of SiC. Accurate values were recorded for each experiment. The internal voidage of the catalyst bed was calculated by the difference in mass between a packed cartridge when dry and when filled with solvent and the density of the solvent.All reactions were performed using a commercial X-Cube™ reactor, which we have previously employed in the aerobic oxidation of alcohols.14 The catalyst was loaded into cylindrical cartridges (4 mm × 70 mm) and mounted into the system, which allows control of reactor temperature, pressure, and volumetric flow rates via two piston pumps and saturation of the reactant solution with O2 at ambient temperature via a gas mixer. Gas is added to maintain a 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 liquid-to-bubble ratio in the flow prior to the catalyst cartridge. The dissolved O2 concentration can be controlled by changing the operating pressure of the system (electronic back pressure regulator). Oxygen concentrations for each set of conditions were predicted using the CAPE-OPEN Flowsheet Environment with a Peng–Robinson model.18
1 liquid-to-bubble ratio in the flow prior to the catalyst cartridge. The dissolved O2 concentration can be controlled by changing the operating pressure of the system (electronic back pressure regulator). Oxygen concentrations for each set of conditions were predicted using the CAPE-OPEN Flowsheet Environment with a Peng–Robinson model.18
In a typical experiment, tert-amyl alcohol (t-AmOH) and oxygen were passed through a packed catalyst cartridge at the required temperature and pressure at 1 mL min−1 for 30 minutes before the flow rate was adjusted to that required for the experiment and the system was allowed to stabilise for a further 5 minutes. The inlet stream was switched to a solution of benzyl alcohol (100 mM in dry t-AmOH) (time = 0) and the fraction collector started simultaneously.
A Mettler-Toledo FlowIR™ instrument, equipped with a diamond window, was employed at the outlet of the reactor to monitor the outlet stream. Spectra were recorded between 4000 cm−1 and 650 cm−1 with a resolution of 8 cm−1 over 30 seconds. Post-reaction analysis of the spectra was performed on the second derivative of the spectrum. Peak area was measured between the local minima of the 2nd derivative either side of the peak at 830 cm−1 and to a baseline drawn between the same points.
A Pharmacia Biotech RediFrac fraction collector equipped with a drop detector was employed after the FlowIR™ to collect samples for analysis by gas chromatography. Samples were collected by setting the sampling time for each fraction, ensuring that a minimum of 0.5 mL was collected. At least three samples were collected at each time point.
Conversion of benzyl alcohol was monitored using an HP6890 gas chromatography system fitted with an HP5 column (30 m × 0.320 mm × 0.25 μm). Samples were diluted with methanol containing a standard (4-tert-butylphenol, 30 mM) and the conversion and selectivity were determined using a calibration plot for products and reactants against known standards.
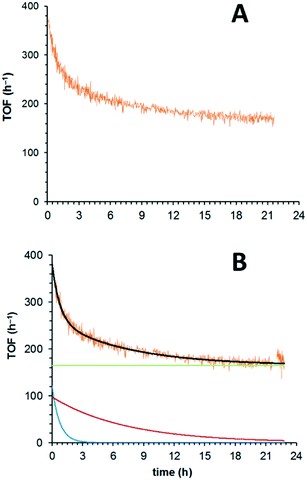
Catalyst activity is presented as Turnover Frequency (TOF) and is plotted against time (min or h). The reaction parameters were carefully adjusted so that the system operated below complete conversion for each single pass. Turnover frequency (TOF) is calculated using the formula:
Data fitting was performed using Origin 201519 using a Levenberg–Marquardt iteration algorithm. The deactivation models used incorporate a term for the stoichiometric flow rate (moles of substrate per mole of metal per hour), ϕ, thus allowing different flow rates and loadings of catalyst to be compared.
Results and discussion
Toluene has been frequently employed as a solvent in the aerobic oxidation of benzyl alcohol in earlier studies.14,15,17 However, it is a poor choice for kinetic and mechanistic studies as it can oxidise to benzyl alcohol, or be formed as a by-product from the disproportionation of benzyl alcohol (to benzaldehyde and toluene).20,21 With this in mind, it was decided that a tertiary alcohol be employed as an alternative solvent to allow a good material balance. Equation of state calculations (Peng–Robinson model) revealed that the expected oxygen concentration in tert-amyl alcohol is comparable to that in toluene across our operating range (Table S1, ESI†). The limiting oxygen concentration (LOC) for combustion is similar to that of toluene at elevated pressures, providing it with similar safety characteristics in these reactions.22 Furthermore, tert-amyl alcohol is a good solvent for organic compounds and remains as a liquid over a wide range of temperatures and pressures, making it particularly suitable for use in a flow reactor (Scheme 2).Catalyst deactivation
The studies were conducted using a commercial (X-Cube™) flow reactor under plug flow conditions.14 The oxidation was initially performed using a full catalyst cartridge of 5 wt% Ru(OH)x/γ-Al2O3 (containing 125 μmol Ru) at three temperatures (120, 150 and 180 °C), to determine if its deactivation profile exhibits temperature dependence. In order to negate the effect of the different O2 solubility at different temperatures, a large excess of dissolved O2 (≥7 equiv.) was applied by pre-saturating the mobile phase under 25 bar of O2, prior to exposure to the catalyst packed bed, i.e. the system is operated as an integral reactor. The catalytic activity (TOF) and selectivity (benzaldehyde vs. benzoic acid) were assessed by monitoring the output of the system over the first 3 hours of exposure to a solution of benzyl alcohol in tert-amyl alcohol (Fig. 1). At 120 °C, catalyst deactivation was rapid: TOF decreased from 13.1 h−1 to 5.7 h−1 (Fig. 1A). Formation of benzoic acid was not observed under these conditions. By raising the temperature to 150 °C, complete single-pass conversion of the alcohol was obtained, but slowly decreasing to 95% over the period of observation. Concomitantly, a small amount of benzoic acid (ca. 0.4%) can be detected in the output throughout the experiment (Fig. 1B). Finally, at 180 °C, complete conversion of benzyl alcohol can be maintained over 3 hours. However, the reaction also becomes less selective, producing up to 4.5% benzoic acid (Fig. 1C).The reduction in rate of deactivation with elevated temperature is indicative of the passivation of the catalytic sites by adsorbates. A more in-depth study requires online monitoring of the TOF over extended reaction times. This was achieved by using an IR detector fitted with a flow cell (FlowIR™), attached to the outlet of the reactor for continuous measurement of the reaction stream. The concentration of benzaldehyde (PhCHO) in the reaction stream was determined by using the area under a diagnostic peak (at 830 cm−1) in the second derivative of the spectrum. Selected samples collected over the period of the experiment were also subjected to GC analysis for secondary verification.
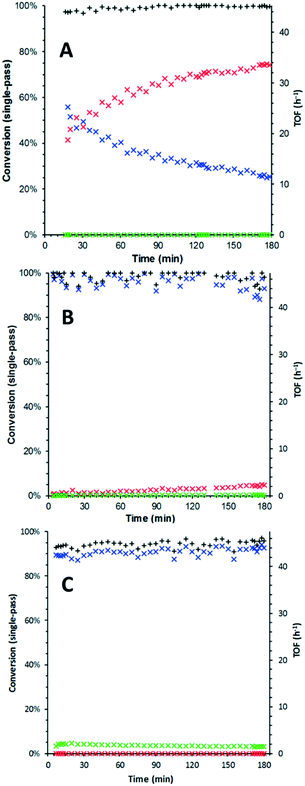
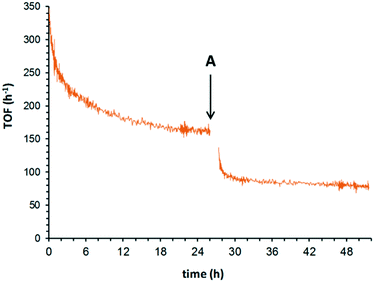
For extended studies, the catalyst was diluted by dispersing in silicon carbide which is chemically inert in the reaction, has high thermal conductivity and whose low porosity ensures a small pressure drop across the cartridge. Reducing the amount of catalyst (approx. 18 times) allowed the deactivation profile to be observed, even at the highest temperature (180 °C). Under these conditions, the initially high activity of the catalyst (TOF: 380 h−1) rapidly reduces (ca. 220 h−1 after 3 h) and approaches a quasi-steady state (TOFSS = 170 h−1) towards the end of the experiment (Fig. 2A). What is clearly apparent is that the deactivation profile does not follow a simple, single exponential decay (eqn (1)), nor can our data be fitted satisfactorily to the extended exponential equation put forward by Mannel et al. (eqn (3)), without relaxing the constraint of initial TOF0 (Fig. S1, ESI†).
Working on the hypothesis that there is more than one deactivation pathway operating in our system, we were able to fit the data to a double first-order decay exponential equation (eqn (4)):
| TOFt = TOFd(e−αρ + e−βρ) + TOFSS | (4) |
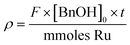
This appears to produce an excellent fit to the experimental data. However, it cannot distinguish the individual effects imposed by each reactant, which were introduced to the catalyst bed sequentially in these experiments. To account for this, eqn (4) can be rewritten as eqn (5), to allow for the different molar flows of benzyl alcohol and O2, with the introduction of an additional time constant (τ) to account for the amount of time the catalyst is exposed to the aerated solvent solution, prior to the introduction of a step change in benzyl alcohol:
| TOFt = TOFd(e−αϕat + e−βϕb(t+τ)) + TOFSS | (5) |
(note: ϕ × t = ρ in the previous equations), α = deactivation rate constant due to benzoic acid poisoning (directly related to the amount of benzyl alcohol), β = deactivation rate constant due to changes in the catalyst's redox state, and τ = delay between the introduction of O2 and benzyl alcohol to the catalyst.
Thus, the overall process can be described as a composite of three underlying processes. Eqn (5) can be fitted to the experimental data to yield information on each of these pathways (Fig. 2B): a fast deactivation, associated with the increased formation of benzoic acid, due to over-oxidation of benzyl alcohol to which the catalyst has been exposed (Fig. 2B, blue exponential curve, α = 3.24 × 10−3). This process is approximately 33 times faster than a simultaneous deactivation associated with O2 (Fig. 2B, red exponential curve,β = 9.95 × 10−5). The system eventually converges upon a final quasi-steady state of 165 h−1 (Fig. 2B, green line, TOFSS). Clearly, TOFss may be affected by other, slower, deactivation processes, but this will require extending the study beyond the current experimental timescale (72 hours) for these to be detected and quantified.
In eqn (5), TOFd directly correlates to, and reflects, the number of catalytic sites that are subjected to the two deactivation processes, and we assume that benzoic acid and O2 compete for and deactivate the same catalyst sites. Alternatively, eqn (5) can also be expanded further to eqn (6):
| TOFt = TOFae−αϕat + TOFbe−βϕb(t+τ) + TOFSS | (6) |
This will allow for each deactivation process to be assessed separately, for it is known that certain catalytic sites/surfaces can be more susceptible to certain deactivation processes. Fitting of eqn (6) to our experimental data does reveal a marginal improvement in terms of fitting error compared to eqn (5) (Fig. S3, ESI†). However, the addition of another parameter is not judged to be warranted at this stage of the work, as we are not sufficiently confident to interpret our data according to a separate site model.
In order to evaluate the parameters in eqn (5), two further experiments were conducted at a different pressure (10 bar) and temperature (120 °C), and the results are summarised in Table 1 (see also Fig. S3–S5, ESI†).
| Conditions | TOF0b/h−1 | TOFd/h−1 | α/× 10−3 | β/× 10−5 | TOFSS/h−1 | R 2 |
|---|---|---|---|---|---|---|
| a General reaction conditions: BnOH (100 mM in t-AmOH), 0.5 mL min−1. b TOF0 = TOFd + TOFss. c Goodness-of-fit. | ||||||
| 180 °C, 25 bar | 282 | 114.8 | 3.24 | 9.95 | 167.2 | 0.979 |
| 180 °C, 10 bar | 337.5 | 115.4 | 2.59 | 53.9 | 222.1 | 0.944 |
| 120 °C, 10 bar | 23.3 | 19.5 | 7.15 | 300 | 3.8 | 0.971 |
At 180 °C and 25 bar of O2, a TOF0 of 282 h−1 may be extrapolated from the fitted data. Reducing the pressure to 10 bar causes an apparent increase in the TOF0.23 This is attributed to the fact that the catalyst bed is exposed to O2 prior to the introduction of the alcohol, i.e. benzyl alcohol is introduced into a catalyst bed that is pre-saturated with O2 at the beginning of the experiment. This can lead to the rapid formation of benzoic acid that can poison the active sites. At lower O2 pressure, this over-oxidation of alcohol to benzoic acid is reduced, which is reflected in a higher observed TOF0.
At the same temperature (180 °C), the values of α are similar at different pressures, indicating that catalyst poisoning by benzoic acid is independent of [O2]. In contrast, β increases by over an order of magnitude at lower pressure, suggesting the reduction of Ru as the secondary deactivation pathway. Overall, the same observed TOFd was observed at 180 °C, indicating that the deactivation by benzoic acid is the dominant process at high temperatures.
As expected, lowering the reaction temperature to 120 °C leads to reduced productivity (TOF0 = 23.3 h−1). Under these conditions, α increases as the desorption of benzoic acid from the active site becomes less favourable. Under these conditions, the second deactivation process becomes even more rapid, to the extent that β becomes competitive with α.
More significantly, larger β values at lower temperatures and pressures are reflective of a process whereby active sites are lost due to insufficient catalyst regeneration by O2. This would suggest that the active catalyst involves Ru in a higher oxidation state, previously proposed as RuO2 or Ru(OH)3(OH2)3.24–26
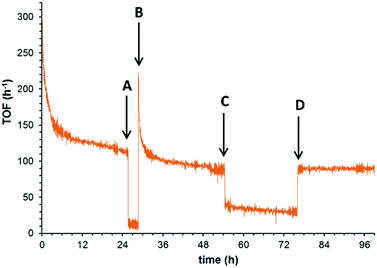
Having identified the two major deactivation pathways, the nature of these processes was further interrogated in situ, by introducing step changes to the reactant feed over the course of an extended experiment. In earlier papers, benzoic acid (an over-oxidation product) has been implicated as a source of catalyst poisoning,12,15 which is supported by the direct observation of benzoic acid in the spent catalyst, and a brief recovery of catalyst activity after rinsing of the catalyst with a basic solution (pH = 12). In this study, the catalytic system was operated at 180 °C under 25 bar of O2 over 24 h, when the TOF decreased from 300 to 114 h−1. The benzyl alcohol feed was then replaced by the solvent (Fig. 3, perturbation A), and the catalyst system was subjected to solvent rinsing for 3 hours while the O2 delivery was maintained. Upon the reintroduction of the benzyl alcohol (perturbation B), a recovery of the TOF was observed (ca. 220 h−1), which quickly returned (α = 6.5 × 10−3) to the level of activity prior to perturbation A, in accordance with previous suggestions that the active site is inhibited by the adsorption of the benzoic acid side product. Furthermore, the underlying slow deactivation process is unaffected by these perturbations, i.e. the loss of catalyst sites by the redox process appears to be irreversible under these conditions. The reversibility of the benzoic acid inhibition is confirmed by switching the reactant feed for a solution containing 5 mM benzoic acid and 95 mM benzyl alcohol in tert-amyl alcohol (perturbation C). As expected, this resulted in a nearly instantaneous drop in TOF. After 21 h, the undoped reactant feed was reinstated, whereupon the TOF immediately returned to its prior level. This shows that the acid poisoning of the active site is a fast and reversible process.
A similar approach was adopted to study the effect of O2 concentration and pressure (Fig. 4). After allowing the catalytic system to establish a quasi-steady state turnover at 180 °C under 25 bar of O2, lowering the O2 pressure to 10 bar (ref. 27) induced an immediate decrease in the TOF from 154 h−1 to 73 h−1. This supports our earlier observations that the reaction has a partial positive order in O2 while it operates in a plug flow reactor.14 This contradicts the result of earlier studies by Yamaguchi et al., where the reaction was reported to be zero order in O2. However, it is noted that the experiments were conducted using a batch reactor, over a small pressure range of 0.2–3 bar.12 Under these conditions, it might have been difficult to observe the order due to significant O2 starvation, i.e. the reaction rate is limited by the rate of diffusion into the liquid phase. Similarly, in the flow reactor system reported by Bavykin et al.,15 it was also claimed that the order in O2 was zero. Closer inspection of their data28 reveals that there was, indeed, a positive order in O2 observed between 4–16 bar. The reaction order for O2 was drawn from data acquired at 16 and 24 bar, where the data are not sufficiently accurate to rule out a partial reaction order.
Reaction order in benzyl alcohol
These observations prompted us to re-examine the reaction order of benzyl alcohol in the quasi-steady state regime, i.e. where catalyst deactivation is no longer a significant process. Under these conditions, the single-pass conversion of benzyl alcohol was obtained at different flow rates, which afforded a zero-order rate plot (Fig. 5, R2 = 0.991) with a kobs of 0.94 mM s−1. The analysis was subsequently repeated at 10 bar and the reaction remained zero order in BnOH (Fig. S6, ESI†), confirming that the observed rate is not subject to mass transfer limitations. This would imply that the first-order dependence observed by previous studies12,14 is most likely the result of (poor) transport of the reactant to the active site. Also, catalyst deactivation was not explicitly taken into account (during which time the number of active catalyst sites decreased rapidly). The experiment was repeated at different temperatures at 10 bar (120–180 °C), to yield an Arrhenius plot (Fig. S7, ESI†), giving an apparent activation energy of 94.9 kJ mol−1 for the oxidation of benzyl alcohol to benzaldehyde in t-AmOH. This value is broadly in agreement with that previously reported, recorded in toluene (78.2 kJ mol−1).15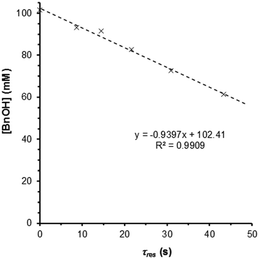 | ||
| Fig. 5 Zero-order rate plot obtained for a Ru(OH)x/Al2O3 catalyst (7.0 μmol Ru), operating in the quasi-steady state region. Conditions: BnOH (100 mM in t-AmOH), 25 bar O2, 0.5–2.5 mL min−1. | ||
Overall mechanism and rate equation
The catalytic process is generally believed to involve 4 distinctive steps (Scheme 3): the active catalyst is a ruthenium hydroxide species that can undergo metathesis with an alcohol (step A) to form a surface alkoxide species. β-Hydride elimination ensues (step B) to generate a surface hydride and an adsorbed benzaldehyde, which is released in the next step. The insertion of O2 into the Ru–H forms an unstable peroxide (step C) that eliminates an oxygen atom to regenerate the active site (step D). The revised kinetic orders (zero order in benzyl alcohol and partial positive order in O2) allowed us to identify step C as turnover-limiting during steady-state operation of the catalyst. The results of the present study allow us to interpolate deactivation pathways to the catalytic cycle (indicated in red in Scheme 3), where a ‘Janus’ effect of O2 is highlighted: while the presence of excess O2 is beneficial for turnover and prevents irreversible loss of active catalyst sites, too much of the gaseous reactant can cause over-oxidation of the product to benzoic acid, which can inhibit catalyst activity by reversible binding.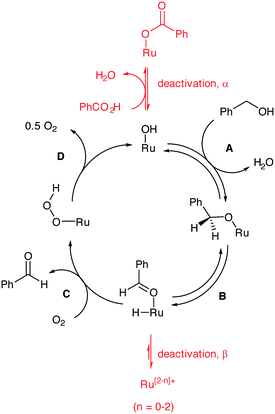 | ||
| Scheme 3 The catalytic cycle for the Ru-catalysed oxidation of benzyl alcohol with deactivation pathways incorporated. | ||
In a previous publication,14 we have shown the kinetics of the catalytic reaction operating via a Mars–van Krevelen-type mechanism, which can be described by two main processes as shown in eqn (6) and (7), from which the rate equation (eqn (8)) can be derived:
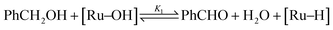 | (7) |
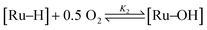 | (8) |
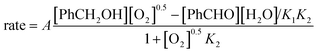 | (9) |
As the catalyst regeneration step is rate-limiting, k2 is small, so K2 ≪ 1; therefore, eqn (9) can be simplified into eqn (10):
| rate = [cat]tot(k1K2[PhCH2OH][O2]0.5 − k−1[PhCHO][H2O]) | (10) |
In this system, the relative number of catalyst sites is much smaller than the amount of benzyl alcohol present ([cat]tot ≪ [Ph2CH2OH]). Hence, the observed order in benzyl alcohol becomes effectively zero. Under these conditions, a partial positive order in O2 becomes evident, particularly at high concentrations of benzyl alcohol at lower pressures. As [O2] increases, the reaction rate will eventually approach zero-order dependency, as observed by Bavykin et al. at high pressures.15
Conclusions
During the oxidation of benzyl alcohol to benzaldehyde, the Ru(OH)x/γ-Al2O3 catalyst deactivates through two parallel mechanisms: a fast process due to adsorption of benzoic acid and a slower process caused by loss of active sites, due to insufficient regeneration of the catalyst by O2. New equations (eqn (5) and (6)) incorporating two deactivation constants α (for inhibition by PhCO2H) and β (loss of active sites by reduction), as well as different molar flow rates of the reactants, have been derived, which allow for each of these processes to be interrogated independently in a plug-flow reactor. These equations can be applied to the study of other aerobic oxidation catalysts operating under continuous flow in different reactor configurations, thus allowing direct comparisons to be made between catalyst performance. Potentially, further correlations can be made to specific catalyst surfaces (by using eqn (6)). By operating in the quasi-steady state regime of the integral plug-flow reactor, we have found the reaction to be zero order in benzyl alcohol and a partial positive order in O2, thus identifying the catalyst regeneration step to be rate-limiting.Our study highlights the importance of on-line deactivation studies as a pre-requisite for the proper investigation of kinetics, which can only be achieved in a flow reactor. We have demonstrated, in this case, that fast deactivation processes may interfere with the correct determination of reaction order, if they are not properly accounted for. With a zero order in benzyl alcohol (at quasi-steady state), our system allows us to determine the intrinsic catalytic activity of Ru(OH)x/γ-Al2O3 that is independent of pre-equilibria, deactivation and transport processes.
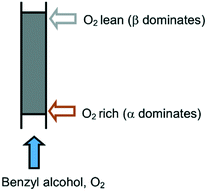
Last but not least, the results from this study call into question the suitability of plug flow reactors for aerobic oxidation reactions. Given that O2 exerts opposing effects on the deactivation processes, the existence of an O2 concentration gradient causes different degrees of deactivation along the length of the reactor (Fig. 6), which may be exacerbated by a high single-pass conversion (integral reactor) and a relatively low concentration of O2. Over time, this will cause speciation of the catalyst species along the packed bed that could compromise both the activity and selectivity of the system. This may be overcome by controlling the exposure of the catalyst to O2, for example, by reversing the flow of the reactant periodically, or by using a membrane reactor to implement an even distribution of O2 along the catalyst bed, such as a tube-in-tube reactor reported recently by Gavriilidis and co-workers.29
Acknowledgements
The work was supported by an EPSRC award (grant number: EP/L003279/1). We are grateful to our industrial collaborators (AstraZeneca, GlaxoSmithKline, Johnson Matthey, Syngenta) for their participation in this project and Mettler-Toledo Autochem for the loan of the FlowIR™ instrument.Notes and references
- S. E. Davis, M. S. Ide and R. J. Davis, Green Chem., 2013, 15, 17–45 RSC.
- R. Ciriminna, V. Pandarus, F. Beland, Y.-J. Xu and M. Pagliaro, Org. Process Res. Dev., 2015, 19, 1554–1558 CrossRef CAS.
- A. Gavriilidis, A. Constantinou, K. Hellgardt, K. K. Hii, G. J. Hutchings, G. L. Brett, S. Kuhn and S. P. Marsden, React. Chem. Eng., 2016, 1, 595–612 CAS.
- B. Pieber and C. O. Kappe, in Topics in Organometallic Chemistry, ed. T. Noel, Springer, 2016, pp. 97–136 Search PubMed.
- C. Kohlpaintner, M. Schulte, J. Falbe, P. Lappe, J. Weber and G. D. Frey, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2000 Search PubMed.
- Liquid Phase Aerobic Oxidation Catalysis: Industrial Applications and Academic Perspectives, ed. S. S. Stahl and P. L. Alsters, Wiley, 2016 Search PubMed.
- C. M. A. Parlett, L. J. Durndell, A. Machado, G. Cibin, D. W. Bruce, N. S. Hondow, K. Wilson and A. F. Lee, Catal. Today, 2014, 229, 46–55 CrossRef CAS.
- Z. Zhao, J. T. Miller, T. Wu, N. M. Schweitzer and M. S. Wong, Top. Catal., 2015, 58, 302–313 CrossRef CAS.
- C. M. Zhou, Z. Guo, Y. H. Dai, X. L. Jia, H. Yu and Y. H. Yang, Appl. Catal., B, 2016, 181, 118–126 CrossRef CAS.
- V. R. Gangwal, J. van der Schaaf, B. F. M. Kuster and J. C. Schouten, J. Catal., 2005, 232, 432–443 CrossRef CAS.
- T. L. Lu, Z. T. Du, J. X. Liu, H. Ma and J. Xu, Green Chem., 2013, 15, 2215–2221 RSC.
- K. Yamaguchi and N. Mizuno, Chem. – Eur. J., 2003, 9, 4353–4361 CrossRef CAS PubMed.
- K. Yamaguchi and N. Mizuno, Angew. Chem., Int. Ed., 2002, 41, 4538–4542 CrossRef CAS PubMed.
- N. Zotova, K. Hellgardt, G. H. Kelsall, A. S. Jessiman and K. K. Hii, Green Chem., 2010, 12, 2157–2163 RSC.
- D. V. Bavykin, A. A. Lapkin, S. T. Kolaczkowski and P. K. Plucinski, Appl. Catal., A, 2005, 288, 175–184 CrossRef CAS.
- It is also important to note that the TOF values were calculated based on a fairly large amount of catalyst (1 g), low conversions of benzaldehyde (20%), and short reaction times (75 min), i.e. the system operates under a pseudo-steady state, whereby the deactivation process (k) is relatively slow, which is asserted by the authors in the selected system..
- D. S. Mannel, S. S. Stahl and T. W. Root, Org. Process Res. Dev., 2014, 18, 1503–1508 CrossRef CAS PubMed.
- http://www.cocosimulator.org/ .
- OriginPro 2015 Sr2 b9.2.272, OriginLab Corporation, Northampton, MA, USA Search PubMed.
- (a) D. M. Meier, A. Urakawa and A. Baiker, J. Phys. Chem. C, 2009, 113, 21849–21855 CrossRef CAS; (b) S. Meenakshisundaram, E. Nowicka, P. J. Miedziak, G. L. Brett, R. L. Jenkins, N. Dimitratos, S. H. Taylor, D. W. Knight, D. Bethell and G. J. Hutchings, Faraday Discuss., 2010, 145, 341–356 RSC.
- A. Villa, D. Ferri, S. Campisi, C. E. Chan-Thaw, Y. Lu, O. Krocher and L. Prati, ChemCatChem, 2015, 7, 2534–2541 CrossRef CAS.
- P. M. Osterberg, J. K. Niemeier, C. J. Welch, J. M. Hawkins, J. R. Martinelli, T. E. Johnson, T. W. Root and S. S. Stahl, Org. Process Res. Dev., 2015, 19, 1537–1543 CrossRef CAS PubMed.
- At 10 bar, the reaction is limited in dissolved [O2] (0.85 equivalents with respect to benzyl alcohol). Nevertheless, 60% conversion of benzyl alcohol may be achieved in a single pass without competitive formation of toluene..
- J. Aßmann, D. Crihan, M. Knapp, E. Lundgren, E. Löffler, M. Muhler, V. Narkhede, H. Over, M. Schmid, A. P. Seitsonen and P. Varga, Angew. Chem., Int. Ed., 2005, 44, 917–920 CrossRef PubMed.
- F. Nikaidou, H. Ushiyama, K. Yamaguchi, K. Yamashita and N. Mizuno, J. Phys. Chem. C, 2010, 114, 10873–10880 CAS.
- K. Yamaguchi and N. Mizuno, Synlett, 2010, 2365–2382 CAS.
- Corresponding to an 8-fold drop in O2 concentration in solution..
- See Fig. 8 in ref. 15..
- G. W. Wu, A. Constantinou, E. H. Cao, S. Kuhn, M. Morad, M. Sankar, D. Bethell, G. J. Hutchings and A. Gavriilidis, Ind. Eng. Chem. Res., 2015, 54, 4183–4189 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental data and data fitting are supplied. See DOI: 10.1039/c6re00208k |
| This journal is © The Royal Society of Chemistry 2017 |