Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tunable thermal conductivities of graphene and graphyne under in-plane torsion†
Yinfeng Li *ab,
Qianling Lina,
Ye Lib and
Daxiang Cui
*ab,
Qianling Lina,
Ye Lib and
Daxiang Cui c
c
aDepartment of Engineering Mechanics, School of Naval Architecture, Ocean and Civil Engineering, State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China. E-mail: liyinfeng@sjtu.edu.cn
bCollaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
cInstitute of Nano Biomedicine and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
First published on 29th November 2017
Abstract
Using the non-equilibrium molecular dynamics method, the thermal properties of two dimensional nanomaterials are investigated by considering graphene and graphyne nanosheets with circular boundaries. The thermal transport efficiency of graphene and graphyne under heat flux from the inner boundary to outer boundary is revealed to be tunable by applying in-plane torsion at the inner boundary, and the tunable range of thermal conductivity for graphyne could be up to 37% (15% for graphene). With the increase of rotation angle, the thermal conductivities of both graphene and graphyne are found to increase at small rotation angles and then decrease after the occurrence of wrinkle deformation. The maximum thermal conductivity appears at the onset of wrinkling which depends on the lattice structure and stiffness of the nanosheets. By systematically investigating the morphological characteristics and the phonon spectra under different torsion angles, the tunable thermal conductivities of both graphene and graphyne are found to be controlled by three factors including surface smoothness, stress concentration and lattice instability. The increase of thermal conductivity with small torsion angles is caused by the suppressed surface fluctuation which decreases the phonon scattering, while the wrinkling and lattice instability occurring under large torsion angles accounts for the deterioration of thermal conductivity. Since the fluctuation of graphyne is efficiently compressed at smaller torsion angles compared to graphene, the maximum thermal conductivity of graphyne appears earlier than graphene. Such correlation between out-of-plane deformation and in-plane thermal conductivity provides new insights into the thermal management of two dimensional nanomaterials.
Introduction
Graphene, as an ideal two dimensional (2D) nanomaterial composed of a single layer of atoms organized in a hexagonal lattice, has attracted wide attention since it was fabricated in 2004.1 Owing to their extraordinary mechanical, thermal, electronic and optical characteristics,2–4 researchers are actively exploiting 2D materials for various applications in next generation electronics,5,6 microchips,7 composites,8,9 biosensors, drug delivery,10 and energy harvesting and conversion systems.11 Graphyne is another form of carbon nanosheet composed of sp and sp2 carbon atoms, which was first predicted by Baughman et al.12 New synthetic methods enable the successful fabrication of graphyne on copper substrates via a cross-coupling reaction using hexaethynylbenzene.13–15 Nowadays, graphyne has become the focus of new investigations because of its promising applications in novel nanoelectronic and optoelectronic devices with highly tunable band gaps, large carrier mobility, and unique transport properties.16–19Own to the structural features, 2D nanomaterials are easily susceptible to out-of-plane deformation and tend to form wrinkles and corrugations during fabrication and application.20–22 These out-of-plane deformations can be seen as a stability mechanism to relax the in-plane strain of thin 2D materials,23,24 and have been reported to affect the electronic and chemical properties by inducing effective magnetic fields and changing local potentials.25–27 Unusual spiral wrinkling patterns has been reported for graphene nanosheets under circular shearing at the inner edge,28,29 and show potential applications as nanosensor, tunable magnetic or electronic devices, as well as patterned stretchable electronics.30–32 The wrinkle characteristic and torque capacity of circular graphene and graphyne under in-plane torsion has been studied by varying approaches. Zhang et al. studied the formation and characteristics of the wrinkles in annular graphene under in-plane rotation combing grillage model and molecular dynamics simulation.32,33 Qin et al. investigated the effect of wrinkles on the surface area of graphene using classical molecular dynamics simulations, and suggested that the high specific surface area of graphene can only be affected up to 2% regardless of loading conditions, geometry, and defects.34 Li et al. reported the wrinkling characteristics of surface functionalized graphene and graphyne under circular shearing at the inner edge.29,35
The keep miniaturization of electronic devices raises a strong demand for high efficient heat dissipation and thermal management to ensure device performance. The thermal conductivity of graphene has been revealed to be sensitive to external loadings such as tension and out-of-plane rotation,36,37 and the largest enhancement of thermal conductivity provided by applied strain is reported up to 40%.38 The effects of non-uniform strain with specific distribution has also been revealed to be associated with the electronic structure and Raman spectra of graphene.39 Thus, in addition to its mechanical response under circular shearing, thermal conductivity of 2D nanomaterials tuned by in-plane torsion is also of crucial interest for its design and practical application. It is necessary to understand how in-plane rotation influences the thermal conductivity of 2D nanomaterials for the design of micro and nano electro-mechanical system devices. In this paper, thermal characteristics of 2D nanomaterials with circular boundaries under in-plane torsion applied at its inner edge are studied using molecular dynamics method. The thermal conductivities of graphene and graphyne annuli under heat flux from inner boundary to outer boundary are calculated at varying in-plane torsion angle. The radial thermal conductivity of both graphene and graphyne shows interesting dependency on the torsion-angle. Systematic analyses on surface morphology and phonon spectra are carried out for the mechanism of such torsion-dependent thermal conductivity. The reported tunable thermal conductivities of graphene and graphyne under in-plane torsion are expected to stand for a wide range of 2D nanomaterials. Our results provide insights for developing next generation nanodevices with tunable thermal conductivity.
Methods
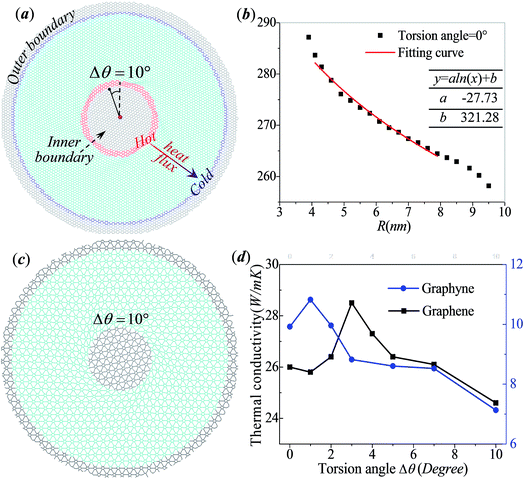
Fig. 1a shows the atomistic model of circular graphene with outer radius Ro = 10 nm under in-plane torsion. Gray atoms inside Ri = 3 nm and outside Ro represent the inner boundary and outer boundary, and cyan atoms in between represent the free carbon atoms of graphene. The torsion angle Δθ applied at the inner radius equals to 10°. Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential40 implemented in the LAMMPS package41 is adopted for the carbon–carbon interactions. Prior to rotation, a relaxation process of 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps with time step Δt = 0.1 fs is carried out for equilibrium. Boundary atoms are free to move in the plane of graphene while the out-of-plane displacement is constrained by enforcing zero force and velocity along out-of-plane direction. During the rotation process, the atoms inside the inner boundary Ri are rotated around the center as a rigid body at constant angular velocity 0.1 rad ps−1 with outer boundary fixed. After rotation, another relaxation process of 500
000 MD steps with time step Δt = 0.1 fs is carried out for equilibrium. Boundary atoms are free to move in the plane of graphene while the out-of-plane displacement is constrained by enforcing zero force and velocity along out-of-plane direction. During the rotation process, the atoms inside the inner boundary Ri are rotated around the center as a rigid body at constant angular velocity 0.1 rad ps−1 with outer boundary fixed. After rotation, another relaxation process of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps with fixed inner and outer boundary is enforced. The relaxing and loading process is performed at room temperature (300 K) under NVT ensemble. Thermal conductivity is then computed by non-equilibrium molecular dynamics method by dividing the free atoms of annulus into concentric loops, where the most inner loop is assigned to be the hot region with fixed temperature 350 K while the most outer loop is the cold one with fixed 250 K. Heat flux J can be calculated from the exchanging of kinetic energy between the cold and hot domains by the equation:
000 MD steps with fixed inner and outer boundary is enforced. The relaxing and loading process is performed at room temperature (300 K) under NVT ensemble. Thermal conductivity is then computed by non-equilibrium molecular dynamics method by dividing the free atoms of annulus into concentric loops, where the most inner loop is assigned to be the hot region with fixed temperature 350 K while the most outer loop is the cold one with fixed 250 K. Heat flux J can be calculated from the exchanging of kinetic energy between the cold and hot domains by the equation:
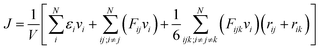 | (1) |
The whole exchanging process is performed under NVE ensemble for 1 ns to reach a steady temperature gradient along radial direction. The temperatures of each loop are determined by:
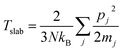 | (2) |
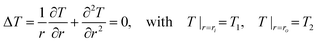 | (3) |
By solving eqn (3), we can get the analytic solution of temperature profile in annulus:
T = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r + b r + b
| (4) |
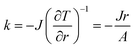 | (5) |
Results and discussion
We first study the dynamic rotation process of the described graphene under in-plane torsion at inner boundary. The graphene sheet is found to remain flat when torsion angle Δθ is small. With the increase of Δθ, the graphene nanosheet buckles suddenly forming a series of spiral wrinkles surrounding the inner boundary. The radial thermal conductivities of circular graphene under different torsion angles are calculated when heat flux from inner boundary to outer boundary. The black in Fig. 1d shows the evolution of the radial thermal conductivity of graphene as a function of the torsion angle Δθ. The thermal conductivity anomalously increases from 26 W mK−1 to 28.5 W mK−1 with the increase of torsion angle in the range of 0° < Δθ < 3° and reach a maximum at Δθ = 3°, which is just the critical point that the spiral wrinkling appears. The maximum thermal conductivity is about 10% higher than that of the graphene annulus at rest. After that, the thermal conductivity decreases to 24.6 W mK−1 with the increase of torsion angle until the final failure of annulus. The total tunable range is about 15% of the pristine value. Furthermore, we repeat the simulation with smaller temperature difference between hot region (350 K) and cold region (310 K). The calculated evolution of radial thermal conductivity is plotted in the Fig. S1.† The evolution of the graphene thermal conductivity with smaller temperature difference also shows an inversed-V-shaped evolution, which is same with the results of circular graphene under larger temperature gradient. Similar wrinkle characteristics are also observed in graphyne as plotted in Fig. 1c. It is noticeable that our calculated thermal conductivity of graphene under torsion angle Δθ = 0° equals to 26 W mK−1, which is smaller than the experimental values of graphene nanoribbons (GNRs) about 2500–5000 W mK−1.42,43 Previous simulations have found that the thermal conductivity of the GNRs is sensitive to the size of graphene nanosheet due to phonon scattering.44 Since the radial length of circular graphene considered in our approach is much smaller than the ultra-long phonon mean free path of experimentally studied graphene (about 1 μm), our simulations focuses on the qualitative discussion about the evolution of thermal conductivity with in-plane torsion. The effect of in-plane torsion is demonstrated by the relative difference between thermal conductivity of graphene under different torsion degree instead of the absolute calculated results.We further study the thermal conductivity of graphyne to see whether the in-plane torsion tuned thermal properties of graphene can be applicable for other two dimensional carbon allotropies with different unit lattice. Fig. 1c shows the atomistic model of circular graphyne under torsion angle Δθ = 10°. Graphyne annulus also presents unusual spiral wrinkling patterns around inner edge under circular in-plane rotation and has lower thermal conductivity as reported by Zhang et al.45 Similar to the evolution of graphene thermal conductivity, the radial thermal conductivity of graphyne also shows an inversed-V-shape evolution. The maximum thermal conductivity occurs at Δθ = 1°, which is earlier than graphene whose max maximum value occurs at Δθ = 3°. As shown by the blue curve in Fig. 1d, the maximum thermal conductivity (10.8 W mK−1) is about 9% higher than that of the graphyne annulus at rest (9.9 W mK−1). After that, the thermal conductivity decreases to 7.1 W mK−1 with the torsion angle, the maximum tunable range of thermal conductivity is up to 37% when torsion angle increases from 0 to 10°.
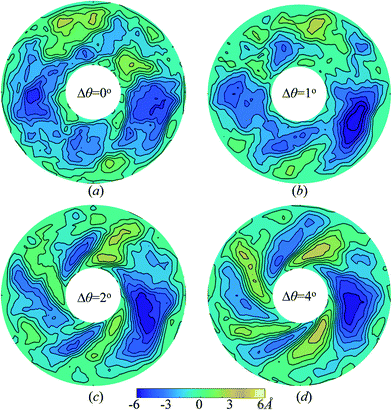
To explain the reason why thermal conductivities of both graphene and graphyne increases anomalously under slight torsion while the peak value occurs at different torsion angle for graphene and graphyne, we further analyze the change of surface morphology of graphene and graphyne under torsion. The change of graphene surface smoothness is noticeable even before the occurrence of wrinkling under small torsion angle. Fig. 2 plots the contour map of graphene annulus by plotting the out-of-plane displacement of carbon atoms. The equilibrated graphene under torsion angle Δθ = 0° exhibits a number of random fluctuations. After the graphene undergoes slight in-plane torsion at inner boundary, the surface morphology is smoothed by in-plane strain and the random fluctuations disappear gradually. Such improvement of surface smoothness contributes to the propagation of the phonon in graphene,46 and leads to the increase of thermal conductivity. With the increase of torsion angle, the severe in-plane strain plays a more and more important role in softening the phonon modes and increasing the lattice anharmonicity, which causes the reduction of thermal conductivity. Furthermore, the enhanced wrinkling amplitude under large torsion angle induces the lattice instability which also contributes to the reduction of thermal conductivity. The contours of graphyne under different torsion angle are also calculated as shown in Fig. S2.† It can be seen that the graphyne annulus also possesses a number of random fluctuations under Δθ = 0°, and the surface morphology is flatted obviously when Δθ = 1°. Due to the difference in lattice structure and stiffness, spiral winkling happens earlier in graphyne annulus than that of graphene annulus. Thus, the maximum thermal conductivity appears at a smaller torsion angle than that of graphene. The atomistic structures of circular graphene and graphyne under in-plane torsion angle Δθ = 0° and 3° are plotted in Fig. S3 and S4† for comparison.
We also carried out detailed analyses on the phonon spectra of graphene and graphyne under different Δθ to elucidate the tuning effect of torsion on thermal transport efficiency. The phonon spectrum function G(ω) can be calculated from the Fourier transform of the velocity autocorrelation function (VACF):
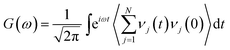 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps after equilibrium.
000 steps after equilibrium.
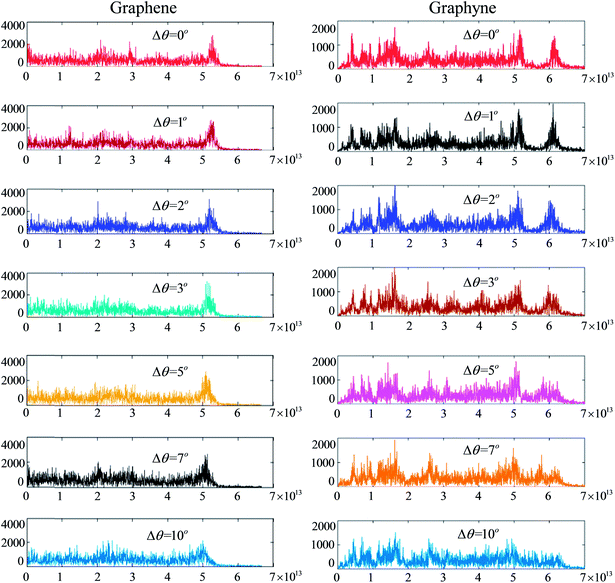
The Fourier transform of the VACF reveals the amount of energy in vibrations at each frequency, which is proportional to the phonon density of states times the occupation of the modes. As shown in Fig. 3a, the phonon spectra of annular graphene under different torsion angles are calculated. Each phonon spectra owns a main peak (G-band) at frequencies around 50 THz, which is consistent with previous result.46 Moreover, the peak frequency shift left with the increase of torsion angle. Fig. 3b shows the phonon spectra of circular graphyne under different torsion angles. The main peak occurs at frequencies around 60 THz.
To present the change of phonon spectra with torsion angle Δθ, the main peak frequency and the corresponding amplitude of each spectrum of graphene and graphyne are recorded as shown in Fig. 4. The peak frequencies of both graphene and graphyne decrease with the increase of torsion angle. The change of peak frequency is slight at small torsion angle while the peak frequency drops dramatically under large in-plane torsion. Previous study has reported that the applied strain could soften the G-band (frequency peaks around 50 THz) of the phonon spectra remarkably, causing a reduction in the phonon group velocities.46 Hence, the thermal conductivity is reduced according to the classical lattice thermal transport theory:
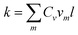 | (7) |
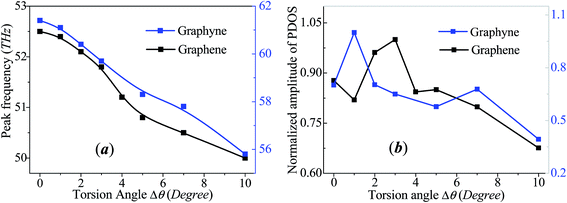 | ||
| Fig. 4 Evolutions of the peak frequency of the phonon spectra (a) and the amplitude of the peak frequency (b) as a function of the torsion angle for circular graphene and graphyne. | ||
The black line in Fig. 4b demonstrates that the amplitude of peak for graphene increases with torsion angle when 0° < Δθ < 3° while decreases with torsion angle when Δθ > 3°. The evolution of amplitude with torsion angle is consistent with that of thermal conductivity with Δθ. The variation of the amplitude of peak frequency can be attributed to the change of phonon scattering which has already been suggested as the main factor for the reduction of thermal conductivity. More severe phonon scattering corresponds to lower frequency amplitude. Under small torsion angle, the thermal conductivity increases with the improvement of surface smoothness of graphene annulus, which reduces the degree of phonon scattering. Meanwhile, the strain induced redshift of the peak frequency of the phonon spectra is too small to change the thermal conductivity, i.e., the decline rate of thermal conductivity due to phonon peak frequency redshift at this stage is small. As a result, the thermal conductivity increases with torsion angle under small torsion angle. With the increasing of torsion angle, the increased in-plane shear strain and lattice instability result in the redshift of peak frequency and the enhancement of phonon scattering. The combined influences provided by the changes of peak frequency and phonon scattering lead to the decrease of thermal conductivity. The overall change of thermal conductivity follows an inverted V-shaped evolution with the increase of rotation angle. For graphyne represented by the blue line in Fig. 4b, the peak frequency amplitude also shows an inverted V-shaped evolution with torsion angle while the maximum value appears at Δθ = 1°. The specified mechanism for the in-plane tuned thermal conductivity is expected to be applicable for 2D nanomaterials of different lattice structures.
Conclusions
In conclusion, the in-plane torsion tuned thermal conductivities of circular graphene and graphyne have been studied systematically. The thermal conductivity shows an interesting inverted V-shaped evolution with the torsion angle, and the tunable range of thermal conductivity for graphyne could be up to 37% (15% for graphene). The evolution of thermal conductivity with torsion angle is interpreted from the perspectives of out-of-plane deformation and the phonon spectra of nanosheets. Under small in-plane torsion angle, the surface morphology of the 2D nanomaterials is flattened and phonon scattering is depressed, which contribute to the increase of thermal conductivity. With the increase of torsion angle, the enhanced in-plane strain causes the occurrence of wrinkling and lattice instability which soften the phonon modes and increases phonon scattering, leading to the deterioration of thermal conductivity. The results show that the in-plane thermal conductivity can be effectively regulated by out-of-plane deformations which affect the phonon spectra. Similar tunable thermal conductivity has also been revealed for graphyne under in-plane torsion. Our results indicate that the described tunable thermal properties as well as the specified mechanism stand for wide range of 2D nanomaterials with different unit lattice structures. The revealed phenomenon and mechanism provides a new route for tailoring the thermal properties of 2D nanosheets, and can also be combined with other approaches, such as surface functionalization, introducing defects and our-of-plane strains for more efficient manipulation of thermal conductivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support of the National Natural Science Foundation of China (No. 11402145), National Key Basic Research Program (973 Project) (Project No. 2017YFA0205300). The computational support for this work was provided by Center for HPC, Shanghai Jiao Tong University.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- L. A. Falkovsky, J. Phys.: Conf. Ser., 2008, 129, 012004 CrossRef.
- Y. Li, D. Datta and Z. Li, Carbon, 2015, 90, 234–241 CrossRef CAS.
- M. Terrones, A. R. Botello-Méndez, J. Campos-Delgado, F. López-Urías, Y. I. Vega-Cantú, F. J. Rodríguez-Macías, A. L. Elías, E. Muñoz-Sandoval, A. G. Cano-Márquez and J.-C. Charlier, Nano Today, 2010, 5, 351–372 CrossRef.
- D. Boukhvalov, M. Katsnelson and A. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035427 CrossRef.
- Y. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- S. Cho and M. S. Fuhrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 081402 CrossRef.
- D. W. Boukhvalov and M. I. Katsnelson, J. Phys.: Condens. Matter, 2009, 21, 344205 CrossRef CAS PubMed.
- A. Salehi-Khojin, D. Estrada, K. Y. Lin, K. Ran, R. T. Haasch, J.-M. Zuo, E. Pop and R. I. Masel, Appl. Phys. Lett., 2012, 100, 033111 CrossRef.
- Y. Li, H. Yuan, A. von dem Bussche, M. Creighton, R. H. Hurt, A. B. Kane and H. Gao, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12295–12300 CrossRef CAS PubMed.
- H. Gao, J. Mech. Phys. Solids, 2014, 62, 312–339 CrossRef CAS.
- R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- E. L. Spitler, C. A. Johnson and M. M. Haley, Chem. Rev., 2006, 106, 5344–5386 CrossRef CAS PubMed.
- C. D. Stevenson, Acc. Chem. Res., 2007, 40, 703–711 CrossRef CAS PubMed.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258 RSC.
- J. Koo, H. J. Hwang, B. Huang, H. Lee, H. Lee, M. Park, Y. Kwon, S.-H. Wei and H. Lee, J. Phys. Chem. C, 2013, 117, 11960–11967 CAS.
- W. Wu, W. Guo and X. C. Zeng, Nanoscale, 2013, 5, 9264–9276 RSC.
- Q. Yue, S. Chang, J. Kang, S. Qin and J. Li, J. Phys. Chem. C, 2013, 117, 14804–14811 CAS.
- J. Chen, J. Xi, D. Wang and Z. Shuai, J. Phys. Chem. Lett., 2013, 4, 1443–1448 CrossRef CAS PubMed.
- W. Bao, F. Miao, Z. Chen, H. Zhang, W. Jang, C. Dames and C. N. Lau, Nature Nanotechnol., 2009, 4, 562–566 CrossRef CAS PubMed.
- Q. Lu and R. Huang, Int. J. Appl. Mech. Eng., 2009, 1, 443–467 CrossRef.
- A. Srivastava, C. Galande, L. Ci, L. Song, C. Rai, D. Jariwala, K. F. Kelly and P. M. Ajayan, Chem. Mater., 2010, 22, 3457–3461 CrossRef CAS.
- J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60–63 CrossRef CAS PubMed.
- S. Scharfenberg, N. Mansukhani, C. Chialvo, R. L. Weaver and N. Mason, Appl. Phys. Lett., 2012, 100, 021910 CrossRef.
- K. Eun-Ah and A. H. C. Neto, EPL, 2008, 84, 57007 CrossRef.
- F. Guinea, B. Horovitz and P. Le Doussal, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 205421 CrossRef.
- F. Guinea, M. I. Katsnelson and M. A. H. Vozmediano, Phys. Rev. B: Condens. Matter, 2008, 77, 075422 CrossRef.
- Y. Li, Q. Lin and D. Cui, Sci. Rep., 2017, 7, 41767 CrossRef CAS PubMed.
- Y. Li, S. Liu, D. Datta and Z. Li, Sci. Rep., 2015, 5, 16556 CrossRef CAS PubMed.
- J. S. Bunch, S. S. Verbridge, J. S. Alden, A. M. van der Zande, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2008, 8, 2458–2462 CrossRef CAS PubMed.
- J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315, 490–493 CrossRef CAS PubMed.
- Z. Zhang, W. H. Duan and C. M. Wang, Nanoscale, 2012, 4, 5077–5081 RSC.
- Z. Zhang, W. H. Duan and C. M. Wang, J. Appl. Phys., 2013, 113, 014902 CrossRef.
- Z. Qin, M. Taylor, M. Hwang, K. Bertoldi and M. J. Buehler, Nano Lett., 2014, 14, 6520–6525 CrossRef CAS PubMed.
- Q. Lin, Y. Li and H. Yao, Phys. Chem. Chem. Phys., 2017, 19, 20049–20056 RSC.
- W. Ning, X. Lanqing, W. Hui-Qiong and Z. Jin-Cheng, Nanotechnology, 2011, 22, 105705 CrossRef PubMed.
- C. Si, G. Lu, B.-Y. Cao, X.-D. Wang, Z. Fan and Z.-H. Feng, J. Appl. Phys., 2017, 121, 205102 CrossRef.
- Y. Kuang, L. Lindsay and B. Huang, Nano Lett., 2015, 15, 6121–6127 CrossRef CAS PubMed.
- C. Si, Z. Sun and F. Liu, Nanoscale, 2016, 8, 3207–3217 RSC.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- S. Panigrahi, A. Bhattacharya, S. Banerjee and D. Bhattacharyya, J. Phys. Chem. C, 2012, 116, 4374–4379 CAS.
- W. W. Cai, A. L. Moore, Y. W. Zhu, X. S. Li, S. S. Chen, L. Shi and R. S. Ruoff, Nano Lett., 2010, 10, 1645–1651 CrossRef CAS PubMed.
- C. Wang, J. Guo, L. Dong, A. Aiyiti, X. Xu and B. Li, Sci. Rep., 2016, 6, 25334 CrossRef CAS PubMed.
- Z. Guo, D. Zhang and X.-G. Gong, Appl. Phys. Lett., 2009, 95, 163103 CrossRef.
- Y. Y. Zhang, Q. X. Pei and C. M. Wang, Comput. Mater. Sci., 2012, 65, 406–410 CrossRef CAS.
- W. Ning, X. Lanqing, W. Hui-Qiong and Z. Jin-Cheng, Nanotechnology, 2011, 22, 105705 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11128b |
| This journal is © The Royal Society of Chemistry 2017 |