Open Access Article
Open Access ArticleAn experiment-based model quantifying antimicrobial activity of silver nanoparticles on Escherichia coli†
Mohammad A. Haquea,
Riku Imamurab,
George A. Browna,
Venkata R. Krishnamurthia,
Isabelle I. Niyonshutib,
Tiffany Marcellea,
Leanne E. Mathurinb,
Jingyi Chen *bcd and
Yong Wang
*bcd and
Yong Wang *acd
*acd
aDepartment of Physics, University of Arkansas, Fayetteville, Arkansas 72701, USA. E-mail: yongwang@uark.edu
bDepartment of Chemistry and Biochemistry, University of Arkansas, Fayetteville, Arkansas 72701, USA. E-mail: chenj@uark.edu
cMicroelectronics and Photonics Graduate Program, University of Arkansas, Fayetteville, Arkansas 72701, USA
dCell and Molecular Biology Program, University of Arkansas, Fayetteville, Arkansas 72701, USA
First published on 12th December 2017
Abstract
Silver nanoparticles (AgNPs) are well known to exhibit antimicrobial effects through plausible interactions with proteins and/or deoxyribonucleic acid inside the bacteria. Yet a quantitative understanding on the antimicrobial activities of AgNPs remains obscure. Here we conducted in-depth kinetic growth assays and colony-forming unit (CFU) assays on Escherichia coli (E. coli) cultured in AgNPs or Ag ion-containing growth media. Compared to the Ag-absent culture medium, it was found that the growth rate of the bacteria remained unaffected but the lag time of the bacterial growth was extended due to the presence of AgNPs or Ag ions. From the CFU-based time-kill curves, we observed that fractions of E. coli were killed exponentially in the presence of AgNPs or Ag ions. Based on the experimental data, a quantitative model was established to describe the antimicrobial activity of AgNPs. The predictions from this model agree well with the experimental results. We also showed that the parameters in our model as well as their dependence on the concentrations of Ag and bacteria could, in turn, be determined experimentally. It is expected that our quantitative model and the associated parameters provide an alternative means to minimum inhibitory concentration values for characterizing the antimicrobial activities of Ag ions and AgNPs.
Introduction
Nobel metals, especially silver (Ag), have long been used as antimicrobial agents, dating back as far as ancient Greece, the Roman Empire and Egypt.1 More recently, colloidal metal nanoparticles have been shown to significantly suppress the growth of bacteria2–24 (reviewed in Durán et al.25). The antimicrobial effect of metal nanoparticles opens a new avenue to fighting against drug resistance of microbes, which has been a severe concern to public health.26–29 In fact, Ag has been included in many healthcare products that are commercially available.30 While some studies reported that metal nanoparticles did not result in obvious resistance in bacteria after long-term exposure to them,12,24 others found the opposite: Ag-resistant or metal nanoparticle-resistant bacteria can occur in a variety of circumstances and environments.31–34 To help to avoid overdose and unnecessary exposure of these nanomaterials, it is important to understand the antimicrobial mechanism of metal nanoparticles.Much effort has been made and various methods have been exploited to investigate how the metal nanoparticles suppress the growth of, or kill, bacteria.3,5,7,20,23,24 It has been found that the shape, size, and surface modifications of metal nanoparticles play important roles in their antimicrobial activities.2,12,15,23,24 Descriptive models have been proposed to explain how metal nanoparticles suppress the growth of bacteria.7,11,22,24 Despite the exciting progresses, little quantitative understanding on the antimicrobial mechanism of metal nanoparticles exists, leaving many basic questions unclear and thus hindering further antimicrobial applications of these nanoparticles. In addition, difficulties currently exist for quantifying the antibiotic activities of metal ions and nanoparticles.
In this work, we focused on developing a quantitative understanding on the antimicrobial activities of silver nanoparticles (AgNPs) and silver ions (Ag ions) using kinetic growth assays and colony-forming-unit (CFU) assays in combination with quantitative modelling. We investigated the kinetic growth curves of Escherichia coli (E. coli) with AgNPs or Ag ions in the growth media, which showed that the growth rate of the bacteria was not affected but the lag time of the bacterial growth was elongated in the presence of AgNPs or Ag ions. In addition, CFU assays and time-kill curves were used to monitor the killing kinetics of bacteria in the presence of AgNPs or Ag ions. Based on these experimental observations, we developed a quantitative model to describe the antibacterial activity of AgNPs. Our model explains the experimental results very well. Furthermore, we quantified the dependence of the parameters in our model on the concentrations of Ag and bacteria experimentally. As an alternative to the minimum inhibitory concentration (MIC) values, our model and its parameters allow us to characterize the antimicrobial activities of Ag ions and AgNPs quantitatively.
Methods and materials
Synthesis and characterization of AgNPs
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich), and 4 mL of 282 mM silver trifluoroacetate (AgTFA, Alfa Aesar) were sequentially added to the reaction flask. Once the LSPR peak reached ∼430 nm (∼35 min after addition of AgTFA), the reaction was quenched in an ice bath. Upon cooling, the product was collected by adding acetone to the reaction solution at a ratio of 5
000, Sigma-Aldrich), and 4 mL of 282 mM silver trifluoroacetate (AgTFA, Alfa Aesar) were sequentially added to the reaction flask. Once the LSPR peak reached ∼430 nm (∼35 min after addition of AgTFA), the reaction was quenched in an ice bath. Upon cooling, the product was collected by adding acetone to the reaction solution at a ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and centrifuging at 6000 rcf for 10 min. The resulting pellet was purified twice with H2O, collected by centrifugation at 20
1 and centrifuging at 6000 rcf for 10 min. The resulting pellet was purified twice with H2O, collected by centrifugation at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rcf for 10 min, and resuspended in 10 mL of H2O for future use.
000 rcf for 10 min, and resuspended in 10 mL of H2O for future use.For the growth-curve measurements with varying Ag concentrations, the initial OD600 of E. coli was set to 0.05, while the concentrations of AgNPs were 0 (negative control), 1, 5, 10, 20, 30, 40 μg mL−1, or the concentrations of AgNO3 were 0 (negative control), 1, 2, 5, 7, 10 μg mL−1 (the corresponding concentrations of Ag ions were then 0.63 × [AgNO3]). For the experiments with varying initial OD600 values of bacteria, the concentrations of AgNPs and AgNO3 were fixed at 20 μg mL−1 and 5 μg mL−1, respectively, while the initial OD600 values of E. coli were 0.001, 0.005, 0.01, 0.05, 0.1, and 0.2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rcf for another 15 minutes. From the second centrifugation, the supernatants were collected and used for measurement of the concentration of Ag ions by inductively coupled plasma mass spectrometry (ICP-MS, Thermal Scientific). Calibration curves for ICP-MS were obtained by AgNO3 solutions (0–100 μg L−1) in 2% (v/v) nitric acid.
000 rcf for another 15 minutes. From the second centrifugation, the supernatants were collected and used for measurement of the concentration of Ag ions by inductively coupled plasma mass spectrometry (ICP-MS, Thermal Scientific). Calibration curves for ICP-MS were obtained by AgNO3 solutions (0–100 μg L−1) in 2% (v/v) nitric acid.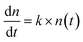 , can be used to describe the growth of bacteria, where k is the growth rate.38 With unlimited resources, k is a constant and the growth of the bacteria is exponential.38 However, under our experimental conditions where growth medium is limited, the growth rate k depends the cell number or cell density,
, can be used to describe the growth of bacteria, where k is the growth rate.38 With unlimited resources, k is a constant and the growth of the bacteria is exponential.38 However, under our experimental conditions where growth medium is limited, the growth rate k depends the cell number or cell density,  , where k0 is the initial growth rate, and A is the asymptotic cell density.38 The equation of the bacterial growth becomes
, where k0 is the initial growth rate, and A is the asymptotic cell density.38 The equation of the bacterial growth becomes  , resulting in a logistic growth curve,
, resulting in a logistic growth curve,
 | (1) |
At t = 0, the cell number starts with n0, while as t → ∞, the cell number approaches the asymptotic value A.38 Note that the cell number is equivalent to the cell density or approximately the OD600 readings,39–41 and thus the OD600 values of a bacterial culture and the cell density follow the same equation (eqn (1)).
To account for the antimicrobial activity of AgNPs and Ag ions, we modelled that E. coli were knocked into a suppressed state, S, upon the addition of Ag (in the form of AgNPs or Ag ions). The treated bacteria went through two possible pathways: some bacteria are killed (into the dead state, D), while some bacteria adapt to the new environment, wake up and go back to the active state (A). After waking-up, the active bacteria then undergo the normal cycles of growth and reproduction. We refer to this model as the Suppressed-Active-Dead (SAD) model. The general idea of our model is that bacteria might develop adaptation to the new Ag-containing environment. Similar ideas of acclimation have been developed to model the lag phase of bacterial growth.42–44 In addition, a previously reported active but nonculturable (ABNC) state45 provides a possible biological account for the S state in our model.
Next, conversions between the three states (S → A and S → D) were introduced into the model. If na, ns, and nd are the numbers of cells in the active, suppressed, and dead states, respectively, then the SAD model can be quantitatively described by the following differential equations
 | (2) |
Results and discussions
Synthesis of AgNPs
The AgNPs used in this study were synthesized by the polyol method in which Ag precursor was reduced by EG using PVP as the capping agent35 as illustrated in the reaction scheme (Fig. 1A). The synthesized AgNPs were imaged using TEM, showing an average size of 39.5 ± 10.7 nm (Fig. 1B). The size distribution was plotted in the Fig. 1C by analyzing the TEM image, indicative of two size population at averages of ∼30 and ∼50 nm, respectively. The shapes of the nanoparticles were irregular with some spheres, short rods, and tetrahedrons. The hydrodynamic diameter of these nanoparticles measured by DLS in aqueous solution was 69.0 nm on average with the polydispersity index (PDI) of 0.327. The DLS measurement may not accurately reflect the size of these irregular nanoparticles because the method assumes that the nanoparticles were spherical in shape; however, the relatively high value of PDI indicates the sample was polydispersed, which agreed with the analysis of the TEM result. The concentration of Ag in the aqueous stock solution was measured by atomic absorption spectroscopy to be 2.5 × 103 ppm (μg mL−1). Fig. 1D displays the X-ray powder diffraction (XRD) pattern of the AgNPs. The peaks at 38.04, 44.22, 64.34, 77.24, and 81.38 degree can be indexed to {111}, {200}, {220}, {311}, and {222} crystallographic planes of face-centered cubic Ag (JCPDS file no. 04-0783). The XRD result confirmed that the samples were made of metallic Ag. The zeta potential was measured to be −8.50 mV ± 2.04 mV, indicating that PVP-capped AgNPs are slightly negatively charged in agreement with the literature report.46Suppressed growth of E. coli by AgNPs or Ag ions via lag-time elongation
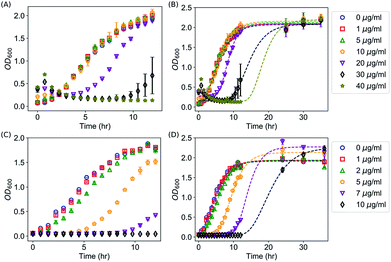
We first confirmed the antimicrobial activities of AgNPs against E. coli as reported in the literature by kinetic growth assays and CFU assays, both of which have been extensively used for investigating the antimicrobial activities of AgNPs and Ag ions.2,3,9,10,13,15,18,20,24,47–51 In the kinetic growth assays, the concentrations of bacteria in the liquid cultures (i.e., OD600) were monitored. In the first 12 hours (with an initial OD600 = 0.05), AgNPs at 40 μg mL−1 were able to completely suppress the growth of the E. coli (Fig. 2A). At lower concentrations (20 or 30 μg mL−1), the growth of the bacteria was inhibited initially but then started off at a later time (Fig. 2A); and no obvious effect was observed for AgNPs below 10 μg mL−1 (Fig. 2A). In addition to the kinetic growth assays, the suppression of the growth of E. coli by AgNPs or Ag ions was also confirmed by CFU assays as shown in Fig. S1.† These observations are consistent with most previous reports.2,12,13,24 It is noted that the OD600 reading of the growth medium was enhanced by the addition of AgNPs (Fig. 2A and 2B). This is expected because of the long tail of the absorbance spectrum of the AgNPs (with a peak around 400 nm, Fig. S2†). It is worthwhile to mention that, although it has been a standard protocol to correct the growth curves with AgNPs by subtracting the OD600 readings of abiotic AgNPs solutions (i.e., AgNPs in media but without inoculation),36,50 the presented data in this study (Fig. 2) were “uncorrected” to emphasize the necessary of complementing the growth curve measurements with CFU assays, and to highlight how this effect brings difficulty in determining the MIC of AgNPs for bacteria. First, as MIC values are defined by checking the “visible growth” of bacteria in the presence of antimicrobial agents,52 the opacity of the culture due to the presence of AgNPs interferes with determining whether there is any visible growth. In addition, growth assays for bacteria with AgNPs at very high concentrations (≥100 μg mL−1) is practically difficult as the OD600 value of AgNPs at 100 μg mL−1 approaches to 1.5. This high optical density is close to the maximum OD600 readings (∼2.0) of E. coli in typical kinetic growth curve assays (Fig. 2), and it compromises the measurement range of typical photometers. On the other hand, we note that the kinetic growth curve assays are practically more convenient and efficient than CFU assays. More importantly, the growth-curve assays are better to represent chronic exposures to Ag, which could be useful in clinical applications.50It was observed that, after 12 hours of suppression, E. coli with AgNPs at 40 μg mL−1 grew again, which indicates that the commonly defined MIC for the E. coli under the described experimental conditions is above 40 μg mL−1, consistent with some of the previously reported MIC values.13,53,54 The OD600 value of this sample reached its asymptotic value before 30 hours (Fig. 2B), while the asymptotic value was similar to that of the wild type and the samples with AgNPs at lower concentrations (Fig. 2B). Simultaneous control experiments ruled out the possibility of any contamination. Therefore, it is likely that the suppression on the growth of E. coli by AgNPs is only transient under these experimental conditions. In addition, we explored whether the transiency of the antibacterial effect of AgNPs is unique, by measuring the kinetic growth of the same bacteria with Ag ions in the growth medium (provided from AgNO3). Silver ions have been reported to cause DNA condensation and inactivate certain proteins in bacteria.45,55 We performed the same growth-curve measurements on the same bacteria with AgNO3 at various concentrations (0, 1, 2, 5, 7, 10 μg mL−1). The antibacterial effects of Ag ions were detected in our experiments (Fig. 2C). More importantly, we found that, similar to AgNPs, the suppression of bacterial growth by the Ag ions is also transient with AgNO3 in the media at concentrations up to 10 μg mL−1 (Fig. 2D): the bacteria that were completely suppressed in the first 12 hours, but they eventually grew at later time points (Fig. 2D). On the other hand, at higher concentrations of Ag ions (≥30 μg mL−1 AgNO3), no growth of E. coli was observed for up to 10 days.
Interestingly, we found that the suppressing effect of AgNPs and Ag ions on bacteria is not through reducing the maximum specific growth rate of the bacteria. Instead, they elongated the lag time of the bacterial growth significantly. This can be seen directly from the growth curves of bacteria shown in Fig. 2. For example, in the presence of 20 μg mL−1 AgNPs, the suppression on the bacterial growth is obvious; however, the growth rate of the bacteria is very similar to that of the wild type (0 μg mL−1) or with lower concentrations of AgNPs (1, 5 and 10 μg mL−1) as shown in Fig. 2A and 2B. Similar results were observed for Ag ions: although 5 μg mL−1 Ag ions delayed the growth of the bacteria for at least 4 hours, the growth rate of the bacteria was not affected significantly by the Ag ions (Fig. 2C and 2D).
To quantify these observations, we extracted the maximum specific growth rate (μm) and the lag time (λ) from the growth curves by fitting them with the Gompertz model,40,41  . As shown in Fig. 3A and B, the maximum specific growth rates μm of the bacteria were the same (within error) with AgNPs or Ag ions at various concentrations in the growth media. In contrast, the lag time of the bacterial growth λ increased significantly as the concentration of AgNPs or Ag ions in the growth media went up (Fig. 3C and D). In addition, it was found that the elongation of the lag time increased quickly as the concentration of AgNPs or Ag ions goes up: the dose dependence of the lag time can be fitted quite well with quadratic functions (Fig. S3†). Furthermore, it is worthwhile to point out that a previous study on the effect of some antibiotic drugs (ciprofloxacin, tetracycline, etc.) on E. coli showed that the maximum specific growth rate of E. coli decreases as the concentration of the antibiotics increased while the lag time did not change significantly.40 The difference between our results with AgNPs and the previous experiments with antibiotics indicates that the antimicrobial mechanism of AgNPs and Ag ions is possibly not the same as that of those antibiotic drugs.40
. As shown in Fig. 3A and B, the maximum specific growth rates μm of the bacteria were the same (within error) with AgNPs or Ag ions at various concentrations in the growth media. In contrast, the lag time of the bacterial growth λ increased significantly as the concentration of AgNPs or Ag ions in the growth media went up (Fig. 3C and D). In addition, it was found that the elongation of the lag time increased quickly as the concentration of AgNPs or Ag ions goes up: the dose dependence of the lag time can be fitted quite well with quadratic functions (Fig. S3†). Furthermore, it is worthwhile to point out that a previous study on the effect of some antibiotic drugs (ciprofloxacin, tetracycline, etc.) on E. coli showed that the maximum specific growth rate of E. coli decreases as the concentration of the antibiotics increased while the lag time did not change significantly.40 The difference between our results with AgNPs and the previous experiments with antibiotics indicates that the antimicrobial mechanism of AgNPs and Ag ions is possibly not the same as that of those antibiotic drugs.40
It has been controversial regarding the roles of AgNPs vs. Ag ions released from AgNPs in the antimicrobial activity of AgNPs.22,36,50,56 To address this question, we determined the concentration of Ag ions released from dissolution of AgNPs in both water and LB growth medium. We measured that the dissolution percentage of our PVP-coated AgNPs ranges from 0.3% to 1.4% in LB growth medium, and from 0.4% to 2.7% in water (Table S1†). The values are consistent with the range of typical values (<10%) reported previously.36,37,50,57 The low concentration of dissolved Ag ions in the AgNPs solutions, <0.3 μg mL−1 Ag ions (equivalently, <0.5 μg mL−1 AgNO3), is likely to be responsible for why AgNPs showed lower toxicity than Ag ions in our experiments (Fig. 2). On the other hand, based on the growth curves in the presence of AgNO3 (Fig. 2), the concentration of dissolved Ag ions is too low to result in any significant suppression on the bacterial growth by the dissolution of AgNPs alone. Therefore, our data indicates that particle-specific effects are likely to play a role in the toxicity of our PVP-coated AgNPs. This observation supports the conclusions from ref. 36 and 56, but is in contradiction to ref. 22 and 50.
Killing of E. coli by AgNPs
Time-kill curves52,58 of E. coli by AgNPs were performed based on the CFU assay to determine whether E. coli were killed by AgNPs. CFU assays were performed for E. coli upon the addition of AgNPs at final concentrations of 0 (negative control), 10, 40 and 80 μg mL−1. Decreased CFU counts, which were proportional to the number of live bacterial cells, were observed in the first few hours (Fig. 4A). The CFU counts for bacteria treated with 40 μg mL−1 AgNPs decreased from 9.5 × 105 per mL to 1.6 × 105 per mL in two hours, indicating that more than 83% of the E. coli were killed. The killing percentages were 88% and 28% for AgNPs at 80 and 10 μg mL−1, respectively. Therefore, AgNPs in the growth media were able to kill a fraction of E. coli. In addition, we noticed that the kinetics of bacterial killing is roughly a straight line in the log-linear plot (dashed line in Fig. 4A), indicating that the killing process by AgNPs and Ag ions in short time scales could be described by a simple differential equation,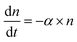 , or n(t) ∼ e−αt, where α is a parameter quantifying the killing rate of the antimicrobial agents.
, or n(t) ∼ e−αt, where α is a parameter quantifying the killing rate of the antimicrobial agents.
The killing rate α can be estimated experimentally from the initial portion of the time-kill curves, which was presented in Fig. 4B. Under our experimental conditions where the concentration of AgNPs ranged from 10 to 80 μg mL−1, the killing rate was roughly independent of the concentration of AgNPs (Fig. 4B). Therefore, we combined the data for AgNPs at different concentrations and fitted them with a single curve, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(t)=−αt + c, which yielded α = 0.77 ± 0.10 h−1. The R2 value for the fitting over the combined data is 0.89, indicating that the use of a single killing rate is reasonable (Fig. 4B).
n(t)=−αt + c, which yielded α = 0.77 ± 0.10 h−1. The R2 value for the fitting over the combined data is 0.89, indicating that the use of a single killing rate is reasonable (Fig. 4B).
It is also noted that the exponential growth phases (i.e., the increasing portions of the curves) were shifted to the right in the presence of AgNPs (Fig. 4A and S1C†), which indicated the time for preparing the bacteria to grow exponentially was longer in the presence of AgNPs than without AgNPs. In other words, the apparent lag phase was elongated due to the addition of AgNPs, consistent with our observations from the kinetic growth assays (Fig. 2 and 3).
Halted growth of E. coli in the exponential phase by AgNPs or Ag ions
The kinetic growth assays showed that the growth of E. coli was suppressed by AgNPs or Ag ions via elongating the lag time, instead of changing the maximum specific growth rate. The experiments were done for E. coli in the lag phase (OD600 was typically 0.05). An interesting question is whether Ag is able to halt the growth of bacteria that are not in the lag phase (e.g. the exponential phase). To address this question, we performed similar kinetic growth curve experiments but AgNPs or Ag ions were added to the E. coli culture when the OD600 values reached ∼0.5. As AgNPs has light absorptions at 600 nm (Fig. S2†), sudden jumps in the OD600 readings of the samples were observed upon the addition of AgNPs (Fig. 5A). It was observed that the growth of E. coli slowed down, as the slopes became flatter, which could be clearly seen after removing the contribution of AgNPs to the OD600 values by subtracting OD600 readings at the addition time of AgNPs (Fig. 5C). Therefore, the growth of bacteria in the exponential phase was halted in the presence of AgNPs. Similar results were observed after the addition of Ag ions to E. coli in the exponential phase. As shown in Fig. 5B and D, the growth of E. coli was completely halted for >10 hours if the concentration of Ag ions is high enough (≥20 μg mL−1).We note that the counts of colonies in CFU assays dropped down significantly in the time-kill curves when the bacteria were treated with Ag (Fig. 4), but the OD600 values in the kinetic growth curves did not decrease significantly upon the addition of AgNPs or Ag ions (Fig. 5). The discrepancy is due to the difference on what exactly the two assays measure. In the CFU assays, only the live bacteria appear as colonies that are counted. In contract, OD600 readings do not distinguish whether the bacteria are alive or dead. As long as the bacterial cells are not lysed, they contribute to the measured OD600 values. Therefore, the observed discrepancy indirectly indicates that most of the bacteria killed by AgNPs or Ag ions were not lysed, which is consistent with a model proposed by Zhou et al.24 and other studies using TEM imaging and X-ray microanalysis.3,55
A plausible quantitative model on the antibacterial activity of AgNPs and Ag ions
We aim to develop a quantitative model in order to promote our understanding on the antimicrobial activity of Ag ions and AgNPs. The model needs to satisfy all the observations from the kinetic growth assays, CFU assays and time-kill curves: (1) the growth of bacteria was slowed down by elongating the apparent lag time (λ) while keeping the maximum specific growth rate μm unaffected; (2) some of the E. coli in the culture were killed by Ag, and the killing rate was roughly independent of the concentration of AgNPs, while the percentage of survivors decreased at higher concentrations of AgNPs; and (3) the growth of E. coli in the exponential phase could be partly or completely halted upon the addition of Ag.Our developed model, termed as the Suppressed-Active-Dead (SAD) model, was described in the Section of Materials and Methods, and shown in Fig. 6A. We solved the SAD model was solved numerically, and it turned out that the SAD model predicted all the key features in our observations of the aforementioned several types of experiments. For example, several examples of growth curves of E. coli with different wake-up rates β, but with a constant killing rate α, were shown in Fig. 6B. Note that all the bacterial cells (nOD = na + ns + nd) were included for plotting the growth curves, as all of them contributed to the OD600 readings, assuming the dead cells were not lysed. The shape of the growth curves in our model was sigmoid, the same as the logistic function of the “wild type” (eqn (1), blue curve in Fig. 6B). Second, it was observed that the exponential growth phases were basically parallel to that of the “wild type” for all the different wake-up rates, indicating that the maximum specific growth rate μm was neither affected by the introduction of the suppressed state, nor by the wake-up rate β. In contrast, the lag time was extended in the SAD model, and the lag time extension was longer for smaller wake-up rates, which presumably correspond to higher concentrations of Ag.
In addition, our SAD model reproduced the time-kill curves based on CFU assays, as shown in Fig. 6C, where the numbers of live bacterial cells (active or suppressed, nCFU = na + ns) were plotted as a function of time with various wake-up rates. The CFU counts from our SAD model decreased in the first few hours and then went up, exactly the same as our experimental observations (Fig. 4A). Furthermore, it was shown from the model that the turning point moved lower vertically and the effective killing time became longer for smaller “wake-up” rates (corresponding to higher concentrations of silver), both of which are consistent with our experimental time-kill curves (Fig. 4A). Interestingly, although a constant killing rate (α) was used to predict the time-kill curves, the killing rates appeared to be slightly different (orange curve vs. purple one in Fig. 6C). Therefore, although the measured decreasing slope for AgNPs at 10 μg mL−1 (green squares in Fig. 4A) appeared to be different from that for the AgNPs at 40 μg mL−1 (blue triangles in Fig. 4A), it is not necessary to assume different killing rates under our experimental conditions. On the other hand, we point out that, in general, the killing rate is expected to depend on concentration of Ag, as well as the physiochemical properties of AgNPs such as the size, shape and surface modifications.
Moreover, the experimental results of halted growth of E. coli in the exponential phase due to the addition of AgNPs or Ag ions could be predicted from our SAD model. For the prediction, the bacterial population was first calculated according to our SAD model with an initial condition that all the bacteria were in the active state. When the OD600 reached 0.5, Ag was added to the culture virtually by forcing all the bacteria to go into the suppressed state. Then the cell density of the culture (nOD = na + ns + nd) was calculated again as a function of time according to the SAD model. As shown in Fig. 6D, our SAD model accurately predicted the halted growth of the bacteria: with smaller wake-up rates (or equivalently higher concentrations of Ag) the growth of bacteria became slower or halted. Again, the prediction of the SAD model is consistent with our experimental observations (Fig. 5).
Our model also predicts that the bacteria halted in the exponential phase would resume to grow with the same growth rate after they wake up (Fig. S4A†). To verify this prediction, we repeated the experiments in Fig. 5 for a longer time: the growth of bacteria with Ag ions added in the exponential phase (10 μg mL−1 AgNO3) was monitored for 36 hours. It was confirmed that, after a long lag time, the bacterial culture resumed growth with the same specific growth rate μm as the control (Fig. S4B†), consistent with our prediction (Fig. 6D and S4A†).
It is worthwhile to point out that our SAD model encompasses both bacteriostatic and bactericidal effects of antimicrobial agents. Note that although the definitions of “bacteriostatic” and “bactericidal” seem straightforward (i.e., inhibiting vs. killing), the two pure categories of antimicrobial agents do not exist in reality:52 bactericidal drugs usually fail to kill every single microorganism within 24 hours, and most so-called bacteriostatic drugs do kill some bacteria within 24 hours.52 The practical difference between the two categories lies mainly on the quantitative side (i.e., below or above 99.9% killing). In principle, our SAD model can predict both bactericidal and bacteriostatic effects by tuning the two parameters, α and β. If α were high enough, the antimicrobial effect would become bactericidal; if β were high enough, the effect would be bacteriostatic. In addition, it is expected that the SAD model can be extended to more complicated models to account for the existence of persisters, which are a small fraction of quiescent bacteria (i.e., the suppressed state in our SAD model) that survive and regrow.59
Determining the wake-up rate in the SAD model experimentally
In our quantitative SAD model, the antimicrobial activity of AgNPs or Ag ions is characterized by two parameters: the killing rate α and the wake-up rate β. While α has been estimated from the CFU assays (Fig. 4), here we determined the wake-up rate from measured kinetic growth curves (Fig. 2).As discussed above, although the killing rate α is expected to depend generally on various factors, it can be treated as a constant under our experimental conditions. Therefore, in this study to avoid over-fitting, we assumed a constant killing rate when estimating the wake-up rate β from measured kinetic growth curves (Fig. 2). Another rationale behind this assumption is that changing the killing rate alone predicted that the turning points move towards lower left (Fig. S5†), conflicting with experimental data in which the turning points shifted towards lower right (Fig. 4A). Therefore, we conclude that the wake-up rate is the major effecting parameter under the current experimental conditions.
The idea for estimating the wake-up rate β is to optimize it in the model (eqn (2), with α fixed at 0.77 in the presence of AgNPs) such that the predicted growth curves from the model matches the measured ones. The optimization process is similar to curve fitting through least-square regression, i.e., by minimizing the squared residuals  where yi are measured values and
where yi are measured values and  are fitted values. However, instead of estimating the fitted values
are fitted values. However, instead of estimating the fitted values  via an explicit function f(xi,β) in least-square curve-fitting, the “fitted” y-values in the optimization here were estimated by numerically solving our model (eqn (2)).
via an explicit function f(xi,β) in least-square curve-fitting, the “fitted” y-values in the optimization here were estimated by numerically solving our model (eqn (2)).
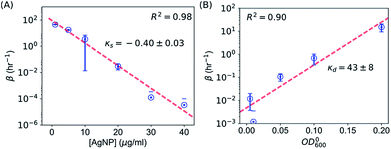
It is possible to determine the dependence of the wake-up rate on the concentration of AgNPs in the growth media by estimating the wake-up rates β for each and every measured growth curve for E. coli in the presence of AgNPs at different concentrations. Note that each growth curve was “fitted” independently, and no prior information about [AgNP] was needed for the “fitting”. However, the independently “fitted” wake-up rates β were clearly dependent on [AgNP] as shown in Fig. 7A. It was found that the logarithm of the wake-up rate was linear to the concentration of AgNPs, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = κs × [AgNP] + θs where κs is the slope and θs is the intercept of the ln
β = κs × [AgNP] + θs where κs is the slope and θs is the intercept of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β ∼ [AgNP] plot. Fitting the β ∼ [AgNP] curve resulted in κs = −0.40 ± 0.03 and θs = 4.5±0.7, with a R2 value of 0.98 (Fig. 7C). The negative slope, κs, indicates that AgNPs at higher concentrations would result in longer lag phases, consistent with our experimental measurements (Fig. 3). We note that, in a previous model, based on energy flux, for the toxicity of metal-based nanoparticles, a parameter termed as the target acclimation energy density was responsible to characterize the dynamics of bacterial acclimation to new environments,42,43 and thus relevant to our wake-up rate β. Our results that β depends on the concentration of AgNPs indicate that the target acclimation energy density in the models by Klanjscek et al.42,43 is likely to correlate with exposure to AgNPs.
β ∼ [AgNP] plot. Fitting the β ∼ [AgNP] curve resulted in κs = −0.40 ± 0.03 and θs = 4.5±0.7, with a R2 value of 0.98 (Fig. 7C). The negative slope, κs, indicates that AgNPs at higher concentrations would result in longer lag phases, consistent with our experimental measurements (Fig. 3). We note that, in a previous model, based on energy flux, for the toxicity of metal-based nanoparticles, a parameter termed as the target acclimation energy density was responsible to characterize the dynamics of bacterial acclimation to new environments,42,43 and thus relevant to our wake-up rate β. Our results that β depends on the concentration of AgNPs indicate that the target acclimation energy density in the models by Klanjscek et al.42,43 is likely to correlate with exposure to AgNPs.
Similarly, we determined the dependence of the wake-up rate β on the initial concentration of E. coli, OD0600. For this purpose, we performed kinetic growth assays for E. coli with a constant concentration of AgNPs (20 μg mL−1) but different initial concentrations of the bacteria. We observed that the growth curves were shifted to the right at lower initial bacterial concentrations (Fig. S6†). Fitting of the growth curves showed that the maximum specific growth rate didn't change much for different OD0600 (Fig. S6 and S7†), but the lag times increased when the initial OD600 of the bacterial cultures decreased (Fig. S6 and S7†). These experimental results could be reproduced qualitatively using our SAD model (Fig. S8†). More importantly, we obtained the wake-up rates at varying OD0600 values from this set of growth curves as described above. Interestingly, the logarithm of the wake-up rate is again roughly linear, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = κd × OD0600 + θd, where κd = 43 ± 8 (the slope) and θd = −5.3 ± 0.9 (the intercept) were fitted parameters from Fig. 7B (R2 = 0.90). The positive slope, κd, indicates that lower initial bacterial concentrations would result in longer lag phases, consistent with our experimental measurements (Fig. S7†).
β = κd × OD0600 + θd, where κd = 43 ± 8 (the slope) and θd = −5.3 ± 0.9 (the intercept) were fitted parameters from Fig. 7B (R2 = 0.90). The positive slope, κd, indicates that lower initial bacterial concentrations would result in longer lag phases, consistent with our experimental measurements (Fig. S7†).
Taking together, we obtained that the wake-up rate was approximately exponential to the concentrations,
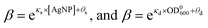 | (3) |
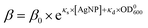 | (4) |
The dependences of the wake-up rate on the concentration of AgNPs and initial concentration of bacteria in the culture provided us an additional way to verify our SAD model. This is because both dependences are from eqn (4) but they are from two independent sets of kinetic growth curves (varying [AgNP] vs. varying OD0600). By comparing eqn (3) and (4), we have
 | (5) |
 | (6) |
As the parameters θs and θd were obtained with OD0600 = 0.05 and [AgNP] = 20 μg mL−1, respectively, if our SAD model is correct, we would expect that
| θs − θd = 0.05κd − 20κs | (7) |
Plugging in the measured values, we found that the left hand side of eqn (7) is θs − θd = 9.8 ± 1.1 and the right hand side is 0.05κd − 20κs = 10.1 ± 0.7. Therefore, both sides of eqn (7) are indeed the same (within error), which strongly justifies the SAD model.
We also note that the exponential dependence of β on the concentration of AgNPs in this study was supported by experimental results reported by others previously.11,22 Using the measured relation between β and [AgNP], the SAD model produced a sigmoid relation between the killing percentage of bacteria and the concentration of AgNPs (Fig. S9†), qualitatively consistent with the experimental results by Xiu et al.22
Conclusions
To conclude, we investigated the antimicrobial activity of AgNPs and Ag ions on the growth of E. coli using kinetic growth assays and CFU assays in combination with quantitative modeling. Kinetic growth assays showed that the presence of AgNPs or Ag ions in the growth media slowed down the growth of E. coli by elongating the apparent lag time (λ) while keeping the maximum specific growth rate μm unaffected. On the other hand, time-kill curves based on CFU assays showed that some of the E. coli in the culture were killed by Ag. Based on these experimental results, a quantitative model (referred to as the SAD model) was developed to describe the antimicrobial activity of AgNPs and Ag ions. This model explained the experimental observations very well, providing a plausible description of the antimicrobial activity of AgNPs. In addition, we showed that the parameters of the SAD model (the killing rate α and the wake-up rate β) could be determined from the experimental data. Furthermore, we estimated the dependences of the wake-up rate β on the concentrations of AgNPs and bacteria experimentally. Our quantitative model provides an alternative way to characterize the antimicrobial activities of AgNPs and Ag ions, other than the commonly used MIC and minimum bactericidal concentration (MBC).Our model provides a phenomenological description and quantification of the antimicrobial activity of AgNPs and Ag ions. The model by itself does not explain how the bacteria were knocked out into the suppressed state by the AgNPs or Ag ions, or what is the suppressed state on molecular basis, or how the bacteria adapt to AgNPs and “wake up” to multiply again. On one hand, it is expected that our model can be extended by integrating mechanistic modeling of the toxicity of AgNPs and Ag ions. For example, the models by Klanjscek et al.42,43 based on energy flux provide a plausible direction. On the other hand, to answer these mechanistic questions, further experimental, mechanistic investigations at single cell and single molecule levels are required. Several studies in the literature using TEM and X-ray microanalysis showed that bacteria were not lysed by AgNPs or Ag ions;3,24,55 instead, the AgNPs or Ag ions caused condensation of DNA, lowered expression level of proteins, aggregation of proteins, or other physical changes.3,24,55 These observations indirectly support our hypothesis of the suppressed state, and indicate the possibilities of bacterial adaptation to AgNPs in the growth medium and the reactivation of the bacteria. To elucidate the molecular mechanism of AgNPs and other metal nanoparticles on bacteria, recent emerging super-resolution fluorescence imaging on live single cells at the molecular level60–65 might be of great help in the future.
Additionally, we emphasize that the killing and wake-up rates in our model generally depend on the physicochemical properties of AgNPs such as size, shape, and surface modifications, which have been shown to play a role in their antimicrobial activities.2,12,15 We expect that our model is ready to take into account various physicochemical properties, and thus applicable to a broad range of metal nanoparticles and ions. Systematic future investigations will address these aspects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Arkansas Biosciences Institute grant (ABI-0189, ABI-0226) to Y. W. We acknowledge partial support from the Center for Advanced Surface Engineering, under the National Science Foundation Grant No. OIA-1457888 and the Arkansas EPSCoR Program, ASSET III. The plasmid pOEGFP2 was a gift from Dr David McMillen at the University of Toronto. We would like to thank E. Pollock and B. J. Shaulis for their help with the ICP-MS analysis at the Trance Element and Radiogenic Isotopic Laboratory, which was supported by the Arkansas Biosciences Institute.References
- J. W. Alexander, Surg. Infect., 2009, 10, 289–292 CrossRef PubMed.
- S. Agnihotri, S. Mukherji and S. Mukherji, RSC Adv., 2014, 4, 3974–3983 RSC.
- H. Bao, X. Yu, C. Xu, X. Li, Z. Li, D. Wei and Y. Liu, PLoS One, 2015, 10, 1–10 Search PubMed.
- J. Bresee, K. E. Maier, A. E. Boncella, C. Melander and D. L. Feldheim, Small, 2011, 7, 2027–2031 CrossRef CAS PubMed.
- A. K. Chatterjee, R. Chakraborty and T. Basu, Nanotechnology, 2014, 25, 135101 CrossRef PubMed.
- M. N. K. Chowdhury, M. D. H. Beg, M. R. Khan and M. F. Mina, Mater. Lett., 2013, 98, 26–29 CrossRef CAS.
- Y. Cui, Y. Zhao, Y. Tian, W. Zhang, X. Lu and X. Jiang, Biomaterials, 2012, 33, 2327–2333 CrossRef CAS PubMed.
- T. Fukuoka, A. Yamaguchi, R. Hara, T. Matsumoto, Y. Utsumi and Y. Mori, in 2015 International Conference on Electronic Packaging and iMAPS All Asia Conference (ICEP-IAAC), IEEE, 2015, pp. 432–435 Search PubMed.
- R. Geethalakshmi and D. V. L. Sarada, Ind. Crops Prod., 2013, 51, 107–115 CrossRef.
- J. S. Kim, E. Kuk, K. N. Yu, J.-H. Kim, S. J. Park, H. J. Lee, S. H. Kim, Y. K. Park, Y. H. Park, C.-Y. Hwang, Y.-K. Kim, Y.-S. Lee, D. H. Jeong and M.-H. Cho, Nanomedicine: Nanotechnology, Biology and Medicine, 2007, 3, 95–101 CrossRef CAS PubMed.
- B. Le Ouay and F. Stellacci, Nano Today, 2015, 10, 339–354 CrossRef CAS.
- X. Li, S. M. Robinson, A. Gupta, K. Saha, Z. Jiang, D. F. Moyano, A. Sahar, M. A. Riley and V. M. Rotello, ACS Nano, 2014, 8, 10682–10686 CrossRef CAS PubMed.
- S. Maiti, D. Krishnan, G. Barman, S. K. Ghosh and J. K. Laha, J. Anal. Sci. Technol., 2014, 5, 40 CrossRef.
- D. Meeker, S. V. Jenkins, E. K. Miller, K. Beenken, A. Loughran, A. Powless, T. Muldoon, E. I. Galanzha, V. Zharov, M. S. Smeltzer and J. Chen, ACS Infect. Dis., 2016, acsinfecdis.5b00117 Search PubMed.
- S. Pal, Y. K. Tak and J. M. Song, Appl. Environ. Microbiol., 2007, 73, 1712–1720 CrossRef CAS PubMed.
- M. Raffi, S. Mehrwan, T. M. Bhatti, J. I. Akhter, A. Hameed, W. Yawar and M. M. ul Hasan, Ann. Microbiol.Ann. Microbiol., 2010, 60, 75–80 CrossRef CAS.
- J. Ramyadevi, K. Jeyasubramanian, A. Marikani, G. Rajakumar and A. A. Rahuman, Mater. Lett., 2012, 71, 114–116 CrossRef CAS.
- J. P. Ruparelia, A. K. Chatterjee, S. P. Duttagupta and S. Mukherji, Acta Biomater., 2008, 4, 707–716 CrossRef CAS PubMed.
- M. Shaalan, M. Saleh, M. El-Mahdy and M. El-Matbouli, Nanomedicine: Nanotechnology, Biology and Medicine, 2016, 12, 701–710 CrossRef CAS PubMed.
- I. Sondi and B. Salopek-Sondi, J. Colloid Interface Sci., 2004, 275, 177–182 CrossRef CAS PubMed.
- Y. Wei, S. Chen, B. Kowalczyk, S. Huda, T. P. Gray and B. A. Grzybowski, J. Phys. Chem. C, 2010, 114, 15612–15616 CAS.
- Z. Xiu, Q. Zhang, H. L. Puppala, V. L. Colvin and P. J. J. Alvarez, Nano Lett., 2012, 12, 4271–4275 CrossRef CAS PubMed.
- Y. Zhao, Y. Tian, Y. Cui, W. Liu, W. Ma and X. Jiang, J. Am. Chem. Soc., 2010, 132, 12349–12356 CrossRef CAS PubMed.
- Y. Zhou, Y. Kong, S. Kundu, J. D. Cirillo and H. Liang, J. Nanobiotechnol., 2012, 10, 19 CrossRef CAS PubMed.
- N. Durán, M. Durán, M. B. de Jesus, A. B. Seabra, W. J. Fávaro and G. Nakazato, Nanomedicine: Nanotechnology, Biology and Medicine, 2016, 12, 789–799 CrossRef PubMed.
- D. Marchaim, T. Chopra, J. M. Pogue, F. Perez, A. M. Hujer, S. Rudin, A. Endimiani, S. Navon-Venezia, J. Hothi, J. Slim, C. Blunden, M. Shango, P. R. Lephart, H. Salimnia, D. Reid, J. Moshos, W. Hafeez, S. Bheemreddy, T. Y. Chen, S. Dhar, R. a. Bonomo and K. S. Kaye, Antimicrob. Agents Chemother., 2011, 55, 593–599 CrossRef CAS PubMed.
- K. M. Papp-Wallace, A. Endimiani, M. A. Taracila and R. A. Bonomo, Antimicrob. Agents Chemother., 2011, 55, 4943–4960 CrossRef CAS PubMed.
- F. Perez and D. Van Duin, Cleveland Clin. Q., 2013, 80, 225–233 CrossRef PubMed.
- D. M. Sievert, P. Ricks, J. R. Edwards, A. Schneider, J. Patel, A. Srinivasan, A. Kallen, B. Limbago and S. Fridkin, Infection Control and Hospital Epidemiology, 2013, 34, 1–14 CrossRef PubMed.
- S. L. Percival, P. G. Bowler and D. Russell, J. Hosp. Infect., 2005, 60, 1–7 CrossRef CAS PubMed.
- L. Deshpande and B. Chopade, BioMetals, 1994, 7, 49–56 CrossRef CAS PubMed.
- J. L. Graves, M. Tajkarimi, Q. Cunningham, A. Campbell, H. Nonga, S. H. Harrison and J. E. Barrick, Front. Genet., 2015, 5, 1–13 Search PubMed.
- X. Z. Li, H. Nikaido and K. E. Williams, J. Bacteriol., 1997, 179, 6127–6132 CrossRef CAS PubMed.
- M. Rai, A. Yadav and A. Gade, Biotechnol. Adv., 2009, 27, 76–83 CrossRef CAS PubMed.
- Q. Zhang, W. Li, L.-P. Wen, J. Chen and Y. Xia, Chem.–Eur. J., 2010, 16, 10234–10239 CrossRef CAS PubMed.
- A. Ivask, A. ElBadawy, C. Kaweeteerawat, D. Boren, H. Fischer, Z. Ji, C. H. Chang, R. Liu, T. Tolaymat, D. Telesca, J. I. Zink, Y. Cohen, P. A. Holden and H. A. Godwin, ACS Nano, 2014, 8, 374–386 CrossRef CAS PubMed.
- E. Navarro, F. Piccapietra, B. Wagner, F. Marconi, R. Kaegi, N. Odzak, L. Sigg and R. Behra, Environ. Sci. Technol., 2008, 42, 8959–8964 CrossRef CAS PubMed.
- A. Juška, G. Gedminiene and R. Ivanec, Biochem. Mol. Biol. Educ., 2006, 34, 417–422 CrossRef PubMed.
- C. Begot, I. Desnier, J. D. Daudin, J. C. Labadie and A. Lebert, J. Microbiol. Methods, 1996, 25, 225–232 CrossRef.
- B. Li, Y. Qiu, H. Shi and H. Yin, Analyst, 2016, 3059–3067 RSC.
- M. Zwietering, I. Jongenburger, F. Rombouts and K. van't Riet, Appl. Environ. Microbiol., 1990, 56, 1875–1881 CAS.
- T. Klanjscek, R. M. Nisbet, J. H. Priester and P. A. Holden, PLOS ONE, 2012, 7, e26955 CAS.
- T. Klanjscek, R. M. Nisbet, J. H. Priester and P. A. Holden, Ecotoxicology, 2013, 22, 319–330 CrossRef CAS PubMed.
- B. P. Hills and B. M. Mackey, Food Microbiol., 1995, 12, 333–346 CrossRef.
- W. K. Jung, H. C. Koo, K. W. Kim, S. Shin, S. H. Kim and Y. H. Park, Appl. Environ. Microbiol., 2008, 74, 2171–2178 CrossRef CAS PubMed.
- K. An Huynh and K. L. Chen, Natl. Inst. Health Public Access, 2012, 45, 5564–5571 Search PubMed.
- S. K. Gogoi, P. Gopinath, A. Paul, A. Ramesh, S. S. Ghosh and A. Chattopadhyay, Langmuir, 2006, 22, 9322–9328 CrossRef CAS PubMed.
- C.-N. Lok, C.-M. Ho, R. Chen, Q.-Y. He, W.-Y. Yu, H. Sun, P. K.-H. Tam, J.-F. Chiu and C.-M. Che, J. Proteome Res., 2006, 5, 916–924 CrossRef CAS PubMed.
- C.-N. Lok, C.-M. Ho, R. Chen, Q.-Y. He, W.-Y. Yu, H. Sun, P. K.-H. Tam, J.-F. Chiu and C.-M. Che, JBIC, J. Biol. Inorg. Chem., 2007, 12, 527–534 CrossRef CAS PubMed.
- J. H. Priester, A. Singhal, B. Wu, G. D. Stucky and P. A. Holden, Analyst, 2014, 139, 954–963 RSC.
- M. Raffi, F. Hussain, T. M. Bhatti, J. I. Akhter, A. Hameed and M. M. Hasan, J. Mater. Sci. Technol., 2009, 24, 192–196 Search PubMed.
- G. A. Pankey and L. D. Sabath, Clin. Infect. Dis., 2004, 38, 864–870 CrossRef CAS PubMed.
- P. Gong, H. Li, X. He, K. Wang, J. Hu, W. Tan, S. Zhang and X. Yang, Nanotechnology, 2007, 18, 285604 CrossRef.
- R. Krishnan, V. Arumugam and S. K. Vasaviah, J. Nanomed. Nanotechnol., 2015, 6, 1–4 Search PubMed.
- Q. L. Feng, J. Wu, G. Q. Chen, F. Z. Cui, T. N. Kim and J. O. Kim, J. Biomed. Mater. Res., 2000, 52, 662–668 CrossRef CAS PubMed.
- E. T. Hwang, J. H. Lee, Y. J. Chae, Y. S. Kim, B. C. Kim, B.-I. Sang and M. B. Gu, Small, 2008, 4, 746–750 CrossRef CAS PubMed.
- X. Yang, A. P. Gondikas, S. M. Marinakos, M. Auffan, J. Liu, H. Hsu-Kim and J. N. Meyer, Environ. Sci. Technol., 2012, 46, 1119–1127 CrossRef CAS PubMed.
- E. Yourassowsky, M. P. van der Linden, M. J. Lismont, F. Crokaert and Y. Glupczynski, Antimicrob. Agents Chemother., 1985, 28, 756–760 CrossRef CAS PubMed.
- Y. Zhang, Emerging Microbes Infect., 2014, 3, e3 CrossRef CAS PubMed.
- E. Betzig, G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz and H. F. Hess, Science, 2006, 313, 1642–1645 CrossRef CAS PubMed.
- J. Fei, D. Singh, Q. Zhang, S. Park, D. Balasubramanian, I. Golding, C. K. Vanderpool and T. Ha, Science, 2015, 347, 1371–1374 CrossRef CAS PubMed.
- M. Heilemann, S. Van De Linde, M. Schüttpelz, R. Kasper, B. Seefeldt, A. Mukherjee, P. Tinnefeld and M. Sauer, Angew. Chem., Int. Ed., 2008, 47, 6172–6176 CrossRef CAS PubMed.
- B. Huang, W. Wang, M. Bates and X. Zhuang, Science, 2008, 319, 810–813 CrossRef CAS PubMed.
- M. J. Rust, M. Bates and X. Zhuang, Nat. Methods, 2006, 3, 793–795 CrossRef CAS PubMed.
- Y. Wang, P. Penkul and J. N. N. Milstein, Biophys. J., 2016, 111, 467–479 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10495b |
| This journal is © The Royal Society of Chemistry 2017 |