Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Desalination by dragging water using a low-energy nano-mechanical device of porous graphene†
Jose L. Rivera *ab,
Francisco Villanueva-Mejia
*ab,
Francisco Villanueva-Mejia c,
Pedro Navarro-Santos
c,
Pedro Navarro-Santos c and
Francis W. Starr
c and
Francis W. Starr d
d
aGraduate School of Engineering Physics, Universidad Michoacana de San Nicolás de Hidalgo, 58000 Morelia, Michoacán, Mexico. E-mail: jlrivera@umich.mx
bFaculty of Chemical Engineering, Universidad Michoacana de San Nicolás de Hidalgo, 58000 Morelia, Michoacán, Mexico
cInstitute of Chemical Biology Sciences, Universidad Michoacana de San Nicolás de Hidalgo, 58000 Morelia, Michoacán, Mexico
dDepartment of Physics, Wesleyan University, Middletown, Connecticut 06459, USA
First published on 22nd November 2017
Abstract
We propose a nano-structured suction system based on graphene sheets for water desalination processes. The desalination system modeled in this work is an alternative process to the commonly employed but energy intensive reverse osmosis process. The nano-structured system generates drag forces, which pull water molecules from the saline solution into a chamber. Our molecular simulations consist of two rigid walls of graphene: one wall with 5 Å pores permeable to water molecules forms the membrane, while the other wall acts as a plunger to induce and control the transfer of desalinated water molecules, which accumulate in a chamber between the two walls. Prior to the desalination process, the chamber is saturated with one monolayer of water molecules. The desalination occurs when the plunger moves to create unsaturated space inside the chamber. At plunger speeds up to 10 cm s−1, the system desalinates saltwater films in the open part of the membrane. At higher plunger speeds, the desalination chamber expands faster than molecules can fill the chamber, resulting in cavitation and poor desalination. At plunger speeds of 0.5 cm s−1, the desalination occurs via a quasi-equilibrium process, which minimizes the energy necessary to drive desalination. Our findings suggest that the desalination process requires less energy than reverse osmosis methods at plunger speeds up to 0.15 cm s−1 (for the chosen pore density). The filling profile of desalinated water molecules inside the chamber occurs via three distinct regimes: the first two regimes correspond to the formation of one and then two monolayers adsorbed to the chamber's walls. The third regime corresponds to the filling of molecules between the adsorbed layers, which approaches a density close to the density of bulk liquid water. Including flexibility in the graphene sheets does not affect the energy consumption for desalination processes occurring after the formation of the second monolayer, but flexible membranes require a slightly larger pore diameter (7 Å) than rigid membranes.
Introduction
Membrane research based on carbon nanostructures,1,2 has been helpful for the development of real separation systems based on these novel materials.3,4 Graphene-based membranes show fluxes one order of magnitude higher than the polymeric membranes used in state-of-the-art reverse osmosis processes.3,5,6 Significant additional improvements can be obtained by increasing the density of pores (which in currently realized systems is ≈1 pore per 100 nm2)3 to approach the physical limit on the order of 1 pore for a few nm2; the technology to build such new materials is currently under development.7 It is expected that clean graphene surfaces will not be degraded by the presence of ozone or chlorine, so that most fouling and scaling problems will be avoided.7Molecular simulations are a useful tool to examine molecular-level properties at aqueous interfaces.8–11 Simulations mimicking the desalination processes have been employed to model desalination using graphene and carbon nanotube membranes, and high-pressure gradients, mimicking reverse osmosis processes.8,12,13 Striolo and collaborators have employed graphene membranes to study the free energy barrier to cross graphene membranes through pores in pristine graphene, and they found that pores with effective diameters ≈0.5 nm effectively block dissolved ions. They also functionalized the pores, and found that the functionalized pores block ions at the cost of a larger free energy barrier for the water molecules.6 Cohen-Tanugi and Grossman have employed high pressure gradients (100–200 MPa) to reproduce the reverse osmosis process, and they also found that narrow membranes effectively reject the ions dissolved in the saline solution, and wider pores functionalized with hydroxyl groups promote water flux through the membrane, reaching fluxes up to three orders of magnitude higher than conventional reverse osmosis membranes.12 Desalination simulations using zwitterion functionalized carbon nanotube/polyamide nanocomposite membranes with a high-density of surface pores also found high fluxes and high salt rejection (through steric effects) at a pressure difference of 3.65 MPa.14
Drawing molecules across membranes is a non-stop process in biological systems, which use specialized nano-machinery to drag, instead of push, molecules and micelles across the membrane.15 Such nano-machinery uses motor proteins, including kinesin,16 myosin,17 and dynein,18 and efforts to produce synthetic molecular motors attempt to reproduce and control the dragging transport capabilities of biological machinery.19
In this work, we examine an alternative approach to desalination, in which molecules are dragged across a membrane by osmotic forces, rather than forced through pores by gradients of pressure exerted on the saline fluid. Specifically, we examine the possibility of controlling the desalination of water through a “nano-syringe” consisting of a graphene membrane and a second graphene wall acting as a plunger. In this approach, one expects the driving force is a “vacuum effect” provided by the movement of the plunger. We show that, over a range of plunger speeds, the nano-syringe can achieve desalination flux rates on the order of those obtained via pressurize-driven flows, but with low-energy consumption.
Methods
We perform the simulations at the ambient temperature of 300 K using the Nose–Hoover algorithm, implemented in the LAMMPS package20 with a time step of 1 fs. We simulate the systems at constant temperature rather than constant energy, because the nanostructures that form the nano-syringes are rigid, and they dissipate heat and momentum as in real systems. We employ up to 300 ns to simulate the desalination processes in non-equilibrium processes at the plunger speed of 0.5 cm s−1. We also simulate systems in equilibrium (the position of the plunger is fixed) to investigate up to how many water molecules can saturate the chamber of the nano-syringe at some points in the dynamic processes of desalination, and for these simulations we employ 1 ns for equilibration, and 10 ns for properties calculation.We use the SPC/E force field to simulate the water molecules, which uses spherical cutoffs for Lennard-Jones and coulombic interactions (10 Å).21 The SPC/E force field reproduces equilibrium interfacial properties of pure water,22–24 and mixtures with non-polar molecules in vapor–liquid equilibrium.11,25,26 Confined water shows slow dynamics,2,27 similar to their behavior in the region of supercooled water, where the SPC/E model also reproduces the surface tension.28 Water–ion interactions also include Lennard-Jones and coulombic interactions, and they are optimized for simulations with the SPC/E model of water.29,30 Corrections due to long-range electrostatic interactions were calculated using the particle–particle particle-mesh Ewald (PPPME) summation technique.31 Carbon atoms in the graphene membrane and plunger form rigid walls with averaged forces (constant speed) in our simulations, and the interaction expression of Lennard-Jones has been used to predict successfully the packing structures in graphite and fullerenes C60 and C70,32,33 as well as the mechanical properties of carbon nanotubes.34,35 We simulate the water–graphene and ions–graphene interactions using the Lorentz–Berthelot mixing rules. To test the effects of flexibility on our findings, we also simulate flexible graphene walls using an intramolecular potential that includes bond, valence, dihedral and improper angles, which previously has been used to simulate water between flexible graphene sheets.36
Results and discussion
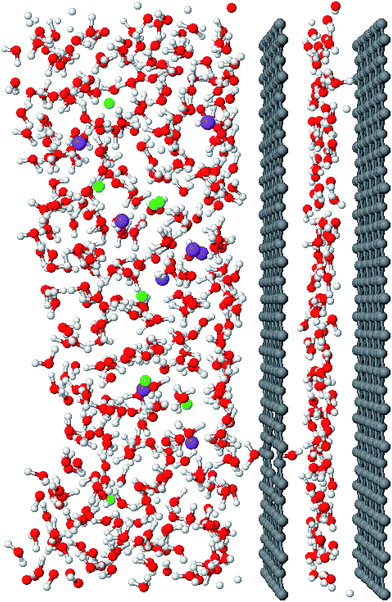
We employ the molecular dynamics methodology to simulate the process of desalination using a nanostructured system based on membranes made of graphene walls containing surface pores. Simulation details are provided in the Methods section. The system replicates the behavior of a “nano-syringe” (Fig. 1), which moves the fluid through the membrane, filtering the saline solution using pores of small diameter created on the graphene surface. The system employs another graphene wall, which has the function of a plunger that expands a chamber to contain the desalinated fluid. A similar nano-syringe system using carbon nanotube pores instead of graphene pores has been studied previously to simulate the rapid transport of water in nanotube-based membranes.2 The drag forces that pull the water molecules from the saline solution into the slit pore chamber are capillary forces, and they result from the movement of the plunger. The pores in the slit and graphene pores are connected, and they form an attractive zone for the water molecules from the saline solution, located in the open part of the membrane. The driving force that carries out the desalination of the saline solution is always present because, when the chamber saturates with newly desalinated water molecules, the plunger moves to create more unsaturated space inside the chamber. During the transfer of water molecules to the chamber, there is a continuous formation/breaking of hydrogen bonds between the two fluids at the membrane pore, as can be seen in the movie of the desalination process provided in the ESI.† The studied systems contain saline solutions of sodium and chlorine with average concentrations close to that present in the seawater (≈35 g L−1), corresponding to ≈51 water molecules for each Na–Cl ion pair.The graphene membrane uses an effective pore diameter of 0.5 nm, which (by periodic boundary conditions in the membrane plane) repeats periodically over the surface of graphene, yielding a density of 0.238 pores per nm2, or one pore by each 4.2 nm2. The area of the simulation cell parallel to the graphene walls is similar to that used in previous studies of membranes constructed from graphene and carbon nanotubes,2,6,7,12 and is large enough to contain a system of water molecules that nearly reproduces the behavior of bulk liquid water away from the interfaces.2
Before we begin the process of desalination, the chamber of the nano-syringe must be filled with a monolayer of water molecules (Fig. 1). Filling of the chamber with pure water molecules prior to desalination is necessary because the saline systems are more cohesive than systems with pure water molecules, and thus water molecules in a saline solution will not spontaneously fill the chamber. However, the filling process does occur spontaneously when we put the membrane in contact with a layer of molecules of pure water located in the open space of the graphene membrane, and we set the separation between the membrane and the plunger large enough to accommodate a monolayer of water molecules.2 Thus, to prefill the system, we start with pure water in the open part of the membrane, and then introduce the saline solution to the open part of the membrane after the chamber has been prefilled. We allow the salinated and pre-filled system to equilibrate for 10 ns, after which the plunger starts to move at constant speed to create the unsaturated space and pull water molecules from the saline solution to the chamber.
The performance of the system as a desalination system was quantified by tracking the number of water molecules transferred from the saline solution to the desalination chamber. Fig. 2 shows the number of transferred water molecules at plunger speeds of plunger from 0.5 to 20 cm s−1. The number of desalinated water molecules shows the expected behavior, as we increase the speed at which the plunger moves, the time needed to desalinate the water molecules decreases. Note that not all water molecules are desalinated because we cannot fully desolvate the ions remaining in the open part of the membrane. Accordingly, roughly 90% (184 of 204) water molecules are transferred to the desalinated chamber at plunger speeds equal or slower than 5 cm s−1. At higher plunger speeds, the fraction of desalinated molecules is reduced. When the plunger moves at a speed of 10 cm s−1, only 70% of the molecules are desalinated, and when the plunger moves to a speed of 20 cm s−1 only a small fraction of water molecules is desalinated (not drawn in Fig. 2). The reduced efficacy of desalination at higher plunger speeds is a result of the loss of cohesion of some water molecules with the plunger wall (cavitation).
 | ||
| Fig. 2 Profiles of number of desalinated water molecules using the dragging desalination system with 204 water molecules at 300 K, and plunger speeds of 0.5, 1.0, 2.5, 5.0, and 10.0 cm s−1. | ||
The desalination at lower speeds is characterized by three regimes. Fig. 2 qualitatively shows these regimes are characterized by different slopes (desalination flux), which is most apparent at speeds below 2.5 cm s−1. As we shall show, the first regime is the gradual expansion of the prefilled monolayer (small slope), followed by the rapid formation (large slope) of a second monolayer beyond a threshold plunger gap. The last and most prolonged regime is the steady filling of molecules in the chamber between the two interfacial layers of water. It is also worth noting that the slower profiles show pronounced dips, which demonstrates that small amounts of water molecules return for short periods of time. In other words, the desalination process at the molecular scale is subject to significant fluctuations, as one might expect at equilibrium. During these short periods, the saline solution on the open side of the membrane reorganizes and is more cohesive than the confined system, attracting some desalinated water molecules from the chamber, but the continuous movement of the plunger creates more unsaturated space and ultimately generates stronger capillary forces, causing more water molecules to be desalinated.
We next show that the desalination process at plunger speeds ≤5 cm s−1 corresponds to a quasi-static equilibrium process, while at speeds ≥10 cm s−1 the desalination is a non-equilibrium process, and thus becomes less effective. To demonstrate this, we consider the number of desalinated water molecules inside the chamber (including the 47 water molecules prefilling the chamber before the desalination process) as a function of the separation between the walls of graphene that form the membrane and the plunger (free space), which delimit the chamber. The separation between the walls of graphene is directly proportional to the free volume inside the chamber because the cross-sectional area is fixed. In Fig. 3, we show three profiles of the number of desalinated water molecules inside the chamber as a function of the separation between the wall of the membrane (free space) and the plunger for the system with initially 204 water molecules and 4 Na–Cl ion pairs, at speeds of 0.5, 1.0, and 5.0 cm s−1 at 300 K. To relate these profiles to equilibrium, we also simulate equilibrium systems with a fixed plunger separation. The initial conformations for the equilibrium simulations are taken from the dynamic system with the plunger moving at a speed of 1.0 cm s−1, which we allow to equilibrate for 1 ns, followed by 10 ns of data collection. The properties appear invariant over this 10 ns “production” run. Fig. 3 shows that the profile of the number of desalinated water molecules at the plunger speeds ≤1.0 cm s−1 all collapse to the same equilibrium master curve for the number of molecules in the chamber. Thus, below a threshold plunger speed the system desalination occurs via equilibrium process, which thus minimizes free energy.
The comparison to the equilibrium data also clearly distinguish the three distinct regimes of the desalination process. At the low plunger speeds where we have a quasi-equilibrium process, the first regime arises from the beginning until the systems reaches a separation of ∼5.2 Å and is characterized by a nearly zero-desalination rate. Between 5.2 and 6 Å a second regime is present, characterized by a large desalination rate, and the last regime occurs from 6 Å onwards, characterized by a moderate desalination rate. At larger speeds when the process is non-equilibrium, these regimes become less distinguishable. The three regimes are still apparent at a plunger speed of 5.0 cm s−1, with the main difference that the second regime shows a smaller desalination rate than the rate observed using a plunger speed of 1.0 cm s−1. As we increase the plunger speed, those regimes fade until they disappear when the plunger speed reaches 10 cm s−1, which has a nearly linear behavior. The final desalination regime exhibits a monotonic increase of desalinated molecules, accompanied by occasional fluctuations, as molecules from the chamber flow back to the solution, with “setbacks” of up to 12 water molecules in a period of 0.5 ns for the profile at a plunger speed of 5 cm s−1, and up to 9 water molecules in a period of 0.2 ns for the profile at a speed plunger of 1 cm s−1. The “setbacks” are also observed in the equilibrium simulations, and are the result of natural fluctuations that make one of the phases in equilibrium transiently more cohesive.2 For the plunger speed of 0.5 cm s−1, there is a periodic “setback” of molecules along the profile due to the slow movement of the plunger, similar to the behavior of the equilibrium simulations.
Snapshots of the conformations at several separations provide a qualitative view of the desalination process. We show conformations in key points of the system in Fig. 4, which correspond to separations (free space) of 3.4, 4.8, 6.0, and 11.8 Å in the profile of Fig. 3 at a plunger speed of 1.0 cm s−1. At a separation of 3.4 Å, the prefilled water forms a monolayer of molecules inside the chamber. As we increase the separation inside the chamber, molecules prefer being close to one of the two walls for short times. At a separation of 6.0 Å, two distinct interfacial monolayers of water molecules form, which adsorb preferentially on each wall of the chamber. At larger separations than 6 Å, additional water molecules coming from the open part of the membrane are no longer located in the adsorbed monolayers, but in a third layer between the two adsorbed monolayers, which gets progressively thicker as we increase the separations between the walls of the chamber.
The filling behavior of the chamber can be quantified by the water density profiles in the chamber along the axis perpendicular to the graphene surfaces forming the desalination system. These density profiles demonstrate the nature of the three regimes of desalination at equilibrium. To obtain the density profiles, we calculate the mean density of the equilibrium simulations in slabs of thickness 0.01 nm along the axis of the separation between the walls. Density profiles were calculated for the characteristic separations of 3.4, 4.8, 6.0, and 11.8 Å, the same separations used in the snapshots of Fig. 4. These profiles are displayed along the curve of number of molecules at equilibrium in Fig. 5. The first regime is bounded by the density profiles at 3.4 and 4.8 Å. At the separation of 3.4 Å, the formation of a single-monolayer of water molecules inside the chamber is clearly observed, which is reflected by the density profile with a single peak with density 4.7 g cm−3 within the chamber; this high density (compared to bulk water) is due to the effects of confinement within the two walls of graphene.37,38 At a separation of 4.8 Å, the monolayer begins to divide into two layers with peaks of density of 1.7 g cm−3. The second regime, up to 6 Å, involves the formation of a second interfacial monolayer. As we increase the separation between the walls, the system is divided into two well-defined peaks with a density of ≈4 g cm−3 (at 6 Å of separation). Beyond 6 Å, the third and final regime, additional water molecules accumulate in an increasingly bulk-like film formed between the two monolayers adsorbed on the graphene surfaces. This central region has density value at a separation of 11.8 Å similar to that observed in bulk liquid water at 300 K, ≈1 g cm−3.
Current experimental devices utilizing nanotubes or graphene have a somewhat lower pore density in the range of ≈1 pore per 100 nm.24 Therefore, we study the effect of the pore density on our simulated desalination. We consider systems with pore densities of one half and one fourth of the original value studied (0.2381 pores per nm2), using the same effective diameter of pore. The pore density using these systems are 0.1191 and 0.0595 pores per nm2, respectively (Fig. 6). We study plunger speeds of 1.0 and 5.0 cm s−1, below and above the threshold plunger speed for equilibrium desalination in our initial study. Note that for the same plunger speed, the rate of increase in the chamber size (per pore) increases as we decrease the pore density. For the smallest pore density (0.0595 pore/nm2), the desalination process fails after the system desalinates only a few water molecules. The failure occurs because, as very low pore density, the pace water molecules are entering through the pore cannot keep up with the increase in unsaturated spaces, leading to cavitation. For the case where we reduce the pore density by half, the dragging system successfully desalinates the system, as shown in Fig. 7. If we compare the original system to the system having half the pore density, we find that the half-density system at a plunger speed of 5.0 cm s−1 shows a desalination profile nearly as linear as the one observed in the single-area system, but the rate of desalination is more than double the value of the original system (2.32), probably due to the larger voids generated in the half-density system, which in turn generates stronger capillary forces. Clearly this is a non-equilibrium process. The desalination profile of the half-density system at a plunger speed of 1.0 cm s−1 shows the three-regime profile seen in the single-area system, and at 50 ns of the desalination run, the desalination rate of the half-density system is double the value of the original system, probably reflecting that these systems run through equilibrium states, since the plunger speed is slow enough that the desalinated water readily fills the chamber.
To combine the effects of the plunger speed and the pore density, we show the average flux of desalinated water molecules in Fig. 8 for each system that did not fail at the beginning of the desalination process. The data show that, in the quasi-equilibrium regime, the flux is a simple function of the plunger speed. Thus, flux of desalinated molecules can be tuned equally well by modulating the pore density or plunger speed, allowing for flexibility within experimental design constraints. Taking into account the pore density, we obtain fluxes between 0.14 and 2.57 molecules per nm2 per ns for speeds between 0.5 and 10 cm s−1. These fluxes represent ∼1/5 of the flux obtained in studies using molecular dynamics simulations of the transport of pure water molecules across carbon nanotube membranes using high pressure gradients (100 MPa).13 Since the flux is smaller than high pressure desalination, we need to consider other potentially important aspects of the plunger system.
To better illustrate the practical value of this desalination approach, we calculate the work done to move the plunger at constant speed. We calculate the mechanical work (W) done to move the plunger at constant speed:
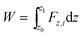 | (1) |
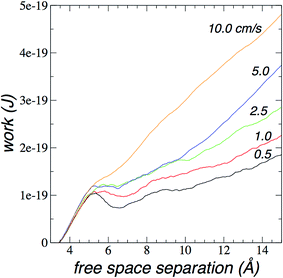
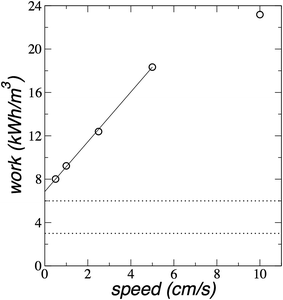
The more important question is the total work needed to complete desalination. We compare the average work done on the plunger to desalinate almost all water molecules (∼180) as a function of the plunger speed in Fig. 10. The plot shows that the average work grows like cube-root of plunger speed.
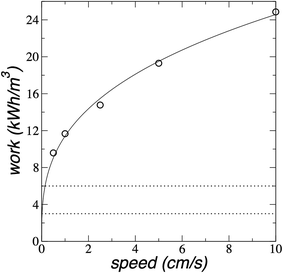 | ||
| Fig. 10 Average work (for 180 water molecules) as a function of the plunger speed for the saline system with 204 water molecules and their correspondent ion pairs at 300 K. The continuous line represents the best non-linear fit (work = c0(speed)1/3). Dotted lines represent the limits of energy consumption of state-of-the-art reverse osmosis.39,40 | ||
Since we wish to minimize the amount of work needed for desalination, we can devise a procedure based on the behavior of the work during desalination. In the first cycle, the system desalinates water from the point where there is only one monolayer of water to the point where we desalinate the whole 180 water molecules. At the beginning (first step), we need work to be done on the plunger to reach the verge of the formation of the second monolayer, which needs ≈1.07 × 10−19 J of total work to desalinate 47 water molecules (≈1.37 kJ mol−1), and is essentially independent of plunger speed (Fig. 9). From this point (second step), we can assume that if the system moves at a very low speed, or if the system is allowed to equilibrate, the system will push the plunger to a separation where the two monolayers are stable. The work done by the system on the plunger in the second step, can be stored through a mechanism to be later employed in the first step in a following cycle, therefore, the system will desalinate water molecules to form a second monolayer at the cost of no work, or a minimum work due to irreversibility. From this point, all desalinated molecules require the same amount of work, and that work will depend on the plunger speed. To reach energy consumptions as the state-of-the-art reverse osmosis, the work should be between 3 and 6 kW h m−3 for the desalination of the 180 water molecules.39,40 which means that the plunger should move between 0.020 and 0.152 cm s−1 (Fig. 10). Below this range of plunger speeds, the dragging desalination will require less work than state-of-the-art reverse osmosis.39,40 At the plunger speed of 0.020 cm s−1, the flux rate is ∼0.05 molecules per ns (Fig. 8), which for 1 m2 of membrane, will produce ∼30 m3 of desalinated water per day at an energy consumption of 3 kW h m−3.
A second cycle will start from the already formed second monolayer, and any water desalination will consume the same amount of work. Fig. 11 shows the average consumption work per molecule in this step as a function of the plunger speed. The only plunger speed that does not follow the linear behavior is the value at the speed of 10.0 cm s−1, which reflects the fact that for this speed, the desalination stops at ∼145 molecules (Fig. 2). The rest of the values follow a linear behavior, and the extrapolation at a plunger speed of 0 cm s−1 reaches a minimum value of 0.74 J per molecule, which represent a consumption of ≈6.9 kW h m−3, which falls into the range of values of state-of-the-art reverse osmosis, but no improvement can be made since it represents the minimum work possible for this cycle. The two cycles will finish when water is expulsed from the confinement and the system returns to the start stage, in which the chamber contains only one or two monolayers of water, depending on the cycle used.
 | ||
| Fig. 11 Average work (for separations between 6.25 and 15 Å) as a function of the plunger speed for the saline system with 204 water molecules and their correspondent ion pairs at 300 K. The continuous line represents a linear regression. Dotted lines represent the limits of energy consumption of state-of-the-art reverse osmosis.39,40 | ||
We consider the effect of flexibility of the graphene41 using two flexible membranes with pore diameters of 5 and 7 Å at 10 cm s−1 (Fig. 12). In the ESI,† we provide animations of the desalination processes using these 2 membranes. The flexible membrane with pore diameter of 5 Å fails to desalinate water due to “dangling” carbons, which prevent water molecules from forming hydrogen bonds across the membrane. Thus, we consider a membrane with a larger pore diameter of 7 Å. The larger pore diameter also has “dangling” carbons, but due to the large diameter the fluctuations of the carbons do not preclude the formation of hydrogen bonds across the membrane, and water molecules readily traverse the membrane. The desalination process for the larger pore, flexible membrane proceeds with a behavior very similar to that of the rigid membrane with pore diameter of 5 Å (Fig. 13). An additional desalination simulation using the rigid membrane and pore diameter of 7 Å produce a slightly faster desalination rate. In short, the desalination process in the flexible case behaves very similar to a rigid membrane with slightly smaller pore diameter.
The work done by the membranes with larger pores is lower than the work done by the rigid smaller pore, no matter if the membrane is rigid or flexible (Fig. 13). The total work done by the flexible membrane is lower than the work done by the rigid membrane to desalinate 204 water molecules. The main contribution to this difference is the work done to create the second layer of waters, which in the rigid membrane is higher because water molecules maintain a rather specific organization relative to the rigid graphene, making it more difficult to transform to a double layer system. In the flexible membrane, distortions of the graphene sheet allow the initial water layer to more readily reorganize and accommodate molecules to form a double layer of waters. Beyond the second monolayer of water, both systems, flexible or rigid, consume to the same amount of work to desalinate the same amount of water molecules, which indicates the water–water interactions and cohesion dominates the desalination processes, so that the interactions with the walls have little effect. The larger pore uses a work of ∼8 kW h m−3 for cycles starting at separations of 6 Å, which is very close to the maximum work done by reverse osmosis membranes.
Conclusions
Molecular dynamics simulations show that desalination using dragging forces created by a graphene layers should be possible with low energy consumption. The nanostructured system designed to carry out the desalination process consists of two surfaces of graphene that function as membrane and plunger. The system reflects the setup of a nano-syringe, which is repeated in a two-dimensional array, producing a surface with a pore concentration of 1 pore by ∼4.2 nm2. Prior to the desalination process, the chamber of the nano-syringe needs to be pre-filled and saturated with water molecules to begin the process of desalination, due to the lower cohesive strength of pure water. Inside the chamber, the fluid with desalinated water underwent several transformations, which can be grouped in 3 regimes, which for the first two correspond to the formation of one, and two monolayers adsorbed to the walls of the chamber. In the third regime, a water film forms between the two monolayers, and when the layer is wide enough it reaches average densities as those present in bulk liquid water.Saline systems were desalinated to the point where only a few molecules of water solvating the ions were left in the open part of the membrane. During the process of desalination, the plunger moves to create an unsaturated phase inside the chamber, and generate dragging forces, which promotes, and drives desalination. A significant amount of water molecules is desalinated at the studied plunger speeds (0.5–10 cm s−1). It is expected that for plunger speeds slower than 0.5 cm s−1, we can also carry out the desalination although these plunger speeds were not studied because of computing time constraints. For plunger speeds below ≈1 cm s−1, the desalination proceeds as a quasi-equilibrium process, which naturally minimizes the necessary work to perform desalination.
The work done to move the plunger wall shows that the energy consumptions for this desalination process (when the plunger moves at speeds between 0.020 and 0.152 cm s−1) is similar to that of state-of-the-art reverse osmosis processes. At the plunger speed of 0.020 cm s−1, the proposed systems would theoretically require an energy of 3 kW h m−3, and generate ≈30 m3 of desalinated water per day for a 1 m2 membrane. More energy is required to move the water out of the confinement, and to maintain the system under isothermal operation, but it is expected that the main energy consumption will be the desalination. If the system works at lower plunger speeds, it will be energetically more efficient, but at the cost of lower desalination rates.
Decreasing the pore density by one half increases the desalination rate more than double, indicating that the movement of the plunger generates larger unsaturated spaces (larger impulse) that attract more strongly the water molecules in the saline solution. On the other hand, the lower pore density limits the speed at which the plunger can be moved before the desalination fails. Any design must be a compromise between pore density and plunger speed.
The flexibility of the graphene membrane allows carbon atoms at the pore edge to move back and forth. For a small pore diameter of 5 Å, this flexibility precludes water hydrogen bonding across the membrane, and thus desalination fails. For a pore diameter of 7 Å, the desalination proceeds in the same fashion as rigid membranes with pore diameters of 5 Å. For pore diameters of 7 Å, the flexibility does not affect the rate of desalination, and the energy consumed is the same when desalinations occur after the formation of the second water monolayer. The findings of this study illustrate the potential promise of the proposed desalination method, as well as fundamental design principles that must be considered.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
JLR thanks CONACYT (México), and UMSNH for research funds. FVM thanks CONACYT (México) for a PhD fellowship.References
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Water conduction through the hydrophobic channel of a carbon nanotube, Nature, 2001, 414, 188–190, DOI:10.1038/35102535.
- J. L. Rivera and F. W. Starr, Rapid Transport of Water via a Carbon Nanotube Syringe, J. Phys. Chem. C, 2010, 114, 3737–3742, DOI:10.1021/jp906527c.
- S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Water desalination using nanoporous single-layer graphene, Nat. Nanotechnol., 2015, 10, 459–464, DOI:10.1038/Nnano.2015.37.
- J. K. Holt, H. G. Park, Y. M. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Fast mass transport through sub-2-nanometer carbon nanotubes, Science, 2006, 312, 1034–1037, DOI:10.1126/science.1126298.
- T. Humplik, J. Lee, S. C. O'Hern, B. A. Fellman, M. A. Baig, S. F. Hassan, M. A. Atieh, F. Rahman, T. Laoui, R. Karnik and E. N. Wang, Nanostructured materials for water desalination, Nanotechnology, 2011, 22, 292001, DOI:10.1088/0957-4484/22/29/292001.
- D. Konatham, J. Yu, T. A. Ho and A. Striolo, Simulation Insights for Graphene-Based Water Desalination Membranes, Langmuir, 2013, 29, 11884–11897, DOI:10.1021/la4018695.
- A. Aghigh, V. Alizadeh, H. Y. Wong, M. S. Islam, N. Amin and M. Zaman, Recent advances in utilization of graphene for filtration and desalination of water: a review, Desalination, 2015, 365, 389–397, DOI:10.1016/j.desal.2015.03.024.
- D. Cohen-Tanugi and J. C. Grossman, Nanoporous graphene as a reverse osmosis membrane: recent insights from theory and simulation, Desalination, 2015, 366, 59–70, DOI:10.1016/j.desal.2014.12.046.
- J. L. Rivera, F. W. Starr, P. Paricaud and P. T. Cummings, Polarizable contributions to the surface tension of liquid water, J. Chem. Phys., 2006, 125, 94712, DOI:10.1063/1.2345063.
- J. L. Rivera, M. Predota, A. A. Chialvo and P. T. Cummings, Vapor-liquid equilibrium simulations of the SCPDP model of water, Chem. Phys. Lett., 2002, 357, 189–194, DOI:10.1016/S0009-2614(02)00527-4.
- J. L. Rivera, C. McCabe and P. T. Cummings, Molecular simulations of liquid-liquid interfacial properties: water-n-alkane and water-methanol-n-alkane systems, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 11603, DOI:10.1103/PhysRevE.67.011603.
- D. Cohen-Tanugi and J. C. Grossman, Water Desalination across Nanoporous Graphene, Nano Lett., 2012, 12, 3602–3608, DOI:10.1021/nl3012853.
- A. Kalra, S. Garde and G. Hummer, Osmotic water transport through carbon nanotube membranes, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180, DOI:10.1073/pnas.1633354100.
- W. F. Chan, H. Y. Chen, A. Surapathi, M. G. Taylor, X. H. Hao, E. Marand and J. K. Johnson, Zwitterion Functionalized Carbon Nanotube/Polyamide Nanocomposite Membranes for Water Desalination, ACS Nano, 2013, 7, 5308–5319, DOI:10.1021/nn4011494.
- M. Schliwa and G. Woehlke, Molecular motors, Nature, 2003, 422, 759–765, DOI:10.1038/nature01601.
- R. D. Vale and R. A. Milligan, The way things move: looking under the hood of molecular motor proteins, Science, 2000, 288, 88–95, DOI:10.1126/science.288.5463.88.
- J. S. Berg, B. C. Powell and R. E. Cheney, A millennial myosin census, Mol. Biol. Cell, 2001, 12, 780–794, DOI:10.1091/MBC.12.4.780.
- A. P. Carter, J. E. Garbarino, E. M. Wilson-Kubalek, W. E. Shipley, C. Cho, R. A. Milligan, R. D. Vale and I. R. Gibbons, Structure and functional role of dynein's microtubule-binding domain, Science, 2008, 322, 1691–1695, DOI:10.1126/science.1164424.
- P. Král and B. Wang, Material drag phenomena in nanotubes, Chem. Rev., 2013, 113, 3372–3390, DOI:10.1021/cr200244h.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular-Dynamics, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The Missing Term in Effective Pair Potentials, J. Phys. Chem., 1987, 91, 6269–6271, DOI:10.1021/j100308a038.
- J. Alejandre, D. J. Tildesley and G. A. Chapela, Molecular-Dynamics Simulation of the Orthobaric Densities and Surface-Tension of Water, J. Chem. Phys., 1995, 102, 4574–4583, DOI:10.1063/1.469505.
- F. Chen and P. E. Smith, Simulated surface tensions of common water models, J. Chem. Phys., 2007, 126, 221101, DOI:10.1063/1.2745718.
- J. Wang and X. C. Zeng, Computer Simulation of Liquid-Vapor Interfacial Tension: Lennard-Jones Fluid and Water Revisited, J. Theor. Comput. Chem., 2009, 8, 733–763, DOI:10.1142/S0219633609005027.
- M. Chen, X. C. Lu, X. D. Liu, Q. F. Hou, Y. Y. Zhu and H. Q. Zhou, Retardation of Water Reorientation at the Oil/Water Interface, J. Phys. Chem. C, 2015, 119, 16639–16648, DOI:10.1021/acs.jpcc.5b03742.
- K. Kadota, T. Wake, K. Gonda, A. Kitayama, Y. Tozuka, A. Shimosaka, Y. Shirakawa and J. Hidaka, Effect of organic solvent on mutual diffusion and ionic behavior near liquid–liquid interface by molecular dynamics simulations, J. Mol. Liq., 2014, 197, 243–250, DOI:10.1016/j.molliq.2014.05.025.
- J. L. Rivera, C. McCabe and P. T. Cummings, Layering behavior and axial phase equilibria of pure water and water plus carbon dioxide inside single wall carbon nanotubes, Nano Lett., 2002, 2, 1427–1431, DOI:10.1021/nl0257566.
- Y. J. Lu and B. B. Wei, A molecular dynamics study on surface properties of supercooled water, Sci. China, Ser. G: Phys., Mech. Astron., 2006, 49, 616–625, DOI:10.1007/s11433-006-2019-6.
- L. X. Dang, J. E. Rice, J. Caldwell and P. A. Kollman, Ion Solvation in Polarizable Water - Molecular-Dynamics Simulations, J. Am. Chem. Soc., 1991, 113, 2481–2486, DOI:10.1021/ja00007a021.
- L. X. Dang and P. A. Kollman, Free Energy of Association of the K+:18-Crown-6 Complex in Water: A New Molecular Dynamics Study, J. Phys. Chem., 1995, 99, 55–58, DOI:10.1021/j100001a011.
- E. L. Pollock and J. Glosli, Comments on P3M, FMM, and the Ewald method for large periodic Coulombic systems, Comput. Phys. Commun., 1996, 95, 93–110, DOI:10.1016/0010-4655(96)00043-4.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, Dreiding - a Generic Force-Field for Molecular Simulations, J. Phys. Chem., 1990, 94, 8897–8909, DOI:10.1021/j100389a010.
- Y. J. Guo, N. Karasawa and W. A. Goddard, Prediction of Fullerene Packing in C60 and C70 Crystals, Nature, 1991, 351, 464–467, DOI:10.1038/351464a0.
- J. L. Rivera, C. McCabe and P. T. Cummings, Oscillatory behavior of double-walled nanotubes under extension: a simple nanoscale damped spring, Nano Lett., 2003, 3, 1001–1005, DOI:10.1021/nl034171o.
- J. L. Rivera, C. McCabe and P. T. Cummings, The oscillatory damped behaviour of incommensurate double-walled carbon nanotubes, Nanotechnology, 2005, 16, 186–198, DOI:10.1088/0957-4484/16/2/003.
- S. A. Deshmukh, G. Kamath and S. K. R. S. Sankaranarayanan, Comparison of the interfacial dynamics of water sandwiched between static and free-standing fully flexible graphene sheets, Soft Matter, 2014, 10, 4067–4083, 10.1039/C3SM53044B.
- T. A. Ho and A. Striolo, Polarizability effects in molecular dynamics simulations of the graphene-water interface, J. Chem. Phys., 2013, 138, 54117, DOI:10.1063/1.4789583.
- T. A. Ho and A. Striolo, Molecular dynamics simulation of the graphene-water interface: comparing water models, Mol. Simul., 2014, 40, 1190–1200, DOI:10.1080/08927022.2013.854893.
- S. A. Stillwell and E. M. Webber, Predicting the Specific Energy Consumption of Reverse Osmosis Desalination, Water, 2016, 8, 601, DOI:10.3390/w8120601.
- M. Elimelech and W. A. Phillip, The Future of Seawater Desalination: Energy, Technology, and the Environment, Science, 2011, 333, 712–717, DOI:10.1126/science.1200488.
- S. Deng and V. Berry, Wrinkled, rippled and crumpled graphene: an overview of formation mechanism, electronic properties, and applications, Mater. Today, 2016, 19, 197–212, DOI:10.1016/j.mattod.2015.10.002.
Footnote |
| † Electronic supplementary information (ESI) available: Movie of the desalination process for the system with 204 water molecules and their corresponding Na–Cl ion pairs at a plunger speed of 1.0 cm s−1. During the transfer of water molecules across the membrane, formation/breaking of hydrogen bonds occur at the membrane entrance. See DOI: 10.1039/c7ra09847b |
| This journal is © The Royal Society of Chemistry 2017 |