A theoretical study of the substituent effect on reactions of amines, carbon dioxide and ethylene oxide catalyzed by binary ionic liquids

Abstract

The reaction mechanisms of one-pot conversion of carbon dioxide, ethylene oxide and amines to 3-substituted-2-oxazolidinones catalyzed by the binary ionic liquids of BmimBr and BmimOAc were investigated using DFT methods. In this work, we focus on exploring how the different substituents in amines affect the yields of 3-substituted-2-oxazolidinones. The comparison of calculated free energy profiles and pathways reveals that the electronic structures of the substitutional groups in amines have a substantial influence on the nucleophilic properties of nitrogen atoms of key intermediates, which leads to a discrepancy in the activation barriers. The comparison of the calculated activation barriers of key steps and experimental yields indicates that an anticorrelation relationship exists between them. The current theoretical study inspires us to design new substrates for CO₂ conversion by modulating the substituents in substrates.

---

1. Introduction

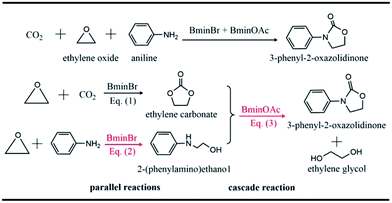
Carbon dioxide (CO₂) is widely recognized as the main component of greenhouse gas.¹ The continuing emission of CO₂ by modern industries has already roused the problem of climatic warming, which results in a threat to the living environment. On the other hand, CO₂ is also an abundant and renewable natural source,^2–5 which can be utilized to produce valuable chemicals. One important conversion of CO₂ in industry refers to the reaction of CO₂ and ethylene oxide to yield carbonate. However, the high thermodynamic stability and kinetic inertness of CO₂ hinder its normal fixation and utilization. Chemists have devoted themselves to developing new strategies^6–10 to fix and convert CO₂. A great number of promising strategies for the utilization of CO₂ have been designed and proposed so far.^4,11,12

The synergistic catalysis in which a few catalysts are combined together is one of efficient strategies to convert CO₂.^13–17 In this strategy, one way is to use various ionic liquids to catalyze CO₂ conversion to oxazolidinone^18–20 whose derivatives are widely used in the pharmaceutical field due to their remarkable bioactivity.^21–24 Recently, Wang et al.¹⁸ reported the one-pot conversion of CO₂, ethylene oxide (EO) and amines to 3-aryl-2-oxazolidinones, which are catalyzed by the binary ionic liquids, 1-butyl-3-methyl-imidazolium bromide (BmimBr) and 1-butyl-3-methyl-imidazolium acetate (BmimOAc). It was found that the reactions of CO₂, EO and amines catalyzed by BmimBr or BmimOAc have low yields of 24% and 70%, respectively. However, it was intriguing that the synergistic catalysis with BmimBr and BmimOAc together led to the high yields beyond 90%. Why did the combination of BmimBr and BmimOAc work well on catalyzing the reaction of CO₂, EO and amines? The experiments¹⁸ indicated that BmimBr might play an important role in catalyzing eqn (1) and (2), while BmimOAc facilitates the reaction of eqn (3), as the reaction of CO₂, EO and aniline shows in Scheme 1.

Scheme 1 Proposed reaction mechanism for the one-pot conversion of CO₂, ethylene oxide and aniline to generate 3-phenyl-2-oxazolidinone and ethylene glycol. The whole complex reaction consists of two parallel reactions eqn (1) and (2) to generate the ethylene carbonate and 2-(phenylamino)ethanol respectively, as well as the cascade reaction eqn (3).

The previous theoretical studies mainly focused on elucidating the mechanisms of reactions of CO₂ and different oxides catalyzed by catalysts. For example, Sun et al.²⁵ calculated the reaction pathways of CO₂ with the propylene oxide catalyzed by the alkylmethylimidazolium chlorine by using the density functional theory (DFT) method. Whiteoak et al.²⁶ performed a DFT calculation on the mechanism of CO₂ conversion to carbonates catalyzed by organocatalysis. Girard et al.²⁷ calculated the mechanism of CO₂ with the styrene oxide catalyzed by BmimBr. Recently, Luo et al.²⁸ performed a detailed DFT calculation on the reaction mechanism of aniline, CO₂ and EO catalyzed by BmimBr and BmimOAc. The free energy profiles calculated by them indicate that the key energy barriers of eqn (1) and (2) catalyzed by BmimOAc are higher than that of BmimBr. The reason lies in the fact that, the acetate group in BmimOAc is a strong nucleophile, so that the intermediates formed in the pathway are too stable to be activated. On the contrary, the reaction of eqn (3) follows a stepwise mechanism instead of a concerted one under the catalysis of BmimOAc. The pathway following the stepwise mechanism have low kinetic barriers so that BminOAc promotes the reaction of eqn (3). The DFT calculation performed by Luo et al.²⁸ provides a reasonable explanation for the synergetic catalysis of the binary ionic liquid of BmimBr and BmimOAc.

Although these reactions presented above have been explored with theoretical calculations, the mechanisms of CO₂ reacting with different amines still remain unknown. For instance, Wang et al.¹⁸ reported that the aromatic amines with electron-withdrawing substituents have higher yields of 3-aryl-2-oxazolidinones than that with electron-donating substituents. Aliphatic amines such as cyclohexylamine give rise to quite low yields of 3-aryl-2-oxazolidinones. In order to explore the influence of different substituents in amines on the yields of 3-substituted-2-oxazolidinones, we performed a comprehensive DFT calculation on the reactions of various amines with CO₂ and EO. In this work, we mainly focus on elucidating how the electronic structures of substituents in amines influence the energetics of intermediates and transition states in the reaction pathways, which lead to the different yields of their final products.

2. Computational methods

All the DFT calculations and natural bond orbital (NBO) analysis²⁹ in this work were carried out with the Gaussian09 software.³⁰ The M06-2X functional^31,32 was chosen for the DFT calculations, since it has been demonstrated that the M06-2X functional could give the accurate description for the noncovalent interactions in small molecules.^33,34 The large 6-311+G* basis set³⁵ combined with the M06-2X functional, denoted as the M06-2X/6-311+G* method, was used for the geometry optimization and frequency calculations of structures of reactants, intermediates, transition states and products in gas phase. The frequency calculations give rise to the free energy ΔG_gas for the optimized structure in gas phase.

To evaluate the solvent effect on the overall reactions, we used the implicit solvation model (SMD) proposed by Truhlar and co-workers.^36,37 Since the previously experimental study¹⁸ reported that the concentration of EO in eqn (1) was much higher than that of aniline in eqn (2) and the reaction in eqn (1) actually reacted faster in solution, it was reasonable to consider that the EC generated from eqn (1) constituted the main component of solvent for the subsequent reactions of eqn (2) and (3). The solvent effect of ethylene carbonate was calculated based on the optimized structures in gas phase at the same level of M06-2X/6-311+G* with the value of dielectric constant being 89.6.³⁸ The total free energy of molecules in solution ΔG_sol is counted as the summation of the free energy ΔG_gas in gas phase and the correction term ΔG_cor due to the solvent effect. The temperature and pressure were set to be 413 K and 2.5 MPa in our calculations, as same to the experimental conditions. The units of the calculated Gibbs free energies throughout this work are in kcal mol⁻¹. The intrinsic reaction coordinate (IRC)³⁹ calculations were carried out to verify that the obtained transition states connect with the correct reactants and products in the forward and reverse directions.

3. Results and discussion

We considered several reactions with the typical amines such as aniline, cyclohexylamine, anisidine and chloroaniline, since it has been noticed that a remarkable difference in yields exists for these amines, ranging from 29% to 99% as reported in experiments.¹⁸ The major difference in these amines lies in the substitutional groups connecting to the central nitrogen atoms in amines. For instance, aniline has an aromatic phenyl group while cyclohexylamine possesses an aliphatic hexyl group. Anisidine has an electron-donating methoxyl group in its phenyl group, while chloroaniline has an electron-withdrawing chloride group. Thus, the divergence in yields could be attributed to the substituent effect of amines.

As shown in Scheme 1, eqn (1) represents the ring-opening reaction of CO₂ and EO without any amine involved in. Thus, the current theoretical calculations were just conducted on the reaction mechanisms of eqn (2) and (3). Our previous theoretical study²⁸ performed on aniline, CO₂ and EO revealed that eqn (2) was primarily catalyzed by BmimBr, while eqn (3) was done by BmimOAc. Therefore, we calculated the reaction mechanisms of eqn (2) and (3) with different amines, compared calculated energy profiles with each other and analyzed the influence of substituents on the energetics of reaction pathways.

3.1 Reactions of EO with aniline and cyclohexylamine

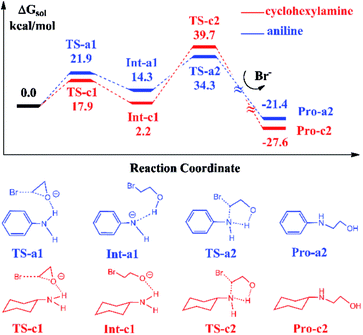
In Scheme 1, the reaction with aniline has a 99% yield of 3-phenyl-2-oxazolidinone,¹⁸ while the reaction with the cyclohexylamine leads to the 29% yield of corresponding product. It is obvious that the substituents in aniline and cyclohexylamine play a determinative role on yields. Our previous DFT calculations²⁸ indicated that the ionic liquid BmimBr was favored by the reaction in eqn (2). In order to explore the substitutional effects, we first calculated the reaction mechanisms of EO with aniline and cyclohexylamine catalyzed by BmimBr. The calculated free energy profiles and reaction pathways are shown in Fig. 1.

Fig. 1 Calculated free energy profiles and reaction pathways of EO reacting with aniline and cyclohexylamine catalyzed by BmimBr, which are denoted by the blue and red curves respectively. The schematic representations of structures of intermediates and transition states are shown below.

The previous NMR experiments performed on eqn (2)¹⁸ indicated that the substrates such as aniline could stabilize EO through the hydrogen-bonding interaction between the NH₂ group aniline and the oxygen atom of EO. Meanwhile, the bromide anion in BmimBr facilitates the ring-opening process of EO by attacking its carbon atom. Based on the experimental suggestions, we optimized the transition structures TS-a1 and TS-c1 in the two pathways, where the distances between the oxygen atoms in EO and H atoms are 1.78 and 2.01 Å, respectively. In the transition states, the C–O bonds in EO tend to be broken, with the assistance of hydrogen bonding interaction and nucleophilic attacking of bromide anions. The ring-opening process via TS-a1 and TS-c1 leads to the formation of the stable intermediates Int-a1 and Int-c1, with their relative free energies of 14.3 and 2.2 kcal mol⁻¹ respectively. Next, the C–N bond addition occurs between the carbon atoms of ring-opened moieties and the deprotonated nitrogen atoms via TS-a2 and TS-c2 with the free energies of 34.3 and 39.7 kcal mol⁻¹, concomitant with the leaving of bromide anions simultaneously. Finally, the C–N bond addition gives rise to the products Pro-a2 and Pro-c2, namely, 2-(phenylamino)ethanol and 2-(cyclohexylamino)ethanol in the aniline-participated pathway and cyclohexylamine-participated pathway, respectively.

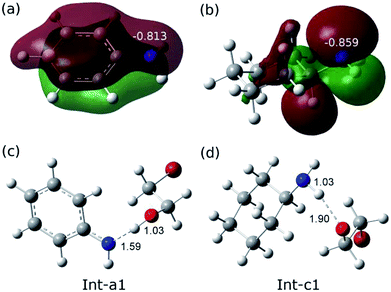
The remarkable difference between the two reaction pathways lies in the intermediates and transition states in the C–N addition steps have different thermodynamic stabilities. Int-c1 is more stable than Int-a1 by 12.1 kcal mol⁻¹, while the energy of TS-c2 is a little higher than TS-a2 by 5.4 kcal mol⁻¹. The energy gap between the two barriers is up to 17.5 kcal mol⁻¹. In order to explain the energy gap between them, we performed a NBO change analysis on the related structures. As shown in Fig. 2(a) and (b), the NBO charges of nitrogen atoms in aniline and cyclohexylamine are −0.813 and −0.859, respectively. Both the nitrogen atoms in two amines adopt an approximate sp²-hybridization. In aniline, the lone pair of electrons of nitrogen could delocalize and conjugate with the π orbital of phenyl group, while the lone pair of electrons in cyclohexylamine localizes around the nitrogen atom due to the unconjugated aliphatic ring, which are indicated by the molecular orbitals in Fig. 2(a) and (b).

Fig. 2 (a) The contour of 20th molecular orbital of aniline and the NBO charge of nitrogen atom is −0.813. (b) The contour of HOMO of cyclohexylamine and the NBO charge of nitrogen atom is −0.859. (c) The bond lengths of N–H and H–O are 1.59 and 1.03 Å, respectively. (d) The bond lengths of N–H and H–O are 1.03 and 1.90 Å, respectively.

The charge of nitrogen atom in aniline is less negative than that of cyclohexylamine by 0.046. Thus, the proton of nitrogen atom is abstracted by the oxygen atom of EO in Int-a1 due to its low electronegativity, while the nitrogen atom in Int-c1 holds the proton and forms the hydrogen bonding interaction with the oxygen atom. Fig. 2(c) and (d) show that the N–H and H–O distances in Int-a1 and Int-c1 are 1.59 and 1.03 Å as well as 1.03 and 1.90 Å, respectively. It can be seen that the nitrogen atoms in Int-a1 and Int-c1 possess different electronegativity, thus leading to the different stability and reactivity of intermediates. Further, it could be understood that the nitrogen atom in Int-a1 is easier for nucleophilic attacking than that in Int-c1 toward the carbon atoms in the ring-opening moiety, because it is chemically unsaturated and active. In contrast, the nitrogen atom in Int-c1 is more stable so that the C–N addition via TS-c2 has a higher barrier of 37.5 kcal mol⁻¹.

3.2 Additions of ethylene carbonate with 2-(phenylamino)ethanol and 2-(cyclohexylamino)ethanol

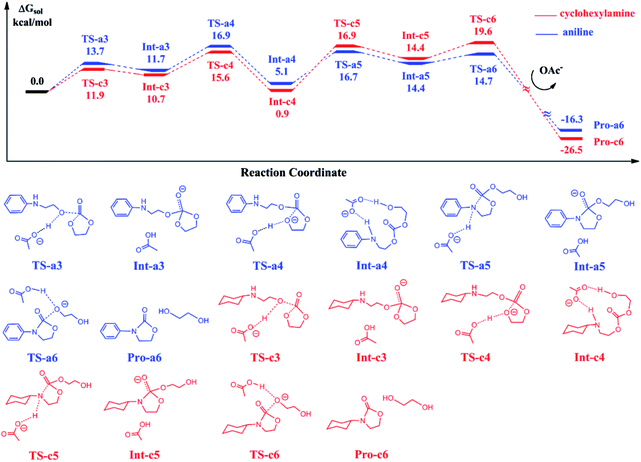
The reaction of ethylene carbonate (EC) with 2-(phenylamino)ethanol and 2-(cyclohexylamino)ethanol in eqn (3) follows a stepwise mechanism catalyzed by BmimOAc. Fig. 3 shows the calculated free energy profiles for EC reacting with the generated Pro-a2 and Pro-c2.

Fig. 3 Calculated free energy profiles and reaction pathways of EC reacting with 2-(phenylamino)ethanol or 2-(cyclohexylamino)ethanol catalyzed by BmimOAc. The schematic representations of structures of intermediates and transition states are shown below.

In the first step, Pro-a2 and Pro-c2 as the nucleophiles attack the carbon atoms in EC via TS-a3 and TS-c3, with the OAc anions acting as a proton acceptor to stabilize the transition states. The nucleophilic addition yields the stable intermediates Int-a3 and Int-c3, where the new C–O bonds form and the OAc anions abstract the protons from hydroxyl groups in substrates. Then, the protons transfer back to the oxygen atoms in the five-member rings, facilitate the five-member ring opening by cleaving the C–O bonds and generate the intermediates Int-a4 and Int-c4 via TS-a4 and TS-c4. Subsequently, the intramolecular ring closure proceeds through TS-a6 and TS-c6, and yield the final products 3-phenyl-2-oxazolidinone and 3-cyclohexyl-2-oxazolidinone respectively, with ethylene glycol. By comparing the two curves with each other, we found that the two energy profiles are quite similar to each other at each elementary step. The intermediates Int-a4 and Int-c4 have an energy difference of 4.2 kcal mol⁻¹. The key barriers for the blue and red curves are 16.9 and 20.5 kcal mol⁻¹, lower than the key barriers of the ring-opening of eqn (2) shown in Fig. 1.

3.3 Reactions of EO with chloroaniline and anisidine

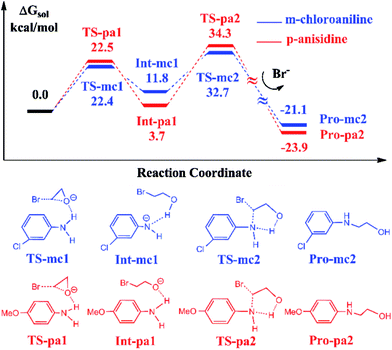
It has been reported that the aniline-participated CO₂ conversion gives rise to the product 3-phenyl-2-oxazolidinone with 99% yield.¹⁸ Nevertheless, it was intriguingly found that the aromatic amines with the electron-donating substituents such as alkyl or alkoxy groups or with the electron-withdrawing substituents such as halides lead to different yields of 3-substituted-2-oxazolidinones. For example, the p-anisidine and m-chloroaniline give 67% and 99% yields in experiments, respectively. Why the aromatic amines with different substituents lead to such a difference of 32% in yield? To answer this question, we chose the reactions participated by p-anisidine and m-chloroaniline for a DFT calculation, since p-anisidine has an electron-donating methoxyl group and m-chloroaniline has an electron-withdrawing chloride group. The theoretical calculations can account for the difference observed in yields.

Fig. 4 shows the calculated energy profiles and pathways of EO reacting with m-chloroaniline and p-anisidine catalyzed by BmimBr, respectively. The two-step reaction process in Fig. 4 is quite analogous to that in Fig. 1. In the first step, the ring-opening of EO takes place through the hydrogen bonding interactions via TS-mc1 and TS-pa1, leading to the ring-opening intermediates Int-mc1 and Int-pa1. Next, the C–N bond addition occurs through TS-mc2 and TS-pa2 and yields 2-(3-chloro-phenylamino)ethanol and 2-(4-methoxy-phenylamino)ethanol, denoted as Pro-mc2 and Pro-pa2, respectively. Fig. 4 shows that the key transition states along the pathways have nearly similar energies. However, it is noticed that the thermodynamic stability of the key intermediates Int-mc1 and Int-pa1 differ from each other. The Int-pa1 is more stable than Int-mc1 by 8.1 kcal mol⁻¹. Thus, the activation barrier of the p-anisidine for the C–N bond addition is 30.6 kcal mol⁻¹, larger than that of m-chloroaniline by 9.7 kcal mol⁻¹.

Fig. 4 Calculated free energy profiles and reaction pathways of EO reacting with m-chloroaniline and p-anisidine catalyzed by BmimBr, which are denoted by blue and red curves respectively. The schematic representations of structures of intermediates and transition states are shown below.

To account for the difference in thermodynamic stability of formed intermediates, we performed a NBO charge analysis on m-chloroaniline and p-anisidine. The NBO analysis indicates that the nitrogen atom in m-chloroaniline carries the negative charge of −0.808, while the nitrogen atom in p-anisidine has a charge of −0.814. It is evident that the charge difference of 0.006 between them is caused by the electron-donating methoxyl group and electron-withdrawing chloride group. As the ring-opening of EC occurs, the oxygen atoms tend to abstract the hydrogen atoms from the amino groups via TS-mc1 and TS-pa1. Since the electronegativity of nitrogen in p-anisidine is stronger than that in m-chloroaniline, the nitrogen atom can hold the hydrogen atom to form a stable Int-pa1, as shown in Fig. 5. In contrast, the hydrogen atom in m-chloroaniline is abstracted by the oxygen atom, which leads to a less stable intermediate Int-mc1. Overall, the calculated results in Fig. 4 indicate that the reaction of eqn (2) with the m-chloroaniline should be more favorable than that of p-anisidine in kinetics. The reason could be that the C–N addition step of p-anisidine is hindered by a large barrier between Int-pa1 and TS-pa2.

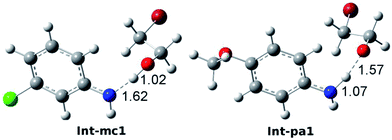Fig. 5 Optimized intermediate structures of Int-mc1 and Int-pa1. The bond lengths of N–H and H–O are 1.62 and 1.02 Å in Int-mc1 and 1.07 and 1.57 Å in Int-pa1.

3.4 Additions of ethylene carbonate with 2-(3-chloro-phenylamino)ethanol and 2-(4-methoxy-phenylamino)ethanol

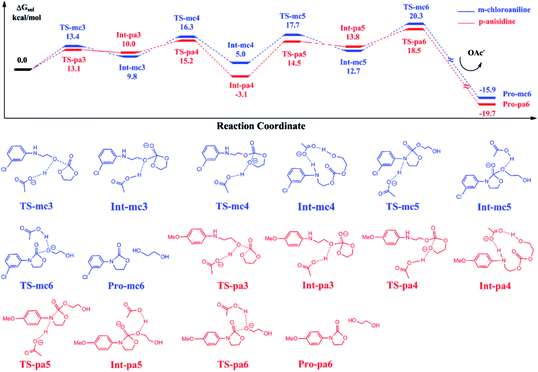
Fig. 6 shows the calculated energy profiles of EC reacting with Pro-mc2 and Pro-pa2 catalyzed by BmimOAc. The whole reactions follow a stepwise mechanism to yield Pro-mc6 and Pro-pa6, namely, 3-(3-chloro-phenyl)-oxazolidin-2-one and 3-(4-methoxy-phenyl)-oxazolidin-2-one, with ethylene glycol. For instance, in the case of C–O bond addition of EC with Pro-mc2, the OAc anion stabilizes the addition transition state TS-mc3 by abstracting a hydroxyl proton, which leads to the stable Int-mc3. Next, the OAc anion assists the ring-opening process via TS-mc4 and ring-closing process via TS-mc5 to yield the intermediate Int-mc5, though the hydrogen bond interaction with the substrates. In Int-mc5, the OAc anion transfers the proton back to the ester oxygen via TS-mc6 to yield the final products Pro-mc6 and ethylene glycol.

Fig. 6 Calculated free energy profiles and reaction pathways of EC and 2-((3-chlorophenyl)amino)ethanol or 2-((4-methoxyphenyl)amino)ethanol catalyzed by BmimOAc. The schematic representations of structures of intermediates and transition states are shown below.

Comparing the energies of key intermediates and the transition states in two pathways, it is found that there is almost no large difference between the two pathways, except the stability of Int-mc4 and Int-pa4. The reason could be that the substitutional groups such as the methoxyl or chloride groups affected the hydrogen bonding interaction between the N–H bond and OAc groups. The key barriers for the blue and red pathways are 16.3 and 21.6 kcal mol⁻¹, lower than that obtained for eqn (2).

3.5 Comparison of key barriers and yields

By comparing the free energy profiles in Fig. 1 and 4 with each other, we found that the key barriers of the ring-opening in eqn (2) for aniline, cyclohexylamine, p-anisidine and m-chloroaniline are 21.9, 37.5, 30.6 and 22.4 kcal mol⁻¹ respectively, which are higher than their corresponding key barriers obtained for eqn (3).

Interestingly, we noticed that the yields of final products are lower if the barriers of key steps in eqn (2) are higher. In order to reveal the relationship existing between them, we calculated the key barriers of eqn (2) for a series of amines, including the data of p-toluidine and 4-ethoxyaniline reported experimentally,¹⁸ as listed in Table 1.

Table 1 Calculated free energy barriers for the key steps of eqn (2) in the reactions of different substrates with CO₂ and EO. The yields with various substrates were extracted from ref. 18

Substrates	Eqn (2)	Yields (%)
Aniline	21.9	100
m-Chloroaniline	22.4	99
p-Toluidine	30.0	77
4-Ethoxyaniline	29.2	75
p-Anisidine	30.6	63
Cyclohexylamine	37.5	29

---

Fig. 7 indicates that the calculated barriers and yields have an anti-correlation relationship, with the fitted correlation coefficient being 0.97. Thus, the data reveal that the ring-opening reaction of EO in eqn (2) might play an crucial role in determining the yields of the whole complex reactions of CO₂ conversion. The reactivity of various amines could be roughly estimated from the free energy difference of key barriers according to the relationship of rate constant and free energy. However, such an anti-correlation relationship in Fig. 7 still needs to be verified by using the experiments of two component reaction of EO and amines in the future.

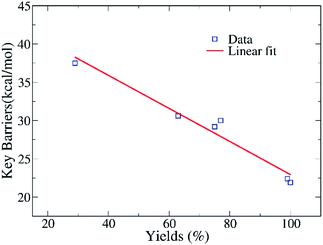Fig. 7 The relationship of the calculated barriers of key steps in eqn (2) and yields of reactions with the substrates presented in Table 1, with a linear fitting in red.

4. Conclusions

The mechanisms of the reactions of CO₂, EO and amines catalyzed by the ionic liquids BmimBr and BmimOAc were explored using the DFT calculations. We compared the free energy profiles of reactions with aniline, cyclohexylamine, m-chloroaniline and p-anisidine with each other and identified the crucial steps to influence the yields of products. The comparison of aniline and cyclohexylamine in Fig. 1 and 3 indicates that the remarkable difference in the pathways between aniline and cyclohexylamine exists in the ring-opening process of eqn (2), rather than the addition reaction of eqn (3). The difference of the key intermediates in the thermodynamic stability could be well explained based on the DFT results. Similarly, the comparison of calculated energy profiles for m-chloroaniline and p-anisidine also indicates that eqn (2) is more important in determining the yields of products than eqn (3).

In a summary, the current theoretical calculations reveal that the ring-opening of EO in eqn (2) is more important in the whole complex reaction of CO₂ conversion catalyzed by binary ionic liquids BmimBr and BmimOAc. The theoretical results based on electronic structure analysis on key intermediates and transition states provide us a deep insight into understanding how the different substituents in amines influence the yields of 3-substituted-2-oxazolidinones. The calculated reaction mechanisms inspire us to design better amines for CO₂ conversion by means of modulating the substituents in substrates.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants No. 21433004 and 21403068). We acknowledge the support of the NYU-ECNU Center for Computational Chemistry at NYU Shanghai. We also thank the supercomputer center of ECNU for providing computer time.

Notes and references

1. K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781.
2. D. H. Gibson, Chem. Rev., 1996, 96, 2063–2096.
3. H. Arakawa, M. Aresta, J. N. Armor, M. A. Barteau, E. J. Beckman, A. T. Bell, J. E. Bercaw, C. Creutz, E. Dinjus, D. A. Dixon, K. Domen, D. L. DuBois, J. Eckert, E. Fujita, D. H. Gibson, W. A. Goddard, D. W. Goodman, J. Keller, G. J. Kubas, H. H. Kung, J. E. Lyons, L. E. Manzer, T. J. Marks, K. Morokuma, K. M. Nicholas, R. Periana, L. Que, J. Rostrup-Nielson, W. M. H. Sachtler, L. D. Schmidt, A. Sen, G. A. Somorjai, P. C. Stair, B. R. Stults and W. Tumas, Chem. Rev., 2001, 101, 953–996.
4. T. Sakakura, J.-C. Chol and H. Yasuda, Chem. Rev., 2007, 107, 2365–2387.
5. M. North, R. Pasquale and C. Young, Green Chem., 2010, 12, 1514–1539.
6. A. Decortes, A. M. Castilla and A. W. Kleij, Angew. Chem., Int. Ed., 2010, 49, 9822–9837.
7. C. J. Liu, J. Y. Ye, J. J. Jiang and Y. X. Pan, ChemCatChem, 2011, 3, 529–541.
8. M. Drees, M. Cokoja and F. E. Kuhn, ChemCatChem, 2012, 4, 1703–1712.
9. C. D. N. Gomes, O. Jacquet, C. Villiers, P. Thuéry, M. Ephritikhine and T. Cantat, Angew. Chem., Int. Ed., 2012, 51, 187–190.
10. D. J. Darensbourg and S. J. Wilson, Green Chem., 2012, 14, 2665–2671.
11. T. Seki and A. Baiker, Chem. Rev., 2009, 109, 2409–2454.
12. F. Jutz, J.-M. Andanson and A. Baiker, Chem. Rev., 2011, 111, 322–353.
13. T. Ema, Y. Miyazaki, J. Shimonishi, C. Maeda and J.-Y. Hasegawa, J. Am. Chem. Soc., 2014, 136, 15270–15279.
14. J. Sun, W. G. Cheng, Z. F. Yang, J. Q. Wang, T. T. Xu, J. Y. Xin and S. J. Zhang, Green Chem., 2014, 16, 3071–3078.
15. N. Eghbali and C. J. Li, Green Chem., 2007, 9, 213–215.
16. H. Zhou, W. Z. Zhang, C. H. Liu, J. P. Qu and X. B. Lu, J. Org. Chem., 2008, 73, 8039–8044.
17. M. S. Liu, K. Q. Gao, L. Liang, J. M. Sun, L. Sheng and M. Arai, Catal. Sci. Technol., 2016, 6, 6406–6416.
18. B. S. Wang, E. H. M. Elageed, D. W. Zhang, S. J. Yang, S. Wu, G. R. Zhang and G. H. Gao, ChemCatChem, 2014, 6, 278–283.
19. B. S. Wang, S. J. Yang, L. J. Min, Y. L. Gu, Y. Y. Zhang, X. P. Wu, L. F. Zhang, E. H. M. Elageed, S. Wu and G. H. Gao, Adv. Synth. Catal., 2014, 356, 3125–3134.
20. M. S. Liu, K. Q. Gao, L. Liang, F. X. Wang, L. Shi, L. Sheng and J. M. Sun, Phys. Chem. Chem. Phys., 2015, 17, 5959–5965.
21. S. Cacchi, G. Fabrizi, A. Goggiamani and G. Zappia, Org. Lett., 2001, 3, 2539–2541.
22. B. Mallesham, B. M. Rajesh, P. R. Reddy, D. Srinivas and S. Trehan, Org. Lett., 2003, 5, 963–965.
23. M. V. Nandakumar, Adv. Synth. Catal., 2004, 346, 954–958.
24. A. Ali, G. S. K. K. Reddy, H. Cao, S. G. Anjum, M. N. L. Nalam, C. A. Schiffer and T. M. Rana, J. Med. Chem., 2006, 49, 7342–7356.
25. H. Sun and D. Zhang, J. Phys. Chem. A, 2007, 111, 8036–8043.
26. C. J. Whiteoak, A. Nova, F. Maseras and A. W. Kleij, ChemSusChem, 2012, 5, 2032–2038.
27. A.-L. Girard, N. Simon, M. Zanatta, S. Marmitt, P. Goncalves and J. Dupont, Green Chem., 2014, 16, 2815–2825.
28. Z. J. Luo, B. S. Wang, Y. Liu, G. H. Gao and F. Xia, Phys. Chem. Chem. Phys., 2016, 18, 27951–27957.
29. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO, Version 3.1.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2009.
31. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
32. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
33. R. Huenerbein, B. Schirmer, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 6940–6948.
34. Y. Zhao and D. G. Truhlar, Org. Lett., 2006, 8, 5753–5755.
35. V. A. Rassolov, M. A. Ratner and J. A. Pople, J. Chem. Phys., 2001, 114, 2062–2066.
36. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543.
37. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
38. M. C. Smart, B. V. Ratnakumar and S. Surampudi, J. Electrochem. Soc., 1999, 146, 486–492.
39. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structures in all figures. See DOI: 10.1039/c7ra09485j

---