Electronic and optical properties of metalloporphyrins of zinc on TiO₂ cluster in dye-sensitized solar-cells (DSSC). A quantum chemistry study

Abstract

Dye-sensitized solar-cell (DSSC) systems have been investigated by calculating light-absorption and electron-injection processes of the LD13 ([5,15-bis(2,6-(1,1-dimethylethyl)-phenyl)-10-4-dimethylaminophenylethynyl-20-4-carboxy phenylethynyl porphyrinato]zinc-(II)) and YD2-o-C8 ([5,15-bis(2,6-dioctoxyphenyl)-10-(bis(4-hexylphenyl)amino-20-4-carboxyphenylethynyl)porphyrinato]zinc-(II)) dyes adsorbed on a TiO₂ cluster simulating the semiconductor. The binding energy of the dyes with the TiO₂ clusters has been calculated at the density functional theory (DFT) level using the B3LYP and CAM-B3LYP functionals. The electronic excitation energies have been calculated at the time-dependent DFT (TDDFT) level for the dyes in the gas and solvent phase employing the B3LYP, CAM-B3LYP and BHLYP functionals. The calculated excitation energies have been compared to values obtained at the algebraic diagrammatic construction through second order (ADC(2)) level of theory. The TDDFT calculations with the B3LYP in tetrahydrofuran solvent with the dye and dye–TiO₂ models yield excitation energies that agree well with the transitions in the experimental absorption spectra. Changes in the free energy for electron injection support the better performance of the dyes on the TiO₂ clusters.

---

Introduction

Dye Sensitized Solar Cells (DSSCs) were proposed in 1991 by Grätzel and O'Regan.^1,2 The DSSCs consist of a light-absorbing dye attached to a semiconductor surface such as titanium dioxide (TiO₂). The dye absorbs solar energy yielding to an electronic excited state that transfers an electron from the dye to the semiconductor.^3,4 The TiO₂ semiconductor has a large band gap, which can be excited only by ultraviolet radiation.^5,6 The role of the dye is to extend the absorption range of the semiconductor to the visible and near-infrared region covering more of the solar spectrum. DSSCs are a cost-effective alternative to the currently commercialized solar cells made of silicon.⁷ The efficiency of the DSSCs can be improved by designing dyes with a broad absorption spectrum and good charge separation properties.

A large number of experimental and computational research groups search for novel dyes with improved efficiency and stability to achieve high photoconversion efficiency.^8–36 The efficiency of the DSSCs is determined by the photophysical properties of the semiconductor, the absorption spectrum of the dye and the ability of the electrolyte regenerator to transport charges. The solar-cell performance is measured by the power conversion efficiency (η), also called photo-conversion efficiency.^2,3 DSSCs based on the sensitization of TiO₂ by the classic ruthenium complexes dyes have a η between 7% and 13%, making practical devices and applications feasible.^8–24 In recent years, ruthenium complexes have been replaced by other dyes that are cheaper as they are based compound with large π-aromatic moieties such as metalloporphyrins (MP).⁵ Metalloporphyrins have been shown to be good dye sensitizers.^8–24 MP based zinc complexes are dyes with good photo-stability and large light-harvesting capabilities.

The η index varies between 6% and 15% depending on the porphyrin substituents which close to the η value of the best ruthenium complexes. The Zn-porphyrins denoted as YD2, YD2-o-C8, ZnPBAT, LD14, LD13, SM315 and SM135 are among the most efficient DSSCs. On the other hand, solar cells based on perovskites such as hybrid alkylammonium lead halide have been found to have a high power conversion efficiency of about 20%.³⁷ However, the lead-containing perovskite is environmentally problematic.

In this work, we employ quantum chemistry methods for studying zinc-porphyrin based dye sensitizers that are attached to the TiO₂ semiconductor surface through an anchor unit consisting of a carboxylic group (COOH).^2–5 The excited state of the dye injects electrons into the semiconductor. Therefore, the energy of the lowest unoccupied molecular orbital (LUMO) of the dye must be above the lower limit of the conduction band of TiO₂ to allow the electron transfer to the semiconductor. The energy of the highest occupied molecular orbital (HOMO) of the dye must be below the potential of the I₃⁻/I⁻ redox pair in order to allow an efficient regeneration of the oxidized dye.^5,13 The interaction of the two zinc porphyrin-based dyes, LD13 and YD2-o-C8, with the (101) plane of TiO₂ (anatase) or a TiO₂ nanocluster has been previously modelled showing that the dyes are attached to TiO₂ via the carboxylate group.^{25–29,33–36}

The aim of this work is to extend the study to systems using the known coordination preference of the LD13 (η = 8.4%) and YD2-o-C8 (η = 12.1%) dyes. We use these two dyes because of their medium sized in comparison to other compounds and their high values of η. We employ computational methods for elucidating which anchor groups should be used for obtaining an improved conjugation of the MP ring with the TiO₂ surface. Using state-of-the-art quantum chemistry methods, the largest molecular systems that we are able to study are about the same size as the light-receptor system of the Grätzel cells.^8–24 The DSSC model systems considered in the present calculations consist of a dye attached to a TiO₂ cluster representing the TiO₂ surface.^25–36 The molecular structures of the DSSC models have been optimized at density functional theory (DFT) levels for identifying and characterizing suitable light-capturing molecules. The ground-state calculations show how the dye binds to TiO₂, whereas single-point quantum chemical calculations of the excitation energies provide information about the vertical excitation processes. The light-absorption processes in the DSSCs have been studied using time-dependent density functional theory (TDDFT) calculations and by performing ab initio correlated calculations at the algebraic diagrammatic construction through second order level (ADC(2)). By determining the properties of the interaction between the LD13 and YD2-o-C8 dyes and TiO₂ one obtains a better understanding of the complete light-absorption mechanism of the DSSCs, which supports the design of future DSSC systems.

Models and computational details

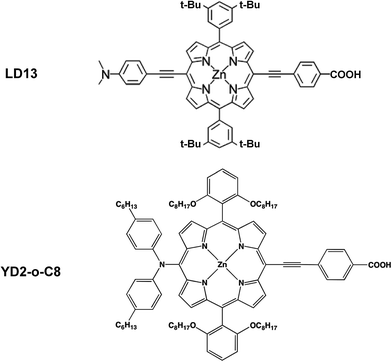
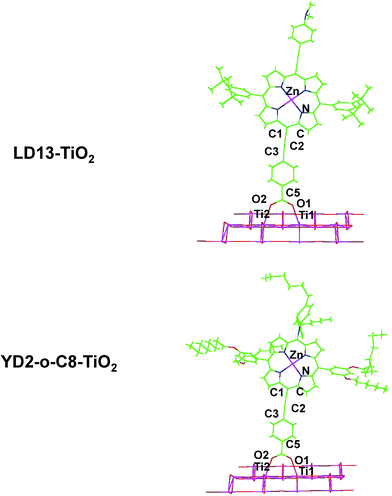
The studied LD13 and YD2-o-C8 models are depicted in Fig. 1. The molecular structures of the ground state were fully optimized without any symmetry constraints at the density functional theory (DFT) level³⁸ using the B3LYP and CAM-B3LYP functionals.^39,40 The structure optimizations were performed with the molecules in a gas phase and for the molecules surrounded by tetrahydrofuran (THF) modelled by using the conductor-like screening model (COSMO) with a dielectric constant (ε) of 7.6.⁴¹ We have used this solvent since the experimental studies of both dyes have been performed with THF as solvent. Acetonitrile is though the most common solvent in DSSCs. Solvent effects must be considered in studies of the absorption energies of the chromophore in DSSCs because the electronic transitions are charge transfer transitions and the excited states are generally charge separated states.³⁵ The fully relaxed structures of the dyes adsorbed on the TiO₂ surface are shown in Fig. 2. The TiO₂ structure was kept fixed in the structure optimization. In previous studies of the dye–TiO₂ interactions, the dyes molecules were modelled with the –COO⁻ group deprotonated.

Fig. 1 Molecular structures of LD13 and YD2-o-C8 dyes porphyrins.

Fig. 2 LD13 and YD2-o-C8 on TiO₂ models.

Experimental and computational studies have shown that the carboxylic acid group of substituted porphyrins is bound to the TiO₂ surface by monodentate or bidentate coordination depending on the dye.^8–36 The [Ti₁₆O₃₄H₄] cluster simulating the TiO₂ surface was constructed by cutting a piece of titanium oxide out from the anatase crystal structure and saturating the dangling bonds with hydrogen atoms.³⁶ TiO₂ clusters of various shapes consisting of 5–80 titanium atoms have previously been used for modelling the TiO₂ surface.^25,26 Small TiO₂ clusters have successfully been used in studies of the interactions between TiO₂ and different dyes such as N749, N3, C101, J3, YD2, LD14, ZnPBAT, ZnPBA and WW3m-WW8m.^25–36

The excitation energies have been calculated for the optimized structures at the DFT level using the time-dependent perturbation theory approach (TDDFT).^42,43 The B3LYP,³⁹ CAM-B3LYP⁴⁰ and BHLYP⁴⁴ functionals have been employed in the TDDFT calculations. Molecular structures optimized at the B3LYP level have been used in the BHLYP calculations of the absorption spectra. We have used several hybrid functionals because some absorption energies of the porphyrins have been found to be sensitive to the employed level of theory. We have not employed pure density functionals, because it has been shown that they yield an incorrect description of the optical properties of the complex metalloporphyrins.^33–36 Excitation energies and oscillator strengths were also calculated for the LD13 dye in the gas and solvent phases at the ADC(2) level^45,46 using the scaled opposite-spin (SOS) approximation.^47,48 The hermitean ADC(2) method belongs to the family of approximate second-order coupled-cluster and configuration-interaction methods.⁴⁶

The calculations were carried out using the Turbomole 7.0,^49,50 Gaussian09 (ref. 51) and Orca 3.0.3 (ref. 52) program packages. We have used the functional B3LYP and ADC(2) with Turbomole. In addition, the B3LYP-CAM and BHLYP functionals were calculated with Gaussian09 and Orca, respectively. For Zn and Ti, the 10 core-electron pseudo-potentials (PP) of Andrae et al.⁵³ were employed. Two d-type polarization and diffuse functions were added to the Zn and Ti basis sets.⁵⁴ The 1s orbitals of C, N and O were also replaced by PPs. Double-zeta basis sets augmented with two d-type polarization and diffuse functions were used for the valence electrons.⁵⁵ For the H atoms, a double-zeta basis set augmented with one p-type polarization function was used.⁵⁶ The employed basis set for Zn consisted of 8s7p6d primitive functions contracted to 6s5p3d (8s7p6d/6s5p3d). The following basis sets were used for the other atoms: Ti (8s7p6d/6s5p3d), O (4s4p1d/2s2p2d), C (4s4p1d/2s2p2d), N (4s4p1d/2s2p2d), and H (4s1p/2s1p). Grimme's semi-empirical dispersion correction term (D3) has also been used.⁵⁷

Results and discussion

Molecular structures

LD13 is a porphyrin with a phenylethynyl group in the meso position as the acceptor and bridging unit between the porphyrin and the carboxylic acid moiety binding to the TiO₂ surface. The porphyrin has ortho-alkoxylated phenyl groups in the two meso positions next to the meso position with the acceptor and anchoring groups. The 4-dimethylaminophenylethynyl donor group is attached to the β position of one of the pyrrole rings on the opposite side of the porphyrin with respect to the acceptor group. The porphyrin chromophore function has a π-bridge in the donor π-conjugate-bridge acceptor (D–π–A) structure. The YD2-o-C8 dye has the same acceptor and anchor group as LD13. It has a 2,6-dioctoxyphenyl group in the two meso-positions closest to the anchor substituent. The donor group attached to the opposite meso position with respect to the anchor group consists of a bis(4-hexylphenyl)amino group. The porphyrin forms a π-bridge in the D–π–A structure. The molecular structures obtained at the B3LYP and CAM-B3LYP levels are very similar. Selected structural parameters and the Cartesian coordinates of the optimized molecular structures are given as ESI see Table S1.†

The LD13 and YD2-o-C8 dyes are linked to the TiO₂ model (see Fig. 2) by binding the carboxylate moiety to the Ti atoms of the (101) plane. The dyes do not undergo any large structural changes when they bind to TiO₂. The largest structural changes occur at the carboxylate group when forming a bidentate bond to TiO₂. The bond distance between the oxygen of the carboxylate group and the titanium atom is 217–221 pm depending on the employed level of theory. The second Ti–O distance of the bidentate bond of 212–215 pm is slightly shorter. The C5–O2 and C5–O1 distances are 127–130 pm, while the O2–C5–O1 angle of 128–129° is wider than for the free dye. The bonds of the COO⁻ group are also slightly conjugated when the dyes are coordinated to the TiO₂ surface. The most relevant geometrical parameters of the optimized structures and the Cartesian coordinates are reported in ESI see Table S2.†

The binding energy of the dye–TiO₂ complex has been calculated at the B3LYP and CAM-B3LYP levels using the counterpoise (CP) method to correct for basis-set superposition errors (BSSE).⁵⁸ The CP corrected B3LYP energies for the LD13–TiO₂ bond are −70.1 kcal mol⁻¹ and −66.8 kcal mol⁻¹ as obtained in the gas-phase and COSMO calculations, respectively. Since the dye binds to two titanium atoms, the average binding energy of the dye with Ti is 35 kcal mol⁻¹, which is weaker than for a typical covalent bond. Similar results have been previously obtained for the YD2 and LD14 dyes.^33,34 At the CAM-B3LYP level, the corresponding binding energies are −68.3 kcal mol⁻¹ and −65.5 kcal mol⁻¹, respectively. B3LYP calculations on the YD2-o-C8–TiO₂ complex yielded equivalent binding energies of −70.4 kcal mol⁻¹ and −66.7 kcal mol⁻¹. The corresponding CAM-B3LYP binding energies for YD2-o-C8–TiO₂ are −68.2 kcal mol⁻¹ and −65.1 kcal mol⁻¹, respectively. The binding energies are practically the same for the two dyes, presumably because they have the same anchoring unit.

Natural Population Analyses (NPA) based on the B3LYP and CAM-B3LYP density matrices for the LD13, YD2-o-C8, TiO₂, LD13–TiO₂ and YD2-o-C8–TiO₂ models in the gas and solvent phases show that 0.4–0.6 electrons are transferred from mainly the carboxylate group of the dyes to the two nearest Ti atoms when binding to the TiO₂ cluster. The most relevant NPA charges are given in the ESI see Tables S3 and S4.† The NPA results and the binding energies show that there is a coordinating bond between the dye and the TiO₂ cluster.

Excitation energy calculations

The UV-Vis spectra have been calculated at the TDDFT level using the B3LYP, CAM-B3LYP and BHLYP functionals. The excitation energies for LD13 were also calculated at the ADC(2) level to assess whether spurious charge transfer states occur for the investigated molecules. Since the electronic coupling between the dye and the semiconductor determines the electron injection rate and the power conversion efficiency (η), it is necessary to study properties of the excited states of the free dye and of the dye attached to TiO₂. For porphyrins, the UV-Vis absorption spectra in the visible region usually consist of a weak Q band in the red part of the spectrum and a strong B (Soret) band at higher energies. Substituted porphyrins can also have a weak T band between the Q and B bands in addition to the vibrational band of the Q band.⁵⁹ The vertical excitation energies calculated for the dyes and the dye–TiO₂ complexes are reported in Table 1. The experimental spectra of LD13 and YD2-o-C8, free and adsorbed on TiO₂, show a Q band maximum between 645 and 672 nm, while the maximum of the B band is between 448 and 472 nm (ref. 14 and 22) in THF solvent.

Table 1 The absorption wavelengths (λ in nm) corresponding to the strong vertical excitation energies of LD13, LD13–TiO₂, YD2-o-C8 and YD2-o-C8–TiO₂ calculated at different levels of theory. Calculations considering solvent effects are indicated with solvent. The strong transitions are assigned to the experimental B, T and Q bands

System	Method	B	T	Q
a Calculated using a [Ti16O34H4] cluster to simulate TiO2.b Measured in THF.
LD13	B3LYP	427		615
LD13	B3LYP (solv)	438		632
LD13–TiO2	B3LYP^a	434		602
LD13–TiO2	B3LYP (solv)^a	445		606
LD13	CAM-B3LYP	384		597
LD13	CAM-B3LYP (solv)	397		615
LD13–TiO2	CAM-B3LYP^a	388		583
LD13–TiO2	CAM-B3LYP (solv)^a	389		591
LD13	BHLYP (solv)	361		557
LD13–TiO2	BHLYP (solv)^a	359		540
LD13	ADC(2)	386		603
LD13	ADC(2) (solv)	401		612
YD2-o-C8	B3LYP	408	533	640
YD2-o-C8	B3LYP (solv)	443	545	690
YD2-o-C8–TiO2	B3LYP^a	415		610
YD2-o-C8–TiO2	B3LYP (solv)^a	454		621
YD2-o-C8	CAM-B3LYP	392		594
YD2-o-C8	CAM-B3LYP (solv)	404		605
YD2-o-C8–TiO2	CAM-B3LYP^a	391		595
YD2-o-C8–TiO2	CAM-B3LYP (solv)^a	393		611
YD2-o-C8	BHLYP (solv)	359		549
YD2-o-C8–TiO2	BHLYP (solv)^a	404		557
YD2-o-C8	CAM-B3LYP^60	397		592
YD2-o-C8	LC-ωPBE^60	399		632
YD2-o-C8	PBE^60	477		879
YD2-o-C8	HSE06 (ref. 60)	420		671
LD13	Exp^b^22	458		672
LD13–TiO2	Exp^b^22	461		668
YD2-o-C8	Exp^b^14	448	581	645
YD2-o-C8–TiO2	Exp^b^14	470		650

---

Similar excitation energies were obtained for the Q band of LD13 at the DFT and ADC(2) levels. The first Q band transition calculated at the B3LYP level is slightly red shifted as compared to the ADC(2) value, whereas the lowest excitation energy of LD13 obtained in the CAM-B3LYP calculation is slightly blue shifted as compared to the ADC(2) one (see ESI†). The second excitation energy obtained at 580 nm in the B3LYP calculation agrees well with the corresponding ADC(2) excitation energy. The oscillator strength for the transition at 580 nm is small implying that it might be hidden in the experimental spectra among the vibrational bands. The B band consists of the third and fourth strong transition at 430 and 427 nm at the B3LYP level. At the ADC(2) level, the corresponding transition wave lengths are 386 and 381 nm, which are almost the same as obtained at the CAM-B3LYP level. At the ADC(2) and CAM-B3LYP levels, there are no other strong transitions above 350 nm, whereas B3LYP calculations yield two strong transitions at 406 and 398 nm and a weak transition at 410 nm.

The comparison of the excitation energies and oscillator strengths calculated at the four levels of theory shows that the excitation energies calculated at the B3LYP level are generally smaller than those obtained in the CAM-B3LYP and ADC(2) calculations. More states are also obtained at the B3LYP level suggesting that there are charge transfer problems in the high-energy region of the visible part of the absorption spectrum. Very similar absorption spectra were obtained at the CAM-B3LYP and ADC(2) levels in the studied energy range. The oscillator strengths calculated at the CAM-B3LYP and ADC(2) levels qualitatively agree for the first four excited states, whereas at the B3LYP level two strong transitions appear at about 400 nm. Such states cannot be identified at the CAM-B3LYP and ADC(2) levels. The same trends are obtained when solvent effects are considered by using COSMO. The excitation energies calculated with COSMO are slightly red shifted as compared to the values obtained in the gas-phase calculations.

The Q band of the LD13 dye attached to the TiO₂ cluster is blue shifted as compared to the Q band for the free LD13 dye. The energy of the third electronic transition corresponding to the B band calculated at the B3LYP level is about 41 nm smaller than obtained at the CAM-B3LYP level. The excitation energies calculated at the B3LYP level are about 62 nm larger than the experimental values for LD13 and LD13 attached to TiO₂. The excitation energies calculated at the BHLYP level are 200 nm larger than the corresponding B3LYP values.

For YD2-o-C8, the Q band calculated at the B3LYP level is redshifted relatively to the value obtained at using the CAM-B3LYP functional (see ESI†). The same holds for the other studied excitation energies. Similar oscillator strengths were obtained at the two levels of theory. At the B3LYP level, the strong B band consists of the fifth to the eighth transitions between 425 and 389 nm, whereas at the CAM-B3LYP level, the third to the sixth transitions between 428 and 392 nm form the B band as two apparently spurious weak states at the B3LYP level are not obtained in the CAM-B3LYP calculations. Solvent effects shift the B band to lower energies. The calculations are summarized in Table 1, where the obtained wave lengths of the Q, T and B bands are compared to available literature data.

The first strong transition is assigned as the Q band and the strong transitions at higher energy form the B band. Comparisons of the excitation energies for YD2-o-C8 attached to the TiO₂ cluster calculated at the B3LYP and CAM-B3LYP levels show that four spurious states are obtained between the Q and B band in the gas-phase calculations. When solvent effects are considered, the Q and B bands are redshifted and seven spurious states are obtained between the Q and B bands at the B3LYP level. However, the transition wave lengths of the strong transitions calculated at the B3LYP level are in better agreement with the experimental values than those obtained at the other computational levels.

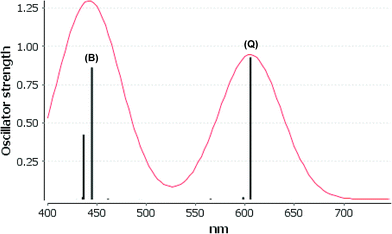
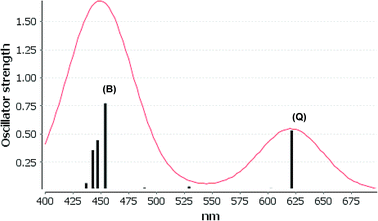
We consider only the strong transitions obtained at the B3LYP level in the discussion of the properties of excited states, since they agree rather well with experimental data and the spurious states are easily identified by comparing the excitation energies with the ones calculated at the other levels of theory. We discuss only the properties of the dye–TiO₂ systems, whereas the corresponding data for the dyes are given in the ESI.† The simulated spectra for LD13–TiO₂ and YD2-o-C8–TiO₂ in THF solution calculated at the B3LYP level are shown in Fig. 3 and 4, respectively. The most important molecular orbitals for describing the electronic transitions are shown in Fig. 5 for LD13–TiO₂ and in Fig. 6 for YD2-o-C8–TiO₂.

Fig. 3 Electronic spectra at the B3LYP level calculated by LD13–TiO₂ in THF.

Fig. 4 Electronic spectra at the B3LYP level calculated by YD2-o-C8–TiO₂ in THF.

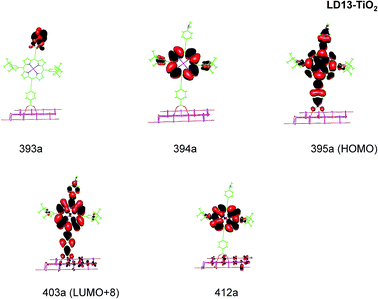Fig. 5 Most important active molecular orbitals in the electronic transitions of LD13–TiO₂ models at the B3LYP level in THF.

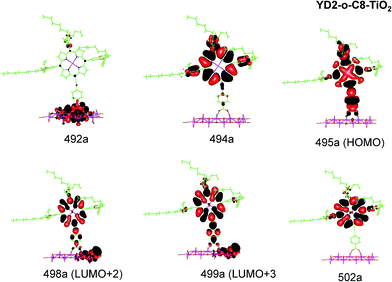Fig. 6 Most important active molecular orbitals in the electronic transitions of YD2-o-C8–TiO₂ models at the B3LYP level in THF.

LD13–TiO₂

The electronic excitations of the LD13–TiO₂ complex are assigned to transitions from the ground state to ligand-to-ligand (LL), metal-ligand-to-ligand (MLL), metal-ligand-to-metal-ligand (MLML) and ligand-to-metal-ligand (LML) charge transfers states using the expansion coefficients obtained in the TDDFT calculation and the composition of the most important molecular orbitals that participate in the absorption process. The excitation character of the strong bands are given in Table 2. Theoretical calculations show good agreement with the experimental results.²² We have used the wave function analysis to study the composition of each molecular orbital involved in electronic sates in the process of absorption.

Table 2 The strongest singlet excitation energies calculated for LD13–TiO₂ and YD2-o-C8–TiO₂ in THF are compared to experimental data.^14,34 The excitation energies and oscillator strengths have been calculated at the TDDFT/B3LYP level using COSMO with ε = 7.6. All calculated excitation energies are reported as ESI. The orbital contributions and the character of the transitions are also given

System	λcalc	λexp	f^a	Contribution^b	Transition type
a Oscillator strength.b The reported values are |coefficient|^2 × 100%.
LD13–TiO2	606 (Q)	668	0.929	395a →403^a (84%)	MLMLCT (dxz/dyz + π → π* + dxz)
	445 (B)	461	0.862	393a → 403^a (60%)	LMLCT (π → π* + dxz)
				394a → 412^a (35%)	LLCT (π → π*)
	437 (B)		0.425	394a → 403^a (42%)	LMLCT (π → dxz + π*)
				393a → 412a (24%)	LLCT (π → π*)
YD2-o-C8–TiO2	621 (Q)	650	0.532	495a → 499a (53%)	MLLMCT (dxz/dyz + π → π* + dTi)
				495a → 498a (29%)	MLLMCT (dxz/dyz + π → π* + dTi)
	454 (B)	470	0.774	494a → 502a (32%)	LLCT (π → π*)
				492a → 499a (21%)	MLLM (π + dTi → π* + dTi)
				492a → 498a (12%)	MLLM (π + dTi → π* + dTi)
	447 (B)		0.446	494a → 499a (30%)	LLMCT (π → π* + dTi)
				495a → 502a (19%)	MLLCT (dxz/dyz + π → π*)
				494a → 498a (14%)	LLM (π → π* + dTi)

---

For the LD13–TiO₂ complex, the absorption bands of the LD13–TiO₂ complex are slight blue shifted as compared to the corresponding absorption bands of the free dye as also observed experimentally. The transition wave lengths, oscillator strengths and transition characters of the strong Q and B transitions are given in Table 2. The corresponding data for the free dye are reported in Table S9 in the ESI.† The calculated spectrum in Fig. 3 and the obtained TiO₂ shifts are in reasonable agreement with experimental data.²² The Q band at 606 nm consists mainly of the transition between HOMO and LUMO+8 on the LD13 dye. The 395a → 403a (d_xz/d_yz + π → π* + d_xz) transition can be assigned as an MLMLCT excitation. The 395a orbital (HOMO) has contributions from porphyrin π orbitals, Zn orbitals, and orbitals of phenylethynyl carboxylic acid moiety. The 403a orbital (LUMO+8) has mainly contributions from porphyrin and the phenylethynyl carboxylic acid moiety. The orbitals are shown in Fig. 5.

The B band at 445 nm also consists of two main orbital transitions. The first one is from 393a to 403a (π → π* + d_xz), which is of LMLCT type. The two orbitals have a π character on the porphyrin ring with a small contribution from TiO₂. The second significant orbital transition from 394a to 412a has LLCT character. The strong contribution to the B band at 437 nm is dominated by the 394a → 403a (π → π* + d_xz) and 394a → 412a orbital transition, which are of the LMLCT and LLCT character, respectively.

YD2-o-C8–TiO₂

The Q band of the calculated absorption spectrum of the YD2-o-C8–TiO₂ complex is slightly redshifted as compared to LD13–TiO₂, whereas in the experimental spectra YD2-o-C8–TiO₂ absorbs at 650 nm as compared to 668 nm for LD13–TiO₂.^14,34 The absorption wave length of the B band of YD2-o-C8–TiO₂ is about 10 nm longer than for LD13–TiO₂. The calculated and measured absorption wave lengths are compared in Table 2. The B band is red shifted and the Q band is blue shifted with attaching YD2-o-C8 to TiO₂, whereas experimentally TiO₂ red shifts the Q and B bands. Since the shifts are small, there is though a reasonable agreement between calculated and experimental absorption spectra for YD2-o-C8 and YD2-o-C8–TiO₂.¹⁴ The band assigned as T band for the free YD2-o-C8 dye disappears in the calculated and experimental spectra when attaching the dye to TiO₂.

The Q band at 621 nm consists mainly of the orbital transition from HOMO (495a) to LUMO+3 (499a) of d_xz/d_yz + π → π* + d_Ti character associated with MLLMCT. The second important orbital transition is from HOMO to LUMO+2 (498a), which is also of MLLMCT type. Orbital 495a (HOMO) has a porphyrin π character, Zn orbitals, diarylamino, and contributions from the phenylethynyl carboxylic acid moiety. Orbital 499a (LUMO+3) has the main contributions centered on the porphyrin, phenylethynyl carboxylic acid and contributions from the d orbitals of Ti on TiO₂. The Zn orbitals do not contribute much to the 498a and 499a orbitals. The frontier orbitals of YD2-o-C8–TiO₂ are shown in Fig. 6.

The band B is formed by electronic transitions to two excited states. The electronic excitation at 454 nm consists mainly of the 494a → 502a (π → π*) orbital transition of LLCT type. The 494a and 502a orbitals have both π orbital character on the porphyrin ring. However, the electronic transition has also significant MLLM character due to orbital transitions from 492a to 499a and to 498a. The second electronic transition of the B band at 447 nm has the largest contribution from the orbital transition between 494a and 499a (π → π* + d_Ti), which is of LLMCT type. Other significant orbital transitions of the second contribution to the B band are 495a → 502a and 494a → 498a, which are of MLLCT and LLM type, respectively.

The calculations show that for the dye–TiO₂ complexes, orbital centered on TiO₂ cluster contribute to the excited states. The orbitals on TiO₂ are the electron accepting of the TiO₂ electrode. The same behaviour has been observed for YD2–TiO₂ (ref. 33) and LD14–TiO₂ (ref. 34) complexes that we have also studied.³⁶ Calculations of the free-energy for the electron injection process are discussed in the next section.

Absorption properties

The electron injection in DSSCs can be understood as a charge transfer (CT) process.⁶⁰ Thus, the Marcus theory can be used for studying the electron transfer in DSSCs.⁶¹ The CT has been associated with the free-energy change for electron injection (ΔG^inject).⁶² This free-energy change is a measure of the electron injection rate in DSSCs. In general, the larger the ΔG^inject, the greater is the electron-injection efficiency (Φ^inject). The injection energy can be calculated as ΔG^inject = E^dye* − E_CB,⁶³ where E_CB is the reduction potential of the conduction band (CB) of the TiO₂. The conduction band is −3.66 eV for the used Ti₁₆O₃₄H₄ cluster of this work. The oxidation potential of the excited state of the dye (E^dye*) is determined by the redox potential of the ground state of the dye (E^dye) and the vertical transition energy (λ_max): E^dye* = E^dye − λ_max. There are two methods to calculate E^dye. The first is from the orbital energy of the HOMO by applying Koopmans' theorem IP ≈ −E_HOMO.⁶⁴ The second is the energy of the orbital that generates the transition.^65,66 The calculated E^dye* and ΔG^inject for the Q and B bands of LD13 and YD2-o-C8 dyes are summarized in Table 3.

Table 3 The calculated oxidized potential of the excited state (E^dye* in eV) and the free-energy change for electron injection (ΔG^inject in eV) for the Q and B absorption bands of LD13 and YD2-o-C8 in the solvent phase. E^dye* and ΔG^inject were calculated at the B3LYP level using COSMO with ε = 7.6 simulating THF. The used E_CB of −3.66 eV is the orbital energy of the LUMO for the TiO₂ cluster

System	Transition	E^dye*		ΔG^inject
		Q	B	Q	B
a E^dye is the energy of the orbital that generates the transition in the band.b E^dye is the absolute value of the HOMO energy.
LD13	Type^a	3.17	2.76	−0.49	−0.90
LD13	Type^b	3.17	2.24	−0.49	−1.42
YD2-o-C8	Type^a	3.18	2.18	−0.48	−1.48
YD2-o-C8	Type^b	3.18	2.18	−0.48	−1.48

---

The results for the YD2-o-C8 dye show that E^dye* for the Q and B bands do not depend on whether the energy of the transition orbital or the HOMO energy is used. The ΔG^inject values are negative, which means that the excited states of YD2-o-C8 with an effective charge transfer excitation character lies above the conduction band edge of TiO₂. The calculated E^dye* and ΔG^inject energies of the Q and B bands for the LD13 dye are listed in Table 3. Even though the magnitudes vary, the favorable electron injection to TiO₂ remains. The YD2-o-C8 dye (η = 12.1%)¹⁴ has a larger charge injection efficiency than to LD13 (η = 8.4%),²² which is also obtained in the calculations. The large free energy for the electron injection implies that the electron injection is fast as also obtained experimentally.^13,65

Conclusions

In this work, we have presented a study of the electronic structures and spectroscopic properties of the dyes LD13 and YD2-o-C8, both free and adsorbed on TiO₂ clusters. The coordination energy between the –COO⁻ anchor group and TiO₂ lies between 66 and 70 kcal mol⁻¹ depending on the calculation level, showing a coordinative bond between dyes and cluster of TiO₂. The charge transfer analysis shows that dye injects electrons to the TiO₂ cluster. The obtained spectra at the B3LYP-D3 TDDFT level demonstrate that this is the most suitable functional for describing the Q and B bands of porphyrins in the dye free and dye–TiO₂ models. The absorption energy is centered on the dye. The LUMO of the dye is delocalized in the region of the TiO₂ cluster conduction band. Finally, using the Marcus theory for electron transfer, the charge transfer can be associated with the free energy change for electron injection (ΔG^inject): i.e. dye and dye–TiO₂ models show a large absolute value, generating greater value for YD2-o-C8 in the same experimental trend as the value η.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support of this work under Conicyt-Aka-ERNC-001 and Fondecyt 1140503, is gratefully acknowledged. The authors thank CSC – IT Center for Science in Finland for computational resources. This work has also been supported by Magnus Ehrnrooth Foundation and the Academy of Finland through projects 266227 and 275845. RM-A Acknowledges financial support from CONICYT-USACH under Proyecto de Atracción e Inserción de Capital Humano Avanzado en la Academia No. 79150043.

References

1. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740.
2. M. Grätzel, Acc. Chem. Res., 2009, 42, 1788–1798.
3. G. K. Singh, Energy, 2013, 53, 1–350.
4. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663.
5. H. Imahori, T. Umeyama and S. Ito, Acc. Chem. Res., 2009, 42, 1809–1818.
6. K. S. Gallagher, Daedalus, 2013, 142, 59–77.
7. F. De Angelis, S. Fantacci, E. Mosconi, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2011, 115, 8825–8831.
8. F. Gajardo, M. Barrera, R. Vargas, I. Crivelli and B. Loeb, Inorg. Chem., 2011, 50, 5910–5924.
9. M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2013, 117, 3685–3700.
10. D. Casanova, F. P. Rotzinger and M. Grätzel, J. Chem. Theory Comput., 2010, 6, 1219–1227.
11. J. Feng, Y. Jiao, W. Ma, M. K. Nazeeruddin, M. Grätzel and S. Meng, J. Phys. Chem. C, 2013, 117, 3772–3778.
12. M. Urbani, M. Grätzel, M. K. Nazeeruddin and T. Torres, Chem. Rev., 2014, 114, 12330–12396.
13. A. Yella, H. W. Lee, H. N. Tsea, C. Y. Yi, A. K. Chandirian, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Grätzet, Science, 2011, 334, 629–634.
14. Y. Chang, C. Wang, Y.-T. Pan, H. Kuo, C. Lo, H. Hsu, C. Lin and E. W. G. Diau, Chem. Commun., 2011, 47, 8910–8912.
15. N. K. Subbaiyan, J. P. Hill, K. Ariga, S. Fukuzumi and F. D'Souza, Chem. Commun., 2011, 47, 6003–6005.
16. T. Bessho, S. M. Zakeeruddin, C.-Y. Yeh, E. W.-G. Diau and M. Grätzel, Angew. Chem., Int. Ed., 2010, 49, 6646–6649.
17. L.-L. Li and W. W.-G. Eiau, Chem. Soc. Rev., 2013, 42, 291–304.
18. K. Kurotobi, Y. Toude, K. Kawamoto, Y. Fujimori, S. Ita, P. Chabera, V. Sundström and H. Imahori, Chem.–Eur. J., 2013, 19, 17075–17081.
19. Y. Chi, K.-L. Wu and T.-C. Wei, Chem.–Asian J., 2015, 10, 1098–1115.
20. S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. E. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 1–6.
21. T. Le Bahers, E. Brémond, I. Ciofini and C. Adamo, Phys. Chem. Chem. Phys., 2014, 16, 14435–14444.
22. C. L. Wang, C. M. Lan, S. H. Hong, Y. F. Wang, T. Y. Pan, C. W. Chang, H. H. Kuo, M. Y. Kuo, E. W. G. Diau and C. Y. Lin, Energy Environ. Sci., 2012, 5, 6933–6940.
23. T. Le Bahers, T. Pauporté, P. P. Lainé, F. Labat, C. Adamo and I. Ciofini, J. Phys. Chem. Lett., 2013, 4, 1044–1050.
24. F. Risplendi, G. Cicero, G. Mallia and N. H. Harrison, Phys. Chem. Chem. Phys., 2013, 15, 235–243.
25. J. Chen, F.-Q. Bai, J. Wang, L. Hao, Z.-F. Xie, Q.-J. Pan and H.-X. Zhang, Dyes Pigm., 2012, 94, 459–468.
26. S. Liu, H. Fu, Y. Cheng, S. Wu, S. Ho, Y. Chi and P. Chou, J. Phys. Chem. C, 2012, 116, 16338–16345.
27. X. Zarate, E. Schott, T. Gomez and R. Arratía-Pérez, J. Phys. Chem. A, 2013, 117, 430–438.
28. E. Mosconi, J. Yum, C. Gómez, M. Nazeeruddin, M. Grätzel and F. De Angelis, J. Am. Chem. Soc., 2012, 134, 19438–19453.
29. T. Gomez, X. Zarate, E. Schott and R. Arratia-Perez, RSC Adv., 2014, 4, 9639–9646.
30. W. Li, Z. Liu, H. Wu, Y. B. Cheng, Z. Zhao and H. He, J. Phys. Chem. C, 2015, 119, 5265–5273.
31. S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. E. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247.
32. N. Klein-Kedem, D. Cahen and G. Hodes, Acc. Chem. Res., 2016, 49, 347–354.
33. F. Mendizabal, A. Lopéz, R. Arratia-Pérez, N. Inostroza and C. Linarres-Flores, J. Mol. Model., 2015, 21, 226–236.
34. F. Mendizabal, A. Lopéz, R. Arratia-Pérez and G. Zapata-Torres, Comput. Theor. Chem., 2015, 1070, 117–125.
35. R. Mera-Adasme, W. H. Xu, D. Sundholm and F. Mendizabal, Phys. Chem. Chem. Phys., 2016, 18, 27877–27884.
36. K. Paredes-Gil, F. Mendizabal, D. Páez-Hernández and R. Arratia-Pérez, Comput. Mater. Sci., 2017, 126, 514–527.
37. J. Burschka, N. Pellet, S. J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319.
38. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
39. A. D. Becke, J. Chem. Phys., 2014, 140, 18A301.
40. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
41. A. Klamt and G. Schüürman, J. Chem. Soc., Perkin Trans. 2, 1993, 5, 799–805.
42. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
43. M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
45. J. Schirmer, Phys. Rev. A, 1982, 26, 2395–2416.
46. C. H. Hatting, Adv. Quantum Chem., 2005, 50, 37–60.
47. Y. Jung, C. Rohini, D. Anthony and M. Head-Gordon, J. Chem. Phys., 2004, 121, 9793–9802.
48. Y. M. Rhee and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 5314–5326.
49. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
50. F. Furche, R. Ahlrichs, C. Häting, W. Klopper, M. Sierka and F. Weigend, Wire, 2014, 4, 91–100.
51. Gaussian 09, Inc., Pittsburgh PA, 2003.
52. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
53. D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141.
54. T. Dunning and P. Hay, in Modern Theoretical Chemistry, ed. H. Schaefer, Plenum Press, 1997, vol. 3, pp. 1–28.
55. A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441.
56. S. Huzinaga, J. Chem. Phys., 1965, 52, 1293–1301.
57. W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871.
58. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
59. D. Sundholm, Phys. Chem. Chem. Phys., 2000, 2, 2275–2281.
60. L.-H. Han, C.-R. Zhang, J. W. Zhe, N.-Z. Jin, Y.-L. Shen, W. Wang, J. J. Gong, Y.-H. Chen and Z.-J. Liu, Int. J. Mol. Sci., 2013, 14, 20171–20188.
61. R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610.
62. W. Fan, D. Tan and W.-Q. Deng, ChemPhysChem, 2012, 13, 2051–2060.
63. J. Preat, C. Michaux, D. Jacquemin and E. A. Perpete, J. Phys. Chem. C, 2009, 113, 16821–16833.
64. T. Koopmans, Physica, 1934, 1, 104–113.
65. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874.
66. M. Torrent-Sucarrat, F. De Proft, P. Geerlings and P. W. Ayers, Chem.–Eur. J., 2008, 14, 8652–8660.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1 and S2 contain main geometric parameters of the LD13, YD2-o-C8, LD13–TiO₂ and YD2-o-C8–TiO₂. Tables S3 and S4 show Natural Population Analysis (NPA) charge on the systems. Tables S5–S8 show the electronic transitions to different methodologies (B3LYP, CAM-B3LYP, BHHLYP and ADC(2)) in gas and solvent phases. Table S9 described the singlet excitation energies calculated for LD13 and YD2-o-C8 in THF. Fig. S1 and S2 calculated B3LYP electronic spectra of LD13 and YD2-o-C8 in THF. Fig. S3 and S4 active molecular orbitals in the electronic transitions of LD13 and YD2-o-C8 at the B3LYP level in a solvent. Fig. S5 and S6 shows frontier orbitals on TiO₂ cluster in systems LD13–TiO₂ and YD2-o-C8–TiO₂ at the B3LYP level. Tables S10–S17 Cartesian coordinates (in angstroms) for the optimized geometries of the systems studied in this work at the B3LYP level. See DOI: 10.1039/c7ra08648b

---